Abstract
The effect of rotational speed and pressure rise on the leakage flow noise radiated by a low-speed axial fan, provided with rotating shroud, has been systematically investigated. The flow in the gap region has been studied by means of particle image velocimetry (PIV) measurements taken in the meridional plane. At low blade loading, the leakage flow is restrained close to the rotor ring and, at higher loading, it forms a wide recirculation zone. In the latter conditions, an unsteady flow separation likely takes place in the blade tip region which may be observed in the instantaneous flow field only. The leakage flow noise generally increases with the blade loading, but is non-monotonic, as the overall sound pressure level (OASPL) growth is interrupted by local minima; such a trend is qualitatively independent of the rotational speed. As the loading increases, the sound pressure level (SPL) spectrum shows important modifications, since the characteristic frequency of the subharmonic narrowband humps related to the leakage noise decreases; furthermore, height and width of the humps vary non-monotonically. Such a complicated behavior is likely related to the modifications in the leakage flow pattern and also to the appearance of the flow separation at the blade tip.
Keywords:
axial-flow fan; rotating shroud; ring rotor; stiff rotor; leakage flow; fan noise; subharmonic humps; PIV 1. Introduction
The axial fans employed in automotive cooling systems are commonly provided with a rotating shroud, i.e., a ring connecting the blade tips, see Longhouse [1]. This ring improves the volumetric efficiency and also strengthens the whole assembly, but it often increases the radiated noise. The reason for this are large-scale flow structures contained in the leakage flow released from the gap between the rotating ring and the stationary enclosure, which are eventually reingested by the rotor. Their interaction with the rotor blades results in noise in the low- to medium-frequency range, with the appearance of narrowband humps at subharmonic frequencies and a general increase of the broadband noise. The leakage flow noise often constitutes the major contribution to the overall radiation and its main features are known, but very few works related to it are available in the literature, e.g., see Fukano et al. [2], Fukano and Jang [3], Piellard et al. [4], Magne et al. [5], Moreau and Sanjosé [6], Zenger et al. [7], Na et al. [8], Canepa et al. [9,10,11,12], Zhu et al. [13] and Sanjosé and Moreau [14]. In order to find effective solutions for noise reduction, a deeper insight in the leakage flow features and in the effect of relevant parameters is necessary. The present paper continues the aerodynamic and acoustic investigation reported in the above cited works by the present authors. That research was conducted on a plastic rotor employed in real cooling units and showed that different patterns may exist for the leakage flow, which also affect the radiated noise. Beyond an obvious dependence of such patterns on both gap geometry and operating conditions, a further, unexpected dependence on both rotational speed and pressure rise was also observed, due to the related rotor deformation. This raised a number of questions on the features of the phenomenon and also on the validity of the acoustic similarity, see Neise and Barsikow [15] or Canepa et al. [10], which allows scaling the results of acoustic measurements related to different rotational speeds. Hence, it has been decided to perform a more systematic investigation on an aluminum rotor, which may be considered stiff. The larger number of investigated operating conditions and rotational speeds provide a more complete picture of the phenomenon. The present paper represents an extended and revised version of Canepa et al. [16], presented at the 13th European Turbomachinery Conference ETC13 2019.
2. Experimental Procedure
2.1. Experimental Facility
Compared to the previous works, see Canepa et al. [9,10,11,12], in the present study, a larger number of operating conditions have been investigated, and a different rotor has been tested, see Figure 1a. It also has nine blades of different geometry but it is an aluminum prototype while the previously studied rotor is a plastic one employed in a real cooling unit. Opposite to the latter, the former rotor may be considered stiff. It has a tip radius rtip = 222 mm, a hub-to-tip diameter ratio rhub/rtip = 0.374, and a chord c which varies between 43 mm and 50 mm from hub to tip.
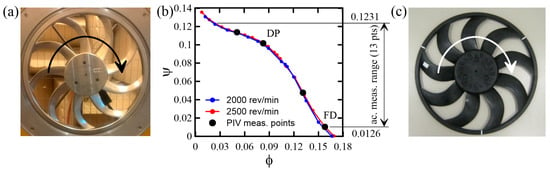
Figure 1.
The low-speed fan. (a) Investigated rotor; (b) non-dimensionalized characteristic curves of the investigated rotor; (c) previously studied rotor.
At the design point (DP), the flow coefficient is 0.0869 and the pressure rise coefficient is 0.0993, with the fan pressure rise (outlet static pressure minus inlet total one). For the previously studied rotor, see Figure 1c, rtip = 227 mm, rhub/rtip = 0.391, φDP = 0.098, and ΨDP = 0.12. Both rotors have been mounted on a test plenum (TP) designed according to the ISO standard 10322 [17]. The TP has a limited interaction with acoustic waves and allows varying the operating point simply varying the width of the TP back slot (BS), see Figure 2a. The non-dimensional characteristic curve of the aluminum rotor, see Figure 1b, has been obtained from measurements taken at Ω = 2000 and 2500 rev/min. The good collapse of the two sets of points shows that overall aerodynamic similarity holds above 2000 rev/min at least, provided that any of φ or Ψ is fixed. Hence, under the realistic assumption that the pressure drop through the BS is proportional to Q2, the rotor is expected to work at fixed operating point (i.e., φ and Ψ do not vary) if the BS width is kept unchanged while Ω varies. During the tests, the pressure inside the TP has been measured and the Ψ trend has been controlled.
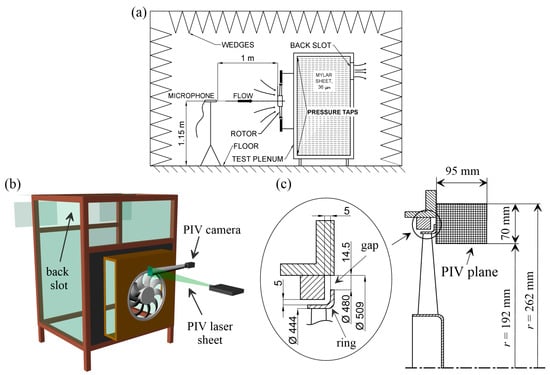
Figure 2.
Experimental facility. (a) Hemi-anechoic chamber and acoustic setup; (b) Test plenum and aerodynamic setup; (c) Particle image velocimetry (PIV) measurement domain and gap geometry (not to scale).
2.2. Acoustic Measurement Procedure and Data Processing Technique
Acoustic measurements have been taken in the DIME hemi-anechoic chamber with a B&K 3560 spectrum analyzer and a ½” free-field microphone with the microphone mounted on-axis 1 m upstream of the rotor, see Figure 2a. Due to the low-frequency loss of anechoicity of the chamber, the part of the spectra below 100 Hz are blanked in the plots. The tests have been done in the range Ω = 1000 ÷ 4000 rev/min at Ω = const and during low-angular-acceleration linear Ω ramps (3000 rev/min variation within 1080 s), for a total amount of 13 Ψ values which include the four conditions at which aerodynamic measurements have been taken, see Figure 1b. In the investigated Ψ range and at Ω = 4000 rev/min, the reference Reynolds number Rec = wtipc/v varies from 52,000 to 69,300 at the rotor hub and from 310,000 to 316,000 at the blade tip; correspondently, the reference Mach number Ma = w/a0 varies from 0.053 to 0.071 at the rotor hub and from 0.272 to 0.276 at the blade tip. a0 is the speed of sound at ambient conditions and w is the reference relative velocity based on the mean axial velocity component . The good collapse of the characteristic curves of Figure 1b suggests that Re effects are independent of Ω and kinematic similarity is respected at the rotor inlet; together with the low Ma values, this indicates that aerodynamic similarity is also respected.
Hence, constancy of Ψ during a speed ramp implies that φ is also constant and that the aeroacoustic similarity should be eventually respected, e.g., see Neise and Barsikow [15] or Canepa et al. [10]. However, noise generation may be strongly affected even by flow details which do not affect the φ − Ψ characteristic curve. Therefore, a preliminary analysis of the sound pressure level (SPL) spectra is required.
Given that is the one-sided power spectral density of the received acoustic pressure, the SPL in the frequency band is given by:
where pref = 20 µPa is the reference acoustic pressure and is the central frequency of the band. If the bandwidth is small enough (typically less than 20 Hz), the sequence with constitutes the SPL spectrum. Alternatively, proportional bands may be employed, i.e., with , being the Strouhal number. SPL strongly increases with Ω and scaling it with 10log10Ω4+∞ allows eliminating the gross dependence on it:
α is an exponent close to one to be tuned case by case; it increases with the flow coherence and hence depends on both the operating point and the noise generating mechanism, that is on the considered part of the spectrum which is identified by . (In fact, Equation (2) applies to SPL spectra computed with proportional bands, while has to be employed if , e.g. see Canepa et al. [10]). In principle, the scaling should result in the same values if the SPL is related to different Ω but to the same St ranges.
As for the leakage flow noise, attention has to be focused on the low-frequency part of the spectrum. A first check consists in the analysis of SPLlow, that is the SPL in the range St = 6 ÷ 90; this range has been chosen since in the present case at St = 90 the SPL value shows little dependence on Ψ. Further information on the active noise generating mechanisms is provided by SPLhigh, the SPL in the high frequency part of spectrum (St = 90 ÷ 300), and by the overall SPL (OASPL) which is related to St = 6 ÷ 300 in the present case. In the computation of SPLlow and SPLhigh, and are obtained substituting the related St values in the relation , resulting in a range with extremes linearly dependent on Ω. If similarity holds, the characteristic frequencies of the noise generating mechanisms scale with Ω. Namely, Spp features such as peaks, humps, dips, etc. are characterized by the same St as Ω varies, resulting in vertical stripes in a St-Ω spectrogram as the one of Figure 3b. Hence, SPLlow,scaled and SPLhigh,scaled linearly depend on and are constant if the actual α value is employed in their scaling.
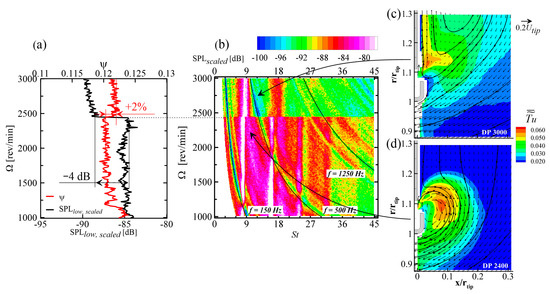
Figure 3.
Measurements on a plastic rotor. (a) SPLlow,scaled and Ψ during a Ω ramp; (b) sound pressure level (SPL) spectrogram during a speed ramp; (c) time-mean velocity field at 3000 rev/min; (d) time-mean velocity field at 2400 rev/min. (Adapted from Canepa et al. [12]).
In fact, for a given rotor and test-rig installed in an anechoic chamber or in an underhood compartment, the characteristic frequencies of acoustic propagation effects such as resonance, diffraction, or reflections scale with the ratio of a0 to a characteristic length such as rtip. As they constitute properties of the test environment, their characteristic frequencies are independent of the noise generating mechanism, i.e., of Ω. They may affect different parts of the SPL spectrum (i.e., different St ranges) if measurements are repeated at different Ω, e.g., see Canepa et al. [10], and should be eliminated as they complicate analyzing the SPL spectra. On the contrary, quantities such as SPLlow and SPLhigh are usually less affected since minima and maxima due to propagation effects compensate due to the large frequency ranges to which SPLlow and SPLhigh are related to. In the present configuration, such effects consist in a number of dips due to the mounting panel (at f = 150, 500, and 1250 Hz), in oscillations due to the TP in the range f = 1900 ÷ 3500 Hz, and in a maximum between 4000 and 5000 Hz, e.g., see Canepa et al. [9,18]. In a St-Ω spectrogram, propagation effects typically appear as crests and valleys aligned along hyperbolas, e.g., see Figure 3b. In order to eliminate them, the method presented by Bongiovì and Cattanei [19] has been employed. Based on measurements taken at the same Ψ and at different Ω, such a method allows to compute the propagation function G(f), which contains the propagation effects. Then, G(f) is subtracted from the SPL spectrum, resulting in the so called filtered SPL:
2.3. Aerodynamic Measurement Procedure and Data Processing Technique
The flow field in the meridional plane close to the tip gap, see Figure 2c, has been investigated in a 70 mm × 95 mm (radial × axial extent) rectangular region by means of a 2D PIV system constituted by a double-cavity Nd:Yag pulsed laser and a Dantec High Sense Mk II digital camera. This has resulted in 6000 instantaneous distributions of 44 × 61 values of and , the axial and radial velocity components respectively. The circumferential component has not been measured. The flow has been seeded by means of a fog generator and measurements have been taken at Ω = 2500 rev/min and at four operating points: Ψ = 0.0126 (maximum BS width, approximating free-discharge conditions (FD)), 0.0488, 0.0993 (DP), and 0.1142.
The ensemble average technique, see Canepa et al. [11], has been employed to extract the unresolved unsteadiness, i.e., that part of the flow unsteadiness not related to the blade passage periodicity. In rotating machinery, it cumulates both small-scale turbulence and non-periodic large-scale flow structures such as the ones released from the gap. In the present case, the unresolved unsteadiness is evaluated by means of the quantity , which is called turbulence intensity for the sake of simplicity; it is based on the rms of the non-periodic part of the velocity fluctuations in the axial and radial direction only as has not been measured:
In a quantitative study of the leakage flow turbulence, the lack of information about would constitute an important drawback, but it does not impair the conclusions of the present work, as is used to identify regions of high unsteadiness relevant to the noise generation only. Due to the large differences between and (not reported for the sake of space), it is expected that also the distribution is different. Considering that is the mean of and and including it in the summation of Equation (4) could lead to values that are likely not representative of the actual ones. Hence, this possibility has been discarded, consistently with the fact that, in the present case, is only aimed at providing an estimation of the unresolved unsteadiness.
3. Experimental Results
3.1. Previous Work
The results of Canepa et al. [11] that constitute the basis for the present work are shortly summarized here, as they show some basic features of the relation between flow and noise patterns. Furthermore, they also show how small geometrical details and/or parameters variation may have a dramatic impact on both flow and noise. PIV measurements were taken at Ω = 2400 and 3000 rev/min at Ψ = ΨFD and ΨDP; opposite to the present study, the investigated domain size was 95 mm × 70 mm (radial × axial extent).
∆p measurements taken during Ω ramps with constant BS width showed a proportionality with Ω2, and this was considered an evidence that similarity was respected, see Canepa et al. [9,10]. Ψ at DP conditions has been recently computed and its trend is reported versus Ω in Figure 3a. Ψ ≅ ΨDP = 0.12 in the range Ω ≅ 1500 ÷ 2450 rev/min, but below 1500 rev/min Ψ is slightly decreasing and above 2450 rev/min a sudden increase of almost 2% takes place. The former variation may be caused by low-Re effects but it is of minor interest as the rotor is usually operated at higher Ω. The latter variation is within the typical uncertainties for such pressure rise measurements but should not be neglected as it is step-like and not random; this becomes apparent observing the trend of SPLlow,scaled, also reported in Figure 3a. The slight fluctuations within the whole speed ramp, possibly due to acoustic propagation effects, may be neglected, but the sudden decrease of about 4 dB which takes place at Ω ≅ 2450 rev/min is unexpected and cannot be explained based on common knowledge on fan noise.
The observed behavior is related to the step in the spectrogram of Figure 3b, which reports the measured SPLscaled, see Equation (2), versus Ω and St. Valleys aligned along hyperbolas are due to propagation effects and may be neglected as only aerodynamic issues are concerned here. The crests at subharmonic frequencies (St ≅ 8.4, 17, 24, 32) are related to the leakage flow noise. Their height should be nearly independent of Ω, provided that a suitable α value has been employed in the scaling, see Canepa et al. [10]. The abrupt SPL decrease at Ω = Ωstep ≅ 2450 rev/min indicates that a sudden modification in the flow pattern must take place. This is confirmed by the time-mean vector plots shown in Figure 3c,d which are related to Ω values above and below 2450 rev/min, i.e., 3000 rev/min and 2400 rev/min, respectively. In the latter case, a recirculation bubble is attached to the rotor ring, and the path followed by the large-scale structures released from the gap before being reingested by the rotor is shorter than in the latter case, where a broad recirculation zone is present and a stronger decay of the turbulent structures is expected. Hence, the observed Ψ variation, though small, is related to a dramatic modification in the leakage flow pattern and related noise. Measurements of the axial position of the ring showed that the combined effect of centrifugal force and blade loading results in a ring displacement in the forward direction: When stationary, the rotor is flush mounted, while it juts out of 3 mm and 4.2 mm at Ω = 2400 rev/min and 3000 rev/min, respectively. Further acoustic tests showed a cross dependence of Ωstep on both Ψ and Ω. This indicated that the broad recirculation zone is typical of high Ψ values, but it did not clarify whether it is characteristic of a rotor jutting out of the mounting panel.
3.2. Preliminary Considerations on the Acoustic Measurements
Ψ has been systematically computed and some of the trends related to speed ramps measurements, taken at constant BS width, are plotted in Figure 4 (each case is identified by means of the corresponding average Ψ value). Below 1800 rev/min, Ψ increases or decreases with a maximum variation smaller than 5% of ΨDP. Above 1800 rev/min, Ψ is almost constant, with maximum variations smaller than 2% of ΨDP, a value which compares to the typical accuracy of such a kind of pressure measurements. Likely, the Ψ variations are due to a slight departure of the pressure drop through the BS from the assumed quadratic behaviour or, possibly, to low-Re effects. However, overall aerodynamic similarity is acceptably respected above 1800 rev/min, as, opposite to previous results, no abrupt steps are present. Acoustic measurements taken at different Ω help verify this assumption.
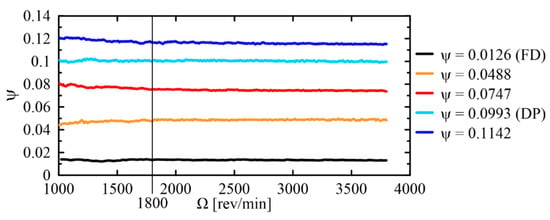
Figure 4.
Acoustic measurements at fixed back slot (BS) width: Ψ trend during different Ω ramps.
The constant-Ω SPL spectra provide a first indication of the operating point effect on the radiated noise. Both original and filtered spectra related to Ω = 2500 rev/min are reported in Figure 5a. The already mentioned propagation effects may be identified in the plot of the propagation function G(f), see Figure 5b. The filtered spectra have smoother trends and show the interesting aspects more clearly. These are the subharmonic, narrowband humps due to the leakage flow, which are present in all of the cases, e.g., see Piellard et al. [4] or Canepa et al. [9]. Due to the leakage flow prerotation, their characteristic St values are smaller than the ones of the blade passing frequency (BPF) harmonics (St = 9, 18, 27, etc.). As the frequency of the i-th BPF harmonic equals , the non-dimensional frequency decrease of a hump from the adjacent BPF harmonic is given by
where both u and vθ are referred to the radial location r where the leakage flow is ingested by the blade, e.g., see Piellard et al. [4].
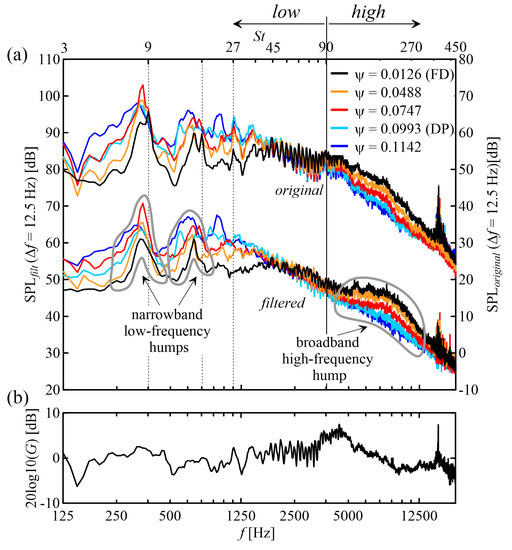
Figure 5.
Acoustic measurements at fixed BS width. (a) Original and filtered SPL spectra at Ω = 2500 rev/min; (b) propagation function.
The apparent growth of the low-frequency part with Ψ is expected as the leakage mass flow increases with Ψ also. However, as Ψ increases, a change in the flow pattern as the one shown in Figure 3 could occur, even more gradually. The variations in humps shape and peak St could be related to such a phenomenon.
The behavior of the high-frequency part of the SPL spectrum is usually related to the boundary layer turbulence. The major contribution is provided by the broad hump between 5 and 10 kHz. According to Henner et al. [20], it could be due to a feedback of the vortex shedding from the blade trailing edge on the boundary layer transition. This explanation is consistent with the hump decrease and eventual disappearance as Ψ increases: Both the adverse pressure gradient on the blade suction side and the turbulence contained in the leakage flow increase with Ψ and may make the boundary layer transition less sensitive to other perturbations.
Some weak tonal components at the 1st, 2nd, and 3rd BPF harmonics are present in the original spectra and are due to the ingestion of ambient turbulence, e.g., see Canepa et al. [21]; they have been eliminated in the filtered spectra, in order to enhance the contribution of the leakage noise. If a smaller ∆f (e.g., 1 Hz instead 12.5 Hz) were employed, higher resolution spectra would result in which such peaks could be clearly distinguished from the narrowband humps.
3.3. Effect of the Operating Conditions on the Radiated Noise
In order to obtain quantitative information on the radiated noise, acoustic measurements have first been taken at Ω = 2500, 3200, and 3900 rev/min. SPLlow, SPLhigh, and the OASPL have been computed employing the original spectra, as propagation effects are less important when the SPL is computed on broad frequency ranges on which G(f) oscillations compensate, see Figure 5b.
First, SPLlow, SPLhigh, and OASPL related to Ω = 3200 rev/min are compared, see Figure 6a. SPLlow, which is representative of the leakage noise, is always larger than SPLhigh, which is related to the boundary layer noise. At low Ψ, SPLhigh causes a 2 dB difference between OASPL and SPLlow, while above Ψ ≅ 0.04 its contribution is negligible and OASPL ≅ SPLlow; this shows that SPLlow provides the major contribution to the radiated acoustic power, thus confirming the importance of the leakage flow noise. Then, the dependence on Ω is considered. To this aim, SPLlow, SPLhigh, and OASPL have been scaled according to Equation (2), see Figure 6b–d. α = 1 has been employed as it has shown the best collapse of the SPLlow,scaled curves below Ψ ≅ 0.09. For larger Ψ values, a higher α (e.g., α = 1.4) would be required. On the contrary, a smaller α (e.g., α = 0.5) would result in a better collapse of the SPLhigh curves, but important discrepancies would remain. In fact, α grows with the coherence of the flow structures causing the noise and, hence, it may vary with both Ψ and St, see Canepa et al. [10]. Thus, as noise is generated by a complicated flow, scaling the SPL with a unique α value is only qualitatively acceptable.
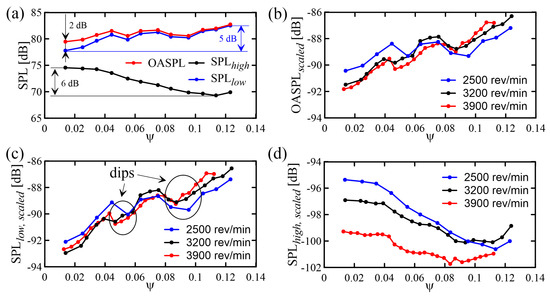
Figure 6.
SPL in different frequency ranges. (a) SPLlow, SPLhigh and overall sound pressure level (OASPL) at Ω = 3200 rev/min; (b) OASPLscaled at Ω = 2500, 3200 and 3900 rev/min; (c) SPLlow,scaled at Ω = 2500, 3200 and 3900 rev/min; (d) SPLhigh,scaled at Ω = 2500, 3200 and 3900 rev/min.
The three SPLhigh,scaled curves have similar trends, but show a spread between 1 and 4 dB which decreases with Ψ; due to the different Ω values, a Re dependence of the boundary layer transition could contribute to such discrepancies. Below Ψ ≅ 0.085, SPLhigh,scaled is always decreasing, then a minimum follows whose width depends on Ω, and, above Ψ ≅ 0.11, it is always increasing. Discrepancies between the three SPLlow,scaled curves are limited to less than 2 dB and the trends are similar. As expected, SPLlow,scaled increases with Ψ since the leakage flow rate increases with Ψ also, but, peculiarly, its trend is not monotonic, as the growth is interrupted by a sudden decrease at Ψ ≅ 0.04 ÷ 0.045 and by a further, smoother decrease between Ψ ≅ 0.075 ÷ 0.0873. Such a behavior is qualitatively independent of Ω. Although the maximum decrease is of a few dB only, these Ψ values are characteristic ones, since important flow pattern modifications may be related to them.
In order to deepen the SPLlow dependence on Ω, the low-frequency part of SPLfilt,scaled has been plotted as a function of both St and Ψ in the spectrogram of Figure 7a, which is related to Ω = 3200 rev/min. Indeed, consistently with the trend of SPLlow, the spectrograms related to 2500 and 3900 rev/min (not reported for the sake of space) show crests, valleys, and plateaus with similar shapes. This qualitative independence of Ω indicates that aeroacoustic similarity is qualitatively respected also. Hence, opposite to the case of the plastic rotor, see Figure 3c,d, no sudden flow pattern modifications take place as Ω grows and the analysis may be continued with reference to one Ω value only.
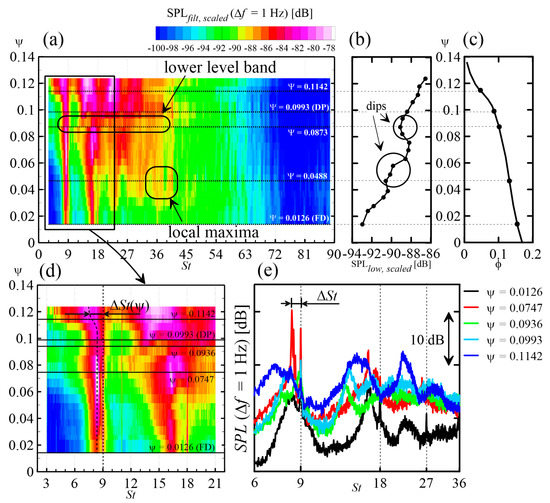
Figure 7.
Acoustic analysis at Ω = const. (a) Spectrogram at 3200 rev/min; (b) SPLlow,scaled at 3200 rev/min; (c) non-dimensionalized characteristic curve of the rotor; (d) low-frequency part of the spectrogram; (e) constant-Ω SPL spectra at 3200 rev/min.
Below St = 45, the SPL spectrum shows the highest values and strongly grows with Ψ, yielding the observed increase of SPLlow. A number of vertical crests are present in the plot, but the ones below St = 9, 18, 27, and 36 are the most important ones, as they are generated by the interaction of the rotor blades with the prerotating large-scale flow structures; the higher-St crests are harmonics of the first one.
They correspond to the narrowband humps observed in the constant-Ω spectra. According to Equation (5), in a first approximation, the lower the characteristic St, the higher the prerotation. Furthermore, a narrow, high crest indicates that the flow structures have a high coherence and viceversa, see the analysis of Majumbdar and Peake [22] on the ingestion of large-scale turbulence by propellers. Up to Ψ ≅ 0.075, the crests widen, their characteristic St seems slightly decreasing, and their height gradually increases; this agrees with the SPLlow trend. The SPLlow dip which takes place at Ψ ≅ 0.04 seems related to the decrease of the maxima between St = 36 and 42 in the spectrogram. Between Ψ ≅ 0.085 and Ψ ≅ 0.095, a horizontal, lower-level band is present which extends up to St = 36; it should be related to the second minimum of SPLlow. Then, as Ψ grows beyond about 0.09, the first crest gradually increases, broadens, and shifts towards lower St, Figure 7d. The change in shape appears in the constant-Ω spectra of Figure 7e more clearly; in the curves related to the Ψ = 0.0126, some peaks at BPF harmonics are present which are likely due the ingestion of ambient turbulence.
These peaks are apparently very prominent since the SPL spectra have been computed with a high resolution (∆f = 1 Hz), resulting in a general decrease in the broadband part and in the narrowband humps. The second crest has a similar trend, while the other ones apparently merge in a plateau extending from St ≅ 12 to St ≅ 36; as Ψ further grows, two new, high and broad crests appear at St ≅ 15 and 22. The characteristic St of the three crests have clearly decreased compared to the values at Ψ < 0.075. Possibly, a change in the flow pattern takes place across Ψ ≅ 0.09, e.g., stronger flow structures with a higher degree of prerotation substitute the ones present at lower Ψ. Evidence that such a hypothesis is correct will be sought in the flow features.
3.4. Relation between Radiated Noise and Flow Pattern
The collapse of the SPLlow,scaled curves of Figure 6c is only fair, as the curves spread in a range of ±1 dB, indicating that aeroacoustic similarity could not be fully respected while Ω varies. However, discrepancies of this magnitude are common in such measurements and it is important to verify whether this depends on the leakage noise. To this aim, the SPL spectrum in the low-frequency range (St < 45) has been measured during Ω-ramps and plotted versus St and Ω in Figure 8. The spectrograms reporting the original SPL scaled with α = 1 (1st row) are strongly distorted by propagation effects which appear as crests and valleys aligned along hyperbolas. As this complicates analyzing the plots, SPLscaled has been filtered according to Equation (3), (2nd row); although some valleys aligned along hyperbolas are still present in all of the plots at low Ω, the main features of the noise generating mechanism may be more clearly observed. The already observed tonal components at BPF harmonics may be identified as sharp, constant-St crests at St = 9, 18, 27; they do not affect the main features of the spectrograms, and, hence, may be neglected in the present analysis. The subharmonic crests are the most interesting aspect of the spectrograms, as the narrowband humps observed in the SPLfilt spectra of Figure 7e are constant-Ω cuts of them. They constitute the major contribution to SPLlow and are present at all Ψ, confirming that the leakage noise is always important for the present rotor. As Ω varies, their characteristic St values remain basically constant and their height variation is gradual. Opposite to the previous work, no abrupt variations are present, thus confirming that the flow pattern is basically independent of Ω although the employed α is not the exact one.
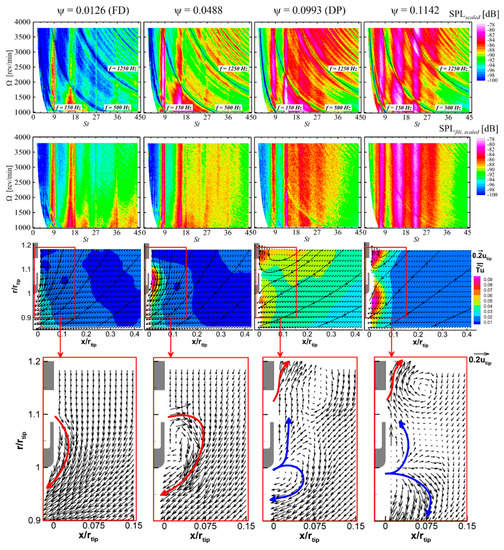
Figure 8.
Measurements taken at Ψ = const. From top to bottom: Spectrograms of SPLscaled and of SPLfilt,scaled during speed ramps, and time-mean and instantaneous flow fields at Ω = 2500 rev/min (→ leakage flow, → blade tip separation). From left to right: Ψ = 0.0126, 0.0488, 0.0993, 0.1142.
At Ψ = 0.0126, only the first three crests seem relevant. The level of all of them decreases with Ω, indicating that the α value employed in the scaling is too large. At the higher Ψ, both height and width of the crests increase with Ω, and a fourth crest arises between St = 27 and 36. If the aeroacoustic similarity were fully respected and the exact α value were employed, characteristic St value and height of such crests would be independent of Ω. The slight Ψ variations during the Ω ramps and some residual propagation effects likely reflect on the trend of the crests, thus preventing them from strictly respecting aeroacustic similarity. Nevertheless, the main features of the spectrograms are qualitatively independent of Ω, showing that, opposite to the case of the plastic rotor studied in Canepa et al. [10,11,12], no important flow pattern modifications take place as Ω grows. Hence, it may be concluded that, for the present rotor, aerodynamic measurements taken at a single Ω value are sufficient to characterize the leakage flow pattern related to a given Ψ.
Such a kind of measurements have been taken in the meridional plane region shown in Figure 2c, at Ω = 2500 rev/min and at the operating points shown in Figure 1b (Ψ = 0.0126, 0.0488, 0.0993, 0.1142). Different aerodynamic quantities are reported in Figure 8: Time-mean vector plots with the contours (3rd row) and instantaneous vector plots (4th row). The latter ones are not representative of the most statistically frequent pattern; rather, they have been arbitrarily chosen since they show a strong instantaneous leakage flow and help explain some flow features, e.g., see Canepa et al. [11]. Extracting further information about large-scale flow structures would require an analysis based on suitable techniques. To this aim, Canepa et al. [11,12] successfully applied the proper orthogonal decomposition algorithm presented in Lengani et al. [23] and Simoni et al. [24] to the leakage flow in the plastic rotor of Figure 1c. Such an analysis goes beyond the purpose of the present work.
As subharmonic narrowband humps are present in the SPL spectra at all of the investigated operating points, it is expected that prerotating large-scale flow structures are always ingested by the rotor and that they are released from the gap. However, both assumptions should be verified.
At low Ψ (0.0126), no reingested leakage flow may be detected in the time-mean vector plots as the flow is centripetal and no velocity component pointing upstream of the rotor may be detected in the gap region. However, in front of the ring, a slightly higher- area is present and the instantaneous vector plot shows that, in the lower part of the gap, the flow points upstream and follows curved streamlines in front of the ring. All this is consistent with the presence of a weak leakage flow.
At Ψ = 0.0488, the time-mean flow is still centripetal but shows a clear deflection and a high in front of the ring; these are evidences of the presence of the leakage flow. The instantaneous flow field shows that, in front of the gap, some velocity vectors point upstream, clearly confirming the leakage flow presence. Furthermore, a recirculation bubble is present in front of the ring; such a bubble must be strongly unsteady, as it is not present in the time-mean flow. This is consistent with the presence of the high zone. On the contrary, in the case of the plastic rotor at Ω = 2400 rev/min and DP conditions, such a bubble is present also in the time-mean flow, due to the higher Ψ, see Figure 3d.
At Ψ = 0.0993 and 0.1142, the time-mean flow pattern is completely different: The leakage flow streams radially outwards along the panel and forms a wide recirculation zone before being reingested by the rotor, a feature already observed in the case of the plastic rotor at Ω = 3000 rev/min, see Figure 3c. This shows that such a flow pattern is present also in case of stiff, flush mounted rotor, i.e., it seems characteristic of the high-Ψ operation of a rotor mounted on a flat panel rather than of the rotor jutting out of it. However, the high- zone in front of the blade tip and of the lower part of the ring is absent in the plastic rotor case and may not be explained based on turbulence convection from the gap towards the rotor entrance. In fact, the instantaneous vector plots show that a reverse flow area is sometimes present at the blade tip. Obviously, the presence of such a separation constitutes an undesired total pressure loss and surely reduces the rotor efficiency, but it does not likely affect the rotor performance, as the kinetic energy loss is likely compensated by a larger static pressure rise, which constitutes the design target for such fans. Such a blade tip separation is not so frequent from the statistical point of view, and, apparently, it does not affect the time-mean velocity field; however, it constitutes an important reason of unsteadiness which results in the observed high zone. At Ψ = 0.1142, such a separated flow is stronger than at Ψ = 0.0993, but both velocity fields are qualitatively similar. In both cases, such a separated flow must have an important prerotation as it directly comes from the rotor, and, eventually, is partly reingested at lower radii. Despite the different origin, such a recirculating flow has likely characteristics similar to the leakage flow ones (positive swirl and presence of unsteady large-scale flow structures). This could be an alternative cause of subharmonic narrowband humps in the SPL spectrum at high loading. Such a hypothesis is consistent with the modifications in the SPL spectrum across Ψ ≅ 0.09, see Figure 7, and also suggests an explanation for the dip observed in SPLlow,scaled, see Figure 6c.
In the spectrograms of Figure 7, at Ψ < 0.09, the 2nd, 3rd, and 4th crests are located at higher St than they are at Ψ > 0.10. In the former case, the main contribution to the noise may be due to the leakage flow, while, in the latter case, the leakage flow is very weak when it is reingested by the rotor, and the related noise becomes weak also. On the contrary, the reverse flow in the blade tip region may strengthen, overwhelming the leakage flow noise and thus providing the major contribution to the noise generation. The larger frequency shift may be ascribed to a stronger prerotation, due to the fact that the separated flow directly comes from the blade region and also follows a shorter path before being reingested. Subharmonic humps in the SPL spectrum of rotors without ring have been reported by Zhu et al. [13], who ascribed them to the leakage flow between blade tip and stationary shroud. Such a reverse flow presents some analogies with the assumed separation at the blade tip of the present shrouded rotor. At Ψ = 0.0936, only the first subharmonic crest may be detected, as the other ones seem to merge in a rather flat valley which extends up to St ≅ 40. At this specific Ψ, the reingested leakage flow and the flow due to the blade tip separation could provide noise of similar level and different frequency, resulting in a rather constant trend. The SPLlow decrease could be due to a pattern transition of the leakage flow from the attached separation bubble to the large recirculation zone, which, similarly to what has been observed by Canepa et al. [11], results in a SPL decrease. The subsequent SPL increase could be due to the appearance and growth of the blade tip separation bubble. Such an explanation for the SPLlow trend has an overall consistency, but requires further evidences in order to be accepted.
4. Conclusions
The leakage flow and related noise in low-speed fans with rotating shroud have been experimentally studied at different operating conditions and rotational speeds by means of both acoustic and PIV measurements. The present work has shown that, in a flush mounted, stiff fan operated during speed ramps, the flow basically respects similarity despite some variations in the pressure rise coefficient. This allows to take measurements at variable rotational speed, which is essential for acoustic measurements, as it provides a large amount of data with a single measurement. The observed variations may result in slight modifications in the SPL spectra, but the flow pattern is basically independent from the rotational speed, since the studied rotor is stiff and low-Reynolds number effects are negligible. This indicates that the aeroacoustic similarity is basically respected for a stiff rotor; on the contrary it may not be the case for plastic rotors employed in real cooling units, as they usually deform during operation.
The leakage flow generally provides the main contribution to the SPL spectrum, and its pattern depends on the pressure rise coefficient and not on the rotational speed. At low blade loading, the leakage flow is restrained close to the rotor ring, while, at high loading, it flows radially outward along the mounting panel forming a broad recirculation zone; as a result, the related noise likely decreases. In the latter condition, an unsteady flow separation in the blade tip region is probably present. It could result in the appearance of new subharmonic narrowband humps in the spectrum, and in a new noise increase, resulting in a non-monotonic trend of the SPL with the loading. Further evidence should be provided in order to support such an explanation. However, this suggests that similar SPL spectrum patterns may be generated by very different flows and that the properties of the noise in the low-frequency range are very complicated. Indeed, it not only depends on the leakage flow, but also on the aerodynamic behaviour of the blade within the whole range of operation.
Author Contributions
E.C., A.C., and F.M.Z. conceived and designed the study, E.C. and F.M.Z. performed the measurements and processed the results, A.C., and F.M.Z. wrote the paper.
Funding
This research received no external funding. The APC was funded by the Euroturbo Association.
Acknowledgments
The authors kindly acknowledge Johnson Electric Asti srl for having provided the tested rotor.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a0 | speed of sound, 340 m/s |
| c | blade chord |
| f | frequency |
| G(f) | acoustic propagation function |
| OASPL | overall SPL, ref. 20 µPa |
| p | acoustic pressure |
| Q | volume flow rate |
| r | radial coordinate |
| Rec | Reynolds number based on blade chord and relative velocity w |
| Spp | one-sided auto power spectral density of p |
| SPL | sound pressure level in a given frequency band (SPL spectrum), ref. 20 µPa |
| St | Strouhal number based on the rotational frequency, |
| Tu | turbulence intensity based on utip |
| u | blade speed |
| components of the absolute velocity | |
| w | reference relative velocity based on the mean axial velocity component |
| α | scaling exponent |
| Δf | bandwidth employed in the SPL computation |
| Δp | pressure rise through the rotor (static outlet minus total inlet) |
| p0 | air density |
| ϕ | flow coefficient, |
| Ψ | pressure rise coefficient, |
| Ω | rotational speed (expressed in rev/min) |
| related to the ensemble average | |
| related to the time average | |
| related to non-periodic instantaneous fluctuations |
Subscripts
| a | related to the axial direction |
| DP | related to design operating conditions |
| filt | related to the filtered SPL, Equation (3) |
| high | related to the range 90 < St < 300 |
| hub | related to the rotor hub |
| low | related to the range 6 < St < 90 |
| r | related to the radial direction |
| scaled | related to the scaled SPL, Equation (2) |
| tip | related to the blade tip |
| x | related to the axial direction (the PIV plots) |
| ϑ | related to the circumferential direction |
References
- Longhouse, R. Control of tip-vortex noise of axial flow fans by rotating shrouds. J. Sound Vib. 1978, 58, 201–214. [Google Scholar] [CrossRef]
- Fukano, T.; Takamatsu, Y.; Kodama, Y. The effects of tip clearance on the noise of low pressure axial and mixed flow fans. J. Sound Vib. 1986, 105, 291–308. [Google Scholar] [CrossRef]
- Fukano, T.; Jang, C.M. Tip clearance noise of axial flow fans operating at design and off-design condition. J. Sound Vib. 2004, 275, 1027–1050. [Google Scholar] [CrossRef]
- Piellard, M.; Coutty, B.; Le Goff, V.; Vidal, V.; Pérot, F. Direct aeroacoustics simulation of automotive engine cooling fan system: Effect of upstream geometry on broadband noise. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014. Paper No. AIAA 2014-2455. [Google Scholar]
- Magne, S.; Moreau, S.; Berry, A. Subharmonic tonal noise from backflow vortices radiated by a low-speed ring fan in uniform inlet flow. J. Acoust. Soc. Am. 2015, 137, 228–237. [Google Scholar] [CrossRef] [PubMed]
- Moreau, S.; Sanjosé, M. Sub-harmonic broadband humps and tip noise in low-speed ring fans. J. Acoust. Soc. Am. 2016, 139, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Zenger, F.J.; Renz, A.; Becher, M.; Becker, S. Experimental investigation of the noise emission of axial fans under distorted inflow conditions. J. Sound Vib. 2016, 383, 124–145. [Google Scholar] [CrossRef]
- Na, G.D.; Kameier, F.; Springer, N.; Mauß, M.; Paschereit, C.O. URANS simulations and experimental investigations on unsteady aerodynamic effects in the blade tip region of a shrouded fan configuration. In Proceedings of the ASME Turbo Expo 2017, Charlotte, NC, USA, 26–30 June 2017. Paper No. GT2017-63680. [Google Scholar]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F.; Milanese, G.; Parodi, D. An experimental investigation on the tip leakage noise in axial-flow fans with rotating shroud. J. Sound Vib. 2016, 75, 115–131. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F. Scaling properties of the aerodynamic noise generated by low-speed fans. J. Sound Vib. 2017, 408, 291–313. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.; Jafelice, F.; Mazzocut Zecchin, F.; Parodi, D. Effect of rotor deformation and blade loading on the leakage noise in low-speed axial fans. J. Sound Vib. 2018, 433, 99–123. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F.; Parodi, D. Large-scale unsteady flow structures in the leakage flow of a low-speed axial fan with rotating shroud. Exp. Therm. Fluid Sci. 2019, 102, 1–19. [Google Scholar] [CrossRef]
- Zhu, T.; Lallier-Daniels, D.; Sanjosé, M.; Moreau, S.; Carolus, T. Rotating coherent flow structures as a source for narrowband tip clearance noise from axial fans. J. Sound Vib. 2018, 417, 198–215. [Google Scholar] [CrossRef]
- Sanjosé, M.; Moreau, S. Fast and accurate analytical modeling of broadband noise for a low-speed fan. J. Acoust. Soc. Am. 2018, 143, 3103–3113. [Google Scholar] [CrossRef] [PubMed]
- Neise, W.; Barsikow, B. Acoustic similarity laws for fans. J. Eng. Ind. Trans. ASME 1982, 104, 162–168. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F. Leakage flow noise and related flow pattern in a low-speed axial fan with rotating shroud. In Proceedings of the 13th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Lausanne, The Switzerland, 8–12 April 2019. Paper No. ETC13-368. [Google Scholar]
- ISO 10302. Acoustics-Method for the Measurement of Airborne Noise Emitted by Small Air-Moving Devices; ISO: Geneva, Switzerland, 1996. [Google Scholar]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F. Installation effects on the tonal noise generated by axial flow fans. J. Sound Vib. 2015, 340, 167–189. [Google Scholar] [CrossRef]
- Bongiovì, A.; Cattanei, A. Spectral decomposition of the aerodynamic noise generated by rotating sources. J. Sound Vib. 2011, 330, 136–152. [Google Scholar] [CrossRef]
- Henner, M.; Franquelin, F.; Demory, B.; Beddadi, Y.; Roland, C.; Serran, A. Hump-shaped broadband noise on a fan at off-design conditions. In Proceedings of the Fan 2015 conference, Lyon, France, 15–17 April 2015. [Google Scholar]
- Canepa, E.; Cattanei, A.; Mazzocut Zecchin, F. Analysis of tonal noise generating mechanisms in low-speed axial-flow fans. J. Therm. Sci. 2016, 25, 302–311. [Google Scholar] [CrossRef]
- Majumdar, S.J.; Peake, N. Noise generation by the interaction between ingested turbulence and a rotating fan. J. Fluid Mech. 1998, 359, 181–216. [Google Scholar] [CrossRef]
- Lengani, D.; Simoni, D.; Ubaldi, M.; Zunino, P.; Bertini, F. Analysis of the Reynolds stress component production in a laminar separation bubble. Int. J. Heat Fluid Flows 2017, 64, 112–119. [Google Scholar] [CrossRef]
- Simoni, D.; Lengani, D.; Ubaldi, M.; Zunino, P.; Dellacasagrande, M. Inspection of the dynamic properties of laminar separation bubbles: Free-stream turbulence intensity effects for different Reynolds numbers. Exp. Fluids 2017, 58, 66. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).