1. Introduction
The hydraulic behavior of centrifugal pumps under normal operating conditions is well known. In normal operating mode, the pumped fluid passes the pump from the suction side to the pressure side while the pump rotates in pump direction. Typically, this behavior is of interest when operating a pump in any system, whether in a closed or an open loop. Almost every pump manufacturer offers head and efficiency curves for their pumps to calculate a stationary duty point as the intersection of the pump head curve and the system resistance curve. Another item of important information is the power consumption related to this operation point. The prediction of the hydraulic performance by means of computational fluid dynamics (CFD) has been shown in recent years to be very reliable. Especially for operating points near the best efficiency point (BEP), the correlation between simulation and experiment is very good [
1,
2]. Performance prediction of pumps in off-design and especially in abnormal operation modes is more complicated, since unsteady phenomena then dominate the flow field.
The abnormal hydraulic performance of a pump is apparent in the case of off-design operating conditions where the direction of flow or rotation may change. An example application is the reverse operation of a pump where the unit is used as turbine. In this specific application, it is necessary to have information on the relationship of turbine head and turbine flow rate for a given speed and efficiency or power output at this special operation. A fundamental investigation of reverse operating pumps was presented by Laux in 1982 [
3]. In his paper, some general aspects for operating pumps as turbines including different fields of applications as well as normalized performance characteristics are presented. A review of research and investigations related to pumps as turbines was carried out by Nautiyal et al. [
4]. In their work, the authors discuss the analytical, experimental and computational work done in the area of pumps working as turbines. Several methods for predicting the behavior of pumps as turbines are presented but the authors state that none of the presented methods is appropriate for the entire range of specific speeds. Stefanizzi et al. [
5] investigated the performance prediction of a pump operating as turbine. They proposed a new model for predicting the turbine mode performance of a pump. Their work is based on a literature survey as well as experimental investigations on a single-stage centrifugal pump.
Another important abnormal operation mode is the pump trip, where the knowledge of the complete pump characteristics is essential. Only if complete information about the pump performance in every possible operation quadrant is known the transient behavior of the machine will be predicted in an accurate way. This information is crucial to calculate reliable system transients (the so-called waterhammer effect), which provides necessary data for pipeline design, like the maximum or minimum resulting internal pressure.
Since extensive testing is required to get all of the necessary information concerning the complete 4-quadrant (4Q) behavior of centrifugal pumps, there is limited information available in the open literature. The publications of Knapp [
6], Wylie and Streeter [
7] or Stepanoff [
8] are well known in the community and their information is often referenced for transient system analysis if no other information is available. This approach leads to inevitable inaccuracies in the prediction of the hydraulic pressure transients since the real pump characteristics are not known.
A reliable numerical calculation of the 4Q pump characteristics is a very challenging task as the abnormal operating conditions lead to complex and unsteady flow phenomena inside the pump. Gros [
9] and Couzinet [
10] investigated the 4Q pump performance by means of numerical simulation and experimental investigations. The results of their unsteady numerical simulations showed good accuracy when comparing them to their experimental results.
This paper presents an additional contribution in obtaining a reliable prediction of the complete pump characteristics by means of CFD calculation.
1.1. The 4-Quadrant Behavior of a Pump and Its Representation
There are several ways to describe the hydraulic behavior of a pump in normal and abnormal conditions. The representation of the 4-quadrant performance of a pump with the head coefficient ψ (Equation (1)) and the flow coefficient φ (Equation (2)) is not preferable since the direction of rotation is not captured. Another disadvantage of this notation appears with blocked impeller, where a singularity in φ and ψ occurs. The IEC 60193 [
11] suggests the illustration of the overall pump behavior with the discharge factor
QED (Equation (3)), the speed factor
nED (Equation (4)) and the torque factor
TED (Equation (5)).
A principle representation of 4Q behavior of a semi-axial pump is shown in
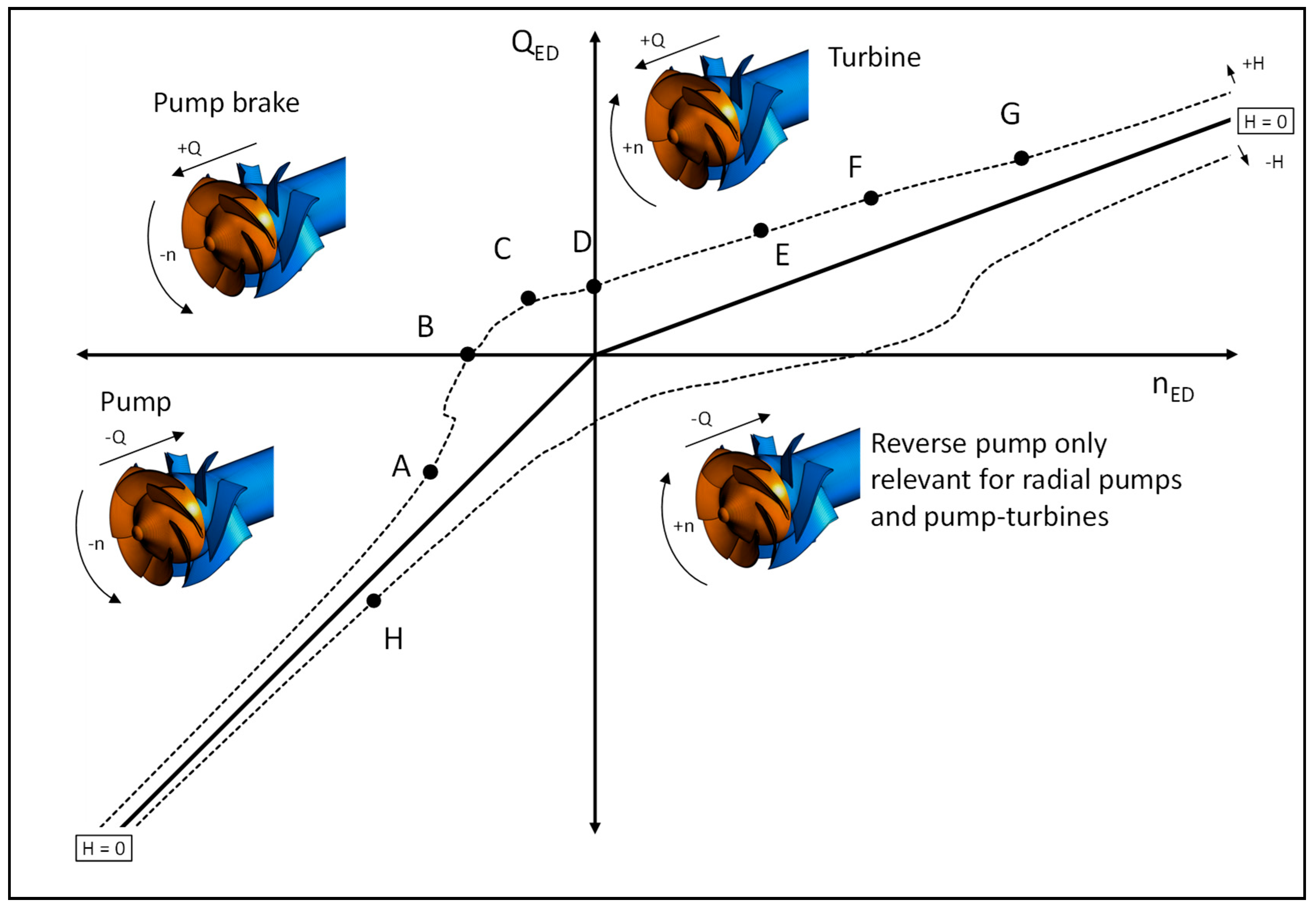
Figure 1 where different operation modes of a pump are marked. The sign convention in the IEC 60193 standard for rotation and flow rate is specified with positive signs for turbine operation. Point A marks the pump operation mode, defined with negative flow and rotation. Point B identifies the zero discharge condition or shut-off point in the pump direction of rotation. The pump brake mode C is characterized by a negative rotation (pump direction of rotation) and a positive flow rate (from pressure side to suction side). The operation of the pump with a blocked impeller and turbine discharge is marked with point D. The pump operating as a turbine with positive flow and rotation direction is identified with mode E, where the unit delivers torque to the machine shaft. The zero torque point F, also known as runaway point in turbine operation, is of essential interest in case of a pump trip to reliably calculate the runaway speed and runaway discharge in case of an emergency. Mode G represents the turbine brake condition were torque must be provided to the unit to rotate in turbine direction with turbine discharge. An additional operation mode may occur in radial machines, which is called the reverse pump mode. With radial pumps and pump turbines it may be possible to pump fluid in pump direction from the suction inlet to the pressure outlet of the machine while the unit rotates in turbine direction.
The curve below the zero head-line (H = 0) is of minor interest since this operation may normally occur only under laboratory conditions. A pump would be a resistance in a hydraulic system if operated at the negative head curve (−H). Point H on curve −H identifies the pump runaway point.
1.2. The Investigated Pump with Variable Pitch
The first pump presented in this paper was designed with variable pitch for a flow rate of 5 m
3/s and a head of 27 m at a speed of 507 rpm, resulting in a specific speed of
nq = 95 [
12]. The mechanical concept of a variable pitch pump is quite complicated as far as the adjustment of the blade is concerned. A spherical hub and shroud contour is therefore needed to allow for the blades to be adjusted during operation.
The benefit of the variable pitch concept is clearly visible in
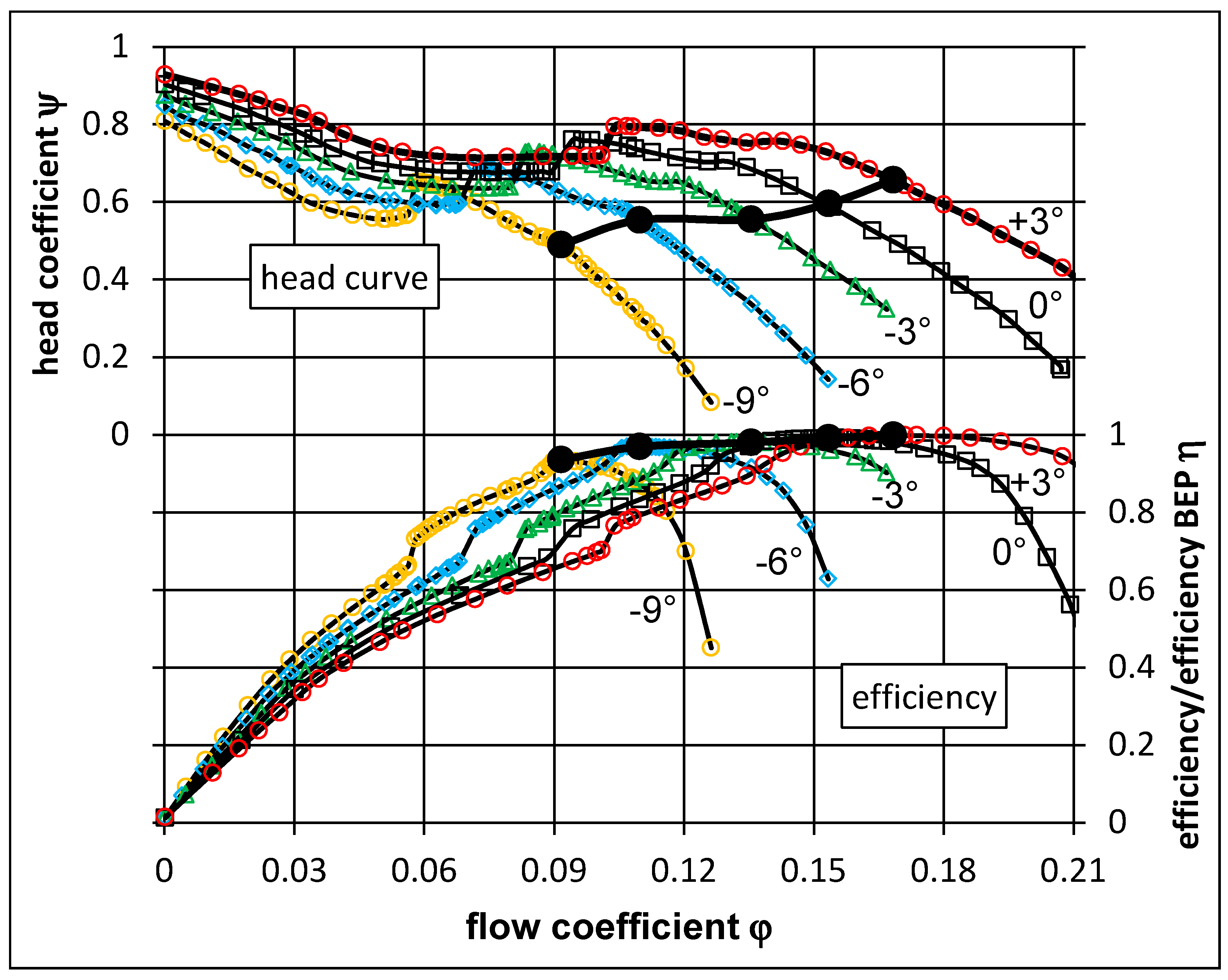
Figure 2, where the envelope of the efficiency as well as the best efficiency points of each head curve for different blade positions are shown. Such pumps are very often used for applications with horizontal system curves. For a variable pitch pump, the blade can be opened for higher flow rates and thus the head does not drop. Towards part load this appears vice versa. The shut-off head is lower for a more closed position, and so the power consumption is lower.
1.3. The Investigated Pump with Low Specific Speed for Multistage Usage
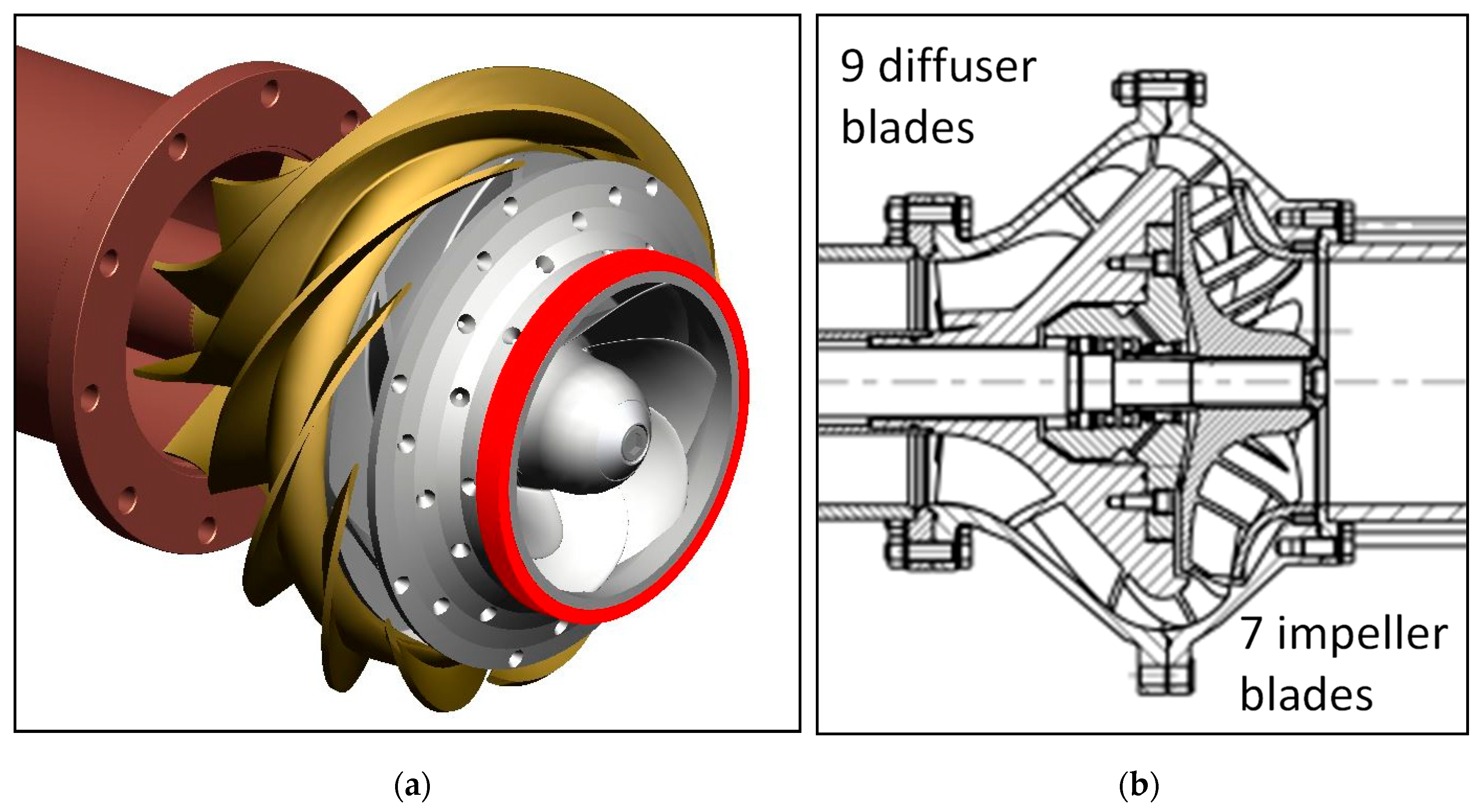
The second pump presented in this paper is a vertical suspended mixed flow diffuser pump with a comparably low specific speed of
nq = 36 [
13]. A stable head curve for flow rates lower than 25%
QDesign and furthermore a shut-off head
H0 in the range of 1.2·
HDesign <
H0 < 1.28·
HDesign were crucial targets for the hydraulic design. The pump was designed so as to be built in a single stage as well as in a multistage arrangement with the same hydraulic design. Besides the above-mentioned hydraulic performance criteria, the pump design is characterized by a comparatively short stage length as well as a limited maximum diffuser diameter. The design of the measured model pump is shown in principle in
Figure 3. It produces a head of 34.5 m at a design flow rate of 0.119 m
3/s and a rotating speed of 1490 rpm.
2. Numerical Method
2.1. Numerical Model
The numerical simulations were carried out with the commercial CFD-code ANSYS CFX15 (Canonsburg, PA, USA). Many different models were generated and analyzed in course of the numerical investigations. The final simulations, which led to the results stated below, were carried out on a full 360° model. The numerical setup (see
Figure 4) consists of the suction bell domain (stationary—including an inlet extension), the impeller domain (rotating) and the stator domain (stationary—including an outlet extension). The different domains were marked with different colors in the left picture in
Figure 4 for a better identification of the positions of the domain interfaces. The impeller domain consists of all impeller passages and the diffuser of all stator passages. Structured hexagonal meshes were generated for each domain. One on one mesh matching has been applied to the periodic faces of the impeller and diffusor domains. Therefore, no additional grid interface is necessary inside one domain. The impeller mesh also includes the tip gap of the semi open impeller for the variable pitch geometry. The runner hub and shroud cavities of the low
nq pump were neglected in the numerical model. The mesh generation for the diffusers and impellers was done with TurboGrid (ANSYS), whereas the mesh for the inlet and suction bell region was generated with ICEM (ANSYS). Near-wall inflation on all meshes was applied to resolve the boundary layer of the viscous flow. The minimum orthogonal element angle is 20° and the maximum aspect ratio is below 3500. A growth rate of 1.25 was applied and the averaged
y+ value for all meshes at a flow rate of the best efficiency point of the pumps is around 20. The mesh statistics for the final simulations are summarized in
Table 1.
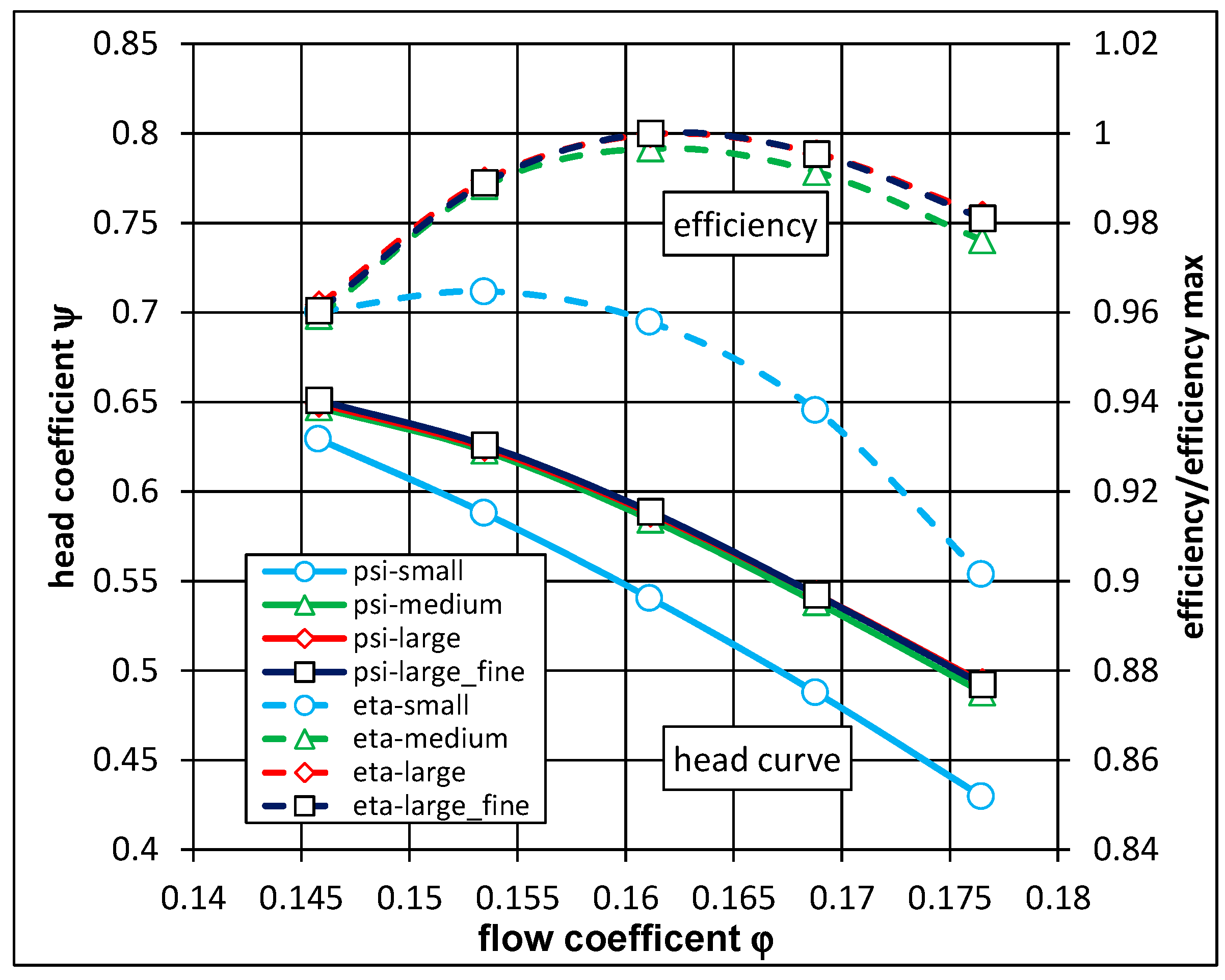
The results of a grid dependency study for the variable pitch pump are shown in
Figure 5. The study was carried out on a single passage model (
Table 2) for both the impeller domain as well as the diffuser domain. Curves for head coefficient and normalized efficiency for different grid sizes on several operating points are shown for the 0 blade position. As shown in
Figure 5, there is no difference for both parameters between the meshes large and large_fine. Thus, beginning with the grid large, the results can be regarded grid-independent. Detailed information on the numerical setup can be found in preliminary works [
12,
13].
For the stationary calculations, a mixing plane approach was chosen for the multiple frames of reference interface between stationary and rotating domains. In the transient CFD simulations, the rotor position is updated at every timestep during the simulation according to the rotors rotational speed. For the inlet boundary condition (BC) (defined at a distance of L = 5·
DInlet away from the pump inlet) the mass flow rate was specified whereas at the outlet (defined at a distance of
L = 5·
DOutlet away from the stator outlet) an average static pressure was applied as boundary condition. As turbulence model the shear stress transport (SST) model developed by Menter et al. [
14] was applied to the stationary calculations. This two-equation approach, based on an eddy-viscosity concept, is commonly used for hydraulic turbomachinery. The transient analyses were carried out with the scale adaptive simulation shear stress transport (SAS-SST) turbulence model [
15]. The concept of the SAS-SST-turbulence model is based on the introduction of the von Karman length scale into the turbulence scale equation. So, the model dynamically adjusts to resolved vortex structures in the URANS (Unsteady Reynolds-Averaged Navier–Stokes) method, which results in a large eddy simulation (LES)-like behavior in unsteady regions of the flow field.
An adaptive timestep was used both in stationary as well as in transient simulations to speed up convergence. In the stationary calculations 500 iterations were calculated. To determine the timestep combinations of the runner speed (
ω) and the blade numbers of the runner (
zr) and the diffuser (
zd) were used (see
Table 3). Convergence was monitored by means of hydraulic efficiency (see Equation (8)). For the transient simulations, a timestep corresponding to a resolution of 12° for the first impeller revolution and 1° for the following revolutions was chosen. The general CFD settings are summarized in
Table 2.
2.2. Post-Processing
The evaluation of the hydraulic performance is executed by means of the key figures as mentioned in the following. In general, the net head is the difference between total pressure head at the outlet and total pressure head at the inlet. Since different flow directions were investigated all results shown were processed with inlet and outlet defined with respect to discharge in pump direction. According to the ISO 9906 standard [
16], the net head represents the difference between the static pressure plus the mean kinetic energy head at outlet and inlet. The post-processing of the CFD results was carried out in a similar way as given in Equation (7).
The head was analyzed with the head coefficient ψ and the flow rate is expressed by the flow coefficient φ. The efficiency η is described by Equation (8) for pump operation.
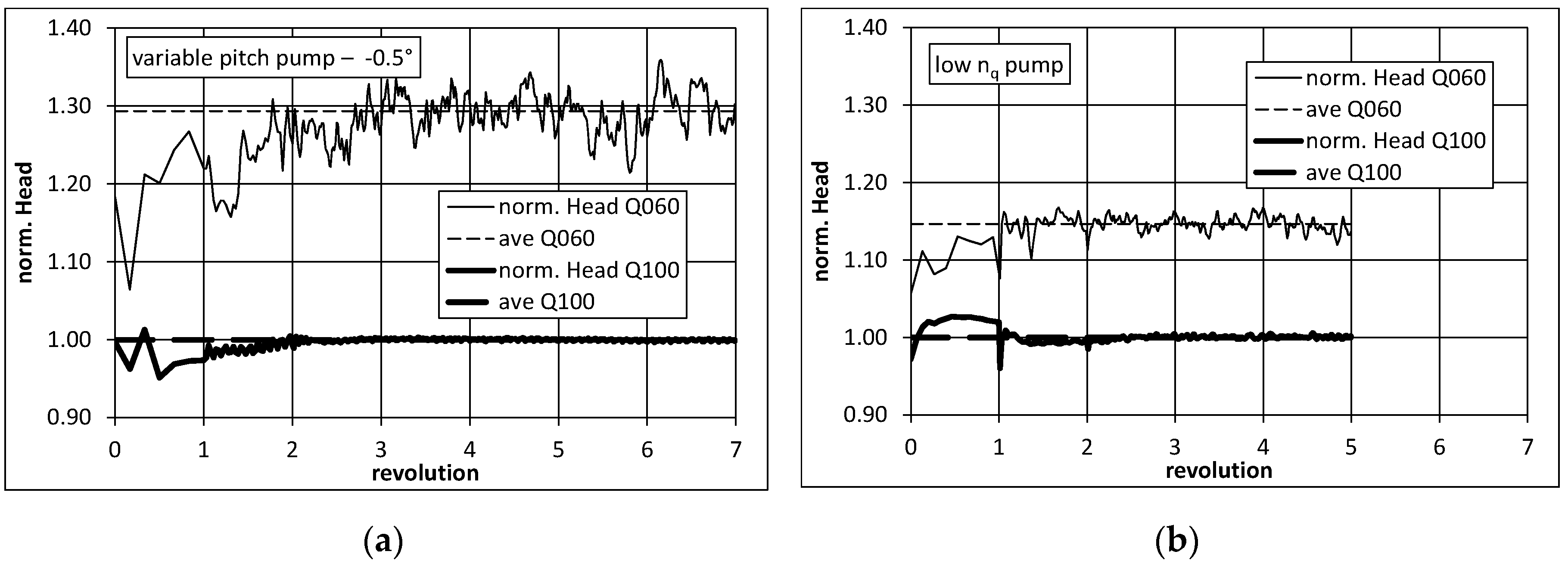
Figure 6 shows the head convergence history of the unsteady simulations for two different operating points at design flow rate (Q100) and at part load at 0.60·
QDesign (Q060). It can be seen that for both investigated pumps, the head increases at the beginning of the transient calculations. This is true for both discussed operating points as well as for both investigated pumps. The increase of head continues for some revolutions until more or less stable oscillations around an average value occur. At least five impeller revolutions were simulated in course of the unsteady calculations. The transient results of the last three revolutions were finally used to calculate a representative average value of head and efficiency in
Section 4.
Furthermore, it turned out that the results of the average head, calculated based on transient simulations are slightly higher than compared to the stationary simulation. Thus, the complete head curves originally calculated by means of stationary CFD were shifted by the found deviations. By applying this approach, an increase in accuracy and reliability of the stationary numerical results compared to measurements is obtained as it is shown in
Section 4.
3. Experimental Setup
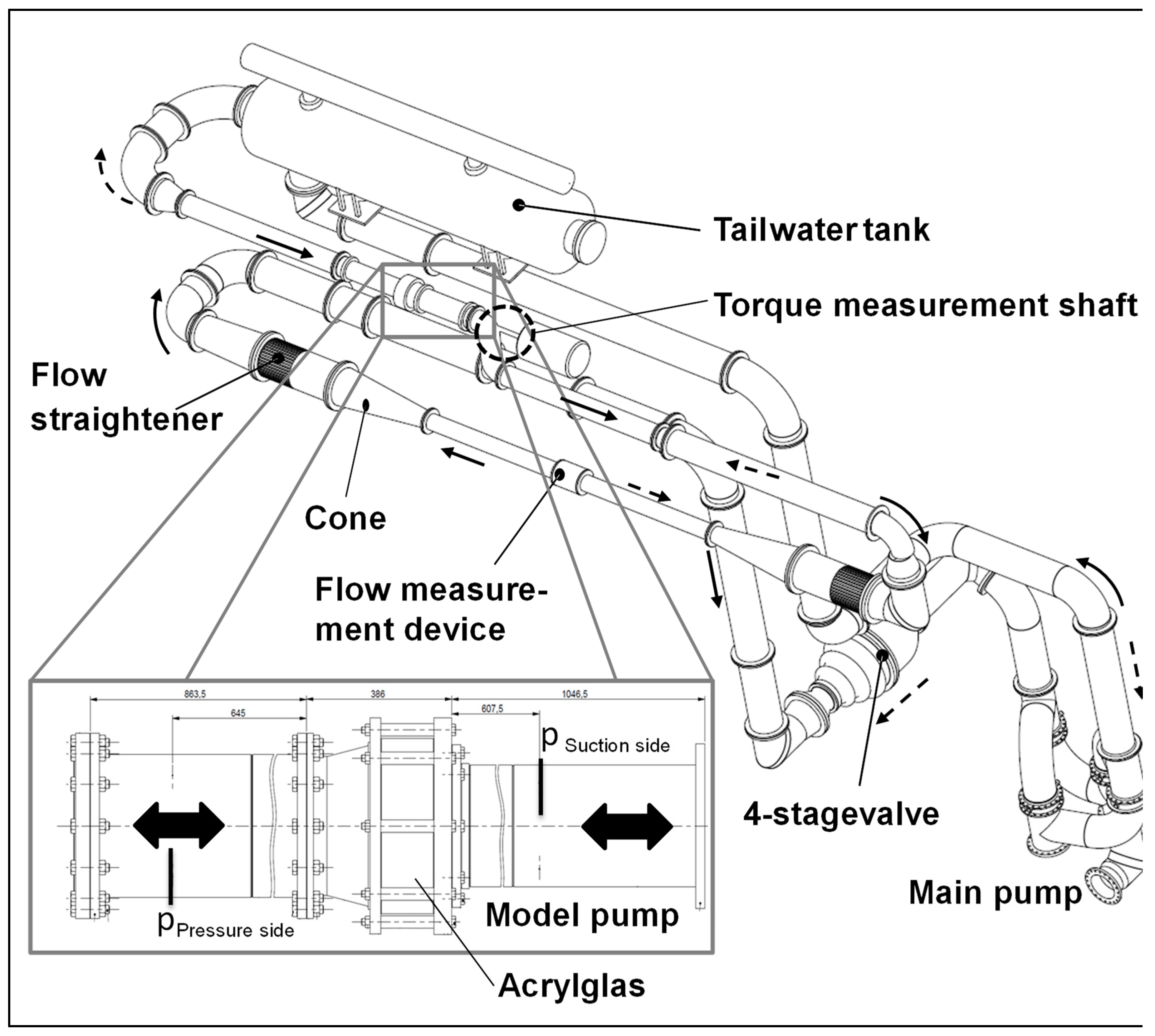
The measurements were carried out on the 4-quadrant test rig of the Institute of Hydraulic Fluid Machinery at Graz University of Technology (Graz, Austria (see
Figure 7)). As the full-size prototype pumps would exceed the performance of the test facility, an adequate model scale was chosen for both pumps. The model size, the experimental setup in general and the measurement instruments meet the requirements for acceptance tests according to the IEC 60193 standard [
11]. The speed of the model pumps were chosen to ensure a Reynolds number higher than 4 × 10
6 for the measurements in pump operation mode [
11].
The model pumps were manufactured at the institute’s workshop and installed on the closed loop test rig shown in
Figure 7. To account for a hydraulic performance test in all normal and abnormal pump operation modes, a speed-regulated pump drive was used, which can also change the direction of rotation. Additionally, the flow direction at the test rig can be reverted to analyze the machine performance with pump (solid arrows) and turbine (dashed arrows) discharge.
The measurement of the flow rate is carried out with an inductive flow meter, and the head is measured with the help of a diaphragm differential pressure transmitter. The pressure on the test rig is measured on four pressure measuring taps, which are being positioned circumferentially around the pipe with an angle of 90° between them. These locations were set 2 diameters away from the flanges as shown in
Figure 7. The torque and the rotational speed are measured with a torque measurement shaft. All measurement devices were calibrated in installed condition at the test rig. The measurement uncertainties regarding the different measurement methods are shown in
Table 4. The total uncertainty for efficiency is calculated according to ISO 9906 [
16] as a root mean square (RMS) value of the individual errors for each method and the random error.
4. Results
4.1. Pump Operation
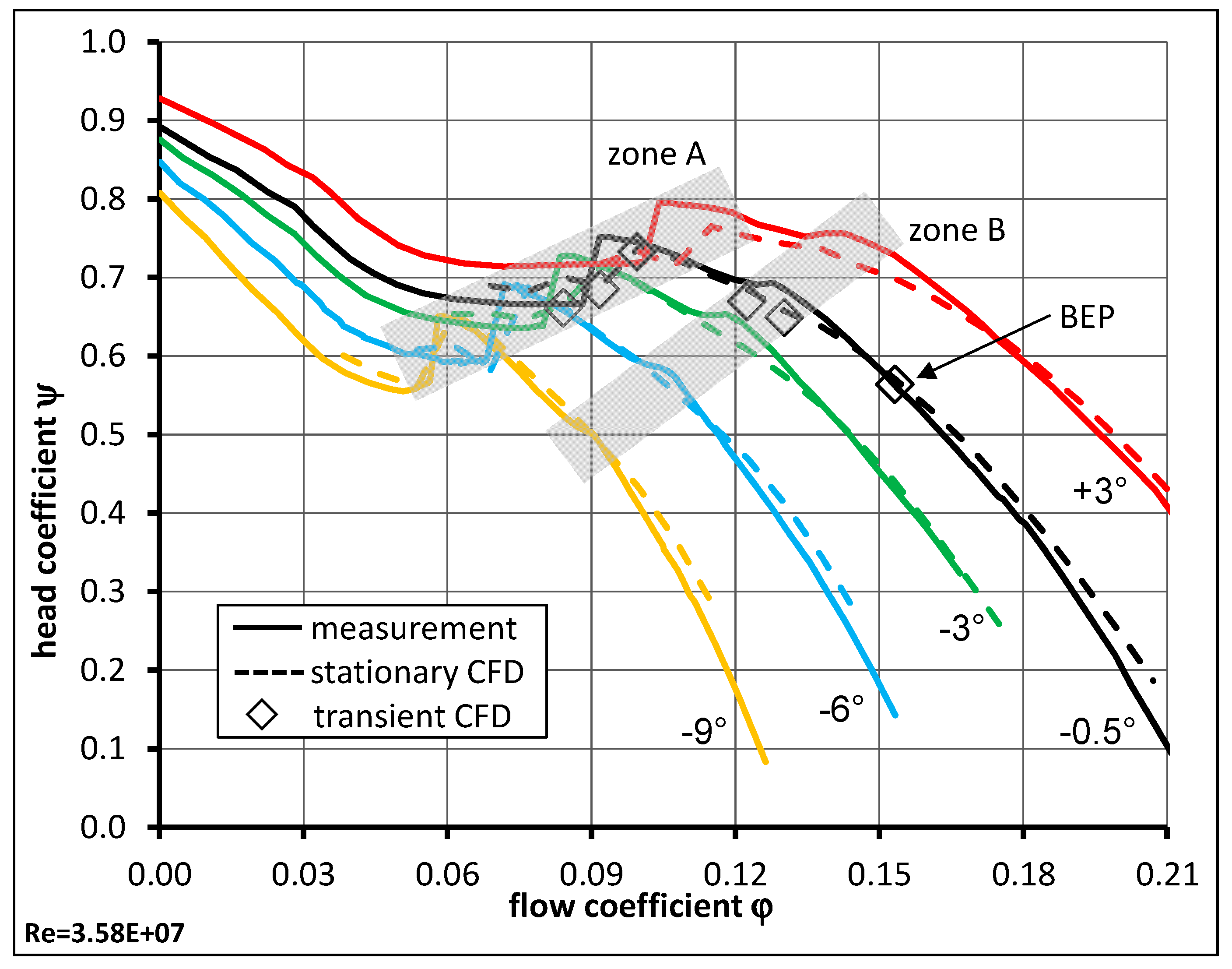
In
Figure 8 the head curves (head coefficient ψ) in pump operation for different blade positions are shown versus the flow rate (flow coefficient φ) for both CFD (dashed) and test rig (solid) results. While the CFD simulations were carried out with the prototype size and speed of the pump, the measurements were performed with above mentioned model size. To allow for a direct comparison of measurement and simulation a dimensional representation of the head curve by means of φ and ψ was required. Additionally, an efficiency scale up according to IEC standard [
11] was applied for the model test data. As it can be seen, a good correlation over the whole operation range was achieved.
Zone A in
Figure 8 indicates the main instability zone of the pump for different blade positions. Usually the pump can only be operated on the right side of this zone, which is generally indicated as operation limit in pump data sheets. The second zone B indicates the diffuser instability and is of minor importance. This zone is not identified as an unstable head curve since the sign of the slope of the curve does not change and so a continuously increasing head with decreasing flow rate is observed. This zone could be eliminated by diffuser modifications (e.g., reduction of diffuser blade numbers and altered diffuser inlet and outlet angles) but would shift the best efficiency point to lower flow rates. The dashed lines indicate the results of CFD calculations in stationary mode. The transient CFD results are marked with diamonds. Especially around BEP, there is a nearly perfect prediction of the pump head. Zone A is also well predicted whereas for zone B larger deviations between measurement and simulation were observed.
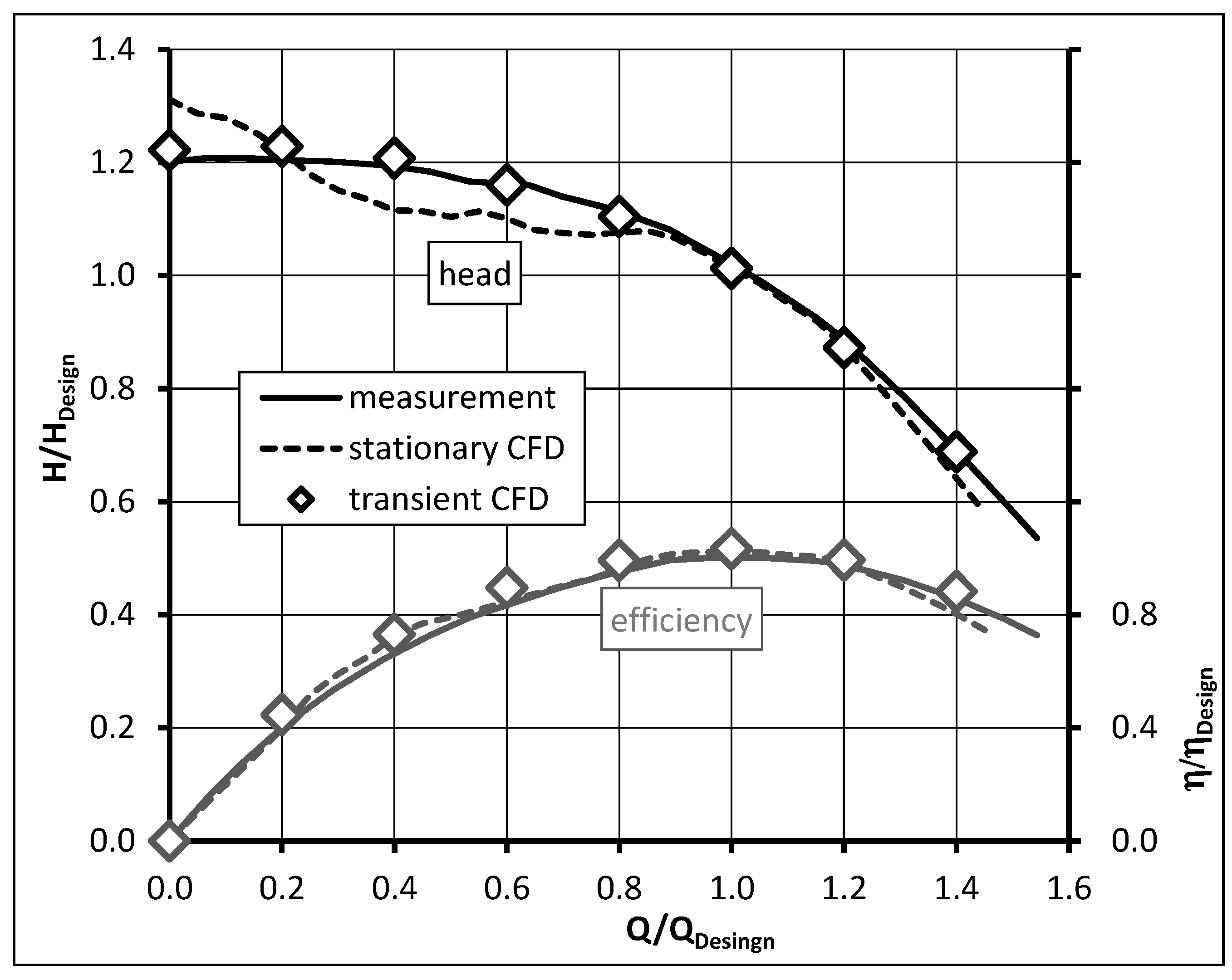
A comparison of the measurements (solid) and the numerical results (stationary CFD—dashed, transient CFD—diamonds) for the low
nq pump is shown in in
Figure 9 for normalized head and normalized efficiency. Normalized head and flow rate instead of head coefficient and flow coefficient were used since the simulations were carried out at model scale for this pump. Therefore, a direct comparison between measurements and numerical results without any scale-up is possible. The dotted lines indicate the results of CFD calculations in stationary mode. Especially around the design point, there is nearly a perfect match between the test rig results and the stationary CFD results. Additionally, the stationary simulation results show a stable head curve. Compared to the transient CFD results, the quality for the stationary calculations is lower in deep part load. Concerning the pump efficiency, there is also a good match between the CFD results and the measurements. Since the CFD setup does not contain the runner side space to reduce the numerical effort as described above, the CFD results do not contain disc friction and leakage losses. Additionally, the numerically calculated efficiency does not include mechanical losses due to sealings and bearings. Thus, it is not surprising that the use of mentioned CFD model yields an overestimated pump performance. At
QDesign the numerically calculated efficiency is two percentage points higher than the one measured on the test rig.
In addition to the stationary calculations, transient calculations for several operating points in pump operation were carried out. These calculation results were evaluated as described in
Section 2.2 and are marked with diamonds in
Figure 8 (for the −0.5° blade position) and in
Figure 9. The transient CFD results show an almost perfect agreement with the measurements over the whole operating range concerning pump head for both investigated pumps. Especially the head drop in zone A of the variable pitch pump is captured well by these transient calculations.
4.2. Experimental and Numerical Results of the Pump Behavior for the Full Operating Range
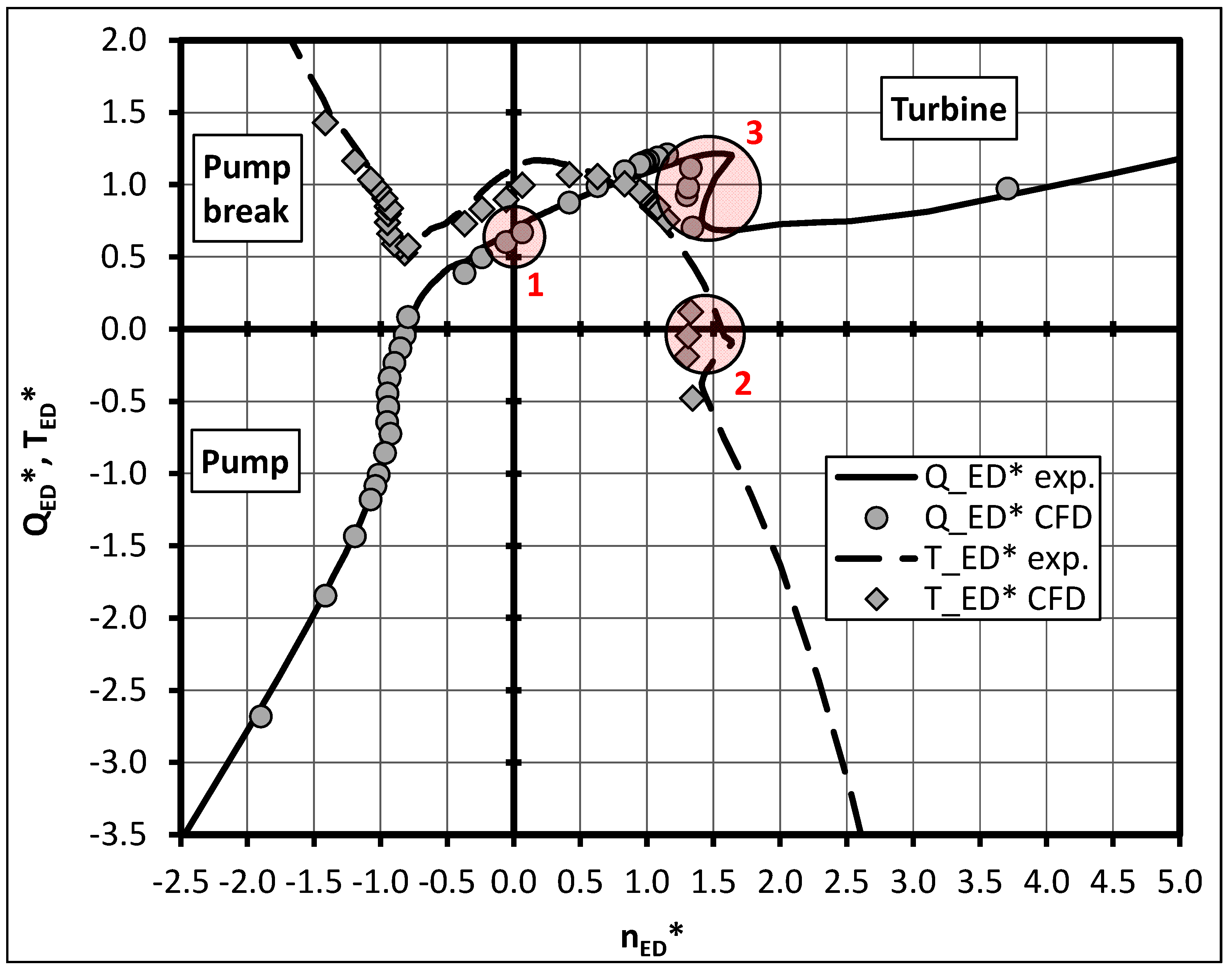
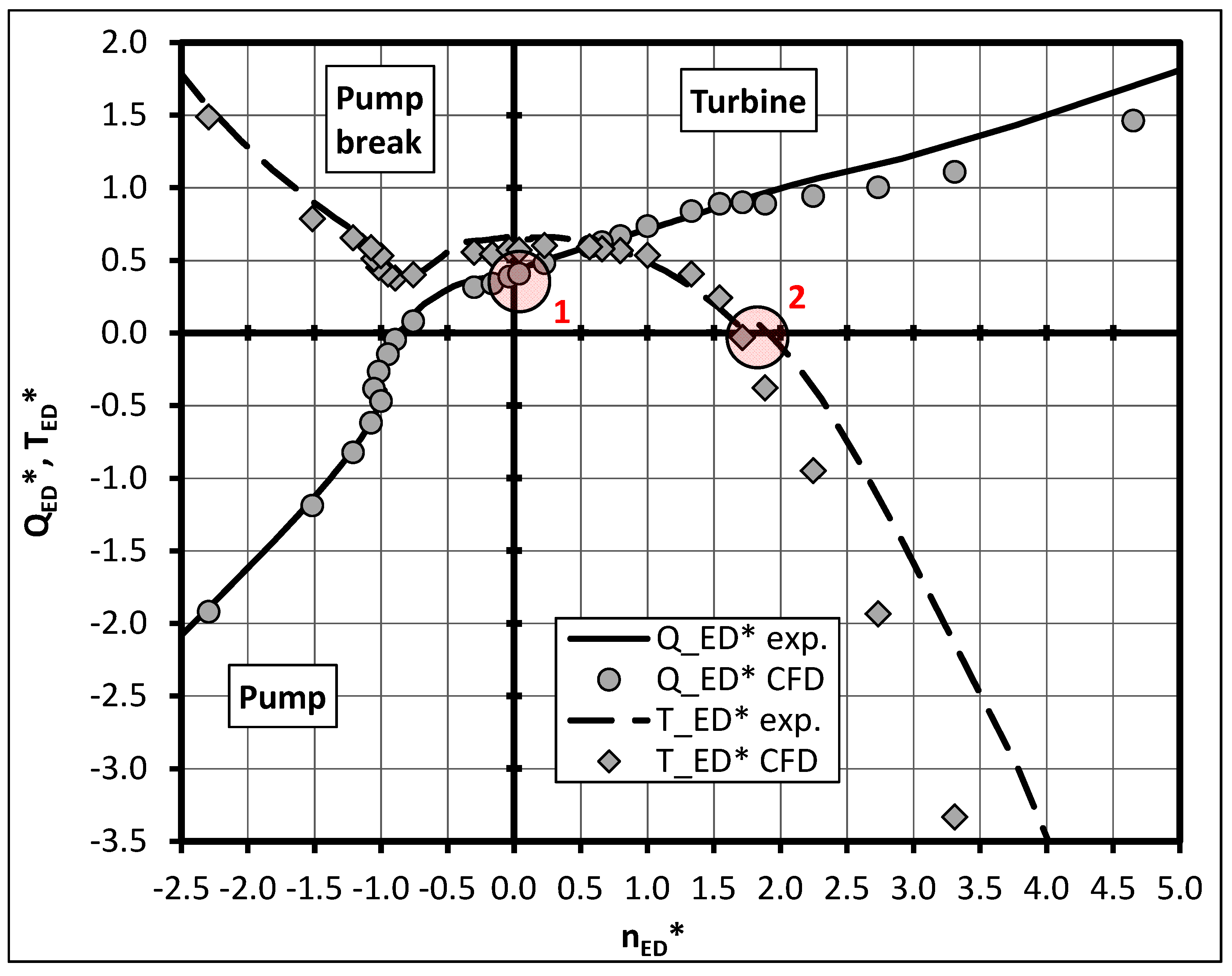
The experimental results of the overall pump performance by means of
QED vs.
nED of the variable pitch pump are shown as solid lines in
Figure 10 for the 0° pitch angle and in
Figure 11 for the −9° pitch angle. The measurements for
TED vs.
nED are shown as dashed lines in these figures. All parameters (
QED,
nED and
TED) were normalized with their values at best efficiency point in pump mode (see Equations (9)–(11)). For the sake of clarity the pump performance at negative head is not shown in these figures since this is also of minor importance.
An instability in the hydraulic behavior in pump operation is presented for both pitch angles shown. These instabilities are indicated by multiple
QED values corresponding to one
nED value. A stable pump operation near these instability regions is not possible. The turbine characteristic for the 0° pitch angle additionally shows a strong instability region in turbine operation near the runaway point (
TED = 0; zone3 in
Figure 10).
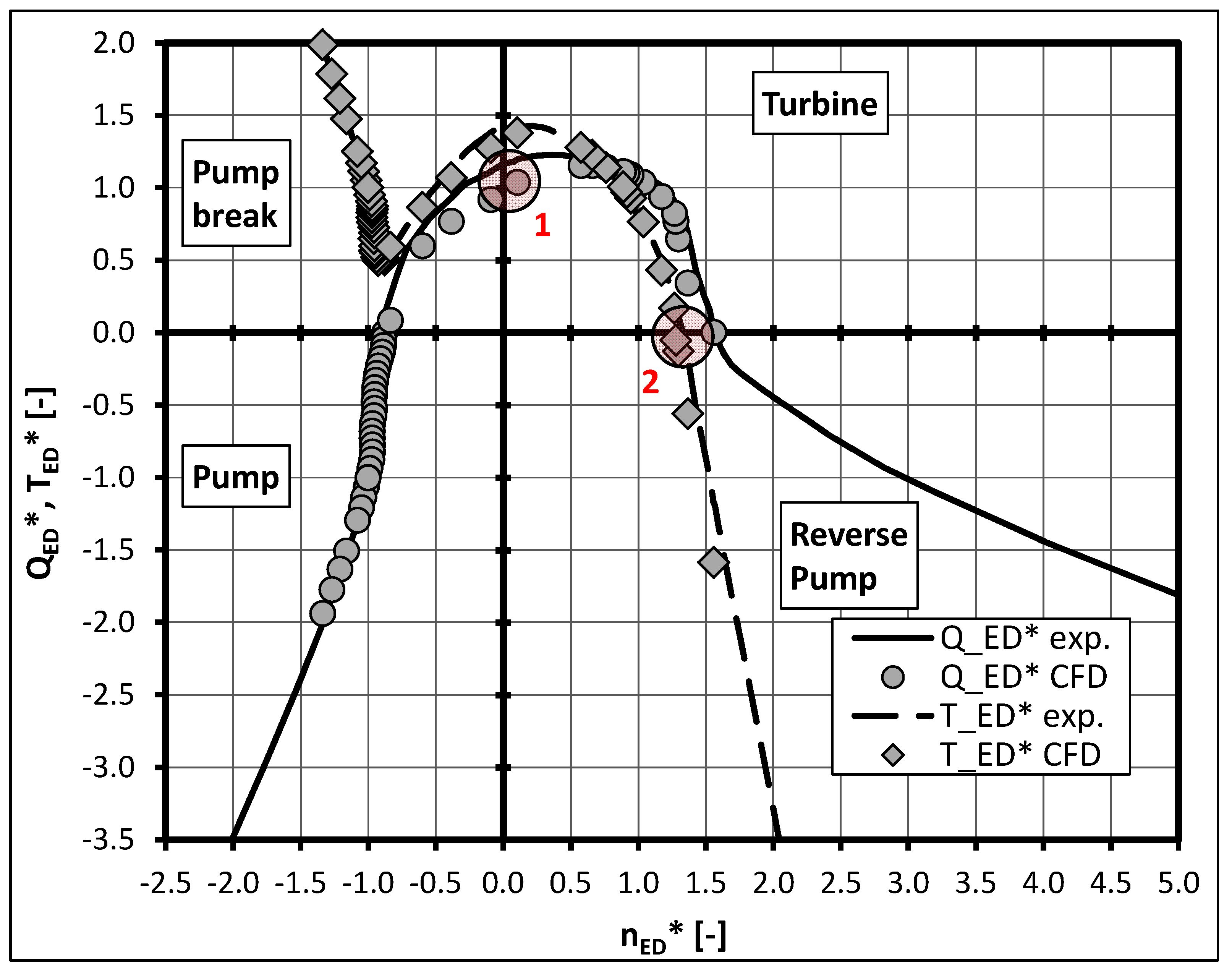
Figure 12 shows the 4-quadrant behavior of the low
nq pump. Again the experimental results for
QED vs.
nED are drawn with solid lines. It turns out that an instability does not occur with this machine in the pump characteristic of this machine nor in turbine operation. Additionally, it can be seen that the low
nq pump enters the reverse pump quadrant, while the variable pitch pump does not show this behavior. Due to the radial impeller, the low
nq pump can pump fluid from the suction side to the pressure side even if rotating in the wrong (turbine) direction.
The results representing the CFD data are marked with circles (
QED) and diamonds (
TED) in
Figure 10,
Figure 11 and
Figure 12 and were obtained by stationary calculations adding the head and efficiency shift stated in
Section 2.2. The numerical prediction of the hydraulic behavior in the pump quadrant shows an excellent correlation between the measurements and the numerical data. Since the pump brake quadrant is of minor importance, only a few operating points were simulated in this region. The numerical results show an acceptable agreement with the experimental data in this quadrant for both investigated pumps. The operating point at blocked impeller (
nED = 0, see zone 1 in
Figure 10,
Figure 11 and
Figure 12) was also captured with satisfactory accuracy by the stationary numerical approach for the variable pitch pump. There is a difference between experimental and numerical data of less than 7% in
QED. For the low
nq pump an under prediction of the discharge factor by less than 15% at this operating point is presented. Moreover, an underestimation of the torque factor is presented in all results. The origin can be found in an error in the pump head for the numerical results at
nED = 0. Thus the discharge factor
QED as well as the torque factor
TED are also affected (see Equations (3) and (5)).
In the turbine quadrant, there is also an adequate prediction of the pump behavior by stationary CFD calculations. The runaway point (
TED = 0, see zone 2 in
Figure 10,
Figure 11 and
Figure 12) was captured with an inaccuracy in
nED of 10% at –9° (see
Figure 11) and 4% for the low
nq pump (see
Figure 12) at this operating point. As for the 0° pitch angle, an instability region could be identified by the numerical approach. The CFD calculated turbine characteristic shows an incorrect location of the predicted instability compared to the experimental data as can be seen in zone 3 in
Figure 10. This results in an inadequate prediction of the turbine runaway point for this blade position. Fifteen-percent of difference between the measured and calculated data in
nED is presented at
TED = 0 for the 0° blade position. Towards the runaway point in the turbine brake region, the accuracy of the CFD-results compared to the experimental data deteriorates for both investigated pumps. It seems that the stationary numerical approach is no longer capable to simulate the flow inside the pump in this operating region.
5. Evaluation of the 4-Quadrant Behavior by Means of a 1D Transient System Analysis
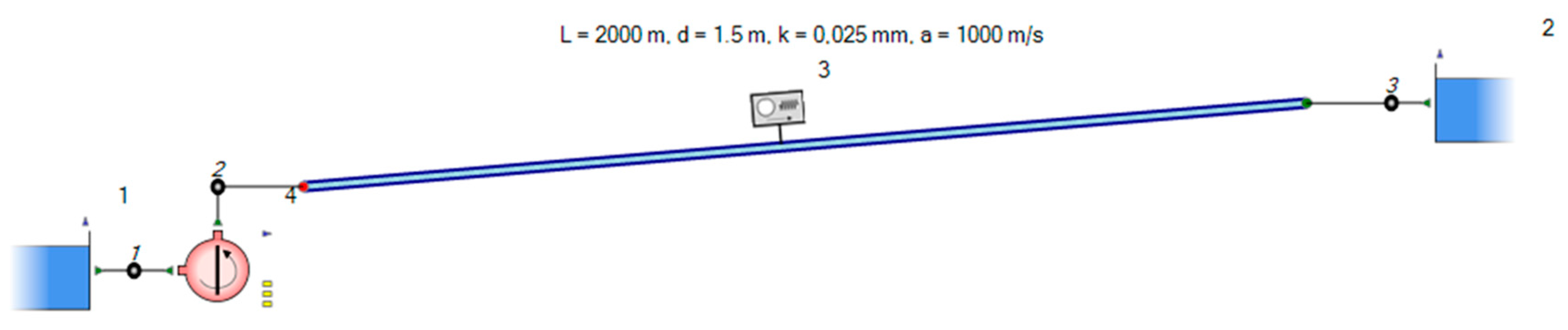
Finally, an exemplary numerical simulation (waterhammer analysis) of a simple hydraulic system according to
Figure 13 was carried out. The idea is to investigate the impact of the discrepancies between experimental and the numerically calculated 4-quadrant curves in case of a pump trip. The example of a hydraulic system consists of two reservoirs with a static head difference of 22 m. The variable pitch mixed flow pump operates at 507 rpm, has a BEP flow rate of 5 m
3/s, produces a head of 27 m at this flow rate and is located directly at the lower reservoir. The
nq = 36 pump runs at 300 rpm and delivers 2 m
3/s at a head of 27 m. A pipe of 2000 m in length and 1.5 m in diameter connects the pump and the upper reservoir. To model the pipe friction, an absolute wall roughness of 0.025 mm was used. No valves or other equipment is installed in this simple exemplary system. The method of characteristics (see [
7]) is used to solve the pipe transients. The wave propagation velocity inside the pipe is set to 1000 m/s and the inertia of the pump including its drive is 1000 kg·m
2 for both pumps investigated. The transient system calculations were carried out with the commercial 1D-CFD software Flowmaster V7 (Mentor Graphics Corp., Wilsonville, OR, USA) with tailor-made numerical models for the hydropower and pumping systems [
17,
18].
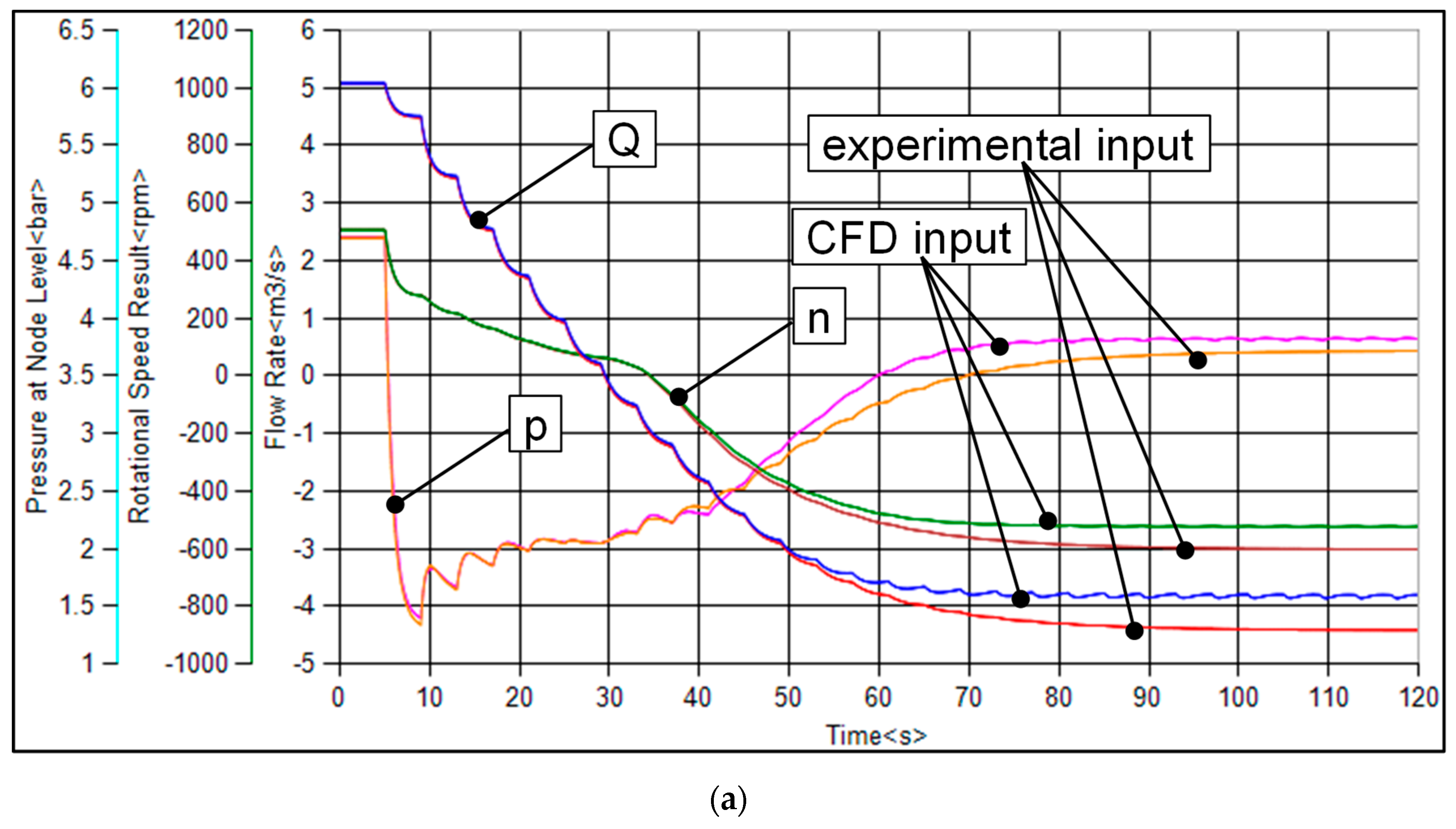
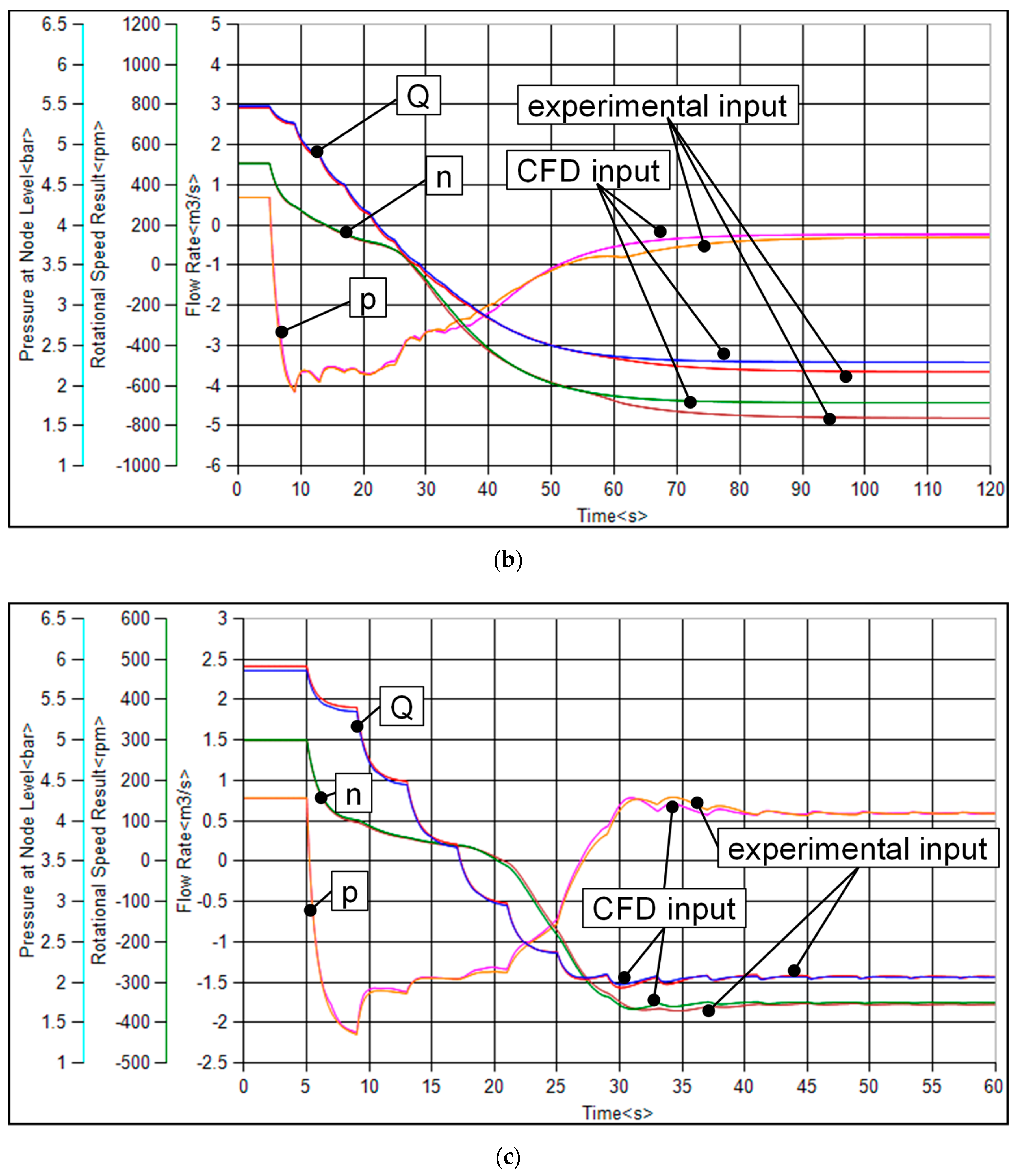
Figure 14 shows the results for a calculated pump trip after 5 s of stationary pump operation of the variable pitch pump with 0° pitch angle (a) and with −9° pitch angle (b) as well as for the low
nq pump (c). All diagrams give a comparison of the system transients for flow rate (
Q), pump rotational speed (
n) and the pressure at the pump outlet (
p) obtained with the experimental 4-quadrant curve and with the 4-quadrant behavior resulting from the CFD calculations according to
Figure 10,
Figure 11 and
Figure 12.
The decreasing rotational speed after the pump trip results in an immediate pressure drop on the pressure side of the pump for all investigated cases. Due to the inertia of the fluid mass inside the pipe, the flow rate decreases slowly compared to the rapid pressure drop after the pump trip.
As it can be seen, there is little difference between the results gained with the experimental input data and the numerically calculated 4-quadrant curves for both investigated pitch angles of the variable pitch pump. Especially for the low nq pump, there is almost no observable difference in the hydraulic transients between the presented results. After the pump changes its direction of rotation and the direction of flow changed as well, a steady state operation in the turbine runaway condition occurs. A slight difference in the runaway speed and flow rate is calculated with the CFD input data compared to the experimental input data for the variable pitch pump. This discrepancy is an effect of the inaccurate prediction of the pump behavior in the CFD calculations near the turbine runaway point (TED = 0).
6. Conclusions
This paper presents an approach to investigate the 4-quadrant behavior of a centrifugal pump by means of CFD calculation. With the help of stationary numerical simulations, good correlation between the numerically obtained pump characteristics and experimental data was found. Together with transient simulations, the accuracy of the numerical data could be increased further and the main instability in pump mode could be calculated in an even better way. The abnormal pump operation—like the pump brake or turbine operation—could also be predicted correctly with the help of stationary CFD calculations. Further transient calculations in this operating region would yield even higher accuracy in this very special pump operation zone, as it becomes interesting in the case of an emergency due to a pump trip. An exemplary transient system calculation proves that the numerically calculated 4-quadrant behavior leads to equally reliable results compared to an analysis with experimental 4-quadrant input data. It shows that the deviation of the numerical simulations from the test bench is fact, but in regions that are not included or from minor importance in the transient system calculations for various operating cases. A CFD calculation of the 4-quadrant characteristic is therefore a very practical and pragmatic approach, since the characteristic of the pump is reproduced with sufficient accuracy.
Author Contributions
Conceptualization, H.B.; Investigation, S.H.; Methodology, S.H.; Project administration, H.B.; Resources, S.H.; Software, S.H.; Supervision, H.J.; Validation, S.H.; Visualization, S.H.; Writing – original draft, S.H.; Writing – review & editing, H.B. and H.J.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | [m2] | Area |
| D | [m] | Diameter |
| E | [m2/s2] | specific Energy |
| H | [m] | Pump head |
| L | [m] | Length |
| Q | [m3/s] | Flow rate, discharge |
| T | [Nm] | Torque |
| cm | [m/s] | Meridional velocity |
| g | [m/s2] | Acceleration due to gravity |
| n | [rpm] | Rotational speed |
| nq | [rpm, m3/s, m] | Specific speed |
| p | [Pa] | Pressure |
| u | [m/s] | Circumferential velocity at reference diameter |
| z | [-] | Number of blades |
| φ | [-] | Flow coefficient |
| η | [-] | Efficiency |
| ρ | [kg/m3] | Density |
| ω | [1/s] | Angular velocity |
| ψ | [-] | Pressure number |
Subscripts and Superscripts
| BEP | Best efficiency point |
| Design | Design point of the pump |
| ED | normalized by specific energy and diameter |
| Ref | Reference |
| r, d | runner, diffuser |
References
- Gehrer, A.; Benigni, H.; Penninger, G. Dimensioning and Simulation of Process Pumps. In Pump Users Technical Forum; VDMA: Karlsruhe, Germany, 2004. [Google Scholar]
- Muggli, F.A.; Holbein, P.; Dupont, P. CFD calculation of a mixed flow pump characteristic from shutoff to maximum flow. ASME J. Fluids Eng. 2002, 124, 798–802. [Google Scholar] [CrossRef]
- Laux, C.H. Reverse-running pumps as energy recovery turbines. Sulzer Tech. Rev. 1982, 2, 23–27. [Google Scholar]
- Nautiyal, H.; Varun, A.K. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Torresi, M.; Fortunato, B.; Camporeale, S.M. Experimental investigation and performance prediction modeling of a single stage centrifugal pump operating as turbine. Energy Procedia 2010, 126, 589–596. [Google Scholar] [CrossRef]
- Knapp, R.T. Complete characteristics of centrifugal pumps and their use in the prediction of transient behavior. ASME Trans. 1937, 59, 683–689. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Stepanoff, A.J. Radial- und Axialpumpen; Springer: Berlin, Germany, 1959. [Google Scholar]
- Gros, L.; Couzinet, A.; Pierrat, D.; Landry, L. Complete pump characteristics and 4-Quadrant representation investigated by experimental numerical approaches. In Proceedings of the ASME-JSME-KSME 2011 Joint Fluids Engineering Conference, Hamamatsu, Japan, 24–29 July 2011. [Google Scholar]
- Couzinet, A.; Gros, L.; Pierrat, D. Characteristics of Centrifugal Pumps Working in Direct or Reverse Mode: Focus on the Unsteady Radial Thrust. Int. J. Rotat. Mach. 2013, 279049. [Google Scholar] [CrossRef]
- ISO. IEC 60193:1999—Hydraulic Turbines, Storage Pumps and Pump-Turbines—Model Acceptance Tests, 2nd ed.; International Electrotechnical Commission: Geneva, Switzerland, 1999. [Google Scholar]
- Höller, S.; Benigni, H.; Jaberg, H. Optimisation of a variable pitch mixed flow diffuser pump with numerical methods and test rig verification. In Proceedings of the Conference on Modelling Fluid Flow, CMFF’15, Budapest, Hungary, 1–4 September 2015. [Google Scholar]
- Höller, S.; Benigni, H.; Jaberg, H. Low specific speed mixed flow API pump for single and multistage usage—Multi-objective design challenge. In Proceedings of the 3rd International Rotating Equipment Conference (IREC), Düsseldorf, Germany, 14–15 September 2016. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. A Scale-Adaptive Simulation Model Using Two-Equation Models. AIAA J. 2005, 271–283. [Google Scholar]
- ISO. ISO 9906:2012—Rotodynamic Pumps—Hydraulic Performance Acceptance Tests—Grades 1, 2 and 3; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- Höller, S.; Jaberg, H. Ein Beitrag zur Druckstoßberechnung von Pumpspeicheranlagen. Wasserwirtschaft 2013, 103, 78–84. [Google Scholar] [CrossRef]
- Höller, S.; Jaberg, H.; Wittwer, B. Increasing Power Output and Flexibility of Kops I High Head Power Plant with the Help of Waterhammer Simulations. In Proceedings of the 20th International Seminar on Hydropower Plants, Vienna, Austria, 14–16 November 2018. [Google Scholar]
Figure 1.
Extended operating range of a semi-axial pump according to the IEC 60193 standard.
Figure 1.
Extended operating range of a semi-axial pump according to the IEC 60193 standard.
Figure 2.
Head curves and relative efficiencies for a variable pitch pump.
Figure 2.
Head curves and relative efficiencies for a variable pitch pump.
Figure 3.
Investigated low-nq pump: isometric view (a) and meridional view (b).
Figure 3.
Investigated low-nq pump: isometric view (a) and meridional view (b).
Figure 4.
Numerical model for the variable pitch pump (a) and the low nq pump (b).
Figure 4.
Numerical model for the variable pitch pump (a) and the low nq pump (b).
Figure 5.
Results for different grid sizes on head coefficient and normalized efficiency.
Figure 5.
Results for different grid sizes on head coefficient and normalized efficiency.
Figure 6.
Head history of unsteady simulations: variable pitch at pump −0.5° (a) low nq pump (b).
Figure 6.
Head history of unsteady simulations: variable pitch at pump −0.5° (a) low nq pump (b).
Figure 7.
Four-quadrant test rig with model pump installed.
Figure 7.
Four-quadrant test rig with model pump installed.
Figure 8.
Head curves for variable pitch pump at different positions, CFD (dashed) vs. test rig (solid).
Figure 8.
Head curves for variable pitch pump at different positions, CFD (dashed) vs. test rig (solid).
Figure 9.
Numerical (dashed) and test rig results (solid) for head and efficiency—low nq pump.
Figure 9.
Numerical (dashed) and test rig results (solid) for head and efficiency—low nq pump.
Figure 10.
Four-quadrant curves: numerical (markers) and experimental data (lines); variable pitch pump 0° blade position.
Figure 10.
Four-quadrant curves: numerical (markers) and experimental data (lines); variable pitch pump 0° blade position.
Figure 11.
Four-quadrant behavior: numerical (markers) and experimental data (lines); variable pitch pump −9° blade position.
Figure 11.
Four-quadrant behavior: numerical (markers) and experimental data (lines); variable pitch pump −9° blade position.
Figure 12.
Four-quadrant curves: numerical results (markers) and experimental data (lines); low nq pump.
Figure 12.
Four-quadrant curves: numerical results (markers) and experimental data (lines); low nq pump.
Figure 13.
Numerical model for the system analysis.
Figure 13.
Numerical model for the system analysis.
Figure 14.
Results of the waterhammer simulations for the variable pitch pump at 0° (a) and at −9° pitch angle (b) as well as for the low nq pump (c).
Figure 14.
Results of the waterhammer simulations for the variable pitch pump at 0° (a) and at −9° pitch angle (b) as well as for the low nq pump (c).
Table 1.
Mesh statistics for final simulations. a
Table 1.
Mesh statistics for final simulations. a
| | Variable Pitch Pump | Low nq Pump |
|---|
| Domain | Elements | Nodes | Elements | Nodes |
|---|
| Inflow | 183 | 191 | 296 | 286 |
| Impeller | 4438 | 4652 | 3727 | 3502 |
| Diffuser | 2547 | 2701 | 5473 | 5147 |
| Global | 7168 | 7544 | 9496 | 8935 |
Table 2.
Mesh statistics for grid dependency study a.
Table 2.
Mesh statistics for grid dependency study a.
| | Grid Small | Grid Medium | Grid Large | Grid Large_Fine |
|---|
| Domain | Elements | Nodes | Elements | Nodes | Elements | Nodes | Elements | Nodes |
|---|
| Inflow | 25 | 27 | 53 | 56 | 132 | 140 | 183 | 191 |
| Impeller | 22 | 25 | 212 | 226 | 511 | 538 | 740 | 775 |
| Diffuser | 19 | 22 | 125 | 136 | 215 | 231 | 364 | 385 |
| Global | 66 | 74 | 390 | 418 | 858 | 909 | 1287 | 1351 |
Table 3.
General computational fluid dynamics (CFD) settings.
Table 3.
General computational fluid dynamics (CFD) settings.
| Option | Stationary CFD | Transient CFD |
|---|
| Inlet BC | Mass Flow Rate | Mass Flow Rate |
| Outlet BC | Average Static Pressure | Average Static Pressure |
| Turbulence Model | SST | SAS-SST |
| Timestep | Iteration 1 to 25: 1/(ω·zr·zd) | revolution 1: 12/360·2π/ω |
| | Iteration 26 to 100: 1/(ω·zr) | revolution 2 to 6: 1/360·2π/ω |
| | Iteration 101 to 500: 1/ω | |
| Coefficient loops | - | 10 |
Table 4.
Measurement uncertainties.
Table 4.
Measurement uncertainties.
| Method/Type | Uncertainty |
|---|
| Flow rate | ±0.167% |
| Head | ±0.104% |
| Torque | ±0.101% |
| Speed | ±0.05% |
| Random error | ±0.15% |
| Total uncertainty | ±0.272% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).