1. Introduction and Literature Review
By now, the common understanding is that rotating stall as well as the resulting noise and vibration within a turbomachine is a dynamic effect. This means that frictional forces lead to boundary layer separation and eventually stall in rotating machines [
1,
2]. This understanding is recently confirmed by Cloos et al. [
3] both experimentally and analytically for the most generic machine, a flow through a coaxial rotating circular tube. According to Cloos et al. [
3],
wall stall—a term coined by Greitzer [
1] in contrast to
blade stall—is caused at part load by the interaction of axial boundary layer and swirl boundary layer flow, i.e., the influence of centrifugal force on axial momentum. For
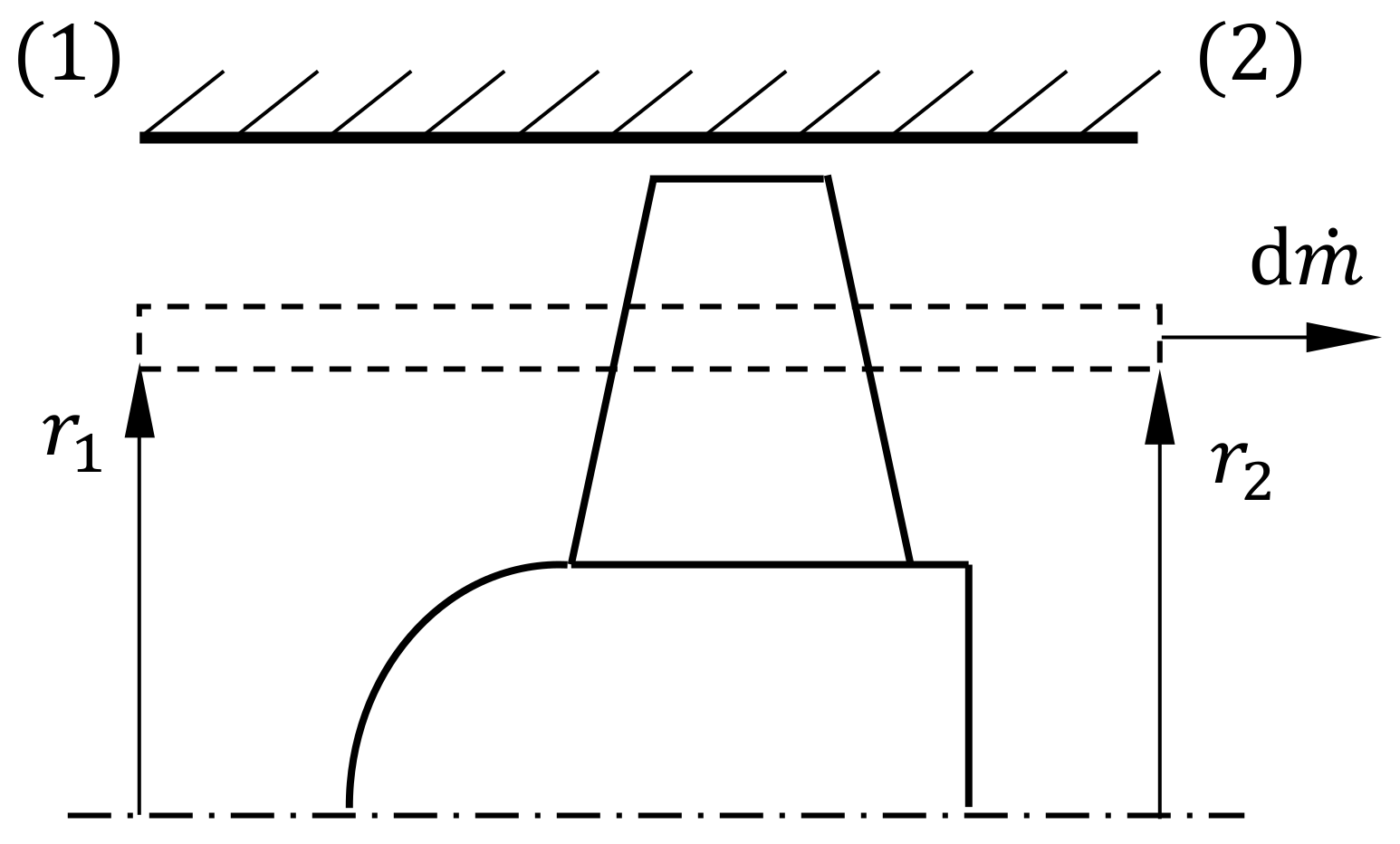
wall stall the axial velocity component
vanishes at the line
,
(axial coordinate in mean flow direction
z, distance
from the reference point on the line of symmetry
, radial coordinate
r and tube radius
a; cf.
Figure 1).
This paper analyzes the flow situation in encased axial turbomachines for small viscous friction. This work shows that
wall stall, i.e.,
can also be a result of kinematics only due to induced velocities of the vortex system superimposed with the axial main flow. The structure of the vortex system, especially the tip vortices, depends on the operating point of the turbomachine. Furthermore, the tip vortices rotate with a sub-synchronous frequency
(Karstadt et al. [
4] and Zhu [
5]). The aim of the present paper is to analyze the influence of the vortex system in encased axial turbomachines and its circulation strength on the observed phenomena yielding the research questions:
To answer these questions, this paper first employs vortex theory for an encased axial turbomachine followed by the application of fundamental solutions. For machines without casing such as wind turbines and screw propellers, vortex theory is well described by Betz [
6], Goldstein [
7], Glauert [
8] and van Kuik [
9]. The method is not yet developed in such a degree for encased turbomachines requiring the flow potential of a vortex ring inside a tube.
In addition, to enlarge the investigation on the whole operating range of a turbomachine, we investigate the structure and kinematics of the vortex system at heavy overload applying theory of functions (complex analysis). For turbomachines, the flow number
defines the operating point (e.g., part load or overload). The flow number is the ratio of axial free-stream velocity
U to the circumferential velocity
where
is the rotational speed (the scaling to
and not to
with the blade tip radius
b is common in the context of turbomachines and therefore used here as well [
10]).
For the nominal operating point and negligible induction, the vortex system of an encased axial turbomachine consists of a hub, Z bound and Z tip vortices, with Z the number of blades. The tip vortices transform into helices with a pitch of .
For part load operation
(see
Figure 1), the
Z helices “roll up” and form a vortex ring, i.e., the pitch of the helices vanishes. The vortex ring is continuously generated by the bound vortex system. Hence, the coaxial vortex ring strength is transient. A nice picture for this vortex ring is that of a thread spool rolling up and gaining strength over time. This picture explains some transient phenomena using kinematic arguments only.
The case of heavy overload occurs for infinitely high flow numbers
(see
Figure 2). The hub, the bound and the tip vortices form a horseshoe, i.e., the pitch of the helices becomes infinite. Both hub and tip vortices are semi-infinite, straight vortex filaments. In real turbomachines, the flow number cannot be adjusted to infinity but is limited to a maximum value
due to flow rate limitations and geometric restrictions. Nevertheless, the analysis of this limiting case is important for the basic understanding of the vortex system in axial turbomachines.
Investigations of vortex systems in fluid dynamics trace back to the work of Helmholtz [
11] who formulated the Helmholtz’s theorems as a basis for the research concerning rotational fluid motion.
Didden [
12] performed measurements of the rolling-up process of vortex rings and compared the results with similarity laws for the rolling-up of vortex sheets.
Besides the investigation of vortex kinematics, a broad research field on vortex structures in turbomachines is the experimental and numerical analysis of acoustic and noise emission of tip vortices [
13,
14,
15,
16]. The noise of a fan is noticeable by a CPU, car or a rail vehicle cooler. All three examples are met in everyday life. One of the main reasons for the noise is the gap
between the housing and the impeller tip. With increasing gap the noise emission and the energy dissipation increase [
17,
18]. Karstadt et al. [
19] and Zhu [
5] investigated noise and dissipation due to tip vortices.
The kinematics for an encased axial turbomachine operating at part load or overload are not fully understood yet. Especially the basic kinematics of these phenomena are not sufficiently analyzed.
To develop physical understanding of the whole picture in detail, the paper is organized as follows.
Section 2 uses vortex theory to determine the strength of the vortices. Subsequently,
Section 3 derives the velocity potential of a coaxial vortex ring within a circular tube at part load and the induced rotating frequency. The flow potential and the induction at overload is introduced in
Section 4. The paper closes with a short outlook to potential applications in
Section 5 and a discussion in
Section 6.
2. Vortex Theory
An encased axial turbomachine with
Z impellers is considered. The sketched vortex system (see
Figure 1 and
Figure 2) results from the
Z bound vortices. The generation of a bound vortex was explained by Prandtl [
20] using arguments of boundary layer theory and Kelvin’s circulation theorem. The presence of viscosity is essential for the creation of the bound vortex but the generation phase is not in the scope of this paper. For vortex generation, we would like to refer the reader to the work of Prandtl [
20].
By vortex theory, each blade
of length
b is represented by its bound vortex of strength
. For simplicity, this investigation assumes
to be constant in radial direction along the blade from
to
. As a vortex filament cannot end in a fluid due to Helmholtz’s vortex theorem, a free, trailing vortex springs at each blade end
and
(see
Figure 1 and
Figure 2). These vortices are of the same strength as the bound vortex. At the inner end
, a straight semi-infinite vortex line
of strength
—the so-called hub vortex—attaches to the blade. The tip vortices at the outer end
are helices. The axial distance of the each helix winding, i.e., the helix pitch, is given by
. Depending on the load, these helices either “wind up”
forming a vortex ring or stretch to infinity
yielding a straight, semi-infinite vortex line.
Regardless of the flow number , the semi-infinite straight vortex line at induces the circumferential velocity at due to the Biot–Savart law. Hence, the induced rotational speed is .
In a next step, this analysis calculates the vortex strength
employing the angular momentum equation and the energy equation. On the one hand, the axial component of the angular momentum equation is
. Here,
M is the axial torque component applied by the turbomachine to the fluid and
the mass flux. A more detailed explanation is given in
Appendix A. Multiplying the momentum equation by
yields
.
is the power applied to the fluid by means of the rotating bound vortices. On the other hand, the energy equation for an adiabatic flow reads
, with
being the difference in total enthalpy experienced by a fluid particle passing the cross-section
. Both arguments result in the relation
.
From turbomachine theory, the expression
can be derived from the equation mentioned above. The dimensionless design parameter
equals the tangent of the blade’s trailing edge angle
, i.e.,
. Hence, the relation between
and
yields
As Equation (
1) shows, the total change in circulation
along the plane of the machine is linked to the flow number
by Euler’s turbine equation.
3. The Vortex System at Heavy Part Load
For the limiting case of interest
, the relation between
and
, Equation (
1), yields
. This results in an induced sub-synchronous frequency
Here, the calculation neglects the self-induction of the vortex ring. This idealization is to some extent inconsistent but allows obtaining a simple solution for the kinematics of an encased axial turbomachine.
The induced frequency, Equation (
2), is in surprisingly good agreement with measured sub-synchronous frequencies
of rotating stall of compressors, fans and pumps at part load operation [
10] and may result in a rethinking of rotating stall from a kinematic perspective.
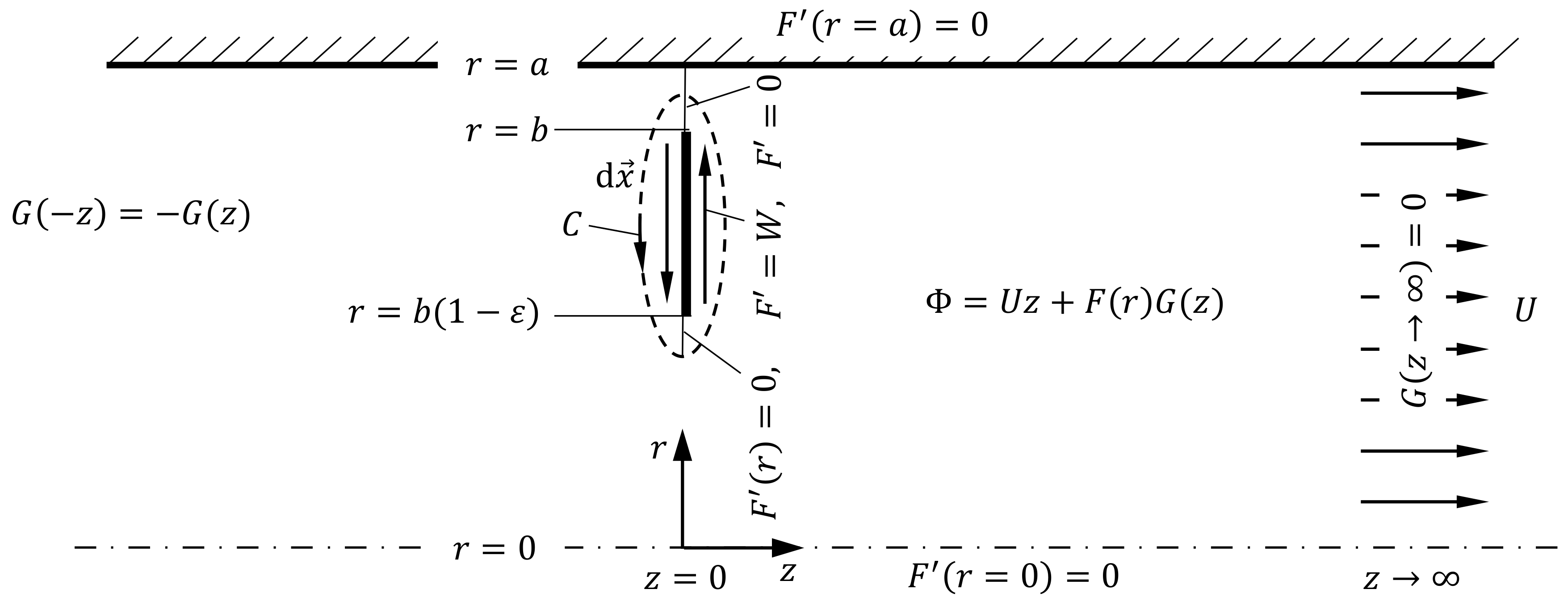
This investigation is now set to analyze the kinematics of coaxial vortex rings of radius
b and maximal strength
, with time
t, as sketched in
Figure 1. By doing so, Laplace’s equation
for the velocity potential
, with
, is solved for an incompressible, axisymmetric flow. The velocity potential for a coaxial ring filament in a circular tube yields
with
the Bessel function of orders 0 and 1, respectively, and
the zeros
of the function
.
Appendix B gives a more detailed derivation for this result. The dimensionless velocity potential
depends on the dimensionless ring radius
and the dimensionless vortex strength
. Since
increases linearly in time,
can also be interpreted as a parametric time of the process.
Stokes stream function for this flow is (using the integrability conditions
and
)
With the stream function, the radial velocity component
and the axial velocity component
are given. The velocity field (Equations (
6) and (
7)) takes the induction of the vortex ring into account. At the stagnation point
, the axial velocity
vanishes for
Equation (
8) is implicit for the stagnation point
.
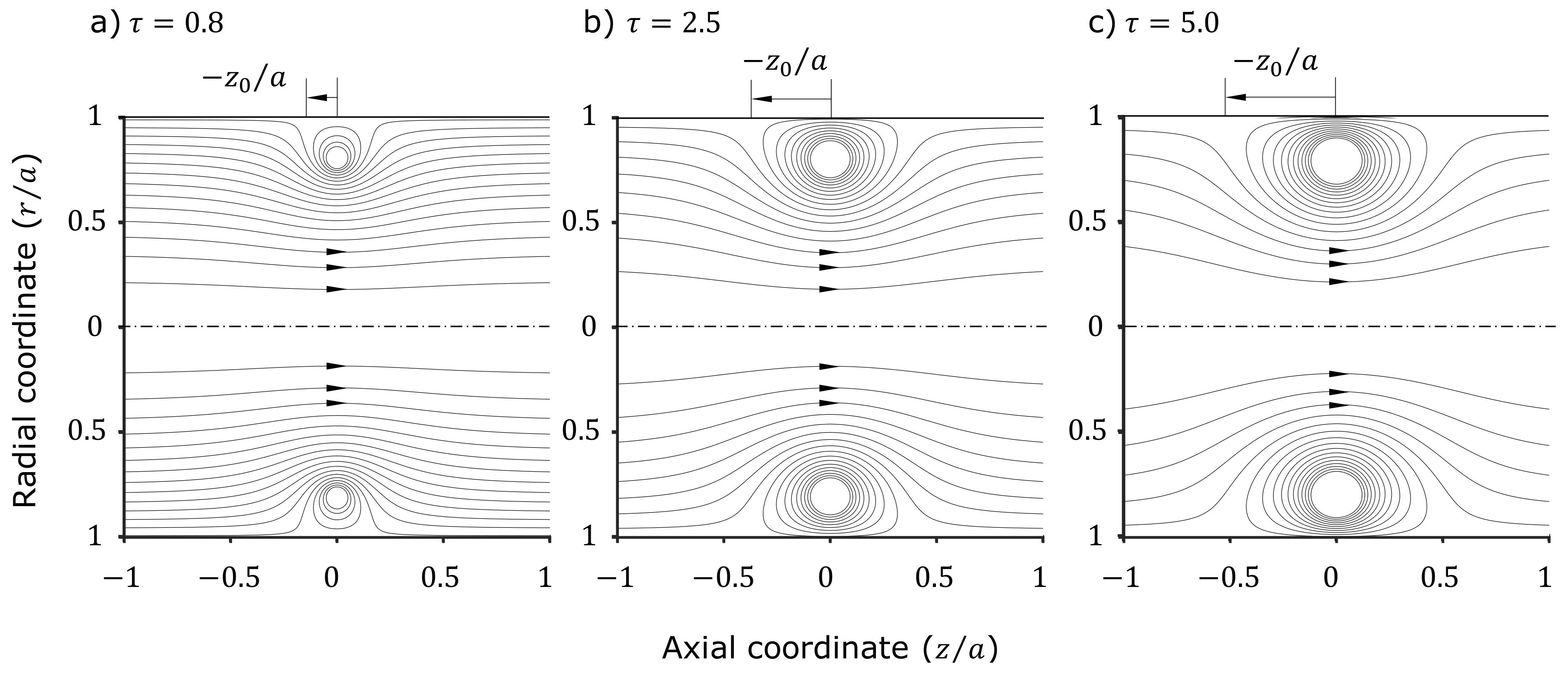
Figure 3 shows Stokes stream function and the stagnation points at
for different circulation strengths
of the vortex for
. With increasing
, the stagnation point
moves away from the plane of the turbomachine
. This is because the induced velocity of the vortex ring increases with respect to the free-stream velocity. Hence, the limiting case
represents an undisturbed flow through a rigid pipe without vortices. For the limiting case
, the free-stream velocity disappears and only the two vortices at
would be visible.
4. The Vortex System at Heavy Overload
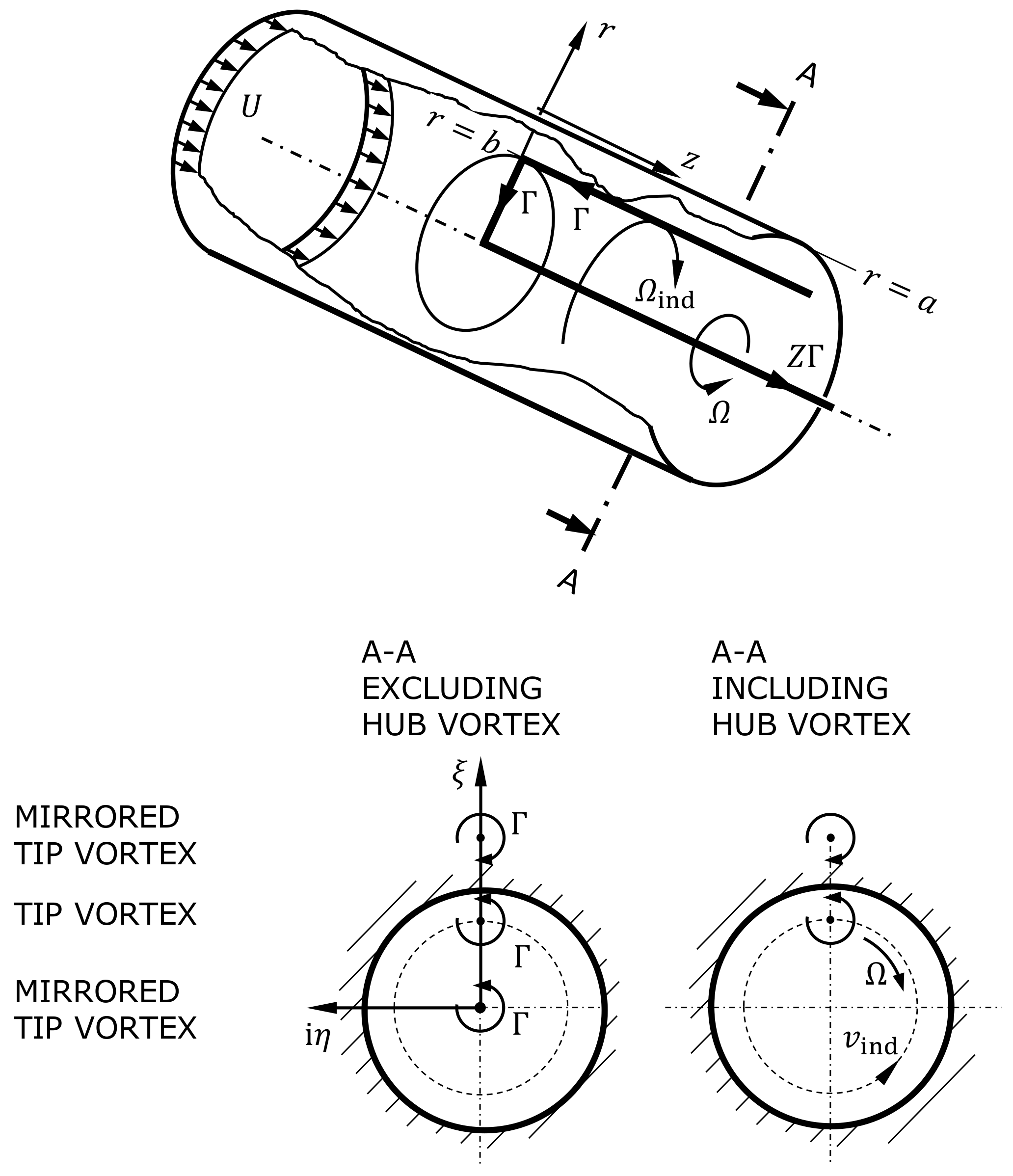
Figure 4 visualizes the vortex system of an axial turbomachine composed of
impeller blade at heavy overload
(
is chosen to improve clarity only). For this limiting case, the flow at cross section A-A far downstream of the machine is a plane potential flow. It can be described using theory of functions (complex analysis) [
21]. Mirrored tip vortices are necessary to fulfill the kinematic boundary condition on the tube wall. These mirrored vortices are located in the housing and on the rotational axis of the turbomachine. Considering the tip vortex and its mirrored conjugates only, i.e., neglecting the hub vortex as a first step, one obtains the system visualized in
Figure 4, bottom left. The vortex on the axis and the hub vortex feature identical magnitude but opposing rotating directions. Adding the hub vortex yielding the complete system hence results in the annulation of these two vortices (see
Figure 4, bottom right).
In the following notation, the complex coordinates are composed of a real part and an imaginary part , with . The complex potential is divided into the real part, which is the velocity potential and the imaginary part which is the stream function . is the complex conjugate of F.
For the considered potential flow, the tip vortex at radial position
yields the complex potential
Here,
s is the dimensionless gap. The Milne–Thomson circle theorem [
22] is applied to derive the complex potential satisfying the kinematic boundary condition at the wall. This theorem postulates a resulting complex potential
for a potential
and the mirrored potential at the surrounding wall. Adding the potential of the mirrored tip vortex on the axis of the turbomachine
(see
Figure 4, bottom right), yields for the complex flow potential
The tip vortex at
with the circulation
necessitates a mirrored vortex at
with the same magnitude of circulation and a mirrored vortex in the housing at
with the same magnitude and inverted direction. Up to now, the hub vortex is excluded from the considerations. Considering the hub vortex as visualized in
Figure 4, bottom right yields for the complex potential
In the following, this analysis shows that an induced movement of the gap vortex occurs against the rotating direction of the turbomachine at heavy overload. A potential vortex induces a velocity on the surrounding flow. The velocity components of a given potential
are calculated by
A straight vortex filament does not induce a velocity on its own due to the Biot–Savart law so the induced velocity at
is only due to the mirrored tip vortex at
. The resulting induced velocity at the position of the tip vortex yields
Assuming a turbomachine with
Z impeller blades, the rotating velocity of the tip vortex is
This is the rotating direction against the rotating direction of the turbomachine. For symmetry reasons, the rotating trajectory defines a circular path at radius
. Hence, the induced frequency at
is
For high flow number
and small gap
, the induced frequency yields
against the rotating direction of the turbomachine.
5. Application for Acoustical Investigations
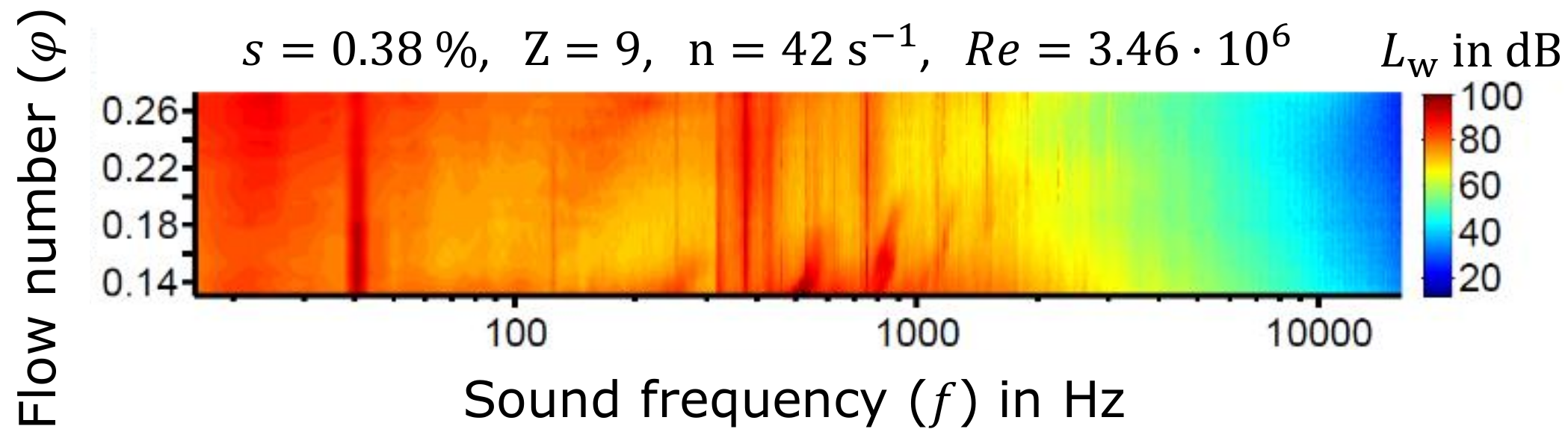
Previous investigations by Karstadt et al. [
4] analyzed the tip clearance noise in axial turbomachines.
Figure 5 shows the frequency spectra over the complete operating range. Remarkable are the peaks at 42 Hz and 375 Hz, which correspond to the rotational speed
n and the blade passing frequency
. Fukano and Yang [
16] showed that the circumferential frequency of the tip clearance noise shifts to lower values with increasing tip clearance
s and decreasing flow number
due to the larger extent of the gap vortex. The present paper investigates the frequency of the tip clearance noise depending on the operating point applying analytical methods. At heavy part load, Equation (
2) indicates that an induced frequency at half the rotation speed of the turbomachine should appear. This frequency was also observed by Karstadt et al. [
4] as
Figure 5 shows a high intensity in the region of 0–50
. Equation (
17) indicates that for heavy overload the induced frequency will increase with decreasing tip clearance. Furthermore, we expect a noise of high frequency due to the small value of
which is common for turbomachines. The broadband drop in the sound power for all flow numbers is clearly visible.
Müller [
23] applied the continuity and the momentum equation and deduced that sound inside a fluid volume is only emitted if the rotation of the velocity field changes in time. The present study applies a similar approach to analyze the tip clearance noise of a turbomachine. Time-consuming simulations as performed by Carolus et al. [
24] surely allow a more profound and accurate insight into the acoustics of turbomachines. The development of an analytical model which predicts main frequencies is yet interesting to generate a deeper understanding of the acoustics in turbomachines.
These findings and the presented analytical model in this paper could be an efficient tool for acoustic design of turbomachines. This is because this analysis separates kinematic and dynamic effects. Up to now, this is not possible for computational fluid dynamics (CFD) calculations. Separating different effects generates a deeper understanding of the underlying physics and allows realizing particularly focused investigations.
6. Summary and Conclusions
An interplay between dynamic and kinematic effects explains flow structures and phenomena. Using computational fluid dynamics, a clear distinction of both effects is often impossible. In contrast, analytical methods allow a more focused picture of fluid mechanics, i.e., they allow a clear distinction of effects. Of course, only generic flows are accessible to analytical methods.
This paper focuses on an analytic model for wall stall so far being explained by dynamics only: boundary layer separation is indeed a dynamic effect. Nevertheless, boundary layer separation is not necessarily the only reason for wall stall. It is shown that kinematics may also explain at least some effects of wall and rotating stall. The used picture for a flow at small flow numbers is a thread spool rolling up the tip vortices resulting from rotating bound vortices. From the fluid mechanics perspective, the thread spool is a coaxial vortex ring of increasing strength connected to a semi-infinite hub vortex (
Figure 1).
Thus far, the velocity potential of a coaxial vortex ring inside a tube was unknown. The solution of Laplace’s equation results in the velocity potential for the vortex filament within a tube (see Equation (
4)).
This study gained three main results, which are due to kinematics only. First, at part load operation the hub vortex induces a sub-synchronous rotation of the vortex ring. The derived rotational speed
of the vortex ring is surprisingly consistent with observed sub-synchronous speeds of rotating stall (cf. [
10]). Second, the vortex ring induces an upstream axial velocity at the wall. Together with the undisturbed flow velocity, this results in a stagnation point upstream and downstream at the wall which may be interpreted as
wall stall (
Figure 3). Third, at overload operation, the induced rotational direction is inverted to the case at part load. The semi-infinite straight vortex filament at the outer blade end rotates against the rotating direction of the turbomachine due to the induction of the hub vortex. The induced frequency yields
.
The presented analytical model may give new arguments and improves the understanding of the vortex system in turbomachines but is also intended to motivate generic experiments. Hence, a test rig will validate the models presented in this paper in the near future.
As a next step, the velocity potential for a coaxial vortex ring filament in a circular tube (Equation (
4)) will be extended to a coaxial vortex layer, yielding a transient behavior of the vortex system. This behavior leads to a change in the circulation over time being responsible for noise emission [
23].