Influence of Pressure Fluctuations on the Mean Value of Different Pneumatic Probes

Abstract

For this study, measurements were carried out in a one-and-a-half stage test turbine. In order to characterize the flow field and to obtain steady flow quantities, five-hole probes are used in the rig in several measurement planes. Although a very high resolution in circumferential and radial direction is possible with five-hole probes, only certain sectors of the flow field can be measured due to quite long measurement times. For this reason, total pressure rakes, which can be traversed 360 degrees in a circumferential direction, were built for this test configuration. During foregoing measurements, differences between the total pressure measured with the rakes and the total pressure measured with a five-hole probes were observed, especially in the measurement plane downstream of the rotor where the flow is highly unsteady. It was found that the measured value for total pressure is particularly influenced by the stochastic pressure fluctuations and turbulence and can therefore deviate significantly from the “real” value.

1. Introduction

For the aerodynamic evaluation of newly designed engine parts as well as the validation of the Computational Fluid Dynamics (CFD) code, rig tests are essential and necessary. Several different probes and measurement devices are used in order to characterize and quantify the flow field. For the determination of steady flow quantities, five-hole probes (5HP) were used during the current measurement campaign. The used 5HP was further equipped with a thermocouple close to the probe head. Based on the five measured pressures, the measured temperature and an appropriate calibration, these probes can be used to determine static and total pressure as well as the flow angles, Mach number and temperature. With five-hole probes, a very high resolution in circumferential and radial direction is possible, but due to quite long measurement times and geometrical constraints at the test facility, only certain sectors of the flow field can be measured during one test run. This is why total pressure and total temperature rakes were built, including several radial measurement positions with a circular Kielhead at each position. Compared to a pneumatic probe, the measurement grid for the rakes is significantly coarser, but due to their smaller design and the shorter measurement time (measurements at several radial positions at the same time; with a probe each radial position has to be measured separately), they can be used for 360 degree traverses. This allows the characterization of the whole flow channel, not only of a limited sector. During foregoing measurements, differences between the total pressure measured with the rakes and the total pressure measured with a five-hole probe were observed, especially in the measurement plane downstream of the rotor where the flow is highly unsteady. This leads to the assumption that, particularly in fluctuating flows, the amplitude as well as the frequency of the pressure fluctuations have an influence on the average pressure values, which are measured by five-hole probes and rakes. Weyer [1], who investigated unsteady flows in transonic compressors, also made similar findings. During his studies, he confirmed his assumption that the measured average values can deviate significantly from the true average value, depending on the pressure amplitude, the time variation of the pressure and the shape of the measurement boring. Therefore, measurements were carried out using rakes, five-hole probes and a Fast Response Aerodynamic Pressure Probe (FRAPP) at three different operating points, where different pressure amplitudes were expected. In order to eliminate the influence of a day-to-day variation of the operating point, all of the measurements were carried out during the same test run, at the same circumferential position and for the same radial positions. While rakes and five-hole probes were used for the determination of the average total pressure, the FRAPP was used to measure the time resolved total pressure and therefore the amplitude of the pressure fluctuations. In addition, the stochastic pressure fluctuations were determined based on the unsteady pressure measurements in order to get an idea on how unsteadiness may influence the measurement results.

Li and Bohn [2] investigated the influence of dynamic effects on flow measurements numerically regarding a three-hole probe. The authors determined, amongst others, calibration coefficients using the quasi-steady and the unsteady numerical results and found significant differences between steady and unsteady calibrations coefficients. This leads to the assumption that a steady probe calibration is not valid anymore if the flow under investigation is highly unsteady. Sieverding et al. [3] stated that many dynamic phenomena could influence the probe response depending on the geometry of the probe head. For cylindrical or spherical probe heads, for example, inertia effects can have a significant influence and should be considered for a correct representation of time varying pressure. To sum up, it can be said that some studies dealing with the influence of unsteady flow on steady probe measurements were already carried out in the past, but still no general approach for measurements in highly fluctuating flows could be given. This makes it necessary to get a deeper insight into this topic, especially when regarding pneumatic probe measurements in complex test rigs where highly unsteady flow phenomena occur. Up to now, cylindrical as well as spherical or wedge probes were investigated, but nearly no studies dealt with Kielhead rakes and the comparison with 5HP results as well as unsteady pressure measurements.

2. Experimental Setup

The regarded one-and-a-half stage test turbine is located at the Institute for Thermal Turbomachinery and Machine Dynamics at Graz University of Technology, Graz, Austria. The flow path of this test rig consists of a high-pressure turbine stage followed by an S-shaped intermediate turbine duct (ITD) and a low-pressure vane row. The air leaves the rig downstream of two outlet guide vane rows (OGV). The aerodynamic measurements presented in this paper were taken downstream of the high pressure (HP) stage (plane B, see Figure 1) under engine relevant conditions at different operating points. This facility is a continuously operating rig, which is used in open circuit operation mode. The rig is driven by pressurized air delivered by a 3 MW electrically driven compressor station, which is placed in the second basement of the institute. The power output of the HP rotor is used to drive a three-stage radial brake compressor delivering additional air. The two mass flows, one originating from the compressor station and one from the brake compressor, are merged in a complex system consisting of a mixer and a tandem cascade at the inlet of a mixing chamber. Therefore, the overall mass flow can be increased. The inlet temperature of the rig can be adjusted between 40 °C and 185 °C by cooling the air coming from the compressor station. However, the mass flow, which is delivered by the brake compressor, cannot be cooled. With the two air flows, an overall mass flow of up to 22 kg/s can be achieved. Due to the design of the mixing chamber, the inlet pressure is limited to 4.5 bar absolute. The maximum shaft speed of the HP rotor is limited to 11,500 rpm. Figure 1 shows a schematic cross-section of the transonic test turbine facility.

Operating Conditions

The measurements with five-hole probe, FRAPP and rakes were carried out at three different operating points, which can be found in

Table 1. Operating Conditions of the Three Different Operating Points.

	Low OP	ADP	High OP
Rotational Speed [rpm]	4840	9710	10,390
Mass Flow [kg/s]	10.7	14.2	16.5
Pressure Ratio [-]	1.33	2.83	3.28

OP: operating point; ADP: aero design point.

. For the lower operating point, the rotational speed as well as the pressure ratio of the HP stage was reduced compared to the aero design point (ADP). Lower turbulence and lower pressure fluctuations were expected for this condition. For the higher operating point (OP) with higher rotational speed of the HP rotor and a higher pressure ratio, the turbulence and fluctuations were expected to increase. These expectations were proven during the measurements (see Figure 2). More details on the operation of the test rig can be found in Hubinka et al. [4].

3. Measurement Technique

3.1. Total Pressure and Total Temperature Rakes

For this measurement campaign, total pressure and total temperature rakes were designed and 3D laser-sintered, which is a very new manufacturing technique for measurement probes. In order to prevent the rakes from corrosion and to guarantee sufficient stability, the rakes were made of stainless steel. For each rake, a leak test was carried out after the instrumentation and no leakages could be found. The measurement points at several radial positions are each located in the center of a Kielhead. The rakes were calibrated for several yaw and pitch angles at different Mach numbers, and, as the whole rake was located in the calibration channel, the same conditions (including for example the effect of the stem) as in the test rig. Due to the new manufacturing method, each Kielhead could be easily aligned to the flow in terms of yaw as well as pitch angle. Preceding CFD calculations were the base for the design of the rakes and the orientation of the Kielheads. Other advantages of 3D printing as a production technology for probes and rakes are the high accuracy concerning the dimensions and the fact that it is a very fast manufacturing method. The short measurement time and the compact design of the rakes make it in principle possible to traverse them over 360 degrees and catch the flow field in the whole annular channel. Besides the rakes, the measurement system includes 15 multi-channel pressure transducers PSI 9016 (Pressure Systems, Hampton, VA, USA) with a total amount of 240 channels and an accuracy of 0.05% full scale and four National Instruments (NI, Austin, TX, USA) Field Point FP TC-120 eight-channel thermocouple input modules as well as a National Instruments cRIO 9067 system with two NI 9214 thermocouple input modules.

3.2. Five-Hole Probe

Parts of the measurement campaign were carried out with a five-hole probe, which was manufactured and calibrated at the Institute for Jet Propulsion and Turbomachinery of the Rheinisch-Westfälische Technische Hochschule (RWTH) Aachen, Germany. One radial line was measured in the plane downstream of the HP stage (plane B in Figure 1). Using a traverse system with two stepping motors, the probe was moved radially and then turned into the flow. This was done in order to guarantee highest accuracy and to ensure to always be within the calibration range of the probe concerning the yaw agle. The used 5HP is calibrated for Mach numbers between 0.2 and 0.8, yaw angles between −20 deg and +20 deg and pitch angles between −16 deg and +20 deg. The correlation between the calibration characteristic and the flow variable to be measured is given by a multi-parameter approximation.

Table 2. Measurement Uncertainties of the Five-hole Probe (5HP).

Parameters	Units	Max	Min
Mach number Ma	[-]	0.005	−0.004
Yaw angle α	[deg]	0.3	−0.3
Pitch angle γ	[deg]	0.5	−0.4
Total pressure pt	[mbar]	3	−3
Static pressure p	[mbar]	5.4	−5.1
Total temperature Tt	[K]	0.6	−0.5
Static temperature T	[K]	0.7	−0.8

shows the measurement uncertainties for the five-hole probe measurements. These values contain the errors due to the approximation and the systematic errors of the PSI modules (see section about total pressure rakes).

3.3. Fast Response Aerodynamic Pressure Probe

Unsteady flow measurements were performed by means of a cylindrical single-sensor FRAPP, operated as a virtual three sensor probe for 2D aerodynamic measurements. Since the three rotational positions are measured at different times, the measurements have to be phase-resolved by means of a phase-locked flow reconstruction. To be able to do this, a trigger signal is acquired with each revolution of the rotor in order to determine the beginning as well as the end of a rotor revolution. A miniaturized piezo-resistive pressure sensor (Kulite XCE-062, Leonia, NJ, USA) is mounted inside the probe head, which has an outer diameter of 1.85 mm. The probe aerodynamic accuracy was evaluated in a calibrated nozzle, giving an extended uncertainty equal to ±0.5% of the kinetic head for the pressure measurements and equal to ±0.3 deg for the flow angle. In order to obtain the transfer function of the probe, a dynamic calibration was carried out in a low-pressure shock tube and, after digital compensation, the probe bandwidth reaches up to 80 kHz. Before digital compensation, the bandwidth is linear in the range from 0 to 20 kHz. In their work, Persico et al. [5] present more about the probe design and calibration.

4. Numerical Setup

In addition to the measurements, a steady state calculation using Ansys^® CFX v16.2 (Canonsburg, PA, USA) was carried out. As a turbulence model, a k-ω-SST (Shear Stress Transport) model with fully turbulent flow was used. The number of elements is approximately 1.5 million with tetrahedral shapes. This number was chosen based on a mesh independence study and being a compromise between resolution and calculation time. In general, CFX uses automatic wall functions with y⁺ ≈ 30 close to the Kielhead surface. While the total pressure rake used in the test rig consists of five radial measurement positions, just one Kielhead and the shaft of the rake were meshed and used for the calculation. This was done in order to remove the possible influence of adjacent Kielheads, as just the impact of turbulence levels on the numerical results was supposed to be evaluated. The dimensions of the Kielhead are exactly the same as for the real pressure rake and the Kielhead was placed in a cylindrical flow channel with a diameter significantly larger than the rake dimensions in order to eliminate any influence of the channel walls.

The goal of these numerical investigations was a variation of turbulence at the inlet plane in order to determine a possible change in total pressure or flow phenomena at the Kielhead inlet due to different turbulence levels.

5. Methods

5.1. Determination of Stochastic Pressure Fluctuations

For the determination of the stochastic pressure fluctuations using a FRAPP, the method of Fourier filtering is adopted as previously described by Lengani et al. [6,7] and Camp and Shin [8]. The post processing tool for FRAPP data is based on the triple decomposition of the measured value (see Equation (1)), which is the total pressure in this case. The measured value is composed of the time average, the periodic fluctuations and the stochastic fluctuations:

$$p\left(t\right)=\overline{p\left(t\right)}+\langle p\left(t\right)\rangle +p^{\prime }\left(t\right).$$

(1)

In order to determine the stochastic fluctuations, the periodic part of the signal, as well as the time average, have to be removed from the signal. Therefore, Fast Fourier Transformations (FFTs) are performed over a sufficiently high number of samples to reach a good frequency resolution. As no trigger signal and no averaging procedure is applied to these FFTs, the spectrum shows peaks at the blade passing frequencies (BPF) of the two rotors and their linear combinations. These amplitudes are set to zero in order to remove the deterministic periodic components of the signal. The time average is removed by setting the amplitude at a frequency of 0 Hz to zero. The new spectrum is then transformed back into the time domain, and the received data just shows the stochastic part of the signal without any periodic component. The results are therefore the time resolved stochastic fluctuations of the total pressure $p_t^{\prime }\left(t\right)$. At the BPFs, it is not possible to distinguish between the deterministic and the stochastic part of the peak. Since the whole peak is set to zero, including also the stochastic part, a small mistake is made at these certain frequencies, and the turbulence intensity based on stochastic pressure fluctuations is underestimated.

5.2. Total Pressure Coefficient

In this paper, no absolute values for total pressure are shown, except for the total pressure coefficient. For the calculation, the following formula was used, whereas $p_t$ is the local total pressure, $\overline{p_{t,ref}}$ and $\overline{p_{ref}}$ the mass-averaged total and the area-averaged static pressure in the reference plane. In this case, plane B—the plane downstream of the rotor—was used as a reference plane. The reference values were taken from 5HP measurements at ADP:

$$C_{pt}=\frac{p_t-\overline{p_{t,ref}}}{\overline{p_{t,ref}}-\overline{p_{ref}}} [-].$$

(2)

5.3. Percentage Fluctuation

The pressure fluctuations are given as percentage of the $p_{t,RMS}$ value referred to the mass-averaged total pressure in the regarded measurement plane B:

$$PF=\frac{p_{t,RMS}}{\overline{p_{t,ref}}}·100 [\%].$$

(3)

6. Results and Discussion

During several foregoing measurement campaigns, deviations between results of 5HP and total pressure rakes could be observed, especially in the measurement plane downstream of an HP rotor. For this reason, measurements were carried out using a 5HP, a total pressure rake and a FRAPP to be able to get a deeper insight into the reasons for these deviations. All of the measurements were performed during one test run at the same circumferential and the same radial measurement positions. 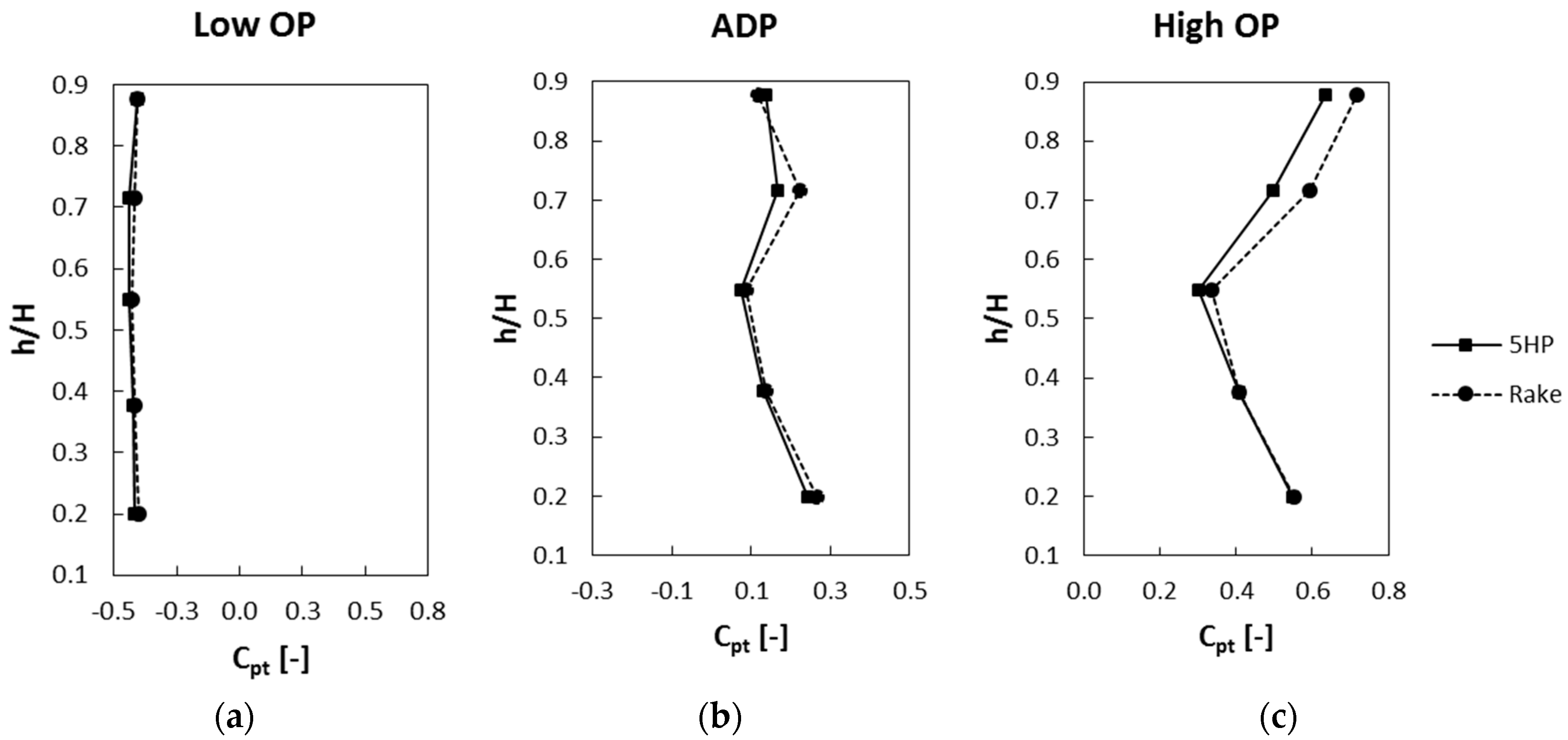Figure 2 shows the comparison of the total pressure coefficient between 5HP and rakes for three different operating points, which were already described in the Section 2.1. On the one hand, it can be seen that the pressure level increases significantly when going from the lowest to the highest operating point. On the other hand, the difference between 5HP and rake results also gets considerably larger, especially for the measurement points in the upper half of the flow channel. While 5HP and rakes show identical results for the lowest operating point, the two measurement techniques start to deviate from each other with increasing mass flow, pressure ratio (PR) and rotational speed. To make this even clearer, the same scaling was used for the abscissa in all three diagrams. In the following, every radial measurement point got a name starting with measurement point (MP) 1 at the inner channel wall and ending with MP 5 at the outer channel wall.

In their von Karman Institute (VKI) Lecture Series, Arts et al. [9] already discussed several parameters that can have an influence on the readings of a Pitot probe. Therefore, the following parameters were investigated:

• Amplitude and frequency of time resolved periodic pressure fluctuations;
• Reynolds number;
• Velocity gradient and wall proximity effects;
• Stochastic pressure fluctuations/turbulence intensity.

This was also done in order to make sure that the deviations in total pressure distribution between different pneumatic probes really originate from high amplitudes of stochastic fluctuations and high turbulence (as assumed a priori), respectively, and that the results are not dominated by the influence of other parameters.

6.1. Amplitude and Frequency of Pressure Fluctuations

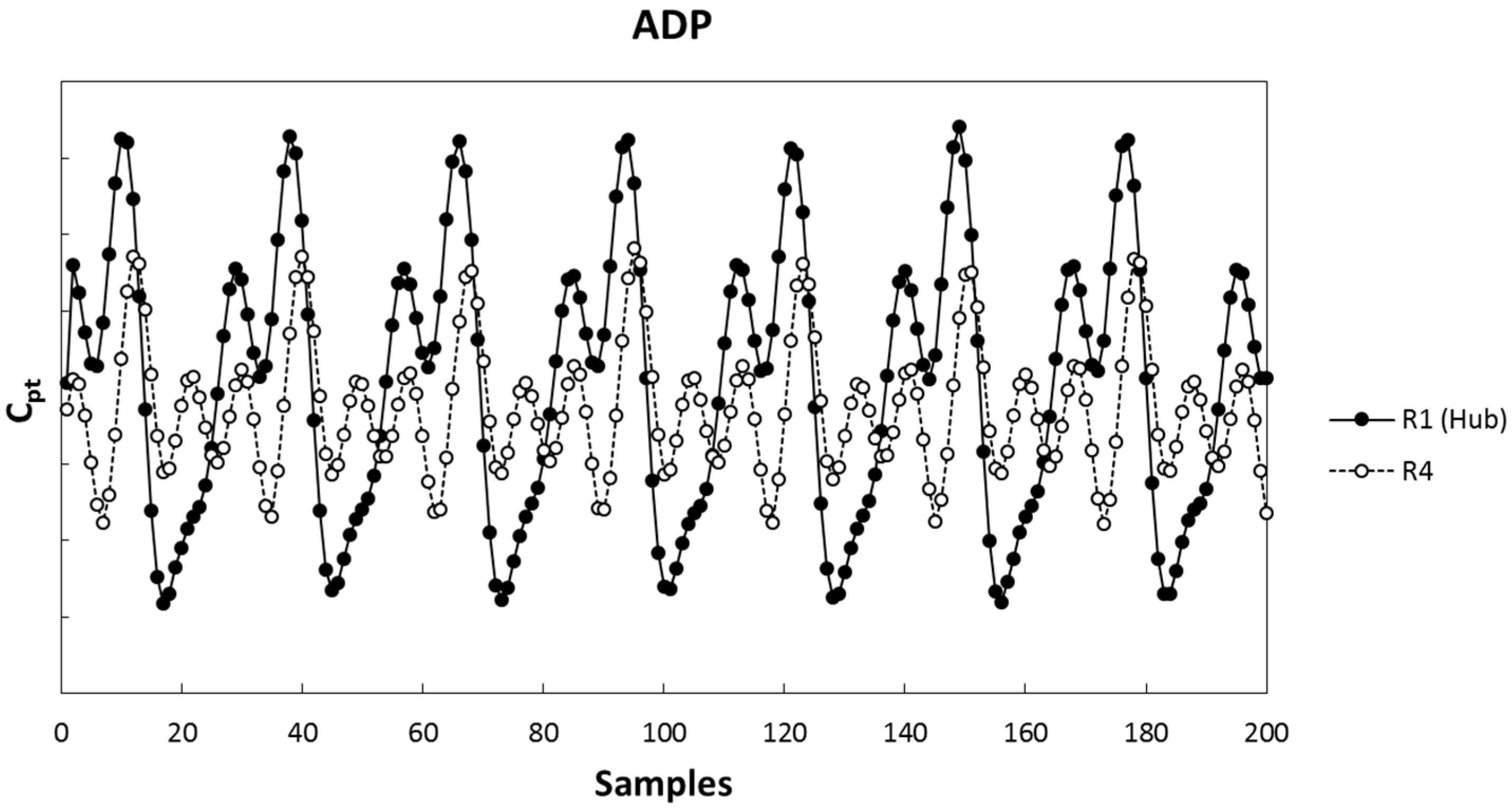
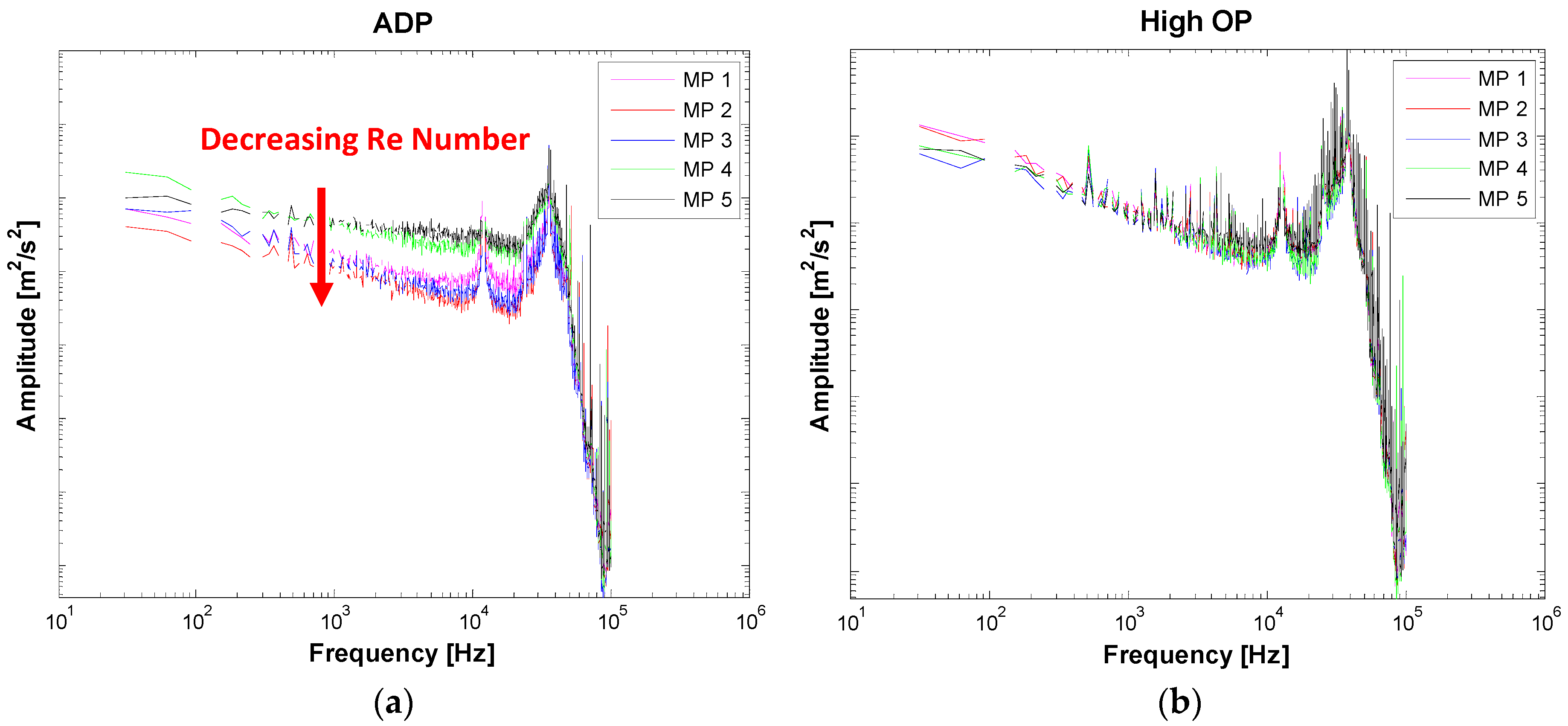
Figure 3 shows the time resolved total pressure coefficient for a certain number of samples obtained from the FRAPP measurement for two radial measurement points at operating point ADP. The results represent the periodic component of the signal, which is obtained through phase averaging of the signal, where the stochastic fluctuations are averaged out. As shown in Figure 2, the largest deviation between 5HP and rake was observed at MP 4. At this point, the amplitudes of the periodic pressure fluctuations are significantly smaller compared to those at MP 1, where the difference between 5HP and rake results is negligible. This means that the amplitude of the periodic part of the signal does not seem to influence the measurement result depending on the shape of the probe head. The same is true for other radial points and operating conditions but is not shown here due to space reasons.

Besides the different amplitudes, Figure 3 leads to the assumption that there is a difference between MP 1 and MP 4 concerning the frequency content. Therefore, an FFT of the raw signal originating from FRAPP measurements was performed. The signal contains both periodic and stochastic parts but is clearly dominated by peaks at the BPF and its harmonics. 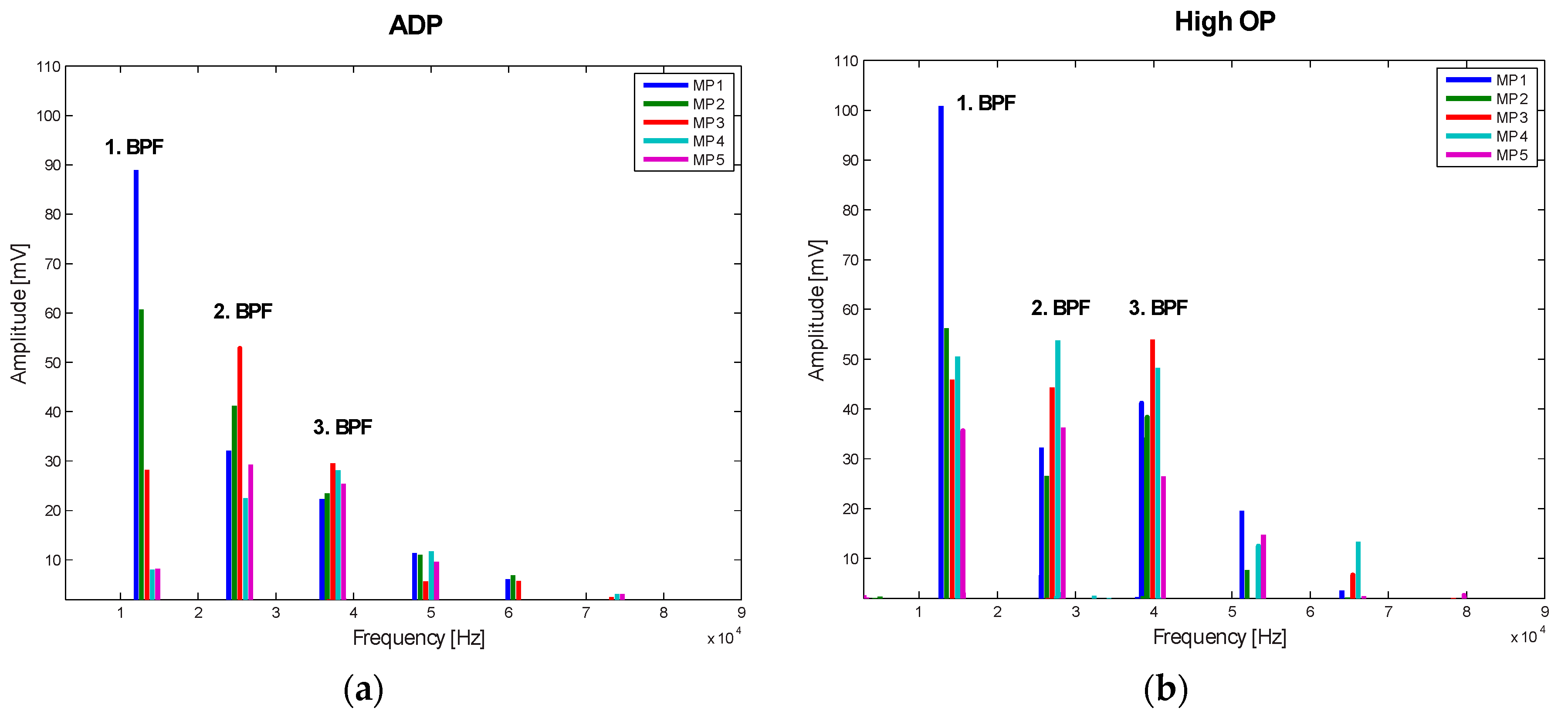This is why the stochastic part of the signal cannot be seen in the two plots in Figure 4, although they are actually present. The spectrum for ADP (Figure 4) shows that the pressure signal at MP 4 is really dominated by a higher frequency content with the highest peak at the third harmonic of the BPF. MP 1 and MP 2, where the differences between 5HP and rake results are negligible, have the highest peak at lower frequencies.

However, MP 3 shows good agreement between the different measurement techniques at ADP, but, nevertheless, the signal at this radial point is composed of higher frequency components with a significant peak at the second BPF. Similar findings can be made for the higher OP: only MP 1 has the largest peak at the first BPF. For all of the other measurement points, peaks with very similar amplitudes can be found at the first, the second and the third BPF. At some of these points, the 5HP and rake results differ significantly from each other, but, at MP 2, the difference is negligibly small, although the signal mainly consists of higher frequencies at this point. To sum up, no clear correlation between the frequency content of the signal and the deviations between the results of different measurement devices can be found, which leads to the assumption that the frequency content of the signal does not seem to influence the result considerably.

6.2. Reynolds Number

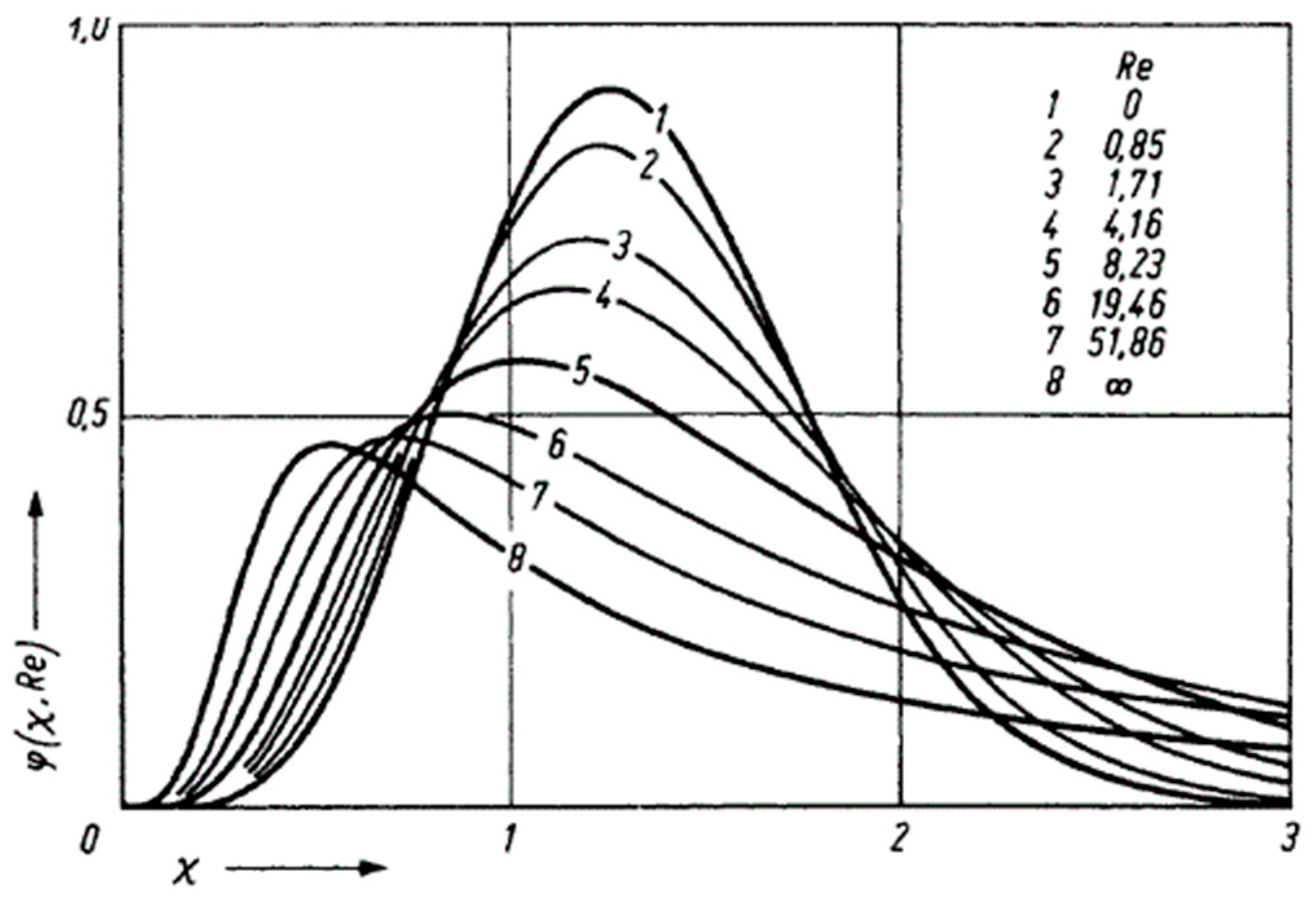
According to Rotta [10], different Reynolds numbers of the flow result in different amplitudes of the energy spectral function, which was calculated using the average of the squared flow velocity assuming isotropic turbulence (see Figure 5). In this figure, the abscissa is represented by a dimensionless value calculated from the wave number times an integral length scale. The ordinate corresponds to a dimensionless function, which depends on the Reynolds number and on χ $=kL$. This dimensionless function is calculated from Equation (4), whereas $E\left(k,t\right)$ is the energy spectral function. The Re number is given as $Re={\left(3\overline{u^2}/2\right)}^{0.5}L/\nu$:

$$E\left(k,t\right)=\frac{3}{2}\overline{u^2}L\phi \left(\chi ,Re\right).$$

(4)

As one can clearly see, the amplitude of the spectral function decreases with increasing Reynolds number. Assuming that the turbulent length scale and the kinematic viscosity stay constant, only a change in flow velocity can change the Re number significantly. If the velocity increases, the Re number increases and so does the energy $E\left(k,t\right)$, but the function $\phi$ decreases (see Figure 5).

Based on this theoretical approach by Rotta, results from unsteady pressure measurements with FRAPP were used to obtain a comparable data representation as shown in Figure 5. For this reason, the velocity fluctuations were calculated from the pressure fluctuations using the method given by Persico et al. [11]. In order to get the energy and intensity of the velocity fluctuations, respectively, the Root Mean Square (RMS) value of the velocity was calculated comparable to Rotta. When plotting now the intensity over the frequency as it was done in Figure 6, the amplitude is larger for high velocities, which corresponds to higher Re numbers. This result is also in accordance with other publications like Rodriguez et al. [12]. The peaks originating from the periodic parts of the signal are still clearly visible in both plots of Figure 6.

Especially in the plot for ADP, a small difference in amplitude and therefore Reynolds number depending on the radial measurement positions is depicted. When regarding the spectrum for ADP, one may assume that higher Re numbers lead to discrepancies between the results of different pneumatic probes, as the two radial points with the largest differences (MP 4 and MP 5) also have the highest Re number as shown in Figure 6. However, this assumption is proved wrong when regarding the spectrum for the high OP, where the Re number seems to be very similar for each radial point, but, according to Figure 2, significant differences in total pressure occur for MP 3, MP 4 and MP 5. Again, no relation between Re number and deviations in measurement results could be determined, which also corresponds to the findings of Arts et al. [9], who just found influences on Pitot probe measurements for very low Re numbers, which usually do not occur in a turbomachine like the currently presented.

6.3. Velocity Gradients and Wall Proximity Effects

Especially in the region of the tip leakage vortex, the total pressure rake (and also the 5HP) sees a large velocity gradient. According to Arts et al. [9], a strong transverse pressure gradient causes a measurement error due to two effects. The first one is the integration of velocity over the orifice and the second more important one is the deflection of streamlines due to the presence of a probe. Both effects lead to an increase in total pressure measured by a Pitot probe. It was assumed by the authors that, in the Kielhead of a total pressure rake, the mixing process due to the velocity gradient is more pronounced than in a Pitot probe, as the Kielhead is significantly larger than the opening of a Pitot probe. Therefore, the pressure after the mixing of two streams was estimated using the formulae given by Denton [13]. For this estimation, the flow into the Kielhead was divided into two streams with constant total temperature and total pressure according to the same gradient that was seen in the measurement data. It was found considering that a mixing process leads to total pressure values that are lower than the arithmetically averaged total pressure value of the two streams. This may be a possible explanation for the trend seen for MP 5 at ADP: the difference between the two measurement techniques is smaller compared to MP 4. It is not as clear for the high OP, but, still, the trend can be seen that the deviation between 5HP and the rake is smaller at MP 5 than at MP 4 with lower values for the rake than expected.

Concerning the wall proximity effects, no influence could be found, as both the Kielhead close to the inner and the one close to the outer casing are located far enough from the walls (see Arts et al. [9]). The same is of course valid for the 5HP measurement positions.

6.4. Stochastic Pressure Fluctuations/Turbulence Intensity

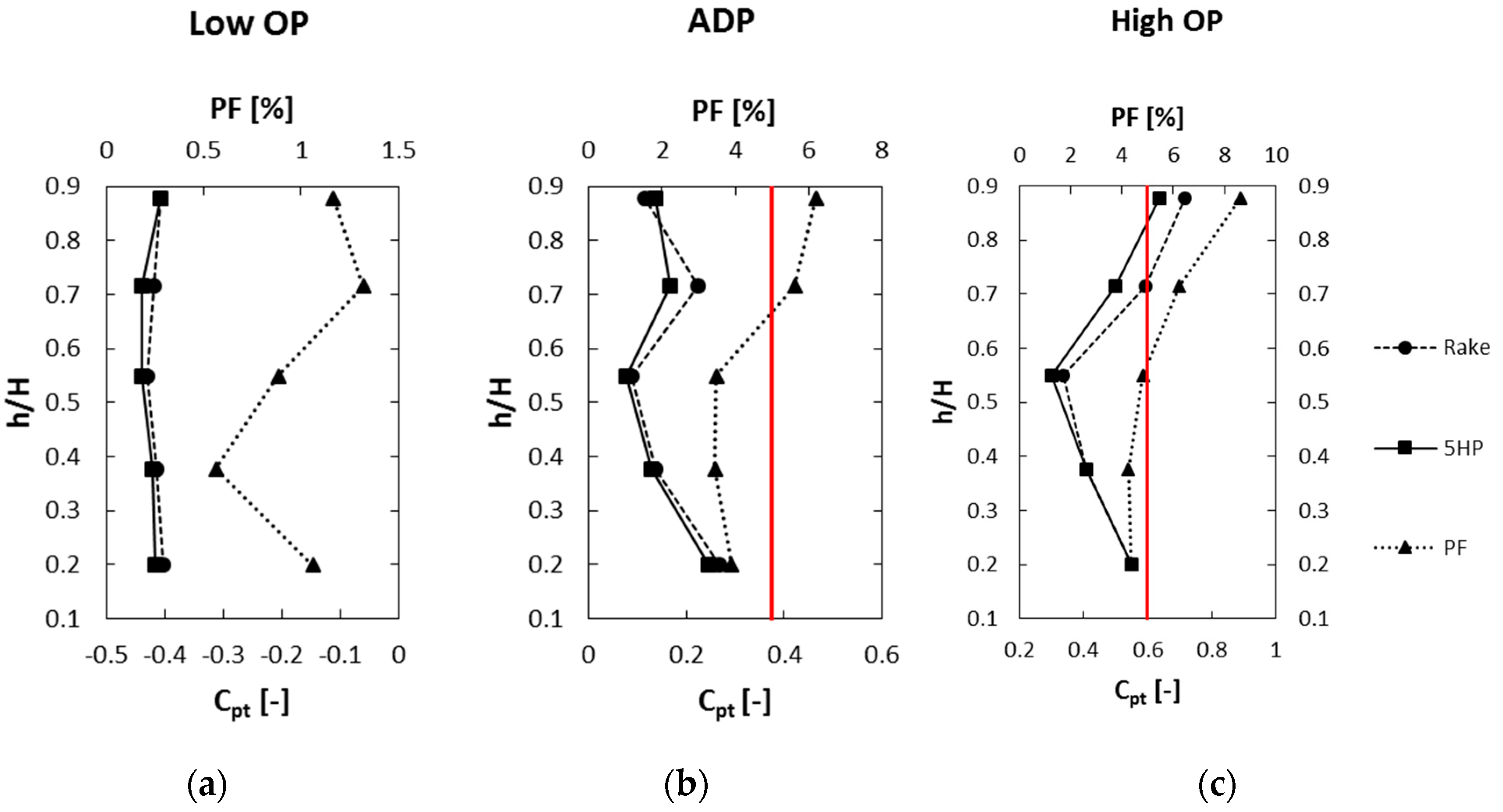
As seen in the foregoing sections, the stochastic pressure fluctuations and the turbulence intensity, respectively, seem to be to most influencing factor concerning increased measurement uncertainty and deviations between pressure readings of differently shaped probes. Figure 7 shows the stochastic pressure fluctuations as a percentage of the average pressure value in the regarded plane (see Equation (3)) after applying Fourier Filtering. The radial line is shown for the three operating points, and, regarding the three plots, the assumption that the amplitude of the fluctuations gets higher with increased mass flow, pressure ratio and rotational speed is confirmed. For the low OP, the percentage fluctuation (PF) values are very small, but also the deviations between 5HP and the rake are negligible. It seems that, from a certain value, which is marked by the red line at about 5% PF, the deviations between 5HP and the rake start to become significant.

Several authors like Bennett [14] or Goldstein [15] already noted that the correct formulation of the measured total pressure is the one according to Equation (5). For reasons of simplicity, $w^{\prime }$ was neglected and the fluctuations were just considered in two spatial directions. Therefore, the measured value of total pressure is composed of the static pressure, the average value of the flow velocity as well as the stochastic velocity fluctuations in two spatial directions. After some rearrangements, the difference $\mathrm{\Delta }{p}_t$ between the measured total pressure and the total pressure according to theory $p_t=p+\frac{1}{2}\rho U^2$ depends on the flow velocity but also on the turbulence intensity. Using the formulae given by Persico et al. [11], it is possible to calculate the stochastic velocity fluctuations from FRAPP results and insert them into Equation (7):

$$p_{t,meas}=p+\frac{1}{2}\rho \left(U^2+{u^{\prime }}^2+{v^{\prime }}^2\right),$$

(5)

$$p_{t,meas}-\left(p+\frac{1}{2}\rho U^2\right)=\frac{1}{2}\rho ({u^{\prime }}^2+{v^{\prime }}^2),$$

(6)

$$\mathrm{\Delta }{p}_t=\rho U^{2}T{u}^2 with Tu=\frac{1}{U}\sqrt{\frac{{u^{\prime }}^2+{v^{\prime }}^2}{2}}.$$

(7)

Bennett [14] goes even further and introduces a factor $A_i$ in relation with the measured dynamic pressure consisting of a steady and unsteady part. He also formulates the static pressure as a sum of an average value and a fluctuating part:

$$p_{t,meas}=\overline{p}+p^{\prime }+\frac{1}{2}\rho A_i\left(U^2+{u^{\prime }}^2+{v^{\prime }}^2\right).$$

(8)

The author relates this coefficient to individual probe response. As total pressure rakes and 5HP have a different shape and different probe response, this factor could explain the difference between the two probes. According to him, these coefficients have to be determined by an appropriate (unsteady) calibration.

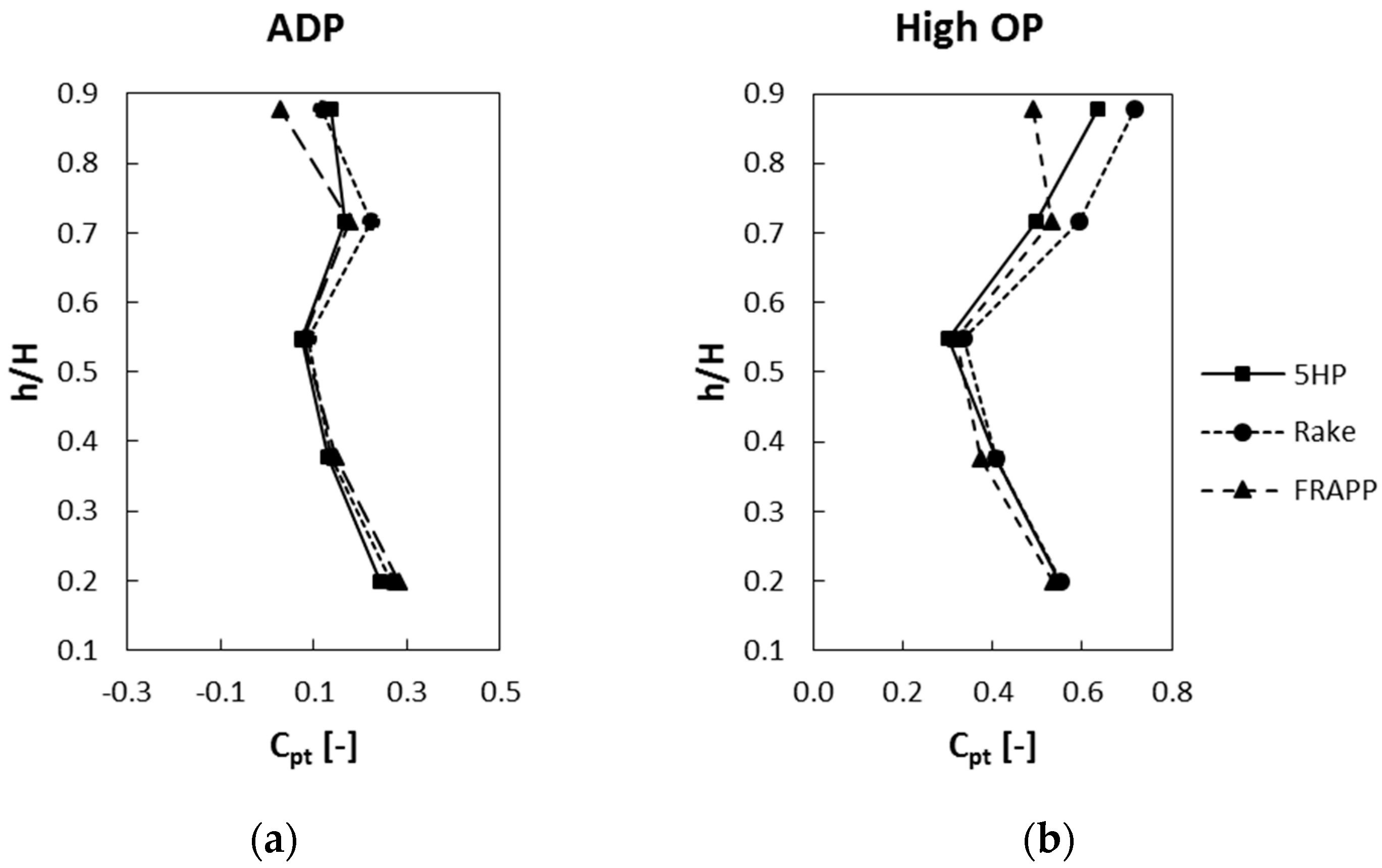
Bennett’s and Goldstein’s findings are reinforced by Figure 8, where 5HP and rake measurements are compared to time averaged results of a FRAPP probe. The FRAPP results are shown after phase averaging, which means that the stochastic fluctuations have been averaged out and the problem with the influence of Tu on the measured value is eliminated. It seems that the 5HP is getting pretty close to the results of the FRAPP, except for the region of the tip leakage. Concerning the rake results, the deviations are significantly larger compared to those of the FRAPP, especially at the measurement points with higher turbulence. Again, this supports the theory presented by Bennett that the measured total pressure depends, amongst others, on a coefficient $A_i$, which, in turn, depends on the probe geometry.

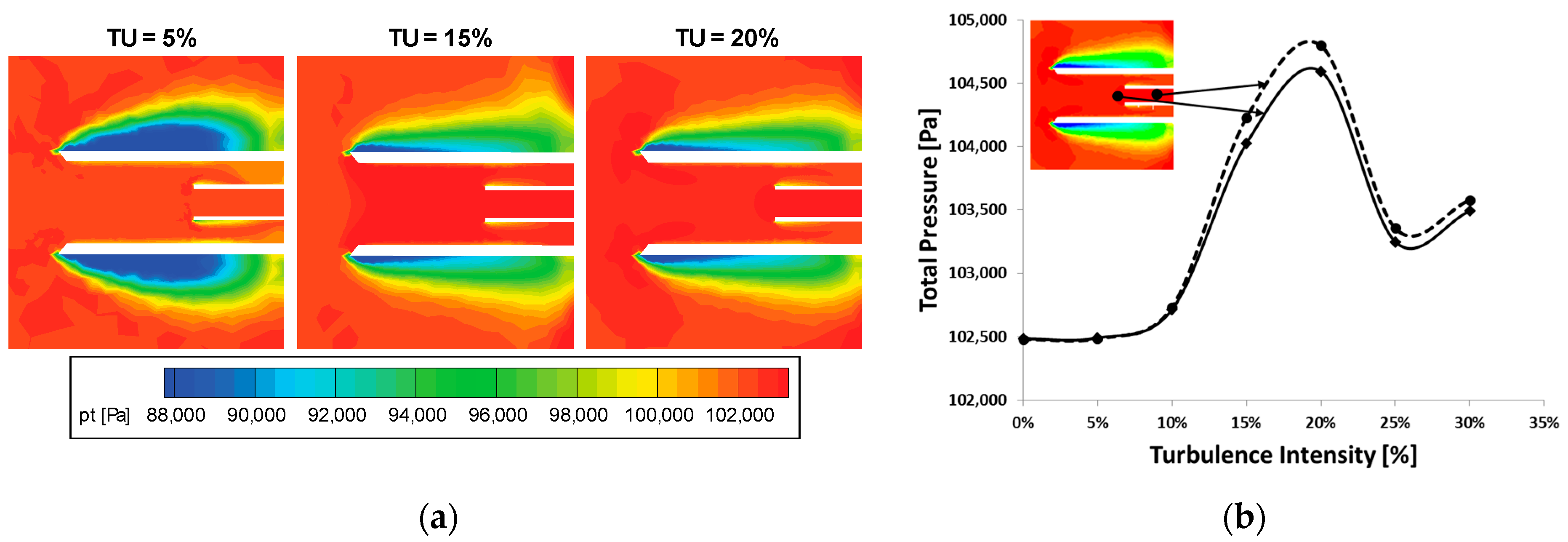
In order to get a deeper insight into the flow inside and around the Kielhead, steady state numerical investigations were carried out. The geometry of the Kielhead was the same as in the test rig, and the compensating bores on both sides of the Kielhead were also modelled but are not shown in the results. For each calculation, the turbulence intensity at the inlet was varied, but all of the other parameters were kept constant. The results of these calculations are depicted in Figure 9. Also in the CFD, the total pressure in the pressure pipe inside the Kielhead increases with increasing turbulence intensity at the inlet. Interestingly, the shape and size of the separation zones outside the Kielhead also change with increasing turbulence.

The diagram on the right side represents the total pressure directly in front and at the end of the pressure pipe for different turbulence intensities, and shows a considerable jump in total pressure between a turbulence intensity of 10% and 15%, whereas the total pressure at 0% and 5% corresponds exactly to the total pressure given as a boundary condition.

Surprisingly, there is another jump to a lower total pressure for turbulence intensities larger than 20%, but the shape of the separation region stays the same as e.g., for 15%. It is also interesting that the difference between the total pressure of the main flow and the total pressure inside the pressure pipe depends on the position inside the pipe: for the point at the end of the pipe, the total pressure deviation is even larger for increasing turbulence than for the point directly in front of the pipe.

7. Conclusions

As foregoing measurements in a turbine test rig showed significant deviations in total pressure measured with different pneumatic probes, investigations were carried out in order to determine the origin of these deviations. Several parameters that can have an influence on total pressure readings of a probe were analysed. It was found that the most important parameters are stochastic pressure fluctuations and turbulence, respectively, as they have a significant influence on the total pressure, especially the one measured by Kielhead probes. It is therefore recommended by the authors that, especially in test rigs with high turbulence intensities, unsteady measurements should be carried out in addition to steady measurements with five-hole probes and rakes. The determination of stochastic fluctuations is inevitable for the evaluation of steady data from pneumatic probes. Still, 5HP and rakes are an appropriate tool for aerodynamic measurements in test rigs, but, in connection with high turbulence, absolute values should be handled with care. In highly unsteady flows, an unsteady calibration of the used probes could also help to solve some of the previously discussed issues.