Abstract
The adjoint method is considered as the most efficient approach to compute gradients with respect to an arbitrary number of design parameters. However, one major challenge of adjoint-based shape optimization methods is the integration into a computer-aided design (CAD) workflow for practical industrial cases. This paper presents an adjoint-based framework that uses a tailored shape parameterization to satisfy geometric constraints due to mechanical and manufacturing requirements while maintaining the shape in a CAD representation. The system employs a sequential quadratic programming (SQP) algorithm and in-house developed libraries for the CAD and grid generation as well as a 3D Navier–Stokes flow and adjoint solver. The developed method is applied to a multipoint optimization of a turbocharger radial turbine aiming at maximizing the total-to-static efficiency at multiple operating points while constraining the output power and the choking mass flow of the machine. The optimization converged in a few design cycles in which the total-to-static efficiency could be significantly improved over a wide operating range. Additionally, the imposed aerodynamic constraints with strict convergence tolerances are satisfied and several geometric constraints are inherently respected due to the parameterization of the turbine. In particular, radial fibered blades are used to avoid bending stresses in the turbine blades due to centrifugal forces. The methodology is a step forward towards robustness and consistency of gradient-based optimization for practical industrial cases, as it maintains the optimal shape in CAD representation. As shown in this paper, this avoids shape approximations and allows manufacturing constraints to be included.
1. Introduction
High fidelity numerical optimization methods have made substantial progress and play an important role in modern industrial design processes. While a wide variety of algorithms have been developed, they can be broadly divided into gradient-free and gradient-based optimization methods. Gradient-free (or stochastic) optimization algorithms, which only require the evaluation of the objective function, are widely used due to their robustness, simple integration into a standard design process, and ability to handle multimodal functions of complex design problems. They have been successfully applied to many turbomachinery applications including multipoint, multiobjective, and multidisciplinary optimization problems [1,2,3,4]. Despite their success, gradient-free optimization techniques are computationally expensive, especially for applications with many design parameters, resulting in a long runtime due to the large number of required function evaluations. This constitutes a major obstacle to industrial design processes where limited resources and time restrictions consequently limit the range of optimal shapes. Gradient-based optimization algorithms, on the other hand, are particularly suited for problems involving large design spaces and generally converge to a local optimum in a few design cycles. However, the computational efficiency of these methods is mainly determined by the gradient calculation. For aerodynamic design problems, the adjoint method [5,6] has emerged as the most efficient approach to evaluate gradients of the cost function with respect to an arbitrary number of shape parameters by solving two sets of equations: the flow equations and the corresponding adjoint equations. The computational cost is essentially independent of the number of design variables and scales only with the number of objective and constraint functions defined in the optimization problem.
Gradient-based optimization methods have been used in turbomachinery applications to optimize axial compressor and turbine configurations, ranging from isolated blade rows [7,8,9,10] including hub endwall contouring [11,12] to multi-row and multi-stage architectures [13,14,15,16]. In most cases, the geometry is parameterized by Hicks–Henne shape functions [17], free-form deformation (FFD) control lattices [18], or even by the surface nodes of the computational grid. These parametrization techniques are very attractive for gradient-based optimization methods since they possess a large degree of freedom and provide sensitivity derivatives at low computational effort. However, they deform the computational grid without a direct connection to the computer-aided design (CAD) model. Given that CAD systems have become an integral part of standard industrial design processes, reverse engineering techniques would need to be utilized to recreate the CAD model from the optimized grid, e.g., [19,20], which may impair the optimality of the design due to fitting or approximation errors. Furthermore, the proper treatment of geometric constraints due to mechanical and manufacturing requirements is crucial for the success of 3D realistic design problems. Using a parametric CAD model facilitates the integration of constraints in the optimization process and allows design parameters to be easily varied while sustaining the geometric features of the original geometry.
The main challenge for CAD models to be included into a gradient-based optimization process is the calculation of the sensitivity of the surface displacements with respect to the design parameters that control the shape. However, several approaches have been undertaken to incorporate a CAD representation directly in a gradient-based optimization loop. A closed-source commercial CAD tool was used by [21] for a 3D air duct and by [22] to optimize a compressor stator under geometric constraints at multiple operating points. In both cases, the gradient information from the grid to the CAD parameters was calculated by finite-difference approximations. To overcome the limitations that are associated with finite-differences, an open-source CAD system was differentiated by [23] using algorithmic differentiation (AD), which was then applied to optimize a U-Bend shape found in high-pressure turbine blades as cooling devices. A trivariate B-spline parameterization was used by [24] for the same test case that allows a rapid meshing of the domain suitable for a one-shot optimization method while the geometry maintains the link to a CAD representation. A different approach was developed by [25,26] that employs the displacements of the control points of non-uniform rational B-spline (NURBS) patches as design parameters, which are available in the STEP file standard used to exchange data in a computer-aided engineering (CAE) framework. This method is not connected to a higher-level parameterization and represents the richest design space a CAD geometry can have. It was applied by [27] to optimize the rotor of a high-pressure turbine stage where, due to the large degree of freedom, special attention is devoted to the treatment of geometric constraints, e.g., continuity of neighboring NURBS patches, minimal blade thickness as well as restrictions on the trailing edge radius for cooling ejection.
In the present work, a CAD integrated approach is presented and applied to a multipoint gradient-based optimization of a turbocharger radial turbine. The system uses a dedicated shape parametrization and in-house flow and adjoint solvers as well as libraries for the CAD and grid generation. This allows (a) to incorporate geometric constraints through a tailored shape generation and (b) the differentiation of the respective routines. The former results in a limited degree of freedom but is essential in radial turbomachinery due to mechanical and manufacturing constraints, e.g., flank milling processes require ruled blade surfaces, while stress limitations often dictate fully radial blades as will be shown in this paper. The differentiation of the CAD and grid generation provides accurate design gradients with respect to parameters that control directly the CAD shape, which is a significant step towards robustness and consistency of gradient-based optimization for industrial purposes. The complex-step method [28,29] is used as proof of concept in the present work that yields machine accurate gradients at low implementation effort [30]. However, other methods that involve the differentiation of the CAD kernel and grid generation by AD have been tested in [31] in order to fully exploit the potential of the current approach.
The remainder of the paper is structured as follows: Section 2 explains the optimization method with the individual components that constitute the algorithm. The objective and constraints of the optimization are presented in Section 3. Results of the optimization are discussed in Section 4 followed by conclusions that are drawn in Section 5.
2. Optimization Methodology
Figure 1 shows a schematic flowchart of the optimization framework. The system uses the optimization package SNOPT [32,33], which is a state-of-the-art optimizer for large scale constrained optimization problems. A sequential quadratic programming (SQP) method is adopted. The algorithm handles constraints by forming a smooth augmented Lagrangian merit function [34], which is solved for the optimal point that satisfies the Karush–Kuhn–Tucker (KKT) [35] optimality condition by a line search procedure. The Hessian of the Lagrangian required by the algorithm is approximated using a limited-memory Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton method. The remaining components of the algorithm shown in Figure 1 evaluate the objective and the constraints as well as their design gradients required by the optimizer. These components are described in more detail in the following sections.
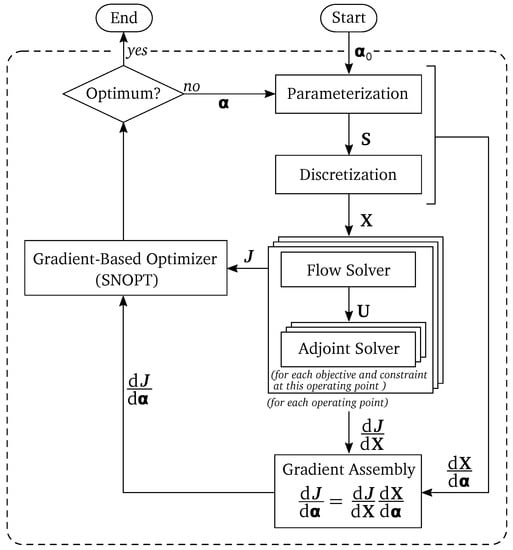
Figure 1.
Flowchart of the gradient-based optimization methodology.
2.1. Parameterization, Design Variables, and CAD Model
The parametrization is one of the crucial steps in every optimization process. On the one hand, the design space should be diverse and large enough in order to include optimal designs; on the other hand, geometric restrictions are invariably imposed due to mechanical and manufacturing limitations. In particular, turbocharger radial turbines have to withstand the harsh environment of high mechanical stresses at high temperatures. Therefore, as illustrated in Figure 2 (left), radial turbines are commonly designed with radial fibered blades in order to avoid bending stresses inside the blades due to centrifugal forces.
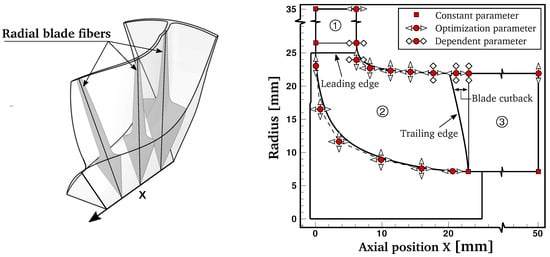
Figure 2.
Radial fibered blade sections of the turbine wheel (left); parameterization of the meridional flow path with three patches ①–③ (right).
In the present study, the parametrization of the radial turbine is tailored to inherently satisfy this geometric constraint through the CAD-based approach where the model is based on NURBS. The 3D geometry is defined by:
- the meridional flow path,
- the camber line surface defined by a blade angle distribution and a trailing edge cutback,
- the blade thickness distribution, which is added normal to the camber line surface, and
- the number of blades.
Figure 2 (right) shows the parametrization of the meridional flow path, which is subdivided into three patches: an inlet patch ①, an intermediate patch ② where the blade is located, and an outlet patch ③. Each patch is defined by a B-spline curve at hub and shroud with an underlying set of control points. The coordinates of the control points are the design parameters that can be modified by the optimization program and the possible variation in axial and radial direction is indicated by arrows in Figure 2 (right). Additionally, the diamond shaped arrows at the shroud represent dependent parameters that are linked to the position of the control points defining the inlet and outlet width of the meridional flow path in order ensure a straight endwall in the respective region.
The camber line surface of the radial blading is defined by a blade angle -distribution with respect to the meridional plane along the machine axis (Figure 3, left). Eight degrees of freedom are used for the blade angle distribution, which allows a large shape variation while guaranteeing the geometric constraint of radial fibered blades.
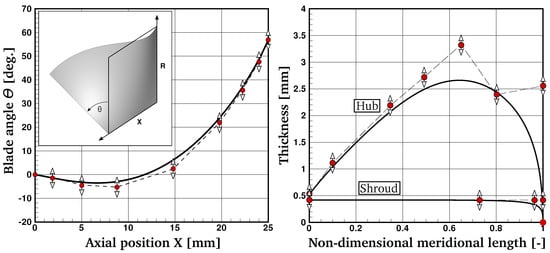
Figure 3.
Blade angle parameterization (left); blade thickness distribution at hub and shroud (right).
Next, the blade pressure side and suction side surfaces are constructed by adding a thickness distribution (Figure 3, right) normal to the camber line surface. The blade thickness is parameterized at hub and shroud in the meridional plane and its span-wise distribution is linearly interpolated. The blade thickness can be modified during the optimization with, in total, 11 optimization parameters. However, due to mechanical considerations, the lower limit of each parameter is restricted by a safety margin. The cutback of the blade at the trailing edge (see Figure 2, right) is one additional design parameter, which has a high impact on mechanical stresses in the trailing edge root. Since stresses are not evaluated during the optimization process, this parameter is fixed in order to keep the stress levels bounded. In total, 40 free design variables are selected for this optimization: 21 parameters for the hub and shroud curves including the inlet and outlet width of the meridional flow path, eight for the blade angle -distribution, and eleven degrees of freedom for the blade thickness distribution. Each parameter can be modified in a prescribed range by the optimization program. The turbine wheel diameter, its axial length, the tip clearance as well as the number of blades are kept constant due to external constraints.
The aforementioned procedure generates the turbine wheel geometry defined by several NURBS, which is shown in Figure 4 for the surfaces of the blade and the hub fillet along with their control points. The blade surfaces are skinned through ten sections in span-wise direction, whereas the hub fillet surfaces are generated by a rolling-ball algorithm involving several CAD operations such as surface intersection, surface off-setting, trimming, and surface lofting [36]. The endwalls at both hub and shroud are axisymmetric surfaces revolved about the x-axis. Using the displacements of the control points shown in Figure 4 directly as optimization parameters would result in a much larger design space as compared to the approach followed in the present work. However, this would require imposing many constraints to ensure a minimum blade thickness as well as geometric continuity at the junction between the fillet and the adjoining surfaces. Furthermore, avoiding bending stresses in the blade due to centrifugal forces requires an equal mass distribution on both sides of the radial fiber at each cross-section along the machine axis (cf. Figure 2, left). In particular, the last requirement would be difficult to realize, while it is inherently satisfied by the approach presented in this paper.
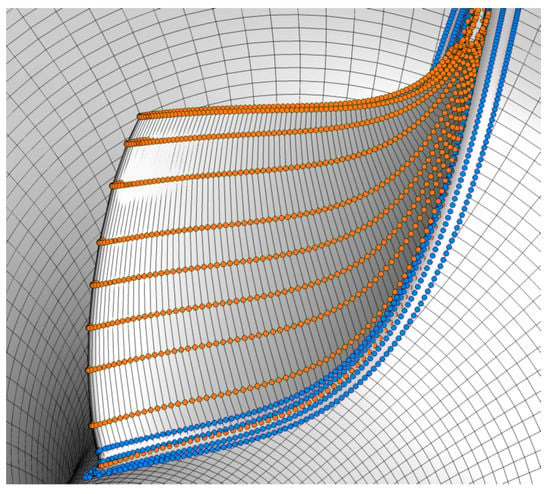
Figure 4.
Non-uniform rational B-spline (NURBS) surfaces of the blade and hub fillet with their control points.
The solid CAD model of the turbine wheel is defined by a boundary representation (BRep) [37] scheme. A BRep is a collection of surface elements in the boundary of the solid and is composed of a topology (faces, edges, vertices) and a geometry (surfaces, curves, points). Each topological entity has an associated geometry, e.g., a face is a bounded portion of a surface. Figure 5 (left) shows the solid model of the turbine wheel in an exposed view to further illustrate that each face is indeed a separate entity. The resulting BRep is watertight and has no overlaps, which is assured by the internal CAD program by extending and trimming curves and surfaces such that each edge is shared by two neighboring faces. Consequently, no repair operation is needed when the model is further processed in a CAE workflow. The export of the BRep model for manufacturing is realized through the STEP file protocol. Figure 5 (right) shows the turbine wheel visualized in a CAD program.
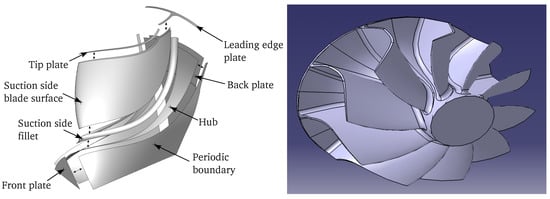
Figure 5.
Exposed view of the boundary representation (BRep) of the solid turbine wheel model (left) and exported through the STEP file protocol to a computer-aided design (CAD) program (right).
2.2. Discretization
Besides the parameterization, the grid generation is often a bottleneck in automatic shape optimization. The process should be robust, fast, and produce high quality meshes even for large geometry changes. In the present work, the three-dimensional multiblock structured grid of the turbine wheel is created by stacking annular surface grids. This approach has proved to be very robust for turbomachinery configurations, while ensuring high grid quality for blades subject to large geometry changes during the optimization process. Additionally, the internal grid generator has direct access to the NURBS surface model, which guarantees a tight link between the actual model and the discretized computational domain for the CFD analysis.
In general, the automatic grid generation process consists of a two-step approach that is illustrated in Figure 6: first, the meridional passage is discretized by a predefined grid point distribution with a boundary layer refinement towards the endwalls at hub and shroud. Each meridional grid line is consecutively converted into a surface of revolution, which is intersected with the blade pressure- and suction-side surfaces. Angle-preserving conformal mapping [38] is used to transform the ()-coordinates of the intersected blade profile on the surface of revolution into an equivalent two-dimensional ()-space (cf. Figure 6, right) and vice versa. Secondly, the two-dimensional body-conformal grids are created by elliptic grid generation [39] by solving the elliptic equations
where are the grid points in the transformed computational space. The source terms of Equation (1) are necessary to control the grid point distribution and several formulations [40,41,42] are used to meet grid quality measures, e.g., first cell spacing and orthogonality, cell skewness and expansion ratio.
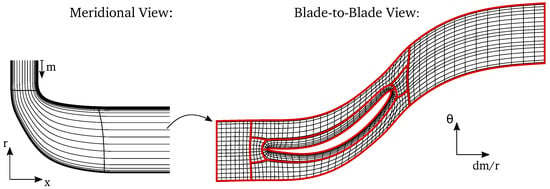
Figure 6.
Schematic diagram of the grid generation process. Meridional grid lines (left) and blade-to-blade mesh in conformal plane (right). Mesh is coarsened for visualization purposes.
Figure 7 shows the final computational domain of the radial turbine with a close-up of the tip clearance mesh. The computational cost is reduced by modeling only one blade pitch and using periodic boundary conditions in circumferential direction. In total, 84 layers of cells are used in span-wise direction, including 20 cells to model the tip clearance. Special care is given to grid independence of the flow solution to avoid any scatter of the results due to grid dependence. To meet common grid quality requirements, the average wall-spacing is and the maximum cell expansion ratio is limited to 1.2 for 20 cells in blade normal direction.
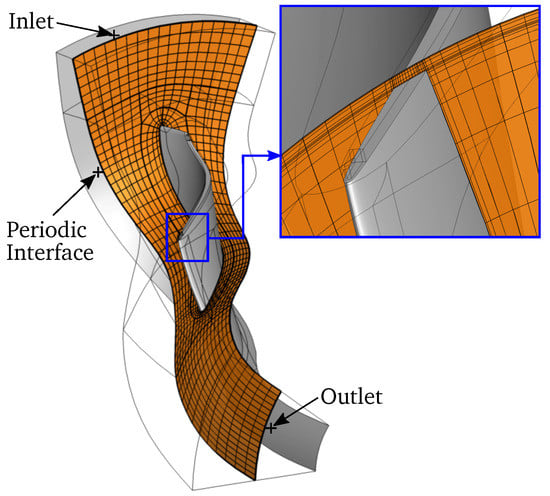
Figure 7.
Computational domain of the turbine wheel with a close-up of the tip clearance mesh with an axial cross section through the 3D grid (every 4th grid line shown).
2.3. Flow and Adjoint Solver
2.3.1. Flow Solver
The governing equations are the compressible Reynolds averaged Navier–Stokes (RANS) equations formulated in a rotating reference frame using absolute flow variables. They are spatially discretized using a cell-centered finite volume method on multiblock structured grids. Convergence to a steady-state solution is obtained with a parallelized implicit time integration scheme accelerated by local time-stepping and geometric multigrid. The fluid is considered as a calorically perfect gas and the eddy-viscosity hypothesis is used to account for the effect of turbulence. The semi-discrete form of the steady-state RANS equations can be written as
where are the conserved flow variables and the residual containing the spatial discretization including the flux balances through the cell interfaces and the source term due to Coriolis forces. The inviscid fluxes are computed by Roe’s approximate Riemann solver [43] with an MUSCL reconstruction [44] of primitive variables for second order accuracy. Oscillations near shocks are suppressed by a van-Albada type limiter [45], while the numerical dissipation of the scheme is controlled with the entropy correction of Harten and Hyman [46]. Viscous fluxes are calculated with a central discretization and the negative Spalart–Allmaras turbulence model [47] is used for the turbulence closure problem assuming a fully turbulent flow from the inlet ( 250,000 based on the turbine wheel diameter).
Boundary conditions are imposed weakly by utilizing the ghost cell concept [48]. Solid walls are considered adiabatic with the no-slip velocity condition and a first-order pressure extrapolation. Characteristic-based subsonic inflow and outflow boundary conditions using Riemann invariants are applied. At the inlet of the computational domain the total pressure, total temperature and flow angles are imposed while, at the outlet, the static pressure with a radial equilibrium formulation is prescribed. For some applications, it is crucial to directly control the mass flow rather than the total pressure at the inlet or static pressure at the outlet. In this case, the mass flow boundary conditions described by [49] are used. Furthermore, to reduce the computational cost, periodic boundary conditions are applied in circumferential direction. Time integration is realized with an adaption of the JT-KIRK scheme [50] that combines Runge–Kutta time-stepping and Krylov methods inside a geometric multigrid cycle. As illustrated in [50], the proposed algorithm enables fully converged flow solutions for some cases where conventional algorithms would fail, and therefore extends the applicability of adjoint-based optimization for marginally stable applications. For a basic multistage Runge–Kutta (RK) method, the algorithm is given by
with the RK-stage coefficient and the system matrix defined as
where () is an approximation to the Jacobian matrix by using a first-order Roe-scheme, to which a fictitious time term is added in order to improve the diagonal dominance of the matrix. The linear system of equations in every Runge–Kutta stage is solved with an ILU(0)-preconditioned GMRES solver of the publicly available PETSc library [51]. However, for efficiency, the system matrix is assembled in the first stage only and then held constant for subsequent stages. Mean-flow and the turbulence model equations are loosely coupled. Equation (3) is applied to the mean-flow equations as smoother inside a multigrid cycle, whereas the turbulence model is updated only on the finest grid level.
2.3.2. Adjoint Solver and Gradient Evaluation
Once the flow equations are solved, the cost function J can be computed, which may be the objective or one of the constraints of the optimization problem. A gradient-based shape optimization method, however, requires in addition to the cost function also its gradients with respect to the geometric design parameters . For aerodynamic applications, the cost function depends on both the flow solution and on the design parameters so that the design gradients can be obtained applying the chain rule as follows:
The partial derivatives in this expression can be computed analytically and are computationally inexpensive. The total derivative (), on the other hand, requires the solution of the linearized flow equations for every design parameter, and thus the computational cost to compute all design gradients scales linearly with the number of design variables. For most applications, in which the number of cost functions is far less than the number of design parameters, the adjoint method is preferred. With this approach, the design gradients are evaluated by linearizing the cost function as
where is the solution of the discrete adjoint equations
and the nonlinear residual vector. The adjoint equations are a linear system that depends on the cost function J, but not on the design parameters and therefore needs to be solved only as many times as the number of cost functions.
In practice, the adjoint equations given by Equation (7) are not solved with a linear solver due to the stiffness of the 2nd-order Jacobian matrix and memory limitations for large three-dimensional cases. Instead, the implemented discrete adjoint solver uses the same time-marching method as the primal flow solver
where is the transposed system matrix of the nonlinear flow solver (Equation (4)) frozen at the steady-state value and the adjoint residual defined as
The differentiated nonlinear residual (), which is a large and sparse matrix, is not explicitly stored in memory but directly multiplied element-by-element with the adjoint vector . This approach has two main advantages: first, the resulting memory footprint of the adjoint solver is similar to the primal flow solver, which is largely determined by the system matrix , while the run-time of the adjoint solver is equivalent to the primal flow solver. Secondly, since the transposed system matrix has the same eigenspectra as , the adjoint solver inherits the convergence rate of the flow solver [50,52,53], which is illustrated in Figure 8 for a radial turbine test case. This is a desirable property as it guarantees convergence of the adjoint problem, provided that primal flow solver converges (i.e., the system matrix at the last iteration of the flow solver is contractive with the magnitude of all eigenvalues less than unity).
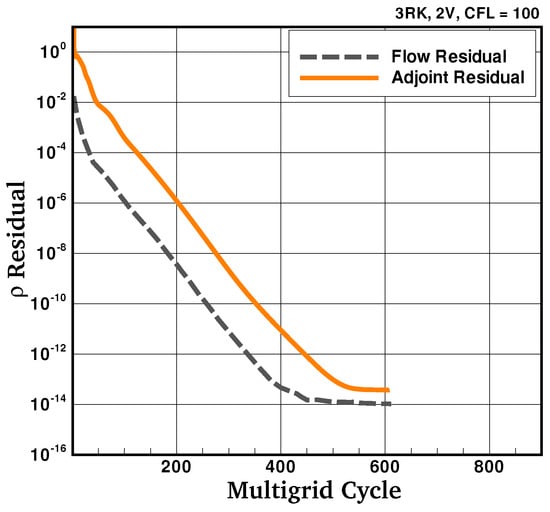
Figure 8.
Convergence history of the density residual of the primal flow solver and of the adjoint solver for a radial turbine test case.
The linearization of the cost function () and the nonlinear residual () in Equation (9) is primarily done by hand-differentiation with selective use of algorithmic differentiation to simplify the development of the adjoint solver, e.g., for the differentiation of the Roe scheme or the linearization of the characteristic-based boundary condition. For this, the source code transformation tool Tapenade [54] was used. To further reduce the development cost, the constant eddy viscosity (CEV) assumption is made, that is, the eddy viscosity is independent from changes of the design. The impact of this approximation was analyzed by [55,56] and is assessed in the course of this section for the present application.
After the adjoint equations are solved, the design gradients are calculated with an alternative formulation of Equation (6) using a two-step approach that decouples the adjoint solver from the geometry and grid generation:
The sensitivity of the cost function with respect to the grid point coordinates () is obtained at a computational cost of solving two sets of equations (the flow and the adjoint equations) while the complementary sensitivity information of the grid to the design variables () is computed with the complex-step method [28,29], which is accurate up to machine round-off precision. Although the computational cost to compute gradients with the complex-step method is proportional to the number of design parameters, it is still considered reasonable given the limited number of design parameters used in this study (40) and the relatively fast grid generation process.
The adjoint-based gradients are validated against exact gradients where the complex-step method is applied to the entire evaluation chain. This is illustrated in Figure 9 showing non-dimensional design gradients of total-to-static efficiency (left) and power (right). Additionally, to quantify the error introduced by the CEV assumption in the adjoint solver, two sets of complex-step gradients are plotted: one where the same approximation is made as in the adjoint solver (circle symbols) and one that provides exact gradients without any approximation (square symbols). As can be seen, both the sign and the magnitude of the adjoint-based gradients agree well with the complex-step gradients using the CEV assumption. For example, the gradient of design variable 29, which is the exit width, suggests that both the efficiency and power increase when enlarging the exit area. The CEV assumption indeed affects the accuracy of the adjoint-based gradients, in particular for design parameters of the shroud meridional contour (design variables 21–24), where this assumption may not be valid due to the tip leakage vortex. However, they are accurate enough for shape optimization as will be shown in Section 4.
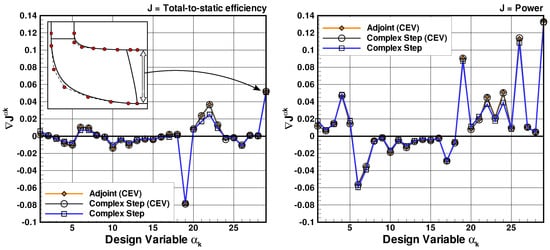
Figure 9.
Comparison of non-dimensional design gradients of total-to-static efficiency (left) and power (right) computed with the adjoint method and complex-step method. CEV: Constant Eddy Viscosity.
3. Objectives and Constraints
The objective of this study is to improve to total-to-static efficiency of the radial turbine at two operating points while constraining the output power at these conditions and ensuring a sufficient swallowing capacity of the machine at high mass flow rate. The operating points are indicated in the performance map of the turbine in Figure 10 and the corresponding boundary conditions are listed in Table 1.
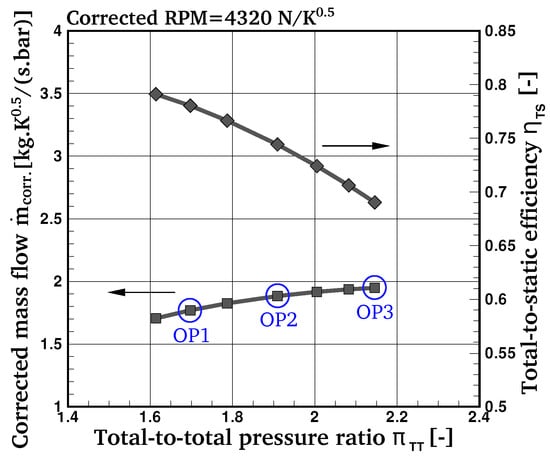
Figure 10.
Performance map of the baseline turbine wheel.

Table 1.
Definition of boundary conditions for the optimization.
The optimization problem can therefore be formulated as follows:
Maximize
Subject to
where the total-to-static isentropic efficiency and power are respectively given by
and
The subscripts 01 and 02 represent mass flow averaged total quantities evaluated at the inlet and outlet of the computational domain, while the static pressure is area averaged at the exit plane. Close examination of Equations (13) and (14) reveals that, for a given mass flow and inlet total temperature at operating conditions OP1 and OP2, higher total-to-static efficiency and constant power are conflicting design requirements. As can be seen, a lower total temperature ratio (/) results in higher efficiency but also increased output power of the turbine. This eventually would lead to a power imbalance between turbine and compressor of the turbocharger, and move the system to a different equilibrium at a higher rotational speed. Therefore, in order to increase the aerodynamic performance while limiting the power, the main task of the optimizer is to find suitable design changes that will reduce pressure losses, and hence will increase the static-to-total pressure ratio (/).
4. Results and Discussion
The optimization converged in 16 design cycles after which no further improvement of the objective could be found by the algorithm while satisfying the imposed constraints. This translates to a run-time of approximately 1.5 days on a multicore workstation using an Intel® Xeon® E5-2690 processor with 2.6 GHz CPU rate. Figure 11 shows the evolution of the weighted objective function as well as the power and mass flow constraints. Each design cycle comprises three flow solutions to compute the objective and the constraints at different operating points and five adjoint solutions: two, respectively, for the total-to-static efficiency and power functional, and one for the mass flow constraint. For the sake of clarity, sub-iterations in which a derivative-free line search was performed to estimate a step size for solving the optimization problem are not included in this plot. In total, the optimizer could improve the objective by approximately 3.4% relative to the baseline geometry already after ten design cycles with minor improvements in the following iterations. As can be seen, the mass flow constraint was not restricting the design progress and the computed mass flow rate at operating point OP3 always exceeds the reference value and therefore satisfies this requirement. The power constraint, on the other hand, was indeed a limiting factor in this optimization. In particular, the power constraint at operating point OP2 was active and reached the upper limit of the imposed bounds. This agrees with the reasoning made in Section 3 that both efficiency and power increase due to the lower total temperature ratio through the machine. However, the optimizer was able to improve the turbine total-to-static efficiency and simultaneously comply with this strict design requirement. Although the turbine geometry undergoes significant changes during the optimization process, each design maintains smooth blade shapes, axi-symmetric endwalls, and is satisfying the geometric constraints due to the CAD-based parameterization as will be shown in the following.
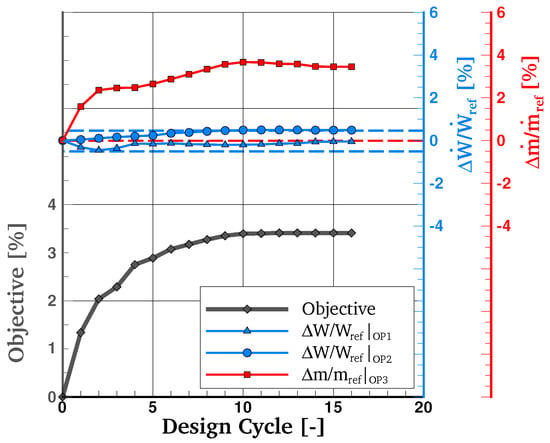
Figure 11.
Optimization history including the weighted efficiency objective and the power and mass flow constraints.
Figure 12 (left) compares the meridional contour of the baseline and the redesigned geometry after 16 design iterations. Additionally, the evolution of the inlet and outlet width during the optimization process is presented in Figure 12 (right), in which the lower and upper limits of each parameter are indicated. The inlet area was slightly increased by the optimization program to reduce the incidence angle with respect to the radial blade leading edge at operating point OP2 from −5.1 to −1.7 and from 6.9 to 6.6 at OP1. The outlet width, on the other hand, was set to its maximum possible value in order to lower the exit Mach number and therefore reduce the exit kinetic energy and consequently increase the turbine total-to-static efficiency.
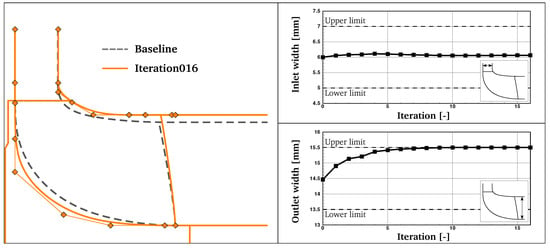
Figure 12.
Comparison of the meridional contour of the baseline and optimized geometry (left). Evolution of inlet and outlet width during the optimization process (right).
Figure 13 (left) shows the modification of the blade angle -distribution between the baseline and the optimized geometry with the corresponding blade shapes on the right-hand side. Here, the design changes are less intuitive to judge because the -angle distribution defines the angular coordinate of the blade with respect to the meridional plane and is therefore not related to the blade metal angle, and hence the relative flow angle. However, the design gradients of the underlying set of control points, which are included in Figure 13 (left), provide better insight into the design problem. Each arrow in this plot indicates the gradient magnitude and direction to higher objective function values (red with filled head) and increased power at operating point OP2 (blue with hollow head). As can be seen, for every design parameter, the respective pair of gradients is pointing in the same direction, which again shows that higher total-to-static efficiency and increased output power are closely related (cf. Section 3). In an unconstrained optimization problem, the blade would be altered until the objective design gradients eventually approach zero. In the present study, however, the power constraint at operating point OP2 has reached its maximum tolerated value (cf. Figure 11) and consequently the blade shape is not further modified by the optimization program in order to fulfill this design requirement.
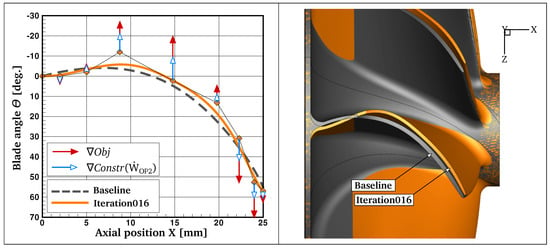
Figure 13.
Comparison of blade angle -distribution of the baseline and optimized geometry (left). The arrows show the design gradients of the weighted objective function (Equation (11)) and power constraint function at operating point OP2. Comparison of the blade shapes (right).
From an aerodynamic perspective, the design changes of the shroud meridional contour have a bigger contribution to the efficiency improvements than the modifications of the hub shape. This is because most of the mass flow is passing the turbine wheel in the shroud region where the blade is subject to the highest aerodynamic loading. Figure 14 shows the relative isentropic Mach number distribution on the blade surface at 90% span of both the baseline and the optimized geometry at operating point OP1 (left) and OP2 (right). As can be seen, the loading has been redistributed in order to reduce the velocity peaks on the suction side surface and therefore the diffusion process and its unfavorable influence on the blade losses. On the front part of the blade, the suction side peak and subsequent deceleration of the flow is removed for the optimized blade at both operating points. Furthermore, due to the lower pressure gradient over the tip gap in the first 20% of the meridional length, the formation of the associated vortex has been weakened. On the rear part of the blade, the onset of the deceleration is delayed from initially for the baseline geometry to for the optimized configuration. Combined with a lower diffusion rate between the velocity peak and trailing edge, this indicates a shorter region in which the flow is subject to a reduced adverse pressure gradient. Finally, the velocity peak due to incidence close to the leading edge is slightly reduced.
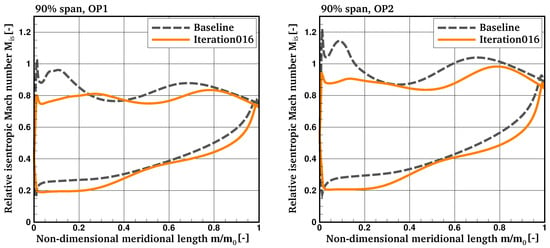
Figure 14.
Relative isentropic Mach number on the blade surface at 90% span of the baseline and the optimized geometry (Iteration016) at operating point OP1 (left) and OP2 (right).
Similar conclusions may be drawn from Figure 15 that shows the entropy generation at 90% span and downstream of the turbine wheel for both configurations at operating point OP1. The loss generation is evidently reduced for the optimized design due to a redistributed blade loading and weaker tip leakage vortex, which is visible in the attenuated wake downstream of the blade near the shroud endwall. This could be further improved using a non-radial fibered blade that has more degrees of freedom to adapt to the flow, but would require a stress evaluation inside the optimization loop to limit the stress levels introduced by the additional bending stresses.
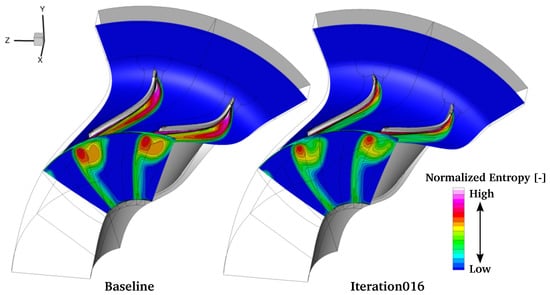
Figure 15.
Comparison of normalized entropy at 90% span of the baseline and the optimized geometry (Iteration016) at operating point OP1.
Table 2 summarizes the performance characteristics of both the baseline and optimized wheel with their relative changes at the three operating points that are also indicated in the performance map in Figure 16. The data reveals that the efficiency gains are largely due to the lower exit Mach number and hence lower exit kinetic energy, which would otherwise be wasted and not recuperated into static pressure by a downstream diffuser. This was achieved by maximizing the diffusion in the turbine wheel (in the absolute frame of reference) and reducing the pressure losses while retaining the output power of the machine at the operating points OP1 and OP2.

Table 2.
Performance summary of baseline and optimized geometry.
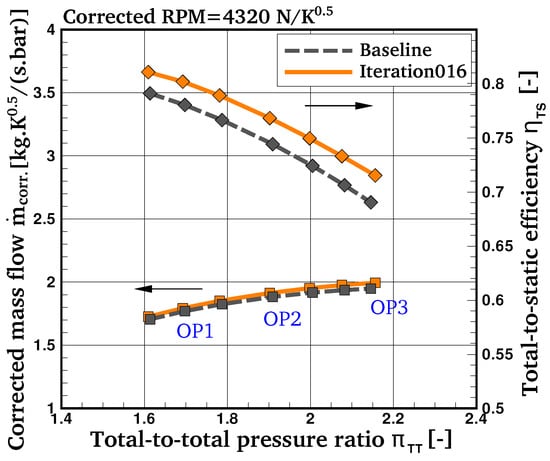
Figure 16.
Performance map of the baseline turbine wheel and the optimized geometry (Iteration016).
To verify the present design approach using radial fibered blades to ensure the mechanical integrity of the turbine in an aerodynamic optimization process, additional stress simulations were conducted with the open source structural solver CalculiX [57] . The simulations were carried out at a bursting speed that is 25% higher than the nominal rotational speed at design condition. The resulting von Mises stresses in the turbine wheel are compared in Figure 17 for both the baseline and the optimal shape, including several axial cross-sections to further illustrate that the mechanical stresses are solely due to centrifugal forces.
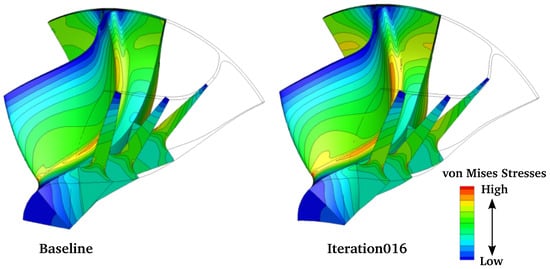
Figure 17.
Comparison of von Mises stresses in the baseline and the optimized turbine wheel (Iteration016).
The maximum von Mises stresses have only increased by approximately 3.5% relative to the baseline design, from 488 MPa to 505 MPa for a nickel based alloy (cf. Table 2), which is remarkable given that no mechanical constraint was imposed apart from the radial fibered blade approach to avoid bending stresses in the turbine wheel. Moreover, the blades have been increased in length to improve the diffusion in the wheel, and hence would explain the increased stress levels. The location of maximum stresses is in the root of the blade and may be reduced by increasing the hub fillet radius without penalizing the aerodynamic performance. The optimized turbine wheel is directly available in a CAD representation and can be used for further vibration analysis or manufacturing without any shape approximation or fitting error that may impair the optimality. Ongoing work, however, will include the stress analysis in the optimization framework to allow for blades that are not radially fibered. This will result in a much richer design space, which can only be solved efficiently by the adjoint method.
5. Conclusions
A CAD integrated adjoint framework is proposed and applied to a multipoint optimization of a turbocharger radial turbine. One of the characteristic features of this approach is a tailored shape parameterization that allows for inherently satisfying geometric constraints due to mechanical and manufacturing requirements. The core components of the algorithm are a 3D Navier–Stokes flow solver, its discrete adjoint counterpart, and libraries for the automatic CAD and grid generation. The differentiation of the CAD and grid generation is realized with the complex-step method as proof of concept in the present work that yields machine accurate design gradients while the complementary gradient information of the cost function with respect to the grid point coordinates is computed by the adjoint method. The resulting gradients have been validated against accurate complex-step gradients computed by the flow solver.
A sequential quadratic programming (SQP) algorithm is used to maximize the total-to-static efficiency of the turbine wheel at multiple operating points while constraining the output power and the choking mass flow of the machine. The optimization converged in a few design cycles in which the total-to-static efficiency could be significantly improved over a wide operating range. Additionally, the imposed aerodynamic constraints with strict convergence tolerances are satisfied and several geometric constraints were inherently respected due to the parametrization of the turbine. In particular, radial fibered blades are used to avoid bending stresses in the turbine blades due to centrifugal forces. The maximum stress levels in the optimized turbine wheel could be limited by this approach and may be reduced in a post-processing step without penalizing the aerodynamic performance.
The methodology is a significant step forward in applying gradient-based optimization to industrial relevant problems, as it maintains the optimal shape within CAD format, which eliminates manual shape approximations and allows for including manufacturing constraints such as ruled surfaces and radial fibered blades. Compared to gradient-free methods where typically one order of magnitude more computational time would be required, the methodology presented here can achieve the optimum at considerably reduced costs.
Author Contributions
Lasse Mueller developed the CFD code, its adjoint, and the grid generation as well as the complex-step implementation. Tom Verstraete developed the CAD kernel. Both authors were involved in the analysis of the results. Lasse Mueller conceived the optimization and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Roman Symbols | |||
| Identity matrix | Residual vector | ||
| J | Cost function | S | Surface |
| m | Meridional length | t | Time |
| M | Mach number | T | Temperature |
| Mass flow | Conservative variables | ||
| P | Pressure | Power | |
| P | Source term | Grid point coordinates | |
| System matrix | y | Non-dimensional wall distanc | |
| Superscripts | |||
| n | Pseudo time step | ||
| m | Number of Runge–Kutta stages | ||
| Subscripts | |||
| 0 | Total condition | m | Number of Runge–Kutta stages |
| 1 | Inlet | ref | Reference |
| 2 | Outlet | TS | Total-to-static |
| is | Isentropic | vM | von Mises |
| Greek Symbols | |||
| Absolute flow angle | Camber line circumferential position | ||
| Runge–Kutta stage coefficient | Grid points in computational space | ||
| Design variables | Pressure ratio | ||
| Difference | Mechanical stresses | ||
| Efficiency | Adjoint variables | ||
| Abbrevations | |||
| AD | Algorithmic Differentiation | ||
| BFGS | Broyden–Fletcher–Goldfarb–Shanno | ||
| BRep | Boundary representation | ||
| CAE | Computer Aided Engineering | ||
| CAD | Computer Aided Design | ||
| CEV | Constant Eddy Viscosity | ||
| Constr | Constraint | ||
| FFD | Free-Form Deformation | ||
| GMRES | Generalized Minimal Residual Method | ||
| ILU(0) | Incomplete Lower Upper factorization with zero fill-in | ||
| JT-KIRK | Jacobian Trained Krylov Implicit Runge–Kutta | ||
| KKT | Karush–Kuhn–Tucker | ||
| MUSCL | Monotonic Upstream-Centered Scheme for Conservation Laws | ||
| NURBS | Non-Uniform Rational Basis-Spline | ||
| Obj | Objective | ||
| OP | Operating Point | ||
| PETSc | Portable, Extensible Toolkit for Scientific Computation | ||
| RANS | Reynolds-Averaged Navier–Stokes | ||
| RPM | Revolutions per minute | ||
| SNOPT | Sparse Nonlinear OPTimizer | ||
| SQP | Sequential Quadratic Programming | ||
| STEP | STandard for the Exchange of Product model data | ||
References
- Verstraete, T.; Amaral, S.; Van den Braembussche, R.; Arts, T. Design and Optimization of the Internal Cooling Channels of a High Pressure Turbine Blade, Part 2 Optimization. J. Turbomach. 2010, 132, 021014. [Google Scholar] [CrossRef]
- Siller, U.; Voß, C.; Nicke, E. Automated Multidisciplinary Optimization of a Transonic Axial Compressor. In Proceedings of the 47th AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Mueller, L.; Alsalihi, Z.; Verstraete, T. Multidisciplinary Optimization of a Turbocharger Radial Turbine. J. Turbomach. 2013, 135, 021022. [Google Scholar] [CrossRef]
- Shahpar, S.; Caloni, S. Aerodynamic Optimization of High-Pressure Turbines for Lean-Burn Combustion System. J. Eng. Gas Turbines Power 2013, 135, 055001. [Google Scholar] [CrossRef]
- Pironneau, O. On Optimum Design in Fluid Mechanics. J. Fluid Mech. 1974, 64, 97–110. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic Design via Control Theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef]
- Campobasso, M.S.; Duta, M.C.; Giles, M.G. Adjoint Calculation of Sensitivities of Turbomachinery Objective Functions. J. Propuls. Power 2003, 19, 693–703. [Google Scholar] [CrossRef]
- Wu, H.-Y.; Liu, F.; Tsai, H.-M. Aerodynamic Design of Turbine Blades Using an Adjoint Equation Method. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Papadimitriou, D.I.; Giannakoglou, K.C. Total Pressure Loss Minimization in Turbomachinery Cascades Using a New Continuous Adjoint Formulation. J. Power Energy 2007, 221, 865–872. [Google Scholar] [CrossRef]
- Marta, A.C.; Shankaran, S.; Holmes, D.G.; Stein, A. Development of Adjoint Solvers for Engineering Gradient-Based Turbomachinery Design Applications. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 8–12 June 2009. [Google Scholar]
- Luo, J.; Liu, F.; McBean, I. Turbine Blade Row Optimization Through Endwall Contouring by an Adjoint Method. J. Propuls. Power 2015, 31, 505–518. [Google Scholar] [CrossRef]
- Corral, R.; Gisbert, F. Profiled End Wall Design Using an Adjoint Navier-Stokes Solver. J. Turbomach. 2008, 130, 021011. [Google Scholar] [CrossRef]
- Wang, D.X.; He, L. Adjoint Aerodynamic Design Optimization for Blades in Multi-Stage Turbomachines: Part 1—Methodology and Verification. J. Turbomach. 2010, 132, 021011. [Google Scholar] [CrossRef]
- Wang, D.X.; He, L.; Li, Y.S.; Wells, R.G. Adjoint Aerodynamic Design Optimization for Blades in Multi-Stage Turbomachines: Part 2—Verification and Application. J. Turbomach. 2010, 132, 021012. [Google Scholar] [CrossRef]
- Shahpar, S.; Caloni, S. Adjoint Optimisation of a High Pressure Turbine Stage for Lean-Burn Combustion System. In Proceedings of the 10th European Conference on Turbomachinery, Fluid Dynamics and Thermodynamics, Lappeenranta, Finland, 15–19 April 2013. [Google Scholar]
- Walther, B.; Nadarajah, S. Optimum Shape Design for Multirow Turbomachinery Configurations Using a Discrete Adjoint Approach and an Efficient Radial Basis Function Deformation Scheme for Complex Multiblock Grids. J. Turbomach. 2015, 137, 081006. [Google Scholar] [CrossRef]
- Hicks, R.; Henne, P. Wing Design by Numerical Optimization. J. Aircr. 1978, 15, 407–412. [Google Scholar] [CrossRef]
- Sonderberg, T.W.; Parry, S.R. Free-Form Deformation of Solid Geometric Models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1986, Dallas, TX, USA, 18–22 August 1986; pp. 151–160. [Google Scholar]
- Leal, N.; Leal, E.; Branch, J.W. Simple Method for Constructing Nurbs Surfaces From Unorganized Points. In Proceedings of the 19th International Meshing Roundtable, Chattanooga, TN, USA, 3–6 October 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 161–175. [Google Scholar]
- Becker, G.; Schaefer, M.; Jameson, A. An Advanced NURBS Fitting Procedure for Post-Processing of Grid-Based Shape Optimizations. In Proceedings of the 49th AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Robinson, T.T.; Armstrong, C.G.; Chua, H.S.; Othmer, C.; Grahs, T. Optimizing Parameterized CAD Geometries Using Sensitivities Based on Adjoint Functions. Comput. Aided Des. Appl. 2012, 9, 253–268. [Google Scholar] [CrossRef]
- Vasilopoulos, I.; Flassig, P.; Meyer, M. CAD-Based Aerodynamic Optimization of a Compressor Stator Using Conventional and Adjoint-Driven Approaches. In Proceedings of the ASME Turbo Expo, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Banovic, M.; Mykhaskiv, O.; Auriemma, S.; Walther, A.; Legrand, H.; Mueller, J.-D. Automatic Differentiation of the Open CASCADE Technology CAD System and Its Coupling with an Adjoint CFD Solver. Optim. Methods Softw. 2017. submitted. Available online: www.optimization-online.org/DB_FILE/2017/03/5931.pdf (accessed on May 2017).
- Verstraete, T.; Mueller, L.; Mueller, J.-D. Adjoint Based Design Optimisation of an Internal Cooling Channel U-Bend for Minimised Pressure Losses. Int. J. Turbomach. Propuls. Power 2017, 2, 10. [Google Scholar] [CrossRef]
- Yu, G.; Mueller, J.-D.; Jones, D.; Christakopoulos, F. CAD-Based Shape Optimization Using Adjoint Sensitivities. Comput. Fluids 2011, 46, 512–516. [Google Scholar] [CrossRef]
- Xu, S.; Jahn, W.; Mueller, J.-D. CAD-Based Shape Optimization with CFD Using a Discrete Adjoint. Int. J. Numer. Methods Fluids 2014, 74, 153–168. [Google Scholar] [CrossRef]
- Xu, S.; Radford, D.; Meyer, M.; Mueller, J.-D. CAD-Based Shape Optimisation of a One Stage Turbine with Geometric Constraints. In Proceedings of the ASME Turbo Expo, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Lyness, J.N.; Moler, C.B. Numerical Differentiation of Analytical Functions. SIAM J. Numer. Anal. 1967, 4, 202–210. [Google Scholar] [CrossRef]
- Martins, J.R.; Sturdza, P.; Alonso, J.J. The Complex-Step Derivative Approximation. ACM Trans. Mathe. Softw. 2003, 29, 245–262. [Google Scholar] [CrossRef]
- Sturdza, P. Complex-Step Guide—C/C++. Available online: http://mdolab.engin.umich.edu/content/complex-step-guide-cc (accessed on April 2016).
- Torreguitart, I.S.; Verstraete, T.; Mueller, L. CAD Kernel and Grid Generation Algorithmic Differentiation for Turbomachinery Adjoint Optimization. In VII European Congress on Computational Methods in Applied Sciences and Engineering, Proceedings of the ECCOMAS Congress, Crete Island, Greece, 5–10 June 2016; Papadrakakis, M., Papadopoulos, V., Stefanou, G., Plevris, V., Eds.; ECCOMAS: Barcelona, Spain, 2016. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. An SQP Algorithm for Large-Scale Constrained Optimization. SIAM J. Optim. 2002, 12, 979–1006. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. User’s Guide for SNOPT Version 7: Software for Large-Scale Nonlinear Programming; University of California: San Diego, CA, USA, 2008. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. Some Theoretical Properties of an Augmented Lagrangian Merit Function; Technical Report SOL 86-6R; Stanford University: Stanford, CA, USA, 1986. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear Programing. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1950; Neyman, J., Ed.; University of California Press: Oakland, CA, USA, 1951; pp. 481–492. [Google Scholar]
- Verstraete, T. CADO: A Computer Aided Design and Optimization Tool for Turbomachinery Applications. In Proceedings of the 2nd International Conference on Engineering Optimization, Lisbon, Portugal, 6–9 September 2010. [Google Scholar]
- Stroud, I. Boundary Representation Modelling Techniques; Springer: London, UK, 2006; Volume 1. [Google Scholar]
- Miller, P.L.; Olivier, J.H.; Miller, P.D.; Tweedt, D.L. BladeCAD: An Interactive Geometric Design Tool for Turbomachinery Blades; Technical Report TM-107262; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1996.
- Thompson, J.F.; Thames, F.C.; Mastin, C.W. Automatic Numerical Generation of Body-Fitted Curvilinear Coordinates for a Field Containing Any Number of Arbitrary Two-Dimensional Bodies. J. Comput. Phys. 1974, 15, 299–319. [Google Scholar] [CrossRef]
- Steger, J.L.; Sorenson, R.L. Automatic Mesh-Point Clustering Near a Boundary in Grid Generation with Elliptic Partial Differential Equations. J. Comput. Phys. 1979, 33, 403–410. [Google Scholar] [CrossRef]
- White, J.A. Elliptic Grid Generation with Orthogonality and Spacing Control on an Arbitrary Number of Boundaries. In Proceedings of the 21st AIAA Fluid Dynamics, Plasma Dynamics and Lasers Conference, Seattle, WA, USA, 18–20 June 1990. [Google Scholar]
- Thomas, P.D.; Middlecoff, J.F. Direct Control of the Grid Point Distribution in Meshes Generated by Elliptic Equations. AIAA J. 1980, 18, 652–656. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the Ultimate Conservative Difference Scheme. V. A Second Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Venkatakrishnan, V. On the Accuracy of Limiters and Convergence to Steady State Solutions. In Proceedings of the 31st AIAA Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
- Harten, A.; Hyman, J.M. Self-Adjusting Grid Methods for One-Dimensional Hyperbolic Conservation Laws. J. Comput. Phys. 1983, 50, 235–269. [Google Scholar] [CrossRef]
- Allmaras, S.R.; Johnson, F.T.; Spalart, P.R. Modifications and Clarifications for the Implementation of the Spalart-Allmaras Turbulence Model. In Proceedings of the 7th International Conference on Computational Fluid Dynamics (ICCFD7-1902), Big Island, HI, USA, 9–13 July 2012. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 2nd ed.; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Jirásek, A. Mass Flow Boundary Conditions for Subsonic Inflow and Outflow Boundary. AIAA J. 2006, 44, 939–947. [Google Scholar] [CrossRef]
- Xu, S.; Radford, D.; Meyer, M.; Müller, J.-D. Stabilisation of Discrete Steady Adjoint Solvers. J. Comput. Phys. 2015, 299, 175–196. [Google Scholar] [CrossRef]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Brown, J.; Brune, P.; Buschelman, K.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; et al. PETSc/Tao. Portable, Extensible Toolkit for Scientific Computation. Available online: http://www.mcs.anl.gov/petsc (accessed on April 2014).
- Nielsen, E.J.; Lu, J.; Park, M.A.; Darmofal, D.L. An Implicit, Exact Dual Adjoint Solution Method for Turbulent Flows on Unstructured Grids. Comput. Fluids 2004, 33, 1131–1155. [Google Scholar] [CrossRef]
- Dwight, R.P.; Brezillon, J. Efficient and Robust Algorithms for Solution of the Adjoint Compressible Navier-Stokes Equations with Applications. Int. J. Numer. Methods Fluids 2009, 60, 365–389. [Google Scholar] [CrossRef]
- Hascoët, L.; Pascual, V. The Tapenade Automatic Differentiation tool: Principles, Model, and Specification. ACM Trans. Math. Softw. 2013, 39, 20. [Google Scholar] [CrossRef]
- Dwight, R.P.; Brezillion, J. Effect of Approximation of the Discrete Adjoint on the Gradient-Based Optimization. AIAA J. 2006, 4412, 3022–3031. [Google Scholar] [CrossRef]
- Marta, A.C.; Shankaran, S. On the Handling of Turbulence Equations in RANS Adjoint Solvers. Comput. Fluids 2013, 74, 102–113. [Google Scholar] [CrossRef]
- Dhondt, G.; Wittig, K. CALCULIX. A Free Software Three-Dimensional Structural Finite Element Program. 1998. Available online: www.calculix.de.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).