Time, Space, and Dynamic Split of Loss Sources in LPT by Means of Phase-Locked Proper Orthogonal Decomposition †
Abstract
1. Introduction
2. Large Eddy Simulation
3. Fundamental Equations
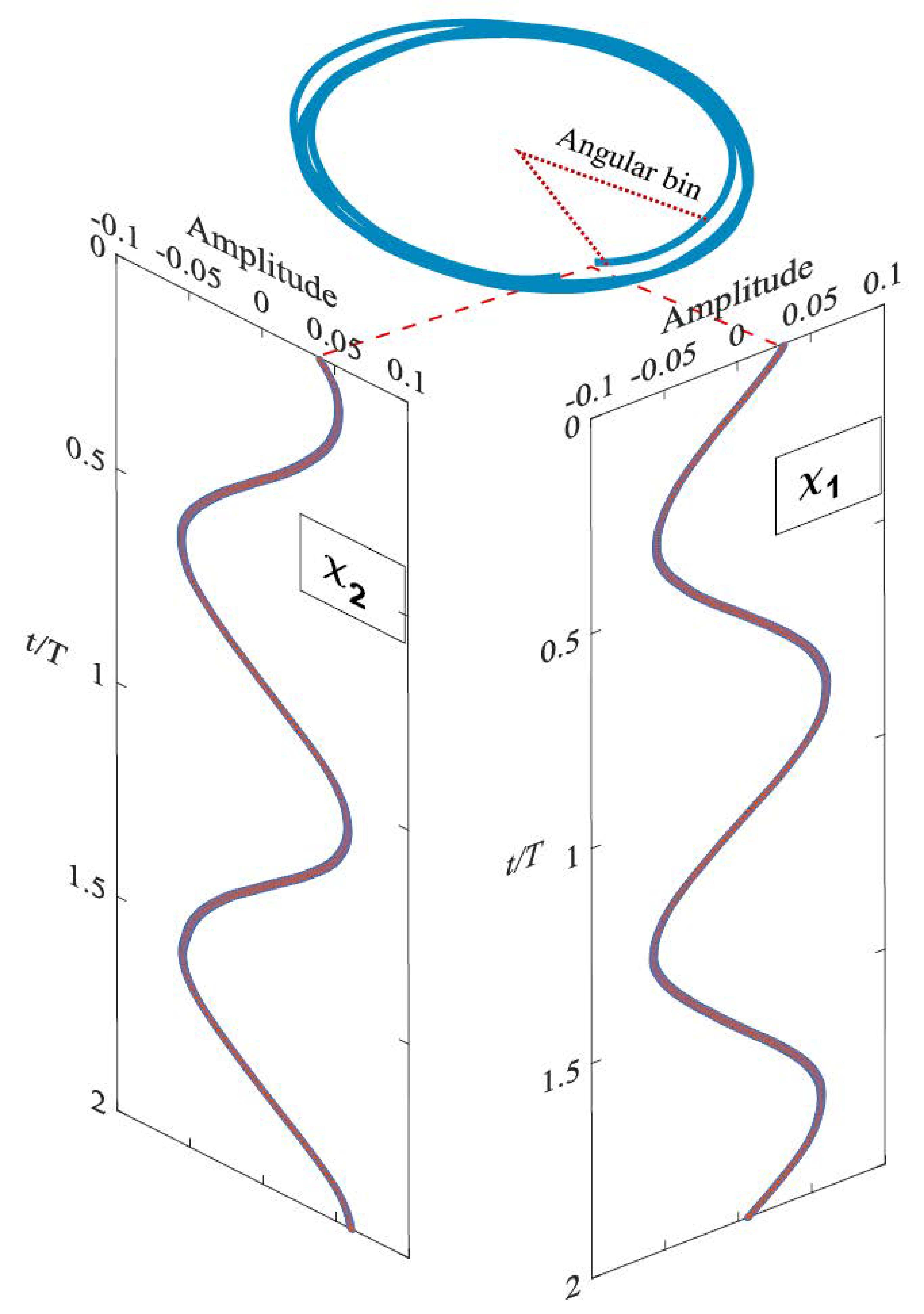
4. Data Processing
5. Results and Discussion
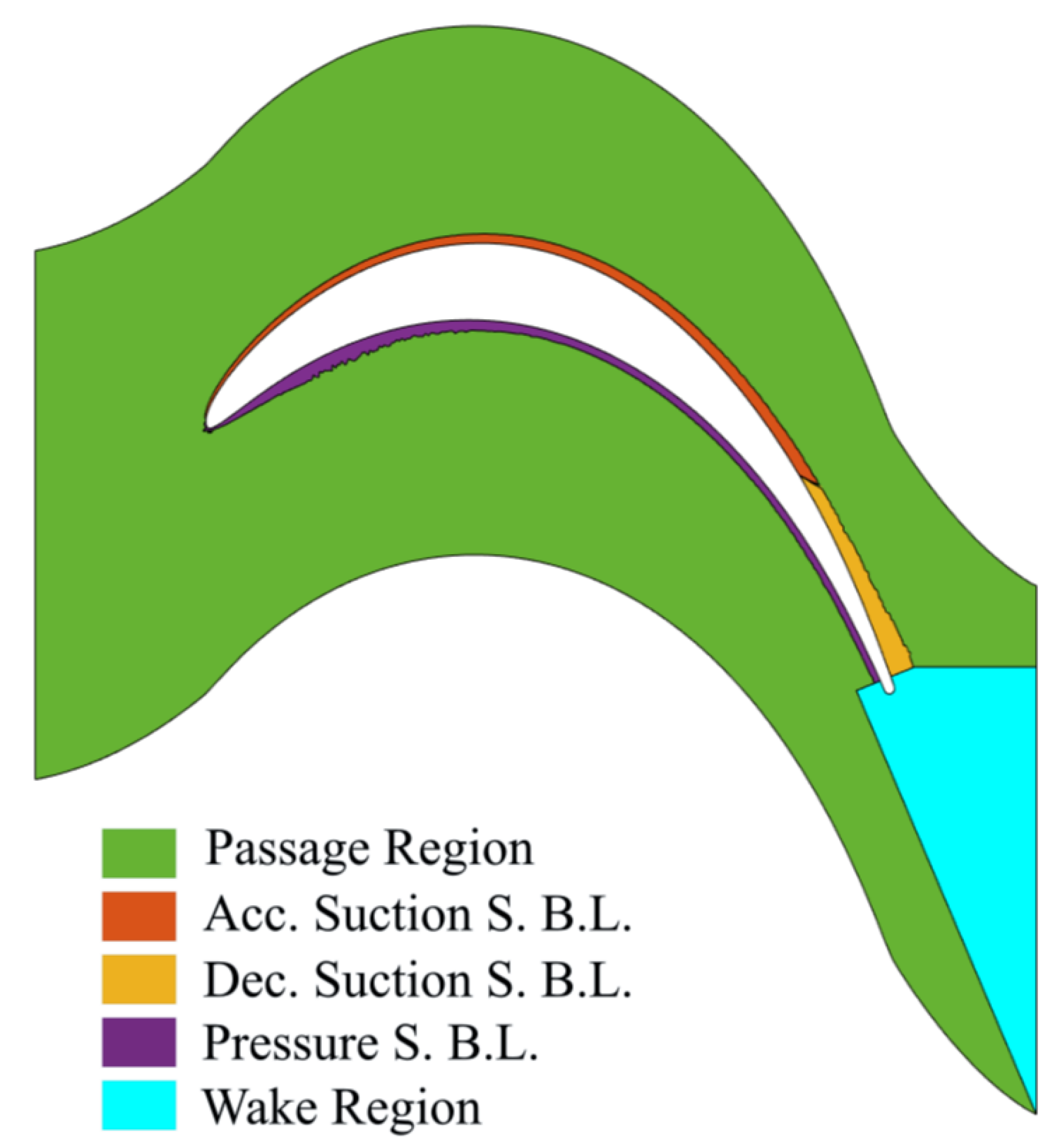
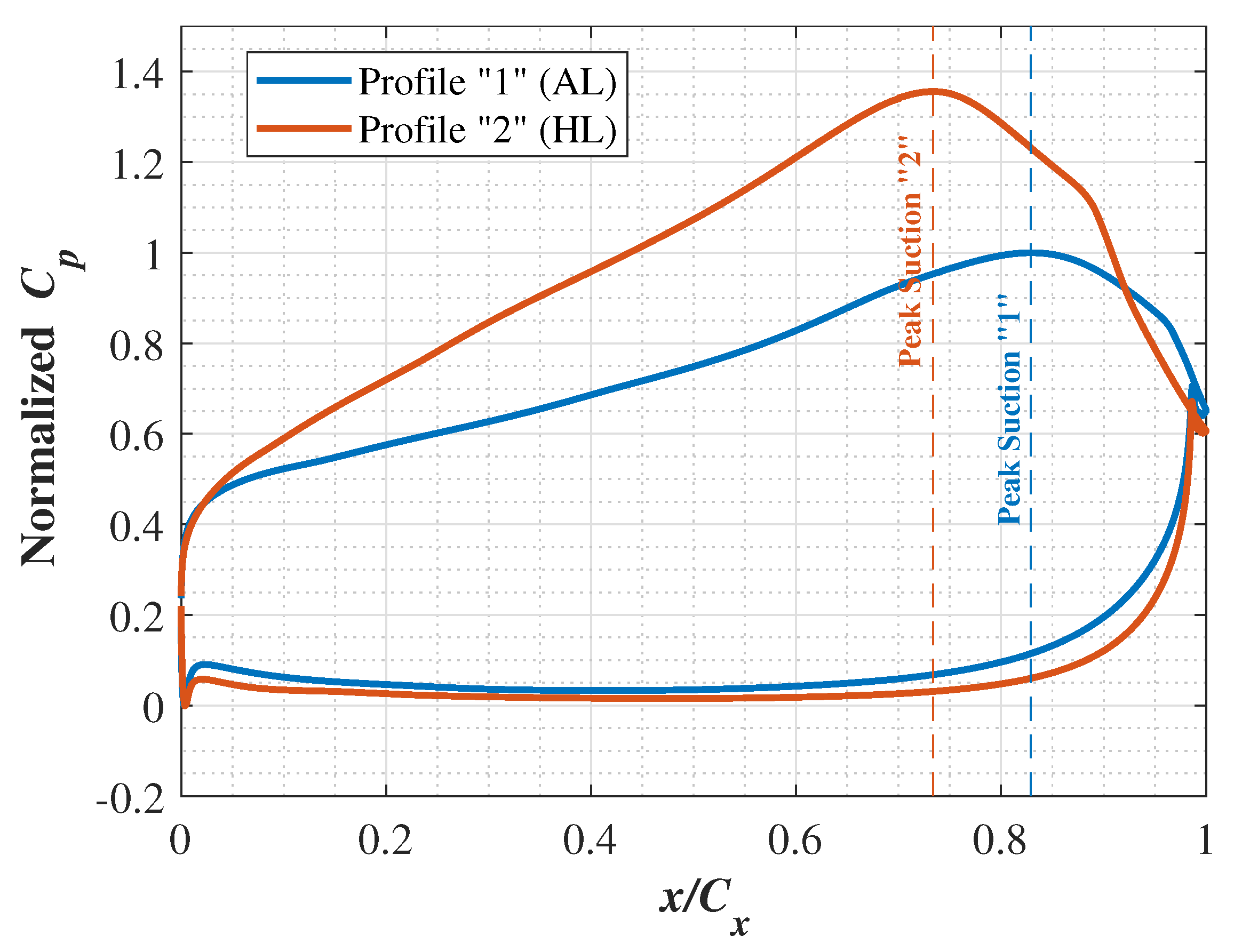
5.1. Overall Performance Analysis
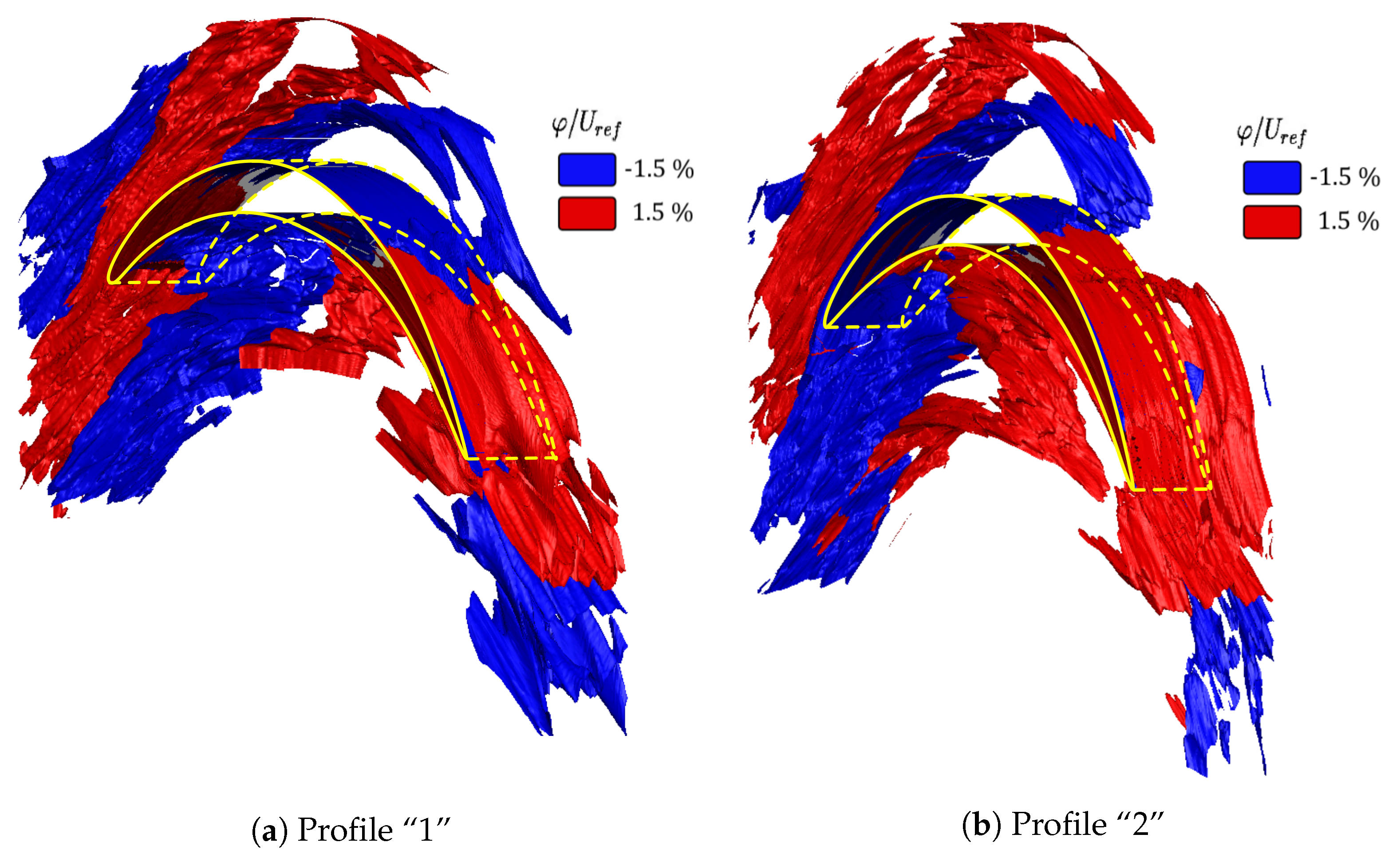
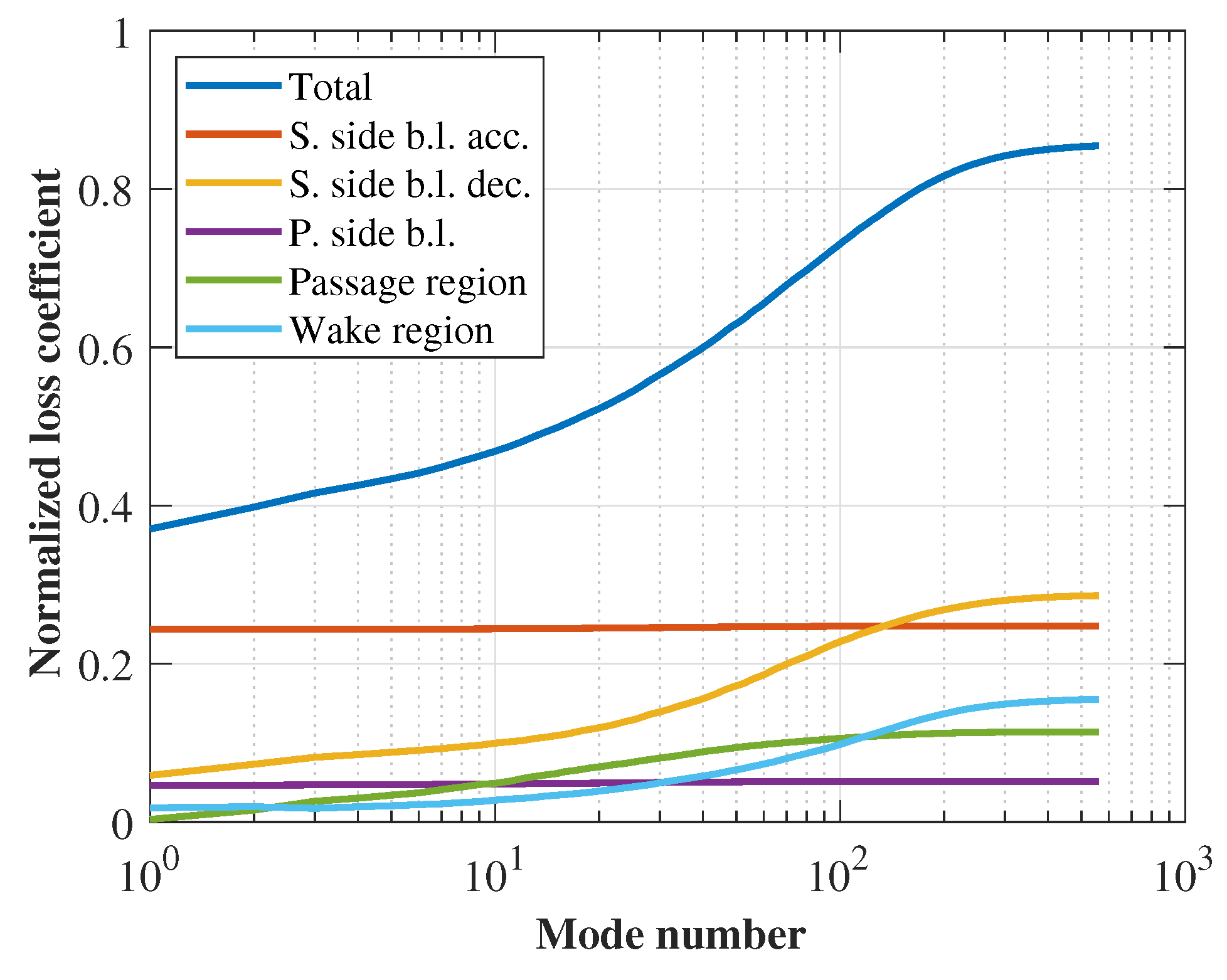
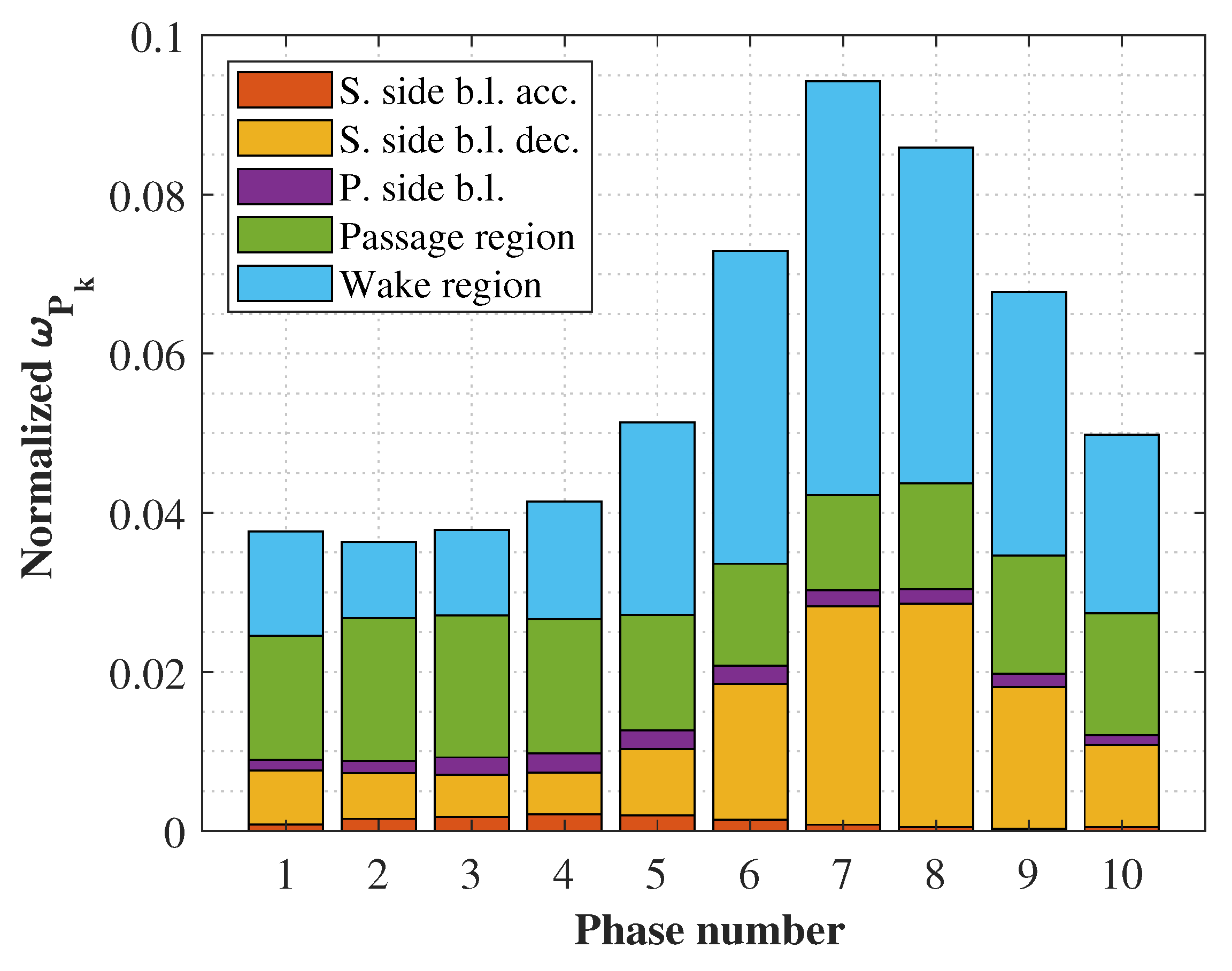
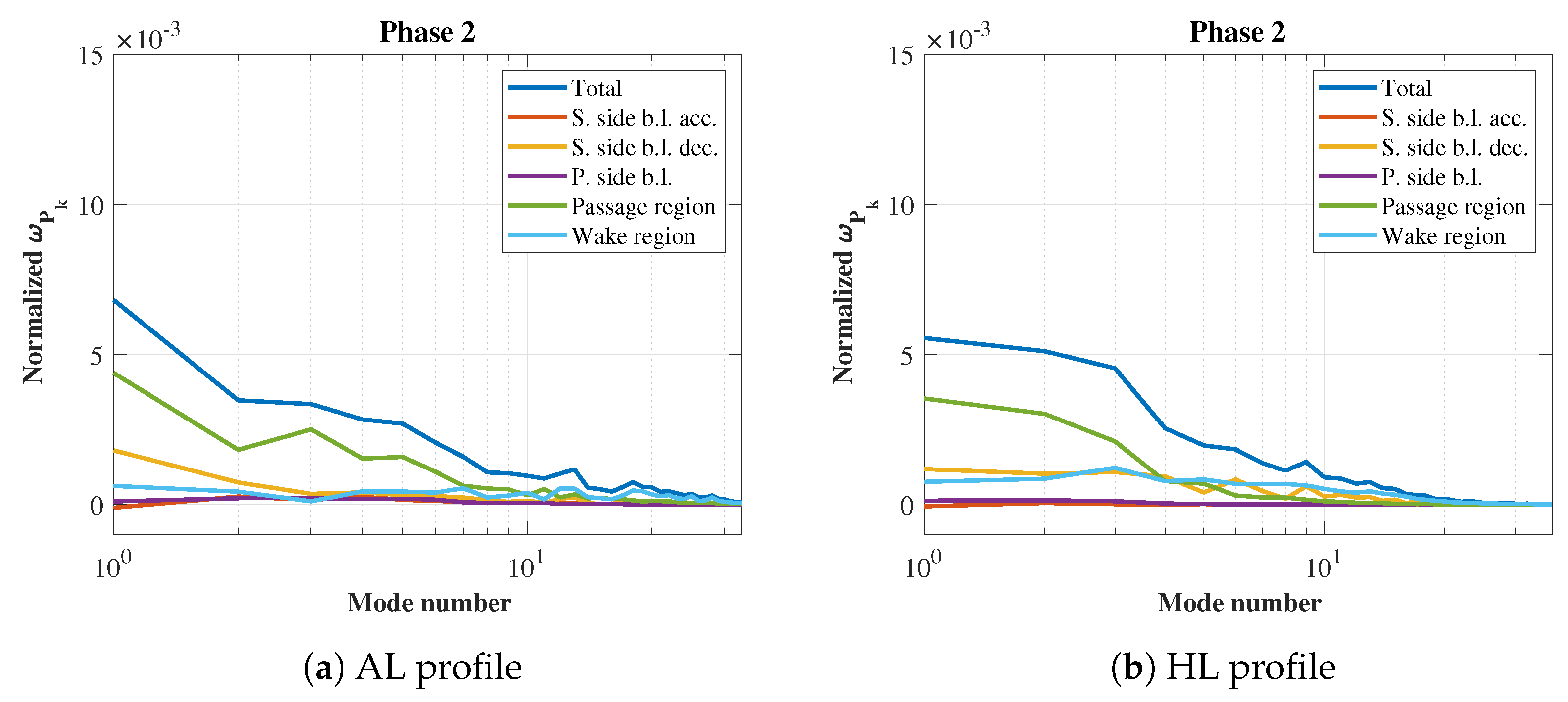
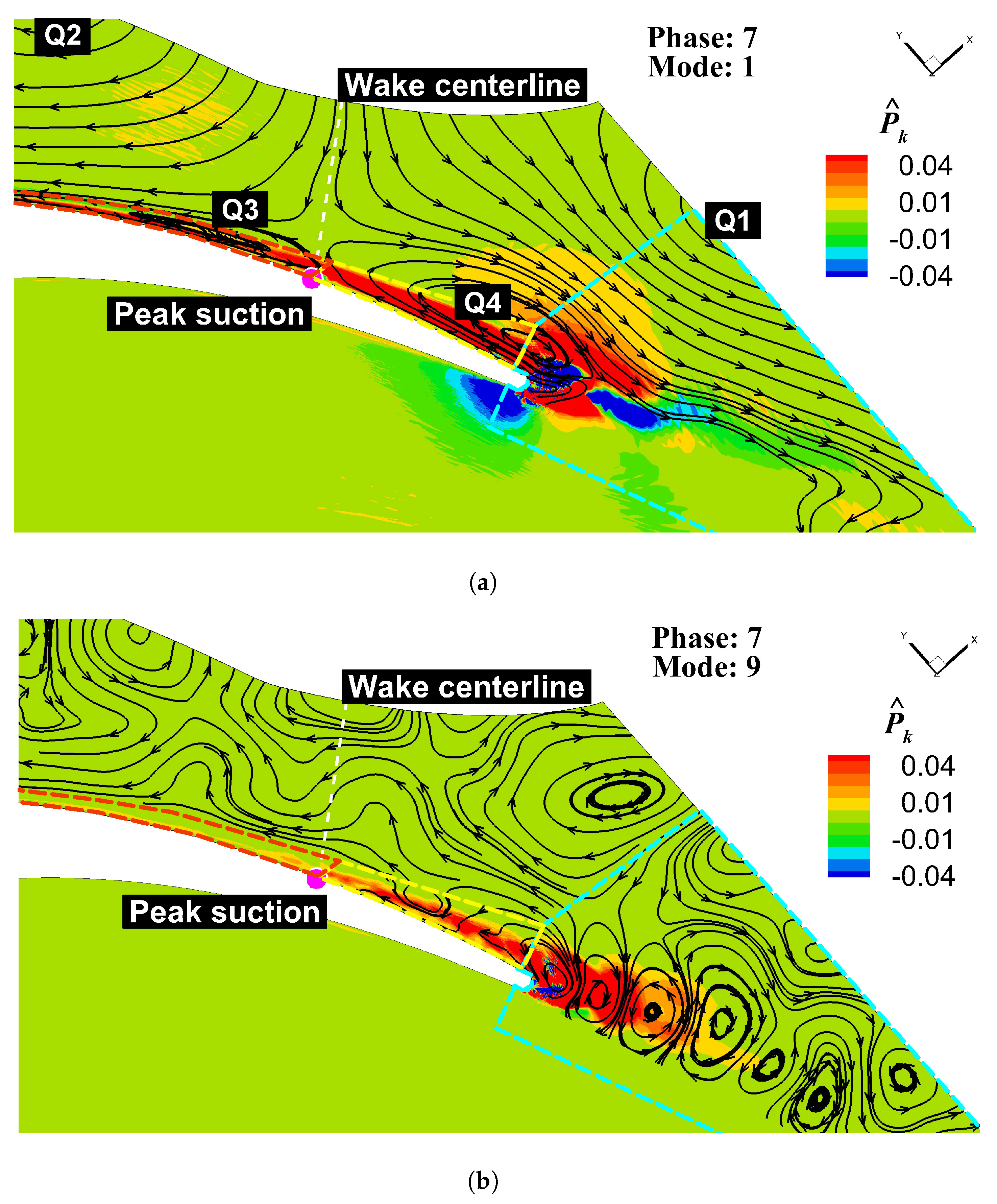
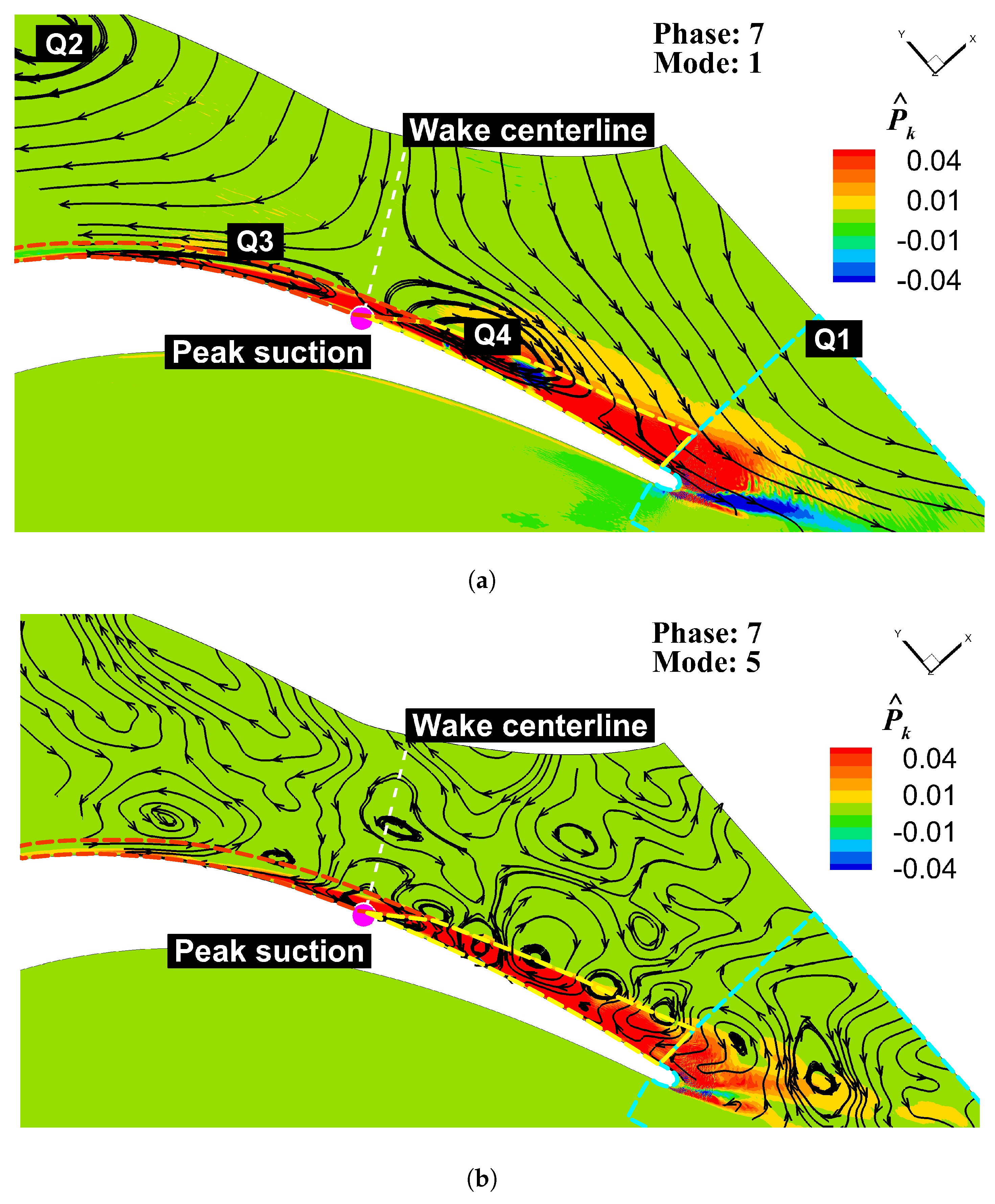
5.2. Loss Distribution Within Wake-Passing Cycle
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman symbols | |
| t | Time [s] |
| p | Pressure [Pa] |
| C | Chord [m] |
| Volume [m3] | |
| k | Turbulent kinetic energy [J kg−1] |
| V | Velocity [m s−1] |
| u | Velocity component [m s−1] |
| Mass flow rate [kg s−1] | |
| Re | Reynolds number, based on outlet velocity |
| Ma | Mach number |
| St | Strouhal number |
| AG | Dimensionless rotor-vane axial gap |
| Greek symbols | |
| ν | Kinematic viscosity [m2 s−1] |
| μ | Dynamic viscosity [Pa s] |
| ρ | Density [kg m−3] |
| τ | Viscous stress tensor [Pa] |
| ϕ | Flow coefficient [-] |
| Subscripts | |
| x | Axial component value |
| Axial chord-defined value | |
| t | Total/stagnation value |
| 1 | Inlet section value |
| 2 | Outlet section value |
| i | x-axis component value |
| j | y-axis component value |
| Superscripts | |
| Time rate value | |
| Time-averaged value | |
| Time-fluctuating component value | |
Abbreviations
| CFD | Computational Fluid Dynamics; |
| LES | Large Eddy Simulation; |
| DNS | Direct Numerical Simulation; |
| URANS | Unsteady Reynolds Averaged Navier–Stokes; |
| WALE | Wall-Adapting Local Eddy-viscosity; |
| FV | Finite Volume; |
| POD | Proper Orthogonal Decomposition; |
| PPOD | Phase-locked Proper Orthogonal Decomposition; |
| TKE | Turbulent Kinetic Energy; |
| LPT | Low-Pressure Turbine; |
| FTT | Flow Through Time; |
| BL | Boundary Layer; |
| HPC | High-Performance Computing; |
| ML | Machine Learning; |
| PIV | Particle Image Velocimetry; |
| F.A.S.P. | Flux of Average Stagnation Pressure; |
| F.T.K.E. | Flux of Turbulent Kinetic Energy; |
| V.D. | Viscous Diffusion; |
| T.D. | Turbulent Diffusion; |
| P.D. | Pressure Diffusion. |
References
- Denton, J.D. Loss mechanisms in turbomachines. J. Turbomach. 1993, 115, V002T14A001. [Google Scholar] [CrossRef]
- Rose, M.G.; Harvey, N.W. Turbomachinery wakes: Differential work and mixing losses. J. Turbomach. 2000, 122, 68–77. [Google Scholar] [CrossRef]
- Stieger, R.D.; Hodson, H.P. The unsteady development of a turbulent wake through a downstream low-pressure turbine blade passage. J. Turbomach. 2005, 127, 388–394. [Google Scholar] [CrossRef]
- Hodson, H.P.; Howell, R.J. Bladerow interactions, transition, and high-lift aerofoils in low-pressure turbines. Annu. Rev. Fluid Mech. 2005, 37, 71–98. [Google Scholar] [CrossRef]
- Sarkar, S.; Voke, P.R. Large-eddy simulation of unsteady surface pressure over a low-pressure turbine blade due to interactions of passing wakes and inflexional boundary layer. J. Turbomach. 2006, 128, 221–231. [Google Scholar] [CrossRef]
- Sterzinger, P.Z.; Zerobin, S.; Merli, F.; Wiesinger, L.; Peters, A.; Maini, G.; Dellacasagrande, M.; Heitmeir, F.; Göttlich, E. Impact of varying high- and low-pressure turbine purge flows on a turbine center frame and low-pressure turbine system. J. Turbomach. 2020, 142, 101011. [Google Scholar] [CrossRef]
- Canepa, E.; Cattanei, A.F.; Mazzocut Zecchin, F.; Milanese, G.; Parodi, D. Experimental study of the effect of the rotor-stator gap variation on the tonal noise generated by low-speed axial fans. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013; p. 2046. [Google Scholar]
- Schulte, V.; Hodson, H.P. Unsteady Wake-Induced Boundary Layer Transition in High Lift LP Turbines. J. Turbomach. 1998, 120, 28–35. [Google Scholar] [CrossRef]
- Wu, X.; Jacobs, R.G.; Hunt, J.C.R.; Durbin, P.A. Simulation of boundary layer transition induced by periodically passing wakes. J. Fluid Mech. 1999, 398, 109–153. [Google Scholar] [CrossRef]
- Lengani, D.; Simoni, D.; Ubaldi, M.; Zunino, P.; Bertini, F. Coherent structures formation during wake-boundary layer interaction on a LP turbine blade. Flow Turbul. Combust. 2017, 98, 57–81. [Google Scholar]
- Sandberg, R.D.; Michelassi, V. Fluid dynamics of axial turbomachinery: Blade- and stage-level simulations and models. Annu. Rev. Fluid Mech. 2022, 54, 255–285. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation; Nauka: Moscow, Russia, 1967; pp. 166–178. [Google Scholar]
- Liu, Z.; Adrian, R.J.; Hanratty, T.J. Large-scale modes of turbulent channel flow: Transport and structure. J. Fluid Mech. 2001, 448, 53–80. [Google Scholar] [CrossRef]
- Kurelek, J.W.; Lambert, A.R.; Yarusevych, S. Coherent structures in the transition process of a laminar separation bubble. AIAA J. 2016, 54, 2295–2309. [Google Scholar] [CrossRef]
- Canepa, E.; Lengani, D.; Nilberto, A.; Petronio, D.; Simoni, D.; Bertini, F.; Rosa Taddei, S. Flow coefficient and reduced frequency effects on low pressure turbine unsteady losses. J. Propuls. Power 2022, 38, 18–29. [Google Scholar] [CrossRef]
- Dellacasagrande, M.; Sterzinger, P.Z.; Zerobin, S.; Merli, F.; Wiesinger, L.; Peters, A.; Maini, G.; Heitmeir, F.; Göttlich, E. Unsteady Flow Interactions Between a High- and Low-Pressure Turbine: Part 2—Rotor-Synchronic Averaging and Proper Orthogonal Decomposition of the Unsteady Flow Fields. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; Volume 2A. [Google Scholar]
- Russo, M.; Carlucci, A.; Dellacasagrande, M.; Petronio, D.; Lengani, D.; Simoni, D.; Bellucci, J.; Giovannini, M.; Granata, A.A.; Gily, M.; et al. Optimization of Low-Pressure Turbine Blade by Means of Fine Inspection of Loss Production Mechanisms. J. Turbomach. 2024, 147, 041005. [Google Scholar] [CrossRef]
- Dellacasagrande, M.; Lengani, D.; Simoni, D.; Ubaldi, M.; Granata, A.A.; Giovannini, M.; Rubechini, F.; Bertini, F. Analysis of Unsteady Loss Sensitivity to Incidence Angle Variation in Low Pressure Turbine. In Proceedings of the ASME Turbo Expo 2023: Turbomachinery Technical Conference and Exposition, Boston, MA, USA, 26–30 June 2023; Volume 13B. [Google Scholar]
- Lengani, D.; Simoni, D.; Pichler, R.; Sandberg, R.D.; Michelassi, V.; Bertini, F. Identification and quantification of losses in a LPT cascade by POD applied to LES data. Int. J. Heat Fluid Flow 2018, 70, 28–40. [Google Scholar] [CrossRef]
- van Oudheusden, B.W.; Scarano, F.; van Hinsberg, N.P.; Watt, D.W. Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 2005, 39, 86–98. [Google Scholar] [CrossRef]
- Perrin, R.; Braza, M.; Cid, E.; Cazin, S.; Barthet, A.; Sevrain, A.; Mockett, C.; Thiele, F. Obtaining phase averaged turbulence properties in the near wake of a circular cylinder at high Reynolds number using POD. Exp. Fluids 2007, 43, 341–355. [Google Scholar] [CrossRef]
- Russo, M.; Dellacasagrande, M.; Satta, F.; Lengani, D.; Simoni, D.; Giovannini, M.; Bellucci, J.; Granata, A.A.; Gily, M. Time, Space and Dynamic Split of Loss Sources in LPT by Means of Phase-locked Proper Orthogonal Decomposition. In Proceedings of the 16th European Turbomachinery Conference, Paper n. ETC2025-188, Hannover, Germany, 24–28 March 2025; Available online: https://www.euroturbo.eu/publications/conference-proceedings-repository/ (accessed on 15 May 2025).
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Benhamadouche, S.; Jarrin, N.; Addad, Y.; Laurence, D. Synthetic turbulent inflow conditions based on a vortex method for large-eddy simulation. Prog. Comput. Fluid Dyn. 2006, 6, 50–57. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Lengani, D.; Simoni, D.; Ubaldi, M.; Zunino, P.; Bertini, F.; Michelassi, V. Accurate Estimation of Profile Losses and Analysis of Loss Generation Mechanisms in a Turbine Cascade. J. Turbomach. 2017, 139, 121007. [Google Scholar] [CrossRef]
- Przytarski, P.; Lengani, D.; Simoni, D.; Wheeler, A.P.S. The Role of Turbulence Transport in Mechanical Energy Budgets. J. Turbomach. 2024, 146, 101008. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures, Parts I, II and III. Quart. Appl. Math. 1987, 45, 561–590. [Google Scholar] [CrossRef]
- Lengani, D.; Simoni, D.; Nilberto, A.; Ubaldi, M.; Zunino, P.; Bertini, F. Synchronization of multi-plane measurement data by means of POD: Application to unsteady boundary layer transition. Exp. Fluids 2018, 59, 1–18. [Google Scholar] [CrossRef]
- Hekmati, A.; Ricot, D.; Druault, P. About the convergence of POD and EPOD modes computed from CFD simulation. Comput. Fluids 2011, 50, 60–71. [Google Scholar] [CrossRef]
- Biassoni, D.; Russo, M.; Viviani, P.; Vitali, G.; Lengani, D. A High-Performance Code for Analyzing Loss Transport Equations in High-Fidelity Simulations. In Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024; Volume 12C. [Google Scholar]
- Leggett, J.; Priebe, S.; Shabbir, A.; Michelassi, V.; Sandberg, R.; Richardson, E. Loss prediction in an axial compressor cascade at off-design incidences with free stream disturbances using large eddy simulation. J. Turbomach. 2018, 140, 7. [Google Scholar] [CrossRef]
- Michelassi, V.; Chen, L.; Pichler, R.; Sandberg, R.; Bhaskaran, R. High-fidelity simulations of low-pressure turbines: Effect of flow coefficient and reduced frequency on losses. J. Turbomach. 2016, 138, 11. [Google Scholar] [CrossRef]
- Simoni, D.; Berrino, M.; Ubaldi, M.; Zunino, P.; Bertini, F. Off-design performance of a highly loaded low pressure turbine cascade under steady and unsteady incoming flow conditions. J. Turbomach. 2015, 137, 7. [Google Scholar] [CrossRef]

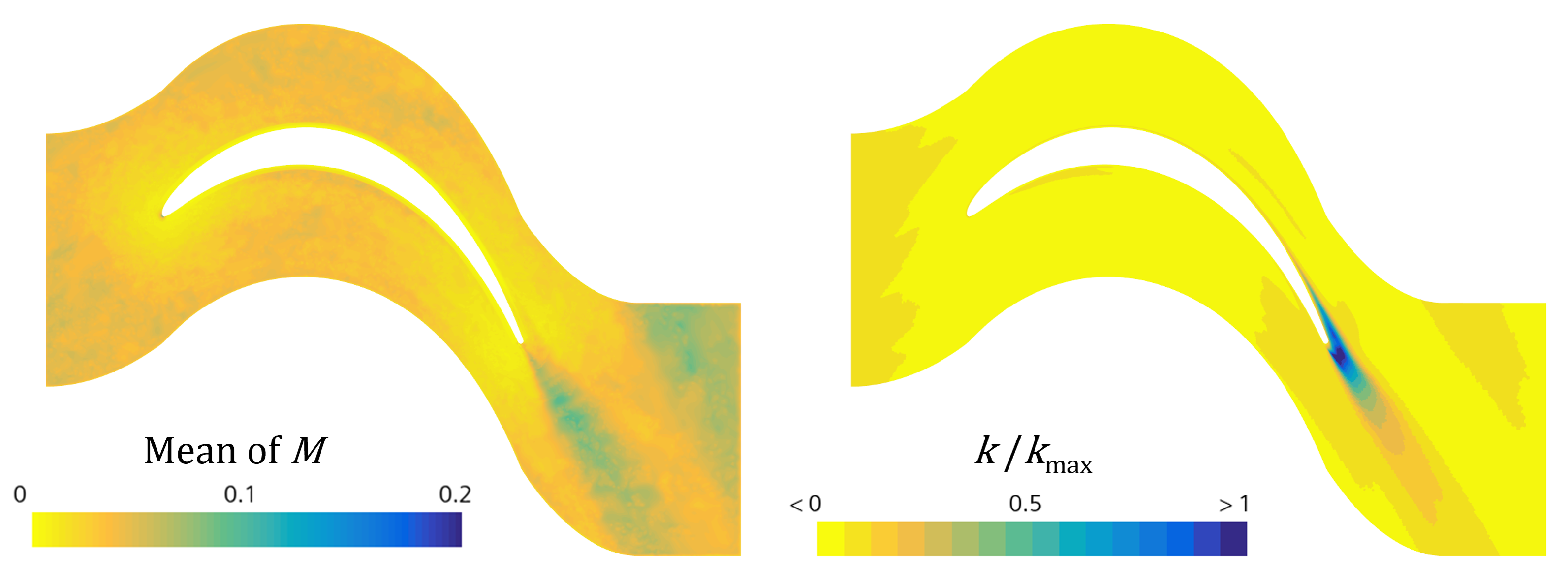




| Profile | “1” | “2” |
|---|---|---|
| 1.1 | 1.1 | |
| 1.11 | 1.11 | |
| St | 1.08 | 0.73 |
| AG | 0.65 | 0.65 |
| Profile | “1” | “2” |
|---|---|---|
| Exp. loss coeff. | 1.00 | 0.79 |
| LES loss coeff. | 0.95 | 0.75 |
| LES-to-exp. ratio | 0.95 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Russo, M.; Dellacasagrande, M.; Satta, F.; Lengani, D.; Simoni, D.; Bellucci, J.; Giovannini, M.; Granata, A.A.; Gily, M. Time, Space, and Dynamic Split of Loss Sources in LPT by Means of Phase-Locked Proper Orthogonal Decomposition. Int. J. Turbomach. Propuls. Power 2025, 10, 25. https://doi.org/10.3390/ijtpp10030025
Russo M, Dellacasagrande M, Satta F, Lengani D, Simoni D, Bellucci J, Giovannini M, Granata AA, Gily M. Time, Space, and Dynamic Split of Loss Sources in LPT by Means of Phase-Locked Proper Orthogonal Decomposition. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(3):25. https://doi.org/10.3390/ijtpp10030025
Chicago/Turabian StyleRusso, Matteo, Matteo Dellacasagrande, Francesca Satta, Davide Lengani, Daniele Simoni, Juri Bellucci, Matteo Giovannini, Angelo Alberto Granata, and Monica Gily. 2025. "Time, Space, and Dynamic Split of Loss Sources in LPT by Means of Phase-Locked Proper Orthogonal Decomposition" International Journal of Turbomachinery, Propulsion and Power 10, no. 3: 25. https://doi.org/10.3390/ijtpp10030025
APA StyleRusso, M., Dellacasagrande, M., Satta, F., Lengani, D., Simoni, D., Bellucci, J., Giovannini, M., Granata, A. A., & Gily, M. (2025). Time, Space, and Dynamic Split of Loss Sources in LPT by Means of Phase-Locked Proper Orthogonal Decomposition. International Journal of Turbomachinery, Propulsion and Power, 10(3), 25. https://doi.org/10.3390/ijtpp10030025






