The Effect of a Variable Cantilevered Stator on 1.5-Stage Transonic Compressor Performance †
Abstract
1. Introduction

2. Investigation Methods
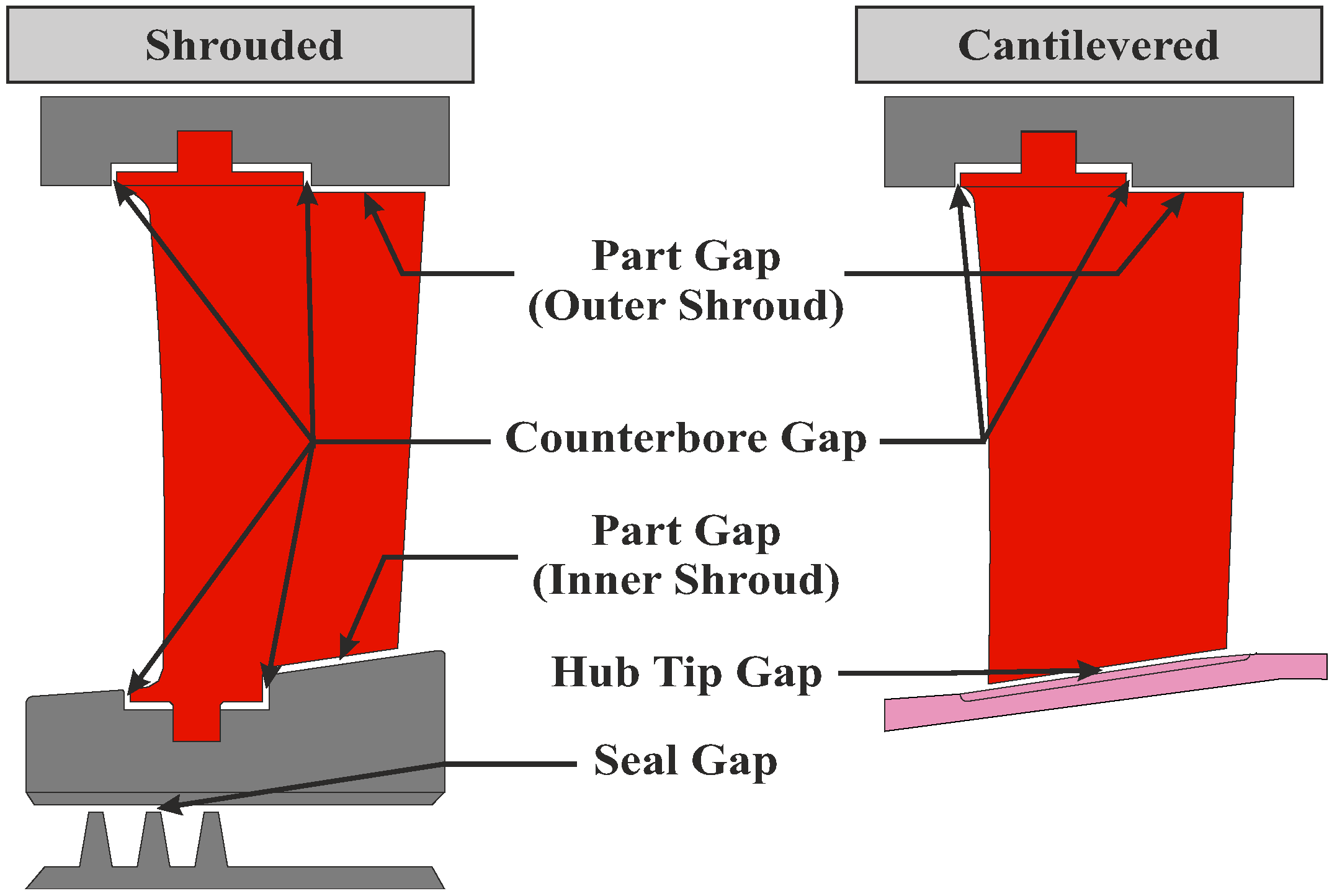
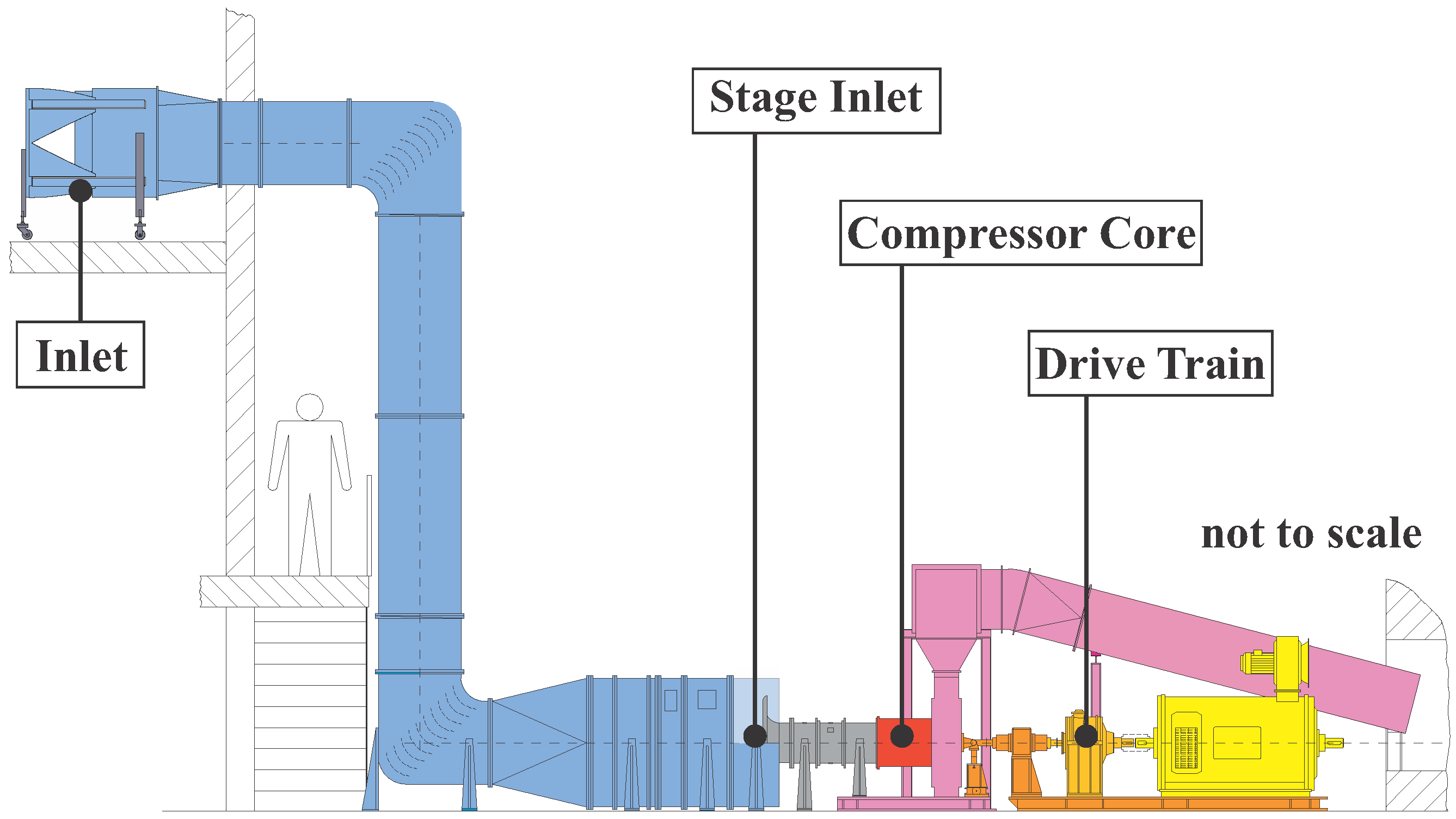
2.1. Experimental Setup
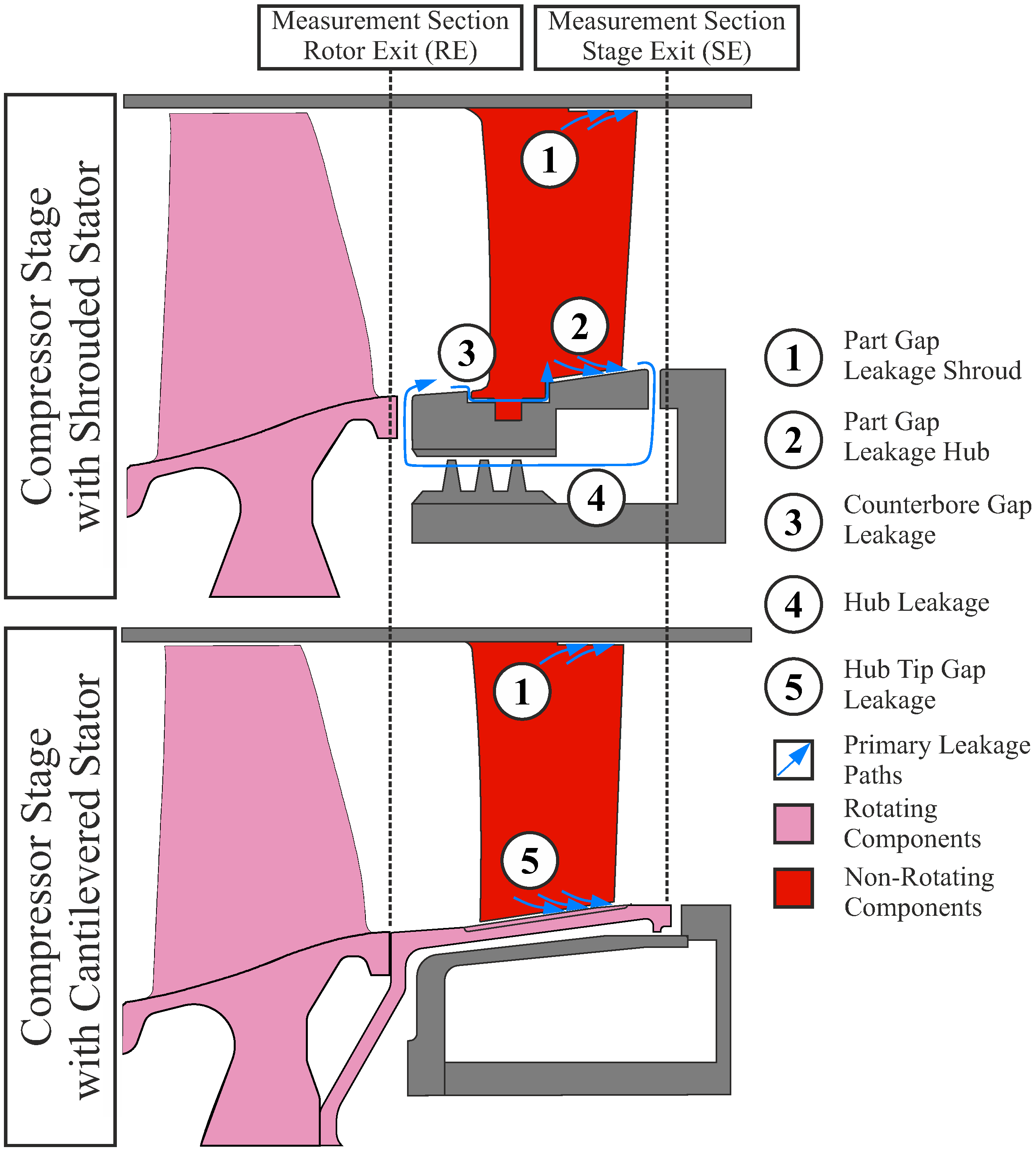
2.2. Instrumentation and Methodology
2.3. Numerical Setup
3. Results
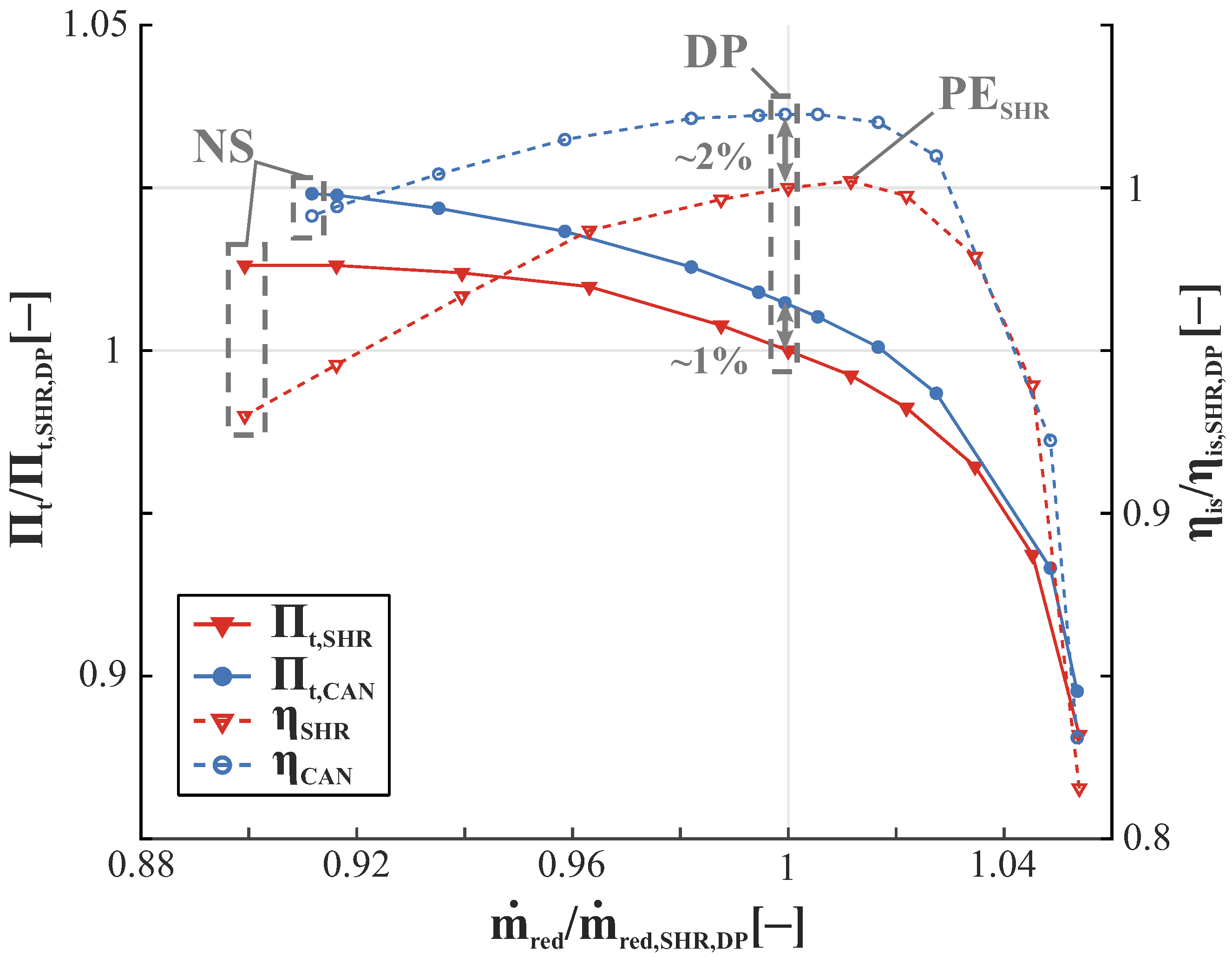
3.1. Global Compressor Performance
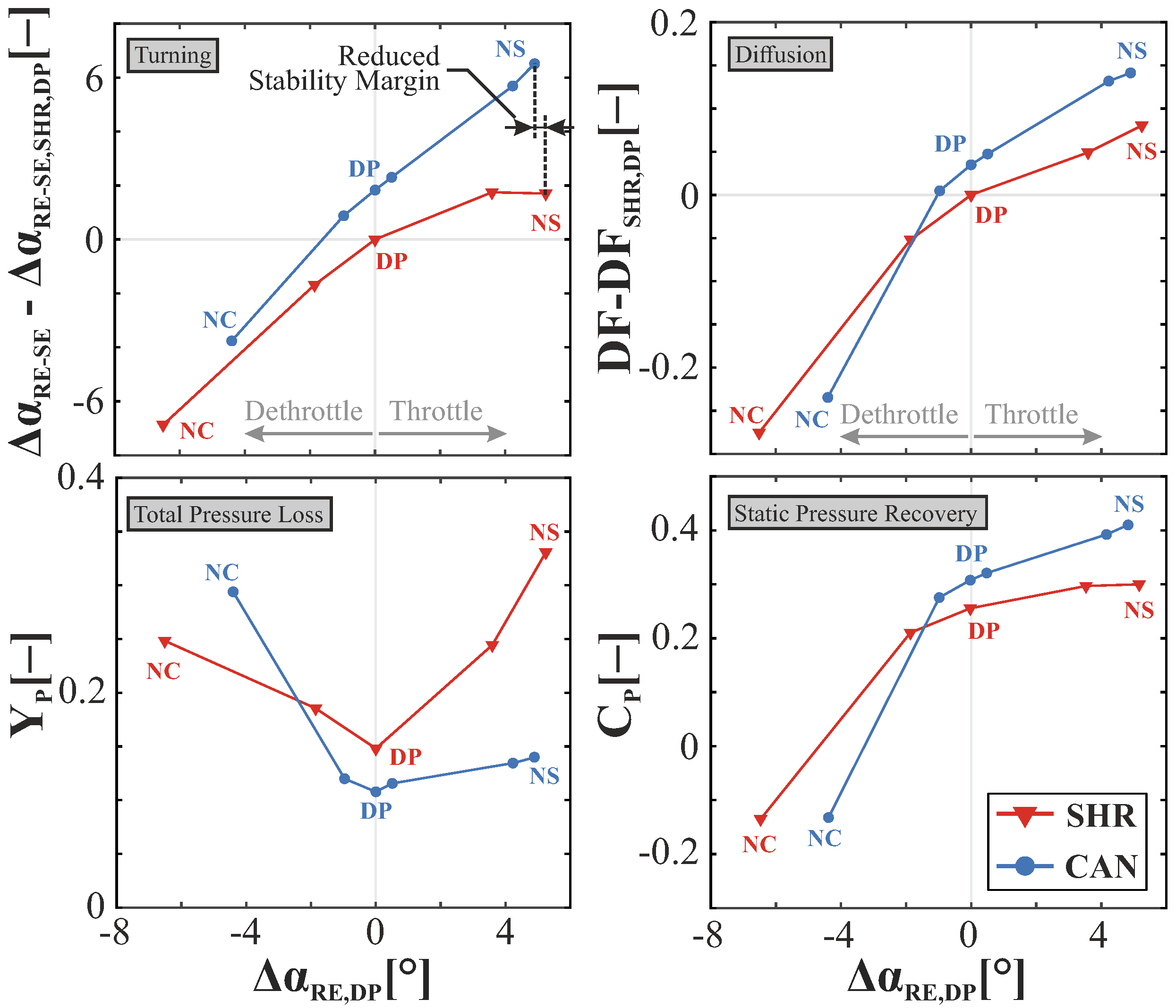
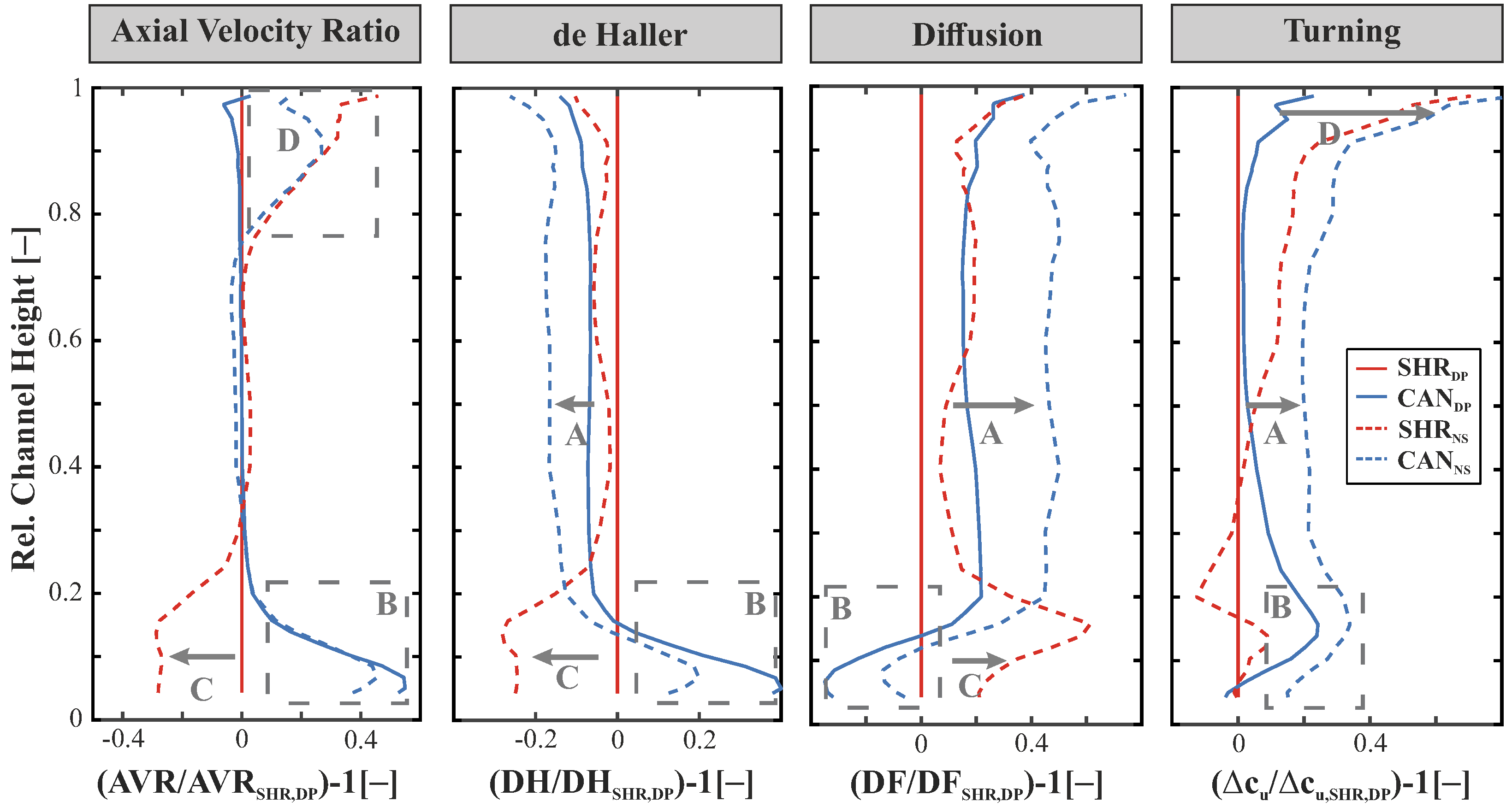
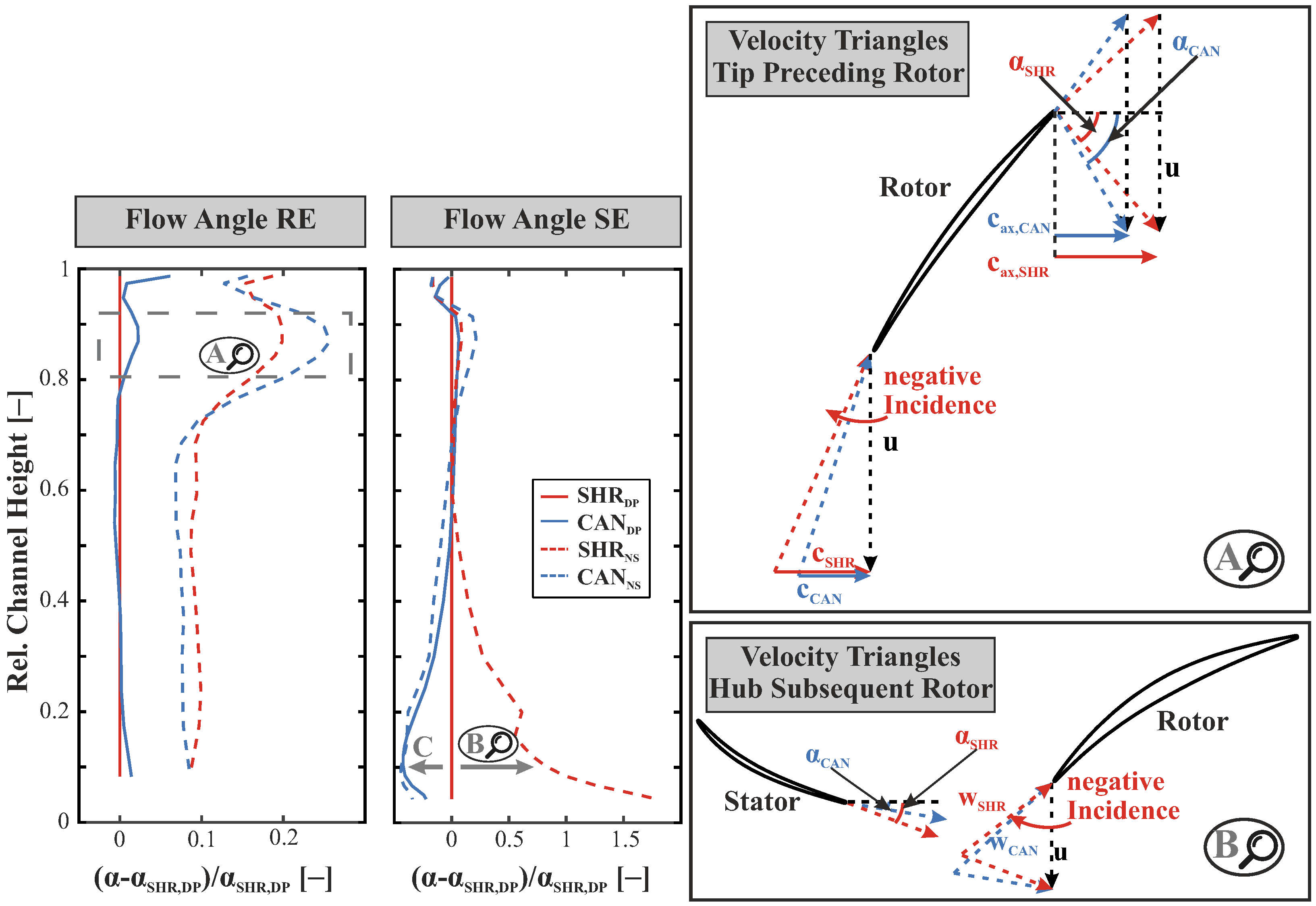
3.2. Aerodynamic Loading
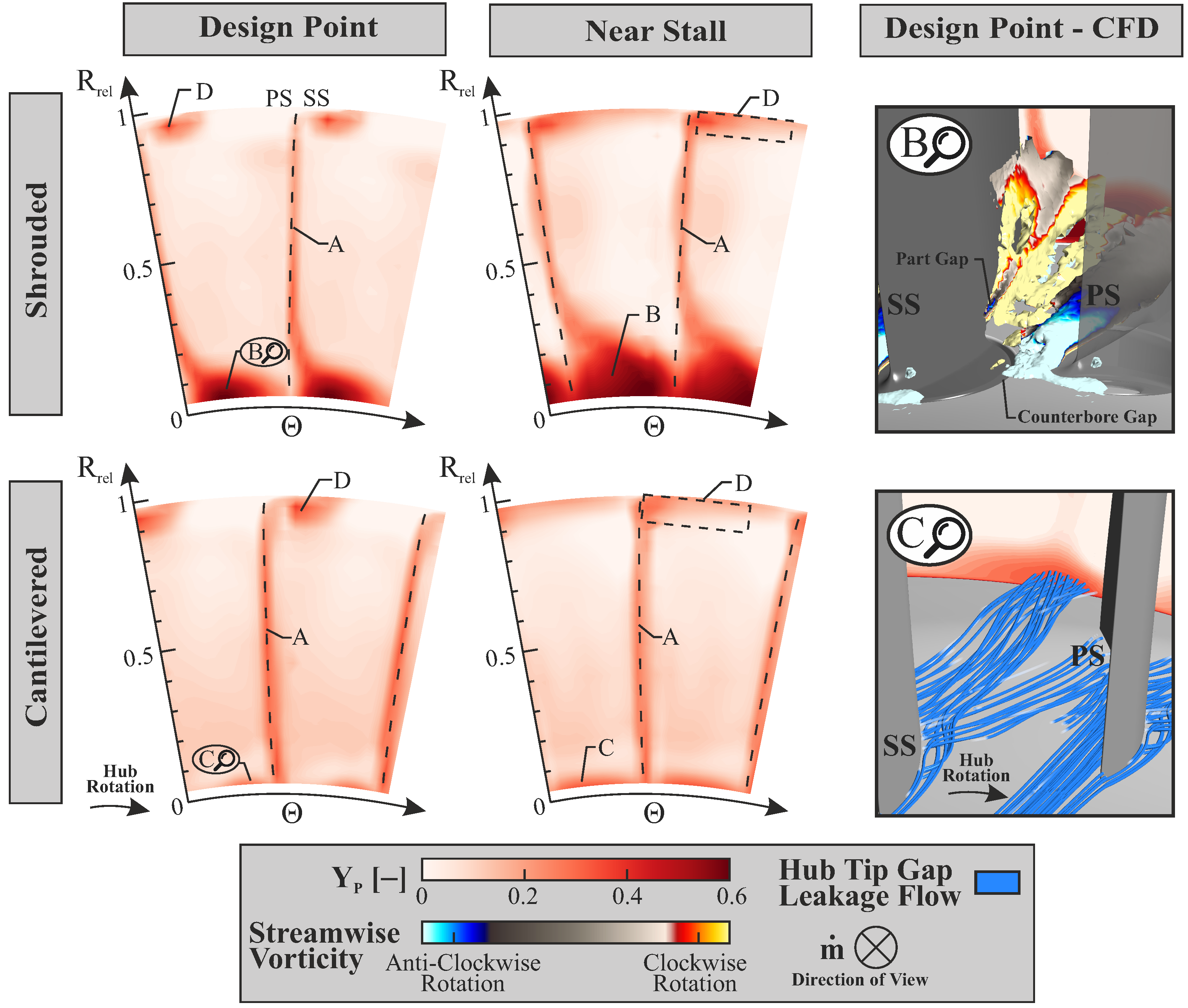
3.3. Loss Determination
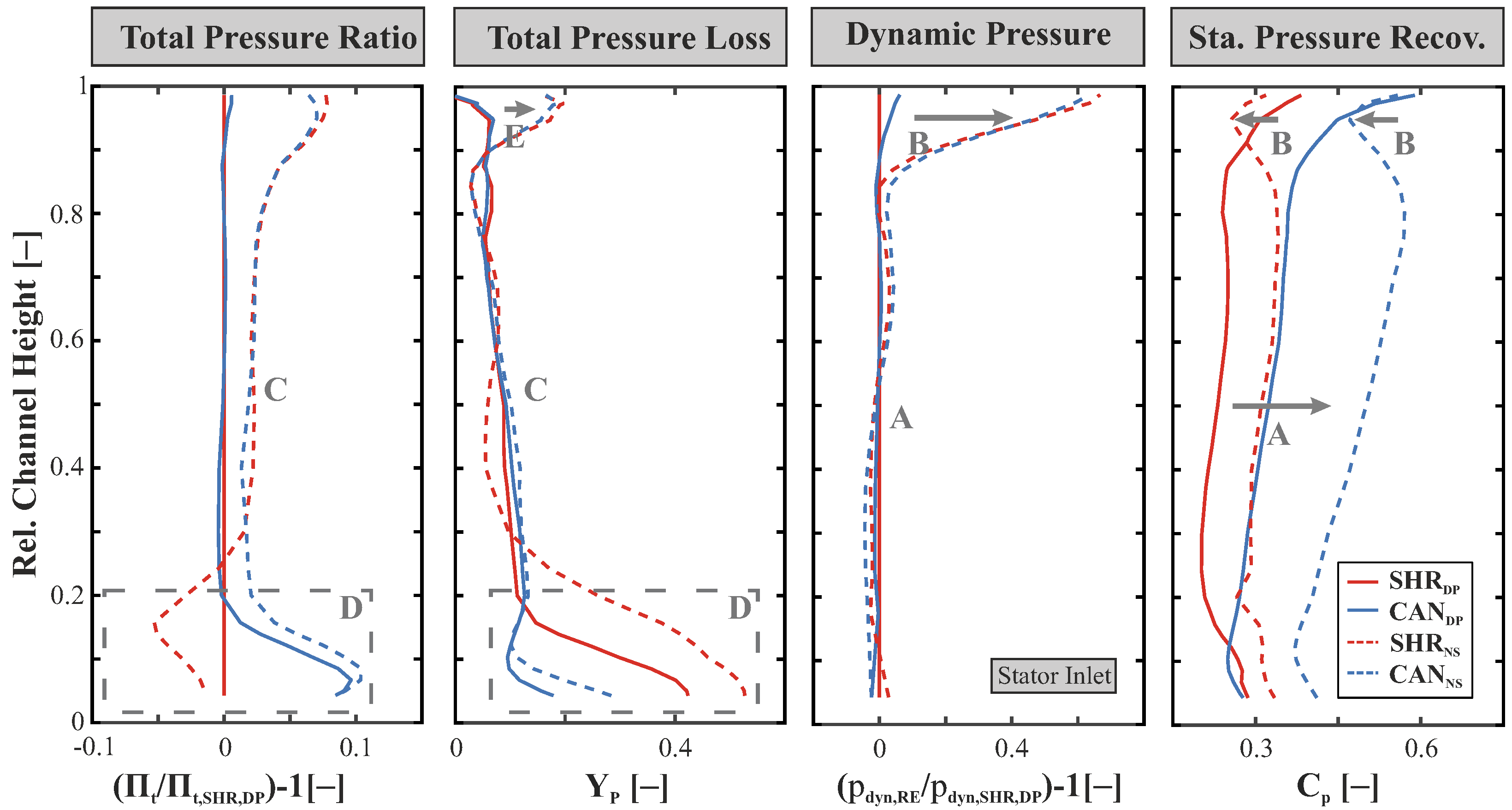
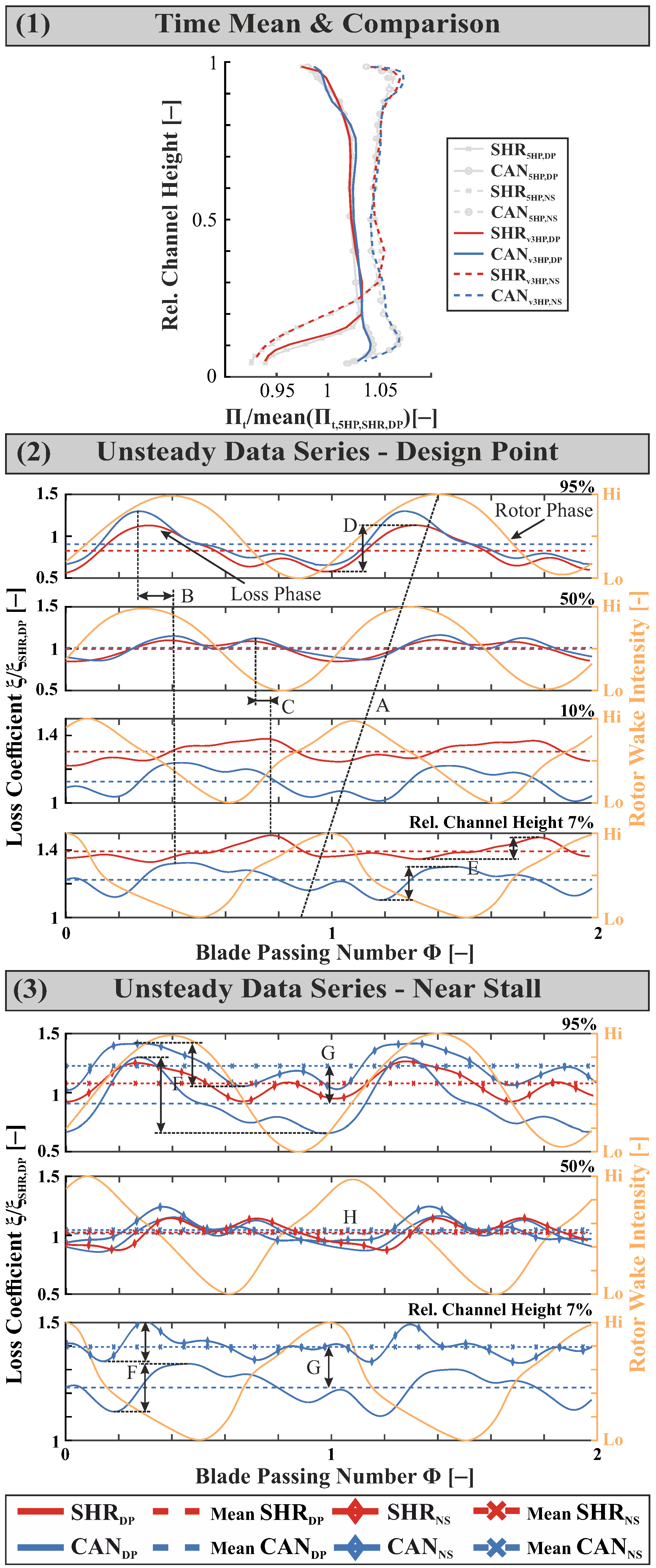
3.4. Unsteady Loss Determination
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Latin | Greek | ||
| A | Area [m2] | Circumferential flow angle [°] | |
| c | Velocity in stationary frame of reference [m/s] | Isentropic efficiency [–] | |
| Static pressure recovery factor [–] | Isentropic exponent [–] | ||
| Specific heat capacity [J/(kg K)] | Total pressure ratio [–] | ||
| Mass flow [kg/s] | Solidity [–] | ||
| p | Pressure [Pa] | Circumferential position [°] | |
| Shaft power [W] | Total temperature ratio [–] | ||
| r | Radius [m] | Vane metal angle [°] | |
| R | Specific gas constant [J/(kg K)] | Loss coefficient [–] | |
| s | Specific entropy [J/(kg K)] | ||
| T | Temperature [K] | Subscripts | |
| Total pressure loss coefficient [–] | area-average | ||
| axial | |||
| Abbreviations | dynamic | ||
| 5HP | Five-hole probe | relative | |
| AVR | Axial Velocity Ratio | static | |
| CAN | Variable Cantilevered Stator | total (stagnated) | |
| DF | Diffusion Factor | circumferential | |
| DH | de Haller-Criterion | ||
| DP | Design Point | ||
| NC | Near Choke | ||
| NS | Near Stall | ||
| PE | Peak Efficiency | ||
| PS | Pressure Side | ||
| RE | Rotor Exit | ||
| SE | Stage Exit | ||
| SHR | Variable Shrouded Stator | ||
| SS | Suction Side | ||
| v3HP | Time-resolving virtual Three-hole Probe | ||
| VIGV | Variable Inlet Guide Vane | ||
| VSV | Variable Stator Vane | ||
Appendix A
References
- Wellborn, S.R.; Okiishi, T.H. The Influence of Shrouded Stator Cavity Flows on Multistage Compressor Performance. In Proceedings of the ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition, Stockholm, Sweden, 2–5 June 1998; ASME: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Campobasso, M.S.; Mattheiss, A.; Wenger, U.; Amone, A.; Boncinelli, P. Complementary Use of CFD and Experimental Measurements to Assess the Impact of Shrouded and Cantilevered Stators in Axial Compressors. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Indianapolis, IN, USA, 7–10 June 1999; ASME: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Swoboda, M.; Ivey, P.C.; Wenger, U.; Gümmer, V. An Experimental Examination of Cantilevered and Shrouded Stators in a Multistage Axial Compressor. In Proceedings of the ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition, Stockholm, Sweden, 2–5 June 1998; ASME: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Rückert, R.; Peitsch, D. Cantilevered Tandem Stator in Annular High Speed Test Rig. Int. J. Turbomach. Propuls. Power 2022, 7, 24. [Google Scholar] [CrossRef]
- Si, X.; Teng, J.; Qiang, X.; Feng, J. Different Effects of Cantilevered and Shrouded Stators on Axial Compressor Performance. In Proceedings of the ASME Turbo Expo: Turbine Technical Conference and Exposition—2017, Charlotte, NC, USA, 26–30 June 2017; ASME: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Freeman, C. Effect of Tip Clearance Flow on Compressor Stability and Engine Performance. In Tip Clearance Effects in Axial Turbomachines; VKI Lecture Series 1985-05; von Karman Institute: Rhode-Saint-Genèse, Belgium, 1985. [Google Scholar]
- Yoon, S.; Selmeier, R.; Cargill, P.; Wood, P. Effect of the Stator Hub Configuration and Stage Design Parameters on Aerodynamic Loss in Axial Compressors. J. Turbomach. 2015, 137, 091001. [Google Scholar] [CrossRef]
- Lange, M.; Mailach, R.; Vogeler, K. An Experimental Investigation of Shrouded and Cantilevered Compressor Stators at Varying Clearance Sizes. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 75–85. [Google Scholar] [CrossRef]
- de Dominicis, I.; Robens, S.; Gümmer, V. Numerical Evaluation of Losses in Shrouded and Cantilevered Stators of a Multi-Stage Axial Compressor. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Online, 7–11 June 2021. Volume 2A: Turbomachinery—Axial Flow Fan and Compressor Aerodynamics. [Google Scholar] [CrossRef]
- Matthews, D.R. The Influence of Stator Endwall Clearances on Multistage Axial Compressor Aerodynamics. Ph.D. Thesis, School of Aeronautics and Astronautics, Purdue University, West Lafayette, IN, USA, 2024; 248p. [Google Scholar] [CrossRef]
- Radermacher, B.; Klausmann, F.; Bargon, J.; Lücke, M.; Schiffer, H.-P.; Becker, B. Aerodynamic Investigation of Different Variable Stator Configurations in a 1.5-stage Transonic Compressor. In Proceedings of the 25th International Society of Air Breathing Engines (ISABE) Conference, Toulouse, France, 22–27 September 2024. Paper No. ISABE-2024-102. [Google Scholar]
- Radermacher, B.; Klausmann, F.; Jung, F.; Bargon, J.; Schiffer, H.-P.; Becker, B.; Grothe, P. The Effect of a Variable Cantilevered Stator on 1.5-stage Transonic Compressor Performance. In Proceedings of the 16th European Turbomachinery Conference, paper No. ETC2025-174, Hannover, Germany, 24–28 March 2025. [Google Scholar]
- Pohl, D.; Janssen, J.; Jeschke, P.; Halcoussis, A.; Wolf, H. Variable Stator Vane Penny Gap Aerodynamic Measurements and Numerical Analysis in an Annular Cascade Wind Tunnel. Int. J. Gas Turbine Propuls. Power Syst. 2020, 11, 44–55. [Google Scholar] [CrossRef] [PubMed]
- Stummann, S.; Pohl, D.; Jeschke, P.; Wolf, H.; Halcoussis, A.; Franke, M. Secondary Flow in Variable Stator Vanes with Penny-Cavities. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; ASME: New York, NY, USA, 2017. Paper No. GT2017-63771. [Google Scholar] [CrossRef]
- Wolf, H.; Franke, M.; Halcoussis, A.; Kleinclaus, C.; Gautier, S. Investigation of Penny Leakage Flows of Variable Guide Vanes in High Pressure Compressors. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; ASME: New York, NY, USA, 2016. Paper No. GT2016-56327. [Google Scholar] [CrossRef]
- Klausmann, F.; Franke, D.; Foret, J.; Schiffer, H.-P. Transonic compressor Darmstadt—Open test case Introduction of the TUDa open test case. J. Glob. Power Propuls. Soc. 2022, 6, 318–329. [Google Scholar] [CrossRef] [PubMed]
- Foret, J. Untersuchung Eines Tandemstators in Einem Transsonischen Axialverdichter. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2023. [Google Scholar]
- Lieblein, S.; Schwenk, F.C.; Broderick, R.L. Diffusion Factor for Estimating Losses and Limiting Blade Loadings in Axial-Flow-Compressor Blade Elements; Research Memorandum; National Advisory Committee for Aeronautics: Washington, DC, USA, 1953. [Google Scholar]
- Saha, U.K.; Roy, B. Experimental investigations on tandem compressor cascade performance at low speeds. Exp. Therm. Fluid Sci. 1997, 14, 263–276. [Google Scholar] [CrossRef]
- Denton, J.D. The 1993 IGTI Scholar Lecture: Loss Mechanisms in Turbomachines. J. Turbomach. 1993, 115, 621–656. [Google Scholar] [CrossRef]
- Baehr, H.D.; Kabelac, S. Thermodynamik: Grundlagen und Technische Anwendungen, 14th ed.; Springer: Berlin/Heidelberg, Germany; Springer Nature: Cham, Switzerland, 2009. [Google Scholar] [CrossRef]
- Bräunling, W.J.G. Flugzeugtriebwerke: Grundlagen, Aero-Thermodynamik, Ideale und Reale Kreisprozesse, Thermische Turbomaschinen, Komponenten, Emissionen und Systeme, 4th ed.; Springer Vieweg: Berlin, Germany, 2015. [Google Scholar]
- Grieb, H. Turboverdichter für Flugtriebwerke; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Hertel, C.; Bode, C.; Kožulović, D.; Schneider, T. Investigations on Aerodynamic Loading Limits of Subsonic Compressor Tandem Cascades: End Wall Flow. In Proceedings of the ASME Turbo Expo 2014: Power for Land, Sea, and Air, Düsseldorf, Germany, 16–20 June 2014. Volume 2A: Turbomachinery; Paper No. GT2014-26978. [Google Scholar] [CrossRef]
- Klausmann, F.S.; Kilian, N.; He, X.; Spieker, D.; Schmidt, B.; Schiffer, H.-P. Transonic Compressor Darmstadt Open Test Case: Experimental Investigation of Stator Secondary Flows and Hub Leakage. J. Turbomach. 2024, 146, 101007. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Kato, M.; Launder, B.L. The modelling of turbulent flow around stationary and vibrating square cylinders. In Proceedings of the Ninth Symposium on Turbulent Shear Flows, Kyoto, Japan, 16–18 August 1993. [Google Scholar]
- Lei, V.; Spakovszky, Z.S.; Greitzer, E.M. A Criterion for Axial Compressor Hub-Corner Stall. ASME J. Turbomach. 2008, 130, 031006. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the EUROTURBO. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Radermacher, B.; Klausmann, F.S.; Jung, F.; Bargon, J.; Schiffer, H.-P.; Becker, B.; Grothe, P. The Effect of a Variable Cantilevered Stator on 1.5-Stage Transonic Compressor Performance. Int. J. Turbomach. Propuls. Power 2025, 10, 24. https://doi.org/10.3390/ijtpp10030024
Radermacher B, Klausmann FS, Jung F, Bargon J, Schiffer H-P, Becker B, Grothe P. The Effect of a Variable Cantilevered Stator on 1.5-Stage Transonic Compressor Performance. International Journal of Turbomachinery, Propulsion and Power. 2025; 10(3):24. https://doi.org/10.3390/ijtpp10030024
Chicago/Turabian StyleRadermacher, Benedikt, Fabian Sebastian Klausmann, Felix Jung, Jonas Bargon, Heinz-Peter Schiffer, Bernd Becker, and Patrick Grothe. 2025. "The Effect of a Variable Cantilevered Stator on 1.5-Stage Transonic Compressor Performance" International Journal of Turbomachinery, Propulsion and Power 10, no. 3: 24. https://doi.org/10.3390/ijtpp10030024
APA StyleRadermacher, B., Klausmann, F. S., Jung, F., Bargon, J., Schiffer, H.-P., Becker, B., & Grothe, P. (2025). The Effect of a Variable Cantilevered Stator on 1.5-Stage Transonic Compressor Performance. International Journal of Turbomachinery, Propulsion and Power, 10(3), 24. https://doi.org/10.3390/ijtpp10030024





