Malaria in Senegal: Recent and Future Changes Based on Bias-Corrected CMIP6 Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Used
2.2.1. Malaria Data Surveillance
2.2.2. Climate Data and Methods
2.3. LMM Malaria Model
3. Results
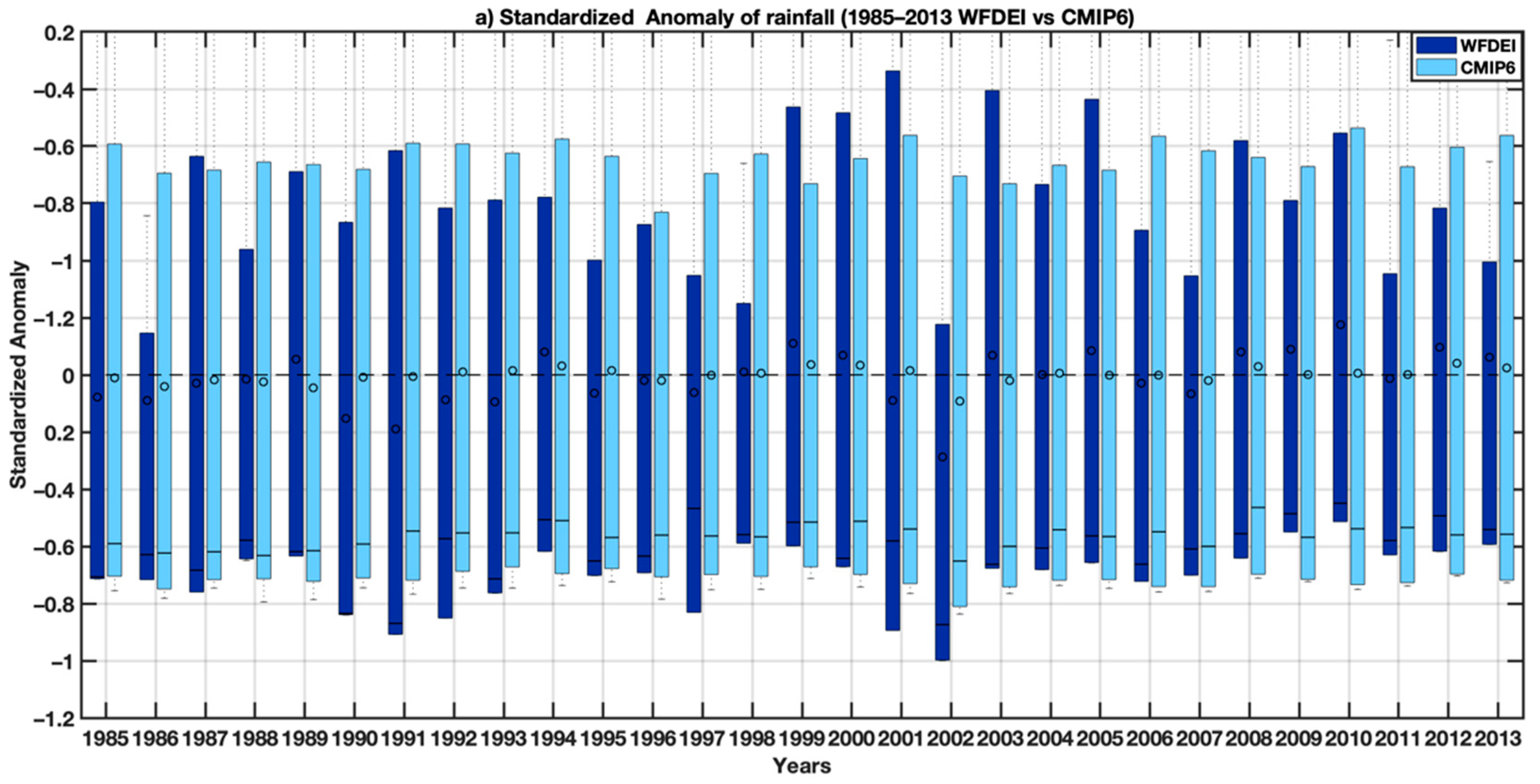
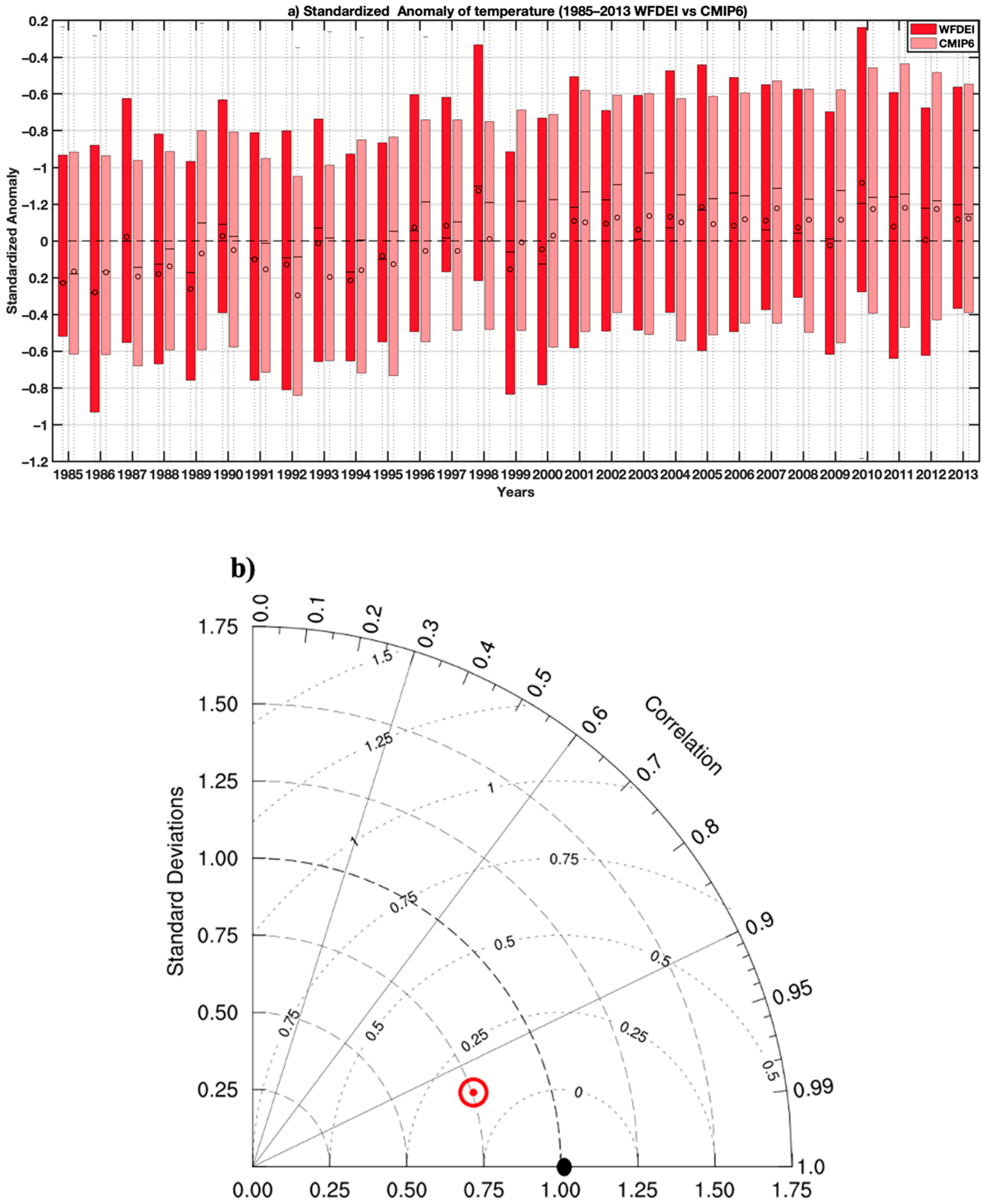
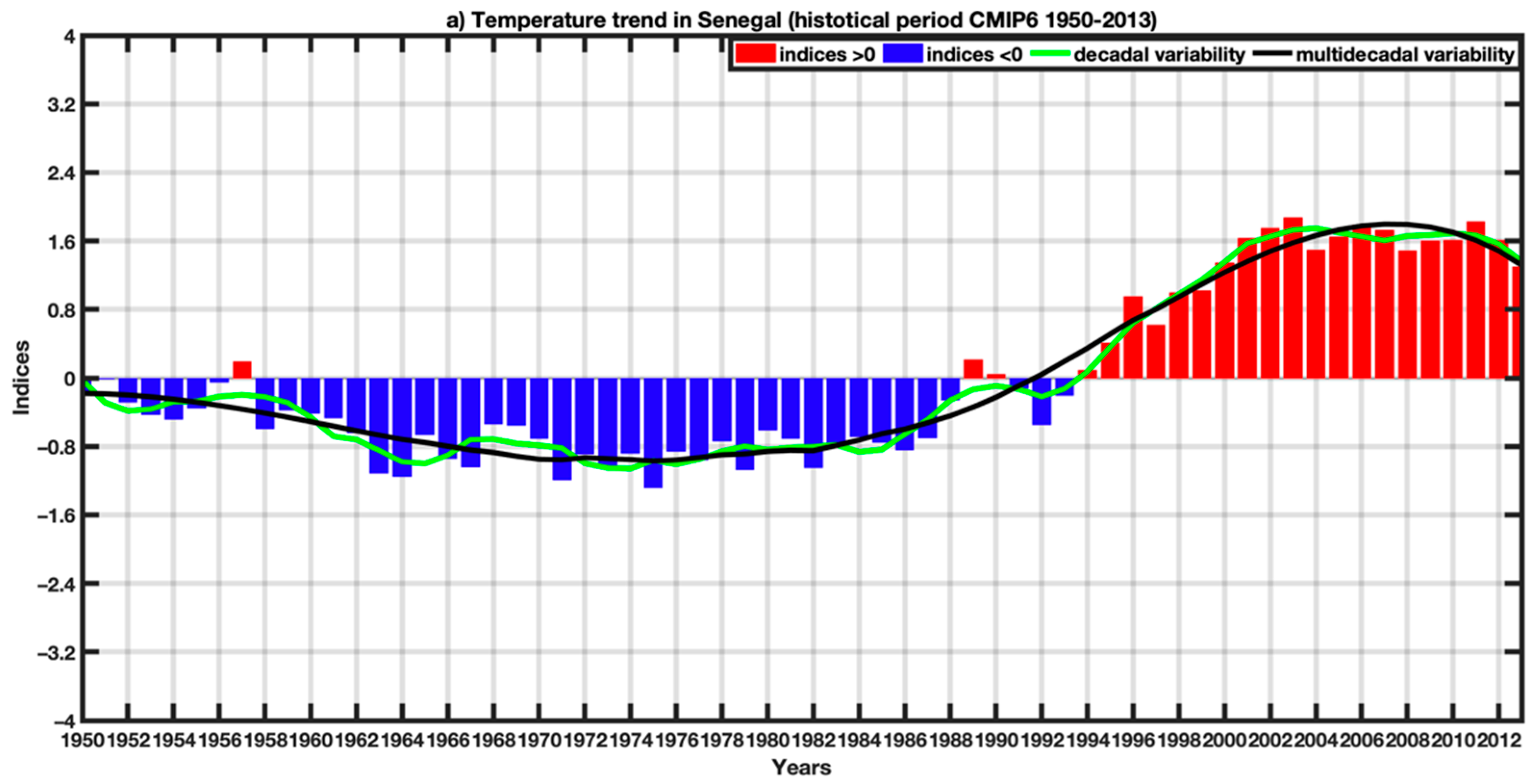
3.1. CMIP6 Models’ Evaluation: Validation of the Rainfall and Temperature Inputs
3.2. Projected Changes in the Spatiotemporal Variability of the CMIP6 Data
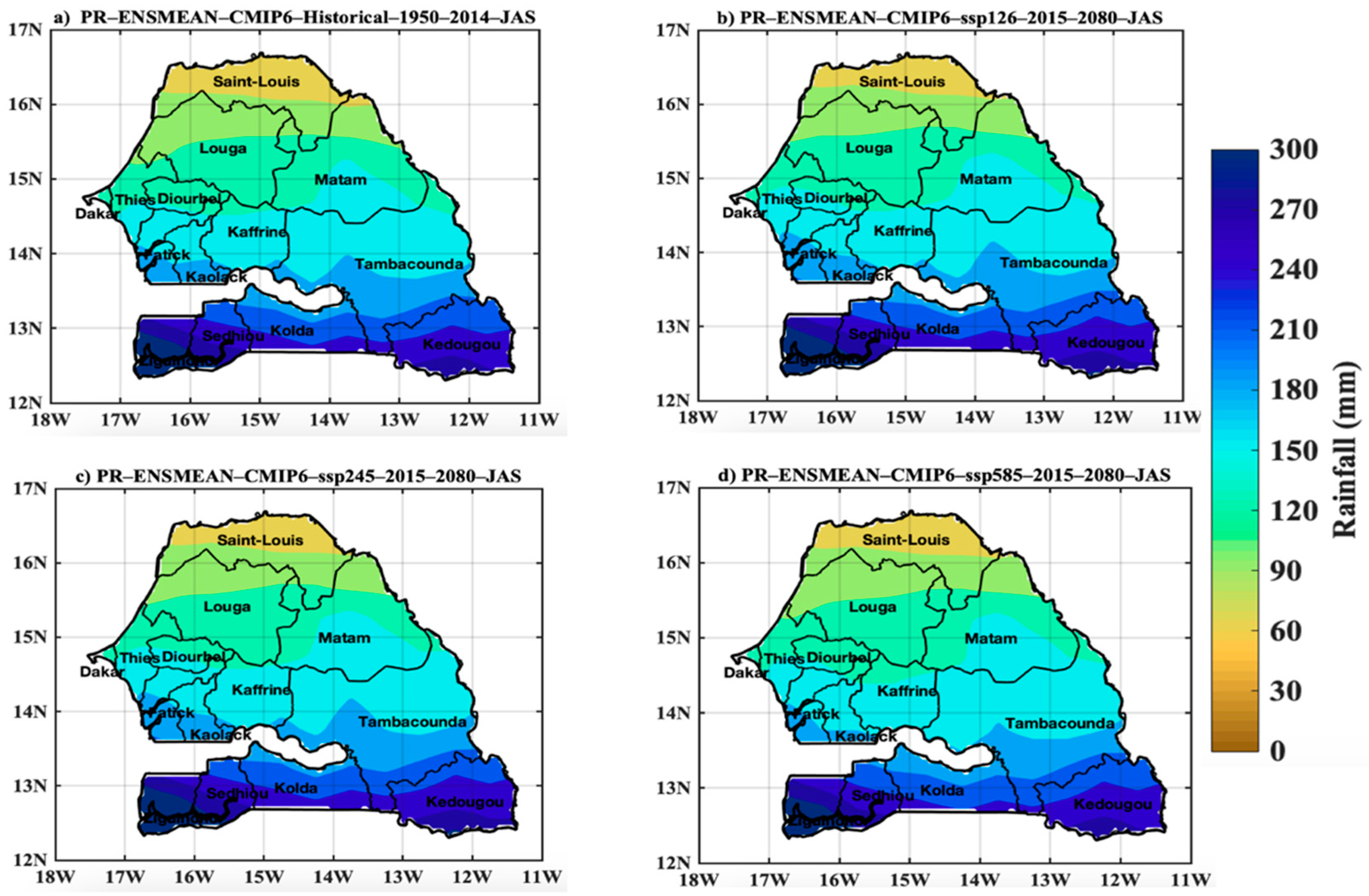
3.2.1. Projected Changes in the Spatiotemporal Variability of the CMIP6 Rainfall
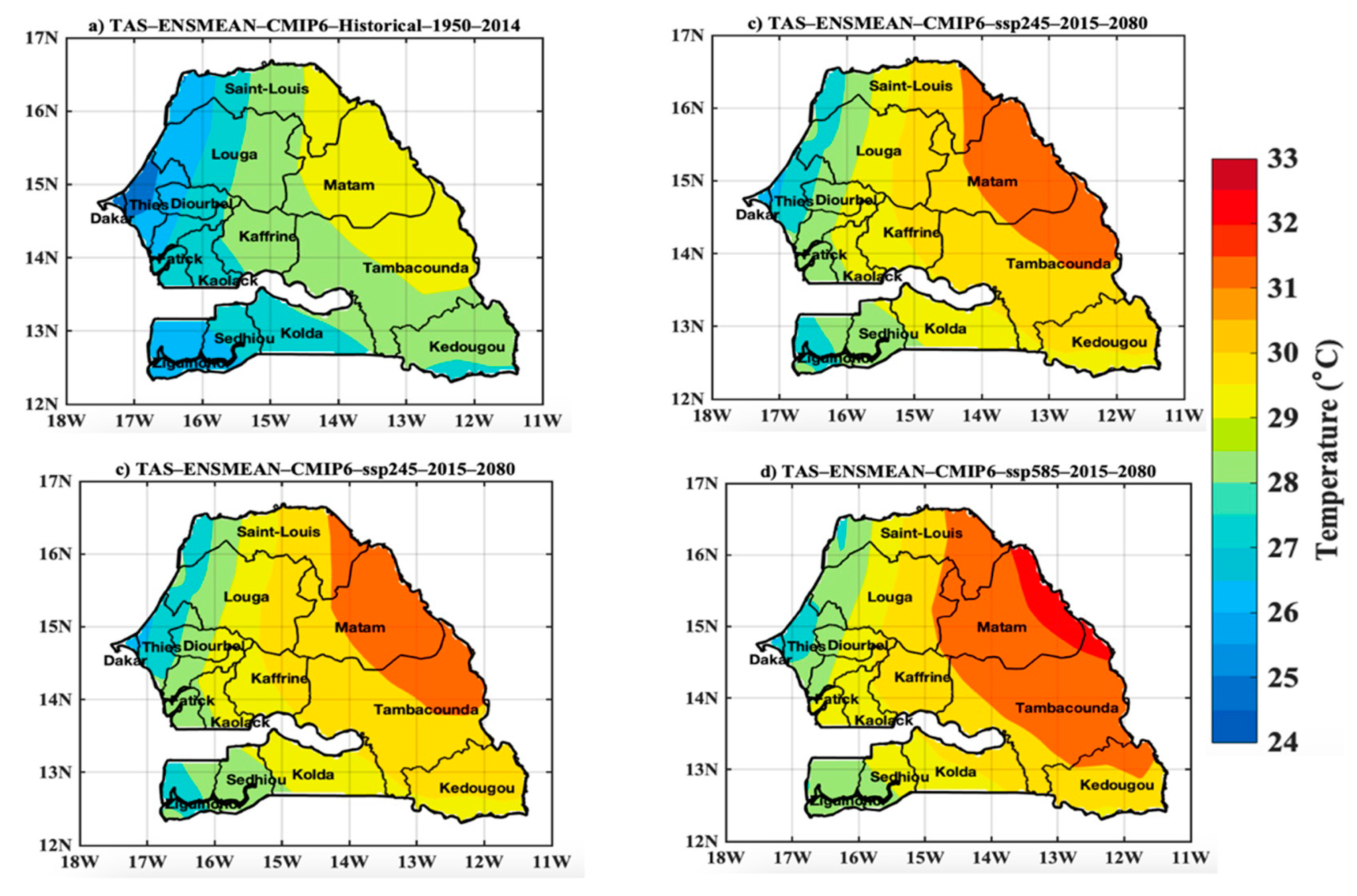
3.2.2. Projected Changes in the Spatiotemporal Variability of the CMIP6 Temperature
- between December and January, there is a period marked by a dry climate and very low temperatures linked to the polar invasions during the winter season.
- between February and May, it is very hot and dry with the first peak in temperature in May; this absolute peak in temperature precedes the start of the rainy season;
- the period from July to September (rainy season) is very rainy and wet with mild temperature due to cloud cover;
- the last period of this classification extends between October and November and is marked by high humidity and slightly high temperature. The second peak of the annual temperature cycle often occurs in October with a peak approaching 32 °C.
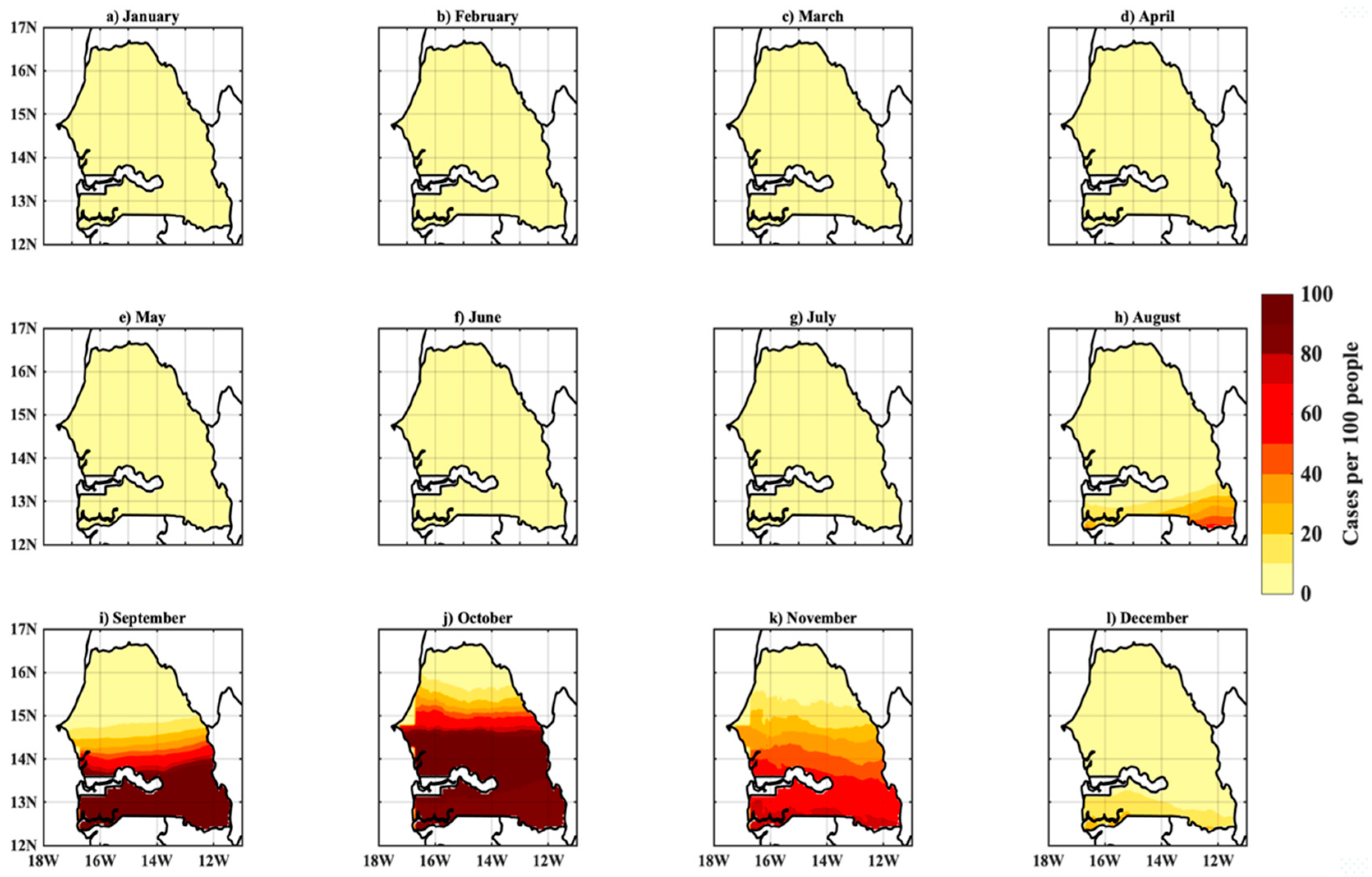
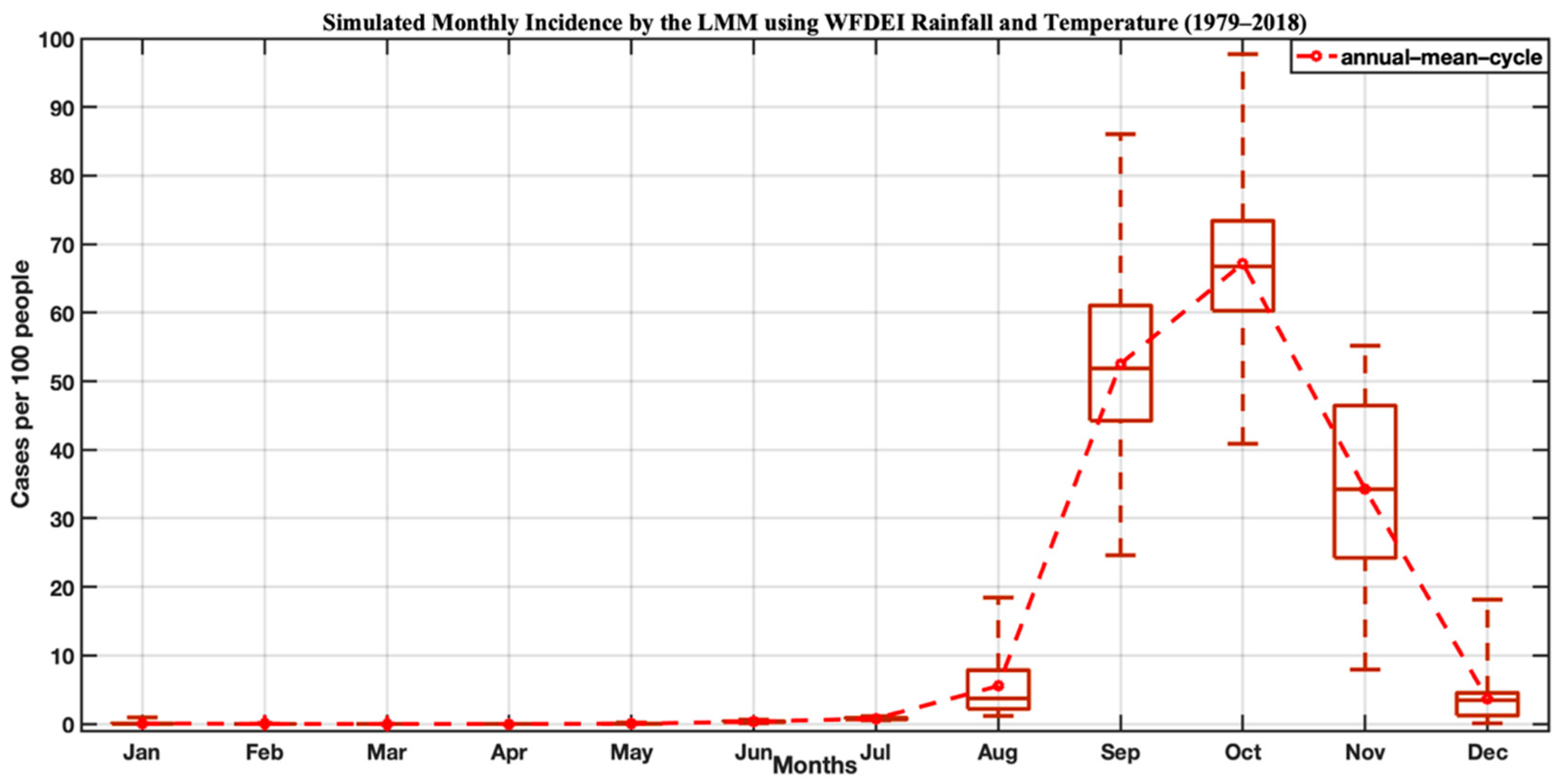
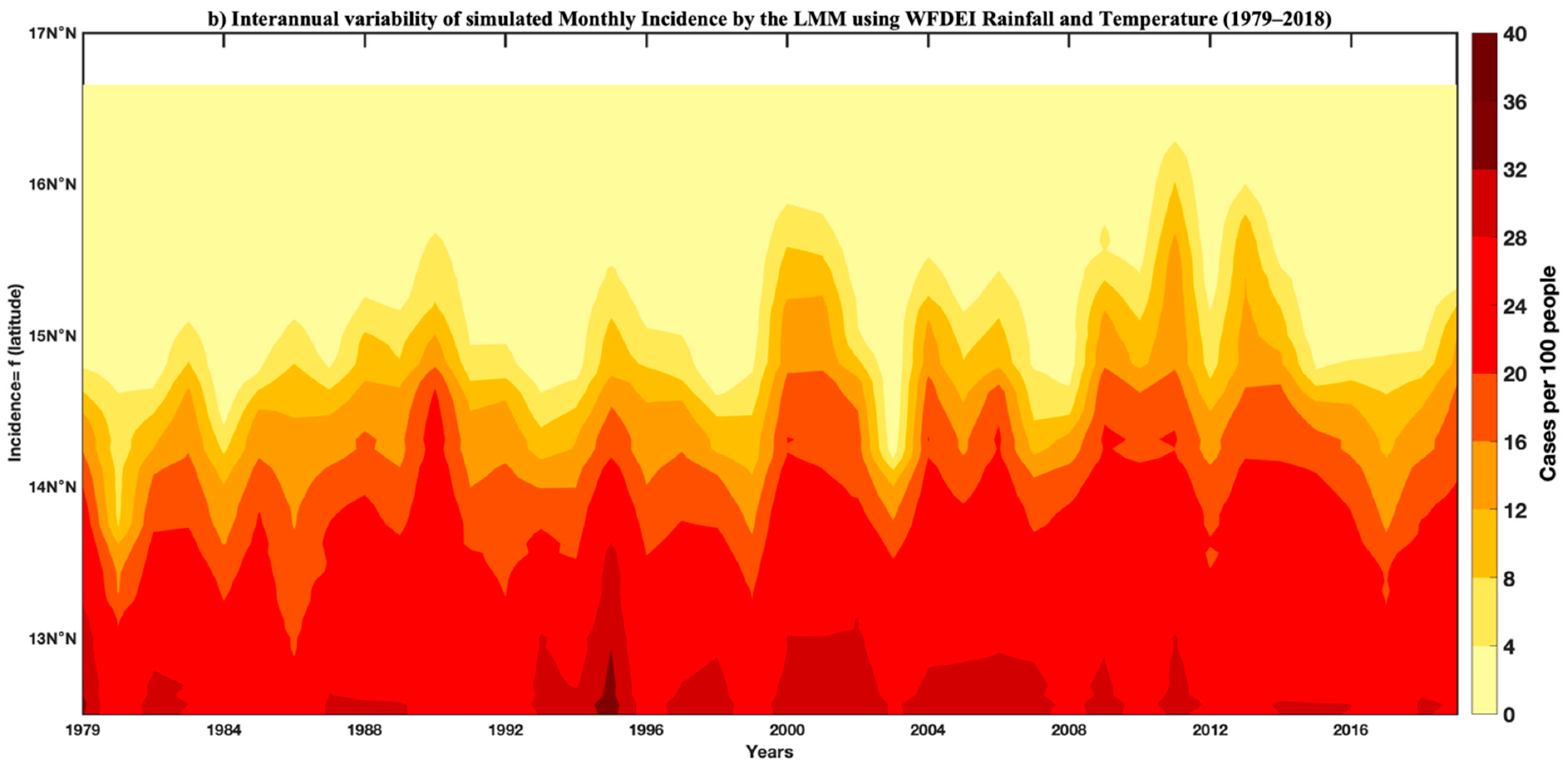
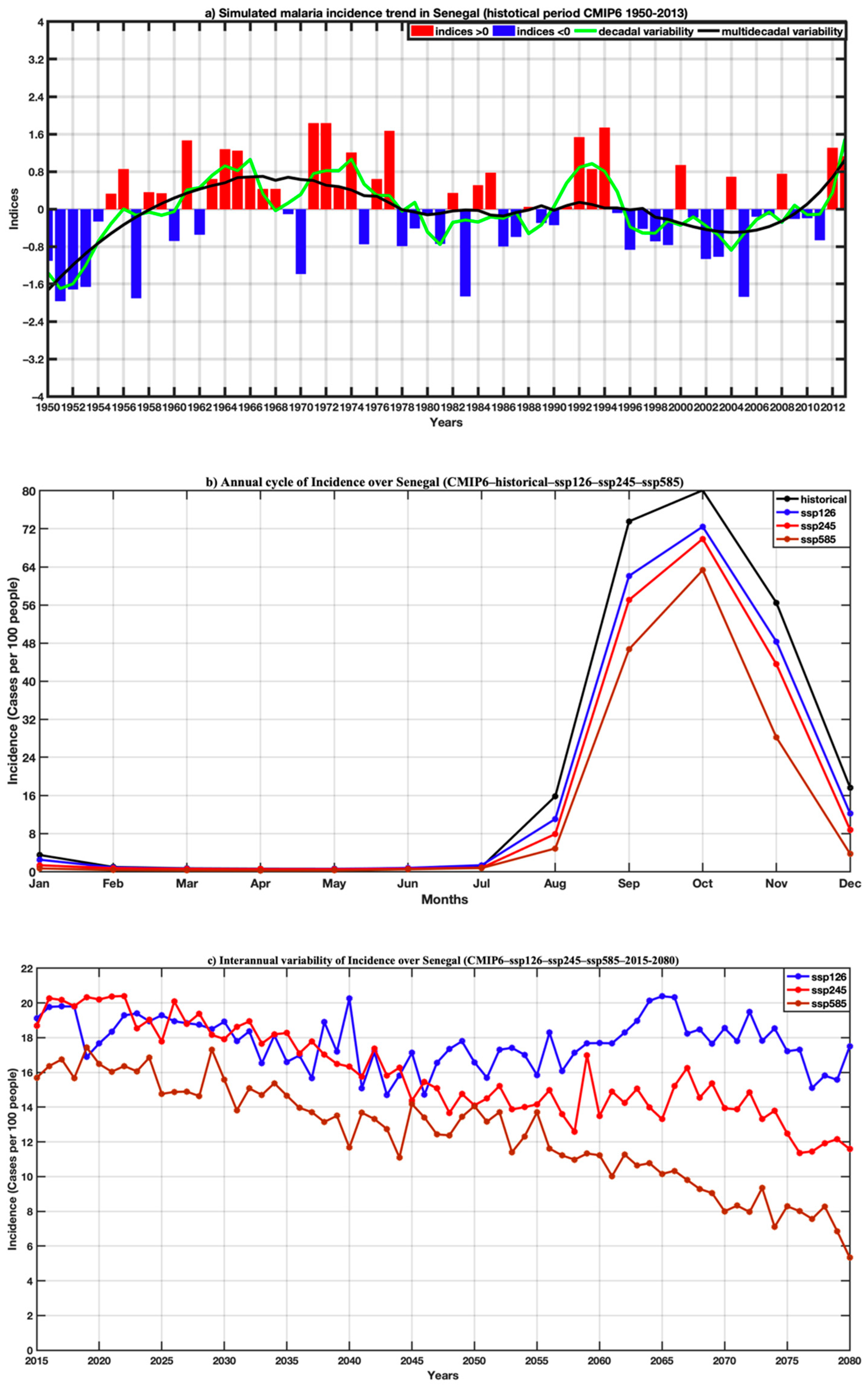
3.3. Simulated Malaria Incidence in Senegal
3.4. Validation of Simulated Malaria Incidence in Senegal
3.5. Projected Changes in Malaria Incidence Based on CMIP6 Data
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caminade, C.; Kovats, S.; Rocklov, J.; Tompkins, A.M.; Morse, A.P.; Colón-González, F.J.; Stenlund, H.; Martens, P.; Lloyd, S.J. Impact of climate change on global malaria distribution. Proc. Natl. Acad. Sci. USA 2014, 111, 3286–3291. [Google Scholar] [CrossRef] [PubMed]
- Chitnis, N.; Hyman, J.; Cushing, J. Determining Important Parameters in the Spread of Malaria Through the Sensitivity Analysis of a Mathematical Model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef] [PubMed]
- Costello, A.; Abbas, M.; Allen, A.; Ball, S.; Bell, S.; Bellamy, R.; Friel, S.; Groce, N.; Johnson, A.; Kett, M.; et al. Managing the health effects of climate change: Lancet and University College London Institute for Global Health Commission. Lancet 2009, 373, 1693–1733. [Google Scholar] [CrossRef]
- Romanello, M.; McGushin, A.; Di Napoli, C.; Drummond, P.; Hughes, N.; Jamart, L.; Kennard, H.; Lampard, P.; Rodriguez, B.S.; Arnell, N.; et al. The 2021 report of the Lancet Countdown on health and climate change: Code red for a healthy future. Lancet 2021, 398, 1619–1662. [Google Scholar] [CrossRef]
- Patouillard, E.; Griffin, J.; Bhatt, S.; Ghani, A.; Cibulskis, R. Global investment targets for malaria control and elimination between 2016 and 2030. BMJ Glob. Health 2017, 2, e000176. [Google Scholar] [CrossRef]
- Diouf, I.; Rodriguez-Fonseca, B.; Deme, A.; Caminade, C.; Morse, A.P.; Cisse, M.; Sy, I.; Dia, I.; Ermert, V.; Ndione, J.-A.; et al. Comparison of Malaria Simulations Driven by Meteorological Observations and Reanalysis Products in Senegal. Int. J. Environ. Res. Public Health 2017, 14, 1119. [Google Scholar] [CrossRef]
- Diouf, I.; Rodríguez-Fonseca, B.; Caminade, C.; Thiaw, W.M.; Deme, A.; Morse, A.P.; Ndione, J.-A.; Gaye, A.T.; Diaw, A.; Ndiaye, M.K.N. Climate Variability and Malaria over West Africa. Am. J. Trop. Med. Hyg. 2020, 102, 1037–1047. [Google Scholar] [CrossRef]
- Diouf, I.; Suárez-Moreno, R.; Rodríguez-Fonseca, B.; Caminade, C.; Wade, M.; Thiaw, W.M.; Deme, A.; Morse, A.P.; Ndione, J.-A.; Gaye, A.T.; et al. Oceanic Influence on Seasonal Malaria Incidence in West Africa. Weather. Clim. Soc. 2022, 14, 287–302. [Google Scholar] [CrossRef]
- Hoshen, M.B.; Morse, A.P. A weather-driven model of malaria transmission. Malar. J. 2004, 3, 32. [Google Scholar] [CrossRef]
- Suárez-Moreno, R.; Rodríguez-Fonseca, B. S4CAST v2.0: Sea surface temperature based statistical seasonal forecast model. Geosci. Model Dev. 2015, 8, 3639–3658. [Google Scholar] [CrossRef]
- Fall, P.; Diouf, I.; Deme, A.; Sene, D. Assessment of Climate-Driven Variations in Malaria Transmission in Senegal Using the VECTRI Model. Atmosphere 2022, 13, 418. [Google Scholar] [CrossRef]
- Cornforth, R.; Parker, D.J.; Diop-Kane, M.; Fink, A.H.; Lafore, J.P.; Laing, A.; Afiesimama, E.; Caughey, J.; Diongue-Niang, A.; Kassimou, A.; et al. The First Forecasters’ Handbook for West Africa. Bull. Am. Meteorol. Soc. 2019, 100, 2343–2351. [Google Scholar] [CrossRef]
- Gaye, A. Caractéristiques Dynamisuqes et Pluviosité des Lignes de Grains en Afrique de l’Ouest. Ph.D. Thesis, Université Cheikh Anta Diop, Dakar, Sénégal, 2002. [Google Scholar]
- Le Borgne, J. La Pluviométrie au Sénégal et en Gambie, Document Multigraphié; ORSTOM, Coopération Française: Dakar, Senegal, 1988. [Google Scholar]
- Russo, S.; Marchese, A.F.; Sillmann, J.; Immé, G. When will unusual heat waves become normal in a warming Africa? Environ. Res. Lett. 2016, 11, 054016. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Michelangeli, P.-A.; Vrac, M.; Loukos, H. Probabilistic downscaling approaches: Application to wind cumulative distribution functions. Geophys. Res. Lett. 2009, 36, L11708. [Google Scholar] [CrossRef]
- Weedon, G.P.; Balsamo, G.; Bellouin, N.; Gomes, S.; Best, M.J.; Viterbo, P. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resour. Res. 2014, 50, 7505–7514. [Google Scholar] [CrossRef]
- Zhongming, Z.; Linong, L.; Xiaona, Y.; Wangqiang, Z.; Wei, L. AR6 Climate Change 2021: The Physical Science Basis; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Ermert, V.; Fink, A.H.; E Jones, A.; Morse, A.P. Development of a new version of the Liverpool Malaria Model. II. Calibration and validation for West Africa. Malar. J. 2011, 10, 62. [Google Scholar] [CrossRef]
- Caminade, C.; Ndione, J.A.; Kebe, C.M.F.; Jones, A.E.; Danuor, S.; Tay, S.; Tourre, Y.M.; Lacaux, J.-P.; Vignolles, C.; Duchemin, J.B.; et al. Mapping Rift Valley fever and malaria risk over West Africa using climatic indicators. Atmospheric Sci. Lett. 2011, 12, 96–103. [Google Scholar] [CrossRef]
- Morse, A.P.; Doblas-Reyes, F.J.; Hoshen, M.B.; Hagedorn, R.; Palmer, T.N. A forecast quality assessment of an end-to-end probabilistic multi-model seasonal forecast system using a malaria model. Tellus A Dyn. Meteorol. Oceanogr. 2005, 57, 464–475. [Google Scholar] [CrossRef]
- Jones, A.E.; Morse, A.P. Application and Validation of a Seasonal Ensemble Prediction System Using a Dynamic Malaria Model. J. Clim. 2010, 23, 4202–4215. [Google Scholar] [CrossRef]
- Béguin, A.; Hales, S.; Rocklöv, J.; Åström, C.; Louis, V.R.; Sauerborn, R. The opposing effects of climate change and socio-economic development on the global distribution of malaria. Glob. Environ. Chang. 2011, 21, 1209–1214. [Google Scholar] [CrossRef]
- Yamana, T.K.; Eltahir, E.A.B. Incorporating the effects of humidity in a mechanistic model of Anopheles gambiae mosquito population dynamics in the Sahel region of Africa. Parasites Vectors 2013, 6, 235. [Google Scholar] [CrossRef] [PubMed]
- Diouf, I.; Adeola, A.M.; Abiodun, G.J.; Lennard, C.; Shirinde, J.M.; Yaka, P.; Ndione, J.A.; Gbobaniyi, E.O. Impact of future climate change on malaria in West Africa. Theor. Appl. Climatol. 2022, 147, 853–865. [Google Scholar] [CrossRef]
- Peterson, A.T. Shifting suitability for malaria vectors across Africa with warming climates. BMC Infect. Dis. 2009, 9, 59. [Google Scholar] [CrossRef]







| Model Name | Institution and Country | Resolution |
|---|---|---|
| BCC-CSM2-MR | Beijing Climate Centre (BCC) and China Meteorological Administration (CMA), China | 1.1° × 1.1° |
| CanESM5 | Canadian Earth System Model, Canada | 2.81° × 2.81° |
| CESM2 | National Centre for Atmospheric Research, Climate and Global Dynamics Laboratory, USA | 1.25° × 0.94° |
| CMCC-CM2-SR5 | The Euro-Mediterranean Centre on Climate Change, Italia | 2.8° × 1.9° |
| CNRM-CM6_HR | Centre National de Recherches Météorologiques-Centre Européen de Recherches et de Formation Avancée en Calcul Scientifique, France | 0.5° × 0.5° |
| FGOALS-g3 | Flexible Global Ocean-Atmosphere-Land System model Grid-point version 3 | 2° × 2.3° |
| GFDL-ESM4 | Geophysical Fluid Dynamics Laboratory, USA | 1.25° × 1.00° |
| IITM-ESM | Indian Institute of Tropical Meteorology, India | 1.9° × 1.9° |
| INM-CM5-0 | Numerical Mathematics, Russian Academy of Science, Moscow 119991, Russia | 2° × 1.5° |
| IPSL-CM6A-LR | Institut Pierre-Simon Laplace, France | 2.5° × 1.3° |
| MIROC6 | Japan Agency for Marine-Earth Science and Technology, Kanagawa 236–0001, Japan | 1.4° × 1.4° |
| MIROC-ES2L | Japan Agency for Marine-Earth Science and Technology, Kanagawa 236–0001, Japan | 2.8° × 2.8° |
| MPI-ESM1-2-HR | Max Planck Institute for Meteorology, High Resolution, Germany | 0.9° × 0.9° |
| NESM3 | Nanjing University of Information Science and Technology, Nanjing, China | 1.9° × 1.9° |
| TaiESM | Research Centre for Environmental Changes, Taiwan | 1.3° × 1° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diouf, I.; Ndione, J.-A.; Gaye, A.T. Malaria in Senegal: Recent and Future Changes Based on Bias-Corrected CMIP6 Simulations. Trop. Med. Infect. Dis. 2022, 7, 345. https://doi.org/10.3390/tropicalmed7110345
Diouf I, Ndione J-A, Gaye AT. Malaria in Senegal: Recent and Future Changes Based on Bias-Corrected CMIP6 Simulations. Tropical Medicine and Infectious Disease. 2022; 7(11):345. https://doi.org/10.3390/tropicalmed7110345
Chicago/Turabian StyleDiouf, Ibrahima, Jacques-André Ndione, and Amadou Thierno Gaye. 2022. "Malaria in Senegal: Recent and Future Changes Based on Bias-Corrected CMIP6 Simulations" Tropical Medicine and Infectious Disease 7, no. 11: 345. https://doi.org/10.3390/tropicalmed7110345
APA StyleDiouf, I., Ndione, J.-A., & Gaye, A. T. (2022). Malaria in Senegal: Recent and Future Changes Based on Bias-Corrected CMIP6 Simulations. Tropical Medicine and Infectious Disease, 7(11), 345. https://doi.org/10.3390/tropicalmed7110345







