Infectious Disease Modeling with Socio-Viral Behavioral Aspects—Lessons Learned from the Spread of SARS-CoV-2 in a University
Abstract
1. Introduction
2. Context
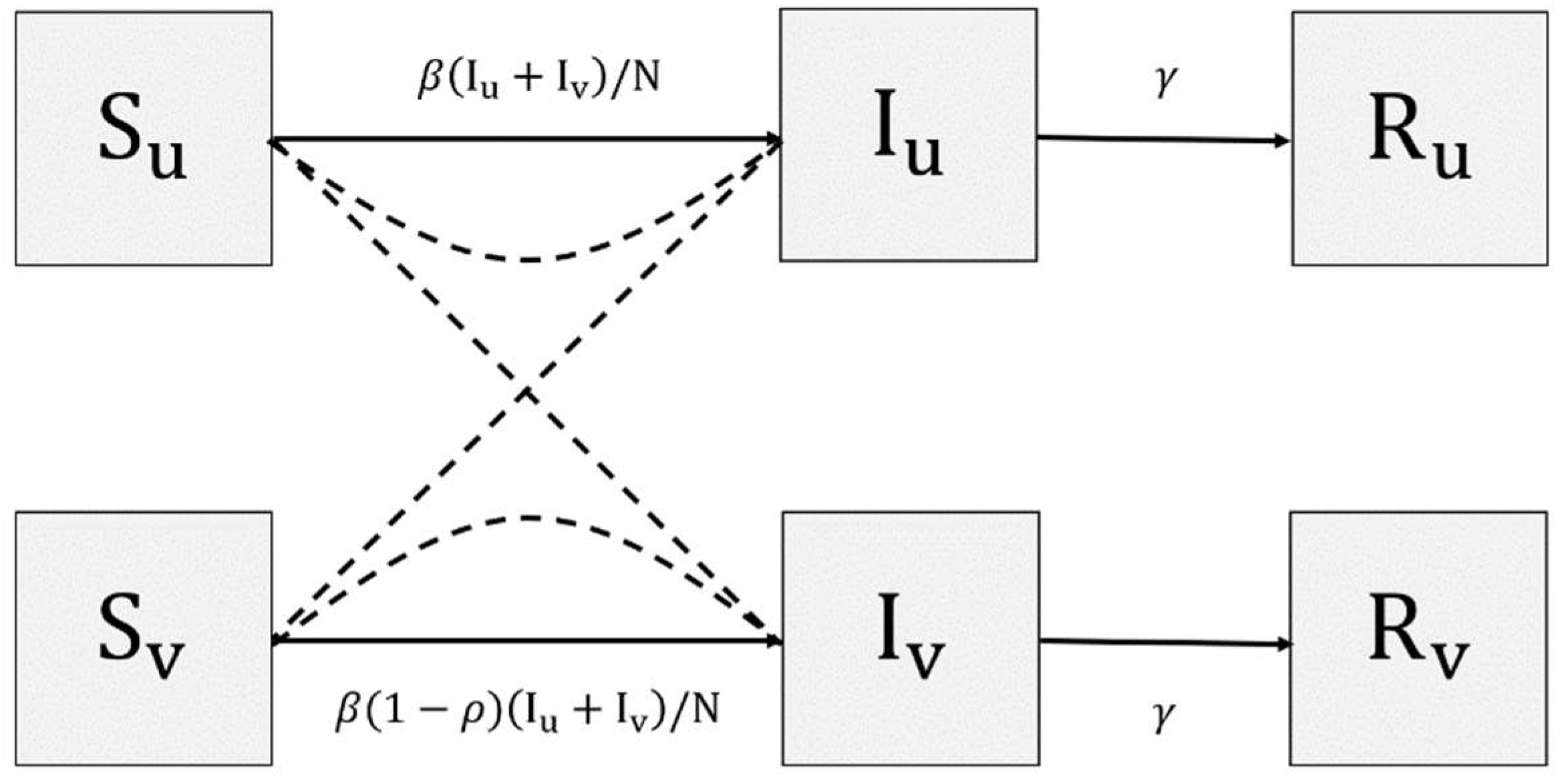
3. Proposed Model
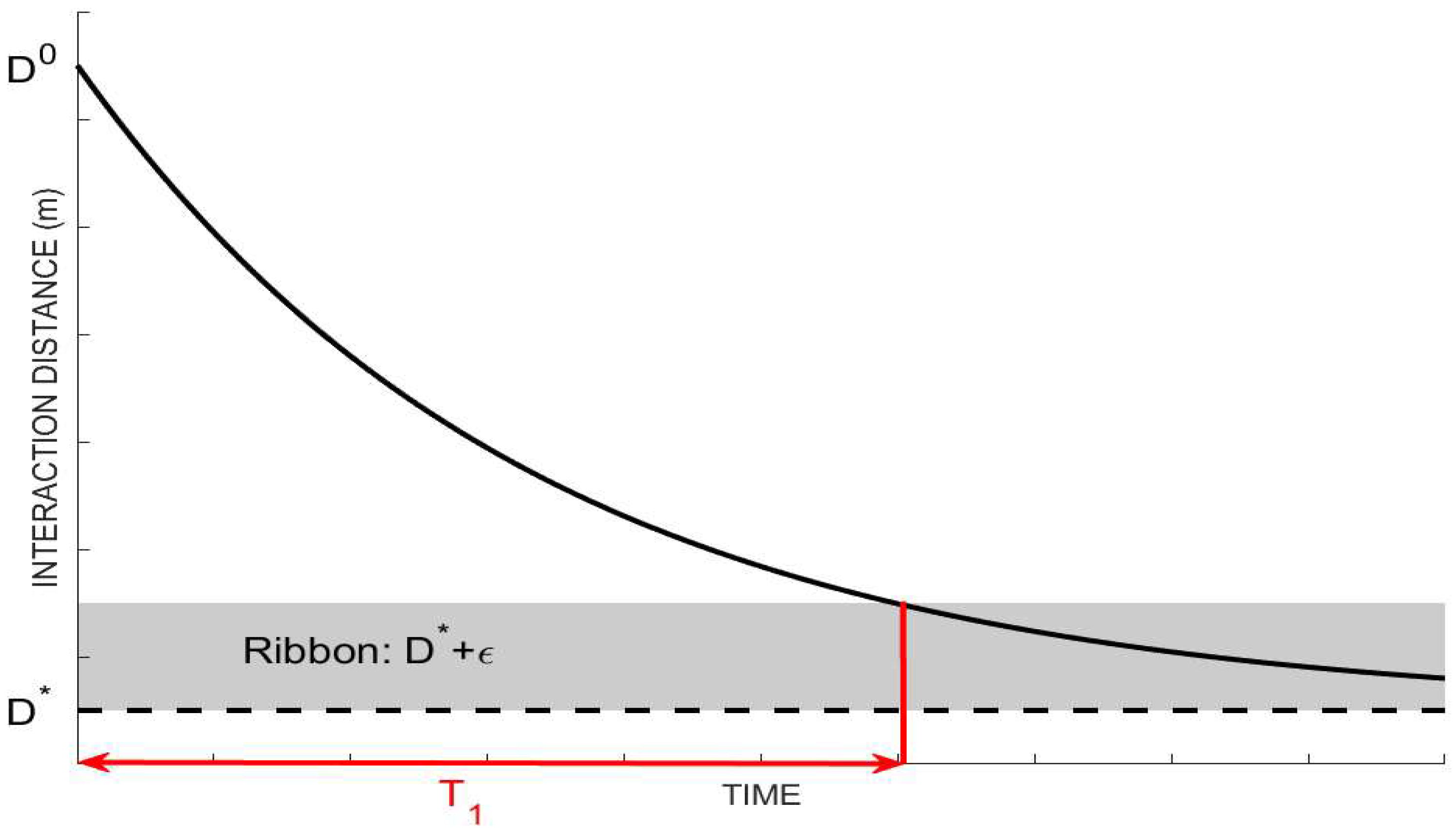
3.1. Observability of Socio-Behavioral Parameters
3.2. Contact and Airborne-Based Transmission Rate
3.3. Recovery Rate
4. Numerical Results
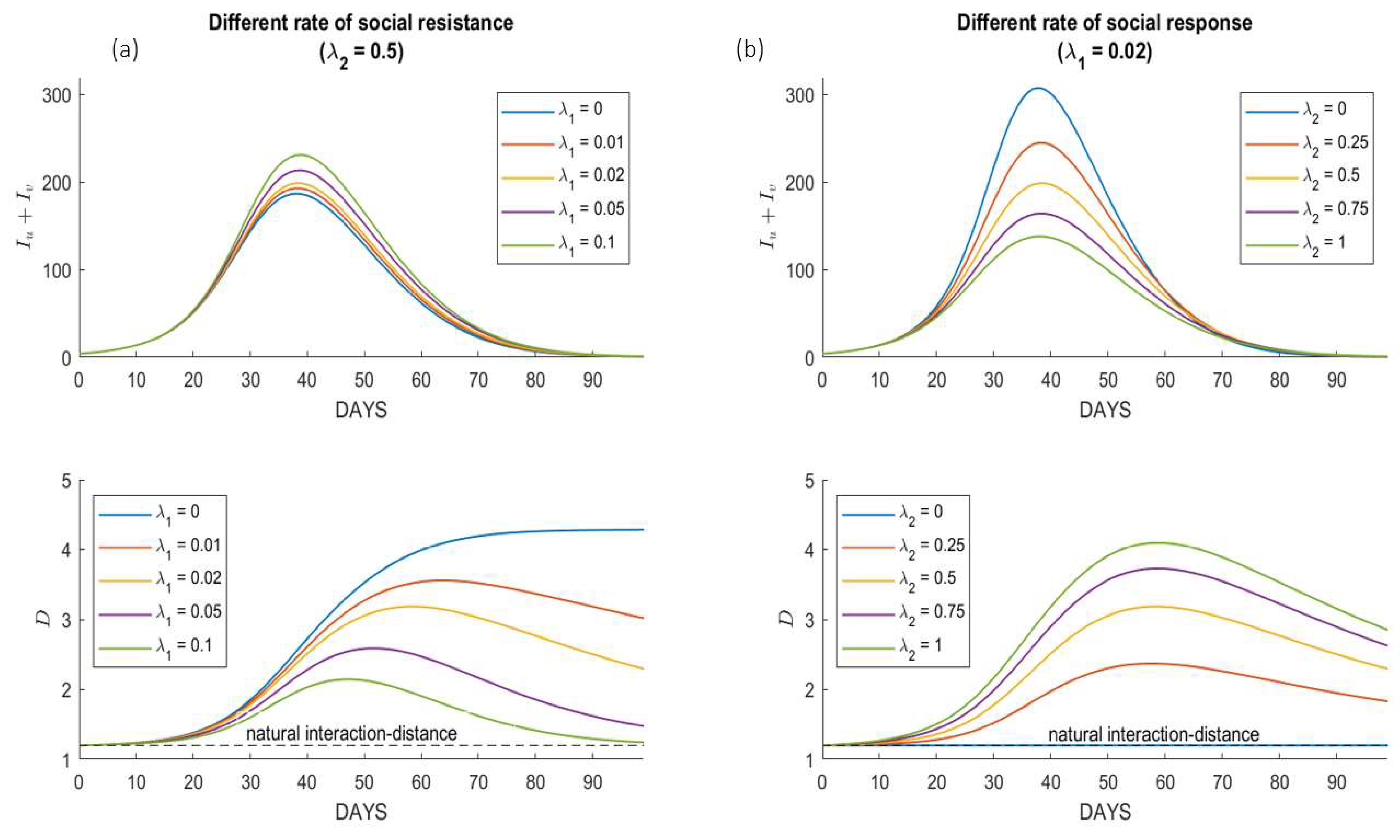
4.1. Variations under Different Society Behaviors
4.2. Variations under Different Pathogen Characteristics
5. Case Study: SARS-CoV-2 Spread in School
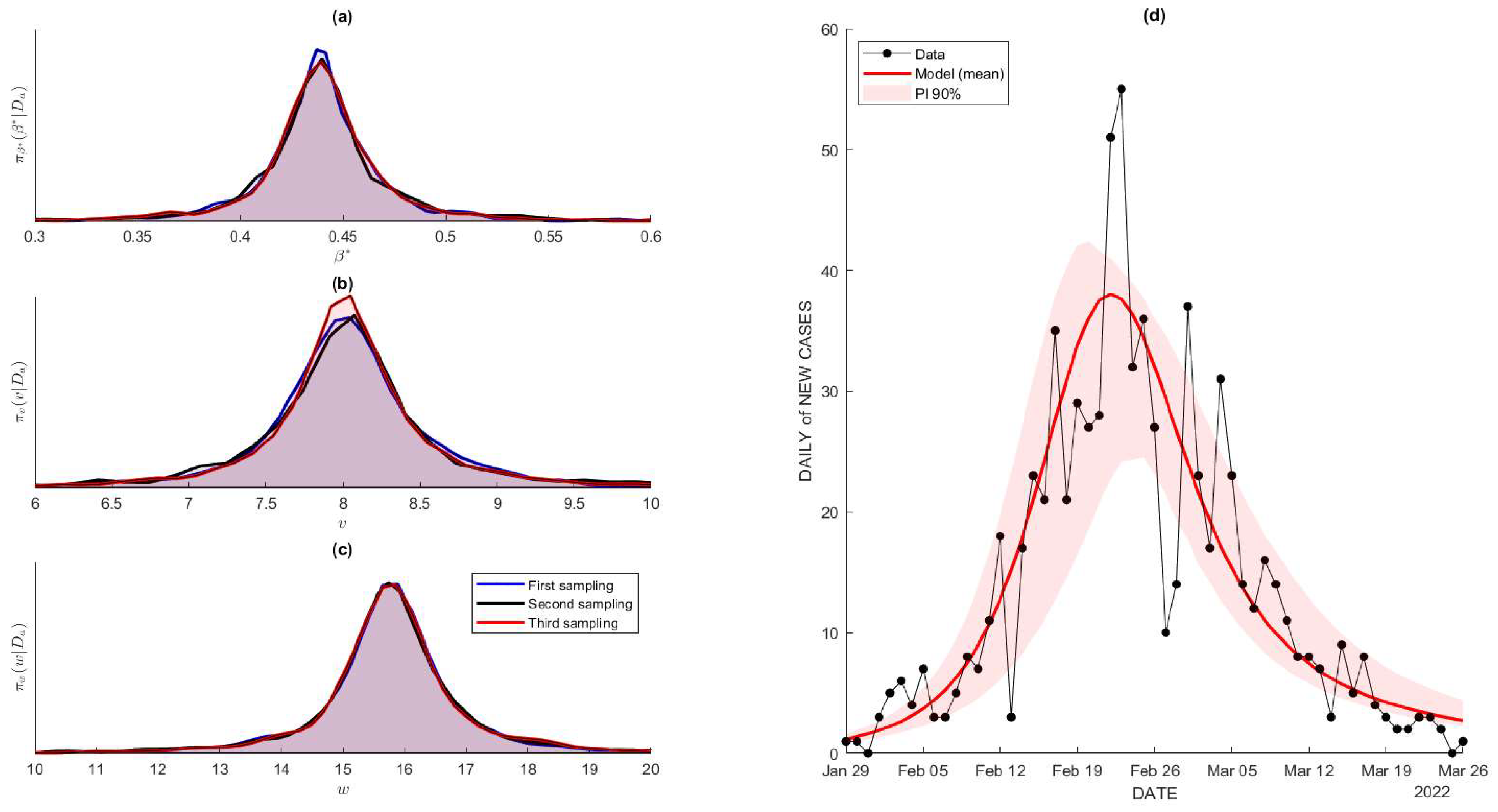
5.1. Dataset and Parameters’ Estimation
5.2. Projected Number of Cases
5.3. Prospective Action Plans
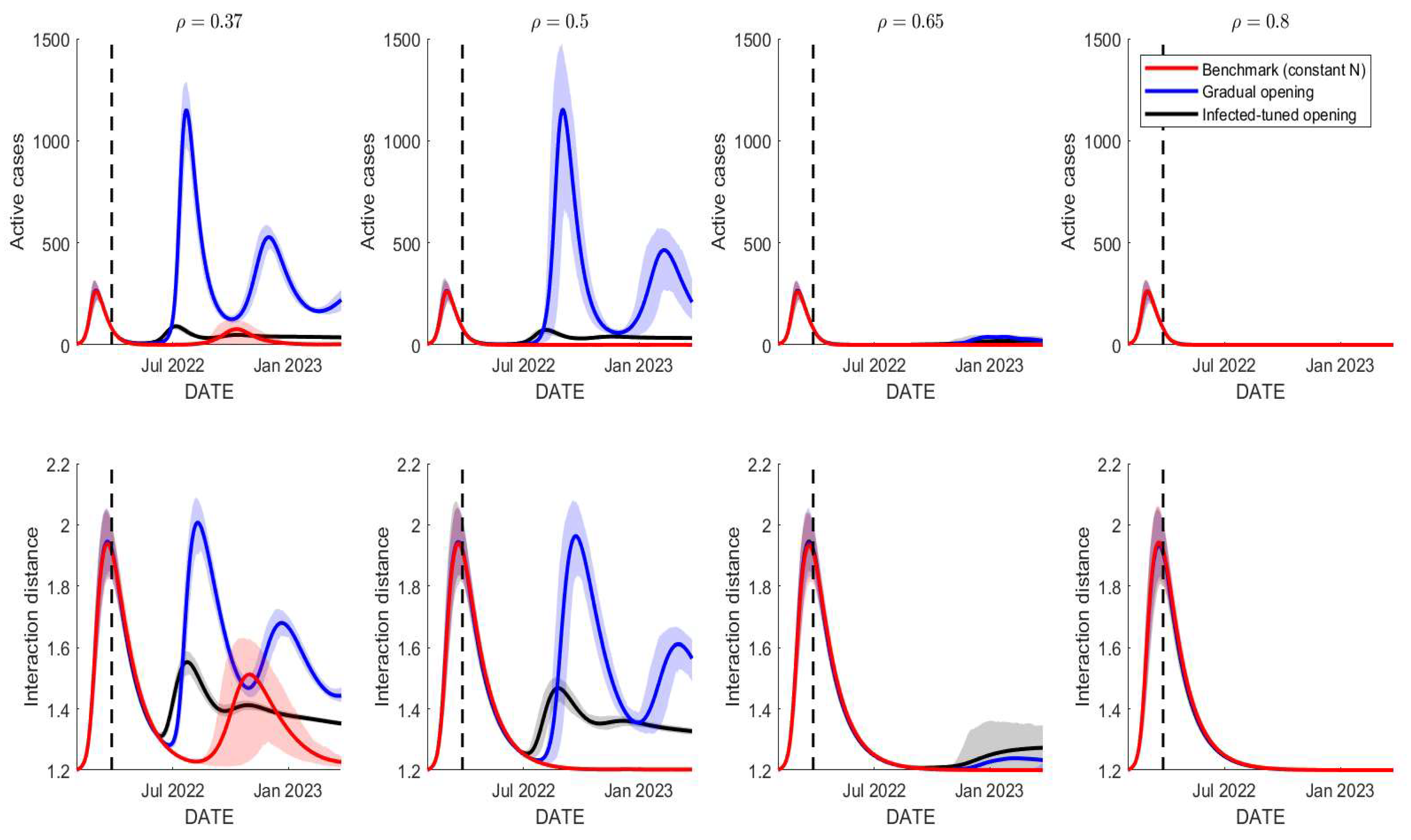
5.3.1. School Reopening Management
- No school reopening (benchmark)We preserve the size of the population as it was used to generate simulations in the previous section. We set for all which leads to the constant population size for all time. This scenario is a benchmark for the other two scenarios.
- Gradual school reopeningA gradual school reopening is a scheme that admits students and academical staff gradually until, at some point, the total number of students and staff is reached. In the Institut Teknologi Bandung (ITB), there are approximately 20,000 students and academical staff at any time for a non-pandemic era, which starts with only 4000 individuals in a pandemic era (January until April 2022). Hence, we choose a simple-bounded linearly increasing function as given by:, with is the training data interval, which uses . However, represents the total school reopening that starts in September 1, 2022, with . The middle period of represents a linearly gradual reopening from 4000 to 20,000. In practice, it is easy to add that and during the period of reopening , and otherwise.
- Prevalence-tuned school openingThe last scenario accommodates the response of the school officials to reduce the school capacity as the disease prevalence level increases. Hence, we assume that the number of should be related to the number of . We chose a negative exponential to represent the relation between and as follows:
5.3.2. Vaccine Coverage and Effectiveness Improvement
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Model Analysis and Threshold Number
Appendix B. Numerical Sensitivity Analysis of the Socio-Behavioral Parameters
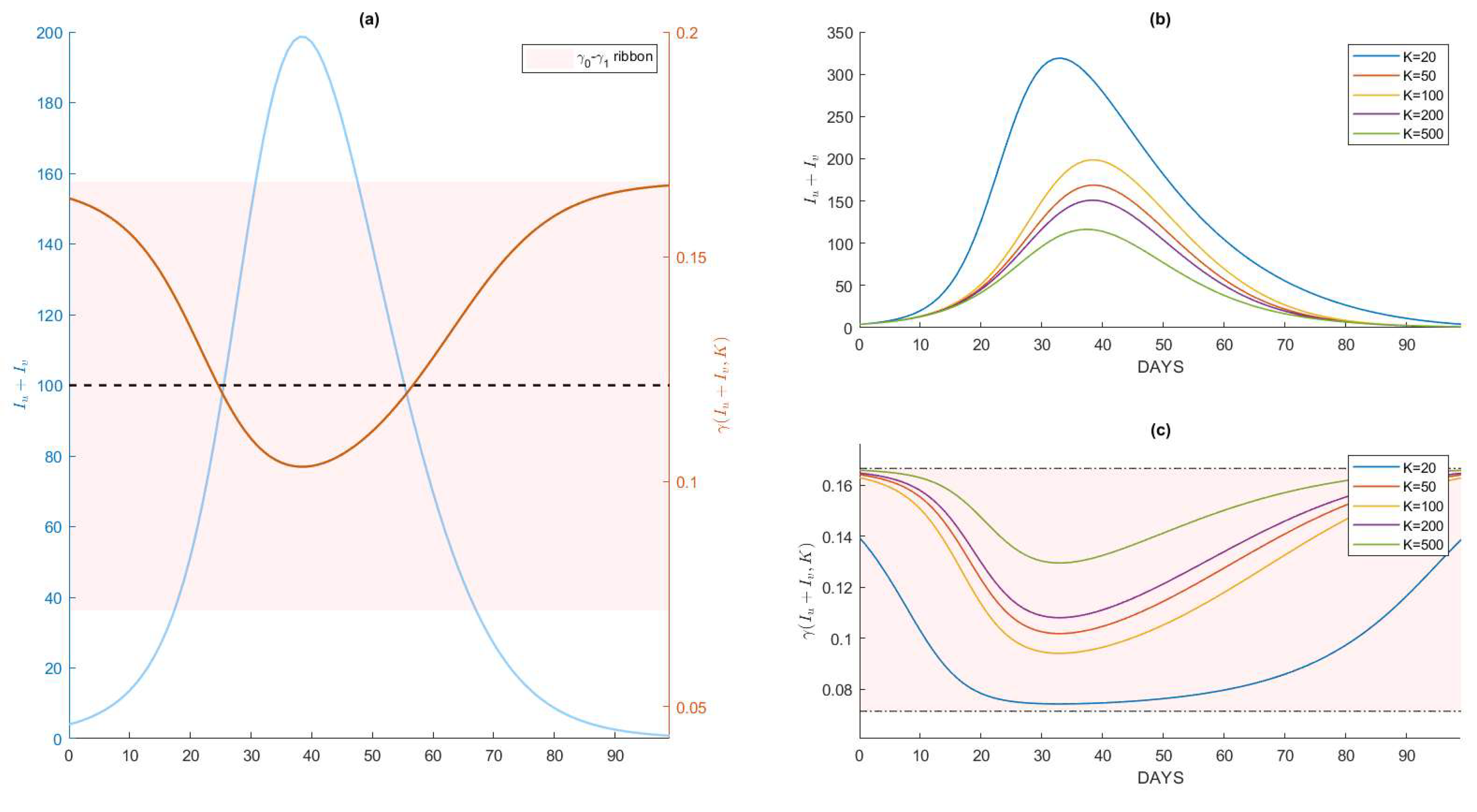
Appendix C. Numerical Simulations under Different Healthcare Capacity
Appendix D. Bayesian Hierarchical for Parameters’ Estimation
References
- Nakamura, G.M.; Martinez, A.S. Hamiltonian dynamics of the SIS epidemic model with stochastic fluctuations. Sci. Rep. 2019, 9, 15841. [Google Scholar] [CrossRef] [PubMed]
- Carcione, J.M.; Santos, J.E.; Bagaini, C.; Ba, J. A Simulation of a COVID-19 Epidemic Based on a Deterministic SEIR Model. Front. Public Health 2020, 8, 230. [Google Scholar] [CrossRef] [PubMed]
- Bjørnstad, O.N.; Shea, K.; Krzywinski, M.; Altman, N. The SEIRS model for infectious disease dynamics. Nat. Methods 2020, 17, 557–558. [Google Scholar] [CrossRef]
- Tolles, J.; Luong, T. Modeling Epidemics with Compartmental Models. JAMA 2020, 323, 2515. [Google Scholar] [CrossRef] [PubMed]
- Milligan, G. Vaccinology: An Essential Guide; Wiley Blackwell: Sussex, UK, 2015. [Google Scholar]
- Susanto, H.; Tjahjono, V.; Hasan, A.; Kasim, M.; Nuraini, N.; Putri, E.; Kusdiantara, R.; Kurniawan, H. How Many Can You Infect? Simple (and Naive) Methods of Estimating the Reproduction Number. Commun. Biomath. Sci. 2020, 3, 28–36. [Google Scholar] [CrossRef]
- Hasan, A.; Nasution, Y.; Susanto, H.; Putri, E.; Tjahjono, V.; Puspita, D.; Sukandar, K.; Nuraini, N.; Widyastuti, W. Modeling COVID-19 Transmissions and Evaluation of Large-Scale Social Restriction in Jakarta, Indonesia. Commun. Biomath. Sci. 2022, 5, 90–100. [Google Scholar] [CrossRef]
- Katul, G.G.; Mrad, A.; Bonetti, S.; Manoli, G.; Parolari, A.J. Global convergence of COVID-19 basic reproduction number and estimation from early-time SIR dynamics. PLoS ONE 2020, 15, e0239800. [Google Scholar] [CrossRef]
- Moein, S.; Nickaeen, N.; Roointan, A.; Borhani, N.; Heidary, Z.; Javanmard, S.H.; Ghaisari, J.; Gheisari, Y. Inefficiency of SIR models in forecasting COVID-19 epidemic: A case study of Isfahan. Sci. Rep. 2021, 11, 4725. [Google Scholar] [CrossRef]
- Allen, L.J.S.; Brown, V.; Jonsson, C.; Klein, S.L.; Laverty, S.M.; Magwedere, K.; Owen, J.C.; Driessche, P.V.D. Mathematical modeling of viral zoonoses in wildlife. Nat. Resour. Model. 2011, 25, 5–51. [Google Scholar] [CrossRef]
- Li, G.-H.; Zhang, Y.-X. Dynamic behaviors of a modified SIR model in epidemic diseases using nonlinear incidence and recovery rates. PLoS ONE 2017, 12, e0175789. [Google Scholar] [CrossRef]
- Okabe, Y.; Shudo, A. A mathematical model of epidemics-a tutorial for students. Mathematics 2020, 8, 1174. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Franco, E.; Mohler, G.; Short, M.B.; Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 16732–16738. [Google Scholar] [CrossRef] [PubMed]
- Wahyudi, B.A.; Palupi, I. Prediction of the peak COVID-19 pandemic in Indonesia using SIR model. J. Teknol. Sist. Komput. 2020, 9, 49–55. [Google Scholar] [CrossRef]
- Weston, D.; Hauck, K.; Amlôt, R. Infection prevention behaviour and infectious disease modelling: A review of the literature and recommendations for the future. BMC Public Health 2018, 18, 336. [Google Scholar] [CrossRef]
- Hufsky, F.; Lamkiewicz, K.; Almeida, A.; Aouacheria, A.; Arighi, C.; Bateman, A.; Baumbach, J.; Beerenwinkel, N.; Brandt, C.; Cacciabue, M.; et al. Computational strategies to combat COVID-19: Useful tools to accelerate SARS-CoV-2 and coronavirus research. Brief. Bioinform. 2021, 22, 642–663. [Google Scholar] [CrossRef]
- Peter, S.; Dittrich, P.; Ibrahim, B. Structure and Hierarchy of SARS-CoV-2 Infection Dynamics Models Revealed by Reaction Network Analysis. Viruses 2020, 13, 14. [Google Scholar] [CrossRef]
- Wisconsin, D. Infection Control and Prevention—Tuberculosis (tb). 2022. Available online: https://www.dhs.wisconsin.gov/ic/tb.htm (accessed on 1 April 2022).
- CDC. Scientific Brief: Sars-cov-2 Transmission. 2022. Available online: https://www.cdc.gov/coronavirus/2019-ncov/science/science-briefs/sars-cov-2-transmission.html (accessed on 1 April 2022).
- CDC. Tuberculosis: General Information. 2022. Available online: https://www.cdc.gov/tb/publications/factsheets/general/tb.htm (accessed on 31 May 2022).
- Van Doremalen, N.; Bushmaker, T.; Morris, D.H.; Holbrook, M.G.; Gamble, A.; Williamson, B.N.; Tamin, A.; Harcourt, J.L.; Thornburg, N.J.; Gerber, S.I.; et al. Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. N. Engl. J. Med. 2020, 382, 1564–1567. [Google Scholar] [CrossRef]
- Oluyori, D.A.; Perez, A.C.; Okhuese, V.A.; Akram, M. Backward and hopf bifurcation analysis of an seirs COVID-19 epidemic model with saturated incidence and satureted treatment response (preprint work). MedRxiv 2020. [CrossRef]
- Cabrera, M.; Córdova-Lepe, F.; Gutiérrez-Jara, J.P.; Vogt-Geisse, K. An SIR-type epidemiological model that integrates social distancing as a dynamic law based on point prevalence and socio-behavioral factors. Sci. Rep. 2021, 11, 10170. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Bush, J.W.M. A guideline to limit indoor airborne transmission of COVID-19. Proc. Natl. Acad. Sci. USA 2021, 118, e2018995118. [Google Scholar] [CrossRef]
- Nuraini, N.; Sukandar, K.; Hadisoemarto, P.; Susanto, H.; Hasan, A.; Sumarti, N. Mathematical models for assessing vaccination scenarios in several provinces in Indonesia. Infect. Dis. Model. 2021, 6, 1236–1258. [Google Scholar] [CrossRef] [PubMed]
- Aini, W.; Sukandar, K.K.; Nuraini, N.; Handayani, D. The Impact of Mass Exodus on the Resurgence of COVID-19 Cases: Case Study of Regions in Indonesia. Front. Appl. Math. Stat. 2022, 8, 912150. [Google Scholar] [CrossRef]
- Sukandar, K.K.; Louismono, A.L.; Volisa, M.; Kusdiantara, R.; Fakhruddin, M.; Nuraini, N.; Soewono, E. A Prospective Method for Generating COVID-19 Dynamics. Computation 2022, 10, 107. [Google Scholar] [CrossRef]
- Fuady, A.; Nuraini, N.; Sukandar, K.; Lestari, B. Targeted Vaccine Allocation Could Increase the COVID-19 Vaccine Benefits Amidst Its Lack of Availability. Vaccines 2021, 9, 462. [Google Scholar] [CrossRef]
- Iachini, T.; Coello, Y.; Frassinetti, F.; Ruggiero, G. Body Space in Social Interactions: A Comparison of Reaching and Comfort Distance in Immersive Virtual Reality. PLoS ONE 2014, 9, e111511. [Google Scholar] [CrossRef]
- Iachini, T.; Coello, Y.; Frassinetti, F.; Senese, V.P.; Galante, F.; Ruggiero, G. Peripersonal and interpersonal space in virtual and real environments: Effects of gender and age. J. Environ. Psychol. 2016, 45, 154–164. [Google Scholar] [CrossRef]
- Matsuda, Y.; Sugimoto, M.; Inami, M.; Kitazaki, M. Peripersonal space in the front, rear, left and right directions for audio-tactile multisensory integration. Sci. Rep. 2021, 11, 11303. [Google Scholar] [CrossRef]
- Salathé, M.; Kazandjieva, M.; Lee, J.W.; Levis, P.; Feldman, M.W.; Jones, J.H. A high-resolution human contact network for infectious disease transmission. Proc. Natl. Acad. Sci. USA 2010, 107, 22020–22025. [Google Scholar] [CrossRef]
- Sorokowska, A.; Sorokowski, P.; Hilpert, P.; Cantarero, K.; Frackowiak, T.; Ahmadi, K.; Alghraibeh, A.M.; Aryeetey, R.; Bertoni, A.; Bettache, K.; et al. Preferred Interpersonal Distances: A Global Comparison. J. Cross-Cultural Psychol. 2017, 48, 577–592. [Google Scholar] [CrossRef]
- Tang, J.W.; Bahnfleth, W.P.; Bluyssen, P.M. Dismantling myths on the airborne transmission of severe acute resporatory syndrome coronavirus-2 (SARS-coV-2). J. Hosp. Infect. 2021, 110, 89–596. [Google Scholar] [CrossRef] [PubMed]
- Escombe, A.R.; Oeser, C.; Gilman, R.H.; Ñavincopa, M.; Ticona, E.; Martínez, C.; Caviedes, L.; Sheen, P.; Gonzalez, A.; Noakes, C.; et al. The Detection of Airborne Transmission of Tuberculosis from HIV-Infected Patients, Using an In Vivo Air Sampling Model. Clin. Infect. Dis. 2007, 44, 1349–1357. [Google Scholar] [CrossRef] [PubMed]
- IHME. COVID-19 Vaccine Efficacy Summary. Available online: https://www.healthdata.org/covid/COVID-19-vaccine-efficacy-summary (accessed on 2 April 2022).
- DDS. Airborne and Direct Contact Diseases. Available online: https://www.maine.gov/dhhs/mecdc/infectious-disease/epi/airborne/index.shtml (accessed on 16 March 2022).
- Hammond, A.; Khalid, T.; Thornton, H.V.; Woodall, C.A.; Hay, A.D. Should homes and workplaces purchase portable air filters to reduce the transmission of SARS-CoV-2 and other respiratory infections? A systematic review. PLoS ONE 2021, 16, e0251049. [Google Scholar] [CrossRef] [PubMed]
- Pyankov, O.V.; Bodnev, S.A.; Pyankova, O.G.; Agranovski, I.E. Survival of aerosolized coronavirus in the ambient air. J. Aerosol Sci. 2017, 115, 158–163. [Google Scholar] [CrossRef] [PubMed]
- Ratnesar-Shumate, S.; Williams, G.; Green, B.; Krause, M.; Holland, B.; Wood, S.; Bohannon, J.; Boydston, J.; Freeburger, D.; Hooper, I.; et al. Simulated Sunlight Rapidly Inactivates SARS-CoV-2 on Surfaces. J. Infect. Dis. 2020, 222, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Riley, E.C.; Murphy, G.; Riley, R.L. Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 1978, 107, 421–432. [Google Scholar] [CrossRef]
- Miller, S.L.; Nazaroff, W.W.; Jimenez, J.L.; Boerstra, A.; Buonanno, G.; Dancer, S.J.; Kurnitski, J.; Marr, L.C.; Morawska, L.; Noakes, C. Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event. Indoor Air 2020, 31, 314–323. [Google Scholar] [CrossRef]
- Gou, W.; Jin, Z. How heterogeneous susceptibility and recovery rates affect the spread of epidemics on networks. Infect. Dis. Model. 2017, 2, 353–367. [Google Scholar] [CrossRef]
- Lee, B.Y.; Bartsch, S.M.; Ferguson, M.C.; Wedlock, P.T.; O’Shea, K.J.; Siegmund, S.S.; Cox, S.N.; McKinnell, J.A. The value of decreasing the duration of the infectious period of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infection. PLOS Comput. Biol. 2021, 17, e1008470. [Google Scholar] [CrossRef]
- Ramatillah, D.L.; Isnaini, S. Treatment profiles and clinical outcomes of COVID-19 patients at private hospital in Jakarta. PLoS ONE 2021, 16, e0250147. [Google Scholar] [CrossRef]
- Kelland, K. One Meter or Two? How Social Distancing Affects COVID-19 Risk. Available online: https://www.reuters.com/article/us-health-coronavirus-distance-explainer-idUSKBN23U22W (accessed on 23 June 2020).
- CBCNews. Some Countries Reconsider 2-Metre Rule for Physical Distancing, But Not Here. 2020. Available online: https://www.cbc.ca/news/health/2-metres-coronavirus-covid-distancing-1.5624439 (accessed on 23 December 2021).
- Henchoz, C.; Coste, T.; Wernli, B. Culture, money attitudes and economic outcomes. Swiss J. Econ. Stat. 2019, 155, 2. [Google Scholar] [CrossRef]





| Countries | Social Distance | Personal Distance | Intimate Distance |
|---|---|---|---|
| Romania, Hungary, Saudi Arabia, Turkey, Uganda | 1.20–1.40 m | 0.90–1.20 m | 0.45–0.90 m |
| Pakistan, Estonia, Colombia, Hong Kong, China, Iran, Malaysia, Czech Republic, Portugal, Kenya, Switzerland, India, Indonesia, Croatia, Ghana, South Korea | 1.05–1.20 m | 0.75–1.05 m | 0.40–0.75 m |
| Norway, Canada, Nigeria, Brazil, England, Mexico, Poland, Germany, USA, Kazakhstan, Italy, Serbia, Greece, Spain | 0.90–1.05 m | 0.60–0.75 m | 0.40–0.60 m |
| Russia, Slovakia, Austria, Ukraine, Bulgaria, Peru, Argentina | 0.70–0.90 m | 0.60–0.70 m | 0.30–0.50 m |
| Media | SARS-CoV-2 | SARS-CoV-1 |
|---|---|---|
| Aerosol | 10.00 2.00 h | 8.00 2.00 h |
| Copper | 11.00 6.00 h | 19.00 7.50 h |
| Cardboard | 39.00 9.00 h | 8.00 5.00 h |
| Stainless steel | 72.00 15.00 h | 50.00 10.00 h |
| Plastic | 90.00 10.00 h | 90.00 10.00 h |
| Countries | Physical Distancing (m) |
|---|---|
| Singapore, United Kingdom, Denmark, France, Hong Kong, China and France | 1 m |
| Australia, Belgium, Greece, Germany, Italy, Spain, Portugal, Switzerland | 1.5 m |
| Canada, United States | 2 m |
| Notation | Description | Values |
|---|---|---|
| COVID-19 recovery rate in the case of a lack of healthcare capacity (in the case of excessive healthcare). This parameter governs the time-dependent recovery rate | 1/14 (1/6) 1/day | |
| Natural interaction distance | 1.2 m | |
| and | Intrinsic transmission rate and the contact and airborne transmission adjuster | Calibrated |
| Current vaccine efficacy, using SinoVac [29] | 0.35 | |
| The rate of social resistance in the observed community | 0.07 1/day | |
| The rate of social response in the observed community | 0.53 m/day | |
| Average concentration of airborne pathogens emitted by one infected individual per day | 24 quanta/(day [24] | |
| Removal rate of airborne pathogens | 2 1/day [21] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuraini, N.; Sukandar, K.K.; Tahu, M.Y.T.; Giri-Rachman, E.A.; Barlian, A.; Suhardi, S.H.; Pasaribu, U.S.; Yuliar, S.; Mudhakir, D.; Ariesyady, H.D.; et al. Infectious Disease Modeling with Socio-Viral Behavioral Aspects—Lessons Learned from the Spread of SARS-CoV-2 in a University. Trop. Med. Infect. Dis. 2022, 7, 289. https://doi.org/10.3390/tropicalmed7100289
Nuraini N, Sukandar KK, Tahu MYT, Giri-Rachman EA, Barlian A, Suhardi SH, Pasaribu US, Yuliar S, Mudhakir D, Ariesyady HD, et al. Infectious Disease Modeling with Socio-Viral Behavioral Aspects—Lessons Learned from the Spread of SARS-CoV-2 in a University. Tropical Medicine and Infectious Disease. 2022; 7(10):289. https://doi.org/10.3390/tropicalmed7100289
Chicago/Turabian StyleNuraini, Nuning, Kamal Khairudin Sukandar, Maria Yulita Trida Tahu, Ernawati Arifin Giri-Rachman, Anggraini Barlian, Sri Harjati Suhardi, Udjianna Sekteria Pasaribu, Sonny Yuliar, Diky Mudhakir, Herto Dwi Ariesyady, and et al. 2022. "Infectious Disease Modeling with Socio-Viral Behavioral Aspects—Lessons Learned from the Spread of SARS-CoV-2 in a University" Tropical Medicine and Infectious Disease 7, no. 10: 289. https://doi.org/10.3390/tropicalmed7100289
APA StyleNuraini, N., Sukandar, K. K., Tahu, M. Y. T., Giri-Rachman, E. A., Barlian, A., Suhardi, S. H., Pasaribu, U. S., Yuliar, S., Mudhakir, D., Ariesyady, H. D., Rosleine, D., Sofyan, I., & Martokusumo, W. (2022). Infectious Disease Modeling with Socio-Viral Behavioral Aspects—Lessons Learned from the Spread of SARS-CoV-2 in a University. Tropical Medicine and Infectious Disease, 7(10), 289. https://doi.org/10.3390/tropicalmed7100289










