Modelling the Use of Vaccine and Wolbachia on Dengue Transmission Dynamics
Abstract
1. Introduction
2. Methods and Results
2.1. Formulation of the Mathematical Model
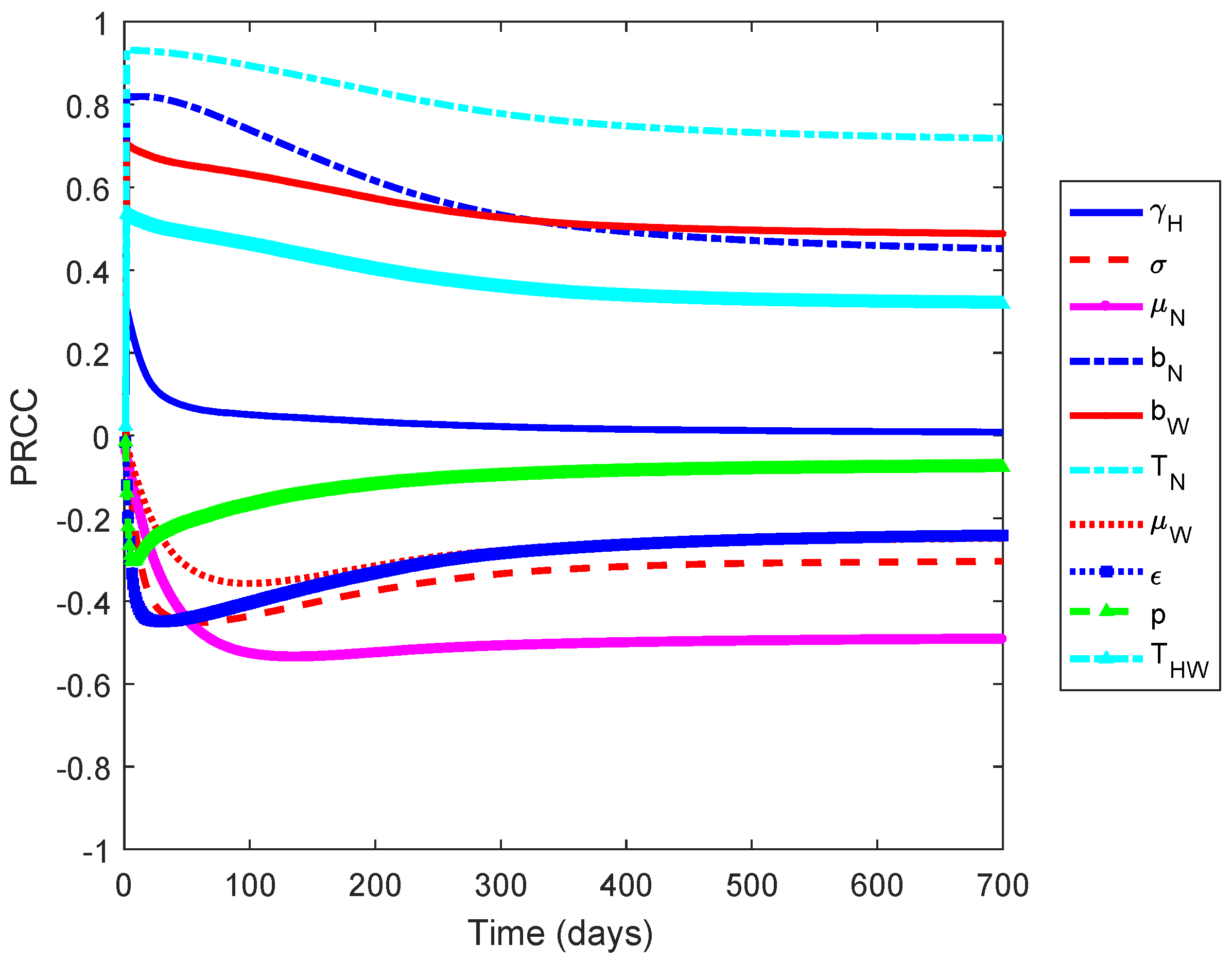
2.2. Sensitivity Analysis
2.3. Numerical Simulations
2.3.1. Dengue Reduction
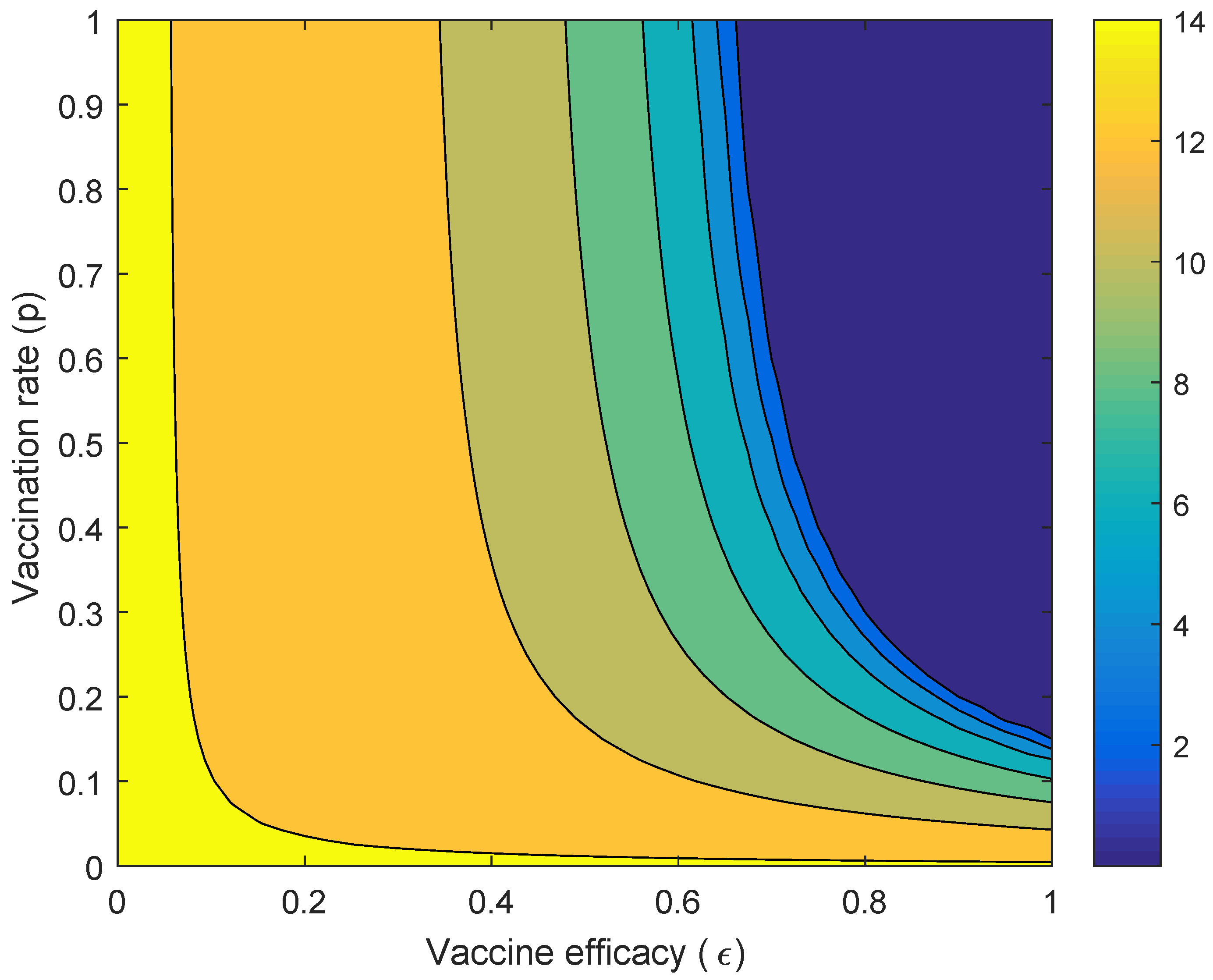
2.3.2. Parameter Exploration
3. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 1476–4687. [Google Scholar] [CrossRef] [PubMed]
- Achee, N.L.; Gould, F.; Perkins, T.A.; Reiner, R.C., Jr.; Morrison, A.C.; Ritchie, S.A.; Gubler, D.J.; Teyssou, R.; Scott, T.W. A Critical Assessment of Vector Control for Dengue Prevention. PLoS Negl. Trop. Dis. 2015, 9, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Anggriani, N.; Tasman, H.; Ndii, M.Z.; Supriatna, A.K.; Soewono, E.; Siregar, E. The effect of reinfection with the same serotype on dengue transmission dynamics. Appl. Math. Comput. 2019, 349, 62–80. [Google Scholar] [CrossRef]
- Katzelnick, L.C.; Gresh, L.; Halloran, M.E.; Mercado, J.C.; Kuan, G.; Gordon, A.; Balmaseda, A.; Harris, E. Antibody-dependent enhancement of severe dengue disease in humans. Science 2017, 358, 929–932. [Google Scholar] [CrossRef]
- Esu, E.; Lenhart, A.; Smith, L.; Horstick, O. Effectiveness of peridomestic space spraying with insecticide on dengue transmission; systematic review. Trop. Med. Int. Health 2010, 15, 619–631. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Hue Kien, D.T.; Clapham, H.; Aguas, R.; Trung, V.T.; Bich Chau, T.N.; Popovici, J.; Ryan, P.A.; O’Neill, S.L.; McGraw, E.A.; et al. Modeling the impact on virus transmission of Wolbachia-mediated blocking of dengue virus infection of Aedes aegypti. Sci. Transl. Med. 2015, 7, 279ra37. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Hickson, R.I.; Allingham, D.; Mercer, G.N. Modelling the transmission dynamics of dengue in the presence of Wolbachia. Math. Biosci. 2015, 262, 157–166. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Allingham, D.; Hickson, R.; Glass, K. The effect of Wolbachia on dengue outbreaks when dengue is repeatedly introduced. Theor. Popul. Biol. 2016, 111, 9–15. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Allingham, D.; Hickson, R.I.; Glass, K. The effect of Wolbachia on dengue dynamics in the presence of two serotypes of dengue: Symmetric and asymmetric epidemiological characteristics. Epidemiol. Infect. 2016, 144, 2874–2882. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Wiraningsih, E.D.; Anggriani, N.; Supriatna, A.K. Mathematical Model as a Tool for the Control of Vector-Borne Diseases: Wolbachia Example. In Dengue Fever; Falcón-Lezama, J.A., Betancourt-Cravioto, M., Tapia-Conyer, R., Eds.; IntechOpen: Rijeka, Croatia, 2019; Chapter 7. [Google Scholar] [CrossRef]
- O’Reilly, K.M.; Hendrickx, E.; Kharisma, D.D.; Wilastonegoro, N.N.; Carrington, L.B.; Elyazar, I.R.F.; Kucharski, A.J.; Lowe, R.; Flasche, S.; Pigott, D.M.; et al. Estimating the burden of dengue and the impact of release of wMel Wolbachia-infected mosquitoes in Indonesia: A modelling study. BMC Med. 2019, 17, 172. [Google Scholar] [CrossRef]
- Dorigatti, I.; McCormack, C.; Nedjati-Gilani, G.; Ferguson, N.M. Using Wolbachia for Dengue Control: Insights from Modelling. Trends Parasitol. 2018, 34, 102–113. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Rodríguez-Barraquer, I.; Dorigatti, I.; Mier-y Teran-Romero, L.; Laydon, D.J.; Cummings, D.A.T. Benefits and risks of the Sanofi-Pasteur dengue vaccine: Modeling optimal deployment. Science 2016, 353, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, M.; Stollenwerk, N.; Halstead, S.B. The Impact of the Newly Licensed Dengue Vaccine in Endemic Countries. PLoS Negl. Trop. Dis. 2016, 10, e0005179. [Google Scholar] [CrossRef] [PubMed]
- Pasteur, S. Sanofi: Dengvaxia®, World’s First Dengue Vaccine, Approved in Mexico. 2015. Available online: https://www.sanofi.com/en/media-room/press-releases/2015/2015-12-09-16-30-00 (accessed on 28 April 2020).
- Gailhardou, S.; Skipetrova, A.; Dayan, G.H.; Jezorwski, J.; Saville, M.; Van der Vliet, D.; Wartel, T.A. Safety Overview of a Recombinant Live-Attenuated Tetravalent Dengue Vaccine: Pooled Analysis of Data from 18 Clinical Trials. PLoS Negl. Trop. Dis. 2016, 10, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Capeding, M.R.; Tran, N.H.; Hadinegoro, S.R.S.; Ismail, H.I.H.M.; Chotpitayasunondh, T.; Chua, M.N.; Luong, C.Q.; Rusmil, K.; Wirawan, D.N.; Nallusamy, R.; et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: A phase 3, randomised, observer-masked, placebo-controlled trial. Lancet 2014, 384, 1358–1365. [Google Scholar] [CrossRef]
- da Costa, V.G.; Marques-Silva, A.C.; Floriano, V.G.; Moreli, M.L. Safety, immunogenicity and efficacy of a recombinant tetravalent dengue vaccine: A meta-analysis of randomized trials. Vaccine 2014, 32, 4885–4892. [Google Scholar] [CrossRef]
- Dorigatti, I.; Aguas, R.; Donnelly, C.A.; Guy, B.; Coudeville, L.; Jackson, N.; Saville, M.; Ferguson, N.M. Modelling the immunological response to a tetravalent dengue vaccine from multiple phase-2 trials in Latin America and South East Asia. Vaccine 2015, 33, 3746–3751. [Google Scholar] [CrossRef]
- Sabchareon, A.; Wallace, D.; Sirivichayakul, C.; Limkittikul, K.; Chanthavanich, P.; Suvannadabba, S.; Jiwariyavej, V.; Dulyachai, W.; Pengsaa, K.; Wartel, T.A.; et al. Protective efficacy of the recombinant, live-attenuated, CYD tetravalent dengue vaccine in Thai schoolchildren: A randomised, controlled phase 2b trial. Lancet 2012, 380, 1559–1567. [Google Scholar] [CrossRef]
- Villar, L.; Dayan, G.H.; Arredondo-García, J.L.; Rivera, D.M.; Cunha, R.; Deseda, C.; Reynales, H.; Costa, M.S.; Morales-Ramírez, J.O.; Carrasquilla, G.; et al. Efficacy of a Tetravalent Dengue Vaccine in Children in Latin America. N. Engl. J. Med. 2015, 372, 113–123. [Google Scholar] [CrossRef]
- Arredondo-García, J.; Hadinegoro, S.; Reynales, H.; Chua, M.; Medina, D.R.; Chotpitayasunondh, T.; Tran, N.; Deseda, C.; Wirawan, D.; Supelano, M.C.; et al. Four-year safety follow-up of the tetravalent dengue vaccine efficacy randomized controlled trials in Asia and Latin America. Clin. Microbiol. Infect. 2018, 24, 755–763. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Anggriani, N.; Supriatna, A.K. Application of differential transformation method for solving dengue transmission mathematical model. AIP Conf. Proc. 2018, 1937, 020012. [Google Scholar] [CrossRef]
- Ndii, M.Z.; Supriatna, A.K. Stochastic Dengue Mathematical Model in the Presence of Wolbachia: Exploring the Disease Extinction. Nonlinear Dyn. Syst. Theory 2020, 20, 214–227. [Google Scholar]
- Supriatna, A.K.; Anggriani, N.; Husniah, H. The optimal strategy of wolbachia-infected mosquitoes release program: An application of control theory in controlling dengue disease. In Proceedings of the 2016 International Conference on Instrumentation, Control and Automation (ICA), Bandung, Indonesia, 29–31 August 2016; 2016; pp. 38–43. [Google Scholar] [CrossRef]
- Cardona-Salgado, D.; Campo-Duarte, D.E.; Sepulveda-Salcedo, L.S.; Vasilieva, O. Wolbachia-based biocontrol for dengue reduction using dynamic optimization approach. Appl. Math. Model. 2020, 82, 125–149. [Google Scholar] [CrossRef]
- Lourenço, J.; Recker, M. Dengue serotype immune-interactions and their consequences for vaccine impact predictions. Epidemics 2016, 16, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lui, R. Releasing Wolbachia-infected Aedes aegypti to prevent the spread of dengue virus: A mathematical study. Infect. Dis. Model. 2020, 5, 142–160. [Google Scholar] [CrossRef]
- Hladish, T.J.; Pearson, C.A.B.; Toh, K.B.; Rojas, D.P.; Manrique-Saide, P.; Vazquez-Prokopec, G.M.; Halloran, M.E.; Longini, I.M. Designing effective control of dengue with combined interventions. Proc. Natl. Acad. Sci. USA 2020, 117, 3319–3325. [Google Scholar] [CrossRef]
- Walker, T.; Johnson, P.H.; Moreira, L.A.; Iturbe-Ormaetxe, I.; Frentiu, F.D.; McMeniman, C.J.; Leong, Y.S.; Dong, Y.; Axford, J.; Kriesner, P.; et al. The WMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature 2011, 476, 450–453. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Turelli, M.; Harshman, L.G. Factors affecting the distribution of cytoplasmic incompatibility in Drosophila simulans. Genetics 1990, 126, 933–948. [Google Scholar]
- Scott, T.W.; Amerasinghe, P.H.; Morrison, A.C.; Lorenz, L.H.; Clark, G.G.; Strickman, D.; Kittayapong, P.; Edman, J.D. Longitudinal Studies of Aedes aegypti (Diptera: Culicidae) in Thailand and Puerto Rico: Blood Feeding Frequency. J. Med. Entomol. 2000, 37, 89–101. [Google Scholar] [CrossRef]
- Gubler, D.J. Dengue and dengue hemorrhagic fever. Clin. Microbiol. Rev. 1998, 11, 480–496. [Google Scholar] [CrossRef]
- Chowel, G.; Diaz-Duenas, P.; Miller, J.C.; Velazco, A.A.; Hyman, J.M.; Fenimore, P.W.; Castillo-Chaves, C. Estimation of the reproduction number of dengue fever from spatial epidemic data. Math. Biosci. 2007, 208, 571–589. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.M.; Macoris, M.L.G.; Galvani, K.C.; Andrighetti, M.T.M.; Wanderley, D.M.V. Assessing the effects of temperature on the population of Aedes aegypti, the vector of dengue. Epidemiol. Infect. 2009, 137, 1188–1202. [Google Scholar] [CrossRef] [PubMed]
- Ndii, M.Z.; Hickson, R.I.; Mercer, G.N. Modelling the introduction of Wolbachia into Aedes aegypti to reduce dengue transmission. ANZIAM J. 2012, 53, 213–227. [Google Scholar]
- Bian, G.; Xu, Y.; Lu, P.; Xie, Y.; Xi, Z. The Endosymbiotic Bacterium Wolbachia Induces Resistance to Dengue Virus in Aedes aegypti. PLoS Pathog. 2010, 6, e1000833. [Google Scholar] [CrossRef] [PubMed]
- Yeap, H.L.; Mee, P.; Walker, T.; Weeks, A.R.; O’Neill, S.L.; Johnson, P.; Ritchie, S.A.; Richardson, K.M.; Doig, C.; Endersby, N.M.; et al. Dynamics of the “Popcorn” Wolbachia Infection in Outbred Aedes aegypti Informs Prospects for Mosquito Vector Control. Genetics 2011, 187, 583–595. [Google Scholar] [CrossRef] [PubMed]
- Turley, A.P.; Moreira, L.A.; O’Neill, S.L.; McGraw, E.A. Wolbachia Infection Reduces Blood–Feeding Success in the Dengue Fever Mosquito, Aedes aegypti. PLoS Negl. Trop. Dis. 2009, 3, e516. [Google Scholar] [CrossRef] [PubMed]
- BPS NTT. Data Nusa Tenggara Timur. Available online: http://fs.fish.govt.nz/Page.aspx?pk=7&sc=SUR (accessed on 30 April 2020).
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F. Vaccination models and optimal control strategies to dengue. Math. Biosci. 2014, 247, 1–12. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Flasche, S.; Jit, M.; Rodríguez-Barraquer, I.; Coudeville, L.; Recker, M.; Koelle, K.; Milne, G.; Hladish, T.J.; Perkins, T.A.; Cummings, D.A.T.; et al. The Long-Term Safety, Public Health Impact, and Cost-Effectiveness of Routine Vaccination with a Recombinant, Live-Attenuated Dengue Vaccine (Dengvaxia): A Model Comparison Study. PLoS Med. 2016, 13, 1–19. [Google Scholar] [CrossRef]
- Moreira, L.A.; Iturbe-Ormaetxe, I.; Jeffery, J.A.; Lu, G.; Pyke, A.T.; Hedges, L.M.; Rocha, B.C.; Hall-Mendelin, S.; Day, A.; Riegler, M.; et al. Wolbachia Symbiont in Aedes aegypti limits infection with dengue, Chikungunya, and Plasmodium. Cell 2009, 139, 1268–1278. [Google Scholar] [CrossRef]
- Aliota, M.T.; Walker, E.C.; Uribe Yepes, A.; Velez, I.D.; Christensen, B.M.; Osorio, J.E. The wMel Strain of Wolbachia Reduces Transmission of Chikungunya Virus in Aedes aegypti. PLoS Negl. Trop. Dis. 2016, 10, e0004677. [Google Scholar] [CrossRef] [PubMed]



| Symbol | Description | Value | Unit | Source |
|---|---|---|---|---|
| Maternal transmission | 0.9 | N/A | [30,31] | |
| Biting rate of non-W | 0.63 | day | [32] | |
| Progression rate from exposed to infectious human | 1/5.5 | day | [33] | |
| Progression from exposed to infectious non-W | 1/10 | day | [34] | |
| Progression rate from exposed to infectious | 1/10 | day | [34] | |
| Adult mosquito death rate (non-W) | 1/14 | day | [35] | |
| Death rate of aquatic non-W | 1/14 | day | [35] | |
| Aquatic death rate | 1/14 | day | [35] | |
| Reproductive rate of non-W | 1.25 | day | [36] | |
| Reproductive rate W | day | [30] | ||
| Recovery rate | 1/5 | day | [33] | |
| Transmission probability | 0.2614 | N/A | [7] | |
| Maturation rate of non-W | 1/10 | day | [35] | |
| Maturation rate of W | 1/10 | day | [35] | |
| Transmission probability from infectious W to human | N/A | [37] | ||
| Death rate of W | 1.1 | day | [30,38] | |
| Biting rates of W | day | [39] | ||
| Natural death rate | day | [40] | ||
| B | Birth rate | day | [40] | |
| p | Vaccination rate | 0.2 | N/A | [41] |
| Vaccine efficacy | 0.538 | N/A | [17,21] | |
| Waning immunity | 0.1 | N/A | [41] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ndii, M.Z. Modelling the Use of Vaccine and Wolbachia on Dengue Transmission Dynamics. Trop. Med. Infect. Dis. 2020, 5, 78. https://doi.org/10.3390/tropicalmed5020078
Ndii MZ. Modelling the Use of Vaccine and Wolbachia on Dengue Transmission Dynamics. Tropical Medicine and Infectious Disease. 2020; 5(2):78. https://doi.org/10.3390/tropicalmed5020078
Chicago/Turabian StyleNdii, Meksianis Z. 2020. "Modelling the Use of Vaccine and Wolbachia on Dengue Transmission Dynamics" Tropical Medicine and Infectious Disease 5, no. 2: 78. https://doi.org/10.3390/tropicalmed5020078
APA StyleNdii, M. Z. (2020). Modelling the Use of Vaccine and Wolbachia on Dengue Transmission Dynamics. Tropical Medicine and Infectious Disease, 5(2), 78. https://doi.org/10.3390/tropicalmed5020078





