Breaking the Cycle of Echinococcosis: A Mathematical Modeling Approach
Abstract
1. Introduction
2. Materials and Methods
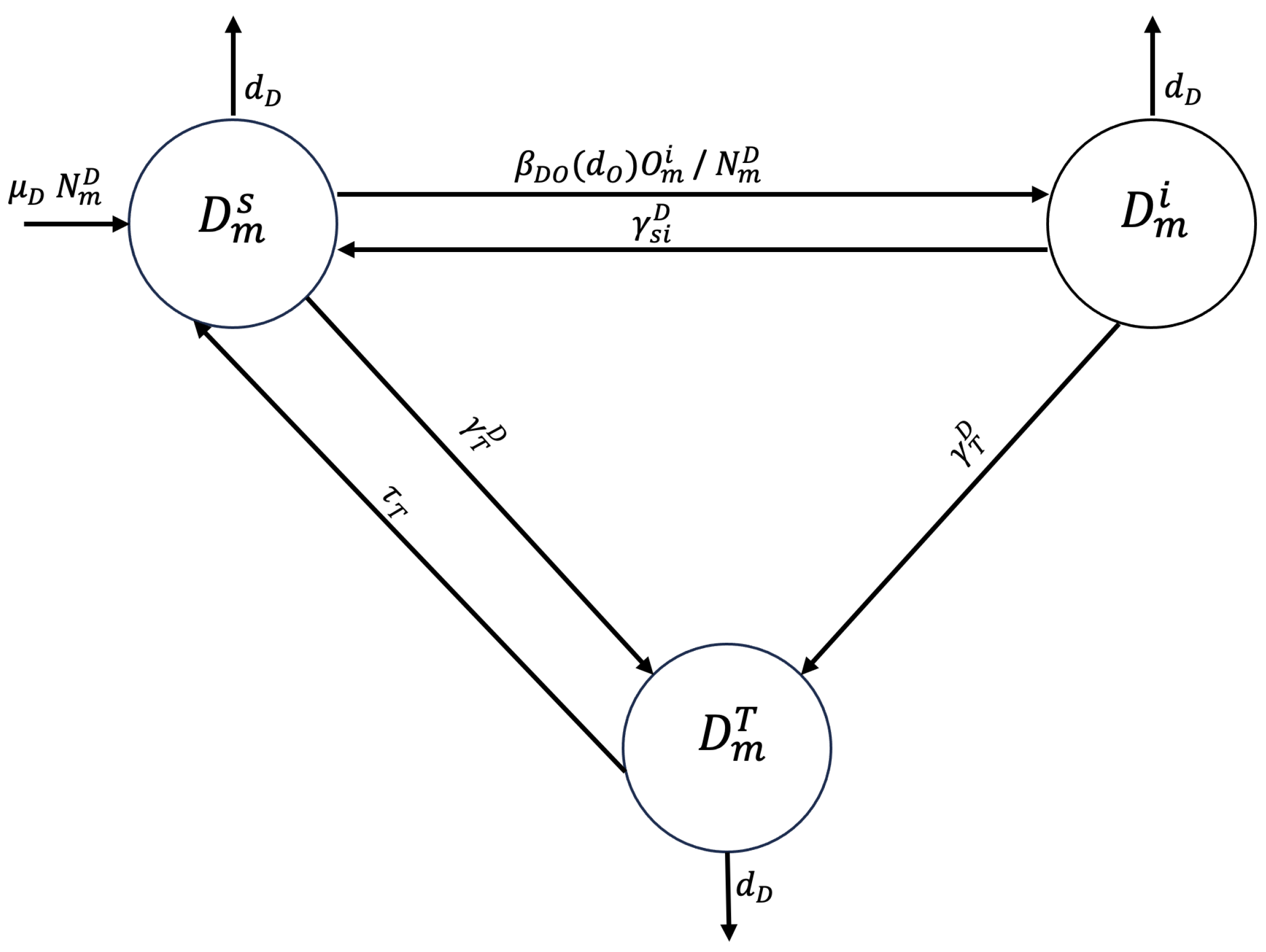
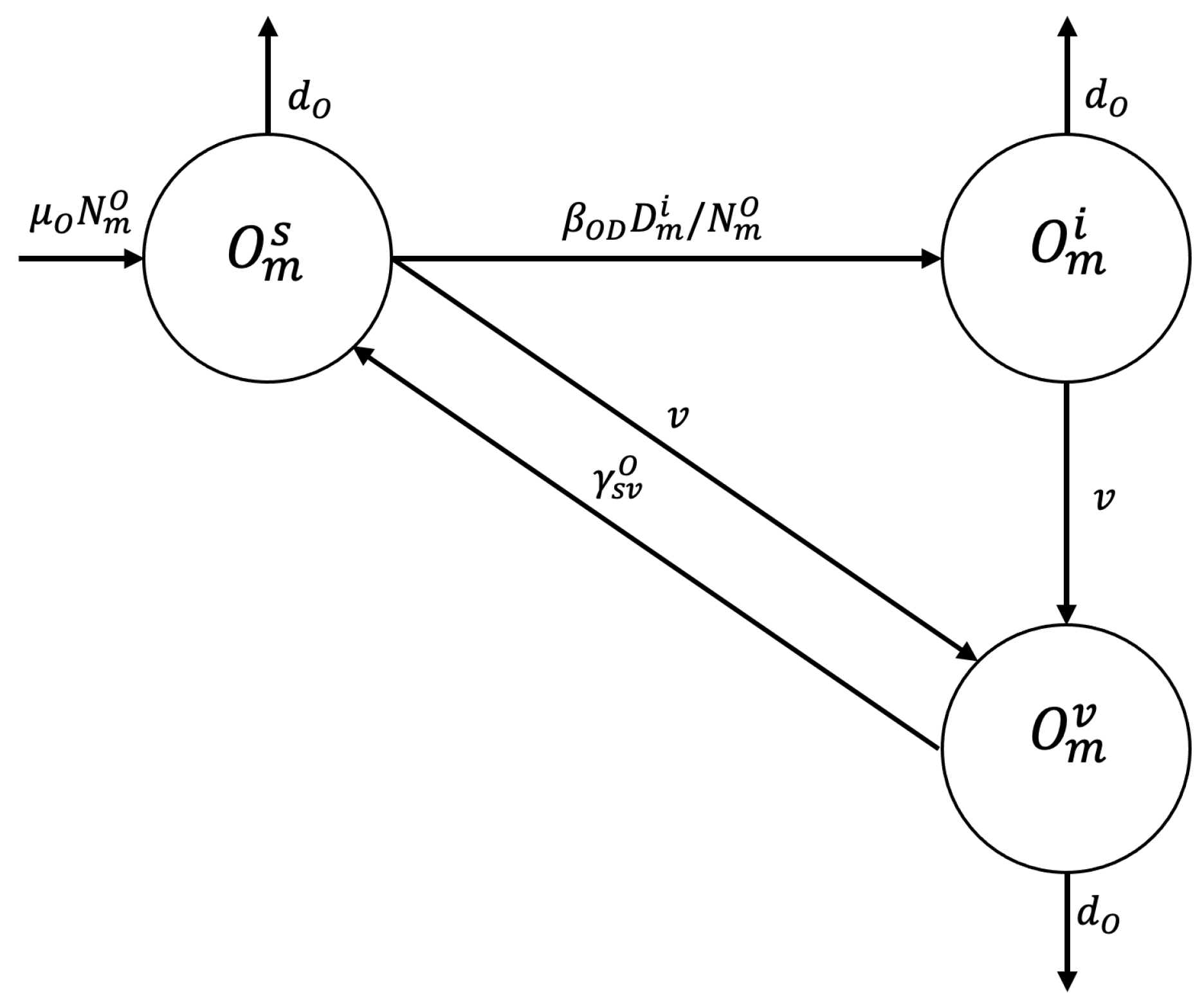
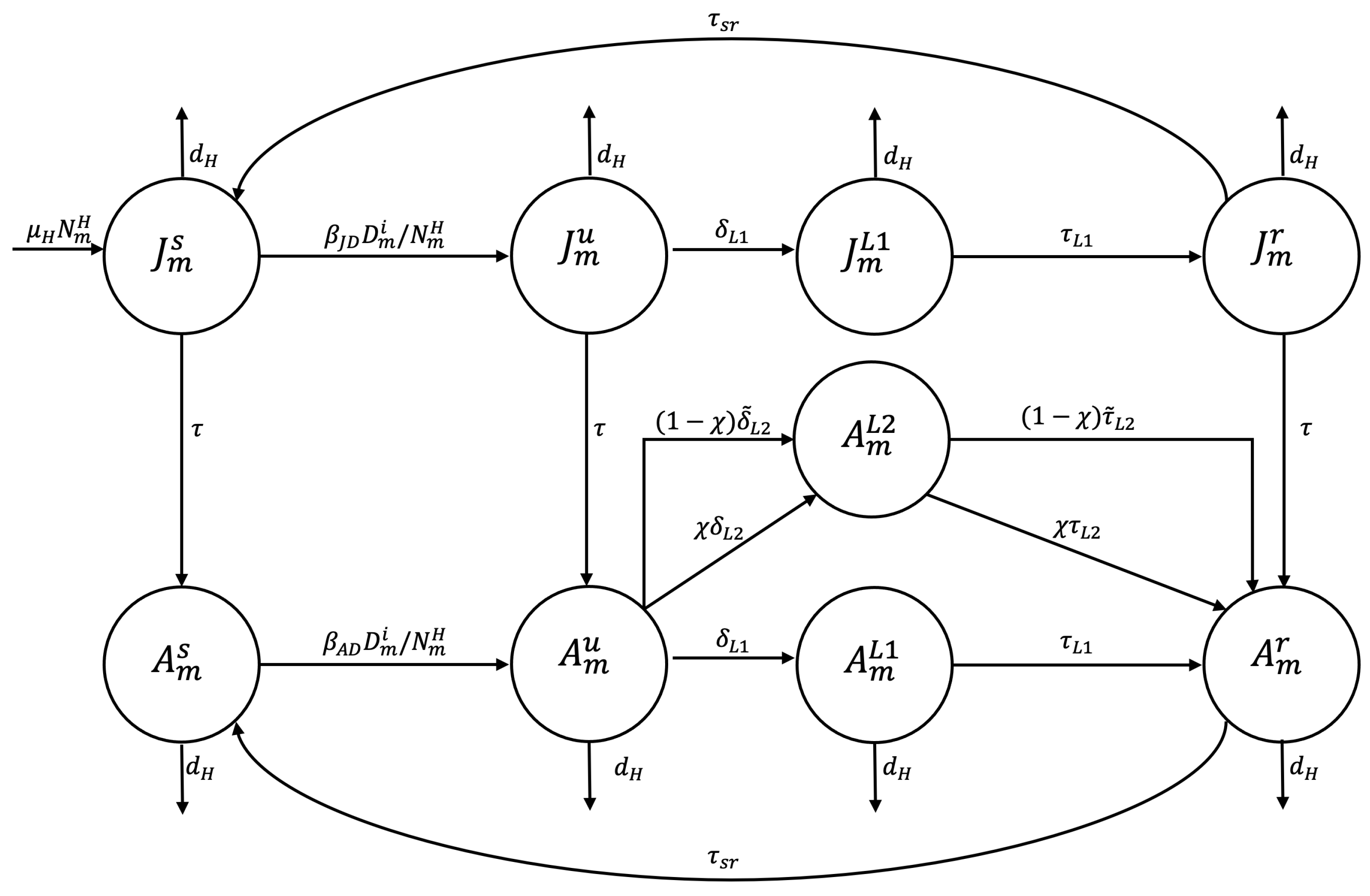
2.1. Compartmental Model
2.2. Dynamics of Disease Transmission Rates
3. Results
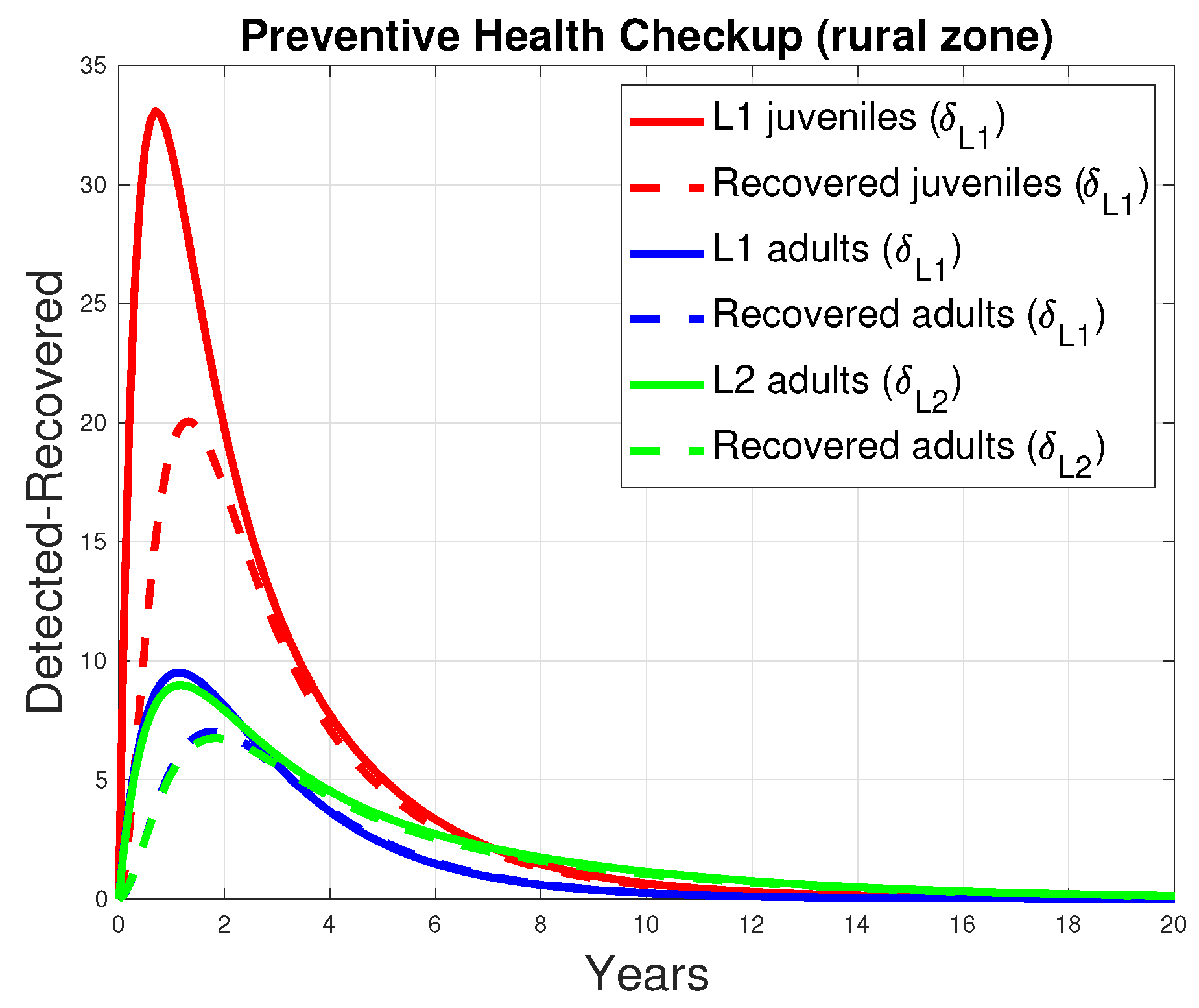
3.1. Simulations for Disease Transmission Rate
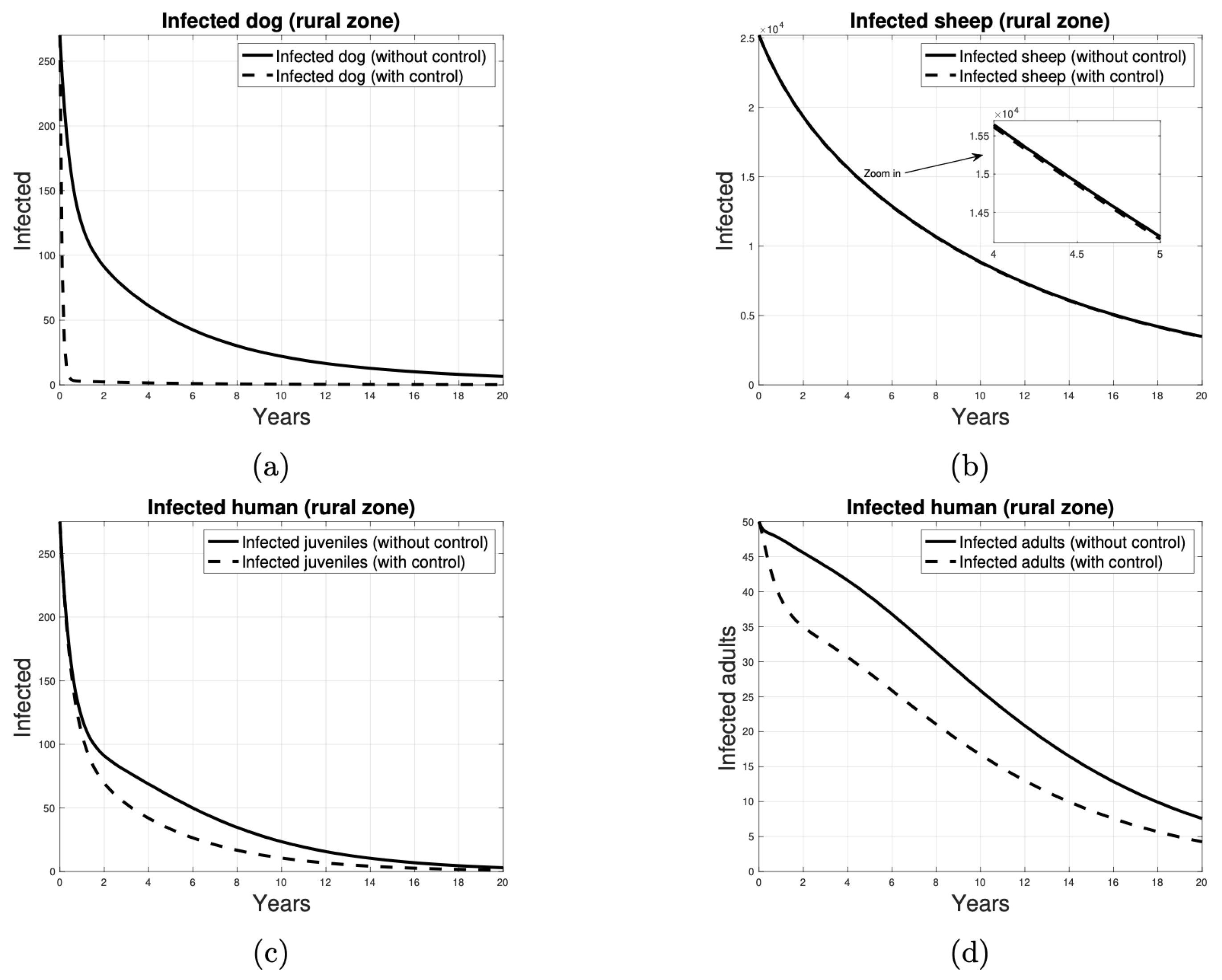
3.2. The Impact of the Control Program on Humans
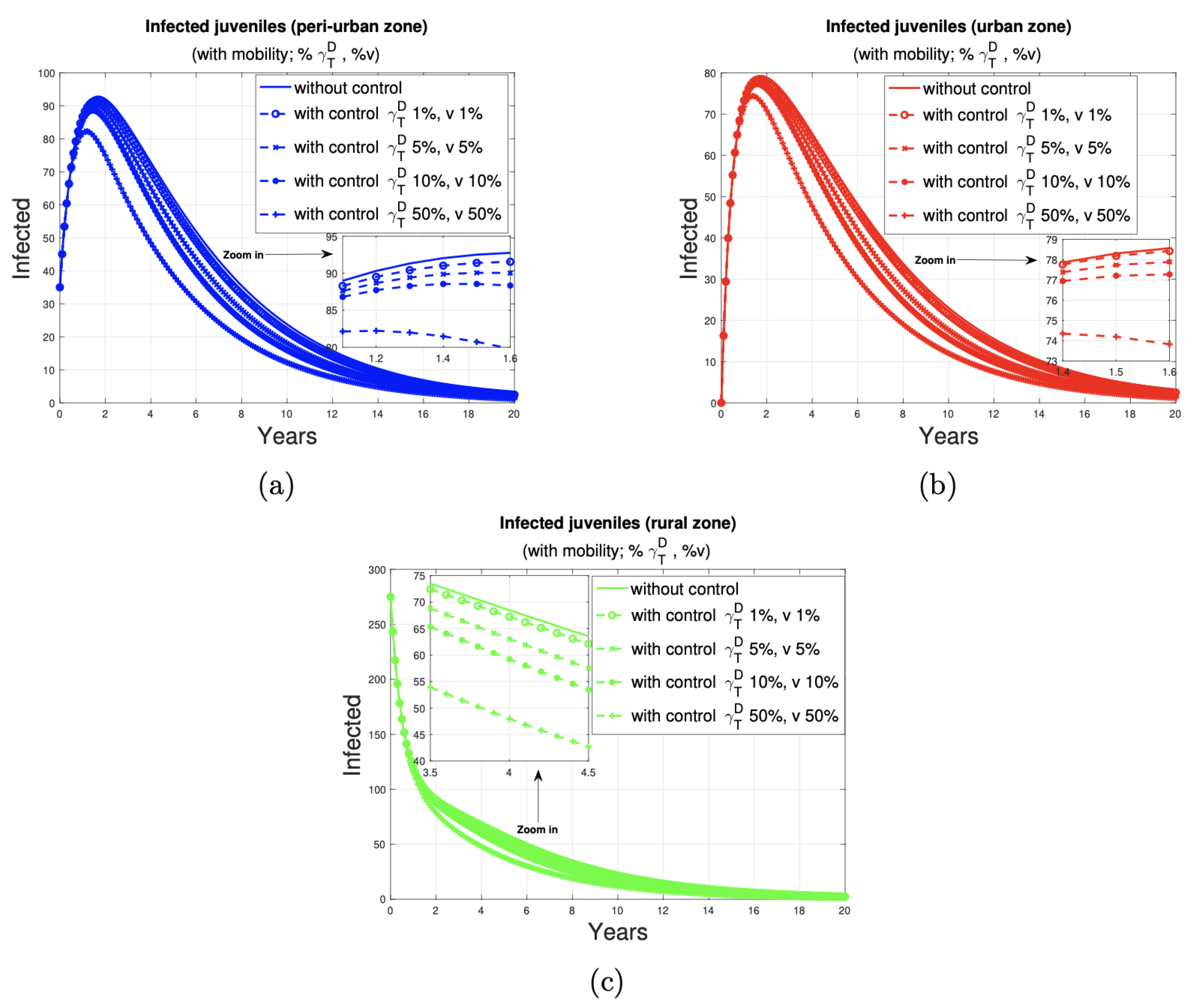
- In the short term, the urban area has the lowest number of affected individuals in all disease control scenarios. An increase in the control ratio from 1% to 5% is associated with a reduction in the number of cases in the peri-urban, urban, and rural areas, with a decrease of three, one, and one cases, respectively. Similarly, an increase in the proportion of controlled animals from 1% to 10% resulted in a reduction of five, two, and three cases in these areas, respectively. Furthermore, an increase in control from 1% to 50% of the proportion of dogs and sheep results in a reduction of 16, 7, and 11 cases, respectively, in the peri-urban, urban, and rural zones.
- In the medium term, the lowest number of human juvenile infections is observed in the urban area when 1%, 5%, and 10% of the dog and sheep populations, respectively, are subjected to deworming and vaccination. When the control ratio is set at 50% of the population, the impact on each zone is consistent, with 19 cases observed in each.
- In the long term, the control of 1%, 5%, and 10% of the dog and sheep population results in a reduction to two cases in each zone. When 50% of the population is dewormed and vaccinated, the number of cases in all zones is reduced to one.
3.3. Effectivity Index
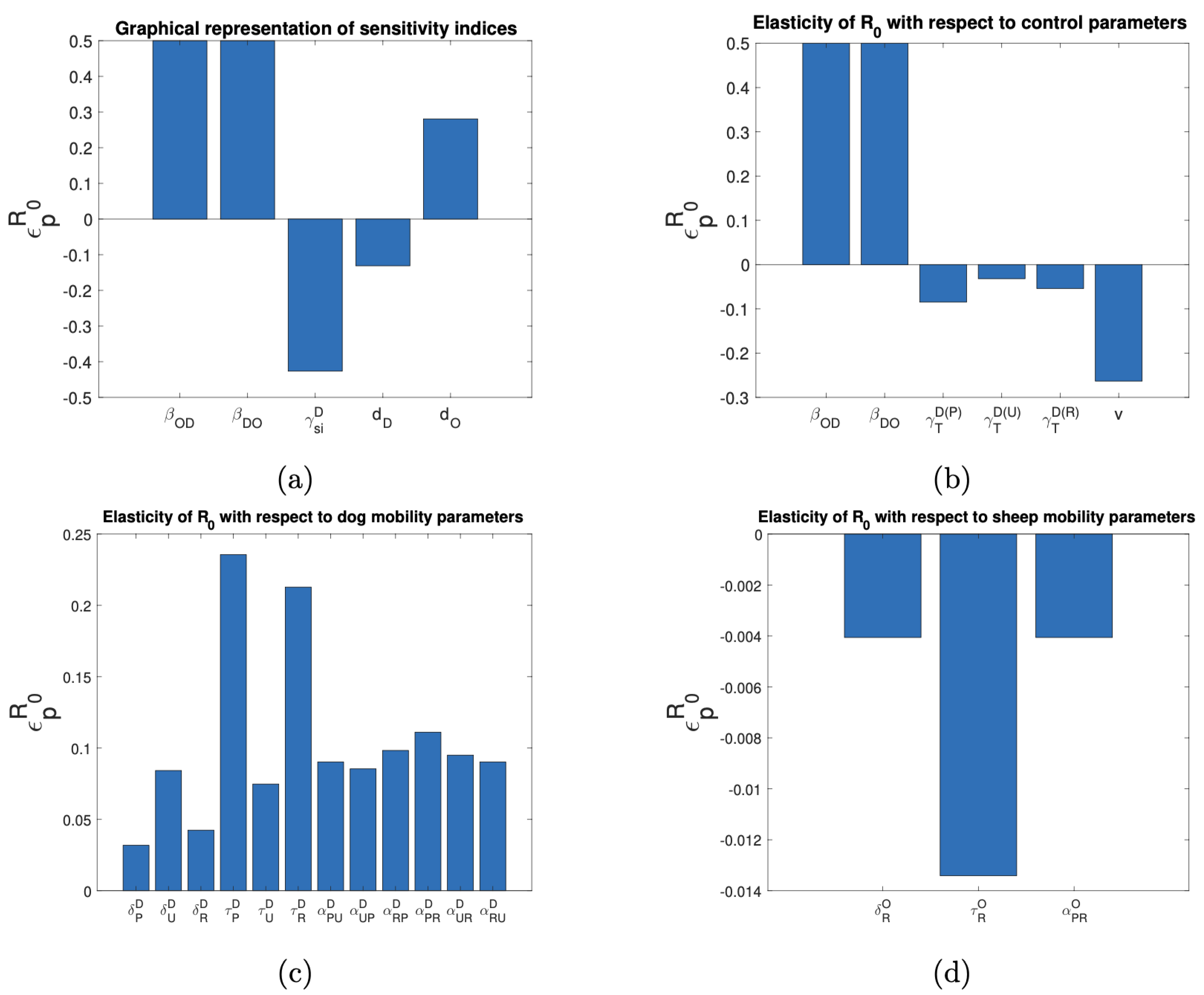
3.4. Sensitivity Analysis of the Basic Reproductive Number and the Target Reproductive Number
3.5. The Impact of Prevention on Humans
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CE | Cystic Echinococcosis |
| WHO | World Health Organization |
| PAHO | Pan American Health Organization |
Appendix A. System of Ordinary Differential Equations, the Next-Generation Matrix, and the Target Reproductive Number
Appendix A.1. Proposed Mathematical Model
Appendix A.2. The Next-Generation Matrix
Appendix A.3. The Target Reproductive Number
References
- Medina, N.; Martínez, P.; Ayala, S.; Canals, M. Distribution and risk factors of human cystic echinococcosis in Aysén 2010–2016. J. Chil. Infectol. 2021, 38, 349–354. [Google Scholar] [CrossRef] [PubMed]
- Larrieu, E.; Belloto, A.; Arambulo, P.; Tamayo, H. Cystic echinococcosis: Epidemiology and control in South America. J. Parasitol. Latinoam. 2004, 59, 82–89. [Google Scholar] [CrossRef]
- Pan American Health Organization. Echinococcosis. 2023. Available online: https://www.paho.org/en/topics/hydatidosis-echinococcosis (accessed on 20 November 2023).
- Larrieu, E.; Mujica, G.; Gauci, C.G.; Vizcaychipi, K.; Seleiman, M.; Herrero, E.; Labanchi, J.L.; Araya, D.; Sepúlveda, L.; Grizmado, C.; et al. Pilot Field Trial of the EG95 Vaccine Against Ovine Cystic Echinococcosis in Rio Negro, Argentina: Second Study of Impact. J. PLoS Neglected Trop. Dis. 2015, 9, e0004134. [Google Scholar] [CrossRef]
- Faúndez, M.; Allende, R.; Pinto, A.; Bustos, G.; Cerda, R.; Ferrada, A.; Sánchez, P.; Vidal, R.; Valladares, R.; Acevedo, M.; et al. Mercado de la carne y lana ovina en Chile; Technical Report; Facultad de Agronomía, Universidad de Concepción: Concepción, Chile, 2013. [Google Scholar]
- World Health Organization; World Organisation for Animal Health. WHO/OIE Manual on Echinococcosis in Humans and Animals: A Public Health Problem of Global Concern, 1st ed.; World Organisation for Animal Health: Paris, France, 2001. [Google Scholar]
- Singh, J.; Vijay, D.; Dhak, P. Textbook of Zoonoses; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2022. [Google Scholar]
- Frider, B.; Larrieu, E.; Odriozola, M. Long-term outcome of asymptomatic liver hydatidosis. J. Hepatol. 1999, 30, 228–231. [Google Scholar] [CrossRef] [PubMed]
- Pinto, P.P.; Mauret, E.; Acuña, M.; Muñoz, E.; Galvez, S.; Vallejos, B.; Jercic, M.I.; Zuñiga, M.; Larrieu, E.; Fuentes, R.; et al. Manual para el Diagnóstico, Tratamiento, Prevención y Control de la Hidatidosis en Chile; Ministerio de Salud de Chile: Santiago, Chile, 2015. [Google Scholar]
- Cifuentes, C. Informe: Situación de la Equinococosis Quística/Hidatidosis en Chile, 2018–2022; Technical Report; Ministerio de Salud de Chile: Santiago, Chile, 2023. [Google Scholar]
- Jensen, O. Hidatidosis: La Vacuna Recombinante Eg95 en Hospederos Intermediarios; Editorial Académica Española: Chisinau, Republic of Moldova Europe, 2021. [Google Scholar]
- Pan American Health Organization. El Programa Regional para la Eliminación de la Equinococosis Quística/Hidatidosis. 2021. Available online: https://www.paho.org/sites/default/files/2022-08/planaccion-equinococosis-2022-2029-191121.pdf (accessed on 25 May 2024).
- Wu, L.; Song, B.; Du, W. Mathematical modelling and control of echinococcus in Qinghai province, China. J. Math. Biosci. Eng. 2013, 10, 425–444. [Google Scholar] [CrossRef]
- Birhan, G.; Munganga, J.; Hassan, A. Mathematical modelling of echinococcosis in human, dogs and sheep with intervention. J. Biol. Dyn. 2022, 16, 439–463. [Google Scholar] [CrossRef]
- Gutiérrez-Jara, J.P.; Muñoz-Quezada, M.T.; Córdova-Lepe, F.; Silva-Guzmán, A. Mathematical Model of the Spread of Hantavirus Infection. Pathogens 2023, 12, 1147. [Google Scholar] [CrossRef]
- Khan, K.; Arino, J.; Hu, W.; Raposo, P.; Sears, J.; Calderon, F.; Heidebrecht, C.; Macdonald, M.; Liauw, J.; Chan, A.; et al. Spread of a Novel Influenza A (H1N1) Virus via Global Airline Transportation. N. Engl. J. Med. 2009, 361, 212–214. [Google Scholar] [CrossRef]
- Córdova-Lepe, F.; Vogt-Geisse, K. Adding a reaction-restoration type transmission rate dynamic-law to the basic SEIR COVID-19 model. PLoS ONE 2022, 17, e0269843. [Google Scholar] [CrossRef]
- Córdova-Lepe, F.; Gutiérrez-Jara, J.P. A Dynamic Reaction-restore-type Transmission-rate Model for COVID-19. WSEAS Trans. Biol. Biomed. 2024, 21, 118–130. [Google Scholar] [CrossRef]
- Acosta-Jamett, G.; Hernández, F.; Castro, N.; Tamarozzi, F.; Uchiumi, L.; Salvitti, J.C.; Cueva, M.; Casulli, A. Prevalence rate and risk factors of human cystic echinococcosis: A cross-sectional, community-based, abdominal ultrasound study in rural and urban north-central Chile. PLoS Neglected Trop. Dis. 2022, 16, e0010280. [Google Scholar] [CrossRef]
- Brunetti, E.; Kern, P.; Vuitton, D.A. Expert consensus for the diagnosis and treatment of cystic and alveolar echinococcosis in humans. Acta Trop. 2010, 114, 1–16. [Google Scholar] [CrossRef]
- Kuehn, R.; Uchiumi, L.J.; Tamarozzi, F. Treatment of uncomplicated hepatic cystic echinococcosis (hydatid disease). Cochrane Database Syst Rev. 2024, 7, CD015573. [Google Scholar] [CrossRef]
- Birhan, G.; Munganga, J.; Hassan, A. Mathematical Modeling of Echinococcosis in Humans, Dogs, and Sheep. J. Appl. Math. 2020, 2020, 8482696. [Google Scholar] [CrossRef]
- Chacha, S.; Stephano, A.; Irunde, I.; Mwasunda, A. Cystic echinococcosis dynamics in dogs, humans and cattle: Deterministic and stochastic modeling. J. Results Phys. 2023, 51, 106697. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, X.; Jin, Z.; Ma, H.; Teng, Z.; Wang, L. Modeling and analysis of the transmission of Echinococcosis with application to Xinjiang Uygur Autonomous Region of China. J. Theor. Biol. 2013, 333, 78–90. [Google Scholar] [CrossRef]
- Bogitsh, B.; Carter, C.; Oeltmann, T. Human Parasitology, 5th ed.; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- The MathWorks Inc. MATLAB Version: 9.12.0.2529717 (R2022a) Update 8; The MathWorks Inc.: Natick, MA, USA, 2024. [Google Scholar]
- Alvarez, J.F.; Ruiz, R.; Ríos, J.; Alvarez Rojas, C.A. Molecular Detection of Echinococcus granulosus Sensu Strict. Environ. Dog Faecal Samples Magallanes Region, Patagonia, Chile. Parasitol. 2021, 1, 238–246. [Google Scholar] [CrossRef]
- van den Driessche, P. Reproduction numbers of infectious disease models. J. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology, 1st ed.; Texts in Applied Mathematics; Springer: New York, NY, USA, 2015; Volume 61, pp. 139–142. [Google Scholar]
- Shuai, Z.; Heesterbeek, J.; van den Driessche, P. Extending the type reproduction number to infectious disease control targeting contacts between types. J. Math. Biol. 2013, 67, 1067–1082. [Google Scholar] [CrossRef]
- Saldaña, F.; Barradas, I. Control Strategies in Multigroup Models: The Case of the Star Network Topology. Bull. Math. Biol. 2018, 80, 2978–3001. [Google Scholar] [CrossRef]
- González-Galeano, A.; Barradas, I.; Villavicencio, J. Beyond R0: Exploring New Approaches. J. Model. Mat. Sist. Biol. 2023, 3, e23R08. [Google Scholar] [CrossRef]
- Shafiei, R.; Mohajerzadeh, M.S.; Masomi, H.F.A.; Tavakoli, M.; Turki, H.; Firouzeh, N. Discordance Therapeutic Protocol of Cystic Echinococcosis With WHO Guideline. J. Ultrasound Med. 2024, 43, 1279–1287. [Google Scholar] [CrossRef]
- Fasihi Harandi, M.; Budke, C.M.; Rostami, S. The Monetary Burden of Cystic Echinococcosis in Iran. PLoS Neglected Trop. Dis. 2012, 6, e1915. [Google Scholar] [CrossRef]
- Lutz, E.; Uhart, M.; Kusch, A.; Vila, A. Increased prevalence of canine echinococcosis a decade after the discontinuation of a governmental deworming program in Tierra del Fuego, Southern Chile. J. Zoonoses Public Health 2023, 70, 213–222. [Google Scholar] [CrossRef]
- Lorca, M.; Garrido, M.; Contreras, M.; Salinas, P.; Alvarez, C.; Ruiz, M.; Soto, P. Human hydatidic seroprevalence in Coquimbo Region. Chile. Parasitol. Latinoam. 2006, 61, 111–116. [Google Scholar] [CrossRef]
- Poggio, T.; Jensen, O.; Chacon, T.; Pino, A.; Boado, L.; Gomez, J.M.; Heath, D. Past and Future Methods for Controlling Echinococcus granulosus South America. J. Echinococcoses 2022, 1, 26–71. [Google Scholar] [CrossRef]
- Liu, B.; Chen, Q.; Cai, J.; Li, J.; Liu, Y. The Effect of Lamb Vaccination Against Echinococcosis on the Scale of Livestock Farming in Northwestern China. Vet. Med. Sci. 2025, 11, e70273. [Google Scholar] [CrossRef] [PubMed]
- Borhani, M.; Fathi, S.; Harandi, M.F.; Casulli, A.; Ding, J.; Liu, M.; Zhang, W.; Wen, H. Echinococcus granulosus sensu lato control measures: A specific focus on vaccines for both definitive and intermediate hosts. Parasites Vectors 2024, 17, 533. [Google Scholar] [CrossRef]




| Parameters | Description | Value | Range | Reference |
|---|---|---|---|---|
| Rate of deworming of dogs | 0.0100 | 0.0100–1.0000 | [11] | |
| Periodicity between deworming | 0.1233 | - | [4] | |
| v | Rate of vaccination of sheep | 0.0100 | 0.0100–1.0000 | [11] |
| Rate of loss of vaccine-induced immunity of sheep | 0.0365 | - | [14] | |
| Detection rate | 0.0010 | 0.0000–1.0000 | [19] | |
| Detection rate | 0.0010 | 0.0000–1.0000 | [19] | |
| Average treatment time | 0.2500 | 0.0000–1.0000 | [20,21] | |
| Average treatment time | 0.5000 | 0.0000–1.0000 | [20,21] | |
| Average time loss of immunity | 0.5000 | - | Assumed |
| Parameters | Description | Value | Range | Reference |
|---|---|---|---|---|
| Dog birth rate | 0.0800 | 0.0800–0.3212 | [13,14,22,23,24] | |
| Sheep birth rate | 0.0833 | 0.0052–0.3333 | [13,14,22,23,24] | |
| Human birth rate | 0.0141 | 0.0141–0.4161 | [13,14,22,23,24] | |
| Dog death rate | 0.0800 | 0.0800–0.3212 | [13,14,22,23,24] | |
| Sheep death rate | 0.0833 | 0.0052–0.3333 | [13,14,22,23,24] | |
| Human death rate | 0.0141 | 0.0141–0.4161 | [13,14,22,23,24] | |
| Human disease-related death rate | 0.1460 | 0.0009–0.1460 | [13,24] | |
| Transmission rate from sheep to dogs | 0.0350 | 5.8 × 10−8–0.0350 | [13,14,22,24] | |
| Transmission rate from dogs to sheep | 0.0860 | 7.4 × 10−8–0.3650 | [13,14,22,24] | |
| Transmission rate from dogs to human children | 0.0430 | 4.2 × 10−11–0.0430 | [13,14,22,24] | |
| Transmission rate from dogs to human adults | 0.0323 | 4.2 × 10−11–0.0430 | [13,14,22,24] | |
| Rate at which exposed sheep progress to infected | 0.1090 | 0.0365–0.1090 | [14,22,23] | |
| Rate at which exposed humans progress to infected | 0.0714 | 0.0693–0.0714 | [14,22,23] | |
| Rate at which infected dogs progress to susceptible | 0.2500 | 0.2500–2.4000 | [2] | |
| Rate at which infected humans receive treatment | 0.5000 | 0.0500–0.5000 | [25] | |
| Average time that a host X from zone Z stays in another zone | 0.5000 | - | Assumed | |
| Rate of exit of host X from area Z | 0.3030 | - | Assumed | |
| Proportion of hosts X moving from area B to area A | 0.5000 | 0.0000–1.0000 | Assumed |
| s Susceptible | i Infected | T Treated | v Vaccinated | u Undetected | Treated Level 1 | Treated Level 2 | r Recovered | |
|---|---|---|---|---|---|---|---|---|
| Peri-urban | ||||||||
| 500 | 20 | 100 | - | - | - | - | - | |
| 8680 | 594 | - | 100 | - | - | - | - | |
| 647 | - | - | - | 35 | 0 | 0 | 0 | |
| 658 | - | - | - | 35 | 0 | 0 | 0 | |
| Urban | ||||||||
| 4000 | 50 | 1000 | - | - | - | - | - | |
| 25,000 | - | - | - | 0 | 0 | 0 | 0 | |
| 25,018 | - | - | - | 15 | 0 | 0 | 0 | |
| Rural | ||||||||
| 1500 | 270 | 150 | - | - | - | - | - | |
| 70,000 | 25,200 | - | 1000 | - | - | - | - | |
| 1520 | - | - | - | 275 | 0 | 0 | 0 | |
| 1556 | - | - | - | 50 | 0 | 0 | 0 |
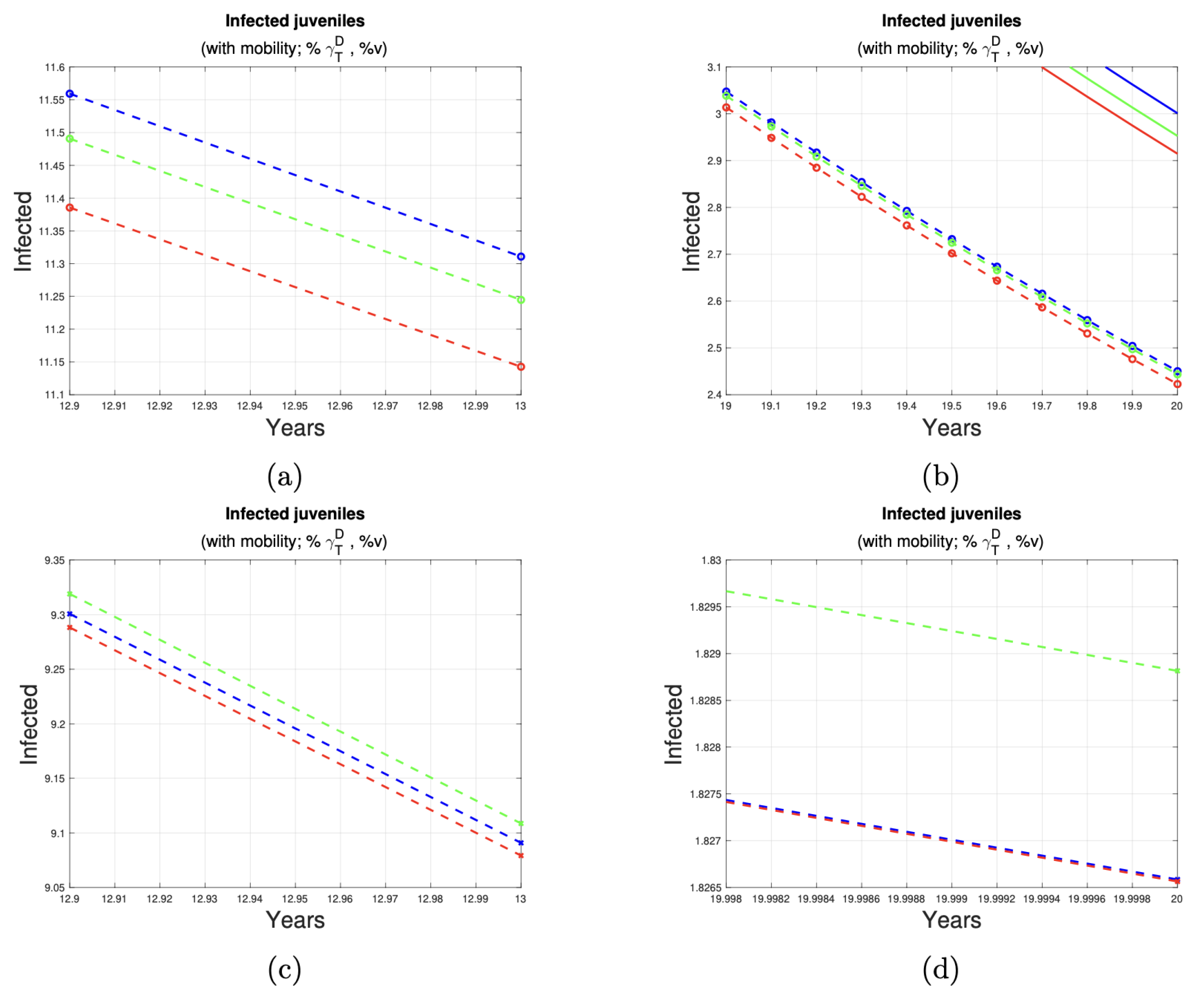
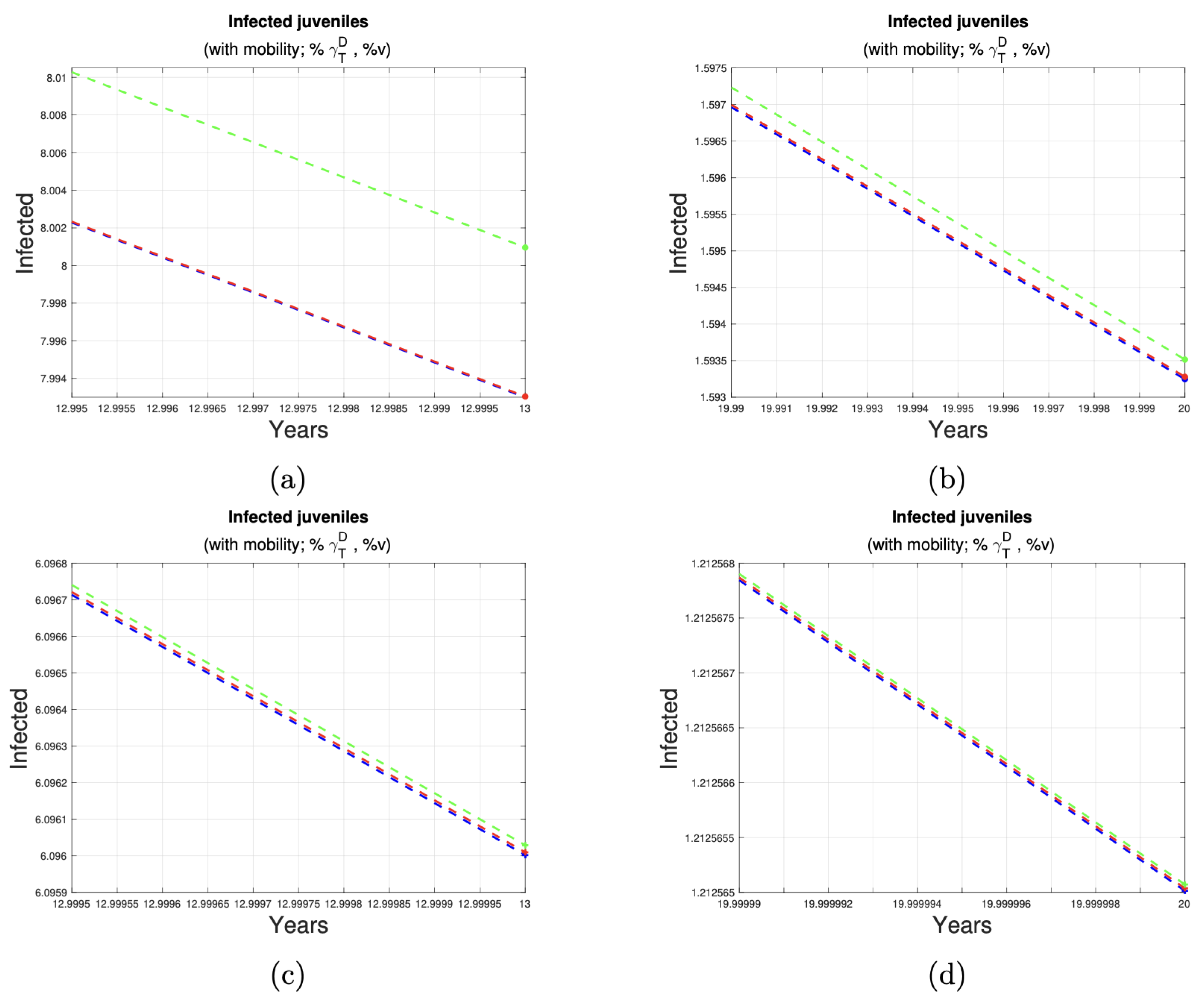
| Ratio of Animals Under Control | Initial Cases (Year 13) | Final Cases (Year 20) | Case Reduction (Approximate) | Figure |
|---|---|---|---|---|
| 11 | 2 | 9 | Figure 7a,b | |
| 9 | 2 | 7 | Figure 7c,d | |
| 8 | 2 | 7 | Figure 8a,b | |
| 6 | 1 | 5 | Figure 8c,d |
| Ratio of Animals Under Control | Cases (Year 2) | Cases (Year 8) | Cases (Year 20) | Zone |
|---|---|---|---|---|
| 91 | 33 | 2 | Peri-urban | |
| 78 | 28 | 2 | Urban | |
| 90 | 32 | 2 | Rural | |
| 88 | 28 | 2 | Peri-urban | |
| 77 | 28 | 2 | Urban | |
| 89 | 28 | 2 | Rural | |
| 86 | 25 | 2 | Peri-urban | |
| 76 | 25 | 2 | Urban | |
| 87 | 25 | 2 | Rural | |
| 75 | 19 | 1 | Peri-urban | |
| 71 | 19 | 1 | Urban | |
| 79 | 19 | 1 | Rural |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lagos, R.; Gutiérrez-Jara, J.P.; Cancino-Faure, B.; Lara-Díaz, L.Y.; Barradas, I.; González-Galeano, A. Breaking the Cycle of Echinococcosis: A Mathematical Modeling Approach. Trop. Med. Infect. Dis. 2025, 10, 101. https://doi.org/10.3390/tropicalmed10040101
Lagos R, Gutiérrez-Jara JP, Cancino-Faure B, Lara-Díaz LY, Barradas I, González-Galeano A. Breaking the Cycle of Echinococcosis: A Mathematical Modeling Approach. Tropical Medicine and Infectious Disease. 2025; 10(4):101. https://doi.org/10.3390/tropicalmed10040101
Chicago/Turabian StyleLagos, Richard, Juan Pablo Gutiérrez-Jara, Beatriz Cancino-Faure, Leidy Yissedt Lara-Díaz, Ignacio Barradas, and Andrei González-Galeano. 2025. "Breaking the Cycle of Echinococcosis: A Mathematical Modeling Approach" Tropical Medicine and Infectious Disease 10, no. 4: 101. https://doi.org/10.3390/tropicalmed10040101
APA StyleLagos, R., Gutiérrez-Jara, J. P., Cancino-Faure, B., Lara-Díaz, L. Y., Barradas, I., & González-Galeano, A. (2025). Breaking the Cycle of Echinococcosis: A Mathematical Modeling Approach. Tropical Medicine and Infectious Disease, 10(4), 101. https://doi.org/10.3390/tropicalmed10040101






