Integrated Hyperparameter Optimization with Dimensionality Reduction and Clustering for Radiomics: A Bootstrapped Approach
Abstract
1. Introduction
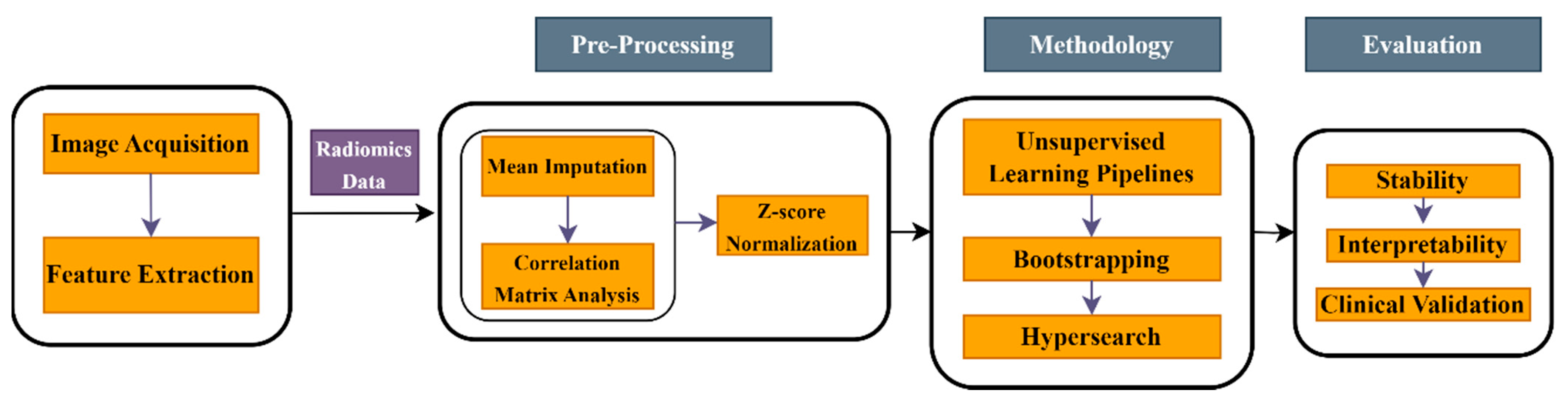
2. Materials and Methods
2.1. Datasets
2.1.1. Clinical Data
Patient Demographics
Preprocessing and Data Extraction
2.1.2. Simulated Data
2.2. Methods
2.2.1. Unsupervised Learning Pipelines
2.2.2. Hyperparameter Tuning
2.2.3. Performance Assessment
3. Results
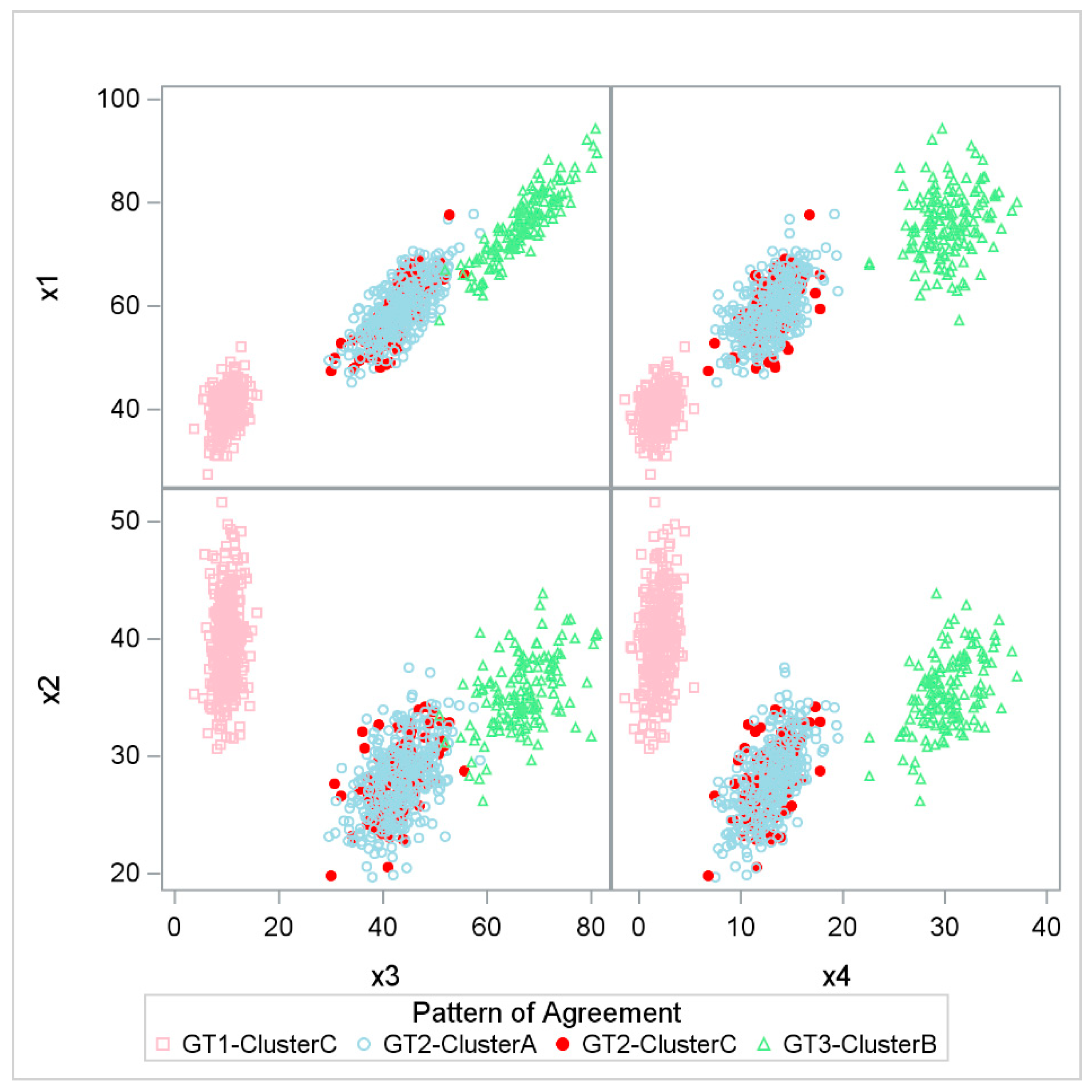
3.1. Simulation Study
3.2. Real-World Data Application
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images Are More than Pictures, They Are Data. Radiology 2016, 278, 563–577. (In English) [Google Scholar] [CrossRef] [PubMed]
- Shur, J.D.; Doran, S.J.; Kumar, S.; Ap Dafydd, D.; Downey, K.; O’Connor, J.P.B.; Papanikolaou, N.; Messiou, C.; Koh, D.M.; Orton, M.R. Radiomics in Oncology: A Practical Guide. Radiographics 2021, 41, 1717–1732. (In English) [Google Scholar] [CrossRef]
- Varghese, B.A.; Cen, S.Y.; Hwang, D.H.; Duddalwar, V.A. Texture analysis of imaging: What radiologists need to know. Am. J. Roentgenol. 2019, 212, 520–528. [Google Scholar] [CrossRef]
- Xv, Y.; Lv, F.; Guo, H.; Zhou, X.; Tan, H.; Xiao, M.; Zheng, Y. Machine learning-based CT radiomics approach for predicting WHO/ISUP nuclear grade of clear cell renal cell carcinoma: An exploratory and comparative study. Insights Into Imaging 2021, 12, 170. [Google Scholar] [CrossRef]
- Kumar, V.; Gu, Y.; Basu, S.; Berglund, A.; Eschrich, S.A.; Schabath, M.B.; Forster, K.; Aerts, H.J.; Dekker, A.; Fenstermacher, D.; et al. Radiomics: The process and the challenges. Magn. Reson. Imaging 2012, 30, 1234–1248. (In English) [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, S.; Dong, D.; Wei, J.; Fang, C.; Zhou, X.; Sun, K.; Li, L.; Li, B.; Wang, M.; et al. The Applications of Radiomics in Precision Diagnosis and Treatment of Oncology: Opportunities and Challenges. Theranostics 2019, 9, 1303–1322. (In English) [Google Scholar] [CrossRef] [PubMed]
- Haldar, D.; Kazerooni, A.F.; Arif, S.; Familiar, A.; Madhogarhia, R.; Khalili, N.; Bagheri, S.; Anderson, H.; Shaikh, I.S.; Mahtabfar, A.; et al. Unsupervised machine learning using K-means identifies radiomic subgroups of pediatric low-grade gliomas that correlate with key molecular markers. Neoplasia 2023, 36, 100869. (In English) [Google Scholar] [CrossRef]
- Rizzo, S.; Botta, F.; Raimondi, S.; Origgi, D.; Fanciullo, C.; Morganti, A.G.; Bellomi, M. Radiomics: The facts and the challenges of image analysis. Eur. Radiol. Exp. 2018, 2, 36. (In English) [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Hwang, Y.-B.; Sumon, R.I.; Rahman, H.; Hyeon, D.-W.; Moon, D.; Carole, K.S.; Kim, H.-C.; Choi, H.-K. Cluster Analysis: Unsupervised Classification for Identifying Benign and Malignant Tumors on Whole Slide Image of Prostate Cancer. In Proceedings of the 2022 IEEE 5th International Conference on Image Processing Applications and Systems (IPAS), Genova, Italy, 5–7 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Oh, J.H.; Apte, A.P.; Katsoulakis, E.; Riaz, N.; Hatzoglou, V.; Yu, Y.; Mahmood, U.; Veeraraghavan, H.; Pouryahya, M.; Iyer, A.; et al. Reproducibility of radiomic features using network analysis and its application in Wasserstein k-means clustering. J. Med. Imaging 2021, 8, 031904. (In English) [Google Scholar] [CrossRef]
- Ullmann, T.; Hennig, C.; Boulesteix, A.L. Validation of cluster analysis results on validation data: A systematic framework. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2022, 12, e1444. [Google Scholar] [CrossRef]
- Lee, C.; Abdool, A.; Huang, C.-H. PCA-based population structure inference with generic clustering algorithms. BMC Bioinform. 2009, 10, S73. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, J.J.; Purdue, M.P.; Signoretti, S.; Swanton, C.; Albiges, L.; Schmidinger, M.; Heng, D.Y.; Larkin, J.; Ficarra, V. Renal cell carcinoma. Nat. Rev. Dis. Primers 2017, 3, 17009. (In English) [Google Scholar] [CrossRef]
- Ged, Y.; Markowski, M.C.; Singla, N.; Rowe, S.P. The shifting treatment paradigm of metastatic renal cell carcinoma. Nat. Rev. Urol. 2022, 19, 631–632. (In English) [Google Scholar] [CrossRef]
- American Cancer Society. Key Statistics About Kidney Cancer-2024. Available online: https://www.cancer.org/cancer/types/kidney-cancer/about/key-statistics.html (accessed on 1 March 2024).
- Sun, E.D.; Ma, R.; Zou, J. Dynamic visualization of high-dimensional data. Nat. Comput. Sci. 2023, 3, 86–100. [Google Scholar] [CrossRef]
- Demirjian, N.L.; Varghese, B.A.; Cen, S.Y.; Hwang, D.H.; Aron, M.; Siddiqui, I.; Fields, B.K.K.; Lei, X.; Yap, F.Y.; Rivas, M.; et al. CT-based radiomics stratification of tumor grade and TNM stage of clear cell renal cell carcinoma. Eur. Radiol. 2022, 32, 2552–2563. (In English) [Google Scholar] [CrossRef]
- Friston, K.J. Statistical parametric mapping. In Neuroscience Databases: A Practical Guide; Springer: New York, NY, USA, 2003; pp. 237–250. [Google Scholar]
- Van Griethuysen, J.J.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.; Fillion-Robin, J.-C.; Pieper, S.; Aerts, H.J. Computational radiomics system to decode the radiographic phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef] [PubMed]
- Katsoulakis, E.; Yu, Y.; Apte, A.P.; Leeman, J.E.; Katabi, N.; Morris, L.; Deasy, J.O.; Chan, T.A.; Lee, N.Y.; Riaz, N. Radiomic analysis identifies tumor subtypes associated with distinct molecular and microenvironmental factors in head and neck squamous cell carcinoma. Oral Oncol. 2020, 110, 104877. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Gao, R.; Pang, J.; Lin, P.; Wen, R.; Wen, D.; Liang, Y.; Ma, Z.; Liang, L.; He, Y.; Yang, H. Identification of clear cell renal cell carcinoma subtypes by integrating radiomics and transcriptomics. Heliyon 2024, 10, e31816. [Google Scholar] [CrossRef]
- Traverso, A.; Kazmierski, M.; Welch, M.L.; Weiss, J.; Fiset, S.; Foltz, W.D.; Gladwish, A.; Dekker, A.; Jaffray, D.; Wee, L.; et al. Sensitivity of radiomic features to inter-observer variability and image pre-processing in Apparent Diffusion Coefficient (ADC) maps of cervix cancer patients. Radiother. Oncol. 2020, 143, 88–94. (In English) [Google Scholar] [CrossRef]
- Kothari, G.; Woon, B.; Patrick, C.J.; Korte, J.; Wee, L.; Hanna, G.G.; Kron, T.; Hardcastle, N.; Siva, S. The impact of inter-observer variation in delineation on robustness of radiomics features in non-small cell lung cancer. Sci. Rep. 2022, 12, 12822. (In English) [Google Scholar] [CrossRef] [PubMed]
- Hershman, M.; Yousefi, B.; Serletti, L.; Galperin-Aizenberg, M.; Roshkovan, L.; Luna, J.M.; Thompson, J.C.; Aggarwal, C.; Carpenter, E.L.; Kontos, D.; et al. Impact of Interobserver Variability in Manual Segmentation of Non-Small Cell Lung Cancer (NSCLC) Applying Low-Rank Radiomic Representation on Computed Tomography. Cancers 2021, 13, 5985. (In English) [Google Scholar] [CrossRef] [PubMed]
- Cross, J.L.; Choma, M.A.; Onofrey, J.A. Bias in medical AI: Implications for clinical decision-making. PLOS Digit. Health 2024, 3, e0000651. [Google Scholar] [CrossRef] [PubMed]
| ccRCC Demographics | ||
|---|---|---|
| Characteristics | Sample Size | |
| Gender | Male | 305 (68.2%) |
| Female | 142 (31.8%) | |
| Age | Mean 60.7 ± 12.6, Median 62 (52 to 70) | |
| Grade | ||
| 110 (24.6%) | |
| 337 (75.4%) | |
| 223 (68.4%) | |
| 103 (31.6%) | |
| 278 (62.2%) | |
| 169 (37.8%) | |
| Method | Hyperparameters |
|---|---|
| K-means | Number of clusters |
| Kernel PCA | Kernels |
| 1. Sigmoid 2. RBF 3. Linear 4. Cosine 5. Polynomial | |
| PCA components | |
| t-SNE | Perplexity |
| NMF | NMF-Components |
| Spectral | Number of clusters |
| Pipelines | Pipelines |
|---|---|
| M1 | K-means |
| M2 | PCA->K-means |
| M3 | NMF-> PCA ->K means |
| M4 | NMF ->K- means |
| M5 | Spectral |
| M6 | PCA-> Spectral |
| M7 | NMF-> PCA ->Spectral |
| M8 | NMF-> Spectral |
| M9 | t-SNE-> PCA ->K-means |
| M10 | t-SNE-> K-means |
| Robustness | Interpretability | Aggressive | Malignant | Risk 1 vs. 23 | Risk 2 vs. 13 | Risk 3 vs. 12 | |
|---|---|---|---|---|---|---|---|
| K-means | 0.43 | 43.62% | 0.6 95% CI (0.54, 0.65) | 0.59 95% CI (0.53, 0.65) | 0.57 95% CI (0.51, 0.63) | 0.56 95% CI (0.5, 0.63) | 0.58 95% CI (0.49, 0.66) |
| PCA-K-means | 0.65 | 68.46% | 0.59 95% CI (0.54, 0.64) | 0.61 95% CI (0.55, 0.67) | 0.54 95% CI (0.49, 0.6) | 0.51 95% CI (0.45, 0.58) | 0.57 95% CI (0.49, 0.64) |
| NMF-PCA-K-means | 0.83 | 62.42% | 0.56 95% CI (0.51, 0.61) | 0.57 95% CI (0.52, 0.63) | 0.57 95% CI (0.52, 0.62) | 0.55 95% CI (0.48, 0.61) | 0.56 95% CI (0.49, 0.63) |
| NMF-K-means | 0.82 | 64.88% | 0.59 95% CI (0.53, 0.64) | 0.56 95% CI (0.5, 0.61) | 0.59 95% CI (0.54, 0.64) | 0.57 95% CI (0.51, 0.64) | 0.57 95% CI (0.49, 0.64) |
| Spectral | 0.36 | Not able to produce | 0.58 95% CI (0.52, 0.63) | 0.63 95% CI (0.58, 0.69) | 0.53 95% CI (0.48, 0.59) | 0.51 95% CI (0.44, 0.57) | 0.52 95% CI (0.44, 0.61) |
| PCA-Spectral | 0.65 | 51.01% | 0.5 95% CI (0.45, 0.55) | 0.52 95% CI (0.46, 0.58) | 0.54 95% CI (0.49, 0.6) | 0.59 95% CI (0.52, 0.65) | 0.52 95% CI (0.45, 0.6) |
| NMF-PCA-Spectral | 0.82 | 69.57% | 0.54 95% CI (0.49, 0.6) | 0.54 95% CI (0.49, 0.6) | 0.51 95% CI (0.45, 0.56) | 0.5 95% CI (0.44, 0.57) | 0.51 95% CI (0.43, 0.59) |
| NMF-Spectral | 0.7 | 69.35% | 0.59 95% CI (0.54, 0.64) | 0.62 95% CI (0.57, 0.68) | 0.54 95% CI (0.49, 0.59) | 0.51 95% CI (0.45, 0.57) | 0.54 95% CI (0.46, 0.63) |
| t-SNE-PCA-K-means | Not stable | 57.05% | 0.56 95% CI (0.51, 0.61) | 0.57 95% CI (0.51, 0.62) | 0.53 95% CI (0.48, 0.58) | 0.53 95% CI (0.47, 0.58) | 0.51 95% CI (0.44, 0.59) |
| t-SNE-K-means | Not stable | 30.20% | 0.53 95% CI (0.48, 0.58) | 0.55 95% CI (0.49, 0.61) | 0.5 95% CI (0.45, 0.55) | 0.53 95% CI (0.46, 0.59) | 0.53 95% CI (0.46, 0.6) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawan, S.J.; Muellner, M.; Lei, X.; Desai, M.; Varghese, B.; Duddalwar, V.; Cen, S.Y. Integrated Hyperparameter Optimization with Dimensionality Reduction and Clustering for Radiomics: A Bootstrapped Approach. Multimodal Technol. Interact. 2025, 9, 49. https://doi.org/10.3390/mti9050049
Pawan SJ, Muellner M, Lei X, Desai M, Varghese B, Duddalwar V, Cen SY. Integrated Hyperparameter Optimization with Dimensionality Reduction and Clustering for Radiomics: A Bootstrapped Approach. Multimodal Technologies and Interaction. 2025; 9(5):49. https://doi.org/10.3390/mti9050049
Chicago/Turabian StylePawan, S. J., Matthew Muellner, Xiaomeng Lei, Mihir Desai, Bino Varghese, Vinay Duddalwar, and Steven Y. Cen. 2025. "Integrated Hyperparameter Optimization with Dimensionality Reduction and Clustering for Radiomics: A Bootstrapped Approach" Multimodal Technologies and Interaction 9, no. 5: 49. https://doi.org/10.3390/mti9050049
APA StylePawan, S. J., Muellner, M., Lei, X., Desai, M., Varghese, B., Duddalwar, V., & Cen, S. Y. (2025). Integrated Hyperparameter Optimization with Dimensionality Reduction and Clustering for Radiomics: A Bootstrapped Approach. Multimodal Technologies and Interaction, 9(5), 49. https://doi.org/10.3390/mti9050049





