Human Perception Measures for Product Design and Development—A Tutorial to Measurement Methods and Analysis
Abstract
:1. Introduction
1.1. Perception Studies for Engineers
1.2. Measuring Perception
- detection—detecting, whether there is a stimulus present or not;
- discrimination—detecting, whether two stimuli are different in one or more parameters;
- identification—identify an unknown stimulus from a given set of stimuli;
- scaling—relation of the size of two or more stimuli (or their parameters).
1.3. Structure of This Paper
2. Study Design
2.1. Hypothesis
- Light emitting diode (LED) technology allows for control of not only brightness and color of white light consisting of different LED colors, but also has an impact on the color rendering of illuminated objects. The energy consumption of LED lightning can be lowered at the expense of the quality of color rendering. Thompson investigates in [7] whether color rendering quality loss is detectable in peripheral and central vision and proposes an optimized dynamic lightning scheme that reduces energy consumption in peripheral vision without affecting the brightness of the scene.
- New automotive lightning systems promise increased sight and visibility, but potentially increase glare of other road users. In [8], Zydek investigates an improved glare-free lightning system and does not find an increased glare of other road users, but a better sight compared to conventional systems.
- The wide use of touch-based interfaces in consumer electronics triggers new applications with haptic feedback in professional contexts. Personal protection gear such as gloves is more wide-spread in professional applications. The question arises of whether these protectional measures have to be considered in the design of professional haptic interfaces. Two recent studies by Seeger et al. [9] and Hatzfeld et al. [10] investigate absolute and differential thresholds for protective and surgical gloves, respectively, and find different parameters with and without gloves, but not necessarily a need to consider these in the design of haptic interfaces.
- The example in Section 6 investigates the perceptual thresholds of damping in rotary controls in combination with other parameters such as detent or user distraction. It aims to find design parameters for clearly distinguishable controls as well as acceptable tolerance values.
2.1.1. Perception Measures
2.1.2. Typical Experiments for Product Development
2.1.3. External Influences
2.2. Classifying Parameters
2.3. Measurement Procedure
2.3.1. Psychometric Methods
2.3.2. Response Paradigms
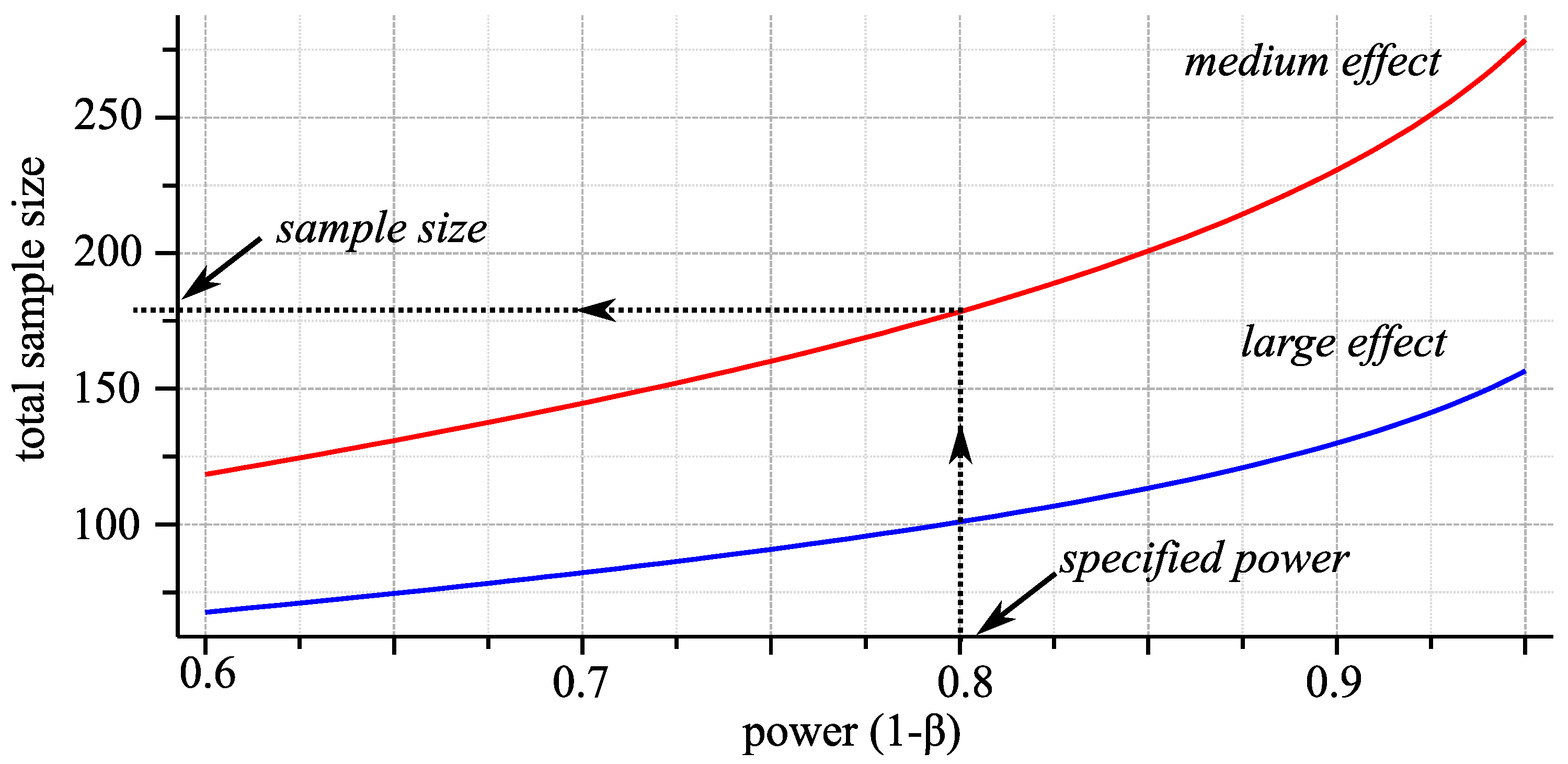
2.3.3. Selection of a Procedure
- Parametric methods like [37] or the Updated-Maximum-Likelihood-Method (UML) [36,42] provide performance benefits for assessing a complete psychometric function. However, they require certain assumptions concerning the psychometric function that may not be available for every kind of experiment [35]. An alternative is the use of the classic Method of Constant Stimuli and finding an acceptable trade-off between accuracy and duration of the experiment.
- For the approximation of the point of the psychometric function, parametric methods are the best choice as well, if an assumption about the form of the function can be made. If that is not the case, one can use the wide-spread adaptive staircase methods, which are easy to implement and only rely on some weak assumptions. An alternative is using approximation methods for stochastic processes such as the ASA procedure [43] or the WUD method [28,38]. These are based on a more complex mathematical basis and can be set to an arbitrary detection probability. Furthermore, they rely on weak assumptions about the psychometric function only and are therefore suitable for experiments with little a priori knowledge about the form and parameters of the psychometric function of the subject.
- For psychometric measures that cannot be described as a parameter of a psychometric function, other types of psychometric procedures must be used. Stevens gives several examples for magnitude estimation tasks [16], in addition to the Method of Adjustment described above.
2.4. Subject Selection
3. Measurement Setup and Errors
4. Conducting the Test
5. Data Analysis
5.1. Checking the Data
5.2. Checking the Hypothesis
5.3. Reporting the Results
6. Example: Haptic Perception of Viscous Damping of Rotary Switches
6.1. Measurement Setup and Stimuli
- Knob diameter: and
- Detent profile: a high-grade detent profile with a maximum torque of 25 , a slope proportion of 1:5 (rise to fall) and a spatial period of 18 can be superimposed on the stimulus. Experimental conditions are activated detent or no detent.
- Distraction: thresholds are either determined as a primary task (no distraction condition), or as a secondary task to a standardized Lane Change Test (LCT) [63] (distraction condition).
6.2. Subjects
6.3. Measurement Procedure
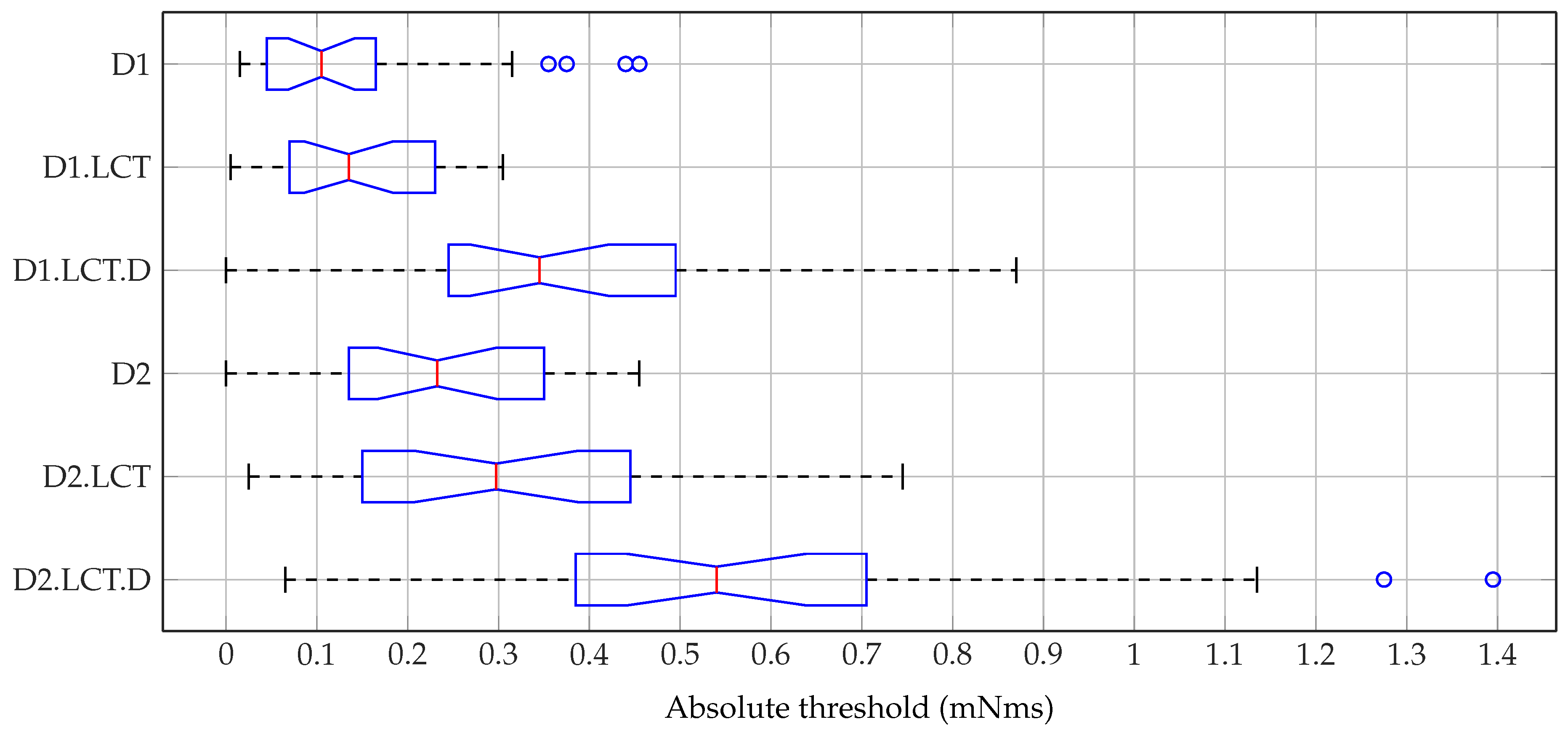
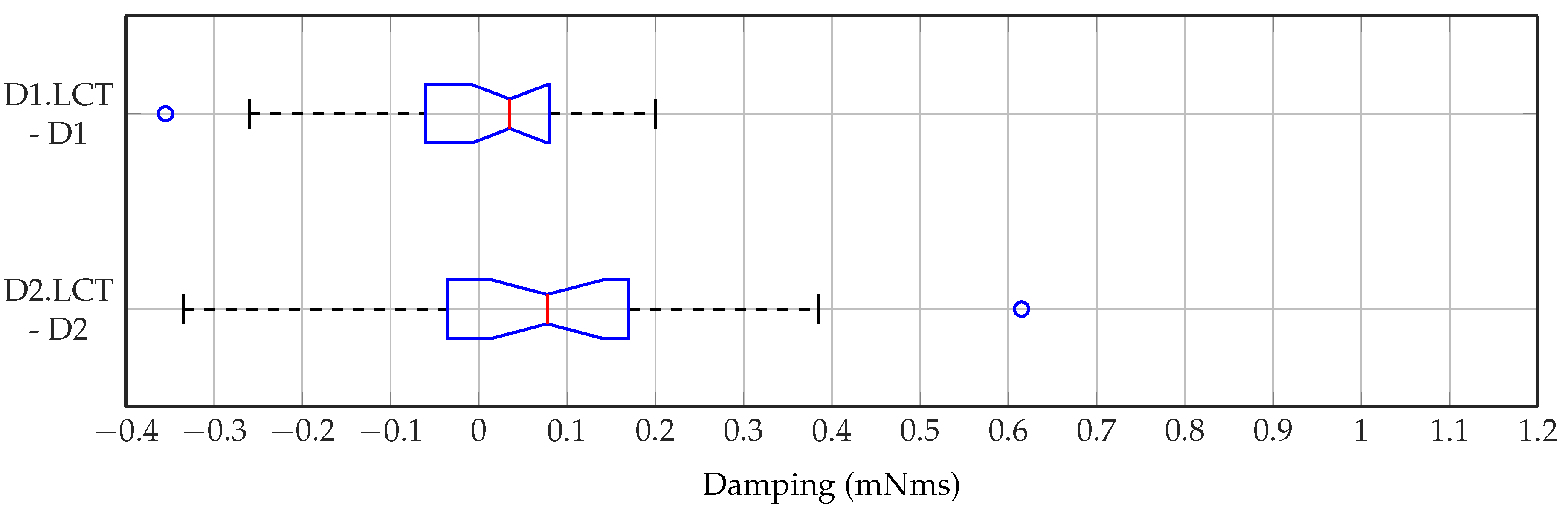
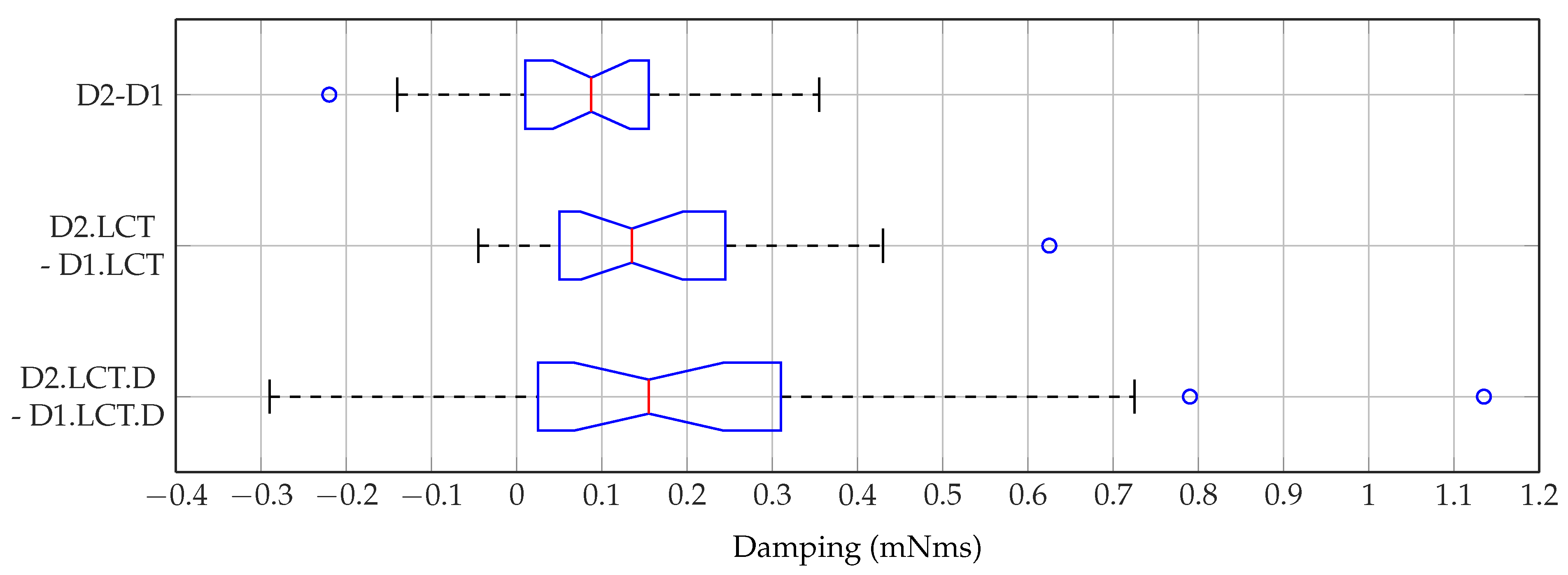
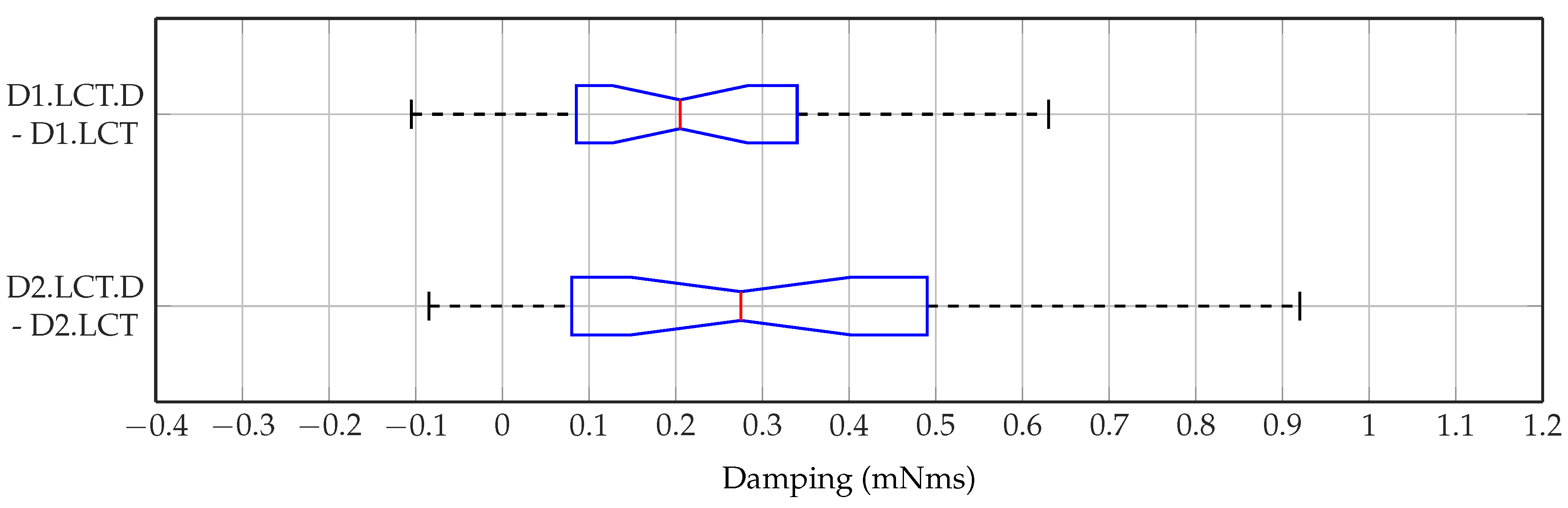
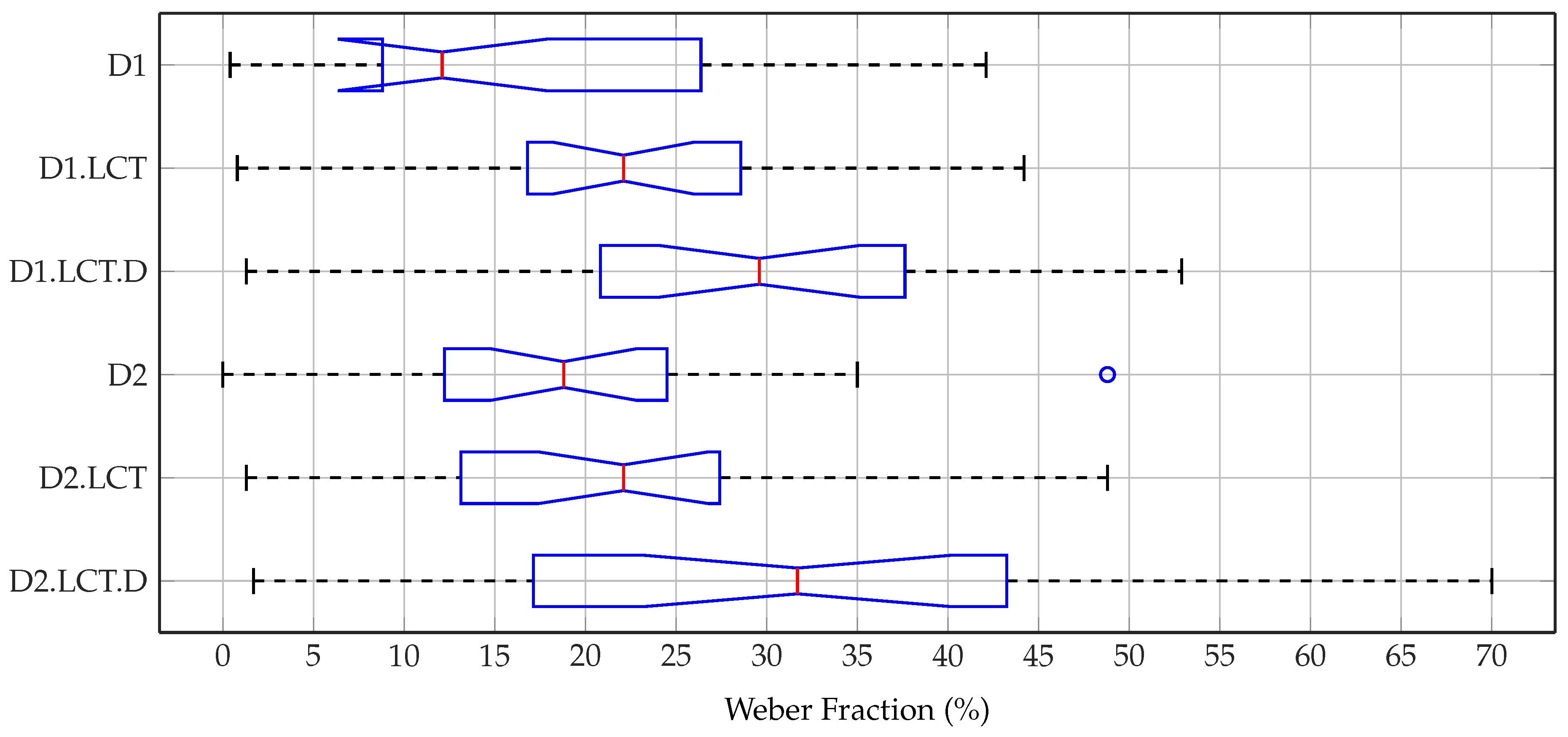
6.4. Results
6.5. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kern, T.A.; Hatzfeld, C. The User’s Role in Haptic System Design. In Engineering Haptic Devices, 2nd ed.; Hatzfeld, C., Kern, T.A., Eds.; Springer: London, UK, 2014. [Google Scholar]
- Weber, E.H. Tastsinn und Gemeingefühl; Engelmann: Leipzig, 1905. [Google Scholar]
- Gall, S.; Beins, B.; Feldman, J. Psychophysics. In The Gale Encyclopedia of Psychology; Gale: Detroit, Michigan, 2001. [Google Scholar]
- Wichmann, F.; Hill, N. The psychometric function: I. Fitting, Sampling, and Goodness of Fit. Percept. Psychophys. 2001, 63, 1293–1313. [Google Scholar] [CrossRef] [PubMed]
- Kühner, M.; Wild, J.; Bubb, H.; Bengler, K.; Schneider, J. Haptic Perception of Viscous Friction of Rotary Switches. In Proceedings of the 2011 IEEE World Haptics Conference (WHC), Istanbul, Turkey, 21–24 June 2011; pp. 587–591. [Google Scholar]
- Kühner, M. Haptische Unterscheidbarkeit Mechanischer Parameter bei Rotatorischen Bedienelementen. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2014. [Google Scholar]
- Do Thompson, M.R. Psychophysical Evaluations of Modulated Color Rendering for Energy Performance of LED-Based Architectural Lighting. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Zydek, B. Blendungsbewertung von Kraftfahrzeugscheinwerfern unter Dynamischen Bedingungen. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2014. [Google Scholar]
- Seeger, M.; Stein, T.; Schmidt, L. Vibrotaktile Wahrnehmung bei der Verwendung von Handschuhen. In Mensch und Computer 2017—Tagungsband; Gesellschaft für Informatik: Regensburg, Germany, 2017. [Google Scholar]
- Hatzfeld, C.; Dorsch, S.; Neupert, C.; Kupnik, M. Influence of surgical gloves on haptic perception thresholds. Int. J. Med. Robot. Comput. Assist. Surg. 2017. [Google Scholar] [CrossRef] [PubMed]
- Prins, N.; Kingdom, F.A.A. Psychophysics: A Practical Introduction; Academic Press: Maryland Heights, MO, USA, 2010. [Google Scholar]
- Macmillan, N.; Creelman, C. Detection Theory: A User’s Guide; Lawrence Erlbaum: London, UK, 2005. [Google Scholar]
- Colman, A. A Dictionary of Psychology, 3rd ed.; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Conner, M.; Booth, D.; Clifton, V.; Griffiths, R. Individualized optimization of the salt content of white bread for acceptability. J. Food Sci. 1988, 53, 549–554. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). ISO 20462-3: Photography—Psychophysical Experimental Methods for Estimating Image Quality; ISO: Geneva, Switzerland, 2012. [Google Scholar]
- Stevens, S.S. Psychophysics; Transaction Books: Piscataway, NJ, USA, 1975. [Google Scholar]
- Theeuwes, J.; Alferdinck, J.W.; Perel, M. Relation between glare and driving performance. Hum. Factors J. Hum. Factors Ergonom. Soc. 2002, 44, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Hatzfeld, C. Haptics as an Interaction Modality. In Engineering Haptic Devices, 2nd ed.; Hatzfeld, C., Kern, T.A., Eds.; Springer: London, UK, 2014. [Google Scholar]
- Zwicker, E.; Fastl, H. Psychoacoustics; Springer: Heidelberg, Germany, 1999. [Google Scholar]
- Drasdo, N. Vision Research: A Practical Guide to Laboratory Methods. Brain 1999, 122, 2000–2002. [Google Scholar] [CrossRef]
- Peters, R.; Hackeman, E.; Goldreich, D. Diminutive Digits Discern Delicate Details: Fingertip Size and the Sex Difference in Tactile Spatial Acuity. J. Neurosci. 2009, 29, 15756–15761. [Google Scholar] [CrossRef] [PubMed]
- Verrillo, R.; Bolanowski, S. The Effects of Skin Temperature on the Psychophysical Responses to Vibration on Glabrous and Hairy Skin. J. Acoust. Soc. Am. 1986, 80, 528–532. [Google Scholar] [CrossRef] [PubMed]
- Gescheider, G.A.; Bolanowski, S.J.; Hall, K.L.; Hoffman, K.E.; Verrillo, R.T. The Effects of Aging on Information-Processing Channels in the Sense of Touch: I. Absolute Sensitivity. Somatosens. Mot. Res. 1994, 11, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Fechner, G.T. Elemente der Psychophysik; Breitkopf und Härtel: Leipzig, Germany, 1860. [Google Scholar]
- Green, D.M.; Swets, J.A. Signal Detection Theory and Psychophysics; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Wickens, T.D. Elementary Signal Detection Theory; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Levitt, H. Transformed Up-Down Methods in Psychoacoustics. J. Acoust.Soc. Am. 1971, 49, 467–477. [Google Scholar] [CrossRef]
- Kaernbach, C. Simple adaptive testing with the weighted up-down method. Atten. Percept. Psychophys. 1991, 49, 227–229. [Google Scholar] [CrossRef]
- Taylor, M.; Creelman, C. PEST: Efficient Estimates on Probability Functions. J. Acoust. Soc. Am. 1967, 41, 782–787. [Google Scholar] [CrossRef]
- Kesten, H. Accelerated Stochastic Approximation. Ann. Math. Stat. 1958, 29, 41–59. [Google Scholar] [CrossRef]
- Tyrrell, R.A.; Owens, D.A. A rapid technique to assess the resting states of the eyes and other threshold phenomena: the modified binary search (MOBS). Behav. Res. Methods Instrum. Comput. 1988, 20, 137–141. [Google Scholar] [CrossRef]
- Leek, M.R. Adaptive Procedures in Psychophysical Research. Percept. Psychophys. 2001, 63, 1279–1292. [Google Scholar] [CrossRef] [PubMed]
- Hatzfeld, C.; Kupnik, M.; Werthschutzky, R. Performance simulation of unforced choice paradigms in parametric psychometric procedures. In Proceedings of the 2015 IEEE World Haptics Conference (WHC), Evanston, IL, USA, 22–26 June 2015; pp. 475–481. [Google Scholar]
- Otto, S.; Weinzierl, S. Comparative Simulations of Adaptive Psychometric Procedures; Jahrestagung der Deutschen Gesellschaft für Akustik: Berlin, Germany, 2009; pp. 1276–1279. [Google Scholar]
- Harvey, L.O. Efficient Estimation of Sensory Thresholds. Behav. Res. Methods 1986, 18, 623–632. [Google Scholar] [CrossRef]
- Shen, Y.; Richards, V.M. A maximum-likelihood procedure for estimating psychometric functions: Thresholds, slopes, and lapses of attention. J. Acoust. Soc. Am. 2012, 132, 957–967. [Google Scholar] [CrossRef] [PubMed]
- Kontsevich, L.; Tyler, C. Bayesian Adaptive Estimation of Psychometric Slope and Threshold. Vis. Res. 1999, 39, 2729–2737. [Google Scholar] [CrossRef]
- Kaernbach, C. Adaptive Threshold Estimation with Unforced-Choice Tasks. Percept. Psychophys. 2001, 63, 1377–1388. [Google Scholar] [CrossRef] [PubMed]
- Prins, N.; Kingdom, F.A.A. Palamedes: Matlab Routines for Analyzing Psychophysical Data. Available online: http://www.palamedestoolbox.org/ (accessed on 28 July 2017).
- Karmali, F.; Chaudhuri, S.E.; Yi, Y.; Merfeld, D.M. Determining thresholds using adaptive procedures and psychometric fits: Evaluating efficiency using theory, simulations, and human experiments. Exp. Brain Res. 2016. [Google Scholar] [CrossRef] [PubMed]
- Madigan, R.; Williams, D. Maximum-Likelihood Psychometric Procedures in Two-Alternative Forced-Choice: Evaluation and Recommendations. Atten. Percept. Psychophys. 1987, 42, 240–249. [Google Scholar] [CrossRef]
- Green, D. Stimulus selection in adaptive psychophysical procedures. J. Acoust. Soc. Am. 1990, 87, 2662–2674. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.J.; Johnson, C.A. Comparison of the ASA, MOBS, and ZEST threshold methods. Vis. Res. 2006, 46, 2403–2411. [Google Scholar] [CrossRef] [PubMed]
- Jäkel, F.; Wichmann, F.A. Spatial four-alternative forced-choice method is the preferred psychophysical method for naïve observers. J. Vis. 2006, 6, 1307–1322. [Google Scholar] [CrossRef] [PubMed]
- Kollmeier, B.; Gilkey, R.H.; Sieben, U.K. Adaptive Staircase Techniques in Psychoacoustics: A Comparison of Human Data and a Mathematical Model. J. Acoust. Soc. Am. 1988, 83, 1852–1862. [Google Scholar] [CrossRef] [PubMed]
- Schlauch, R.; Rose, R. Two-, Three-, and Four-Interval Forced-Choice Staircase Procedures: Estimator Bias and Efficiency. J. Acoust. Soc. Am. 1990, 88, 732. [Google Scholar] [CrossRef] [PubMed]
- Cascio, C.; McGlone, F.; Folger, S.; Tannan, V.; Baranek, G.; Pelphrey, K.A.; Essick, G. Tactile Perception in Adults with Autism: a Multidimensional Psychophysical Study. J. Autism Dev. Disord. 2008, 38, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Grunwald, M.; Ettrich, C.; Krause, W.; Assmann, B.; Dähne, A.; Weiss, T.; Gertz, H.J. Haptic perception in anorexia nervosa before and after weight gain. J. Clin. Exp. Neuropsychol. 2001, 23, 520–529. [Google Scholar] [CrossRef] [PubMed]
- Keppel, G. Design and Analysis: A Researcher’s Handbook; Pearson Education: Old Tappan, NJ, USA, 1991. [Google Scholar]
- Faul, F.; Erdfelder, E.; Lang, A.G.; Buchner, A. G* Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 2007, 39, 175–191. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Standardization (ISO). ISO/IEC Guide 98-3: Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Declaration of Helsinki—Ethical Principles for Medical Research Involving Human Subjects. Technical Report. World Medical Association, 2013. Available online: http://www.wma.net/en/30publications/10policies/b3/ (accessed on 28 July 2017).
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ai, M.; Li, K.; Liu, S.; Lin, D.K. Balanced incomplete Latin square designs. J. Stat. Plan. Infer. 2013, 143, 1575–1582. [Google Scholar] [CrossRef]
- Christensen, R. Testing Fisher, Neyman, Pearson, and Bayes. Am. Stat. 2005, 59, 121–126. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Wallenstein, S.; Zucker, C.L.; Fleiss, J.L. Some statistical methods useful in circulation research. Circ. Res. 1980, 47, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Field, A. Discovering Statistics Using IBM SPSS Statistics, 4th ed.; Sage Publications: New York, NY, USA, 2014. [Google Scholar]
- Levine, T.R.; Hullett, C.R. Eta squared, partial eta squared, and misreporting of effect size in communication research. Hum. Commun. Res. 2002, 28, 612–625. [Google Scholar] [CrossRef]
- Olejnik, S.; Algina, J. Generalized eta and omega squared statistics: Measures of effect size for some common research designs. Psychol. Methods 2003, 8, 434–447. [Google Scholar] [CrossRef] [PubMed]
- Nitsch, V.; Färber, B. A Meta-Analysis of the Effects of Haptic Interfaces on Task Performance with Teleoperation Systems. IEEE Trans. Hapt. 2012, 6, 387–398. [Google Scholar] [CrossRef] [PubMed]
- Hogan, N. Impedance Control: An Approach to Manipulation. ASME J. Dyn. Syst. Meas. Control 1985, 107, 1–24. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). ISO 26022: Road Vehicles—Ergonomic Aspects of Transport Information and Control Systems—Simulated Lane Change Test to assess in-Vehicle Secondary Task Demand; ISO: Geneva, Switzerland, 2010. [Google Scholar]
- Kühner, M.; Bubb, H.; Bengler, K.; Wild, J. Adaptive Verfahren in der Psychophysik. In Ergonomie; Lehrstuhl für Ergonomie, Technische Universität München: München, Germany, 2012; p. 26. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]



| Type of Variable | Haptics | Vision |
|---|---|---|
| Dependent variable | Psychophysical construct in terms of JND, PSD etc. | |
| Independent variable | Stimulus parameter (frequency, intensity etc.), contact area [21], contact force, masking stimuli | Stimulus parameter (size, intensity), time of adaption |
| Controllable variable | Skin moisture, skin temperature [22], test person’s age [23], test person’s sex | Amblyopia, spectral power distribution (SPD) of the stimulus, adaption field |
| Confounding variables | Fatigue, experience of test person, other modalities, change of experimenter, non-thought-of variables | |
| Condition | Absolute Threshold (mN m s) | ||||||
|---|---|---|---|---|---|---|---|
| Min. | Median | Max. | |||||
| D1 | 0.015 | 0.046 | 0.105 | 0.164 | 0.455 | 0.148 | 0.135 |
| D1.LCT | 0.005 | 0.07 | 0.135 | 0.225 | 0.305 | 0.149 | 0.087 |
| D1.LCT.D | 0.065 | 0.255 | 0.355 | 0.495 | 0.87 | 0.386 | 0.216 |
| D2 | 0.035 | 0.135 | 0.235 | 0.35 | 0.455 | 0.245 | 0.128 |
| D2.LCT | 0.025 | 0.161 | 0.298 | 0.439 | 0.745 | 0.312 | 0.184 |
| D2.LCT.D | 0.065 | 0.386 | 0.54 | 0.703 | 1.395 | 0.598 | 0.349 |
| Condition | Weber Fraction (%) | ||||||
|---|---|---|---|---|---|---|---|
| Min. | Median | Max. | |||||
| D1 | 0.40 | 10.00 | 17.90 | 30.85 | 50.40 | 19.79 | 13.95 |
| D1.LCT | 0.85 | 17.10 | 22.30 | 31.56 | 44.15 | 22.84 | 10.72 |
| D1.LCT.D | 1.25 | 22.20 | 29.80 | 38.11 | 52.90 | 28.86 | 14.57 |
| D2 | 1.65 | 15.00 | 18.75 | 27.90 | 48.75 | 20.91 | 10.96 |
| D2.LCT | 1.25 | 13.96 | 21.88 | 27.40 | 48.75 | 22.00 | 11.63 |
| D2.LCT.D | 1.65 | 20.01 | 29.58 | 41.03 | 70.00 | 30.98 | 17.36 |
| Effect | Significance | Mean Effect Size |
|---|---|---|
| Absolute Threshold | ||
| Distraction | no | 0.172 |
| Detent | yes | 1.126 |
| Knob diameter | yes | 0.796 |
| Differential threshold | ||
| Distraction | no | 0.164 |
| Detent | yes | 0.571 |
| Knob diameter | no | 0.098 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatzfeld, C.; Kühner, M.; Söllner, S.; Khanh, T.Q.; Kupnik, M. Human Perception Measures for Product Design and Development—A Tutorial to Measurement Methods and Analysis. Multimodal Technol. Interact. 2017, 1, 28. https://doi.org/10.3390/mti1040028
Hatzfeld C, Kühner M, Söllner S, Khanh TQ, Kupnik M. Human Perception Measures for Product Design and Development—A Tutorial to Measurement Methods and Analysis. Multimodal Technologies and Interaction. 2017; 1(4):28. https://doi.org/10.3390/mti1040028
Chicago/Turabian StyleHatzfeld, Christian, Manuel Kühner, Stefan Söllner, Tran Quoc Khanh, and Mario Kupnik. 2017. "Human Perception Measures for Product Design and Development—A Tutorial to Measurement Methods and Analysis" Multimodal Technologies and Interaction 1, no. 4: 28. https://doi.org/10.3390/mti1040028
APA StyleHatzfeld, C., Kühner, M., Söllner, S., Khanh, T. Q., & Kupnik, M. (2017). Human Perception Measures for Product Design and Development—A Tutorial to Measurement Methods and Analysis. Multimodal Technologies and Interaction, 1(4), 28. https://doi.org/10.3390/mti1040028




