Administrative Boundary Effect of Housing Prices in Hangzhou City and Changes Under District Adjustment Policies: Applying a Spatial Discontinuity Regression Method

Abstract

The continuous expansion of China’s cities has led to a divergence in economics, population, and public service levels among different districts within the city. This has led to different housing prices, due to the resulting impact on housing supply and demand. Previous studies, although taking into account the possible differences in housing prices among different districts, have not focused on the extent to which districts affect housing prices. This study analyzes the housing price boundary effects among different districts in Hangzhou, China, using spatial discontinuity regression methods and data on newly built housing transactions from 2010 to 2021. This study also examines the impact of the integration policy, which acts to integrate suburban counties with the main urban area of Hangzhou, and whether that policy decreases the district boundary effect. The results show that the administrative boundary effect of housing prices in Hangzhou is significant, with most districts experiencing a house price boundary effect exceeding 10%. Encouraging regional integration policies effectively reduces the housing price gap that results from internal administrative divisions within the city.

1. Introduction

The gradual expansion of urban areas is bringing increased attention to the problem of unbalanced development within cities. Within China’s administrative division system, cities comprise municipal districts. As the core urban entities and centers of regional development, these districts are required to maintain a minimum population threshold of 250,000 residents. Spatial differences in resource endowments and location conditions, and the administrative barriers formed by the division of districts, have somewhat hindered the flow of resources and factors between regions. Different districts within cities have gradually started to differ with respect to economic development and population concentration levels [1], resident per capita disposable income, and basic public service provision and satisfaction levels [2].

In this context, the boundary of interest is a physical division between two districts and reflects the differences between them. The resulting boundary effect has become an important topic in administrative division research [3]. However, few studies have examined the boundary effect of administrative division on housing prices. The theory of housing market segmentation focuses on intra-city differences in housing markets. The division of the housing submarket is based on the characteristics of the housing structure, the characteristics of the demander group, and the geographical boundary. The latter are mainly based on spatial orientation [4] and school districts, as well as census tracts [5] in constructing housing segment markets. These studies show that more detailed spatial decomposition significantly improves the accuracy of housing price model predictions. The reasons behind spatial differences in housing prices, however, are often socio-demographic factors and urban growth differences. Under China’s administrative system, urban public services, including education, healthcare, and a significant portion of municipal infrastructure, are financed and provided by district-level governments, and the supply of land is also controlled by district-level governments; therefore, housing prices are strongly influenced by the built environment and the financial capacity of the district, and the industry and public opinion often consider the characteristics and prices of the real estate market in terms of districts. Scholars have also paid attention to house price differences in districts, and these studies usually include district dummy variables in their house price model or construct separate models for transaction samples in different districts. However, these studies cannot accurately reveal the house price differences caused by districts, and the house price differences within each district also blur the differences between districts to a certain extent. Boundary effect theory and the spatial discontinuity regression method can reveal the house price differences near the district boundaries, which provides a new idea for this study. To explore the district boundary effect of intra-city housing prices, a discontinuity regression method based on geographical boundaries may be useful.

In addition, as the economic volume generated by cities continues to expand, there is an increased demand for urban space expansion. Abolishing counties (cities) and developing new districts has become an important urban expansion approach. This encourages the urbanization of land and population growth, but may also create problems with respect to integrating new districts with the original main urban areas. Recent studies have begun to focus on the impact of administrative division adjustments on the regional real estate market; studies have examined the removal of counties, the establishment of districts [6], and the merger of jurisdictions [7]. Regional integration adjustment policies help accelerate the economic growth rate of new districts and improve the quality of regional economic development. This may help decrease the administrative boundary effect on housing prices.

Hangzhou is a leading city among China’s new first-tier cities. It has a superior industrial base and strong economics, with increasing development resilience and vitality, and a beautiful humanistic living environment. It consistently attracts a large non-local population, and the real estate market has been more active, with housing prices ranking among the top in the country. However, there are significant differences in housing price levels among districts. In 2001, Hangzhou underwent a major administrative reorganization. This reorganization abolished the XS and YH counties, and re-established them as districts, which were integrated into the overall development of Hangzhou. However, these two districts still maintain financial autonomy, and many policies or initiatives in the main city of Hangzhou often overlook or exclude the XS and YH districts. The housing price levels in these districts are significantly lower compared with the original six districts of the main city. In January 2015, Hangzhou issued an adjustment policy to further accelerate the integration of the XS and YH districts with the main urban area. The adjustments, along with integration promotion policies, provide an opportunity to analyze the potential effects of regional integration policies on the administrative district boundary effects of housing prices.

The remaining parts of this study are organized as follows. Section 2 provides a literature review exploring the boundary effect of intra-city housing prices and describing the spatial discontinuity regression method. Section 3 describes the data and develops a discontinuity regression model. In Section 4, we measure the administrative district boundary effect on housing prices in Hangzhou. Section 5 investigates the impact of regional integration policies on the boundary effect of housing prices. Finally, Section 6 presents the conclusions drawn from this study.

2. Literature Review

Housing prices show a circle-like divergence around urban centers [8], a divergence in different directions along the urban development axis, and other divergence patterns based on administrative divisions [9]. City-level studies mainly focus on supply and demand theory [6] and urban economy theory; the most common influencing factors considered include the level of economic development [10], population change, land supply [11], and the level of public infrastructure, such as healthcare, education, and transportation [12,13]. In contrast, studies focusing on intra-city heterogeneity mostly apply hedonic price models to analyze the heterogeneity of distribution and influence of factors, such as buildings, location, and neighborhood characteristics in urban space [14]. The influence at the district level is usually expressed simply in terms of district fixed effects [15].

Studies have found that housing market models based on census tracts or districts generate more accurate predictions compared with models driven by data or expert experience [5,16]. Lee et al. [17] revealed that districts with higher levels of commercialization and greater park area ratios were associated with a stronger willingness to pay for houses in Taipei. Some studies have focused on the intra-city real estate market and changes resulting from administrative boundary adjustments. Shi and Xu [7] and Yu et al. [3] examined the impact of jurisdictional mergers on the regional integration of the real estate market and economic fundamentals. They found that administrative boundary adjustment had a positive, but limited, impact on real estate prices. A study analyzing nationwide jurisdictional merger cases found that the merger of removed counties and districts significantly improved the equalization of house prices between the merged counties and urban areas [18].

New Economic Geography (NEG) theory posits that the spatial distribution of economic activity emerges endogenously from market forces—such as scale economies, transportation costs, and factor mobility—spontaneously forming core and peripheral regions through the processes of agglomeration and regional differentiation. Conversely, border effect theory emphasizes that administrative boundaries impede the cross-border flow of production factors, goods, services, and capital, thereby restricting economic interaction and influencing cross-border economic behavior. This manifests in phenomena such as “higher domestic than cross-border trade volumes” [19] and greater price disparities for urban commodities between cross-border cities than between domestic cities [20]. Local governments exercise power within their jurisdictions through instruments like land policies, household registration systems (hukou), and tax incentives. This inter-jurisdictional competition fundamentally alters the dynamics of agglomeration. By linking access to high-quality public services (e.g., education, healthcare) to property ownership within specific administrative divisions, these boundaries effectively endow housing with the value of “access rights to public services,” thus creating significant price gaps across districts. Several studies have examined intra-city disparities. Variations in the physical environment, socio-economic conditions, infrastructure accessibility, and communication coverage were found across districts, leading to social polarization [21,22]. Kallingal et al. [23] analyzed development inequalities across 279 local self-governing areas within Kerala, India. The findings revealed significant disparities in socio-demographic characteristics, employment opportunities, and housing infrastructure development among the settlements. Bourassa’s [24] study of Sydney and Melbourne and Law’s [9] analysis of London both identified housing price submarkets at the district level and, in some cases, down to the street level. Similarly, other studies integrated different indicators, including value-added services, total retail sales, disposable income per urban resident, and total import–export value at the district and county levels in Chinese cities [1,25], and highlighted differences in these indicators across different districts.

Regression Discontinuity (RD) is a randomized test method that evaluates treatment effects. It leverages the fact that the probability of individuals receiving treatment exhibits a discontinuous function at a known critical point. Spatial Regression Discontinuity (SRD) is a specific type of discontinuity regression design that uses geospatial boundaries as precise discontinuities for identification. Black [26] first introduced the approach by studying samples of houses on both sides of school district boundaries. The study assumed the samples were similar, except for differences in educational quality. Many scholars have since applied boundary discontinuity regression to assess the impact of education quality on housing prices [27,28,29,30,31]. This approach helps mitigate the influence of unobserved omitted variables, and has led to the consistent conclusion that spatial discontinuity regression reduces the coefficient associated with the effect of school quality on housing prices, compared with the traditional hedonic price regression approach.

Discontinuity regression has been widely applied to investigate other policy boundaries, including environmental governance policies [32], real estate regulatory policies [33,34], and public funding policies [35]. The method examines data from samples on both sides of a boundary, thereby enabling the assessment of treatment effects resulting from policy implementation.

Unlike previous studies that considered district in house price models as a control dummy variable, this study focuses on the differences in house prices across district boundaries. This study innovatively applies the spatial discontinuity method to measure the administrative boundary effect on housing prices in Hangzhou, China. Specifically, by combining discontinuity regression and difference-in-difference regression methods, this study measures the dynamic changes in the district boundary effect on housing prices in response to major regional integration policy. This study analyzes whether policy adjustments in each period have promoted the integration and development of the real estate market. This expands the current research to assess the spatial differentiation patterns of intra-city housing prices and their influencing factors.

3. Data and Models

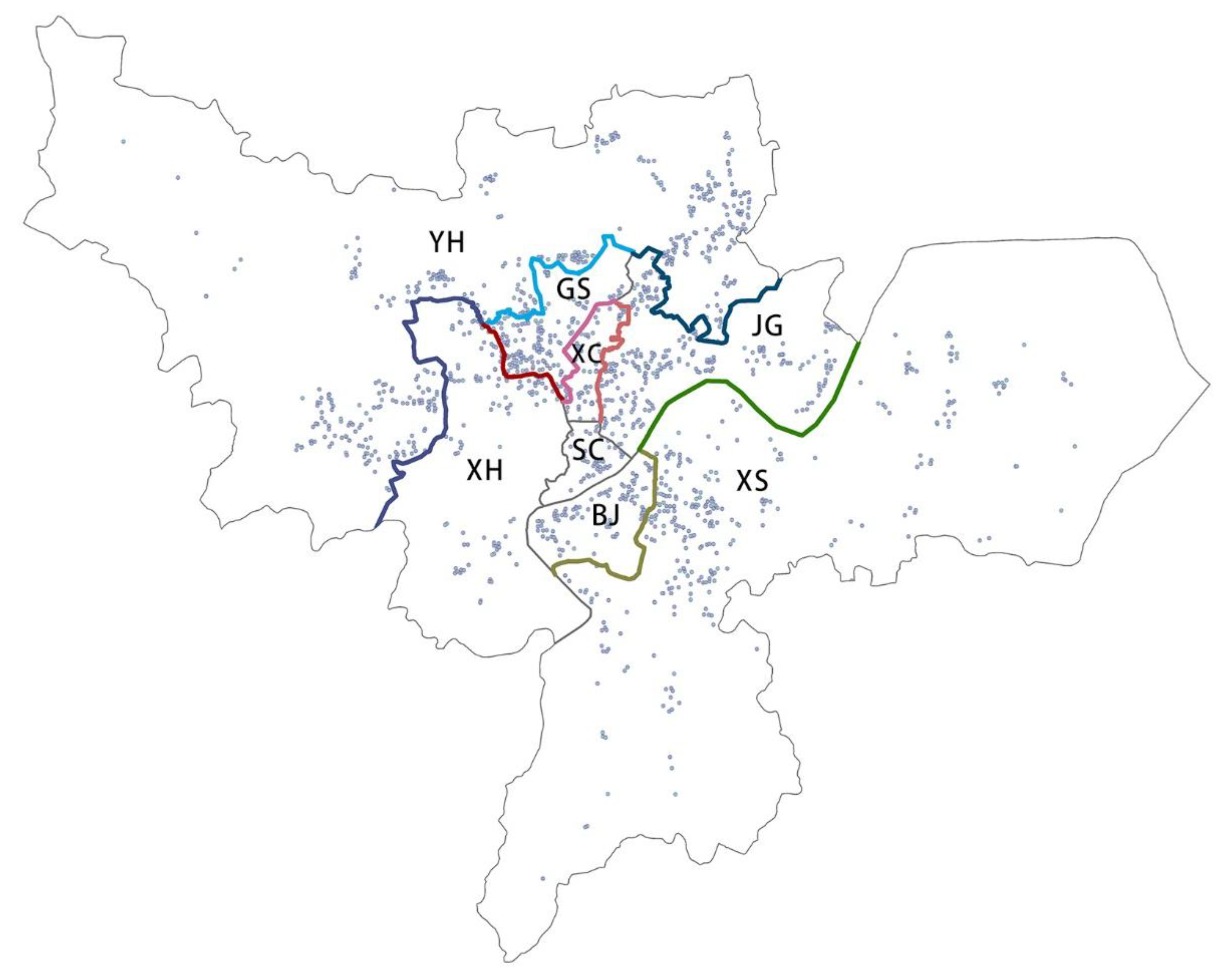
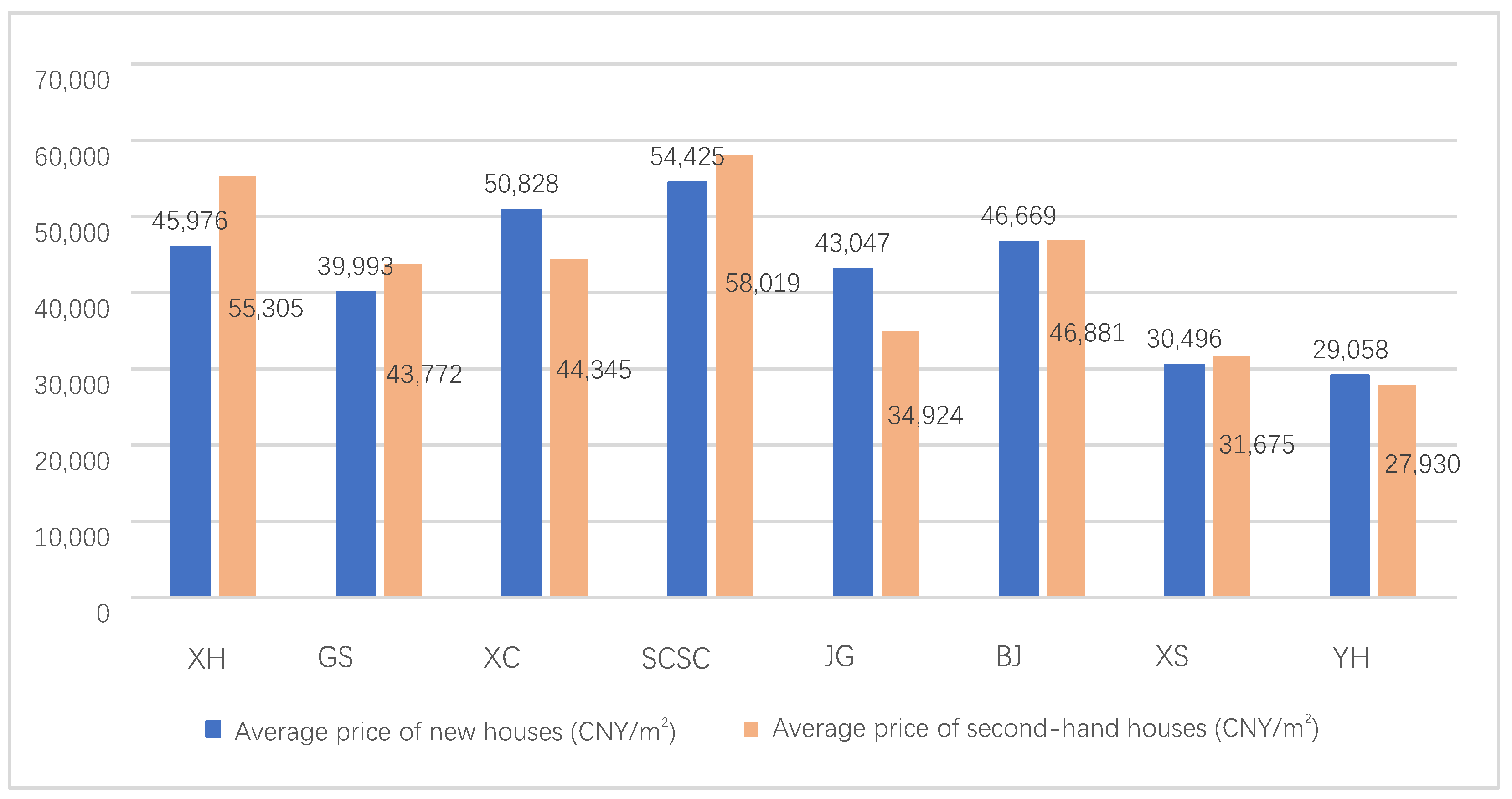
The research area includes the eight urban districts in Hangzhou in 2021. These districts include Shang Cheng (SC), Xia Cheng (XC), Xi Hu (XH), Gong Shu (GS), Bin Jiang (BJ), Jiang Gan (JG), Xiao Shan (XS), and Yu Hang (YH). Figure A1 in the Appendix illustrates the average prices of newly built and second-hand house transactions in each district, based on data obtained from the national house price quotation website (https://www.creprice.cn, accessed on 8 April 2022) for the year 2021. The data show significant disparity in average transaction prices among the districts: SC, XC, XH, and BJ have relatively high prices; and XS and YH (which are located in the suburbs) show notable differences compared with the other six districts within the main city. This study analyzes eight borders (Figure A2), which involves five borders between districts in the suburbs and the main city (YH–XH, YH–GS, YH–JG; XS–BJ, XS–JG) and three borders between districts in the main city (GS–XH, GS–XC, IG–XG). Some other boundaries were not included in the study scope because the samples of housing transactions on both sides were too small.

This study included collecting single-unit transaction information about newly built housing in Hangzhou from 2010 to 2021. Based on previous research and data availability, this study also considered 20 control variables. Data on housing prices, green ratio, plot ratio, parking space allocation ratio, and developer data were obtained from the CRIC (Chinese Real Estate Information Corporation, Beijing, China) database. Variables related to residential location and neighborhood characteristics were determined using Hangzhou electronic map data, from the Hangzhou Geographic Information Center. Referring to Yu [3], a sample of neighborhoods within 5 km of the proposed study boundary was selected, resulting in 875,403 transaction-related data points. The variable definition and descriptive statistics are presented in

Table 1. Descriptive statistics of residential characteristic variables.

Variable	Definition	Avg	Min	Max	Std
Area	Building area of the house	112.729	20.000	400.000	35.594
Floor	Floor where the house is located	11.117	1.000	48.000	7.330
Greenery rate	Green space area/total site area (%)	31.056	10.000	70.000	3.968
Plot ratio	Ratio of total residential construction area to site area	2.507	0.280	8.300	0.600
Car parking ratio	Number of parking spots/total number of households in the residential project	1.083	0.200	3.600	0.309
Brand developer	Whether the developer ranks among the top 100 real estate development enterprises in China, dummy variable of 0 or 1	0.216	0.000	1.000	0.412
Subway	Whether there is a subway station within 1 km, dummy variable of 0 or 1	0.289	0.000	1.000	0.453
Bus	Number of bus stations within 1 km of the neighborhood	14.472	0.000	108.000	13.699
Hospital	Whether there is a first-class hospital within 1 km of the neighborhood, dummy variable of 0 or 1	0.053	0.000	1.000	0.214
Key elementary schools	Whether there is a key primary school within 1 km, dummy variable of 0 or 1	0.377	0.000	1.000	0.224
Key high schools	Whether there is a key high school within 1 km of the neighborhood, dummy variable of 0 or 1	0.056	0.000	1.000	0.229
University	Whether there is university within 1 km of the neighborhood, dummy variable of 0 or 1	0.033	0.000	1.000	0.178
Park	Whether there is a park within 1 km of the neighborhood, dummy variable of 0 or 1	0.243	0.000	1.000	0.429
Scenic	Whether there is a scenic spot within 1 km of the neighborhood	0.231	0.000	1.000	0.421
Grocery Stores	Number of grocery stores within 1 km of the neighborhood	14.734	0.000	81.000	12.120
Supermarkets	Number of supermarkets within 1 km of the neighborhood	12.500	0.000	92.000	12.425
Shopping Center	Whether there is a shopping center within 3 km of the neighborhood, dummy variable of 0 or 1	0.784	0.000	1.000	0.412
Distance to West Lake	Logarithm of distance from residence to West Lake (famous landscape in Hangzhou) (km)	2.366	−0.429	3.476	0.423
Distance to Qianjiang CBD	Logarithm of distance from residence to the new city center (Qianjiang CBD) (km)	2.321	−0.683	3.427	0.458
Distance to Wulin	Logarithm of distance from residence to the traditional city center (Wulin Square) (km)	2.381	−0.080	3.443	0.523

.

This paper first investigates whether there is a boundary effect with respect to housing prices at administrative boundaries, using a spatial discontinuity regression model taking the following form:

Inprice_it = β₀ + β₁ ∙ boundary + (geographic location_i) + β₂ ∙ X_i + μ_t + ε_it

(1)

In this expression, the dependent variable lnprice_it is the unit price of a single dwelling i transacted at time t (taken as logarithm). The boundary is the spatial boundary dummy variable (treatment variable), where boundary = 1 when dwelling i is located on the designated side of the district boundary and boundary = 0 when a dwelling is located on the other side. The parameter β₁ is the coefficient of the boundary effect to be estimated; and X_i is the relevant characteristic affecting the housing price variable. The term (geographic location_i) is a polynomial constructed based on the location of the sample in relation to the boundary.

The driving variables are applied in both linear distance and latitude and longitude forms. The polynomial order is set with reference to the method by Gelman and Imbens [36], which applies both a linear form and a quadratic term form. The polynomial form based on latitude and longitude is set with reference to Dell [37], who found that model results are more robust using simple no-interaction terms. This results in setting the first order (geographic location_i) = lat + lng and the second order (geographic location_i) = lat + lng + lat² + lng² + lat*lng, where lat denotes latitude and lng is longitude. The term μ_t is the time fixed effect, including month fixed effect and year fixed effect, and ε_it is the random error term.

This article focuses on regional policy that may impact the border effect of housing prices. On 5 January 2015, the Hangzhou government issued “Opinions on Further Accelerating the Integrated Development of XS and YH districts and the Main Urban Area.” The document stated that nine key operational fields for XS and YH were to be integrated with the main urban area. To analyze the effect of the regional integration policy on the house price boundary effect of districts, the differential discontinuity regression model form is set as follows, based on Persson and Rossin-Slater (2019):

Inprice_it = β₀ + β₁ ∙ boundary + β₂ ∙ t + β₁′ ∙ treat ∙ boundary + (geographic location_i) + β₃ ∙ X_i + γ_t + ε_it

(2)

The sample of dwelling-related transactions before policy implementation is used as the control group, with the dummy variable treat = 0. The sample of transactions after policy implementation is the treatment group, with the dummy variable treat = 1. The regression coefficient β₁′ of the interaction term of the boundary dummy variable and the policy implementation dummy variable comprise the policy treatment effect.

4. Measurement of Boundary Effects of Housing Prices

The sample was restricted to a distance of 5 km from both sides of the eight boundaries. However, even controlling the sample within this specific range could result in samples that may significantly differ with respect to variables such as housing quality, location advantages, and neighborhood convenience. To narrow the differences in other sample characteristics and to reveal the influence of the administrative districts on house prices, the samples on both sides of the boundaries were first matched using the propensity score matching method (PSM). To reduce sample loss, a pair of four nearest neighbor matches (i.e., k = 4) was chosen. After this process, the mean deviation between the matched treatment group and the control group was significantly reduced, and the mean deviation of most of the housing characteristic variables on both sides of the boundary was less than 10%. As such, this study further selected the matched samples for the spatial discontinuity regression analysis. After removing the unmatched samples, 486,984 transactions were retained.

4.1. Boundary Effects of XS, YH, and the Main Urban Area

After XS and YH were abolished as autonomous counties and were established as districts in the suburbs of Hangzhou city, the difference in house prices between them and the former main urban area were obvious. First, we examined whether the border effect between the two districts and the main urban area is significant. YH borders XH, GS, and JG (three boundaries) and XS borders BJ and JG (two boundaries). ArcGIS software was used to establish buffer zones on both sides of the proposed study boundaries. The transaction samples identified within 5 km, 3 km, and 2 km on each side of the boundaries after propensity score matching (PSM) were retained for regression (Equation (1)). The boundary dummy variable was set to 0 if the location belonged to the YH or XS districts and assigned to 1 if it belonged to another main urban area. The Spatial Regression Discontinuity Design (RDD) was implemented using Stata 16.

The regression coefficients of β₁ for the YH–GS boundary are shown in

Table 2. Regression results of housing price boundary effects for the YH–GS border.

	5 km				3 km				2 km
	Linear Distance		Longitude and Latitude		Linear Distance		Longitude and Latitude		Linear Distance		Longitude and Latitude
	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic
β1	0.269	0.212	0.164	0.177	0.234	0.402	0.138	0.139	0.204	0.380	0.177	0.156
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
R2	0.897	0.898	0.902	0.904	0.916	0.920	0.919	0.921	0.951	0.952	0.951	0.953
AIC	−78,306	−79,079	−81,860	−82,924	−65,231	−67,150	−66,773	−67,811	−45,018	−45,578	−44,919	−45,906
Obs	72,723	72,723	72,723	72,723	47,134	47,134	47,134	47,134	27,331	27,331	27,331	27,331

Note: the numbers in parentheses represent the significance level p value.

. To save space, the results of the control variables are not shown here and can be provided upon request. Most variables pass the 1% significance level test, indicating that the model fits well. The linear and quadratic regression results of the linear distance and latitude/longitude models are robust within different bandwidths of the boundary, and the β₁ (boundary effect) estimates are positive and remain significant at the 1% level. Using Black et al. [38], the estimation results of the smallest Akaike information criterion deficit pool criterion are selected under different bandwidth samples and judged in conjunction with the model goodness-of-fit. The results show that after controlling for the relevant characteristic variables affecting housing prices, housing prices on both sides of the boundary differ significantly based on the districts they belong to. For example, housing with similar characteristics has a higher transaction price, at about 13.9 to 17.7% more, because it belongs to GS rather than YH.

The results of the price discontinuity effect at other boundaries between suburbs and the main city are shown in the upper part of

Table A1. Regression results of housing price boundary effects (β₁).

	5 km				3 km				2 km
	Linear Distance		Longitude and Latitude		Linear Distance		Longitude and Latitude		Linear Distance		Longitude and Latitude
	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic
YH–XH	0.089 (0.000)	0.084 (0.000)	0.145 (0.000)	0.026 (0.000)	0.129 (0.000)	0.174 (0.000)	0.084 (0.000)	−0.083 (0.000)	0.327 (0.000)	0.225 (0.000)	0.167 (0.000)	0.135 (0.000)
YH–JG	0.152 (0.000)	−0.019 (0.000)	0.122 (0.000)	0.107 (0.000)	0.053 (0.000)	0.001 (0.000)	0.121 (0.000)	0.111 (0.000)	0.113 (0.000)	0.105 (0.000)	0.146 (0.000)	0.130 (0.000)
XS–BJ	0.119 (0.000)	0.149 (0.000)	0.163 (0.000)	0.163 (0.000)	0.168 (0.000)	0.285 (0.000)	0.252 (0.000)	0.266 (0.000)	0.139 (0.000)	0.187 (0.000)	0.086 (0.000)	0.089 (0.000)
XS–JG	0.311 (0.000)	0.663 (0.000)	0.233 (0.000)	0.260 (0.000)	0.601 (0.000)	−0.626 (0.000)	0.235 (0.000)	0.261 (0.000)	−1.018 (0.000)	0.098 (0.000)	−0.260 (0.000)	−0.039 (0.000)
GS–XH	−0.202 (0.000)	−0.391 (0.000)	−0.079 (0.000)	−0.081 (0.000)	−0.382 (0.000)	−0.310 (0.000)	−0.022 (0.000)	−0.030 (0.000)	−0.286 (0.000)	−0.612 (0.000)	0.005 (0.446)	0.013 (0.000)
GS–XC	0.108 (0.000)	0.055 (0.000)	0.058 (0.000)	0.062 (0.000)	0.008 (0.197)	0.118 (0.000)	0.0009 (0.000)	0.044 (0.000)	0.089 (0.000)	−0.073 (0.000)	0.054 (0.000)	0.063 (0.000)
JG–XC	0.018 (0.000)	0.132 (0.000)	0.074 (0.000)	0.089 (0.000)	0.096 (0.000)	0.307 (0.000)	0.137 (0.000)	0.138 (0.000)	0.275 (0.000)	0.255 (0.000)	0.152 (0.000)	0.149 (0.000)

Note: the numbers in parentheses represent the significance level p value.

. The results indicate that the housing prices in the XH district are significantly higher compared with YH because of the differences in the districts. The estimated boundary effect is 2.6–13.5%. The magnitude of the boundary effect of housing price in YH–JG is about 10.7–13%. In other words, given similar architectural, location, and neighborhood characteristics, home buyers are willing to pay 10.7–13% more for housing located in the JG district. The estimated results of housing price boundary effects for the XS and BJ boundary are all positive, with the magnitude of boundary effects ranging from 8.9 to 26.6%. The regression results for the 5 km and 3 km boundaries between the XS and JG districts indicate that the housing price gap is about 26%. The regression results for the 2 km sample are not significant possibly due to the small transaction sample size.

4.2. Boundary Effects Between Within the Main City

There are relatively small differences in the housing prices within the main urban area. The house prices of the SC, XC, XH, and BJ districts (45,976–54,425 CNY/m²) can be roughly included in the first gradient of house prices in the main urban area, while in the GS and JG districts, the house price level is slightly lower at 43,772 CNY/m² and 34,924 CNY/m², respectively (see Figure A1).

Next, this study further applies the boundary effect model to examine whether there are differences in house prices within the main city, due to the districts to which they belong. The GS–XH, GS–XC, and JG–XC boundaries are selected; the boundary dummy variable “Boundary” is set as 0 if the housing is located in the GS or JG district, and 1 if otherwise. As shown in the lower half of Table A1, the estimated house price boundary effect for the JG–XC boundary is significantly positive, with a boundary effect of 8.9 to 14.9%. The GS–XC boundary effect is about 4.4%–6.3%. However, the estimated results are not significant under the two models within the 3 km bandwidth. The boundary coefficient of the GS–XH boundary at 5 km and 3 km is −0.030 and −0.391, respectively; as with other similar housing characteristics, the GS district is 3.0–39.1% higher compared with the XH district, while the boundary effect is positive under the 2 km bandwidth.

The empirical results reveal two key findings. First, there is a significant house price boundary effect between the newly incorporated XS and YH districts and the main urban area. Second, there is a gap in housing prices between some borders of the former main city. The size of this boundary effect between JG–XC is not smaller compared with those between the new districts and the main city borders. In contrast, the boundary effect of the GS–XC and GS–XH borders are somewhat ambiguous. This is consistent with the feelings of the residents. The economy and school quality of the JG district are significantly weaker than those of the other main urban areas, and the housing prices have always been the lowest. However, the GS district is different. The southern part of this district is almost seamlessly connected to XC and is located in the traditional city center. In recent years, a large number of high-end residential complexes have been newly developed in the northwest of GS. Moreover, it has excellent school districts and several well-known junior high schools and primary schools, making it highly attractive.

4.3. Robustness Tests

To further show that the house price effects described above are indeed caused by district boundaries and that the results are not affected by possible omitted spatial variables, this section tests the robustness of the results in three ways.

(1) “Pseudo-boundary” test

Based on Black [26], Gibbons et al. [28], and Huang, Bin et al. [39], this study includes a “pseudo-boundary” test, by shifting the boundary 2 km into the district. Using transaction samples with a bandwidth of 2 km, the samples are then restricted within a single district. Samples near the original assignment of 1 with respect to the district are assigned a value of 1; otherwise, the sample is assigned a value of 0. Spatial discontinuity regression is conducted using the same control variables, with latitude and longitude as the driving variables, and with a quadratic polynomial.

The regression results of some “pseudo-boundaries” are no longer significant, including the dummy boundaries obtained from shifting the XS–BJ boundary to the inner BJ district; the XS–JG boundary to the inner XS district; the XS–JG boundary to the inner JG district; and the JG–XC boundary to the inner JG district. A few “pseudo-boundary” estimates of the boundary effects are likely to come from the differentiation in development level within the districts. In addition, most of the significant boundary coefficients are small or close to zero. The test results indicate that the boundary effects estimated by the original model are mainly from district differences, rather than from other spatial differences.

(2) Use different forms of fixed effects

To eliminate the potential impact of neglected, spatially different variables on house prices (such as community characteristics), district boundaries are divided by 500 m equal lengths and boundary dummy variables are included to control unobserved spatial factors. This study also adds dummy variables associated with the street where the housing is located to the spatial discontinuity regression model. This is introduced to control the differences in economic and social characteristics at the sub-district level. The estimation results of boundary effects remain robust. This indicates that omitted variables do not significantly affect the estimation results.

(3) Using inverse distance weights

Samples closer to the boundary are more similar in unobservable features. Therefore, based on Koster et al. [33], a weighted regression using inverse distance weights is conducted in a spatial discontinuity regression model to assign greater weights to samples closer to the boundary. Taking the second order latitude and longitude model with a 5 km bandwidth as an example, the estimated results of the housing price boundary effect for the rest of the borders are significant and are generally consistent with the previous estimation results using uniform weights. Due to space limitations, these results are not presented and can be provided upon request.

5. Impact of Regional Integration Policy

(1) Policy effect of the integration of the new suburb districts and main city

In 2001, the XS and YH counties became districts but retained provincial direct administration, maintaining independent finances and unaligned public policies. Hangzhou often excluded them from policies, hindering urban integration. In January 2015, Hangzhou issued an integration policy covering nine aspects, including household registration management, employment and social security, social assistance, education, public health, citizen card service, provident fund system, public transportation, and industrial policy, enhancing connectivity with the main city.

To assess the policy’s impact on housing price boundaries, we used a differential discontinuity model (Model 3.2). The 2010–2014 sample served as the control group, and 2015–2021 as the treatment group. Robustness tests were then conducted based on samples from different time spans [40,41]. Using latitude/longitude and second-order polynomials,

Table 3. Effect of integration policy between XS, YH, and the main city (β₁′).

		2010–2021				2010–2019				2010–2017
	5 km	3 km		2 km	5 km	3 km		2 km	5 km	3 km		2 km
XS	−0.005	−0.060		−0.021	−0.057	−0.132		−0.061	−0.112	−0.149		−0.080
	(0.015)	(0.000)		(0.000)	(0.000)	(0.000)		(0.000)	(0.000)	(0.000)		(0.000)
YH	−0.004	0.032		0.033	0.010	0.042		0.055	0.030	0.049		0.044
	(0.006)	(0.000)		(0.000)	(0.000)	(0.000)		(0.000)	(0.000)	(0.000)		(0.000)
	2010–2021				2010–2020				2010–2019
	5 km		3 km		5 km		3 km		5 km		3 km
YH (2018)	−0.050 (0.000)		−0.024 (0.000)		−0.038 (0.000)		−0.013 (0.000)		−0.030 (0.000)		−0.006 (0.000)

Note: the numbers in parentheses represent the significance level p value.

shows robust negative effects for XS–main city boundaries (including XS–BJ, XS–JG), with price gaps shrinking by 0.5–14.9%. The effect weakened over time, stabilizing at 0.5–2.1%. However, YH–main city boundaries (including YH–GS, YH–XH, YH–JG) saw no significant decline, with only a 0.4% drop at 5 km; some models even showed increased boundary effects.

Regional integration is a gradual process requiring sustained policy implementation. Taking employment and social security as an example, while the 2015 policy mandated integration with the main urban area, a phased approach was adopted with full municipal-level integration targeted by January 2018.

In contrast, industrial policies and transportation investments yield more immediate effects. Accelerated industrial development and improved transit accessibility directly stimulate population concentration and real estate market growth. The integration policy proved more effective in narrowing the XS–main urban housing price gap than YH’s, attributable to two key factors.

First, in 2015, XS district was selected as the main venue for the 2016 G20 Summit and 2022 Asian Games, which triggered rapid urban development. The Olympic Sports Expo Center and surrounding commercial hubs attracted high-value enterprises, elevating the district’s overall investment appeal.

Second, critical transportation upgrades occurred earlier in XS. The 2014–2015 openings of Metro Line 2’s southeast section and Line 4 significantly enhanced XS–main city connectivity. YH district lagged in both industrial clustering and transportation integration, explaining its weaker policy response.

(2) The lagging changes in boundary effects between YH district and the main city

The year 2018 was a special time point with respect to the integration of YH district into the main city. Employment, social security, and education were continuously and deeply promoted through the integration policy. Furthermore, the successive opening of highways and subways connecting the main city and the expansion and upgrading of the Future Science and Technology City provided favorable conditions for integrating YH district into Hangzhou. This included the introduction and prioritization of the intelligent logistics platform “Cainiao” and Alibaba’s “five new” innovation achievements. This advancement propelled the Future Science and Technology City into a high-speed development stage. Using the differential discontinuity regression model, with 2018 as the time point, housing transaction data were selected for 2010–2021, with transaction samples from 2010 to 2017 as the control group and transaction samples from 2018 and later as the treatment group. The samples were restricted to those within 5 km and 3 km near the boundary between YH district and the main urban area. The second-order longitude and latitude polynomials were used to estimate the results, shown in Table 3.

The house price boundary effect between YH and the main urban area after the upgrading of the Future Science and Technology City decreases by 0.6 to 5.0% after policy implementation. The house price boundary effect between YH district and the main urban area significantly decreases under different time spans. The dampening effect of the industrial upgrading and expansion on the boundary effect between YH district and the main urban area gradually increases as time passes, and the size of the boundary effect is lowered by about 0.6–3.0% between the study period start time and 2019. The policy dampening effect then increases to 2.4–5.0% over time, until 2021.

(3) The policy effect of the “merger of small districts” within the main city

In April 2021, the Hangzhou government issued the “Notice on Adjusting the Administrative Division of Hangzhou City”, which involved the dissolution of the SC and JG districts to establish a new SC district, and the dissolution of the XC and GS districts to establish a new GS district. Thus, the originally smaller SC and XC districts were merged with their adjacent districts, respectively. This paper still uses the difference-in-discontinuity regression model (2) to measure the impact of the “small district merger type” adjustment on the integration of the real estate market. The transaction samples from 2020 to 2021 were selected. For transactions that occurred in April 2021 and later, t = 1; otherwise, t = 0. For the merger of the XC and GS districts, the samples within a 5 km range of the original boundary of the XC and GS districts were retained. However, due to the short boundary between the SC and JG districts resulting in a small sample, the samples at the boundary between the JG and XC districts were selected for regression to explore whether the integration of JG into the SC district has narrowed the housing price gap between them. The results are shown in

Table 4. Impact of “merger of small districts” on the boundary effect (β₁′).

	5 km				3 km
	Linear Distance		Longitude and Latitude		Linear Distance		Longitude and Latitude
	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic	Linear	Quadratic
GS–XC boundary (XC merger into GS):
β1′	−0.00002	−0.009	−0.002	0.003	0.002	0.006	0.005	0.006
	(0.994)	(0.001)	(0.368)	(0.219)	(0.428)	(0.005)	(0.007)	(0.005)
JG–XC boundary (JG merger into SC):
β1′	−0.011	−0.005	−0.006	−0.057	−0.047	−0.047	−0.095	−0.124
	(0.002)	(0.140)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)

Note: the numbers in parentheses represent the significance level p value.

.

For the housing price model at the boundary between the JG and XC districts, the results are robust under different bandwidths, different driving variables, and different orders. The estimated β₁′ remains significant at the 1% significance level, indicating that after JG was merged into the SC district, the housing price gap with the district (XC) with higher housing prices in the main city has narrowed. The policy’s weakening effect on the boundary effect is approximately 3.8% to 6.0%. However, for the merger of the XC and GS districts, the regression results of the 5 km bandwidth samples show that the β₁′ coefficient is not statistically significant in most cases. In the 3 km bandwidth samples, under different driving variables and polynomial orders, the estimated β₁′ is positive but close to zero, suggesting that the impact of the merger on the boundary effect is negligible.

The different policy effects may be due to the fact that, relatively speaking, the development gap between the JG and SC districts is large. After the merger, it is beneficial for the high-quality economic and social resources of SC district to flow to the relatively weaker JG district. In particular, JG district can share the radiation of high-quality educational resources from SC district, which is conducive to narrowing regional differences and guiding the real estate market towards a balanced development. However, the housing price difference at the original boundary between the XC and GS districts was not very stable, and thus the regional integration did not have a significant impact on the house price difference.

6. Conclusions

This paper measures the house price boundary effects between different urban areas within Hangzhou, China, using spatial discontinuity regression. Controlling for housing characteristics and location factors indicates that administrative boundaries lead to significant differences in house prices within the boundaries of suburb districts (XS and YH) and the main city. There is also a distinct housing price boundary effect between JG district, which is relatively backward within the main city, and XC district in the city center. The size of the boundary effect varies between administrative districts: the size of the boundary effect within a 2 km bandwidth is between 2.6% and 26.6%. The difference in the size of the boundary effect may be due to diverse economic factor resource levels and public service allocations, especially quality education between districts.

This study further analyzes the effects of regional integration and administrative division adjustment policies on the house price boundary effect by including the different SRD methods. The regional integration policy has a significant dampening effect on the house price boundary effect between XS and the main urban area. In contrast, the house price difference between YH and the main city has a dampening effect with a lag in time. Within the main urban area, after the relatively backward JG district is merged into the central district, it will be conducive to narrowing the housing price gap between it and other areas. This parallels the experience of Greater Paris, where housing prices in peripheral areas increased following the administrative reorganization in 2016 [42]. Promoting regional integration and real estate market integration takes time to achieve and requires the sharing of economic factors and equalizing public services. The administrative boundary effect of housing prices reflects the impact of differences in the quality of district development on housing prices. The level of economic development, population size and structure, and the availability of public facilities in districts are important fundamentals that affect regional housing supply and demand. This results in differences in housing prices between districts. The functional layout of the city and administrative system and other policy factors also play a pivotal role in influencing the housing price between districts. The link between cross-district housing price discontinuities and the economic development trajectories and policy frameworks of administrative districts merits deeper investigation in future studies.

Since the samples examined in this study are the residential prices within a limited range on both sides of the district boundaries, their location characteristics and some neighborhood characteristics are similar. The facilities such as medical care, commercial facilities, and subways nearby can all be shared across districts. Judging from the price gap revealed and the weakening of the gap brought about by the administrative division adjustment, the main reasons might be educational resources and the differences in urban interface images, as well as the district impressions caused by the long-term differences in district economic development levels. Because education is segmented among districts and there are significant disparities, previous studies have proved that it has a significant impact on housing prices. The improvement of road facilities and urban appearance, as well as the implementation of urban renewal, are financially supported by the district government. The deep impression of remote and previously underdeveloped areas will have a psychological anchoring effect on home buyers [43]. Achieving the balanced and healthy development of the real estate market requires coordinating regional economic development and improving the level of equalization of public services. Maintaining a degree of stability in regional development policies is also critical. Implementing a regional integration policy helps narrow the development quality gap between districts and helps shape the development of the regional real estate market in the direction of equalization. The optimal adjustment of urban planning layout and the equalization of transportation and quality education resources may effectively adjust the house prices in districts. This is of great significance in addressing the current problem of high house prices in China’s big cities.