Optimal Placement of Electric Vehicle Stations Using High-Granularity Human Flow Data

Abstract

Suboptimal placement of charging infrastructure is a major barrier to the transition to sustainable transportation, even with the growing popularity of electric vehicles (EVs). The research addresses this challenge by proposing a novel hybrid genetic algorithm (GA) to solve the NP-hard Multiple-Choice Multidimensional Knapsack Problem (MMKP) for computationally derived optimal charging station placement and configurations in Sapporo, Japan. The methodology leverages high-granularity human flow data to identify charging demand and a Traveling Salesperson Problem (TSP)-based encoding to prioritize potential station locations. A greedy heuristic then decodes this prioritization, selecting charger configurations that maximize service capacity within a defined budget. The results reveal that as the budget increases, the network evolves through distinct phases of concentrated deployment, expansion, and saturation, with a nonlinear increase in covered demand, indicating diminishing returns on investment. The findings demonstrate the efficacy of the proposed model in providing a strategic roadmap for urban planners and policymakers to make cost-effective decisions that maximize charging demand coverage and accelerate EV adoption.

1. Introduction

The pursuit of sustainable transportation has emerged as an essential focus for urban development, motivated by the urgency to mitigate environmental degradation and enhance energy efficiency, offering a viable approach to decreasing greenhouse gas emissions and air pollutants while also promoting greater accessibility and public health benefits [1,2,3,4,5]. Among the strategic initiatives advancing this agenda, electric vehicles (EVs) are particularly prominent for their potential to transform urban mobility and lessen dependence on fossil fuels [6,7]. However, a primary barrier to widespread EV adoption is the critical insufficiency of public charging infrastructure, often resulting from suboptimal placement and configuration that undermines user confidence and limits vehicle utility [8]. Strategic planning for charging infrastructure addresses not only technical challenges, including the impact on power grids and the optimal positioning of charging stations, but also significantly influences public trust and confidence in the practicality and usability of EVs [9,10,11].

The global proliferation of EVs has occurred rapidly, driven by policy incentives, technological innovations, and increasing environmental awareness. In Europe, projections indicate that EVs will dominate the passenger vehicle sector by 2031. Leading nations, such as Norway, Iceland, and China, are at the forefront of EV adoption, whereas countries like India are actively transitioning away from internal combustion engine (ICE) vehicles to achieve climate objectives [12,13,14,15]. Japan has actively enhanced its EV infrastructure since 2021 to promote widespread adoption, acknowledging the pivotal role of EVs in the transition toward a decarbonized society. The government has set an ambitious goal for zero-emission vehicles to account for all new passenger car sales by 2035.

Despite these strategic initiatives, the rate of EV adoption in Japan remains comparatively low on the global scale, with residential circumstances, such as residency in multi-dwelling units (MDUs), posing significant barriers to EV adoption [16]. Domestic companies have contributed to promoting EV adoption by establishing dependable public charging infrastructure and providing financial incentives, which support EV owners without access to private charging facilities and encourage customers to consider transitioning to EVs. The International Energy Agency [8] emphasizes that the expansion of public charging infrastructure is pivotal for facilitating the transition to EVs, particularly in urban areas with high population density, where there is a limitation in private parking options [17,18].

This research investigates the near-optimal placement and configuration of EV charging stations within urban settings, specifically focusing on Sapporo city. Sapporo is a particularly compelling case study due to its status as a major northern Japanese metropolitan area, facing unique challenges related to its urban density patterns that create complex, concentrated demand centers [19,20]. By integrating high-resolution spatial activity data with detailed facility information, this research formulates a mathematical model to strategically allocate chargers according to realistic demand patterns. The model incorporates travel behavior, facility proximity, and station service capacity limitations. This research proposes a novel hybrid genetic algorithm (GA) that models the station placement problem as a Multiple-Choice Multidimensional Knapsack Problem (MMKP) and employs a Traveling Salesperson Problem (TSP) encoding to determine the prioritization of station installations. In this model, each potential site can accommodate only one of the feasible charging station configurations, each varying in installation cost and service capacity. This approach effectively captures the practical trade-offs involved in site selection, charger type, and budget limitations. Given the NP-hard classification of the MMKP and TSP, and the complexity posed by dense urban environments, meaning that checking every possible combination of chargers and locations is computationally intractable for large instances, the GA is utilized to efficiently identify solutions that are nearly optimal. It provides a robust metaheuristic framework capable of managing the nonlinear relationships, diverse configuration options, and combinatorial decision processes inherent in charger deployment strategies.

The extensive objective of this research is to leverage high-granularity spatial activity data and a novel hybrid optimization framework to strategically determine the near-optimal placement and configuration of EV charging stations in a real-world urban setting, thereby providing a robust, data-driven planning strategy for policymakers. To achieve this objective and contribute to the existing literature, this study is structured around the following research questions:

• How can the location and configuration of EV charging stations be optimized under varying budget constraints to maximize realistic charging demand coverage in a dense urban environment?
• What is the functional relationship between the total investment budget and network spatial evolution, and where is the critical point of diminishing returns?
• What actionable, phased investment strategy can be derived from the optimization results to guide municipal infrastructure planning toward a cost-effective and sustainable network?

Despite the widespread emphasis on optimizing EV charging infrastructure, this research contributes to the literature by (i) developing a novel hybrid GA-TSPMMKP optimization framework that simultaneously solves the location, configuration, and demand assignment problem; (ii) utilizing high-granularity human flow data derived from mobile phone networks to capture realistic, dynamic urban mobility patterns, moving beyond static demand models; and (iii) applying the model to the context of Sapporo city to derive near-optimal solutions and practical, cost-effective policy recommendations.

The present approach offers valuable insights for developing sustainable transportation strategies in urban environments. The remainder of this paper is structured as follows: Section 2 reviews the relevant literature and justifies the methodological approach. Section 3 details the datasets, model construction, and proposed hybrid GA-TSPMMKP framework. Section 4 presents the optimization results and sensitivity analysis across all budget scenarios. Section 5 discusses the findings and policy implications, and Section 6 concludes this paper with a summary of limitations and future research directions.

2. Literature Review

2.1. The Strategic Challenge of EV Charging Infrastructure Planning

EV charging stations comprise key components, including charger type, installation cost, and spatial placement, all of which markedly impact user experience and operational efficiency [21]. The deployment of fast chargers is particularly essential in public or high-traffic locations to accommodate short-duration charging requirements [22]. The design of infrastructure must prioritize accessibility, reliability, and user compatibility to facilitate sustained adoption [23,24]. Strategic decisions regarding station locations are crucial, as they directly affect charger utilization rates and service coverage, highlighting the significance of effective spatial planning.

In the Japanese context, a recent survey by ENECHANGE Ltd. [25] identifies key concerns among users, centering on the insufficient development of charging infrastructure and the limited availability of public charging stations, even for EV users with home charging options. This challenge is particularly pronounced in urbanized areas like Japan due to limited spatial resources. Planning is complex because it requires determining mutually exclusive configurations for each location (e.g., a mix of fast and normal chargers) while managing space constraints and the need for charger variety. Similar findings are reported in the Netherlands by Wolbertus and Van Den Hoed [26], who demonstrate that fast chargers serve different user needs; specifically, they support quick, opportunistic charging and are not interchangeable with other charger types in infrastructure planning. These findings underscore that the strategic placement of EV charging stations is a fundamental challenge in location optimization, as it aims to achieve an effective balance among coverage, demand fulfillment, and financial considerations.

The issues surrounding accessibility and equity in the deployment of EV charging infrastructure have garnered increasing scholarly attention. Research by Du et al. [27] and Huang et al. [28] demonstrates that distributing public charging points strategically leads to an increased utilization rate among EV users. Çelik and Ok [29] demonstrate that minimizing walking distances through optimized location modeling can significantly improve user satisfaction and the overall efficacy of charging infrastructure. Within the framework of strategic facility placement in urban environments, Mateus et al. [30] explore various heuristic approaches inspired by smart city principles, ranging from random allocation strategies to pseudo-greedy algorithms that leverage real-time traffic flow data. Meanwhile, Singh et al. [31] utilize interpretive structural modeling to identify and prioritize the key determinants influencing location selection in semi-urban settings. These studies highlight the growing necessity for integrative, data-driven planning approaches that not only enhance operational efficiency but also advance broader objectives related to sustainability and social equity. Optimizing charging station placement is a vital strategic measure. By increasing accessibility and aligning with user needs, it directly increases station efficiency and fosters greater EV adoption.

2.2. Critical Review of Demand Models and the Role of Genetic Algorithms

The challenge of placing EV charging stations efficiently, while considering constraints such as budget limitations, spatial coverage, and demand density, has drawn parallels to classic facility location optimization problems. Existing studies often focus on different objectives, such as maximizing demand coverage [32,33] or minimizing installation and operational costs [34,35]. Studies have proposed different solutions to the challenge of locating EV charging stations, each employing distinct contexts and approaches. For instance, Padmanabhan et al. [36] apply Reinforcement Learning (RL) to identify optimal locations for a charging station in New York City. Alhussan et al. [37] utilize graylag goose optimization (GGO) to assign EV charging demand. Frade et al. [33] employ the Maximal Covering Location Problem (MCLP) framework to determine the necessary number and capacity of charging stations, as well as optimize demand coverage with an appropriate level of service in Lisbon, Portugal.

Building upon these diverse methodological efforts, attention has been shifted toward more established heuristic techniques, notably the GA, which offer proven effectiveness in solving complex, multi-variable optimization problems [38,39]. The GA, originally introduced by Holland [40], operates by iteratively evolving a population of solutions through processes such as selection, crossover, and mutation, facilitating a balance between exploration and exploitation within the solution space. Central to the GA is the fitness function, which determines how solutions are evaluated and selected. The processes of crossover and mutation significantly impact the search trajectory toward the optimal solution, although determining the exact appropriate rates remains challenging. However, the suitability of these rates can often be inferred from the population size [41]. This adaptability enables the GA to effectively address nonlinear, discrete, and multi-constraint optimization scenarios. A key strength of the GA lies in its adaptability and robustness when applied to complex real-world problems, making it a valuable tool in the field of optimization.

The GA was specifically selected for this optimization problem due to the nonlinear, multimodal nature of the search space and the presence of discrete decision variables. Unlike single-solution methods, such as Simulated Annealing (SAA), the GA’s population-based structure enhances global exploration and maintains diversity, reducing the risk of premature convergence. Compared with other population-based techniques like Particle Swarm Optimization (PSO), the GA offers greater flexibility for discrete and combinatorial optimization through its specialized operators (selection, crossover, and mutation). Numerous studies have employed the GA to optimize their charging station placements with various objectives [32,42,43,44,45]. These algorithms demonstrate the advantage of strategically deploying charging stations and optimizing charger configurations, particularly in urban EV scenarios where trade-offs among station quantity, charger types, and service coverage require the evaluation of hundreds of competing solutions. For instance, Dong et al. [46] not only optimize public chargers by simulating driver travel patterns and behavior but also demonstrate that the GA outperforms other optimization approaches in terms of accuracy and efficiency, operating under the premise that installing chargers in densely populated areas improves visibility and accessibility. Consequently, the GA is proficient in offering a promising framework for exploring large solution spaces efficiently, especially in situations where exact solutions are computationally infeasible or require excessive processing time.

2.3. The Novel GA-TSPMMKP Framework and Data Strategy

While the GA demonstrates considerable potential for EV infrastructure planning, its effectiveness is often further improved through hybridization with other heuristic methods to address problem-specific requirements, a practice noted by Bodenhofer [47] as leading to significant enhancements. For example, hybrid models, such as the GA combined with the Simulated Annealing method (GA-SAA) [48], GA with fuzzy logic (GA-FL) [49], and GA with Particle Swarm Optimization (GA-PSO) [50], have been proposed to address specific optimization challenges. Despite these advancements, certain hybrid GA approaches encounter limitations, particularly when incorporating specific logical rules and conditions essential for realistic planning scenarios. For instance, the placement of EV chargers requires selecting a single configuration from multiple options at each site while simultaneously satisfying various resource constraints. These complex requirements pose challenges for traditional GAs, often requiring computationally expensive techniques like specialized decoders or repair algorithms. These methods can struggle to apply diverse rule sets and tend to be effective only within narrowly defined problem contexts [51], limiting their suitability for complex infrastructure planning.

A notable advancement in related fields, particularly in combinatorial optimization, is the use of TSP-based encodings [52]. This approach, where the chromosome represents a permutation of nodes or items, has been successfully applied for testing optimization problems like the Multidimensional Knapsack Problem (MKP) and vehicle routing [53]. By representing a solution as a prioritized order of stations, the GA can efficiently explore a diverse range of location subsets. These observations indicate that the GA can be further enhanced by embedding more domain-specific knowledge and decision-making structures for more precise and contextually relevant evaluations of solutions. GA optimization problems related to EV charging infrastructure often center on maximizing key performance indicators, such as demand coverage, service accessibility, or overall system efficiency, while respecting strict budgetary and resource constraints. For instance, studies by Ameer et al. [54] and Huang and Kockelman [35] focus on maximizing the utilization and profitability of EV charging station placement. These studies highlight that the primary objective of such optimization efforts often centers on identifying the best combination of alternatives to achieve maximum benefit within limited resources.

When a problem involves multiple resource constraints (a multidimensional nature) and requires exclusive selections from a set of options (a multiple-choice aspect) at each potential site, such as determining the specific number and types of chargers to install, the resulting optimization problem adopts a more structured form, aligning with MMKP formulations. Typically, this involves mutually exclusive configuration choices for each distinct location, alongside the simultaneous consideration of overarching resource constraints, such as budget and available space. To effectively address these complex decision-making and resource allocation challenges, the integration of GA with the MMKP combinatorial optimization framework is proposed in this research. This hybrid approach capitalizes on the maximization objective inherent in the structure of the MMKP, facilitating efficient management of grouped decision variables and multiple resource constraints commonly encountered in the planning of EV charging stations. The MMKP is an NP-hard extension of the classic Knapsack Problem that is a highly relevant framework for resource-constrained decision-making [55,56]. The problem requires the selection of exactly one item from each group, where each item has a value and resource consumption, while ensuring that the total resource consumption remains within a set capacity. In this research, each candidate charging station is conceptualized as a distinct group of knapsacks, with each feasible charging configuration treated as an item within that group. The value of an item is represented as the charging demand expected to be fulfilled, and its resource requirements correspond to the associated costs. Since each charging station can be configured in various valid ways (e.g., different numbers of fast and normal chargers) and only one configuration can be selected per station, the problem naturally conforms to a multiple-choice Knapsack Problem framework. This MMKP structure is well-suited for the fitness evaluation of the GA, especially in scenarios involving EV charging station infrastructure and configuration types under spatial and budget constraints.

The principal innovation of this research lies in its novel hybrid GA-TSPMMKP framework. While the GA is widely employed to address MMKPs [56,57,58], the methodology proposed here introduces a unique implementation for EV optimization by combining a TSP-based chromosome encoding with an MMKP-based fitness evaluation. The TSP encoding separates the search for an optimal station sequence from the decoding process. A chromosome in the proposed GA represents a prioritized list of potential charging stations, similar to the tour in the TSP. This allows the GA to efficiently explore a wide range of location subsets by evolving the order of this priority list. The MMKP structure is then embedded within the GA’s fitness evaluation process as a structured decision-making model. This integration effectively manages the complex planning tasks involved in selecting optimal charger configurations across multiple dimensions and exclusive choices. Unlike previous hybrid GA-based approaches (e.g., GA-SAA, GA-FL) that primarily enhanced performance through modified search operators, our contribution lies in reformulating the problem itself. Additionally, this explicit decoupling of station prioritization by TSP-based chromosome encoding from configuration selection via MMKP evaluation distinguishes our approach from earlier hybrid models. This two-stage approach allows the GA to simultaneously optimize broader placement strategies while accurately considering detailed configuration decisions. This integration enhances computational efficiency, ensures solution stability, and provides a more comprehensive interpretation of the near-optimal charger deployment than traditional optimization models.

The efficacy of any optimization model, particularly in the context of complex urban infrastructure planning, fundamentally relies on the quality and detail of the input data. While numerous existing studies incorporate various data sources for demand estimation and spatial context, the innovation in data utilization of this research is also a significant contribution through its integration of high-resolution human mobility data and comprehensive Zenrin geospatial data. For mobility insights, this research utilizes GEOTRA Activity Data (GAD), a GPS-based dataset derived from anonymized smartphone location records that track individual movement trajectories, transportation modes, stopping points, and trip purposes, providing a more precise and dynamic representation of potential charging demand than traditional static or coarse population density data [59,60]. Concurrently, comprehensive Zenrin geospatial data, renowned for its highly detailed mapping of urban environments in Japan, provides point-based representations of buildings and properties with granular classifications and spatial attributes [61,62]. This enables the precise identification of locations for public and commercial facilities, road networks, and critical points of interest, which is especially important for detailed spatial planning and constraint modeling in densely populated urban areas such as Japan. These integrated datasets, which serve as the foundation for defining the feasible search area, provide essential spatial context and support the development of the proposed GA-TSPMMKP model. This rich input data enables the model to produce a highly accurate, demand-driven, and spatially optimized solution for EV charging station placement and configuration that accurately reflects the complexity of the urban environment in Sapporo.

3. Materials and Methods

This section details the construction of the EV charging optimization framework, including the necessary datasets, parameter settings, and mathematical model. We first introduce the high-granularity human mobility data and facility information used to define realistic demand and candidate locations. We then formalize the placement challenge using the MMKP formulation, followed by a detailed explanation of the novel hybrid GA that integrates a TSP-based encoding to efficiently derive near-optimal solutions.

3.1. Datasets

This research employs two main spatial datasets to support its analysis. The first dataset focuses on human mobility activity, capturing individual trip behaviors within the research area. The second dataset comprises data on various facilities, detailing multiple points of interest throughout the research area. By integrating these datasets, this research provides comprehensive input for the GA-TSPMMKP model to facilitate the evaluation of charging demand coverage and the identification of near-optimal locations for establishing EV charging infrastructure.

3.1.1. Human Mobility Activity Data

Human mobility patterns are analyzed using the GEOTRA Activity Data (GAD) as the primary source for identifying locations of charging demand. This high-granularity human flow data is a proprietary dataset developed by GEOTRA Co., Ltd. (Tokyo, Japan), which utilized its proprietary data processing and aggregation system to collect and process GPS location information from a large, anonymous sample of smartphone users in Japan. The data was acquired on weekdays in November 2022. The data was acquired with user permission and provides a dynamic, high-frequency record of travel. The dataset is compiled through a multi-stage process. First, raw GPS data is aggregated onto a fine-grained mesh with a minimum unit of 125 m to map detailed travel routes. The system defines “places to stay” as locations where a person remains for more than 15 min, with the movements between these points categorized as “trips.” Second, using synthetic data generation technology, the dataset estimates various travel attributes, such as transportation mode (e.g., car, train) and trip purpose (e.g., commuting, shopping). For privacy protection, data for teenagers and younger people is excluded. The resulting data reflects the average movements on weekdays and holidays during the acquisition period, enabling a comprehensive analysis of traffic flows [60,63]. In this research, this dataset is filtered to include only trips made by private car users, representing a realistic cluster of potential EV users. The analysis focuses specifically on trips with the longest activity duration outside the home activity, as this represents the most likely time for users to charge their EV at public charging stations. To ensure the analysis accurately reflects practical charging scenarios, trips with activity durations shorter than 30 min are excluded, as such brief periods are considered insufficient for practical charging opportunities.

3.1.2. Facility Data

Facility data is derived from the comprehensive Zenrin geospatial database [64], which offers detailed spatial information regarding various locations. The classification of all facilities from the dataset is shown in Appendix A. To determine the suitable sites for EV charging stations, potential locations are primarily selected from facilities classified within public sectors, including business and commercial facilities, such as commercial buildings, shopping centers, government premises, or parking lots, given their accessibility and appropriateness for public utilization. Residential facilities are considered private spaces and are consequently excluded from the planning considerations for public charging infrastructure in this research.

3.2. Proposed Model Construction

3.2.1. Assumptions of the Problem and Parameter Settings

The parameters associated with the EV charging infrastructure within the proposed model are established based on hypothetical, yet plausible assumptions tailored to the context of typical deployment conditions observed in urban areas of Japan. The model considers two categories of charger configurations, defined as fast chargers and normal chargers, each associated with distinct service capacities and cost implications. The station’s service capacity is determined by estimating the daily operational throughput of a charger, which defines its maximum serving capacity per day. This estimation is obtained through a simulation of a single charger’s daily operation, which is divided into 30 min intervals over a 24 h period, resulting in 48 time slots. The simulation for precompute capacities processes the charging demand sequentially from a sorted list by arrival time, using the pre-existing data on the number of occupied slots for each demand to determine the required charging duration under 30 min intervals. Charging durations are assumed to be between one and three hours (2–6 slots) for fast chargers, and between three and six hours (7–12 slots) for normal chargers. For trips with a stay exceeding six hours, the charging duration is capped at six hours. The simulation, using these parameters, estimates the daily service capacity for each charger type at 15 vehicles per day for fast chargers and 4 vehicles per day for normal chargers. These values represent the maximum number of vehicles that a single charger of the specified type can service within a day, assuming demand aligns with the charger’s operational availability. Such estimates serve as upper bounds for service capacity and are incorporated into the model’s charger capacity constraints during the time-based demand-driven assignment process. Each potential candidate for the charging station is assumed to support a limited number of chargers, with a maximum of two fast chargers and four normal charger units per site. Additionally, a no-installation configuration is included for each candidate station, representing the option of not installing any chargers at that location. This configuration has zero installation cost and zero service capacity, allowing the algorithm to optimally exclude stations if deemed non-beneficial under budget constraints.

Installation costs are approximated using figures from industry reports and official sources. The cost per unit is set at JPY 2 million for a normal charger and JPY 10 million for a fast charger. According to CEO Insight Asia, the cost of installing and operating fast charging stations in Japan can be as high as JPY 10 million due to the strict safety regulations required for handling high-voltage currents [65]. Similarly, the Next-Generation Vehicle Promotion Center [66] reports that the average cost for a normal 6 kW charger is approximately JPY 2 million, which includes JPY 700,000 for the unit itself and JPY 1.3 million for associated construction costs. They also note that the cost of installing a quick charger varies widely, with unit costs ranging from JPY 830,000 to JPY 5 million and construction costs from JPY 1 million to JPY 7 million, for a total of JPY 1.83 million to JPY 12 million. The optimization process is conducted across five budget scenarios (JPY 10 billion, JPY 50 billion, JPY 100 billion, JPY 150 billion, and JPY 200 billion) to assess how varying financial resources influence deployment outcomes and the overall charging demand coverage within the research area.

Table 1. Hypothetical parameters for the charging infrastructure.

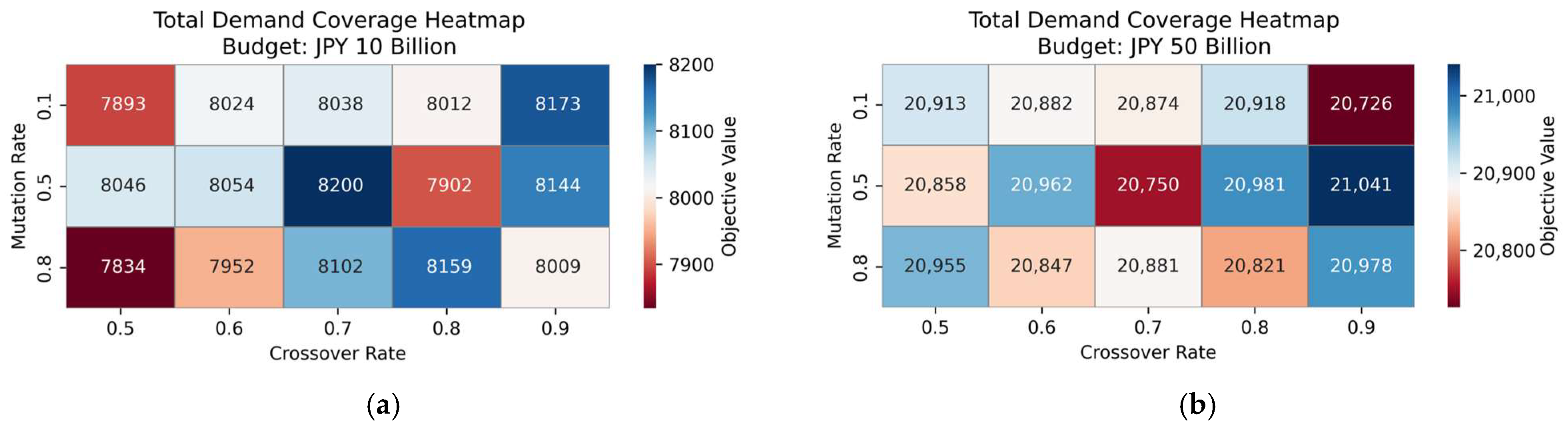
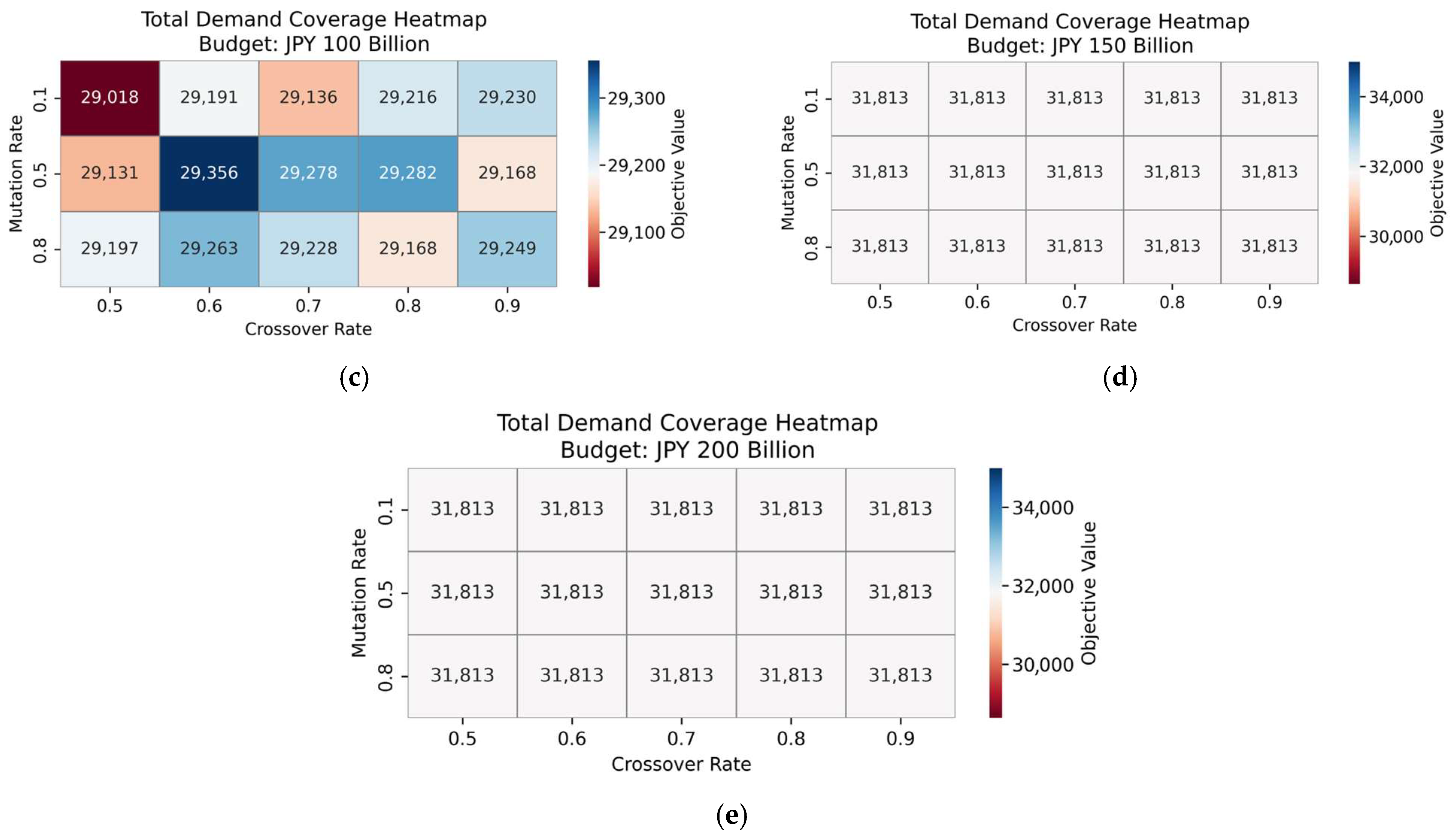
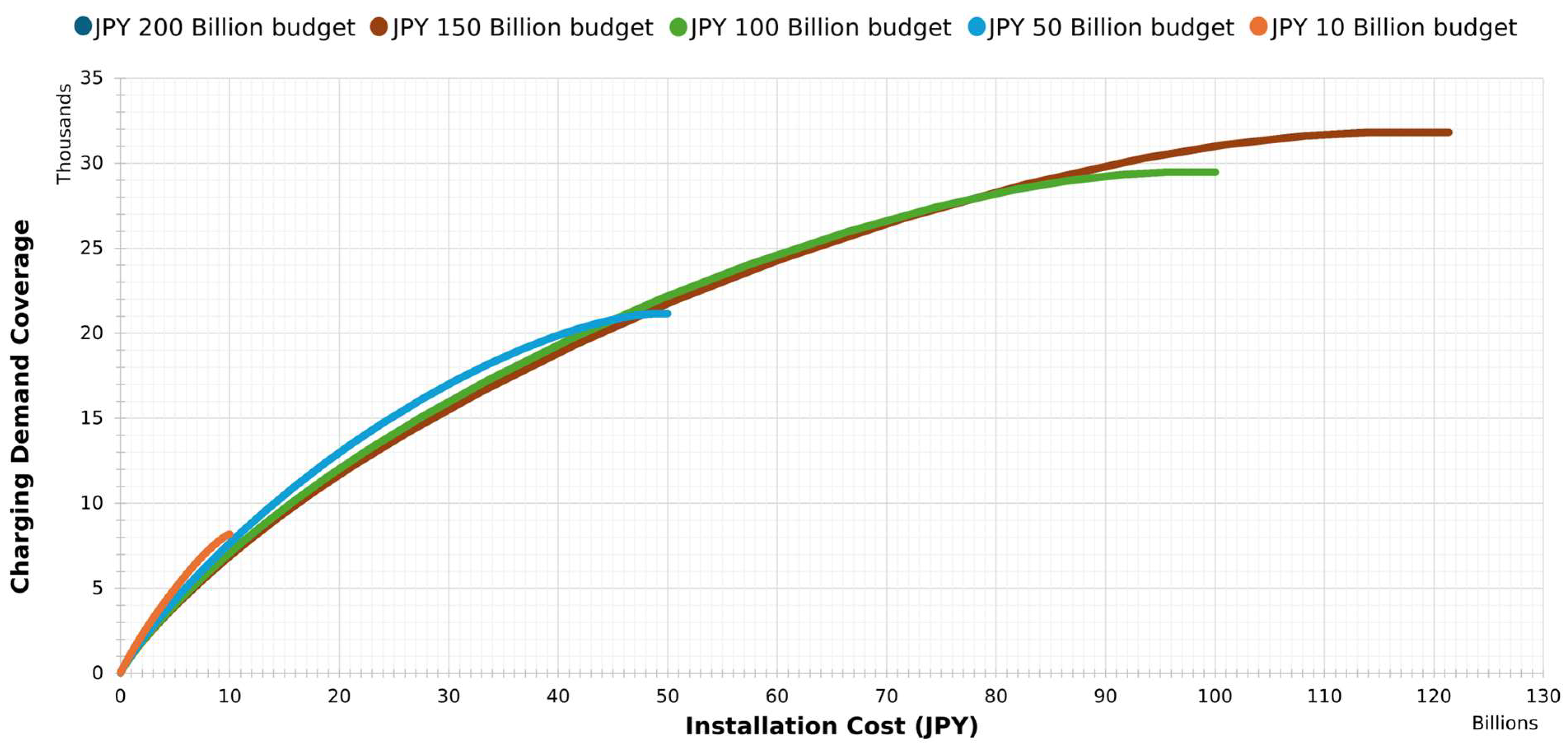
Parameter	Fast	Normal	Unit
Maximum chargers per station	2	4	Charger units
Charging duration occupation	2–6	7–12	30 min interval slots
Station service capacity per unit	15	4	Vehicles per day
Installation cost per unit	10	2	JPY Million
Total available budget	10/50/100/150/200		JPY Billion

provides a summary of all parameters incorporated into the optimization model.

3.2.2. Optimization Model and Objective Function

The optimization problem addressed in this research is to determine the computationally derived optimal placement and configuration of charging stations to maximize demand coverage under budget constraints. This complex task is mathematically formulated as an MMKP, which is known to be NP-hard. This problem is solved using a hybrid genetic algorithm that combines a TSP approach for station prioritization with a greedy decoding logic for charger configuration. This section outlines the mathematical model and the objective function, defining the core components that guide our optimization efforts.

Let $I$ denote the set of candidate facility locations, $J$ the set of demand points, and $K$ the set of charger configurations available for each station (e.g., combination of fast and normal chargers). The decision variable $x_{ik}$ is a binary variable representing the selection of configuration $k$ for location $i$, the coverage variable $y_{ij}$ indicates whether demand point $j$ is assigned to location $i$, and the activation variable $z_i$ indicates whether a station is established at location $i$. The model is subject to several constraints that ensure feasibility and reflect operational limitations and real-world planning considerations.

Table 2. Description of notations.

Variable	Description
Sets and indices
$i\in I$	Set of candidate station locations
$j\in J$	Set of demand points
$k\in K$	Set of charger configurations
Parameters
$d_j$	Charging demands for demand point $j$
$S_k$	Service capacity of a charger configuration $k$
$C_k$	Installation cost of a charger configuration $k$
$B$	Total available budget for station installation
Decision variables
$x_{ik}\in \{0, 1\}$	1 if charger configuration $k$ is selected for station $i$, 0 otherwise
$y_{ij}\in \{0, 1\}$	1 if demand point $j$ is assigned to station $i$, 0 otherwise
$z_i\in \{0, 1\}$	1 if charger configuration is installed at station $i$, 0 otherwise
Objective value
$D$	Total charging demands covered by selected stations

summarizes the notations for the mathematical model.

The objective is to maximize the total charging demand covered by selected stations:

$$maxD={\sum }_{i\in I}{\sum }_{j\in J}{d}_j·y_{ij}$$

(1)

subjective to the following:

• Charger assignment constraint: Station $i$ is activated only if a configuration is installed:

  $$\sum _{k\in K}{x}_{ik}=z_i, \forall j\in J$$

  (2)
• Service capacity constraint: The total charging demand assigned to station $i$ must not exceed its total service capacity:

  $$\sum _{j\in J}{d}_j·y_{ij}\le \sum _{k\in K}{S}_k·x_{ik}, \forall i\in I$$

  (3)
• Budget constraint: The total installation cost across all stations must not exceed the available budget $B$:

  $$\sum _{i\in I}\sum _{k\in K}{C}_k·x_{ik}\le B$$

  (4)
• Demand assignment constraint: A demand point can only be assigned to a station if that station is activated:

  $$y_{ij}\le z_i, \forall i\in i, j\in J$$

  (5)
• Unique demand coverage constraint: Each demand point can be assigned to at most one station:

  $$\sum _{i\in I}{y}_{ij}\le 1, \forall j\in J$$

  (6)

3.2.3. Genetic Algorithm with TSPMMKP-Based Charging Station Placement

The proposed MMKP-based maximization optimization problem is solved using a hybrid GA to manage the complexities of selecting charging station locations and configuring charger types under resource constraints. The objective is to determine the near-optimal set of candidate locations for charging station installation such that total charging demand coverage is maximized while overall installation costs remain within the available budget. The GA adopts a hybrid approach, using a TSP-based encoding to guide the search for a near-optimal sequence of station locations and a greedy decoding logic for charger configuration. This integration leverages the evolutionary power of the GA to find a near-optimal prioritization of stations, which is then translated into a feasible, budget-constrained solution. Finally, the actual demand assignment and charging demand coverage are evaluated for the final solution from the GA loop, using the detailed time-based demand assignment simulation to ensure compliance with real-world constraints, such as geographic proximity and time-dependent station-level service capacity.

• Chromosome Representation and Population Initialization.

The genetic algorithm’s efficiency depends on a well-defined chromosome structure that can effectively encode a potential solution. In the proposed GA-TSPMMKP model, a TSP-based encoding is utilized as a core concept for the population initialization process, where each chromosome represents a prioritized permutation of all potential candidate station locations. This approach ensures that every potential solution includes a unique ordering of all candidate stations. The length of each chromosome is the total number of candidate stations (4334 in this research). The chromosome is represented as a sequence of genes, where the position of a gene in the permutation determines its priority for the station installation. Each gene’s value is the unique identifier of a candidate station location, allowing the GA to explore a vast solution space by evolving the installation priority of all potential stations.

2.

Decoding and Feasibility.

A separate decoding process is used to transform the prioritized chromosome into a feasible solution. The relationship between the TSP-based encoding and this greedy decoding method serves to efficiently solve the problem by decoupling strategic prioritization from practical selection. The decoder iterates through the prioritized list of stations from the chromosome, greedily selecting a valid charger configuration for each station based on predefined integer indices (as shown in

Table 3. List of indices for charger configurations.

Index	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Fast	0	0	0	0	0	1	1	1	1	1	2	2	2	2	2
Normal	0	1	2	3	4	0	1	2	3	4	0	1	2	3	4

) until the total budget is fully consumed. Table 3 shows a separate set of integer indices representing the predefined charger configurations corresponding to a specific combination of fast and normal chargers $\left(x_{ik}:x_{i,fast},x_{i,normal} \right)$ with their upper bound based on station installation constraints. This approach ensures that every evaluated solution is both valid and a cost-effective representation of the chromosome’s potential. The process prioritizes configurations with a higher value that fit the remaining budget. A tie-breaker rule is utilized to choose the one with the lower cost if the values are equal. This systematic approach ensures that a valid and budget-compliant solution is consistently achieved.

3.

Fitness Evaluation.

The fitness evaluation of each chromosome is a dual-tiered process designed to ensure both the quality and feasibility of a solution. This process first assesses whether a solution respects the given budget constraint, and then, if feasible, calculates the solution’s quality based on its objective function. The first tier of the evaluation, which occurs within the GA’s main evolutionary loop, calculates the preliminary proxy fitness score for every chromosome. This proxy score is an estimate of a solution’s quality based on the total service capacity of the stations selected by the greedy decoder. The decoder iterates through the prioritized list of stations in the chromosome, greedily selecting a valid charger configuration for each station. This process terminates when the cumulative budget is met, effectively cutting off the remaining lower-priority stations. The proxy fitness value for each chromosome is the total service capacity achieved by the stations selected up to that cut-off point. This preliminary score is used for parent selection to guide the GA toward promising regions of the solution space. The second tier is for the final, best solution identified by the GA after it has converged. At this stage, a final real fitness score is computed by performing a detailed time-based demand assignment, which is a more accurate measure of the total served demand based on the actual availability of chargers at specific times. This final calculation provides the definitive performance metrics for the best solution, including the total served demand and the exact budget used.

4.

Genetic Operators.

Parent selection is performed using tournament selection on the population of TSP-based chromosomes, a method that chooses parent chromosomes based on a natural competition process. This selection process is repeated until the number of selected parents is equivalent to the population size, effectively balancing the exploration of the new solutions with the exploitation of high-quality individuals while maintaining population diversity. Following the selection process, a specialized crossover operator for permutations, such as Partially Matched Crossover (PMX), is employed to recombine genetic material from two parent chromosomes, resulting in two new offspring, to maintain the integrity of unique station indices. SwapMutation is subsequently applied to introduce random variations into the population. The mutation operator randomly swaps the positions of two station indices within the chromosome, guided by a mutation probability, facilitating the discovery of new combinations that may not be generated through crossover alone and ensuring the search continues exploration of the broader solution space. The tuning strategy for balancing the crossover and mutation probabilities significantly impacts the algorithm’s ability to find better local optimal solutions [41]. Therefore, the process involves experiments with dynamic operator probabilities to perform sensitivity analysis.

5.

Evolutionary Cycle and Termination.

Each complete iteration of the genetic operations, including selection, crossover, mutation, and decoding, constitutes a single generation. Within each generation, the fitness of the newly formed population is evaluated to determine the quality of the offspring, after which the population is updated through replacement. This iterative cycle progressively evolves the population toward solutions that optimize spatial coverage of charging demand while satisfying cost constraints. The algorithm terminates when a convergence criterion is met, which is defined as the absence of significant improvements in the best fitness score over a specified patience parameter within a maximum number of generations.

6.

Final Decoding and Assessment.

Following the identification of the best-performing solutions by the GA, the configuration and the number of chargers at each station are extracted from the final best TSP-based chromosome. Subsequently, a detailed time-based assignment of charging demand points to the selected stations is performed. This step is essential for accurate assessment, as it considers both the spatial proximity measured by the Haversine distance and the dynamic, time-dependent service capacity of each station. The charging demand points are processed chronologically according to their arrival time and assigned to the nearest selected station within the service radius with an available charging slot of the required charger type. This particular process ensures the final validated results for charging demand coverage and installation cost. The procedural flow and framework of the proposed algorithm are visualized in Figure 1 and summarized in Appendix B.

4. Results

To validate the performance of the proposed GA-TSPMMKP model, experiments are conducted under five distinct budget scenarios: JPY 10 billion, JPY 50 billion, JPY 100 billion, JPY 150 billion, and JPY 200 billion. The optimization model is used to identify configurations of EV charger installations across 4334 candidate charging stations in Chuo-ku, Sapporo, with the objective of maximizing demand coverage from 96,427 spatial demand points derived from high-granularity human flow of urban mobility in Sapporo. Each candidate station could be equipped with a combination of up to two fast chargers and four normal chargers, with unit costs set at JPY 10 million and JPY 2 million, respectively. The GA is structured with a population size of 500 individuals and evolved over a maximum of 1000 generations, incorporating a patience mechanism set at 100 generations to prevent premature convergence and ensure thorough exploration of the solution space. Two independent runs were executed for each parameter combination and budget scenario to account for the stochastic nature of the GA, resulting in identical findings. The evaluation focuses on key output metrics, including total demand coverage, the number of selected stations, the total chargers installed, and budget utilization.

4.1. Travel Demand Distribution in Chuo-Ku, Sapporo

The analysis of high-resolution human mobility data, obtained from the GEOTRA GPS-based smartphone dataset, reveals the temporal and spatial characteristics of potential EV charging demand within Sapporo. The spatial distribution of travel demand within the central district, Chuo-ku, is examined to provide context for the optimization model. The figures illustrate how charging demand density varies throughout the day. Figure 2 depicts the spatial distribution of travel demand hotspots during typical morning and evening commute periods. The morning period of 6–7 a.m. (Figure 2a) demonstrates a concentration of travel demand spread throughout the Sapporo area, primarily originating from residential zones as individuals begin their daily activities. The evening period of 5–6 p.m. (Figure 2b) shows a high density of travel demand concentrated in Chuo-ku, the central business district that is the location of numerous commercial and business facilities. This concentration highlights a significant charging opportunity as users conclude their work or leisure activities. The insights from this analysis of temporal travel demand shifts, from residential areas in the morning to the central business district in the evening, highlight the necessity for a strategically placed network that can adapt to the dynamic mobility patterns of the urban population. Consequently, Chuo-ku is selected as the research area to ensure the model can effectively address the significant spatial and temporal variability in charging demand.

4.2. Model Validity and Sensitivity Analysis

A comprehensive sensitivity analysis is performed on multiple combinations of two core evolutionary operators, i.e., crossover probability and mutation probability, to validate the robustness and behavior of the GA search process and explore its responsiveness to parameter changes. The parameters systematically varied are the crossover probability (0.5 to 0.9 in increments of 0.1) and the mutation probability (0.01, 0.1, and 0.5). This analysis is conducted for all budget scenarios, evaluating how these parameter choices influence the final GA performance in terms of best fitness score (i.e., demand coverage), solution feasibility, and convergence behavior. The model successfully identified feasible solutions across all five budgetary scenarios, a crucial validation of its adaptability to varying financial constraints. The heatmaps in Figure 3 collectively demonstrate the GA-TSPMMKP model’s adaptability, visually representing the best total demand coverage achieved for different combinations of crossover and mutation probability under each budget scenario. The optimal parameter settings for the GA are shown to be context-dependent, shifting based on the budget and the complexity of the solution space.

For the JPY 10 billion budget, the highest demand coverage of 8181 was attained with a mutation rate of 0.5 and a crossover rate of 0.5. This result suggests that within this stringent budget, a higher mutation rate might be necessary to escape local optima and find the most valuable initial station placements. For the JPY 50 billion budget, the maximum demand coverage of 21,156 was achieved with a mutation rate of 0.1 and a crossover rate of 0.6. The shift to a lower mutation rate from the previous scenario suggests that as the budget and complexity increase, the GA benefits from more focused exploitation of promising solution regions. For the JPY100 billion budget, the optimal solution with the best performance of 29,456 was attained with a mutation rate of 0.1 and a crossover rate of 0.5. Across both the medium and high budgets, the consistently high performance with a mutation rate of 0.1 reinforces its effectiveness in balancing solution diversity and refinement as the solution space becomes more complex. For the JPY 150 billion and JPY 200 billion budgets, the results reveal a critical finding that the model reached a point of saturation. As shown in the respective heatmaps, the maximum served demand is identical at 31,813 for both budgets, regardless of the crossover or mutation rate combination. This indicates that at JPY 121.352 billion, the model allocates chargers to all 4334 candidate stations, and the demand coverage cannot be further increased with the current set of potential locations. This analysis confirms the robustness of the model and its ability to converge on high-quality solutions across diverse financial and operational constraints while also identifying the point of diminishing returns.

Beyond the individual parameter sensitivity shown in the heatmaps, the overall effectiveness of the GA-TSPMMKP model across varying budget constraints is critically demonstrated by the cumulative demand coverage curves presented in Figure 4. This figure graphically illustrates the trade-off between cumulative installation cost and the achieved charging demand coverage. The X-axis represents the cumulative installation costs (in billions of Japanese yen), while the Y-axis shows the total charging demand served (in thousands of charging demand counts), providing a visual representation of the efficiency curve for each budget scenario.

The curve for the JPY 10 billion budget, represented by the orange line, shows a rapid initial increase in demand coverage with relatively low investment. This indicates that the most cost-effective stations with the highest demand are prioritized first. The curve rapidly reaches its maximum coverage of approximately 8 thousand charging demands as the budget threshold is met. This scenario proposes that, within tighter budget constraints, the model prioritizes high-impact installations but faces limitations in expanding charging demand coverage due to cost limitations. The JPY 50 billion budget scenario, shown by the blue line, demonstrates a higher overall demand coverage capability. The curve shows a similar initial steep ascent, but it continues to capture more charging demand for a longer duration of cumulative cost. It covers approximately 21 thousand charging demands, reaching its budget limit. The JPY 100 billion budget, represented by the green line, achieves over 29 thousand charging demand coverage. And the curves for the JPY 150 billion and JPY 200 billion budgets, the purple and gray lines, respectively, reveal a critical insight. They follow a similar trajectory to the lower budget curves but begin to flatten out significantly around the JPY 120 billion mark, reaching a final coverage of over 31 thousand charging demands. The overlap of these two curves confirms the saturation point identified in the previous section. The findings from the cumulative cost by budget scenarios identify the upper limit of feasible investment. It shows that beyond a certain investment level with the given set of candidate charging station locations, the model has exhausted all available opportunities to serve additional charging demands.

4.3. Optimization Results and Scenario Interpretation

The optimization outcomes across the five budget scenarios demonstrate the effectiveness of the GA-TSPMMKP approach in identifying substantial demand coverage.

Table 4. Summary of GA-TSPMMKP optimization results by budget scenario.

Budget (JPY Billion)	Served Demand	Demand Coverage	Station Selected	Chargers Installation (Fast/Normal)	Budget Used (JPY Billion)
10	8181	8.48%	358	2144 (714/1430)	10.000
50	21,156	21.94%	1787	10,714 (3571/7145)	50.000
100	29,456	30.55%	3572	21,428 (7143/14,285)	100.000
150	31,813	32.99%	4334	26,004 (8668/17,336)	121.352
200	31,813	32.99%	4334	26,004 (8668/17,336)	121.352

presents a summary of the best-performing solutions, achieved with their highest charging demand coverage across all budget scenarios. The results indicate the GA-TSPMMKP model is capable of effectively deploying resources to maximize demand coverage up to the available budget limit.

A key finding of this analysis is the emergence of a saturation point as the budget increases. As the budget increases from JPY 10 billion to JPY 100 billion, there is a clear and proportional increase in demand coverage, demonstrating the model’s ability to efficiently scale the infrastructure deployment. However, the results for the JPY 150 billion and JPY 200 billion scenarios reveal a critical insight that the model achieved identical demand coverage and charger installations, despite the significant difference in the allocated budget. In both cases, the model fully utilized all 4334 candidate stations, reaching the highest served demand of 31,813, with a coverage of 32.99%. The cost of this saturation point was JPY 121.352 billion, with a remaining budget unused, indicating that the maximum possible coverage for the current set of candidate locations is achieved at this cost, and any additional budget does not yield any additional demand coverage, as all feasible installation opportunities have been exploited. This pattern across budgets reveals that higher investment significantly increases the charging demand coverage, but it also highlights a clear saturation point. While even the lowest budget yields a feasible solution, it demonstrates that a minimum threshold of investment is required to achieve meaningful demand coverage. Furthermore, the underutilization of the budget in the JPY 150 billion and JPY 200 billion scenarios confirms that the model does not simply spend money but makes a strategic, objective-driven decision to stop installing chargers when no additional demand can be met. The model’s optimization strategy consistently prioritizes a balanced network to serve both short-stay (fast chargers) and longer-stay charging (normal chargers), aligning with the observed bimodal demand distribution. The ability to find robust solutions across all budget levels, including a clear saturation point, validates the model’s adaptability and operational feasibility for city-scale EV infrastructure planning in urban settings, as in the case of Sapporo.

4.4. Spatial Distribution of EV Charging Stations and Charging Demand Coverage

The strategic placement of electric vehicle charging stations and the corresponding demand served are critical outcomes of the proposed GA-TSPMMKP model. The spatial distribution of the selected charging stations provides a visual representation of the model’s performance and its placement strategy under varying budget constraints. The results are presented as a series of geospatial maps for four budget scenarios of JPY 10 billion, JPY 50 billion, JPY 100 billion, and JPY 150 billion. The scenario with a budget of JPY 200 billion is not shown, as its results are identical to the JPY 150 billion scenario, indicating a point of diminishing returns.

In the low-budget scenario of JPY 10 billion, the model prioritizes placing stations in areas with the highest demand density. As shown in Figure 5a, the stations are clustered in central, high-activity areas of the city. This strategy ensures that limited resources are allocated to maximize the initial served demand, focusing on a few key locations that serve the greatest number of trips. The size of the markers, which is proportional to served demand, confirms that these stations are strategically positioned to handle high traffic volumes. As the budget increases to JPY 50 billion, the model expands its coverage to encompass a wider geographic area. Figure 5b shows that while the core cluster in the city center remains a priority, new stations are additionally selected to serve charging demands in adjacent neighborhoods. At the JPY 100 billion budget level, the network of charging stations achieves significant spatial saturation. Figure 5c shows a further densification of charging stations, filling in gaps within and around the established urban areas. Stations are placed not only in high-demand zones but also at strategic intermediate points, suggesting an emphasis on creating a comprehensive network that supports both short and long trips within the urban area. The increased number of stations leads to greater redundancy and resilience in the network. This saturation point indicates that additional investment yields smaller gains in served demand, a trend that is consistent with the diminishing returns observed in the cumulative cost–demand curve. At a higher budget level, the marginal increase in demand served begins to decrease relative to the cost, signaling the approach of a saturation point where most of the high-value demand has been addressed. Finally, at the JPY 150 billion budget level, the model’s final and most extensive configuration is established. As seen in Figure 5d, the network covers the widest spatial area. The new additional stations are often located in lower-density, peripheral zones. While this configuration maximizes total demand coverage, the increase in demand served per additional station is minimal, highlighting a clear point of diminishing returns. This final map represents a comprehensive, but cost-intensive, infrastructure solution that extends charging access to nearly all feasible demand locations, ensuring that a high percentage of trips can be served with minimal detour.

5. Discussion and Conclusions

This research presents a novel and comprehensive framework for the computationally derived optimal placement and configuration of EV charging stations by integrating high-granularity human flow data with a hybrid GA-TSPMMKP optimization model. By leveraging real-world travel data derived from mobile phone networks, our model moves beyond traditional, simplified demand estimations to capture realistic and dynamic urban mobility patterns. The results demonstrate the model’s effectiveness in strategically allocating resources under varying budget constraints to maximize the charging demand satisfaction, providing a robust, near-optimal solution for a complex facility location problem.

A key finding is the progressive relationship between the investment budget and the spatial evolution of the charging network, which can be categorized into three distinct phases. The model’s initial strategy, as observed in the JPY 10 billion scenario, focuses on concentrated deployment within a few high-demand urban centers to maximize early returns on investment. As the budget increases to JPY 50 billion, the network enters an expansion phase, strategically branching out from the core to serve a wider, more dispersed geographic area. The increase in investment budget from JPY 10 to 50 billion results in a substantial addition of approximately 13 thousand in covered charging demand, representing a high return on investment. Finally, in the JPY 100 billion and JPY 150 billion scenarios, the network achieves spatial saturation, filling in gaps and extending into lower-density peripheral zones. Increasing from JPY 100 billion to JPY 121 billion (the saturation point) yielded only approximately 2300 additional charging demand coverage. Furthermore, increasing the investment to JPY 150 and 200 billion yielded zero marginal return on investment. This final phase clearly illustrates the diminishing returns and the transition from the expansion phase to the saturation phase. The identification of these distinct investment phases, containing concentration, expansion, and saturation, provides a robust, structured approach and a strong theoretical foundation for incremental policy intervention in electric vehicle (EV) infrastructure. Moving the discussion beyond simple cost–benefit ratios, this phased strategy aligns with established public investment theory, which emphasizes the critical importance of investment efficiency over mere scale. This theory suggests that the marginal benefits of public capital are known to diminish or cease once a certain threshold is crossed [67,68]. Consequently, this finding not only defines clear strategic milestones for policy intervention but also supports contemporary arguments for an actionable, sequenced, and cost-effective resource allocation strategy in modern infrastructure development [69].

To provide a strategic roadmap for municipalities, our results suggest a phased approach to investment. For cities with nascent EV infrastructure, the initial investment should focus on the concentration phase of up to JPY 50 billion, as in the context of our model, prioritizing the top 5 to 10% of high-demand hotspots for the most cost-effective coverage. Once this core network is established, the policy could be shifted to a broader expansion phase (e.g., JPY 50 to 100 billion), where investments can be decentralized to cover more of the city’s secondary demand centers. The finding provides critical, data-driven insights for urban planners to identify a near-optimal budget that effectively balances cost-effectiveness with the goal of extensive coverage. The strength of our approach lies in its ability to simultaneously solve multiple facets of the EV infrastructure problem, including location, charger configuration, and demand assignment, within a single framework while using real-world data to anchor its decisions. This integrated methodology offers a significant improvement over traditional single-objective models and provides a more realistic and actionable best-performing solution for cities planning their EV transition.

6. Limitations and Future Work

This research presents a robust spatial optimization framework for EV charging infrastructure planning using a GA-TSPMMKP formulation, offering valuable insights into demand-responsive and cost-efficient deployment strategies. While the model successfully captures key spatial characteristics of charging demand and infrastructure allocation under budgetary constraints, several aspects present opportunities for future enhancement.

The model’s current limitations relate primarily to technical assumptions and the simplification of real-world charging dynamics. First, the model employs generalized assumptions for charger specifications and installation parameters, which, although suitable for an exploratory analysis, do not yet account for specific technical features, such as state of charge (SOC), battery capacity variations, or real-world charger performance profiles. Furthermore, the demand management simulation relies on simplified assumptions regarding charging times, neglecting the varying power output of chargers available on the market and complex actual user behavior, such as frequent short charging times. Incorporating such details in future versions could improve the precision of demand–supply matching, especially in operational planning stages. This research focuses on spatial demand coverage derived from activity–travel behavior, which offers a strong foundation for long-term infrastructure planning. However, the model currently relies on static demand distributions and simplified time allocation. It does not yet incorporate dynamic temporal factors, such as hourly demand variation, peak hour usage patterns, or queuing behavior at stations, all of which can significantly impact the operational utility and efficiency of the infrastructure in practice.

Several limitations concerning the data, scope, and objective function must also be acknowledged. The GEOTRA data lacks a clear assessment of its representativeness or any potential sampling biases, meaning the results are constrained by the underlying data sample. Furthermore, the parameters adopted (e.g., installation costs, service capacity) are hypothetical, and a detailed sensitivity analysis of these assumed values is necessary to ensure the robustness of the derived near-optimal solutions. This research is limited to a single district of Chuo-ku, Sapporo, meaning the specific best-performing infrastructure configuration is limited by the area’s unique spatial characteristics, though the strategic phases identified are generalized to other urban areas. Methodologically, the model is single-objective, neglecting a crucial multi-criteria analysis (MCA) that would consider the impact on the electricity grid, the need for spatial equity (e.g., covering low-income areas), and minimizing total user costs (e.g., travel time). Additionally, the obtained results were not compared with other optimization methods or contexts in this research due to the area’s unique spatial characteristics, prioritizing the in-depth, context-specific application.

Future work will focus on addressing these limitations. Expanding the model to capture these temporal dimensions and user charging behaviors would enhance its applicability in real-time or demand-shifting scenarios. The integration of pricing strategies, user preferences, and behavioral responses to station availability or travel detours also represents a promising direction, aligning the model with emerging research in user-centric and market-driven EV infrastructure planning. Future work will also explore the integration of parking-based activity data to identify more realistic and policy-relevant candidate station locations. We will also conduct a quantitative performance comparison to assess the actual computational advantages of the proposed GA-TSPMMKP framework against established metaheuristics, specifically using the metrics of convergence speed, solution quality (demand covered), and stability across various budget scenarios. Of these future directions, the most critical next step for improving the model’s realism is the integration of real-time grid load data. This will ensure that the near-optimal locations are not only accessible and high-demand areas for drivers but are also electrically feasible, preventing the creation of infrastructure that could destabilize the power distribution network during peak charging times and thereby strengthening the cost-effectiveness and practicality of the final solution. These refinements would collectively allow the framework to support more granular, flexible, and responsive planning strategies for cities aiming to develop sustainable and equitable EV charging networks.