A Dynamic Model of Profit Maximization for Carsharing Services: Astana, Republic of Kazakhstan

Abstract

This study considers building a dynamic model of profit maximization for a carsharing system and its verification based on the case of implementing such a system in Astana, Republic of Kazakhstan. The region, bounded by the administrative boundaries of Astana, was divided into subregions that covered the region with regular hexagons placed side by side. A dataset was built with information on 1168 trips to Astana from January to March 2023. The Kepler visualization service constructed maps of the beginning and end of the trips to the region and a map of trips binding to the hexagonal grid cells. Each cell of the grid corresponds to a specific subregion, for which the quantitative parameters necessary for solving the profit maximization problem in the carsharing system are calculated. Stations with cars are placed in the cells of the grid, which are available to carsharing service customers. Based on the collected data, dynamic (four periods per day) and static profit maximization models in the carsharing system were built. Modeling was carried out based on the built models in the case of Astana. It was established that using a dynamic profit maximization model in the carsharing system increases profit by 3.7%. The obtained results are important for the development of the infrastructure of the capital of Kazakhstan and for finding a solution to the problems of urban science in this region.

1. Introduction

The global sharing market has been growing dynamically, especially in the last decade. In 2019, it was valued at nearly $400 billion. Moreover, in 2024, according to some estimates, the global market value of the sharing economy may reach more than 1.5 trillion dollars. The annual growth rate is higher than 30% [1]. According to some estimates, the sharing market will add 160 to 572 million euros to the economy of the European Union in the next few years [2]. Some analytical calculations regarding the growth of the sharing market are described in [3]. The changes associated with the rapid development of the sharing market are a crucial aspect of the evolution and transformation of transport systems. The authors of [4] investigated how the sharing market potentially leads to reduced emissions, congestion, etc. This has a positive effect on the development of cities, which leads to an increase in the quality of life of the residents of these cities.

One of the essential components of the sharing market is carsharing. The basis of the carsharing system is a client’s short-term use of a car for a fixed fee. A client can travel by car without being tied to the movement of public transport for sufficiently long distances. An essential advantage of using the carsharing service is that clients pay only for the time using the car and do not pay for its maintenance, insurance, parking, etc. The cost of using carsharing is generally lower compared to using taxi services. In addition to carsharing, micro-sharing systems are being considered. However, such systems are designed for different sectors of customers and have their own characteristics, which are not considered in this work.

In order to make a profit, the owner of the carsharing system must calculate the total cost of car maintenance, transporting cars to different parts of the city, etc. That is, many components of the system must be calculated, which determine the price policy of the owner and the system of restrictions for the user. The task of managing a carsharing system is complex. The influence of various factors can quickly lead to an imbalance of the system, potentially leading to unprofitability. Management should occur in real-time and in different regions of the city network in different ways. When building a carsharing system, several problems arise at the same time. The first of them is the division of regions into subregions according to specific criteria, which would simplify the management of system parameters. Next, one needs to calculate the characteristics that determine the balance of the system and ensure their dynamic calculation. The second task is to build a model for maximizing the profits of the carsharing system, taking into account the specified characteristics and distribution into subregions.

The obtained results in this direction are essential for solving urban network planning problems within urban science. This especially applies to the development of carsharing and micro-sharing services, which aims to increase the sustainability of a city’s development given rapid population growth and improve a city’s ecological situation. The metro area population of Astana in 2022 was 1,254,000. Astana has an annual population growth of 3.5% to 4%. This characterizes the city as one whose population is overgrowing. Accordingly, applying urban science approaches in the implementation of carsharing services will help make the city more ecologically clean and more comfortable for living.

The study aimed to build a dynamic optimization model for maximizing the profit of carsharing services. For this, one must solve two problems:

-

Building the optimal division of the region into subregions following the features of the location of the city infrastructure and the needs of system users;

-

Defining and adjusting the parameters that will be integrated into each subregion’s dynamic profit maximization model.

2. Literature Review

Building an effective carsharing system and organizing an excellent carsharing service is an urgent task for both the user and the owner. From the owner’s point of view, such a system can be profitable, given the dynamics of market development in this direction in recent years. Also, the potential profitability of the system is determined by the peculiarities of the region in which it is implemented and the client’s needs from the carsharing service. From the customer’s point of view, such a system is an excellent alternative to personal transport, taxi services, and public transport. The functioning of the carsharing system within a specific region has a positive effect on reducing traffic jams, reducing air pollution, increasing revenues to the regional budget, etc. [5]. This obviously has a positive effect on improving the comfort of the region’s residents.

Building an optimization model of profit maximization for carsharing services must be completed and requires a separate study. The creation of such a model is closely related to the requests of the system’s owner. Therefore, parameters that affect the owner’s profit should be reflected in the model, considering regional characteristics, demand, and customer needs. Also, the maximization model depends on the type of carsharing, which exerts influence and profitability of the system in different regional and geographical conditions. In particular, [6] describes the system of carsharing using electric cars. This study found that such a system still needs to be fixed since electric cars need a long time to charge. This leads to a decrease in the profitability of such a system over time compared to a traditional carsharing system. The paper [7] describes a model of electric carsharing and micro-mobility, as well as the potential impacts of these types of carsharing. However, the problem of maximizing the profitability of such systems needs to be described. The positive impact on the development of city infrastructure and the improvement of the quality of life of city residents is determined by the effective functioning of such a carsharing system, which is beneficial to the system’s owner. Otherwise, there is no point in investing in developing this type of service.

For the effective functioning of the carsharing system, operational decisions must be made constantly. Some of them require solving relevant optimization problems. In particular, Ref. [4] describes a profit maximization model of a carsharing system and a mathematical programming method for finding its solution. In this model, cars do not move without the participation of customers. In [8], a simulation model for evaluating options for such movements was developed. However, the specified model is static and does not consider the change in demand for cars in different parts of the region and times of day. This is important for a rational calculation of the potential profit of the system, taking into account the built-in restrictions. The paper [9] describes a mixed integer programming model for establishing the sequence of actions for moving cars in a carsharing system. In works [10,11], systems for optimizing the movement of vehicles are considered.

Work [12] describes the problem of maximizing the profit of the carsharing system, which considers car maintenance costs. Integer programming was used to solve the problem. The problem of linear programming for maximizing the profits of the carsharing system is described in [13]. An overview of scientific studies on modeling and optimization for the carsharing system is described in [14], where the authors classify the literature into three categories: strategic, tactical, and operational, according to the level of decisions made in optimization tasks. Optimization models and solution methods proposed in existing studies are considered for each category. In particular, in the category of studies on state strategic planning, [15,16,17] are critical publications that aim to maximize profits. Other works discuss the category of making operational decisions on managing the carsharing system to optimize profits [18,19,20]. The problem of profit maximization related to the relocation of cars is described in works [21,22,23]. Related problems must also be solved, such as user verification [24,25,26] and the problem of managing a complex transport system [27].

Study [28] carried out a systematic review of the literature in the field of vehicle sharing, in particular carsharing. A meta-analysis of studies showed that dynamic carsharing services reduce travel costs and demand for parking and improve the ecology of the city. The development of carsharing and micro-sharing services contributes to the urban development of cities. The development of carsharing systems can contribute to sustainability as well as social and transport justice. The authors of study [28] advocate for the consolidation of urban transport policy to achieve the desired results for solving the problems of urban mobility. The study also shows that the field of urban mobility is not sufficiently studied.

Study [29] shows that the carsharing market is not sufficiently developed in the Republic of Kazakhstan. Since the country’s population is growing fast, the implementation of such systems will make the quality of living in large cities and towns of this country more comfortable and convenient.

In [30], it is shown that optimal planning of the location of the infrastructure of charging stations and the distribution of the car fleet and the operation of moving vehicles in a city contribute to increasing profits. The importance of taking into account the uncertain time-varying demand in the input parameters of the profit maximization model is also shown. This significantly increases the efficiency of carsharing systems by 5.3%. Study [30] was conducted on the case of New York City. A similar study is necessary for other large cities with dense transport infrastructure. However, unlike the New York City, data on other cities (for example, Astana) are missing or access is restricted. This complicates research in this direction. There are few studies that take into account the dynamics in the functioning models of carsharing systems. This study is a development in the direction of urban science in terms of filling the gap in the use of dynamic models for maximizing the profit of carsharing systems, in particular in the Central Asian region. This study considers building a profit maximization model for a carsharing service for the capital of the Republic of Kazakhstan, Astana. Regional aspects and needs of customers in this region have determined the need to develop this type of service. Moreover, it is about the development of carsharing services. Micro-services in this region may be less popular due to the significant distances that city residents travel daily, which is related to the vastness of the city and the peculiarity of the location of urban infrastructure facilities.

3. Methods and Data

3.1. Basic Concepts

Ensuring the effective functioning of a carsharing system depends on many internal and external factors, including geographical features of the region, economic parameters, restrictions, and the conditions under which the system is implemented. The theory of sets was used to formalize the parameters that can influence the maximization of profits of the carsharing system. The hexagonal tessellation method was used to cover the area of the region. The theory of discrete optimization was used to create a profit maximization model. This study continues the authors’ previous study published in paper [5].

This study built a profit maximization model of the carsharing system for Astana, Republic of Kazakhstan. There is no accessible information about trips within the city of Astana. A separate task in the study was the collection of data on trips within the city of Astana at different times of the day. This was necessary to implement a dynamic model of profit maximization of the carsharing system. Obtaining results based on this model is important for the development in the direction of urban science, in particular for cities that are growing rapidly.

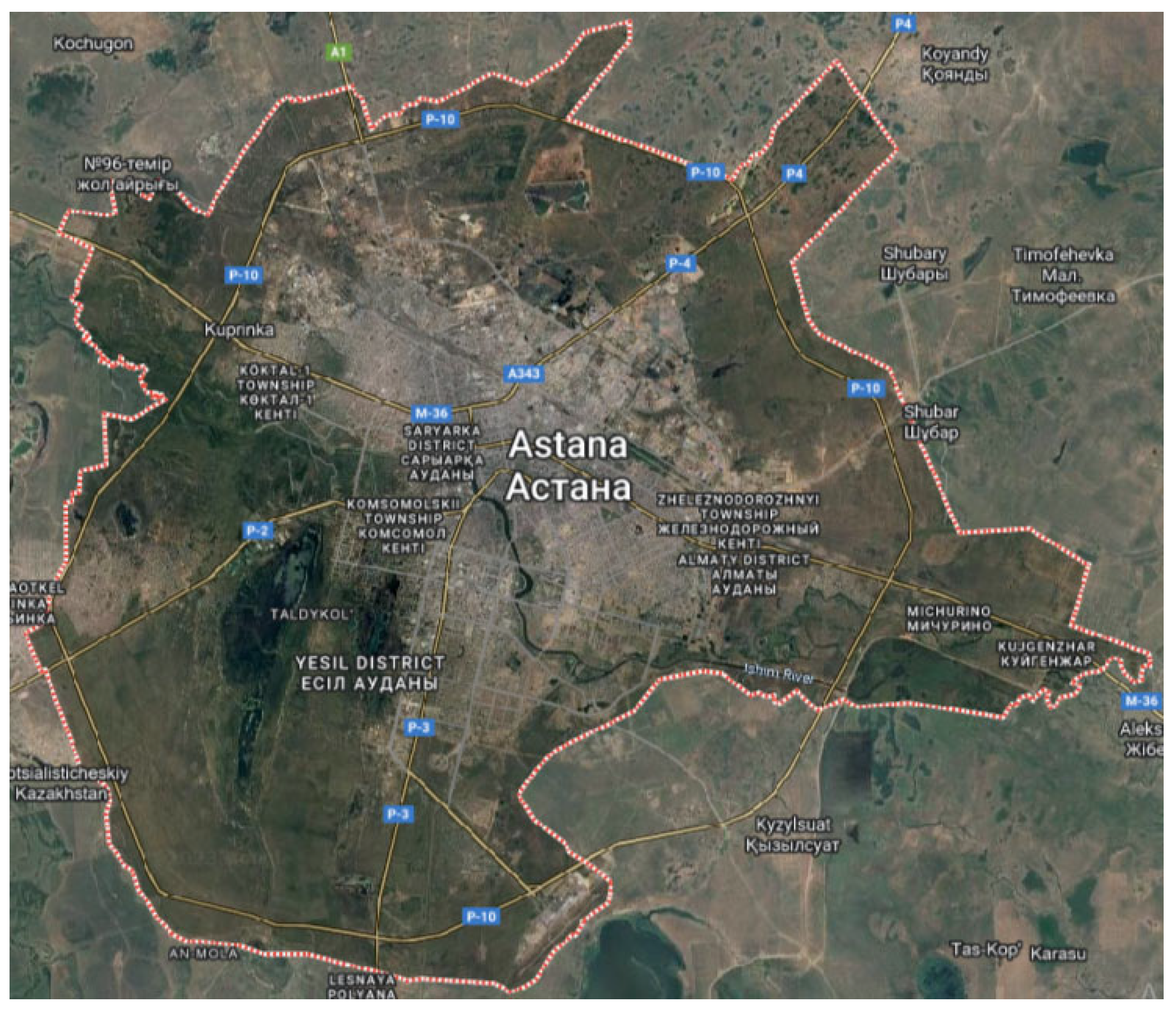
3.2. The Method of Selecting Subregions Using Hexagonal Tessellation

The first task for building a dynamic model of profit maximization of carsharing services is to build an optimal division of the region into subregions following the features of the location of city infrastructure and the needs of system users. Also, this task is related to presenting and storing geo-informational data.

Methods of presenting and storing geo-informational data were investigated in [5]. This is necessary for selecting subregions in the region where the carsharing system is implemented. For each subregion, it is common to calculate the parameters, highlight the restrictions, and place the stations. This has a qualitative effect on the support of operational decisions on the management of this system. It was established that a rational way of presenting data is to cover the region with a grid. Moreover, the properties of the objects will be stored in the grid cell that covers them.

An urgent task was to choose a method of covering the region with a grid. A simple method is administrative, where streets, district boundaries, geographic objects, etc., determine cell boundaries. This method accurately reflects the data of the region, but its disadvantage is the complex shapes of the cell boundaries. Keeping the region’s boundary broken requires significant amounts of data, and the variety of cell boundaries significantly complicates the processing of algorithms. Methods of tessellation with uniform grids allow for solving this problem. The basis of tessellation methods is covering the region with a grid, each cell of which has the shape of a regular n-sided polygon, particularly a triangle, square, or hexagon [31].

The frameworks H3 from Uber [32] and S2 from Google [33] were analyzed to cover the region with geometric shapes of different areas. As a result of the comparison, it was established that both frameworks could be used to cover any region and provide an opportunity to choose a grid scale within vast limits. A significant difference between the H3 and S2 frameworks is the shape of the grid. The main advantage of covering the area with a hexagonal grid is that the distance between the centers of neighboring cells is constant. This property significantly simplifies algorithms for finding the shortest paths between cells. First, one needs to specify the region’s borders to cover the map with hexagons using the H3 framework. The data on the boundaries of the regions provided by the GADM service [34] were used. The Kepler service [35] was used to visualize the coverage.

3.3. Mathematical Model of the Profitability of the Carsharing System

Let us consider the parameters that must be determined for the effective functioning of the carsharing system. Since the carsharing system functions cyclically, that is, every day in the system, depending on the type of system, cars may be relocated to those areas that are in demand by users at the appropriate time. Let T be the number of periods into which one iteration of the cycle of the carsharing system is divided. We will assume that after the completion of the iteration, the system returns to the initial state. The system’s initial state can be determined by relocating a certain number of cars to certain areas. As the demand for carsharing services in these areas changes, the system’s initial state changes in a new cycle. We assume that one cycle iteration is divided evenly into T periods $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$, $\mathrm{i}=\overline{0,\mathrm{T}-1}$, that is, we determine the state of the carsharing system at moments in time $〈{\mathrm{t}}_0,{\mathrm{t}}_1,\dots ,{\mathrm{t}}_{\mathrm{T}}〉$.

Let the carsharing system be implemented in region R. Let us divide region R into subregions $\left({\mathrm{r}}_0,{\mathrm{r}}_2,\dots ,{\mathrm{r}}_{\mathrm{n}-1}\right)$. The distribution can be performed using the hexagonal tessellation method. For each subregion ${\mathrm{r}}_{\mathrm{j}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$ for the corresponding period $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$, $\mathrm{i}=\overline{0,\mathrm{T}-1}$, and we calculate the following parameters:

-

${\mathrm{K}}_{\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the number of occupied cars in subregion ${\mathrm{r}}_{\mathrm{j}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$;

-

${\mathrm{k}}_{\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the number of free cars in subregion ${\mathrm{r}}_{\mathrm{j}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$;

-

${\mathrm{C}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the number of cars that traveled from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$, $\mathrm{q}=\overline{0,\mathrm{n}-1}$, $\mathrm{j}\ne \mathrm{q}$;

-

${\mathrm{p}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the probability of a car trip from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$, $\mathrm{q}=\overline{0,\mathrm{n}-1}$, $\mathrm{j}\ne \mathrm{q}$;

-

${\mathrm{g}}_{\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the maintenance costs (repair, washing, etc.) of cars in subregion ${\mathrm{r}}_{\mathrm{j}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$;

-

${\mathrm{P}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the cost of a car trip from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$, $\mathrm{q}=\overline{0,\mathrm{n}-1}$, $\mathrm{j}\ne \mathrm{q}$;

-

${\mathrm{L}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the expenses for a car trip from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$, $\mathrm{q}=\overline{0,\mathrm{n}-1}$, $\mathrm{j}\ne \mathrm{q}$.

The cost of a car trip from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$ for the relevant period $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$, $\mathrm{i}=\overline{0,\mathrm{T}-1}$, can be calculated using the following formula:

$${\mathrm{P}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)=\mathrm{\tau }\left({\mathrm{t}}_{\mathrm{i}+1}\right)\cdot {\mathrm{u}}_{\mathrm{j}\mathrm{q}},$$

where ${\mathrm{u}}_{\mathrm{j}\mathrm{q}}$ is the length of the route when traveling from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$, and $\mathrm{\tau }\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the fare to travel to the neighboring subregion for the relevant period $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$, $\mathrm{i}=\overline{0,\mathrm{T}-1}$. When using the hexagonal tessellation method, the adjacent subregion is defined by a hexagon whose side is directly adjacent to the hexagon that defines the current subregion.

Expenses for a car trip from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$ for the relevant period $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$, $\mathrm{i}=\overline{0,\mathrm{T}-1}$, can be calculated using the following formula:

$${\mathrm{L}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)=\mathrm{\beta }\cdot {\mathrm{C}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)\cdot {\mathrm{u}}_{\mathrm{j}\mathrm{q}},$$

where $\mathrm{\beta }$ is the coefficient that considers the fuel cost for travel to the neighboring subregion.

After calculating the system of parameters, it is possible to determine the objective function that will determine the maximization of the carsharing system implemented in the specified region:

$${\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{q}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{T}-1}{\mathrm{P}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}}}-{\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{q}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{T}-1}{\mathrm{L}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}}}-{\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{T}-1}{\mathrm{g}}_{\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}}\to \max ,$$

(1)

where ${\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{q}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{T}-1}{\mathrm{P}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}}}$ is the income received from all trips from each subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$ for the complete cycle of the carsharing system, i.e., for the period $\left({\mathrm{t}}_0,{\mathrm{t}}_{\mathrm{T}-1}\right)$; ${\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{q}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{T}-1}{\mathrm{L}}_{\mathrm{j}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}}}$ is the total costs of all trips from each subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$ for the complete cycle of the carsharing system, i.e., for the period $\left({\mathrm{t}}_0,{\mathrm{t}}_{\mathrm{T}-1}\right)$; and ${\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{T}-1}{\mathrm{g}}_{\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}}$ is the car maintenance costs in each subregion ${\mathrm{r}}_{\mathrm{j}}$ for the complete cycle of the carsharing system, i.e., for the period $\left({\mathrm{t}}_0,{\mathrm{t}}_{\mathrm{T}-1}\right)$.

The task is to find the optimal distribution of cars in all subregions at the initial moment. Such distribution can be determined based on statistical data on customers’ trips in these subregions at specific points in time. For example, one can cover a region with hexagons, and for each hexagon corresponding to the corresponding subregion, determine the number of taxi orders in the morning period. Next, one can distribute the cars available in the carsharing system proportionally across these subregions. That is, at the initial moment, the distribution of cars takes place according to the following formulas:

$${\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\mathrm{k}}_{\mathrm{j}}\left({\mathrm{t}}_0\right)}=\mathrm{\gamma },$$

(2)

$${\displaystyle \sum _{\mathrm{j}=0}^{\mathrm{n}-1}{\mathrm{k}}_{\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}\le \mathrm{\gamma },\mathrm{i}=\overline{0,\mathrm{T}-1},$$

(3)

where $\mathrm{\gamma }$ is the total number of cars that are available, ${\mathrm{k}}_{\mathrm{j}}\left({\mathrm{t}}_0\right)$ is the number of free cars at the initial time point in subregion ${\mathrm{r}}_{\mathrm{j}}$, $\mathrm{j}=\overline{0,\mathrm{n}-1}$, ${\mathrm{k}}_{\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the number of free cars at the initial time point in subregion ${\mathrm{r}}_{\mathrm{j}}$, and $\mathrm{j}=\overline{0,\mathrm{n}-1}$ for the period $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$.

At the following points in time, the distribution of cars will be determined according to the formulas that determine the restrictions on the use of free cars in the subregions. In particular, the number of cars that customers use for trips from a subregion ${\mathrm{r}}_{\mathrm{j}}$ to other subregions cannot exceed the number of free cars in this subregion:

$${\displaystyle \sum _{\mathrm{q}=0}^{\mathrm{n}-1}{\mathrm{C}}_{\mathrm{s}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}={\mathrm{k}}_{\mathrm{s}}\left({\mathrm{t}}_{\mathrm{i}}\right)+{\displaystyle \sum _{\mathrm{q}=0}^{\mathrm{n}-1}{\mathrm{C}}_{\mathrm{q}\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}}\right)}-{\displaystyle \sum _{\mathrm{q}=0}^{\mathrm{n}-1}{\mathrm{C}}_{\mathrm{s}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}}\right)},\mathrm{i}=\overline{0,\mathrm{T}-1},\mathrm{s}=\overline{0,\mathrm{n}-1},$$

(4)

$${\mathrm{C}}_{\mathrm{q}\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}}\right)=0,\mathrm{q}=\overline{0,\mathrm{n}-1},\mathrm{j}=\overline{0,\mathrm{n}-1},$$

(5)

where ${\mathrm{C}}_{\mathrm{q}\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}}\right)=0$ is the condition that determines that at the initial moment, cars do not make trips; ${\mathrm{k}}_{\mathrm{s}}\left({\mathrm{t}}_{\mathrm{i}}\right)$ is the number of free cars in subregion ${\mathrm{r}}_{\mathrm{s}}$ for the period $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$, $\mathrm{i}=\overline{0,\mathrm{T}-1}$,$\mathrm{s}=\overline{0,\mathrm{n}-1}$; ${\mathrm{C}}_{\mathrm{s}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)$ is the number of cars that left subregion ${\mathrm{r}}_{\mathrm{s}}$ for subregion ${\mathrm{r}}_{\mathrm{q}}$ during the period $\left({\mathrm{t}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}+1}\right)$; ${\mathrm{C}}_{\mathrm{q}\mathrm{j}}\left({\mathrm{t}}_{\mathrm{i}}\right)$ is the number of cars that left subregion ${\mathrm{r}}_{\mathrm{q}}$ for subregion ${\mathrm{r}}_{\mathrm{j}}$ during the period $\left({\mathrm{t}}_{\mathrm{i}-1},{\mathrm{t}}_{\mathrm{i}}\right)$; and ${\mathrm{C}}_{\mathrm{s}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}}\right)$ is the number of cars that left subregion ${\mathrm{r}}_{\mathrm{s}}$ for subregion ${\mathrm{r}}_{\mathrm{q}}$ during the period $\left({\mathrm{t}}_{\mathrm{i}-1},{\mathrm{t}}_{\mathrm{i}}\right)$.

The relationship between the a priori probability of a car trip from subregion ${\mathrm{r}}_{\mathrm{s}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$ and the number of free cars in subregion ${\mathrm{r}}_{\mathrm{s}}$ is defined by the function

$${\mathrm{C}}_{\mathrm{s}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)=\mathrm{f}\left({\mathrm{p}}_{\mathrm{s}\mathrm{q}}\left({\mathrm{t}}_{\mathrm{i}+1}\right),{\mathrm{k}}_{\mathrm{s}}\left({\mathrm{t}}_{\mathrm{i}}\right)\right).$$

(6)

Analytically, such a function is difficult to describe, so it is common to use simulation modeling to find it. The trips of each free vehicle from each subregion over period $\left({\mathrm{t}}_{\mathrm{i}-2},{\mathrm{t}}_{\mathrm{i}-1}\right)$ were simulated. We generated ${\mathrm{k}}_{\mathrm{s}}\left({\mathrm{t}}_{\mathrm{i}}\right)$ times a pseudorandom number from the interval $\left[0,1\right)$. If the number fell into the interval $\left[0,{\mathrm{p}}_{\mathrm{s}1}\left({\mathrm{t}}_{\mathrm{i}+1}\right)\right)$, then we simulated a car trip to subregion ${\mathrm{r}}_1$; if the number fell into the interval $\left[{\mathrm{p}}_{\mathrm{s}1}\left({\mathrm{t}}_{\mathrm{i}+1}\right),{\mathrm{p}}_{\mathrm{s}1}\left({\mathrm{t}}_{\mathrm{i}+1}\right)+{\mathrm{p}}_{\mathrm{s}2}\left({\mathrm{t}}_{\mathrm{i}+1}\right)\right)$, then we simulated a car trip to subregion ${\mathrm{r}}_2$, etc.; if the number fell into the interval $\left[{\displaystyle \sum _{\mathrm{u}=1}^{\mathrm{q}-1}{\mathrm{p}}_{\mathrm{s}\mathrm{u}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)},{\displaystyle \sum _{\mathrm{u}=1}^{\mathrm{q}}{\mathrm{p}}_{\mathrm{s}\mathrm{u}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)}\right)$, then we simulated a car trip to subregion ${\mathrm{r}}_{\mathrm{q}}$, etc.; and if the number fell into the interval $\left[{\displaystyle \sum _{\mathrm{u}=1}^{\mathrm{n}-1}{\mathrm{p}}_{\mathrm{s}\mathrm{u}}\left({\mathrm{t}}_{\mathrm{i}+1}\right)},1\right)$, then we simulated a car trip to subregion ${\mathrm{r}}_{\mathrm{n}}$. After carrying out the simulation modeling procedure, we obtained the integer linear programming problems (1)–(5). To find a solution to these problems, one can use the CPLEX application [36].

4. Results

4.1. Collection of Data

Carsharing systems were developed in the EU, the USA, Canada, and Japan. At the same time, there is a sufficient amount of data to analyze and improve these systems considering the changes that are taking place. This research was focused on building a model of profit maximization in the region of Astana, for which there needs to be more information on passenger transportation in free access. Therefore, data collection was a separate task.

As part of the project on which this study was based, cars were purchased with the appropriate equipment for recording the number of trips, the transportation route of passengers, and other necessary parameters. These cars were used on a test basis to transport passengers in Astana in the mode of a taxi service from 30 January 2023 to 11 March 2023. Data were collected on 1168 trips within the administrative boundaries of Astana. Towns that are satellites of the city of Astana were considered. For each trip, several parameters were fixed:

-

The time and coordinates of the start of the trip;

-

The time and coordinates of the end of the trip;

-

The cost of the trip;

-

The number of passengers.

This mode of transportation allows one to obtain essential indicators since transportation is not fixed by specific routes, as in public transport. Passengers with average wealth also use this mode of transportation. This category of city residents is considered in the carsharing system for which the model was built in this study. The obtained results make it possible to identify the subregions of the city in which the most calls for cars were made, the subregions of the city where the transportation service users moved the most, and at what time of day. Other recorded parameters are essential for building a dynamic model of profit maximization of the carsharing system considering regional characteristics.

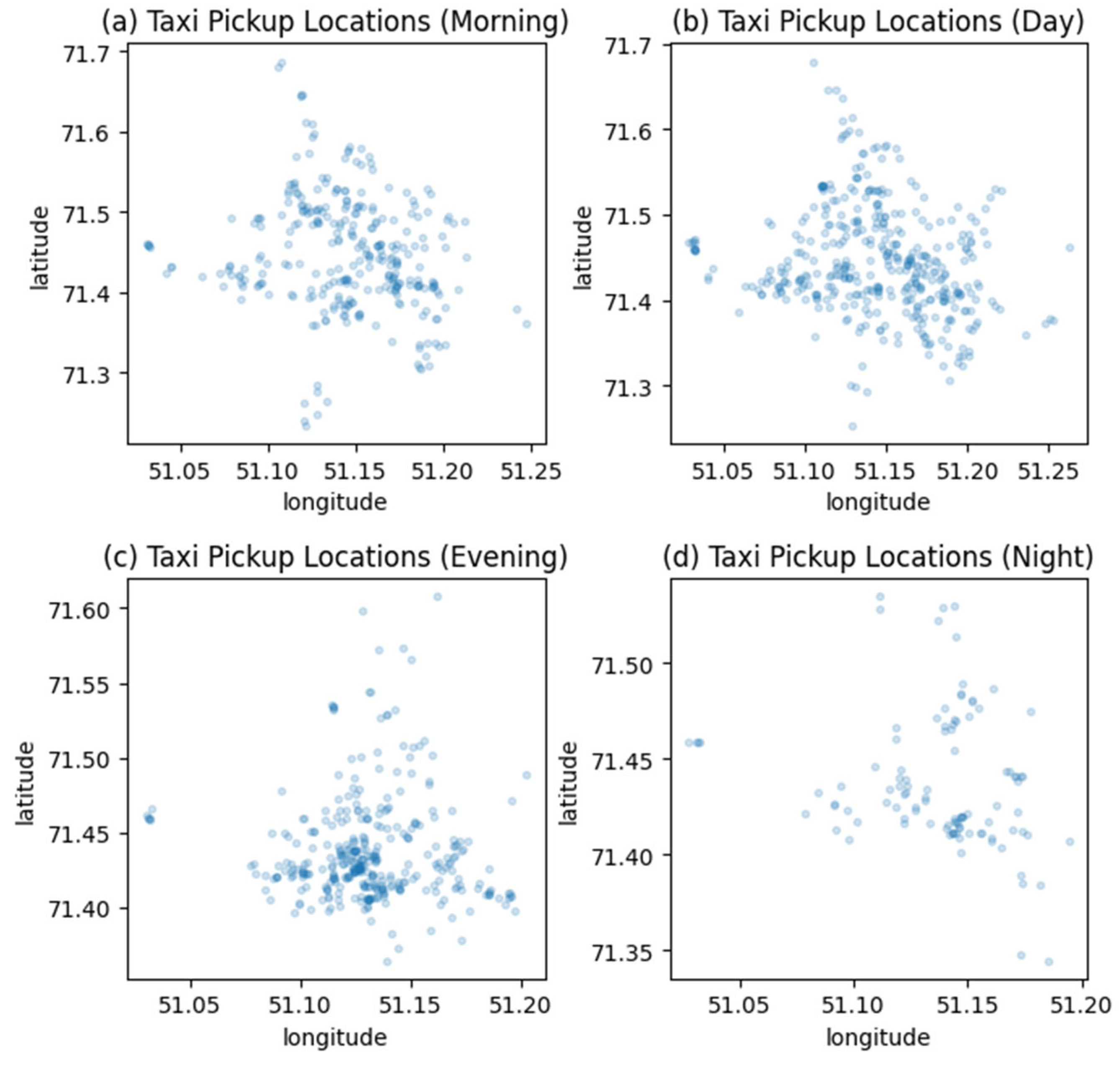
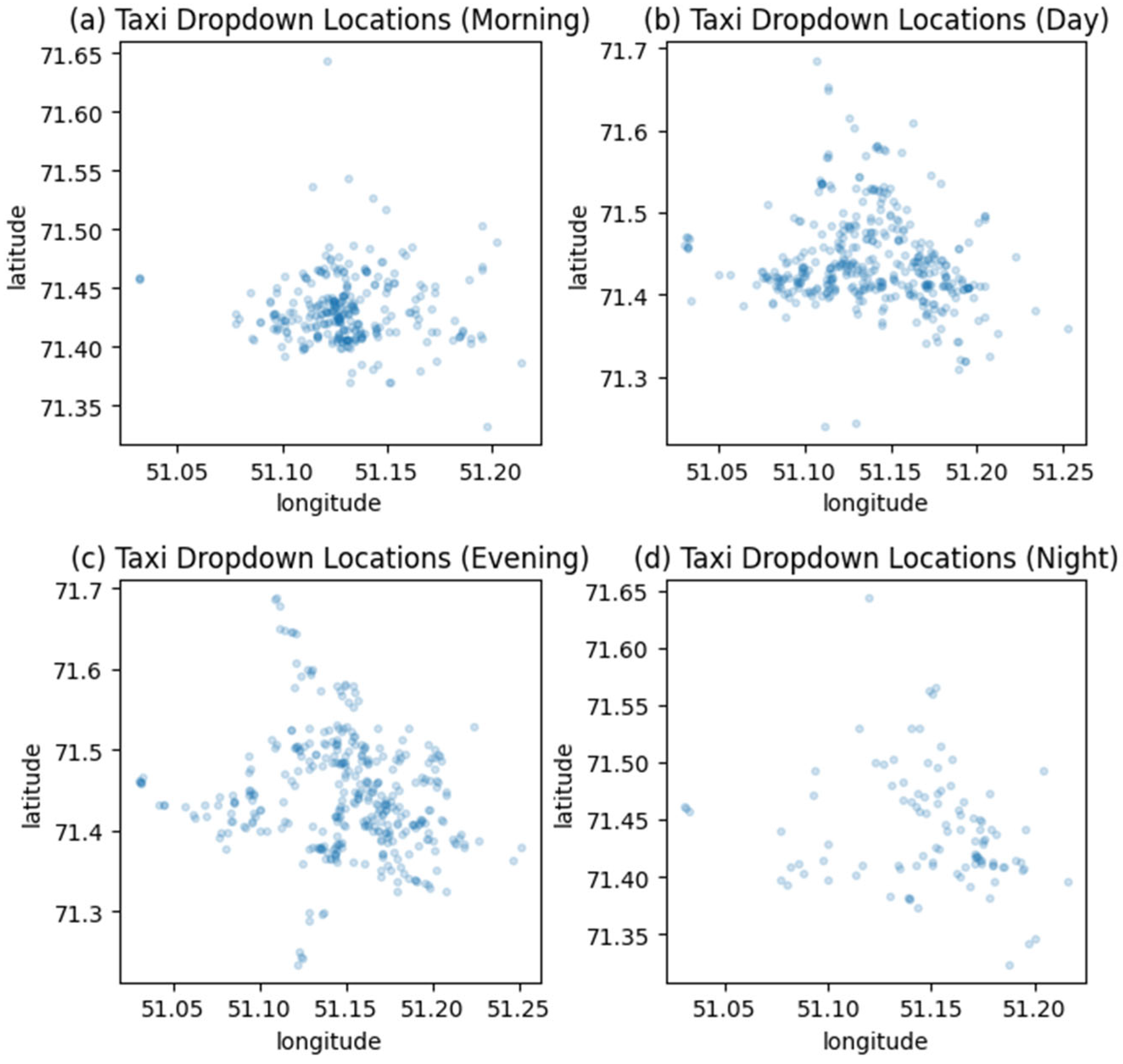
4.2. The Results of Building a Dynamic Model of Profit Maximization of the Carsharing System in the City of Astana

Collected data on trips within the city of Astana in the taxi service mode from 30 January 2023 to 11 March 2023 were processed. Figure 1 shows a city map in administrative boundaries, visualized using Google maps. In total, information on 1168 trips was processed. All trips were divided into four groups, depending on the start time of the trip:

-

A (trip start recorded from 5:00 a.m. to 11:00 a.m.);

-

B (trip start recorded from 11:00 a.m. to 5:00 p.m.);

-

C (the start of the trip was recorded from 5:00 p.m. to 11:00 p.m.);

-

D (the start of the trip was recorded from 11:00 p.m. to 5:00 a.m.).

The number of trips in each group is shown in

Table 1. Number of trips in the groups A, B, C, D.

Group	Number of Trips
A	300
B	403
C	362
D	103
All	1168

. Most trips were recorded between 11:00 a.m. and 5:00 p.m. (group B). The fewest trips were recorded between 11:00 p.m. and 5:00 a.m.

The dataset includes information on the coordinates of the start and end locations of trips and the time of the start of trips. The dataset does not contain personal information about customers.

The coordinates of the start and end locations of trips in these groups were visualized using the Python language’s mathplotlib library and are shown in Figure 2 and Figure 3.

As can be seen from the visualization, the distribution of boarding and disembarking points differed significantly at different periods of the day. The coordinates of the start and end locations of the trips were tied to the corresponding cells of the hexagonal grid. The probability of a trip was calculated as the ratio of the number of trips from subregion ${\mathrm{r}}_{\mathrm{j}}$ to subregion ${\mathrm{r}}_{\mathrm{q}}$ to the total number of trips in the region in one day. Using the Kepler visualization service [35], a hexagonal tessellation of the selected region (the city of Astana, Republic of Kazakhstan) was constructed and visualized based on the collected dataset for the period from 30 January 2023 to 11 March 2023 (Figure 4). The number of trips related to the corresponding cell is displayed in colors. The lighter the color of the cell, the greater the number of trips. Accordingly, the probability of ordering a car in this subregion will be greater. This information is essential for placing stations with cars in the appropriate subregions and determining the number of cars in each subregion at a particular time.

As can be seen from the visualization, the hexagonal grid evenly covers almost all of Astana. The number of trips for each cell varies from 1 to 10. It can also be established that the number of trips to cells located in the city center exceeds the number of trips to cells located on the outskirts.

The average fare of Astana taxi services is about $1.2 per passenger boarding and about $0.1 per kilometer of travel. After a survey of stakeholders working in this field in the city of Astana, several parameters were established, which were empirically included in the profit maximization system: the tariff value is 0.1 ≤ τ(t) ≤ 0.3 and the β coefficient in the profit maximization model can be estimated to be between 0.05 and 0.07. When building a dynamic profit maximization model, it was assumed that β = 0.06.

A value of eight for the mass tab of grid cells was chosen during the hexagonal tessellation of the Astana region using the H3 framework. This value was chosen because it provides the necessary detail at the level of city blocks. The size of a city quarter is determined on average by a hexagon with a width of 400–500 m. At this scale, the hexagon’s side size is 461 m. If one chooses a smaller variable value, such an optimization problem is challenging due to the large number of variables in the maximization model. The placement of hexagons was determined automatically by the H3 framework.

5. Discussion

5.1. Findings

A dynamic profit maximization model for the carsharing system was built. Data on passenger trips in the taxi service mode were also collected to adjust this model to the region where the system is being implemented (Astana). The region bounded by the administrative borders of the city of Astana was covered by a hexagonal grid, each cell of which defines a separate subregion. For this, the H3 framework [32] was used to choose different scales for the required number of subregions. Several parameters reflecting changes in customer behavior in dynamics were calculated for each subregion. A visualization of the movement of taxi service customers in the city at different times of the day was carried out. The dynamic model of profit maximization of the carsharing system was built based on calculated parameters. The model built in this way considers the change in the demand for trips of customers of the carsharing system during the day.

Two cases were considered to verify the results of developing a dynamic model of profit maximization of the carsharing system. The first case concerns finding the maximum profit of the carsharing system for the city of Astana if the data on the time of the customers’ trips are not taken into account, but the coordinates of the start and end locations of the trips are taken into account. To find the maximum profit of the carsharing system, models (1)–(5) with the value of the parameter T = 1 were applied. In this case, the system ceases to be dynamic and becomes static. The static model does not consider data on the start time of customers’ trips during the day, so this model less accurately reflects the actual demand for cars in the carsharing system.

The second case concerns finding the maximum profit of the carsharing system for the city of Astana if the data on the start and end times of the trip, as well as the coordinates of the trips, are taken into account. For this, models (1)–(5) were used. All trips were grouped into four periods: A (the start of the trip recorded from 5:00 a.m. to 11:00 a.m.), B (the start of the trip recorded from 11:00 a.m. to 5:00 p.m.), C (the start of the trip recorded from 5:00 p.m. to 11:00 p.m.), and D (the start of the trip recorded from 11:00 p.m. to 5:00 a.m.). The value of the parameter T = 4. Each case was considered for a different number of cars available in the carsharing system ($\mathrm{\gamma }=1,\dots ,20$). The initial allocation of cars was carried out based on collected data on customer trips to Astana (Figure 3). The results of calculating the profit of the carsharing system in the city of Astana based on the static (T = 1) and dynamic (T = 4) models are shown in

Table 2. Calculation of the profit of the carsharing system based on static and dynamic models of maximization in the city of Astana.

γ	T = 1	T = 4	Difference
1	1207	1291	6.5%
5	4824	4954	2.6%
10	8227	8427	2.4%
20	15,665	16,201	3.3%

.

As a result, it was established that using a dynamic profit maximization model increases it by an average of 3.7%. The dynamic profit maximization model ensures profit maximization, reflecting the actual car demand in the carsharing system during the day more accurately than the static model.

In [30], it is indicated that the use of dynamic models of profit maximization compared to static ones allows increasing the profit by an average of 5.3%. Such results were obtained for the city of New York. The result that was obtained by the profit maximization model of the carsharing system for the city of Astana is equal to 3.7%, which is a commensurate value.

Simulation modeling was used to calculate the parameters used in the profit maximization model, since function (6) is not specified explicitly in this study. As a result, the parameters found with the help of simulation modeling (carried out 10 times) were averaged and adjusted according to the requirements specified in Section 3.3 and included in the profit maximization model of the carsharing system.

5.2. Limitations and Future Research Lines

The built dynamic model is unidirectional. That is, costs for the distribution of cars by subregions after the completion of the trip cycle are not taken into account in the model. These costs, as shown in [8], will be nonzero. The limitations of the built dynamic model are that the number of periods and subregions should be small. This is explained by the complexity of calculations, which will grow exponentially for discrete optimization. The work did not focus on selecting the optimal method for solving problems (1)–(5), which is the subject of further research.

This study did not consider an upper limit on the number of potential customers in each subregion. Instead, a system maximization model was considered from the perspective of the system owner, subject to constraints on the number of cars in the respective subregions. For $\mathrm{\gamma }<20$, the limit on the number of customers is not significant. If the number of cars in the system is more than 20, then this parameter must be considered in the profit maximization model. This is a separate research task.

Pandemics, particularly COVID-19, can affect the intensification of customers’ transition from using public transport to the carsharing service.

The obtained results play an essential role in the development of carsharing systems. Such systems are crucial in reducing environmental pollution in large cities such as Astana. The obtained results can be used in the development of environmental Kuznets curve (EKC) models, including renewable energy consumption (REC) and other independent variables such as economic freedom (EF) and economic policy uncertainty (EPU) [37].

6. Conclusions

The method of covering the region with geometric shapes, which divides the region into subregions, was described. For this problem, the rational choice was to cover the region with regular hexagons that are placed side by side. A dataset with information about trips within Astana was built. We then constructed maps of the start and end locations of trips in the region and a map of trips bound to the hexagonal grid cells using the Kepler visualization service. Each cell of the grid corresponds to a specific subregion, for which quantitative parameters are calculated, including the number of free cars in the subregions, the probability of a car trip from one subregion to another, the costs of car maintenance and operation, and the income from the trip.

The objective function of profit maximization in the dynamic model was determined, and the restrictions were established considering the peculiarities of passenger transportation in Astana. The simulation was carried out based on the constructed profit maximization model for the carsharing system using the case of Astana. For this, two cases were considered. The first case corresponds to the static model (T = 1), and the second corresponds to the dynamic model (T = 4). It was established that using a dynamic profit maximization model in the carsharing system increases the profit by 3.7%.

As a result of the study, the city of Astana within the administrative borders was covered with a hexagonal grid. The necessary information was collected for each cell of the grid, the analysis of which allows the following conclusions to be drawn:

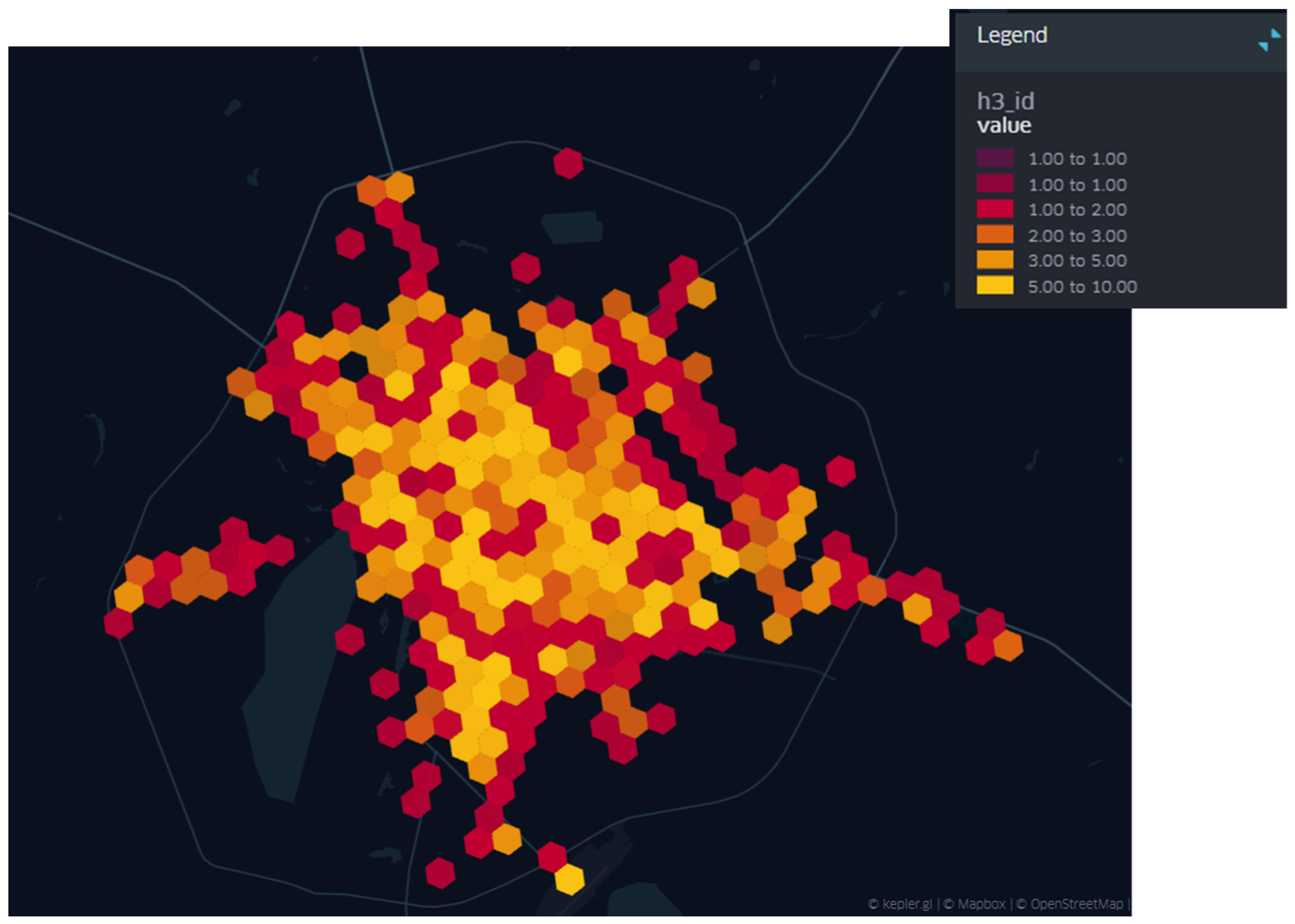
1.

In the areas limited by cells with many trips (light cells in Figure 4), stations with a higher throughput should be established. This should be considered in the city’s development plan, as appropriate city areas should be allocated to these stations.

2.

Information on the number of trips to the polling stations reflects user demand. Since this information is determined for different times of the day, the demand changes cyclically during and throughout the week, month, etc. Accordingly, for the effective functioning of the carsharing system, it is recommended that the cars of the system be moved to the stations determined by the discharge cells at the right time. For example, moving cars to the appropriate areas is recommended in the morning and evening when exceptionally high demand is recorded, in the morning to residential areas and in the evening to business areas.

3.

The described model can be considered by the city administration for urban development and by private companies interested in maximizing profits from the implementation of carsharing systems in large cities, particularly in Astana.