A Two-Period Model of Coastal Urban Adaptation Supported by Climate Services
Abstract
1. Introduction
2. Methods
2.1. Overview of the Coastal Urban Adaptation Model
- i.
- The quantitative projections of future SLR provided by climate science are uncertain;
- ii.
- Future climate damage is also assessed with substantial uncertainty.
2.2. Model Equations
3. Results
3.1. An Analytically Tractable Particular Case: Simplifying Assumptions
3.2. Solution in a Particular Case
3.3. Derivation of Model Solution in a Particular Case
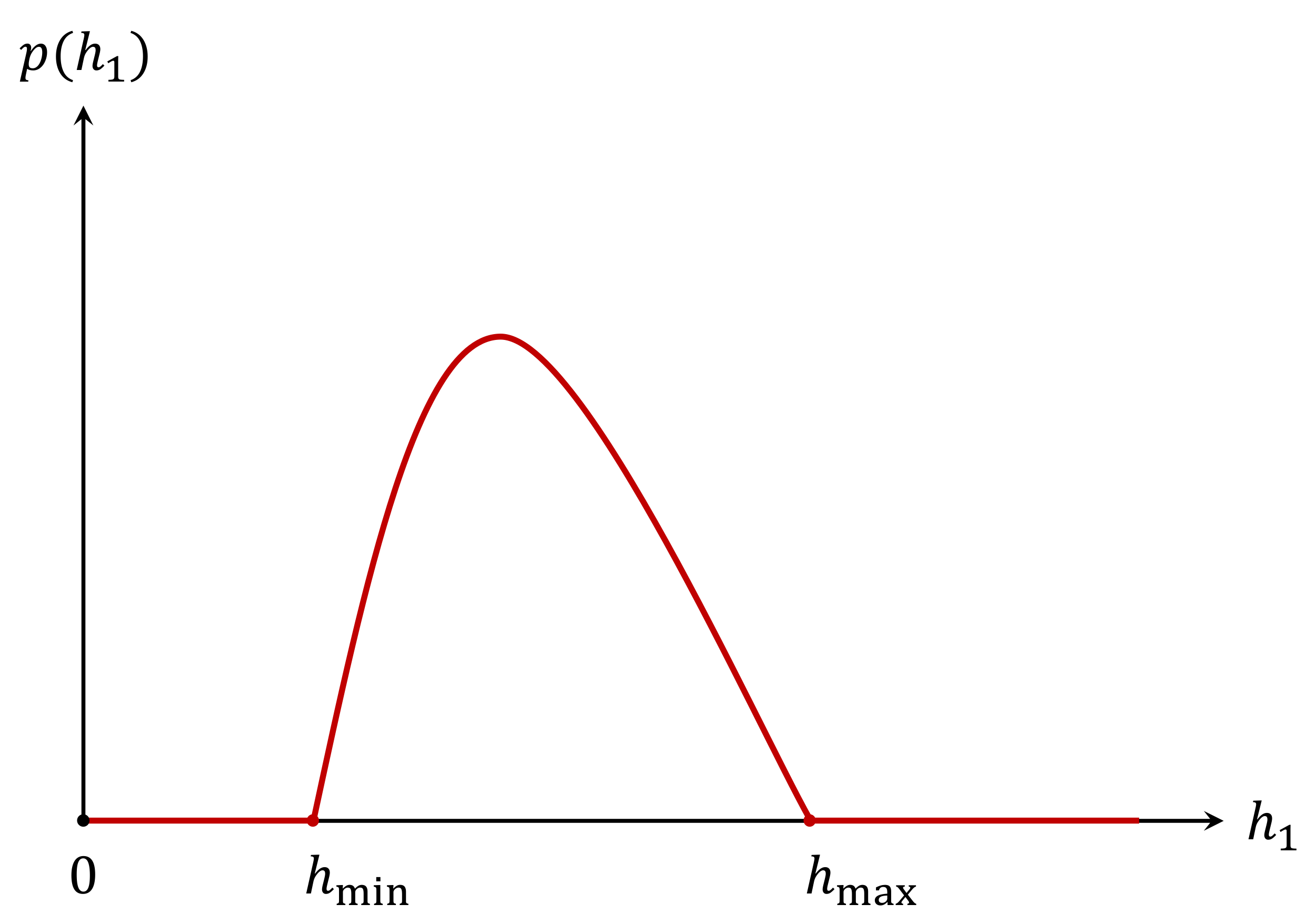
3.4. An Exemplary Uniform PDF for SLR
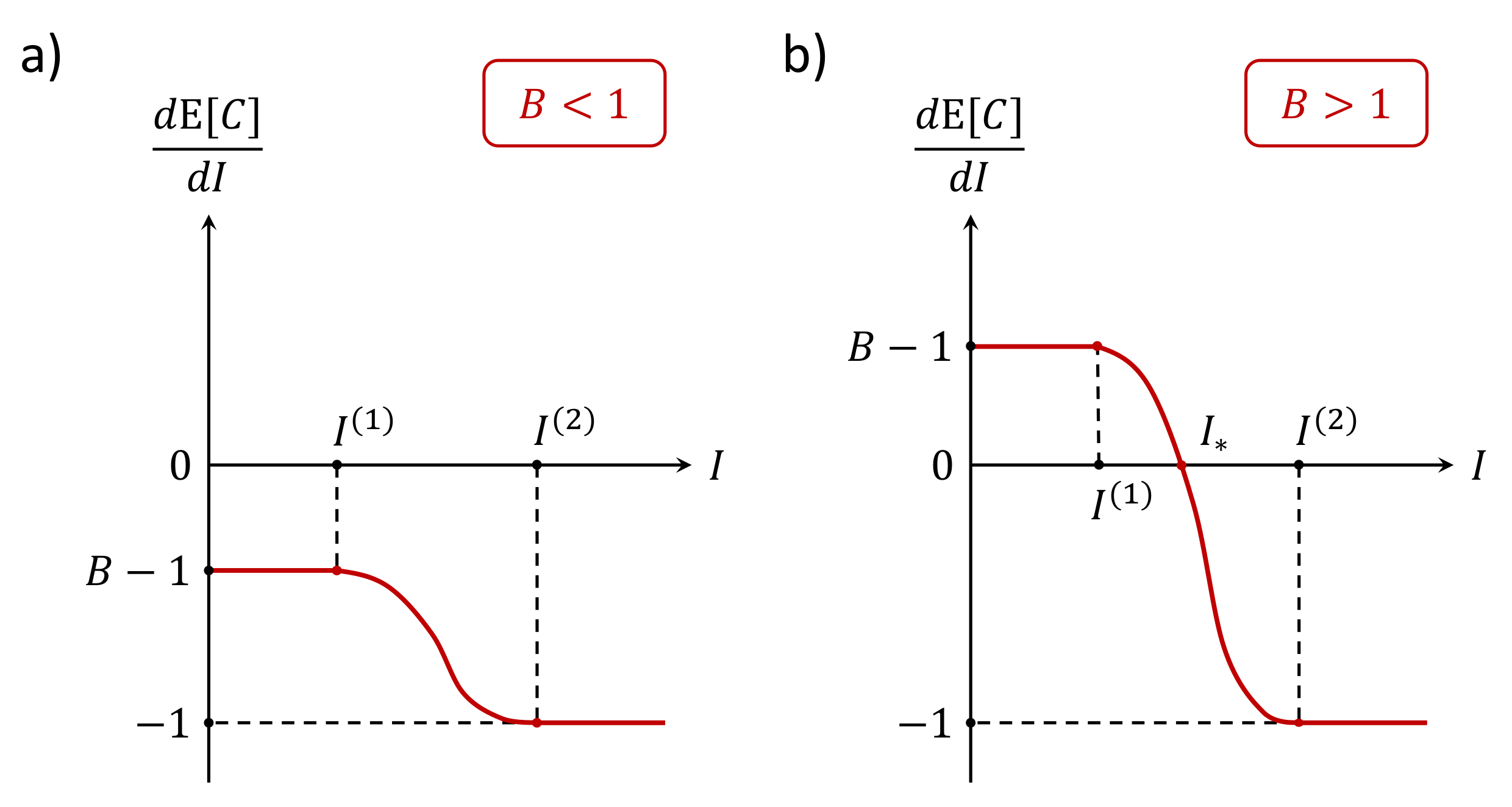
4. Discussion: The Role of Coastal Climate Services
- i.
- The form and parameters of the probability distribution function (PDF) for SLR;
- ii.
- The form and parameters of the climate damage function.
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BaU | ‘business-as-usual’. |
| CDF | Cumulative distribution function. |
| Probability density function. | |
| SLR | Sea-level rise. |
| VIABLE | Values and Investments from Agent-Based interaction and Learning in |
| Environmental systems. |
References
- Rosenzweig, C.; Solecki, W.D.; Romero-Lankao, P.; Mehrotra, S.; Dhakal, S.; Ibrahim, S.A. Climate Change and Cities: Second Assessment Report of the Urban Climate Change Research Network; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Yang, L.E.; Chan, F.K.S.; Scheffran, J. Climate change, water management and stakeholder analysis in the Dongjiang River basin in South China. Int. J. Water Resour. Dev. 2018, 34, 166–191. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- IPCC. Sea level rise and implications for low-lying islands, coasts and communities. In The Ocean and Cryosphere in a Changing Climate: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2022; pp. 321–446. [Google Scholar] [CrossRef]
- Pugh, D.; Woodworth, P. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Hoegh-Guldberg, O.; Jacob, D.; Taylor, M.; Bolaños, T.G.; Bindi, M.; Brown, S.; Camilloni, I.A.; Diedhiou, A.; Djalante, R.; Ebi, K.; et al. The human imperative of stabilizing global climate change at 1.5 °C. Science 2019, 365, eaaw6974. [Google Scholar] [CrossRef]
- Von Szombathely, M.; Albrecht, M.; Antanaskovic, D.; Augustin, J.; Augustin, M.; Bechtel, B.; Bürk, T.; Fischereit, J.; Grawe, D.; Hoffmann, P.; et al. A conceptual modeling approach to health-related urban well-being. Urban Sci. 2017, 1, 17. [Google Scholar] [CrossRef]
- Yang, L.E.; Scheffran, J.; Süsser, D.; Dawson, R.; Chen, Y.D. Assessment of flood losses with household responses: Agent-based simulation in an urban catchment area. Environ. Model. Assess. 2018, 23, 369–388. [Google Scholar] [CrossRef]
- Smirnov, V.; Ma, Z.; Volchenkov, D. Invited article by M. Gidea Extreme events and emergency scales. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105350. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; in press. [Google Scholar]
- Cortekar, J.; Bender, S.; Brune, M.; Groth, M. Why climate change adaptation in cities needs customised and flexible climate services. Clim. Serv. 2016, 4, 42–51. [Google Scholar] [CrossRef]
- Rölfer, L.; Winter, G.; Máñez Costa, M.; Celliers, L. Earth observation and coastal climate services for small islands. Clim. Serv. 2020, 18, 100168. [Google Scholar] [CrossRef]
- Jacob, D.; Kotova, L.; Teichmann, C.; Sobolowski, S.P.; Vautard, R.; Donnelly, C.; Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Damm, A.; et al. Climate impacts in Europe under +1.5 °C global warming. Earth’s Future 2018, 6, 264–285. [Google Scholar] [CrossRef]
- Teichmann, C.; Bülow, K.; Otto, J.; Pfeifer, S.; Rechid, D.; Sieck, K.; Jacob, D. Avoiding extremes: Benefits of staying below +1.5 °C compared to +2.0 °C and +3.0 °C global warming. Atmosphere 2018, 9, 115. [Google Scholar] [CrossRef]
- Koldunov, N.V.; Kumar, P.; Rasmussen, R.; Ramanathan, A.; Nesje, A.; Engelhardt, M.; Tewari, M.; Haensler, A.; Jacob, D. Identifying climate change information needs for the Himalayan Region: Results from the GLACINDIA Stakeholder Workshop and Training Program. Bull. Am. Meteorol. Soc. 2016, 97, ES37–ES40. [Google Scholar] [CrossRef]
- Preuschmann, S.; Hänsler, A.; Kotova, L.; Dürk, N.; Eibner, W.; Waidhofer, C.; Haselberger, C.; Jacob, D. The IMPACT2C web-atlas—Conception, organization and aim of a web-based climate service product. Clim. Serv. 2017, 7, 115–125. [Google Scholar] [CrossRef]
- Akhtar, N.; Geyer, B.; Rockel, B.; Sommer, P.S.; Schrum, C. Accelerating deployment of offshore wind energy alter wind climate and reduce future power generation potentials. Sci. Rep. 2021, 11, 11826. [Google Scholar] [CrossRef]
- Weisse, R.; Bisling, P.; Gaslikova, L.; Geyer, B.; Groll, N.; Hortamani, M.; Matthias, V.; Maneke, M.; Meinke, I.; Meyer, E.; et al. Climate services for marine applications in Europe. Earth Perspect. 2015, 2, 3. [Google Scholar] [CrossRef]
- Nordhaus, W. A Question of Balance: Weighing the Options on Global Warming Policies; Yale University Press: New Haven, CT, USA, 2014. [Google Scholar]
- Landry, C.E. Coastal erosion as a natural resource management problem: An economic perspective. Coast. Manag. 2011, 39, 259–281. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Landry, C.E.; Smith, M.D.; Whitehead, J.C. Economics of coastal erosion and adaptation to sea level rise. Annu. Rev. Resour. Econ. 2016, 8, 119–139. [Google Scholar] [CrossRef]
- Forrester, J.W. Urban Dynamics; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Meadows, D.; Randers, J.; Meadows, D. Limits to Growth: The 30-Year Update; Chelsea Green Publishing Co.: Vermont, VT, USA, 2004. [Google Scholar]
- Fiddaman, T. Dynamics of climate policy. Syst. Dyn. Rev. 2007, 23, 21–34. [Google Scholar] [CrossRef]
- Hallegatte, S.; Ghil, M. Natural disasters impacting a macroeconomic model with endogenous dynamics. Ecol. Econ. 2008, 68, 582–592. [Google Scholar] [CrossRef]
- Kellie-Smith, O.; Cox, P.M. Emergent dynamics of the climate—Economy system in the Anthropocene. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2011, 369, 868–886. [Google Scholar] [CrossRef]
- O’Neill, W.D. Estimation of a logistic growth and diffusion model describing neighborhood change. Geogr. Anal. 1981, 13, 391–397. [Google Scholar] [CrossRef]
- Kovalevsky, D.V.; Volchenkov, D.; Scheffran, J. Cities on the coast and patterns of movement between population growth and diffusion. Entropy 2021, 23, 1041. [Google Scholar] [CrossRef] [PubMed]
- Hasselmann, K. Detecting and responding to climate change. Tellus Chem. Phys. Meteorol. 2013, 65, 20088. [Google Scholar] [CrossRef]
- Hasselmann, K.; Kovalevsky, D.V. Simulating animal spirits in actor-based environmental models. Environ. Model. Softw. 2013, 44, 10–24. [Google Scholar] [CrossRef]
- Hasselmann, K.; Cremades, R.; Filatova, T.; Hewitt, R.; Jaeger, C.; Kovalevsky, D.; Voinov, A.; Winder, N. Free-riders to forerunners. Nat. Geosci. 2015, 8, 895–898. [Google Scholar] [CrossRef]
- Scheffran, J. Conflict and cooperation in energy and climate change: The framework of a dynamic game of power-value interaction. In Jahrbuch für Neue Politische Ökonomie, Band 20: Power and Fairness; Holler, M., Kliemt, H., Schmidtchen, D., Streit, M., Eds.; Mohr Siebeck: Tübingen, Germany, 2002. [Google Scholar]
- Scheffran, J. Adaptive management of energy transitions in long-term climate change. Comput. Manag. Sci. 2008, 5, 259–286. [Google Scholar] [CrossRef]
- BenDor, T.K.; Scheffran, J. Agent-Based Modeling of Environmental Conflict and Cooperation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Benenson, I.; Torrens, P. Geosimulation: Automata-Based Modeling of Urban Phenomena; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Filatova, T.; Verburg, P.H.; Parker, D.C.; Stannard, C.A. Spatial agent-based models for socio-ecological systems: Challenges and prospects. Environ. Model. Softw. 2013, 45, 1–7. [Google Scholar] [CrossRef]
- Aerts, J.C.; Botzen, W.J.; Clarke, K.C.; Cutter, S.L.; Hall, J.W.; Merz, B.; Michel-Kerjan, E.; Mysiak, J.; Surminski, S.; Kunreuther, H. Integrating human behaviour dynamics into flood disaster risk assessment. Nat. Clim. Change 2018, 8, 193–199. [Google Scholar] [CrossRef]
- Tobler, W.R. Cellular geography. In Philosophy in Geography; Springer: New York, NY, USA, 1979; pp. 379–386. [Google Scholar]
- White, R.; Engelen, G. Cellular automata and fractal urban form: A cellular modelling approach to the evolution of urban land-use patterns. Environ. Plan. Econ. Space 1993, 25, 1175–1199. [Google Scholar] [CrossRef]
- Hewitt, R.; van Delden, H.; Escobar, F. Participatory land use modelling, pathways to an integrated approach. Environ. Model. Softw. 2014, 52, 149–165. [Google Scholar] [CrossRef]
- Sekovski, I.; Armaroli, C.; Calabrese, L.; Mancini, F.; Stecchi, F.; Perini, L. Coupling scenarios of urban growth and flood hazards along the Emilia-Romagna coast (Italy). Nat. Hazards Earth Syst. Sci. 2015, 15, 2331–2346. [Google Scholar] [CrossRef]
- Song, J.; Fu, X.; Gu, Y.; Deng, Y.; Peng, Z.R. An examination of land use impacts of flooding induced by sea level rise. Nat. Hazards Earth Syst. Sci. 2017, 17, 315–334. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, J.M.; Schickhoff, M.; Sengupta, S.; Scheffran, J. Technological and social networks of a pastoralist artificial society: Agent-based modeling of mobility patterns. J. Comput. Soc. Sci. 2021, 4, 681–707. [Google Scholar] [CrossRef]
- Volchenkov, D.; Blanchard, P. Markov chain methods for analyzing urban networks. J. Stat. Phys. 2008, 132, 1051–1069. [Google Scholar] [CrossRef]
- Blanchard, P.; Volchenkov, D. Mathematical Analysis of Urban Spatial Networks; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Volchenkov, D.; Smirnov, V. The City of Lubbock is running away. Integration and isolation patterns in the wandering city. J. Vib. Test. Syst. Dyn. 2019, 3, 121–132. [Google Scholar] [CrossRef]
- Vrijling, J.; van Hengel, W.; Houben, R. Acceptable risk as a basis for design. Reliab. Eng. Syst. Saf. 1998, 59, 141–150, Risk Perception Versus Risk Analysis. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Coastal Processes with Engineering Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sorensen, R.M. Basic Coastal Engineering; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kind, J. Economically efficient flood protection standards for the Netherlands. J. Flood Risk Manag. 2014, 7, 103–117. [Google Scholar] [CrossRef]
- World Bank Group. Managing Coasts with Natural Solutions: Guidelines for Measuring and Valuing the Coastal Protection Services of Mangroves and Coral Reefs; Technical Report; The World Bank: Washington, DC, USA, 2016. [Google Scholar]
- Schueler, K. Nature-Based Solutions to Enhance Coastal Resilience; Technical Report; Inter-American Development Bank: Washington, DC, USA, 2017. [Google Scholar]
- Costanza, R.; Anderson, S.J.; Sutton, P.; Mulder, K.; Mulder, O.; Kubiszewski, I.; Wang, X.; Liu, X.; Pérez-Maqueo, O.; Luisa Martinez, M.; et al. The global value of coastal wetlands for storm protection. Glob. Environ. Change 2021, 70, 102328. [Google Scholar] [CrossRef]
- OECD. Responding to Rising Seas; Technical Report; OECD: Paris, France, 2019. [Google Scholar] [CrossRef]
- Rovenskaya, E. One-step optimization model of warming-driven damage of economic growth. In Proceedings of the DEGIT Conference Papers c016_062, DEGIT, Dynamics, Economic Growth, and International Trade, St. Petersburg, Russia, 8–9 September 2011; Available online: https://econpapers.repec.org/paper/degconpap/c016_5f062.htm (accessed on 18 August 2022).
- Sengupta, S.; Scheffran, J.; Kovalevsky, D. Agent adaptation in an urban coastal scenario: Applying the VIABLE Framework. In Proceedings of the DKT-12-22, 12. Deutsche Klimatagung, Online, 15–18 March 2021. [Google Scholar] [CrossRef]
- Sengupta, S.; Scheffran, J.; Kovalevsky, D. A Single-Agent Urban Coastal Adaptation Model: Adaptive decision-making within the VIABLE modeling framework. In Proceedings of the EGU21-12752, EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Kovalevsky, D.; Scheffran, J. A coastal urban adaptation model with time-discounting, optimizing and satisficing decision making. In Proceedings of the EGU21-12228, EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalevsky, D.V.; Scheffran, J. A Two-Period Model of Coastal Urban Adaptation Supported by Climate Services. Urban Sci. 2022, 6, 65. https://doi.org/10.3390/urbansci6040065
Kovalevsky DV, Scheffran J. A Two-Period Model of Coastal Urban Adaptation Supported by Climate Services. Urban Science. 2022; 6(4):65. https://doi.org/10.3390/urbansci6040065
Chicago/Turabian StyleKovalevsky, Dmitry V., and Jürgen Scheffran. 2022. "A Two-Period Model of Coastal Urban Adaptation Supported by Climate Services" Urban Science 6, no. 4: 65. https://doi.org/10.3390/urbansci6040065
APA StyleKovalevsky, D. V., & Scheffran, J. (2022). A Two-Period Model of Coastal Urban Adaptation Supported by Climate Services. Urban Science, 6(4), 65. https://doi.org/10.3390/urbansci6040065






