Industry Interconnectedness and Regional Economic Growth in Germany
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data and Sources
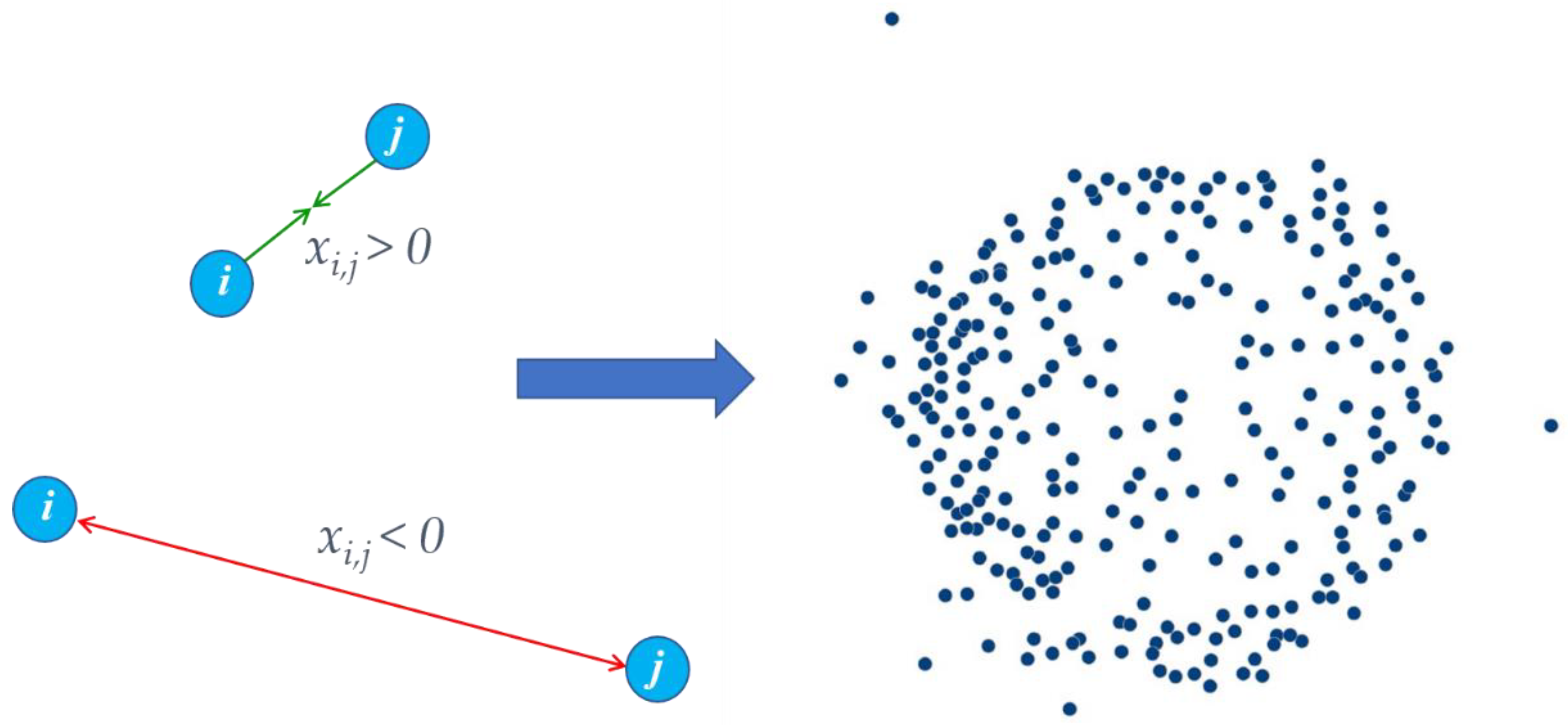
2.2. Quantifying Interdependence, a Pairwise Measure of Industry Interdependence
2.3. Quantifying Tightness, a Regional Aggregate Measure of Industry Interdependence
2.4. Designation of Time Periods
2.5. Empirical Treatments
3. Results and Discussion
3.1. Industry Interdependence
3.2. The German Industry Network
3.3. LMRs and Tightness
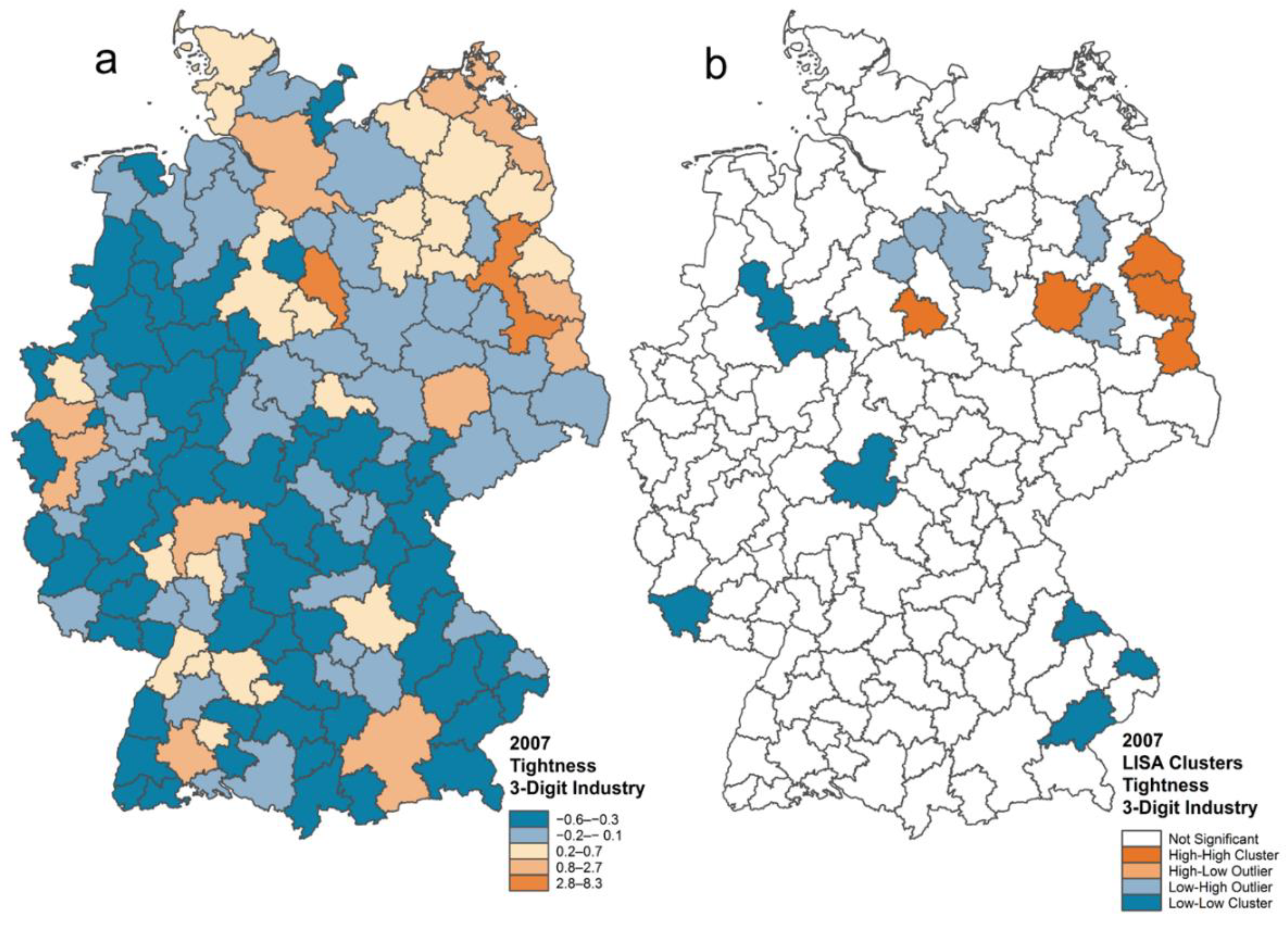
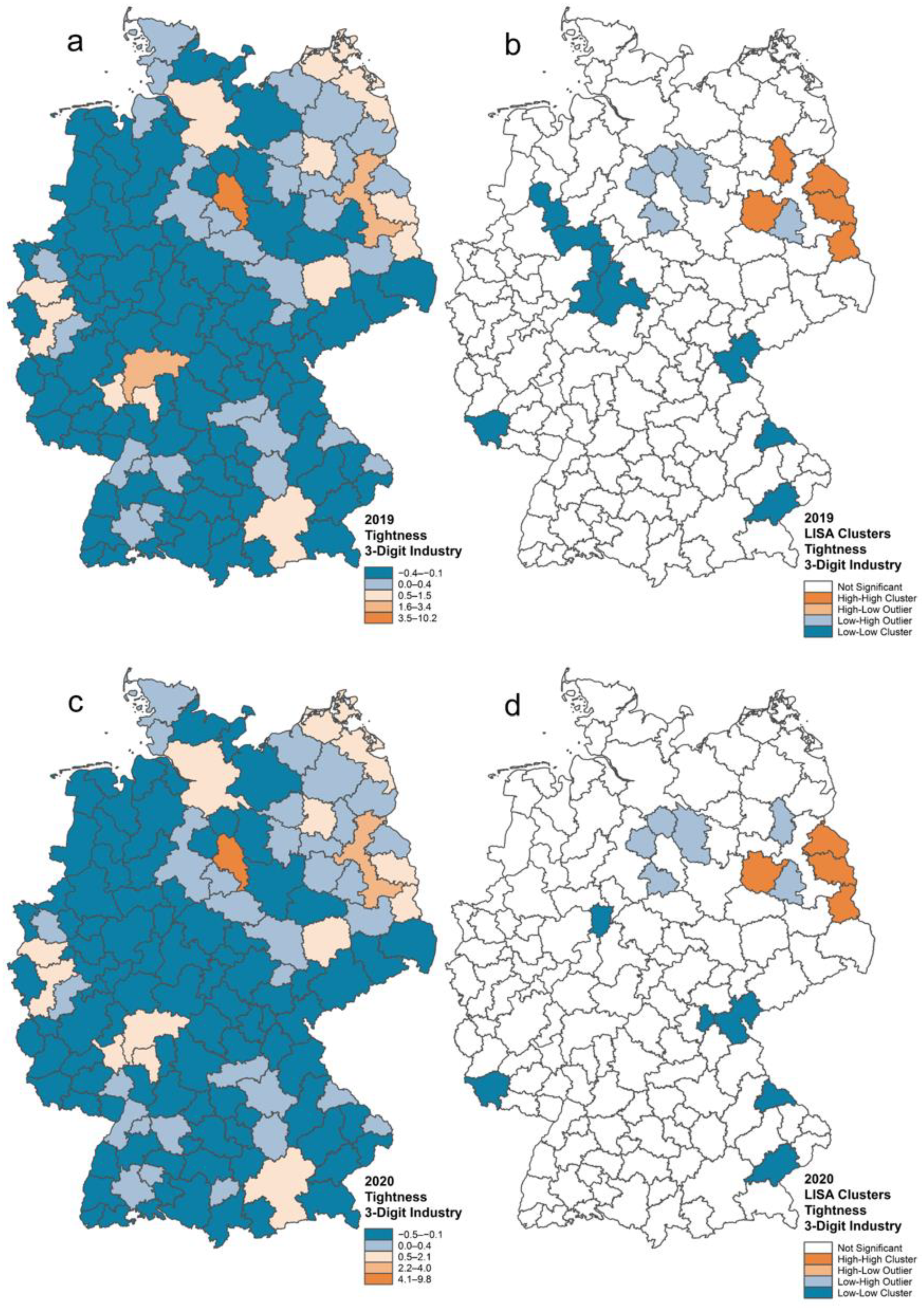
3.4. Spatial Distribution and Autocorrelation of Tightness
3.5. Tightness, Productivity, and Economic Shocks
3.6. A First Comparison of Tightness Effects and COVID-19 Implications
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buhaug, H.; Urdal, H. An urbanization bomb? Population growth and social disorder in cities. Glob. Environ. Chang. 2013, 23, 1–10. [Google Scholar] [CrossRef]
- President’s Council of Advisors on Science and Technology. Technology and the Future of Cities; Executive Office of the President of the United States: Washington, DC, USA, 2016.
- Vandecasteele, I.; Baranzelli, C.; Siragusa, A.; Aurambout, J.P. (Eds.) The Future of Cities–Opportunities, Challenges and the Way Forward; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Batty, M. Inventing Future Cities; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Healy, P. Urban Complexity and Spatial Strategies: Towards a Relational Planning for Our Times; Routledge: London, UK, 2007. [Google Scholar]
- Batty, M. The New Science of Cities; The MIT Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Lobo, J.; Alberti, M.; Allen-Dumas, M.; Arcaute, E.; Barthelemy, M.; Bojorquez Tapia, L.A.; Brail, S.; Bettencourt, L.; Beukes, A.; Chen, W.Q.; et al. Urban Science: Integrated Theory from the First Cities to Sustainable Metropolises. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- McPhearson, T.; Haase, D.; Kabisch, N.; Gren, Å. Advancing understanding of the complex nature of urban systems. Ecol. Indic. 2016, 70, 566–573. [Google Scholar] [CrossRef]
- Barthelemy, M. The Structure and Dynamics of Cities: Urban Data Analysis and Theoretical Modeling; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Neal, Z.P. The Connected City: How Networks Are Shaping the Modern Metropolis; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Shutters, S.T.; Lobo, J.; Strumsky, D.; Muneepeerakul, R.; Mellander, C.; Brachert, M.; Fernandes, T.F.; Bettencourt, L.M.A. The relationship between density and scale in information networks: The case of urban occupational networks. PLoS ONE 2018, 15, e0196915. [Google Scholar] [CrossRef] [Green Version]
- Shutters, S.T.; Muneepeerakul, R.; Lobo, J. Quantifying urban economic resilience through labour force interdependence. Palgrave Commun. 2015, 1, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Shutters, S.T.; Waters, K. Inferring Networks of Interdependent Labor Skills to Illuminate Urban Economic Structure. Entropy 2020, 22, 1078. [Google Scholar] [CrossRef]
- Waters, K.; Shutters, S.T. Industrial structure and a tradeoff between productivity and resilience. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- Dustmann, C.; Fitzenberger, B.; Schönberg, U.; Spitz-Oener, A. From Sick Man of Europe to Economic Superstar: Germany’s Resurgent Economy. J. Econ. Perspect. 2014, 28, 167–188. [Google Scholar] [CrossRef] [Green Version]
- Heise, S.; Porzio, T. Spatial Wage Gaps in Frictional Labor Markets; Federal Reserve Bank of Minneapolis: Minneapolis, MN, USA, 2019. [Google Scholar]
- Bade, F.-J.; Alm, B.; Weins, S. Employment Effects of Investment Subsidies by German Regional Policy; ZBW-Leibniz Information Centre for Economics: Hamburg, Germany, 2020. [Google Scholar]
- Otto, A.; Nedelkoska, L.; Neffke, F. Skill-relatedness und Resilienz: Fallbeispiel Saarland. Raumforsch. Raumordn. 2014, 72, 133–151. [Google Scholar] [CrossRef]
- Holling, C.S. Understanding the Complexity of Economic, Ecological, and Social Systems. Ecosystems 2001, 4, 390–405. [Google Scholar] [CrossRef]
- Simmie, J.; Martin, R. The economic resilience of regions: Towards an evolutionary approach. Camb. J. Reg. Econ. Soc. 2010, 3, 27–43. [Google Scholar] [CrossRef] [Green Version]
- Gunderson, L.H.; Holling, C.S. (Eds.) Panarchy: Understanding Transformations in Human and Natural Systems; Island: Washington, DC, USA, 2002. [Google Scholar]
- National Science Foundation Sustainable Urban Systems Subcommittee. Sustainable Urban Systems: Articulating a Long-Term Convergence Research Agenda. A Report from the NSF Advisory Committee for Environmental Research and Education; U.S. National Science Foundation: Washington, DC, USA, 2018.
- Kosfeld, R.; Werner, D.-Ö.A. Deutsche Arbeitsmarktregionen–Neuabgrenzung nach den Kreisgebietsreformen 2007–2011. Raumforsch. Raumordn. 2012, 70, 49–64. [Google Scholar] [CrossRef]
- Muneepeerakul, R.; Lobo, J.; Shutters, S.T.; Gomez-Lievano, A.; Qubbaj, M.R. Urban Economies and Occupation Space: Can They Get “There” from “Here”? PLoS ONE 2013, 8, e73676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, G.; Wong, L.; Chua, H.N. Complex discovery from weighted PPI networks. Bioinformatics 2009, 25, 1891–1897. [Google Scholar] [CrossRef] [PubMed]
- Tokuyama, T. Algorithms and Computation. In Proceedings of the 18th International Symposium, ISAAC 2007, Sendai, Japan, 17–19 December2007. [Google Scholar]
- Burda, M.C.; Hunt, J. What Explains the German Labor Market Miracle in the Great Recession? Brook. Pap. Econ. Act. 2011, 42, 273–319. [Google Scholar] [CrossRef] [Green Version]
- Harari, D. Recession and Recovery: The German Experience; UK Parliment, House of Commons Library: London, UK, 2014. [Google Scholar]
- Frenken, K.; Van Oort, F.; Verburg, T. Related Variety, Unrelated Variety and Regional Economic Growth. Reg. Stud. 2007, 41, 685–697. [Google Scholar] [CrossRef] [Green Version]
- Hidalgo, C.A.; Balland, P.-A.; Boschma, R.; Delgado, M.; Feldman, M.; Frenken, K.; Glaeser, E.; He, C.; Kogler, D.F.; Morrison, A.; et al. The Principle of Relatedness. In Research and Innovation Forum 2020; Springer: Singapore, 2018; pp. 451–457. [Google Scholar]
- Content, J.; Frenken, K. Related variety and economic development: A literature review. Eur. Plan. Stud. 2016, 24, 2097–2112. [Google Scholar] [CrossRef]
- Corrigendum. Reg. Stud. 2015, 49, 1938–1940. [CrossRef] [Green Version]
- Essletzbichler, J. Relatedness, Industrial Branching and Technological Cohesion in US Metropolitan Areas. Reg. Stud. 2013, 49, 752–766. [Google Scholar] [CrossRef] [Green Version]
- O’Clery, N.; Heroy, S.; Hulot, F.; Beguerisse-Diaz, M. Unravelling the forces underlying urban industrial agglomeration. arXiv 2019, arXiv:1903.09279v2. [Google Scholar]
- Marshall, A. Principles of Economics; MacMillan: London, UK, 1920. [Google Scholar]
- Ellison, G.; Glaeser, E.L.; Kerr, W.R. What Causes Industry Agglomeration? Evidence from Coagglomeration Patterns. Am. Econ. Rev. 2010, 100, 1195–1213. [Google Scholar] [CrossRef] [Green Version]
- MATLAB. Nonclassical Multidimensional Scaling Using Mdscale; The Mathworks Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Anselin, L. Local Indicators of Spatial Association-LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Fotheringham, S. Trends in quantitative methods I: Stressing the local. Prog. Hum. Geogr. 1997, 21, 88–96. [Google Scholar] [CrossRef]
- Farinha, T.; Balland, P.-A.; Morrison, A.; Boschma, R. What drives the geography of jobs in the US? Unpacking relatedness. Ind. Innov. 2019, 26, 988–1022. [Google Scholar] [CrossRef] [Green Version]
- Alabdulkareem, A.; Frank, M.R.; Sun, L.; AlShebli, B.; Hidalgo, C.; Rahwan, I. Unpacking the polarization of workplace skills. Sci. Adv. 2018, 4, eaao6030. [Google Scholar] [CrossRef] [Green Version]
- Kogler, D.F.; Rigby, D.L.; Tucker, I. Mapping Knowledge Space and Technological Relatedness in US Cities. Eur. Plan. Stud. 2013, 21, 1374–1391. [Google Scholar] [CrossRef]

| Rank | Labor Market Region (LMR) | T1 |
|---|---|---|
| 1 | Wolfsburg (007) | 8.27 |
| 2 | Berlin (109) | 5.10 |
| 3 | Frankfurt am Main (043) | 2.68 |
| 4 | Frankfurt an der Oder (110) | 2.05 |
| 5 | Cottbus (118) | 1.68 |
| 137 | Trier (054) | −0.61 |
| 138 | Koblenz (049) | −0.61 |
| 139 | Kleve (027) | −0.62 |
| 140 | Minden (036) | −0.64 |
| 141 | Passau (086) | −0.64 |
| Labor Market Regions (N = 141) | Counties (N = 401) | |||
|---|---|---|---|---|
| Industry Level | 3-digit | 4-digit | 3-digit | 4-digit |
| T (2007) vs. GDP change, 2007–2009 | −0.22 ** | −0.19 * | −0.20 *** | −0.09 n/s |
| T (2009) vs. GDP change, 2009–2011 | 0.34 *** | 0.25 ** | 0.27 *** | 0.14 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shutters, S.T.; Seibert, H.; Alm, B.; Waters, K. Industry Interconnectedness and Regional Economic Growth in Germany. Urban Sci. 2022, 6, 1. https://doi.org/10.3390/urbansci6010001
Shutters ST, Seibert H, Alm B, Waters K. Industry Interconnectedness and Regional Economic Growth in Germany. Urban Science. 2022; 6(1):1. https://doi.org/10.3390/urbansci6010001
Chicago/Turabian StyleShutters, Shade T., Holger Seibert, Bastian Alm, and Keith Waters. 2022. "Industry Interconnectedness and Regional Economic Growth in Germany" Urban Science 6, no. 1: 1. https://doi.org/10.3390/urbansci6010001
APA StyleShutters, S. T., Seibert, H., Alm, B., & Waters, K. (2022). Industry Interconnectedness and Regional Economic Growth in Germany. Urban Science, 6(1), 1. https://doi.org/10.3390/urbansci6010001







