1. Introduction
1.1. Urban Development and Phase Transitions
Urban areas are now the main habitat we are living in: 55% of the world’s population currently lives in urban areas and two-thirds of world population is projected to live in cities by 2050 [
1]. Understanding how cities and regions evolve is one of the grand challenges of 21st century science [
2]. Improved understanding of how cities and region change and grow over time would support more effective planning and sustainable urbanisation. However, predicting future urban development is very challenging in the face of nonlinearity and complexity [
3] and so new methods of analysis are needed to further our understanding of urban dynamics. Urban systems are known to exhibit a form of discontinuous change known as a phase transition [
4]. This is a concept borrowed from physics, which refers to a significant change in one part of a system caused by a small change elsewhere. Langton [
5] describes a phase transition as a critical balance point. The simplest example of this is the transition from water to ice with a small change in temperature. Urban modellers use this concept to better understand radical changes that take place over the course of urban development, associated with discontinuities of urban changes, such as the transition from rural to urban or from monocentric to polycentric cities. Historical examples include the transition from “socially disconnected” to connected settlements in ancient civilisations [
6]. Other examples include: the transition from corner shops to supermarkets in 1950s UK retailing [
7], and the appearance of out of town shopping centres, due to a reduction in the cost of car travel. Gentrification is also an example of a phase transition in the social demographic makeup of an area related to house prices [
8].
Identifying these phase transitions could provide a better understanding of the past and a more complete picture of the future potential of urban development, as it is widely agreed that the future evolution of a region could move in one of a number of different directions depending on small changes caused by urban development or external factors such as a changing climate. However, the phase transitions of urban development are not yet fully understood—how, when and why these discontinuous changes occur is still the subject of much research in urban modelling. Complicated interactions and interdependencies between parts of the system make analysis of future situations more difficult [
3].
1.2. Dynamic Urban Models and the BLV Approach
Urban modelling has emerged from several different traditions [
9,
10], such as ecology and economics, including land use/land cover change models, land use and transportation models, system dynamics models and landscape dynamics models. The first models were static [
11,
12,
13] and later dynamic models were developed mainly as a result of increasing computing power [
4,
14,
15] Dynamic urban models are increasingly applied to explore possible future scenarios of urban development to achieve sustainability [
16,
17]. Dynamic urban models explore how urban development reaches a future state from a current one and so allows exploration of the reasons why phase transitions might occur. Analytical approaches to understanding dynamic urban models have helped to advance the theory in a formal way but have not yet provided a way of fully analysing these models largely due to the nonlinearities that exist in urban systems (see [
3] for a fuller explanation).
Numerical simulation paired with visualisation is one of the most common methods for making progress with dynamic models. Clear and effective visualisation of dynamic model runs is important so that we can intuitively see and interpret the modelled behaviour(s) [
18]. Dynamic urban models tend to either be bottom-up (ABM or CA) or top-down aggregate (BLV or similar). Bottom-up modelling supports the generative approach [
19] which allows large scale structure to emerge. Top-down models contain fewer degrees of freedom but are more amenable to analytical approaches and, in general, require much less computing power especially when applied to urban systems given the size and complexity of most cities and regions. In this paper we focus on top-down aggregate BLV models in order to make use of the low numbers of variables and quick run times in these more parsimonious model types.
The BLV retail model [
20,
21] is a well-established top down dynamic urban model. It is a combination of the entropy-based retail spatial interaction model and Lotka–Volterra-type dynamics. There is a lot of complexity in the dynamics which are controlled by a system of nonlinear simultaneous differential equations. Progress has been made in terms of analysing the number of solutions in the state space of a BLV model [
22] as well as particular kinds of bifurcations [
23]. There are many other models in the complete family of BLV-models including house price dynamics and housing provision dynamics [
24]. Wilson [
4] provides a thorough introduction to the analysis of the dynamics in this kind of model from the point of view of both catastrophe theory and bifurcation theory, which can be further analysed using modern simulation and data visualisation techniques. Wilson [
17] provides a useful overview of the current state of the art in terms of dynamic modelling. A phase transition in BLV retail model terms is defined as a zone changing from being feasible to not feasible (or vice versa) and this concept can be explored at system level involving multiple zones [
21]. Retail model zone-graphs help to explain zonal phase transitions [
20]. Zone graphs for a residential BLV model [
8] demonstrate that there is the potential to apply similar analytical techniques across multiple different kinds of subsystem. Progress has been made in developing simulations that include multiple linked BLV-type subsystems [
8]. This is important for real-world planning applications because looking at how the whole urban system evolves provides more insight into possible futures than just looking at one system. The BLV retail model has been used to explore phase transitions within retail systems [
25,
26].
The type of urban structures that emerge from a wide range of possible exogenous parameter values across the parameter space of the BLV retail model has been explored [
25,
26]. As a result of this exploratory work, we know that phase transitions often occur at critical values of the main parameters. The analogue of parameter space exploration for the endogenous variables in a BLV retail model is state space exploration. This may be a useful area to explore given how successful the parameter space exploration is.
1.3. State Space and Basins of Attraction
State space, also called phase space, is fundamental to the understanding of dynamical systems. It is an abstract space that contains all possible system states. As a system changes over time it moves through the state space. It is helpful to understand how one state transitions to another, as so-called tipping points represent critical thresholds in dynamic systems [
27]. Although the use of state space has been widely applied in the study of system’s dynamics in many branches of science, including a wider range of social system behaviour [
28], ecology [
29,
30], management [
31], etc., it is not sufficiently generalized and applied in urban science to understand how urban systems change over time. A state space representation of the BLV retail model was presented in the original Harris and Wilson [
20] paper and further developed in Wilson [
4]. Vandermeer and Yodzis [
29] used state space features to model discontinuous change in ecosystems, looking specifically at how basin boundaries can collide and cause discontinuous change to occur. A state space approach was used by Weidlich and Haag [
32] for a dynamic model of migration between zones. The three-zone version of the model was restricted to a triangular hyperplane because of a constant total regional population. By drawing the trajectories in state space, the behaviour of the model with different levels of agglomeration could be explored and phase transitions identified. The urban systems we deal with here have every initial condition evolving towards a stable attractor. Building on this, groups of initial conditions that all evolve to the same stable attractor are called a basin of attraction. The boundaries of these basins indicate where a dynamical system will start to evolve in a completely different “direction”. An example of this might be a system evolving towards a centralised retail system changing direction to start evolving towards a more decentralised pattern.
1.4. Aim of This Work
In this paper, we begin to address the question of whether a state space view of a BLV retail model can offer any new insights into urban evolution, especially phase transitions. The aim in this study is not to make a full-scale detailed and realistic-looking urban system, of the sort that might be used by planners. Instead we aim to explore the qualitative nature of the state space of regions containing two or three shopping centres (i.e., zones). By exploring a number of state spaces under different conditions, we can identify regularities and differences. The main features of state space that we are interested in this paper are initial conditions, trajectories, basins of attraction and attractors. We are looking for qualitative features of state space that will enable us to make progress in the analysis of the system.
2. Method
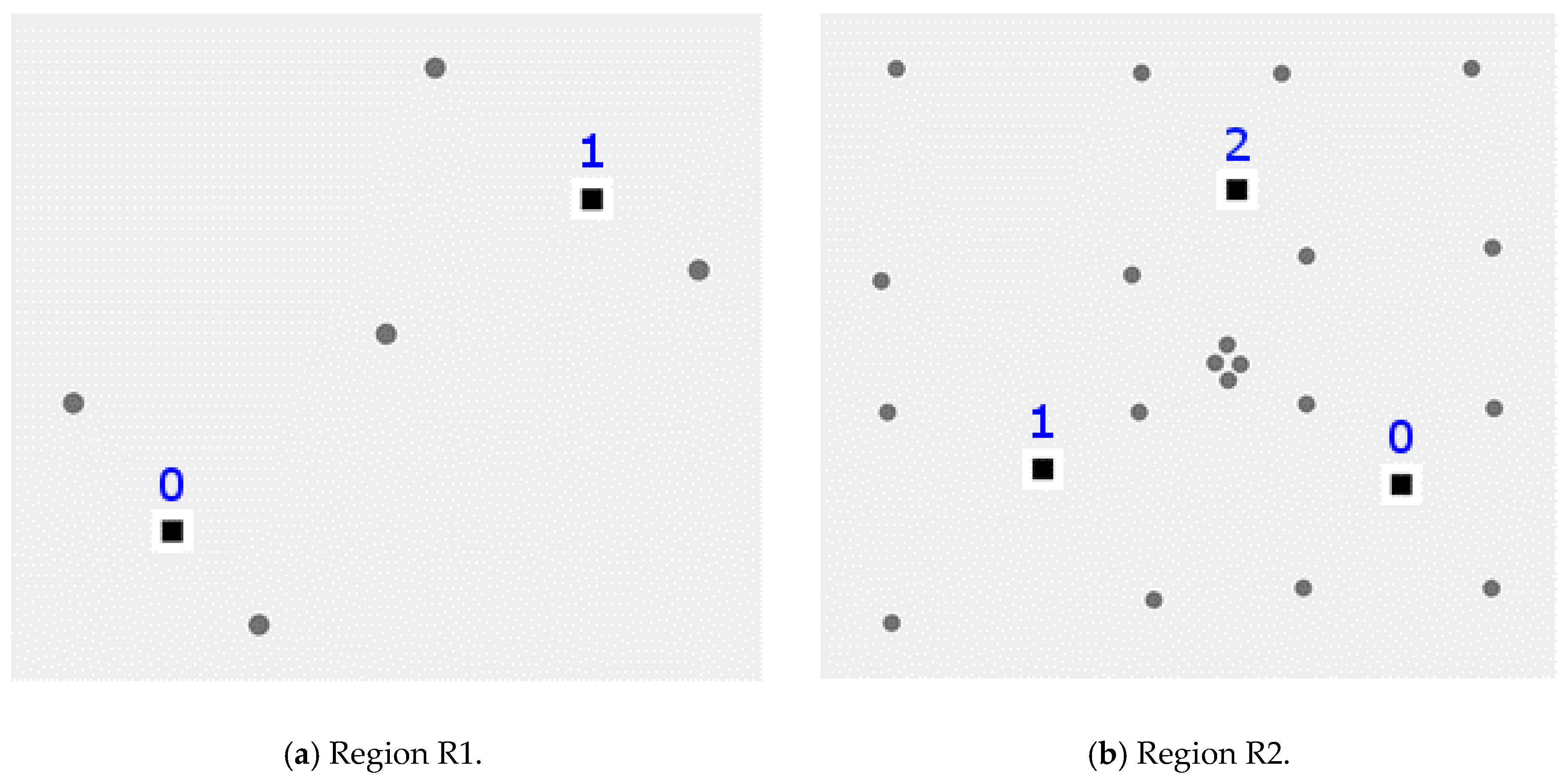
In order to explore the insights available from state space, we construct two hypothetical regions: region R1 with two retail zones (0 and 1) and five residential zones, and region R2 with three retail zones (0, 1 and 2) and 20 residential zones.
Appendix A contains full details about each region. The spatial arrangement of zones in each region is shown in
Figure 1.
We then apply the BLV retail model to construct the associated state space. The model software is written in C# and C++ to allow for fast model runs. The intention of the BLV retail model is to identify profitable locations and sizes for retailers in a region of interest. The main model equations for the BLV retail model are specified as follows. For a retail zone
the attractiveness is
which is normally specified as the floorspace. For a residential zone
the spending per head on retail is
and the total population is
. The travel cost between each pair of zones
and
is given by
. The parameter
represents the impact of size on consumer decisions about where to shop. The parameter
represents the impact of travel cost on consumer decisions about where to shop. The flow of money from residential zone
to retail zone
is
:
The balancing factor
enforces a constraint that the total money flowing out of a residential zone should equal the total spending power there (here the index
ranges across all retail zones in the region):
The total money flowing into a centre is
:
is the retail centre running cost for a unit of floor space. The dynamics given below will determine the rate of change of each retail zone size:
The parameter
determines the rate of response of retailers to market forces. The general assumption here is that if a retail zone is profitable it will grow and if it is not profitable it will shrink. The equilibrium position of each zone is given by:
We explore the state space of each hypothetical region by running a BLV model for each unique point on a regular grid covering the entire state space. The resolution of the grid is important: if the spacing is too large we may miss important details of state space features; if the spacing is too small we will not be able to compute the result in a reasonable amount of time. If we choose the grid resolution to be M samples along each dimension then we are sampling M possible sizes of each shopping centre. From the point of view of urban planning we are seeking to identify critical thresholds in the sizes of the retail zones and so we need to use a large enough number of sampling points to identify them accurately. In two dimensions we explore an M × M grid and in three dimensions we explore an M × M × M grid. We can vary the resolution of our sampling grid to fit each situation. The values of and used for these hypothetical regions lie within the plausible parameter ranges for this model and were in all cases chosen to demonstrate some phenomena of interest in the hypothetical model state space being viewed.
Each model run ends once it moves through a pre-specified number of iterations N with no change in any endogenous variable greater than x% where x is very small (e.g. 0.001). There are significant problems with wrongly characterising very low velocity regions of state space as attractors—we overcame this by setting parameter N very large. We save the start and end point of each model run and then group the trajectories by the attractor they reach—from this we can build the basins of attraction. One useful feature of state space exploration is that it is a perfectly parallelizable technique given that the workload is made up of large numbers of unrelated model runs that vary only in the initial conditions. This makes it very fast when run on parallel computing platforms, e.g., multi-core CPUs or GPUs.
Our main method of investigation is using interactive data visualisation which is a key method for detecting patterns in large amounts of data due to benefits including but not limited to panning, zooming and brushing. The figures presented here are static but illustrate the display output of the software. Linking this with fast simulations of the BLV model in software allows users to generate new results on demand in real-time and customise the visualisation in ways that enable new insights to be detected. The visualisation methods we will make use of are based on vector fields and streamlines. We visualise the square state space area for two zones and state space volume cube for three-zones, as each zone adds one more dimension to the state space.
3. Results and Analysis
3.1. Supply-Demand Balancing Hyperplane
The state space of a BLV retail model even with two or three dimensions is a challenge to comprehend due to the large amount of data present—information overload is a distinct possibility and so effective visualisation is key. We use a 30 × 30 grid to explore velocity vectors and a 50 × 50 grid to explore streamlines. At these resolutions the two dimensional state space includes hundreds, or even thousands, of model runs.
Figure 2 shows the state space of the two-zone region R1 for two values of the
parameter. The two values of
were chosen to demonstrate an interesting change in a hypothetical model state space. The attractor for each basin is shown as a black circle within the associated basin area. As the
parameter changes from 1.3 (
Figure 2a) to 1.4 (
Figure 2b) the green basin disappears and the other two basins expand significantly.
The attractors in the BLV model’s state space always exist on a supply-demand balancing hyperplane because the model is in equilibrium when
(i.e., when total region spending power equals total running costs of all shopping centres combined). The streamlines in
Figure 2c,d show how rapidly the two-zone system moves back to a supply-demand balancing hyperplane if the initial conditions are away from this. The lines use a colour ramp for slow to fast through black, red, yellow, white and cyan. The system is not necessarily at equilibrium when on this hyperplane but the equilibrium solutions are definitely somewhere on the hyperplane. The hyperplane is a system-level feature and when the system is away from the hyperplane the whole system will correct a supply-demand mismatch for the whole region by moving back to the hyperplane. Below the hyperplane there is undersupply of retail facilities in the region and above the hyperplane we have oversupply. The subsequent move to an equilibrium solution on the hyperplane then addresses supply-demand mismatches for each and every zone.
For a retail system it appears intuitive that if the spending power of each residential zone is increased by an equal percentage then the structure of state space would remain the same given that the relationships between retail zones are maintained. In
Figure 2 the complete shape of each basin could be predicted from the basin data on the supply-demand balancing hyperplane because the basin boundaries are linear. As a result, the hyperplane can be used to describe the complete dynamics of the system. The linearity of the basins in the complete two zone state space comes from the fact that the size-based attractiveness (
) of each retail zone relative to all others in the system is constant when the entire system is scaled (in terms of total floor space supported). In the two-zone case for a particular point on the hyperplane the two zones
and
are in constant ratio
. Equation (7) shows that regardless of the absolute size of each
the same ratio (
) holds constant. In other words we are dealing with the same dynamical system regardless of the total system floor space. This appears to also hold in the three-zone case but needs to be explored for higher numbers of zones.
By exploring just the hyperplane we can know that we have identified all possible attractors for the current set of exogenous parameters. Calculating only the hyperplane part of a state space allows for a great reduction in the workload. Assuming a uniform sampling grid resolution of 100 then for a three-zone system you would need to sample one million points (1003) for the full state space but only 5050 if you choose only those points in the uniform sampling grid that fall on the hyperplane. This reduction in workload by three orders of magnitude is obviously very significant given that each sample point represents a model run to equilibrium. The workload reduction is even greater at higher numbers of dimensions, however, visualisation then becomes a significant challenge.
With a three-zone system much of the data has the potential to be occluded in the viewport. We remove the problem of occlusion by showing only the initial conditions on the
supply-demand balancing hyperplane as discussed above.
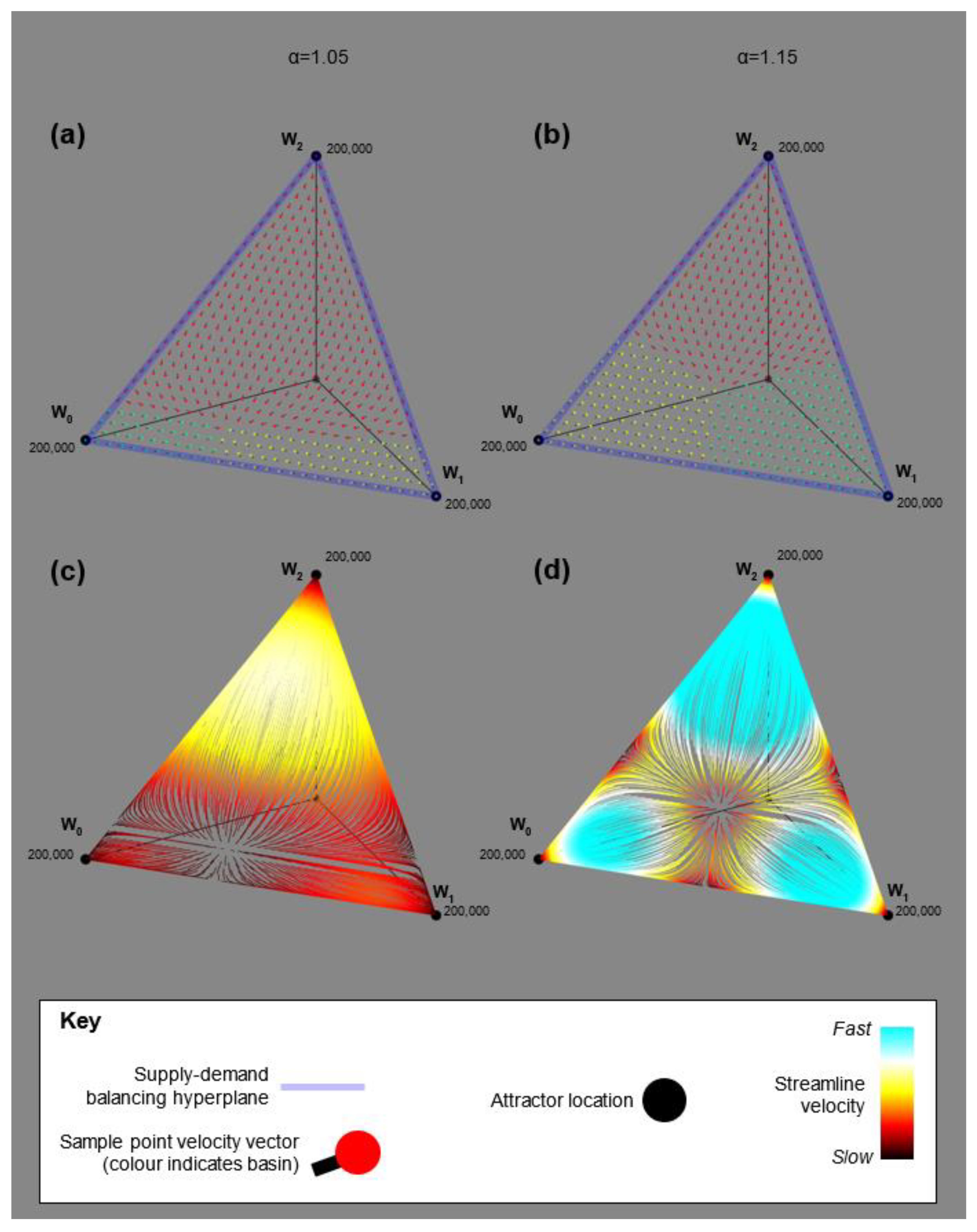
Figure 3 shows how the state space with three-zones varies across two values of
. One retail zone (retail zone 2) in this example sits alone in the north of the region and so has the advantage of being the closest centre for much of the population. Similar with the two-zone case the state space changes smoothly with the red basin shrinking and the yellow and green basins growing. The shrinking of the red basin is caused by the increase in the
parameter meaning that distance becomes increasingly less important and so retail zone 2 starts to lose its prior advantage of being the closest centre for a large percentage of the consumers in the region. The hyperplane is a triangle in this case. Above this triangle (away from the origin) there is oversupply of retail facilities and below it (towards the origin) there is undersupply. With three zones the dynamics have the potential to be more complicated. The streamlines in
Figure 3c,d show that there is the potential for trajectories within one basin to reverse their direction on one or more axes. This suggests strong competition for business between pairs of retail zones that can result in one winning out, and so the other one becomes a non-viable retail zone and shrinks to zero. This shows that in retail dynamics the route from initial conditions to equilibrium is potentially a turbulent one and not just a smooth growth or decline along each dimension. The high values of
and low
value in this example mean that there is no co-existence of retail zones.
3.2. Velocity in State Space
It is useful to explore the rate at which the system travels within the state space, as the speed of urban evolution varies considerably from basin to basin and/or within one basin. This variation relates to the amount of pressure exerted by the market on retail zones, whether it is pressure to grow due to high levels of profit or pressure to shrink due to high levels of loss. This is a vector of values—one for each retail zone. The magnitude of this vector appears to vary considerably across each state space and also between different state spaces, implying that the exogenous parameter values affect the rate of growth in retail systems and how it varies across the state space. It is important to study velocity because it is a key feature of state space and has the potential to provide many insights into the dynamics of the BLV model.
Figure 2,
Figure 3 and
Figure 4 all illustrate how velocity changes across one state space and also how it changes with parameter modification.
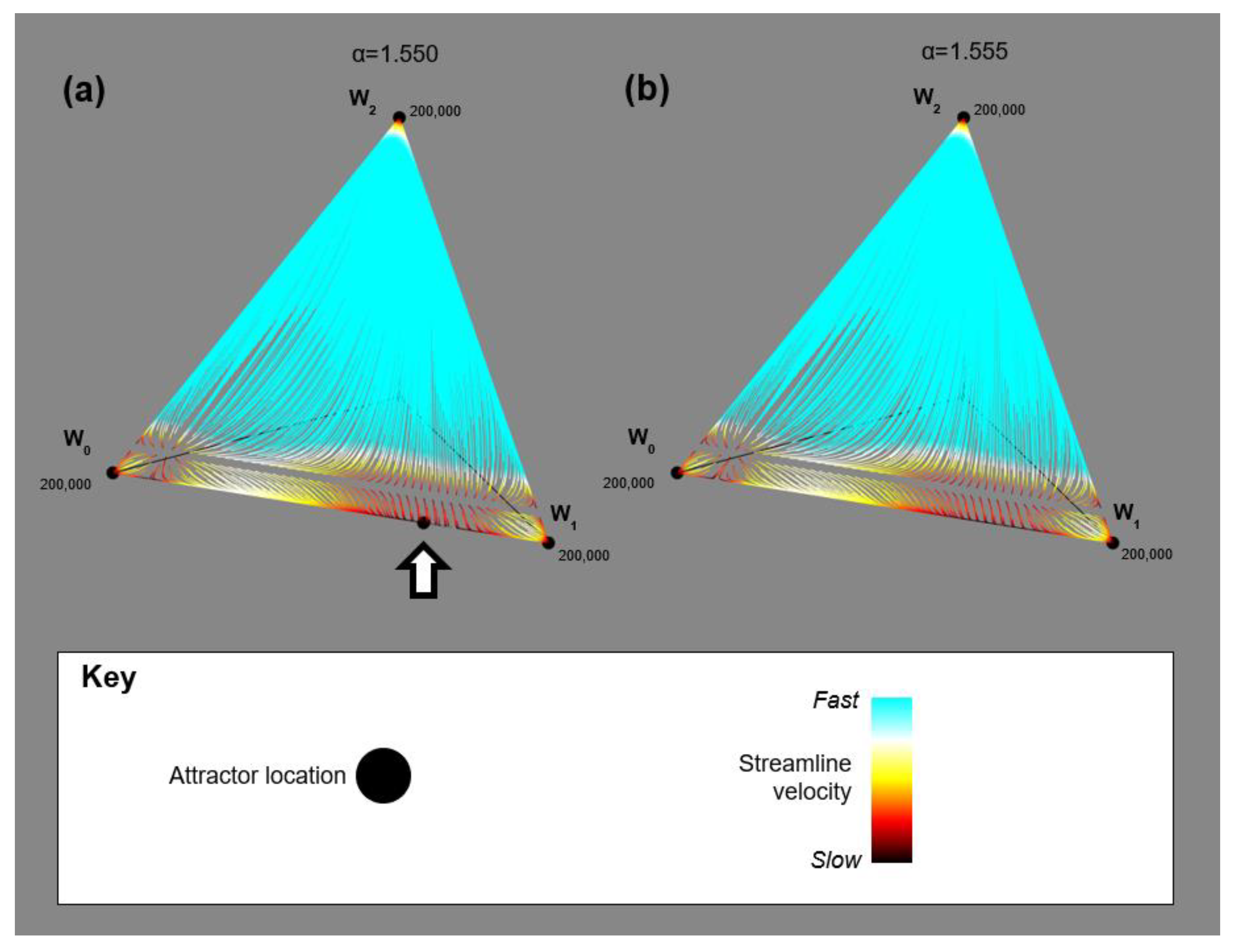
Exploring the state space of a BLV retail model using interactive data visualisation makes clear the way that basins change shape and appear/disappear from state space when exogenous parameter values change gradually. Basins often change shape smoothly and continuously maintaining many, if not all, of the main characteristics and just warping the existing features slightly. New basins may appear anywhere in the state space. As state space is changed through smooth parameter changes a stable attractor can disappear leaving a very slow subpart of state space in its place. All the initial conditions that previously moved to the attractor that disappeared now move to another attractor. The reverse is also possible—then a small portion of an existing basin might “slow down” until a new stable attractor appears, capturing many initial conditions nearby. This phenomenon of attractor appearance/disappearance is demonstrated in
Figure 4 where a single attractor appears/disappears with a small change in the
parameter. Slow subparts of state space can also exist on the boundary between two basins and are potentially the site of unstable equilibrium positions. There is one well-known contrasting situation to that described above: for low values of
we know that small parameter changes across the
= 1 line result in the entire state space changing abruptly. This can be explained by
zone graph analysis—see Dearden and Wilson [
33] for details.
3.3. State-Space-Related Causes of Phase Transitions
It is possible to identify two different causes of phase transitions in model terms. This may help to unpick cause and effect in model runs, something that is often difficult especially in large, complicated simulations. In the BLV retail model there appear to be two possible causes for phase transitions: (A) exogenous change and (B) endogenous change. Details of each cause is given in
Table 1. An example of a Type A phase transition would be expansion of an existing shopping centre which results in the system being placed into a new basin of attraction. The expansion will likely result in oversupply in the retail system but the basin crossing argument still applies and the system is likely to be under pressure to proceed quickly back to the hyperplane. An example of a Type B phase transition would be construction of a new motorway affecting travel cost in the region which then changes the basins in the state space so that the system is then contained by a new basin. Simultaneous endogenous and exogenous change might actually prevent a phase transition from occurring if the system is manually moved in state space to stay in the same basin. This relates to the idea that an urban planner might seek to avoid some phase transitions while welcome others depending on how well they meet the master plan [
3]. Wilson [
4] first explored the idea of phase transitions that cross a separatrix or basin boundary. Our work here is similar but we are using numerical experiments to delineate the boundaries for hypothetical systems.
3.4. Large Numbers of Zones
In order to extend the analysis to real systems with large numbers of zones (i.e., more than three) we introduce the equilibrium-size graph [
8]. This is constructed by probing the state space along one dimension from a point of interest (e.g., the current system state). This is a great simplification for higher numbers of dimensions where the state space is too difficult to comprehend but allows us to use the terminology of state space, e.g., basin boundaries and attractors.
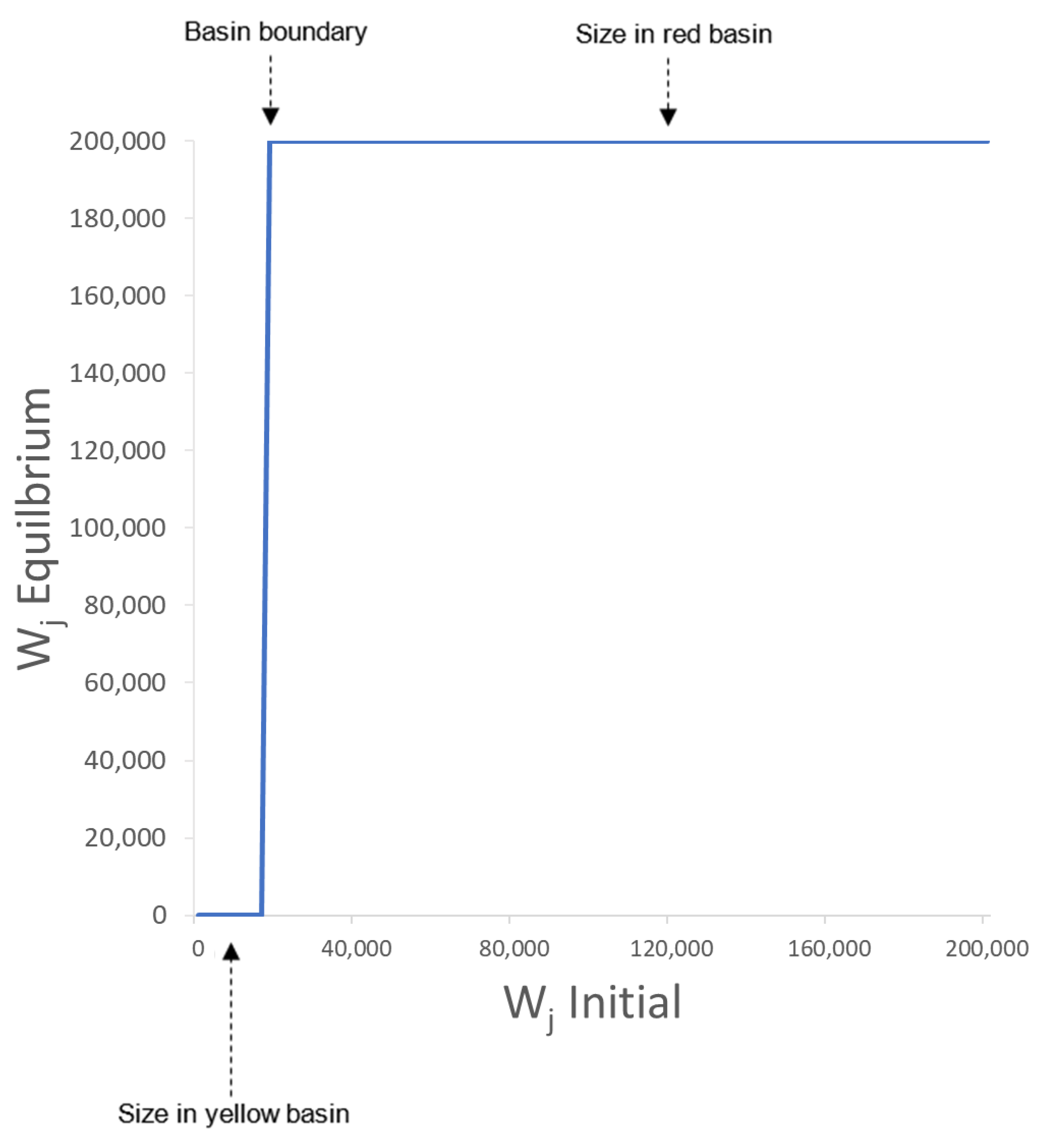
Figure 5 shows an equilibrium-size graph constructed from the centre point of the state space shown in
Figure 3a along the
zone dimension. The chart shows that below a critical size of ~18,000 m
2 retail zone
is zero at equilibrium. More importantly this shows a one-dimensional view of state space and allows us to identify the boundary between two basins. In one basin retail zone
is zero at the attractor and in the other basin it is 200,000 m
2 at the attractor. The benefit of using this graph is to know the nearby and reachable “other basins” and so identify other possible potential development paths for the current city, e.g., by opening a new shopping centre. In more complicated state spaces this kind of chart could identify more than the two basins shown in this simple example. There is a great potential to explore the state space of more complicated models using this technique, e.g., a multi-system BLV model. The chart is really only exploring on the hyperplane because however far above or below it gets from the current hyperplane it will just find the same set of basins on another identical hyperplane.
4. Discussion
This study proposed exploring (with interactive data visualisation) the range of output available when the initial conditions vary. Our methodology provided new insights into the following areas:
The dynamics of the BLV retail model is largely constrained to a supply-demand balancing hyperplane.
The causes of BLV retail model phase transitions can be usefully categorised and described using state space into those caused by endogenous change and those caused by exogenous change.
The landscape of state space can change in both gradual and abrupt ways.
New attractors can appear in regions of state space where velocity is very low (the reverse would mean an attractor would disappear leaving a region of low velocity state space).
Equilibrium-size graphs can extend the analysis to systems with more than three zones.
Rather than being merely a description of what happened during large numbers of model runs, the state space actually contains a large amount of information about the system dynamics—the basin boundaries are critical thresholds that determine the direction of evolution of the whole region. On one side of a basin boundary a particular configuration of stable sizes is present (whether zero or non-zero) and on the other side these stable sizes are different (again whether zero or non-zero). All positions in state space represent some ratio of the retail centre sizes and these lines or surfaces are no different. In two-dimensional models this will be a constant ratio along an exactly straight basin boundary. In three zone models the ratio is likely to vary as you move along the boundary between two basins. The reason for this is the interactions and interdependence between centres because each shopping centre’s size and position affects all the other shopping centres.
State space provides a way of mapping the possible phase transitions for a system—these are visible as basin boundaries in both the phase space for the current parameter set and also in all other parameter sets. State space analysis renders in detail the idea of urban systems that are far from an equilibrium solution which may then cross critical thresholds during their evolution. If a retail system is not at an attractor its natural inclination to move towards equilibrium could potentially be disrupted by type A or type B phase transitions which then cause it to move towards a different equilibrium state. This study provides the state space equivalent of the parameter space exploration shown in Dearden and Wilson [
33], where parameter space exploration is used to demonstrate the range of output of an urban model when varying the exogenous parameters. An exploration of parameter space in this way can be categorised as exploring type B phase transitions in the methodology developed in this study. Although currently it is not possible to visualise the state space of models with more than three zones, there is the potential to build on this study and work towards presenting the information in a manageable way for systems with large numbers of zones. The state space of the kind shown here is similar to a bifurcation diagram, which shows all the stable states possible for one specific zone across a range of parameter values. However, an interactive state space view provides more detail on a particular parameter set, for example, we can see critical sizes/basin boundaries, detail on multiple zones at the same time, and information on how particular solutions relate to each other.
As already demonstrated, equilibrium-size graphs can in some cases identify a critical size below which a zone is not present at equilibrium. This study has allowed us to explain the graph in state space terms. This kind of analysis can help identify both types of causes for phase transitions as demonstrated in Dearden and Wilson [
8] where the critical size of a retail zone changes in this kind of graph when external conditions (the exogenous parameters) are modified manually—implying a basin boundary moving over the current initial conditions. This points the way forward for using the insights that state space offers in higher dimensional systems—the examples given in Wilson and Dearden [
26] work with a 215-dimensional retail system and explore different ways to present the data, e.g., plotting the critical size for each zone on a map of the retail system. Equilibrium-size graphs and the idea of a critical minimum viable size for a retail zone also help to explain how thin basins can occur along a state space edge where at least one zone is zero size across the whole basin—something regularly visible in the outputs of the BLV retail model state space software in use for this study.
The results presented in this paper show how state space can be used to identify why particular phase transitions occur and categorise them based on the underlying reasoning. The categorisation of causes of phase transition is related to the modelling framework containing exogenous and endogenous components. We cannot make everything in a model endogenous and so this is always likely to be the case. This does not take away from the categorisation it is just a way of simplifying an otherwise very complicated situation and allows us to regard some factors as external to the situation being analysed. Phase transitions caused by apparently external factors may become ever more likely as cities and regional areas are more connected distant cities and places (e.g., as a result of globalisation, faster transportation systems interlinking cities, telecommunications, etc.). Generally exploring the qualitative nature of low dimensional versions of urban models appears to provide new insights into the dynamics of cities and regions and aid hypothesis generation for future studies. More specifically it can help us build an intuitive grasp of how the state space of a model changes with exogenous parameter change—potentially laying the groundwork for a higher-level understanding of the structure of state space.
5. Conclusions
In this study we analysed the qualitative features of state space in a hypothetical BLV retail model containing two or three shopping centres. In particular we categorised the causes of phase transitions depending on how they relate to state space features and changes. All phase transitions that occur in the BLV model are analysable from a state space point of view whether by looking at the “current” state space or by exploring the difference between one state space map and another (produced by exogenous parameter change). Examining all possible configurations of an urban system in a region allows us to identify the potential for growth in future. The benefit of this approach is that it provides a relatively intuitive “map” of the abstract space through which an urban system moves when it evolves. This is feasible because BLV model solutions can be calculated very quickly on modern desktop computers. We also identified the hyperplane in state space as being a strong indicator of the nature of the dynamics off the hyperplane and explored qualitatively how state space changes across the parameter space.
There is the potential to compare and contrast the qualitative nature of state space of different urban models in order to gain insights. For example, how do the dynamics of different urban subsystems (that may exist together in the same state space) vary in their response times and how do the shape of the basins differ between for example retail, house price and housing provision BLV models. A limitation is that high dimensional state spaces cannot be visualised easily. Dearden et al. [
34] offers a starting point for extending this methodology to higher dimensional systems using linked viewports and high dimensional visualisation techniques such as parallel coordinates, node-link graphs and vector field matrices. Already mentioned is the use of equilibrium-size graphs [
26] to identify basin boundaries in systems with large numbers of zones. Stochastic versions of the BLV model [
35] are potentially interesting to explore in phase space because the basin boundary would be fuzzy to some extent with the impact of the noise potentially determined by the direction and magnitude of the velocities along each boundary. Validating the theory relating to urban models and development is difficult and in the case of abstract structures like state space. A way of exploring this might be to calibrate a model for a historical system, build the state space and then see if the combination of “natural evolution” and known interventions result in what actually happened at that point in history. By visualising how state space changes as exogenous parameters are changed across a range of values, we can better understand the potential for stabilising different retail system configurations. A planned alteration to a retail system could potentially be synchronized with other external changes to ensure that a stable attractor was moved as close as possible to the hoped-for stable situation. More generally, this type of analysis can potentially offer insights into the nature of the dynamics in any dynamical-systems-type urban model. This is critical in increasing our understanding of the evolution of city regions, as well as helping stakeholders and policy-makers to plan for future urban changes.
Author Contributions
A.W. developed the model. J.D., A.W., M.J. developed method and framework. J.D. coded the software and visualised results. J.D. and Y.G. drafted the manuscript, with inputs and contribution from all authors.
Funding
This work was partially funded by a Leverhulme Grant (REF: RPG-2013-190).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Hypothetical Region Details
In both regions each travel cost is calculated from the straight-line distance between the two zones.
Region R1:
= 0.01.
Contains two retail zones and five residential zones.
Each population zone has a spending power () of £100,000.
Retail rent is £25 per m2.
Total floor space (and also the maximum for any retail zone) is 20,000 m2.
Approximately 5 km2.
Table A1.
Zone centroids for region R1.
Table A1.
Zone centroids for region R1.
| Zone Type | Easting | Northing |
|---|
| Retail zone | 805.317 | 1482.571 |
| Retail zone | 4229.061 | 4181.103 |
| Population zone | 0 | 2523.716 |
| Population zone | 1512.762 | 720.295 |
| Population zone | 2949.575 | 5249.2522 |
| Population zone | 5098.8824 | 3605.135 |
| Population zone | 2549.174 | 3085.36 |
Region R2:
= 0.001.
Contains three retail zones and twenty residential zones.
Each population zone has a spending power () of £1,000,000.
Retail rent is £25 per m2.
Total floor space (and also the maximum for any retail zone) is 200,000 m2.
Approximately 25 km2.
Table A2.
Zone centroids for for region R2.
Table A2.
Zone centroids for for region R2.
| Zone Type | Easting | Northing |
|---|
| Retail zone | 24,616.26953 | 4712.624512 |
| Retail zone | 13,196.95117 | 5207.200195 |
| Retail zone | 19,375.79492 | 14,098.28516 |
| Population zone | 8380.838867 | 303.7167053 |
| Population zone | 16,732.50195 | 1039.698975 |
| Population zone | 21,493.98047 | 1416.083252 |
| Population zone | 27,483.04297 | 1408.50293 |
| Population zone | 26,849.22656 | 17,960.45898 |
| Population zone | 8531.53125 | 17,949.98438 |
| Population zone | 16,337.5332 | 17,813.20313 |
| Population zone | 20,803.79883 | 17,797.17188 |
| Population zone | 8256.461914 | 7010.077148 |
| Population zone | 8051.920898 | 11,194.38477 |
| Population zone | 27,569.38672 | 7136.017578 |
| Population zone | 27,517.85156 | 12,246.12109 |
| Population zone | 16,263.23535 | 7014.057617 |
| Population zone | 16,034.69727 | 11,383.87207 |
| Population zone | 21,596.27539 | 7273.370605 |
| Population zone | 21,595.03516 | 11,985.95703 |
| Population zone | 18,686.56055 | 8580.121094 |
| Population zone | 19,485.07031 | 8537.147461 |
| Population zone | 19,103.83203 | 8030.766113 |
| Population zone | 19,065.60547 | 9156.870117 |
References
- United Nations. World Urbanization Prospects: The 2018 Revision. Available online: https://population.un.org/wup/ (accessed on 10 January 2019).
- Wilson, A.G. The Science of Cities and Regions: Lectures on Mathematical Model Design; Springer: Dordrecht, The Netherlands, 2012; ISBN 9400722656. [Google Scholar]
- Wilson, A.G. Complex Spatial Systems: The Modelling Foundations of Urban and Regional Analysis; Routledge: London, UK; New York, NY, USA, 2014; ISBN 0582418968. [Google Scholar]
- Wilson, A.G. Catastrophe Theory and Bifurcation: Applications to Urban and Regional Systems; Croom Helm Series in Geography and Environment; Croom Helm: New York, NY, USA, 1981; ISBN 9780709927020. [Google Scholar]
- Langton, C.G. Computation at the edge of chaos: Phase transitions and emergent computation. Phys. D Nonlinear Phenom. 1990, 42, 12–37. [Google Scholar] [CrossRef]
- Flores, J.C. A phase-transition model for the rise and collapse of ancient civilizations: A pre-ceramic Andean case study. Phys. A Stat. Mech. Appl. 2015, 440, 155–160. [Google Scholar] [CrossRef]
- Wilson, A.G.; Oulton, M.J. The Corner-Shop to Supermarket Transition in Retailing: The Beginnings of Empirical Evidence. Environ. Plan. A 1983, 15, 265–274. [Google Scholar] [CrossRef]
- Dearden, J.; Wilson, A.G. Explorations in Urban and Regional Dynamics: A Case Study in Complexity Science; Routledge: London, UK; New York, NY, USA, 2015; ISBN 1317698533. [Google Scholar]
- Clarke, K.C. Why simulate cities? GeoJournal 2014, 79, 129–136. [Google Scholar] [CrossRef]
- Berling-Wolff, S.; Wu, J. Modeling urban landscape dynamics: A review. Ecol. Res. 2004, 19, 119–129. [Google Scholar] [CrossRef]
- Von Thünen, J. Der isolierte Staa in Beziehung auf Landwirtschaft und Nationalökonomie; Perthes: Hamburg, Germany, 1826. [Google Scholar]
- Weber, A. Theory of the Location of Industries; University of Chicago Press: Chicago, IL, USA, 1929. [Google Scholar]
- Lowry, I.S. Model of Metropolis; RAND Corporation: Santa Monica, CA, USA, 1964; ISBN RM-4035-RC. [Google Scholar]
- Allen, P.M.; Sanglier, M. Urban Evolution, Self-Organization, and Decisionmaking. Environ. Plan. A 1981, 13, 167–183. [Google Scholar] [CrossRef]
- Haag, G.; Dendrinos, D.S. Toward a Stochastic Dynamical Theory of Location: A Nonlinear Migration Process. Geogr. Anal. 1983, 15, 269–286. [Google Scholar] [CrossRef]
- Wilson, A. New roles for urban models: Planning for the long term. Reg. Stud. Reg. Sci. 2016, 3, 48–57. [Google Scholar] [CrossRef]
- Wilson, A.G. The Future of Urban Modelling. Appl. Spat. Anal. Policy 2018, 11, 647–655. [Google Scholar] [CrossRef] [Green Version]
- Kornhauser, D.; Wilensky, U.; Rand, W. Design guidelines for agent based model visualization. Jasss 2009, 12, 1. [Google Scholar]
- Epstein, J.M. Agent Based Models and Generative Social Science. Complexity 1999, 4, 41–60. [Google Scholar] [CrossRef]
- Harris, B.; Wilson, A.G. Equilibrium Values and Dynamics of Attractiveness Terms in Production-Constrained Spatial-Interaction Models. Environ. Plan. A Econ. Space 1978, 10, 371–388. [Google Scholar] [CrossRef]
- Wilson, A.G. Boltzmann, Lotka and Volterra and spatial structural evolution: An integrated methodology for some dynamical systems. J. R. Soc. Interface 2008, 5, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Rijk, F.J.A.; Vorst, A.C.F. On the Uniqueness and Existence of Equilibrium Points in an Urban Retail Model. Environ. Plan. A Econ. Space 1983, 15, 475–482. [Google Scholar] [CrossRef]
- Osawa, M.; Akamatsu, T.; Takayama, Y. Harris and Wilson (1978) Model Revisited: The Spatial Period-Doubling Cascade in an Urban Retail Model. J. Reg. Sci. 2017, 57, 442–466. [Google Scholar] [CrossRef]
- Wilson, A. Urban and Regional Dynamics from the Global to the Local: Hierarchies, ‘DNA’, and ‘Genetic’ Planning. Environ. Plan. B Plan. Des. 2010, 37, 823–837. [Google Scholar] [CrossRef]
- Clarke, M.; Wilson, A.G. The Dynamics of Urban Spatial Structure: The Progress of a Research Programme. Trans. Inst. Br. Geogr. 1985, 10, 427–451. [Google Scholar] [CrossRef]
- Wilson, A.; Dearden, J. Phase transitions and path dependence in urban evolution. J. Geogr. Syst. 2011, 13, 1–16. [Google Scholar] [CrossRef]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; Van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Nowak, A.; Ormerod, P.; Rosewell, B.; Zhang, Y.-C. Non-Equilibrium Social Science and Policy; Springer: Cham, Switzerland, 2017; ISBN 978-3-319-42422-4. [Google Scholar]
- Vandermeer, J.; Yodzis, P. Basin Boundary Collision as a Model of Discontinuous Change in Ecosystems. Ecology 1999, 80, 1817–1827. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef] [PubMed]
- Forrester, J.W. Industrial Dynamics. J. Oper. Res. Soc. 1997, 48, 1037–1041. [Google Scholar] [CrossRef]
- Weidlich, W.; Haag, G. A Dynamic Phase Transition Model for Spatial Agglomeration Processes. J. Reg. Sci. 1987, 27, 529–569. [Google Scholar] [CrossRef] [PubMed]
- Dearden, J.; Wilson, A. A Framework for Exploring Urban Retail Discontinuities. Geogr. Anal. 2011, 43, 172–187. [Google Scholar] [CrossRef]
- Dearden, J.; Jones, M.W.; Wilson, A. DynaMoVis: Visualization of dynamic models for urban modeling. Vis. Comput. 2015, 31, 1079–1088. [Google Scholar] [CrossRef]
- Ellam, L.; Girolami, M.; Pavliotis, G.A.; Wilson, A. Stochastic modelling of urban Structure. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).