1. Introduction
The relationship between urban design and science has always been highly debatable [
1,
2,
3,
4]. Using analytical methods in urban design has been a challenging question since they do not easily become part of the process [
5,
6]. Despite the difficulties, several authors claim that urban design should be more evidence-based [
7,
8,
9,
10], especially because of the increasing availability of data for cities and analytical tools, which opens up the possibility of a science of cities [
11,
12].
In such a context, it is worthy to review some of the Christopher Alexander’s theories. He is an architectural theorist pioneer in trying to find out better ways to design. Since the 1960’s, he has been outlining a theory of built space design that seeks to overcome the architectural/urban production as something conceived purely in arbitrary and subjective terms. Although he is best known by his seminal work
A Pattern Language [
13], the focus here relies on the theories presented in
The Nature of Order [
14], and related work [
15,
16]. In his recent work [
14,
15,
16], Alexander has proposed very instigating theories about the harmony and beauty seen in natural and man-made artefacts, although his concepts remain very hard to grasp and difficult to translate to practical applications. Here we try to bring such concepts closer to a science-based urban design development. First, we briefly introduce the main theories.
Wholeness is the central concept in recent Alexander’s work [
14,
15,
16]. It can be defined as a global structural character of a given configuration existing in space, both in natural and man-made things. Alexander also calls it a living structure because it emerges from an incremental process. He argues that everything has some degree of life. Of course, he refers to non-biological sense. His meaning for life is more related to coherence and harmony.
Wholeness structure is composed of primary entities called centres. Those centres support and intensify each other through the repeated occurrence of fifteen geometric properties: levels of scale, strong centers, boundaries, alternating repetition, positive space, good shape, local symmetries, deep interlock and ambiguity, contrast, gradients, roughness, echoes, the void, simplicity and inner calm, and not-separateness. Such properties describe how the centres interact with each other. Properties help to increase the coherence and the strength of any given centre and to generate new ones. Alexander believes that the fifteen properties play a major role in making the wholeness of a system, because of the recurrence of them in all the coherent systems observed by him through many decades.
Wholeness is, therefore, a recursively defined structure composed of centres, which in turn are composed of other centres. The successive application of transformations, in other words, computations, based on the fifteen properties lead to the formation of living structures. Such a process is harmony-seeking or wholeness-extending oriented [
16] since it seeks to preserve the previous structure. However, it only happens when transformations are based on the fifteen properties [
16].
As we can note, the idea of wholeness addresses the underlying structure of systems, namely its hidden quality. The existence of sub-structures—the centres and the sub-centres—addresses a scaling hierarchy. Such understanding helps to bring design process closer to a complex sciences approach. According to Alexander [
15], scientists who study biology and physical phenomena, for example, are passive in regards to the aspect of creation. The architects, on the other hand, are key proponents, whose project errors interfere in the lives of many people so they should be aware of the design process. Therefore, the creation of complex structures—which is the case of architecture and urbanism—should become an important scientific topic. Alexander suggests that aesthetic plays a key role in the co-evolution of complex systems since the transformations that lead to the emergence of harmony and beauty in nature obey universal rules—the 15 properties. If it is true, such a process should be understood in order to be applied to the design process.
Finally, Alexander [
14,
15,
16] argues that wholeness, namely the degree of life of a given configuration, is measurable since the properties can be objectively observed and described. However, the author himself admits that we still do not have a mathematical language or a computational method to achieve this. According to Alexander [
14] (pp. 364–367), although the measurement of wholeness relies necessarily on the human observer, it is not just a cognition problem, but something objective that exists in space. The author admits that we need a more objective and mathematical way to support the task of measuring wholeness in spite of his deep concern for human intuition, especially when analysing complex artefacts such as cities and building. He proposes a new research agenda to operationalise the harmony-seeking process [
16].
Therefore, the main challenge would be to establish some way of describing and modelling the harmony-seeking process, the fifteen properties and the idea of wholeness. A reduced number of authors [
17,
18,
19,
20] have attempted to embark on the path outlined by Alexander. Salingaros [
17] have suggested the first mathematical treatment for the degree of life. His measures are quite simple and present some limitation that indeed was highlighted by Alexander [
14] (pp. 469–472). Ekinoglu and Kubat [
20] and Jiang [
18,
19] have proposed interesting methods for measuring wholeness, the former based on entropy measure and the latter based on a complex network approach.
In line with Jiang’s research, this paper discusses the possibilities and drawbacks of operationalizing Alexander’s concepts from a network analysis perspective. We argue that there are much more possibilities to explore towards a configurational approach than previously exposed by Jiang [
18,
19]. We emphasize that a network approach is just one of the possible ways to explore Alexander’s ideas. Obviously, there is a diversity of possible approaches, although in a reduced number of scientific papers, as we have just referred to above.
The aim of this paper is contributing to the discussion of how to operationalise the harmony-seeking and centering process based on network analysis. This kind of research is important because it can lead to the development of a tool for assessing wholeness, in other words, a tool for supporting urban design decisions.
Firstly, we attempt to bring Alexander’s theories closer to an urban design context. Moreover, we attempt to bring it closer to an urban network perspective since we are concerned about configurational issues of urban design. Then, we highlight the diversity of spatial network analysis available in the field of urban configurational studies. It is illustrated with a case study, where we apply network modelling methods. Finally, we discuss possibilities of increasing the potentialities of a network approach to operationalising Alexander’s concepts. The paper concludes with the main drawbacks, challenging issues, and possibilities for future research.
2. Bringing Alexander’s Concepts to an Urban Design Context
Alexander’s theories, as previously exposed, are too abstract and generic to be straightforwardly applicable to urban design processes, or any kind of design process at all. Consequently, some interpretation is required, especially if we are committed to operationalizing measures. In order to make his concepts more concrete, we assume some delimitation.
The first one is to discuss wholeness and the properties within an urban design realm. In fact, urban design is still a broad field to deal with, since it covers a wide range of scales and aspects. Seen in these terms, urban design can embrace small details from streetscape, buildings typology, green areas and activities distribution, networks of infrastructures and even entire cities—to cite just a few examples. Fortunately, the broadness of Alexander’s work is not limited to a single scale. However, dealing with such a wide range of scales would be impossible. Thus, the scale addressed in the present study is the whole city scale, in other words, the urban planning scale. Defining a scale makes it easier to define what are the sub-components of the system, namely, the centres. If we are considering a city as the whole system, we can define the streets and built forms as the primary elements. Streets and buildings are precisely the key features in the structuring of urban morphology at this scale.
Several studies have shown that the configuration of the streets is a primary aspect in the structuring and dynamics of the cities and it has been explored extensively through a network approach in the urban configurational studies [
21,
22,
23,
24,
25]. Thus, the interconnectedness of the streets can be considered one of the most important aspects of the urban design in the scale we are addressing here. Similarly, the built forms can be considered as connected elements. Together with streets, buildings also contribute to give rise and to support the global character of the urban structure. Put it in other words, the built forms are as important as the street network, although studies attempting to include built forms are scarcer in the literature in the urban configurational literature [
26,
27,
28].
The main aspect we focus on is the configuration of the core elements of the urban structure: street and built forms. We are concerned about how the spatial elements connect to each other, as typically approached in configurational studies. Thus, we assume an urban network approach, in which the streets and built elements play a major role. Graphs are the principal mathematical language to describe properties of connected components [
29,
30]. Moreover, graph theory has been broadly used in urban studies [
6,
21,
23,
24,
25,
26,
27,
28,
31,
32,
33,
34,
35,
36]. This kind of work can be considered a particular field of urban morphology as it essentially addresses the configuration and the relationship between urban components. The main advantage is that the network properties of urban components can be mathematically manageable. In this sense, we argue here that this well-established research field can be useful to operationalise some of Alexander’s abstract concepts.
Besides, Alexander’s recent theories are very suggestive of a network approach. According to Alexander, the degree of life of a given centre is defined not by the centre itself but by its position in the entire field of centres [
14] (p. 459). The author gives us others clues that make us believe that a network approach seems to capture the fundamental idea of wholeness and degree of life. Alexander suggests that each centre—as a bit of geometry in the space—affects and changes the other centres [
14] (p. 415).
Another bridge between Alexander’s theories and a network approach is the scale-free property [
19]. Some complex networks present far more less-connected elements than well-connected ones so that their degree of connectivity reveal a power law distribution. It is called a scale-free network [
37]. Such property also has already been explored in urban studies [
25,
32,
33,
35,
36]. The underlying structure and scaling hierarchy of artefacts are some of the key points in Alexander’s theory, as previously exposed. In this sense, the network approach used in urban systems studies may be helpful to achieve it.
Finally, a network perspective on Alexander’s wholeness has already been suggested [
18,
19]. Jiang defines wholeness as a hierarchical graph, in which centres are described as nodes and their relationships as links. The author suggests a mathematical model for wholeness, in which: (a) PageRank score can measure the degree of life for each centre, and (b) ht-index [
38] can characterize the degree of wholeness for the whole system. PageRank (PR) score is an algorithm used to measure the centrality of websites. Jiang [
18] applies it to measure the centrality of nodes in order to capture the hierarchy of the components. Ht-index is based on head/tails breaks, which is a clustering algorithm for data with heavy-tail distribution. It can be used for classification and visualization of data, helping to characterize the levels of scale. Values are ranked in decreasing order and broken down by the average. Those above the average constitute the head and those below are the tail. This breaking process continues recursively for the head until the notion of far more small things is no longer present. Thus, ht-index can be defined as “the number of times that the scaling pattern of far more small things than large ones recurs” [
38] and can be used for comparing different systems.
The main problem in using PR is that it grasps only one characteristic of urban structure and it is not clear whether it is the best way to capture hierarchy. In fact, it is not clear if there is a better way to capture hierarchy since there are several different methods to measure urban centrality and obtain spatial differentiation. Besides, each centrality measure reveals different distribution patterns [
33,
34,
35]. Therefore, many measures other than PR could be used to identify hierarchy in a graph.
In this paper, we assume that Jiang’s suggestion is true, and that network analysis can bring a suitable mathematical language for dealing with Alexander’s insights. In the following sections, we discuss possibilities of improving such approach, considering the diversity of techniques in urban configurational studies unexplored to the task of measuring wholeness.
3. Urban Configurational Studies
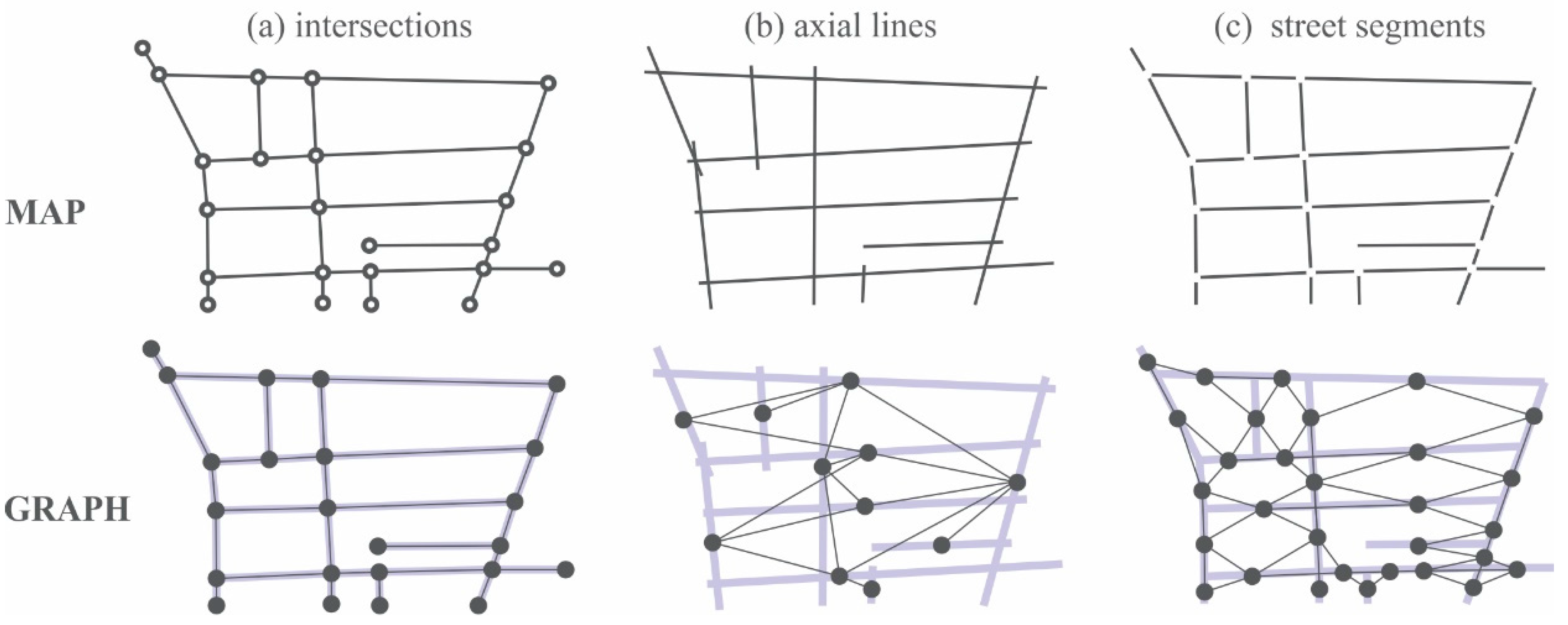
Typically, urban configurational studies use discrete components to represent the urban system, so that each component correspond to nodes and their connection links in a graph. There are three types of criteria used to define the discrete components [
39]: (a) preservation of geographic features, (b) maximum morphological units, and (c) minimum morphological units. In
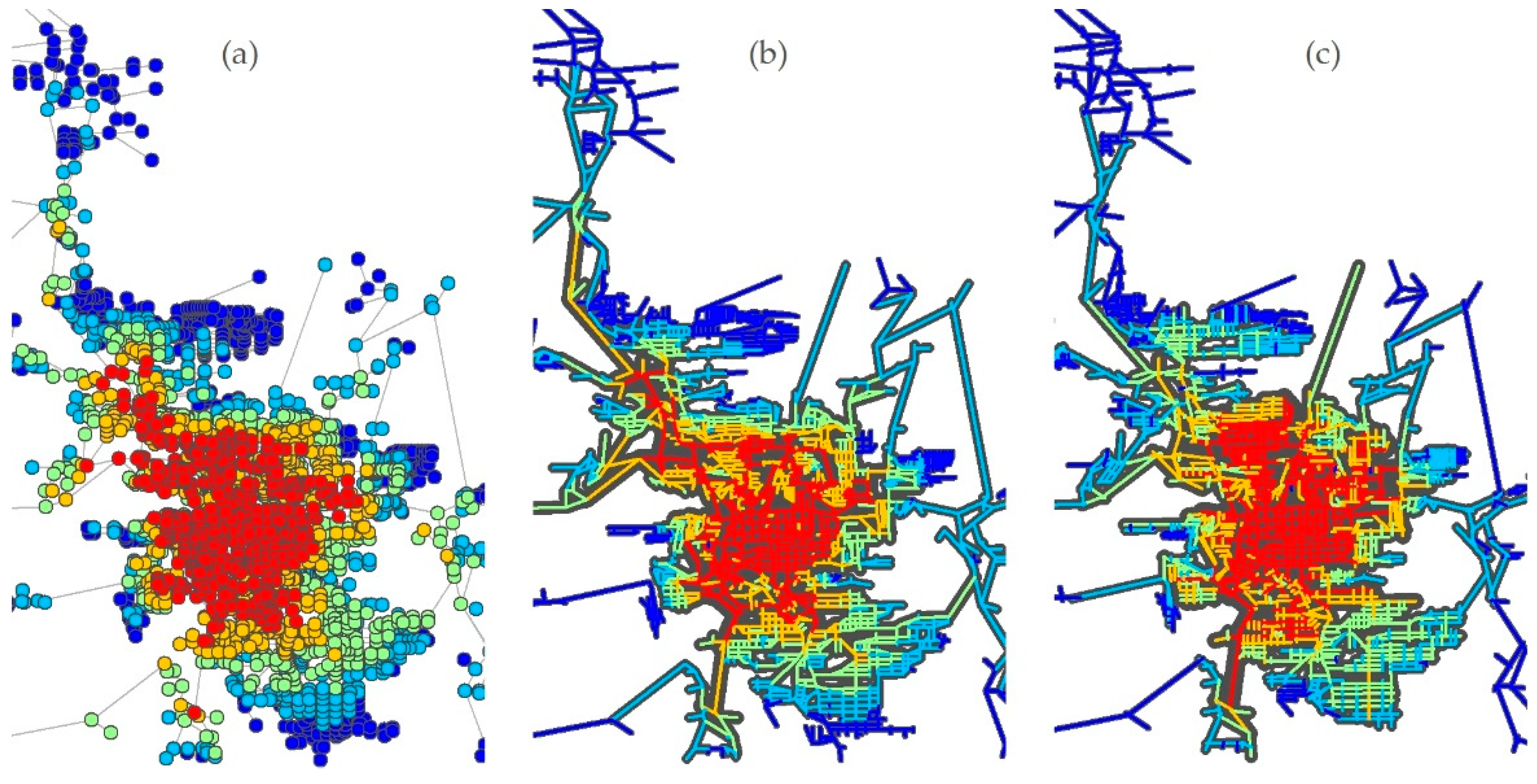
Figure 1, we can see one example of each criterion: (a) intersections, which preserves geographic features—distances between nodes; (b) axial lines, as maximum morphological units; (c) street segments, as minimum morphological units of streets network.
The first one “a” is useful when Euclidean distances are important, because the corresponding graph is equal to the map, as we can see in
Figure 1. This kind of representation is also known as a primal approach [
33,
34]. Both “b” and “c” are known as a dual approach [
35] since the graph is different from the map. In this case, Euclidean distances are deformed.
Descriptive systems like “b” and “c” give priority to streets network. The main difference between them is the level of aggregation of components. Maximum morphological units, such as axial lines [
21,
31] and continuity lines [
40], are highly aggregated models because the primary units—the street segments—are merged according to a criterion, which is usually cognitive. Meanwhile, minimum morphological units can be viewed as a disaggregated form of axial representation [
39].
Choosing the best descriptive system to model any problem is paramount because it strongly affects the results [
33,
34,
35,
39]. In fact, one of the crucial points to operationalise Alexander’s theories is how to represent the parts of a system. The parts, namely the centres, are the components of the urban graph. The examples in
Figure 1 address essentially the street network. However, we know that other features should also be considered as primary entities, at least the built forms since they are key components of the urban design.
One of the core ideas to Alexander is that assembled centres compose wholeness structure. Thus, the recognition of the parts of the system is an important step to operationalise wholeness. The discrete components of graphs, as simplified representations of reality, already do this job. The descriptive system presented in
Figure 1, commonly used in urban studies, can be considered as objective ways of recognising centres if we assume that each centre is a node in the graph.
Besides distinct descriptive systems, urban configurational studies have produced several graph-based methodologies to measure network properties of cities. We can group them into two types [
39]: (a) accessibility-based models, such as closeness centrality [
33,
34,
41] and integration [
21,
31]; and (b) centrality-based models, such as choice [
21,
31], betweenness centrality [
33,
34,
42] and the centrality measure developed by Krafta [
28]. The first type is also known as distance-based measures and the second as relative position-based. Each measure gives us a different picture of the urban structure, showing spatial differentiation among centres. If we combine different measures with the different descriptive system showed above, we will have a set of distinct schemes to grasp spatial differentiation. In other words, we have a number of different ways of identifying the hierarchical relationship between the entities.
4. Material and Methods
In the present paper, we will not suggest new methods. Rather, we will illustrate how the distinct measures and descriptive systems often used in urban configurational studies can produce different results. Thus, the following case study aims at illustrating some of the models described before. Moreover, this case study helps to discuss the possibilities of using the resulting patterns as analogies for some of the properties. We argue that such understanding is crucial to the development of new methods to grasp Alexander’s properties.
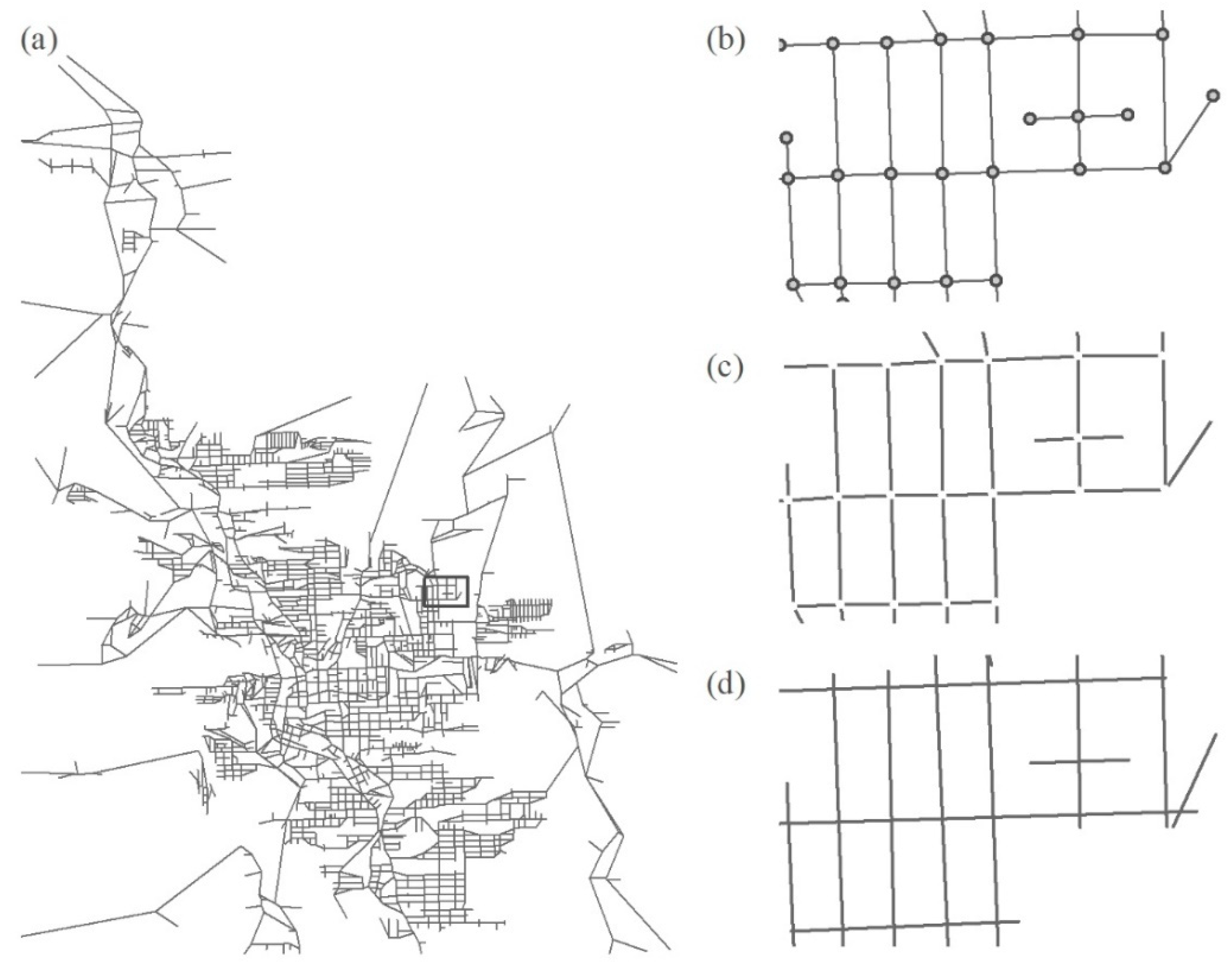
We model a real urban system, a medium-sized city in Brazil, which was chosen mainly because of its size. It is not too small nor too big. We divide the methodology into two steps. First, we explain the descriptive systems and the centrality measurement applied in this case, corresponding to the different manners to identify a hierarchical relationship in the urban system. Second, we suggest different manners to explore the results of the centrality scores from which we can identify possible connections with the geometric properties outlined by Alexander.
4.1. Descriptive Systems and Centrality Measures
The street network of the studied city is described in three different ways (
Figure 2): intersections, street segments, and axial lines. Each one has a corresponding graph, with a different number of units. We can consider each vertex of the graph as a centre. Then, we calculate three different centrality measures for each type of representation: closeness, betweenness and information centrality. These are classical centrality measures already used in urban studies [
33,
34]. They were chosen because they are capable of grasping the global properties of a system.
In network analysis, the nodes are classified in a range of values according to the score that is being used. Therefore, with this set of measures, we have three different way of identifying the hierarchical relationship between the nodes, namely the centres. Closeness centrality measures “to which extent a node is near to all the other nodes along the shortest paths” [
34]. Betweenness centrality measures to which extent a node lies in the shortest paths connecting other couples of nodes [
34]. Information centrality measures the drop in the network efficiency when removing a node, therefore it can be related to the capability of the network to respond to the deactivation of nodes [
34]. Mathematical formulation and deeper explanation of those metrics can be found in the literature [
33,
34,
41,
42].
We perform the measures using Morphometrics [
43], which is a software for urban network analysis developed by researchers from the Federal University of Rio Grande do Sul and the Federal University of Pelotas.
4.2. Exploration of the Centrality Measures Results
After performing the centrality measures, we have three different ways to characterize hierarchy among elements in three different descriptive system. Entities are ranked by values obtained through centrality models. In spite of that, the main question remains unaddressed. How can we measure the fifteen properties of Alexander—at least some of them?
Jiang [
18,
19,
38] uses the Ht-index to capture the levels of scale of a system. Whether it is a proper way of quantifying wholeness is arguable. However, it is certainly a good way to grasp the property levels of scale. It is at the same time an index and a visualization scheme. And most importantly, it is done from the statistical distribution of the centrality metrics. Consequently, we claim that analysing the distribution of the results, spatially as well as statistically, is an important step of operationalizing Alexander’s ideas since the statistical distribution and the spatial patterns can enable us to identify some of the fifteen properties, other than levels of scale.
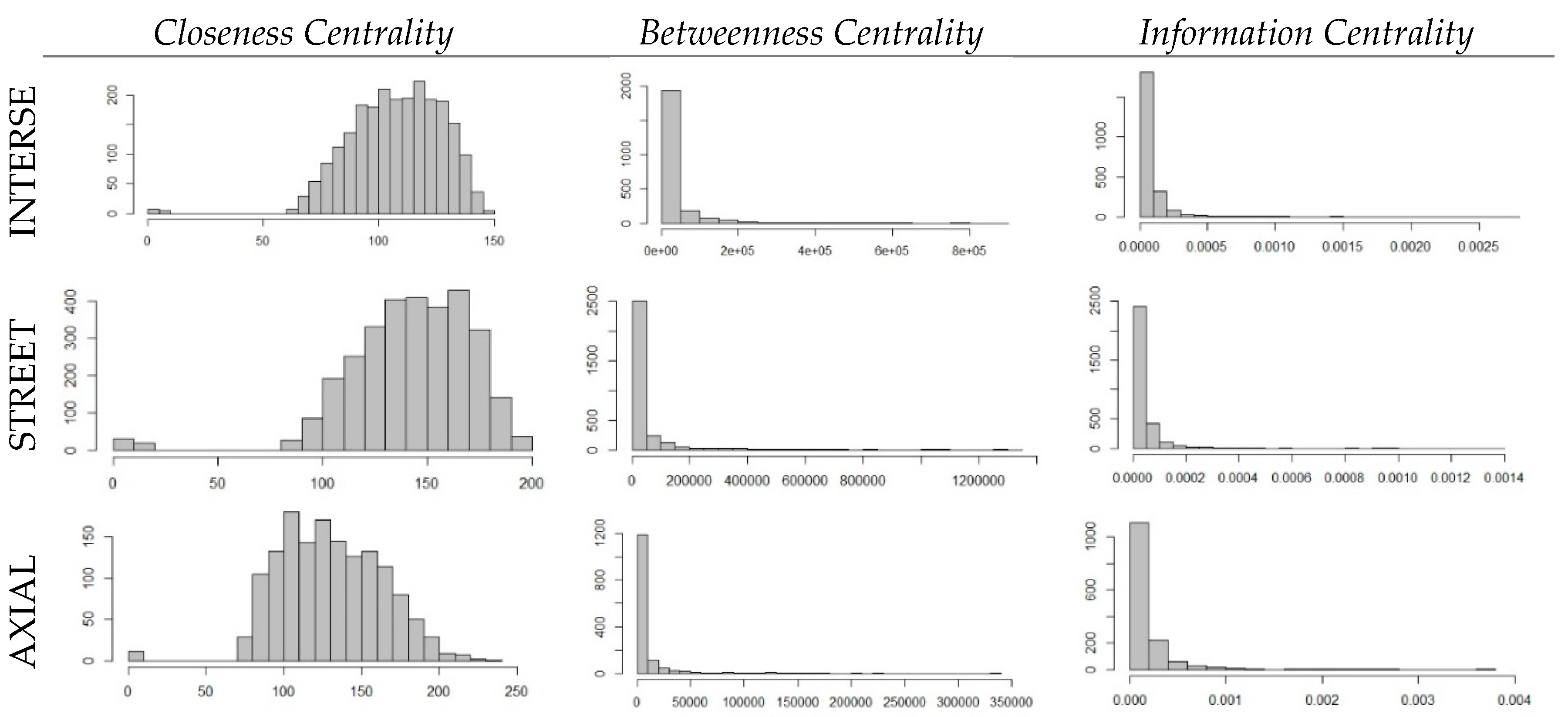
Here we have explored the results of the centrality measures in two ways so that we could see how different measures and different descriptive systems affect them. The first one is the spatial distribution of the results, which enables a visual analysis. The spatial distribution of the centrality measures can be visualized through Geographical Information Systems (GIS). The second one is the statistical distribution of centrality measures, which is analysed by histograms built in RStudio.
5. Results
5.1. Spatial Distribution
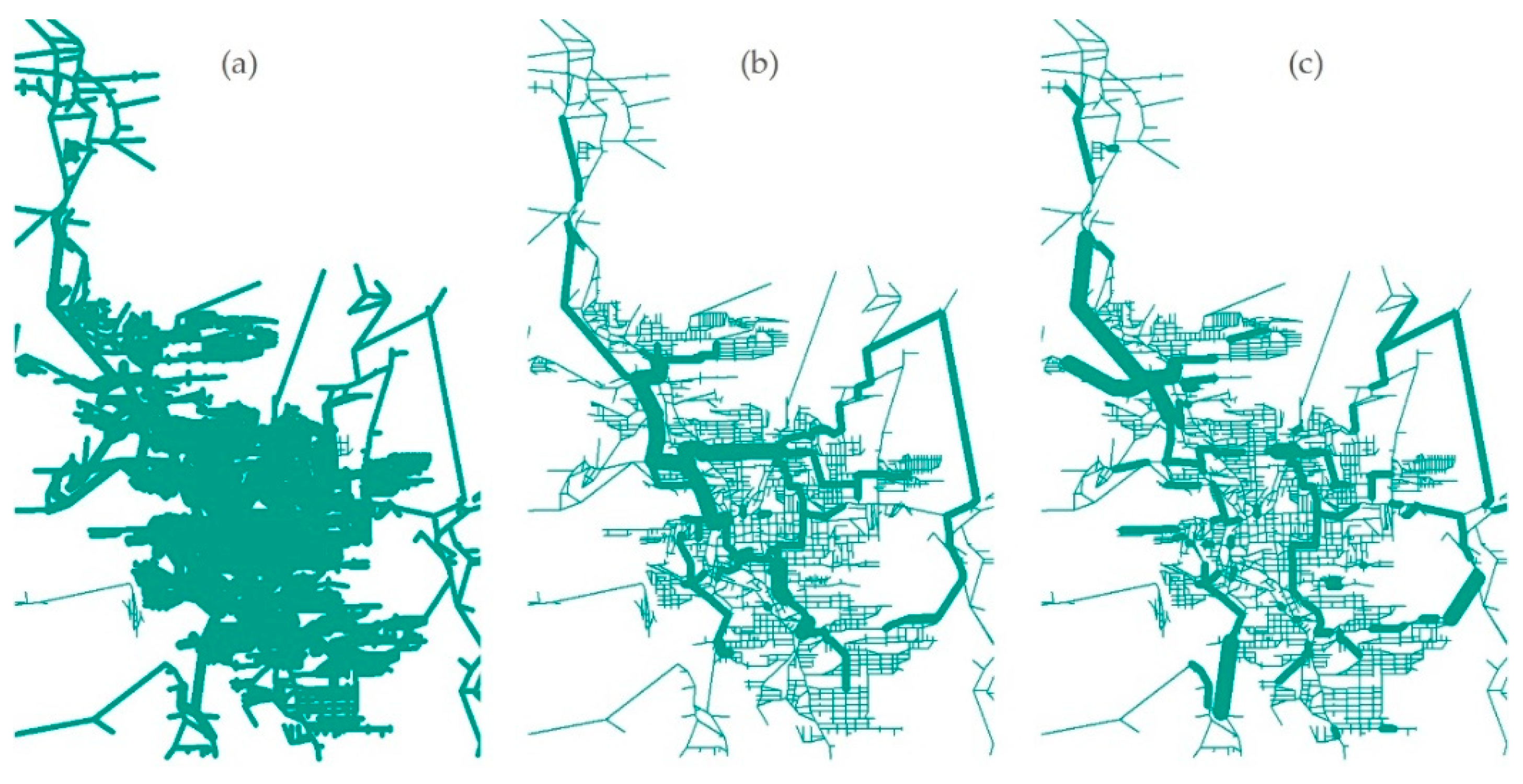
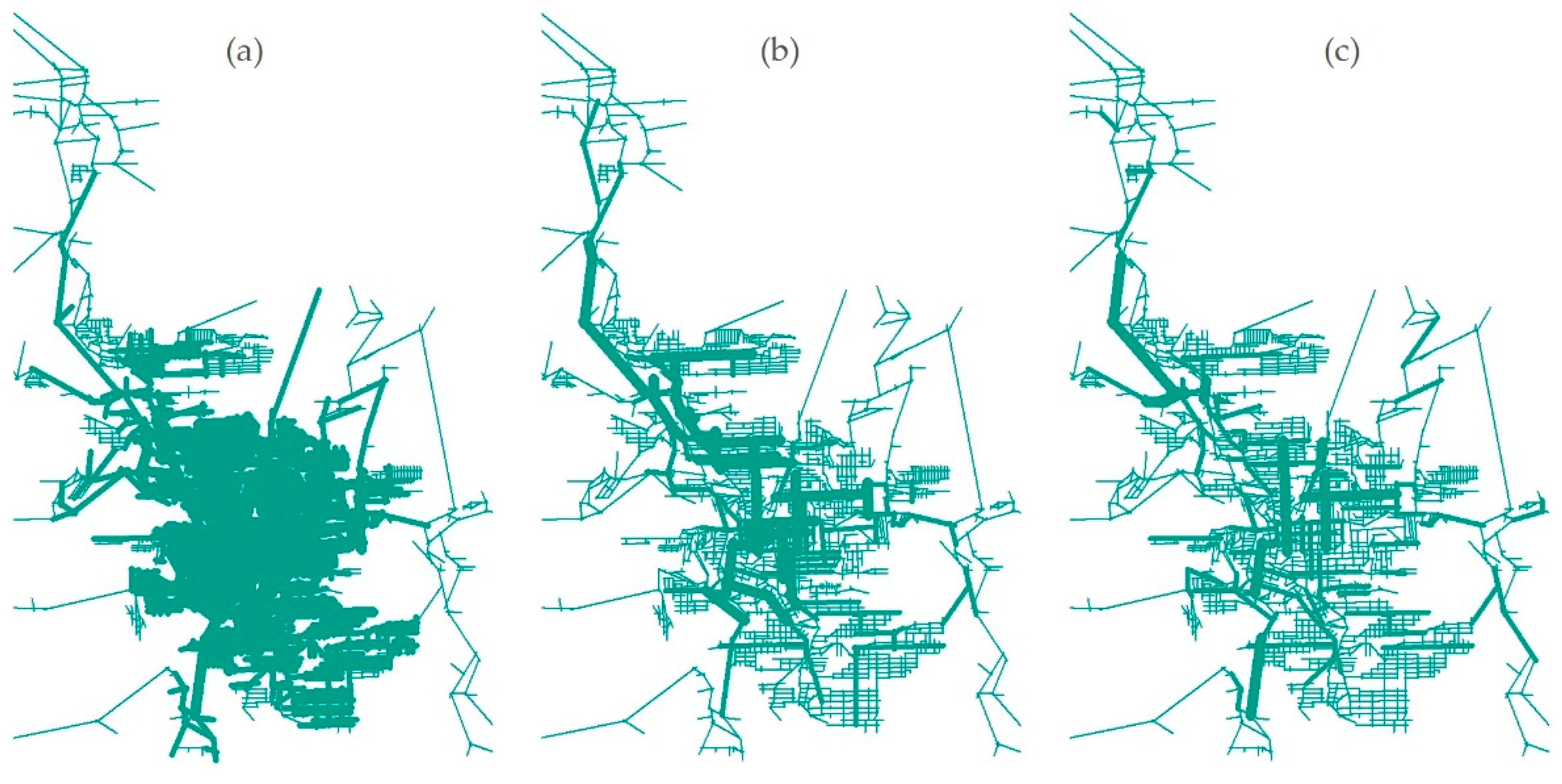
We have standardized the visualization in order to make it easier to compare the different descriptive systems. In spite of building the maps with different types of features, like lines or dots, we display all of them as graduated symbols. Hence, the larger features correspond to greater values, while the smaller ones correspond to lower values. Graduated symbols allow revealing the hierarchy of the values better than colour ranges, for most of the cases. The statistical method used to obtain the intervals is Natural Breaks.
As we can see in
Figure 3,
Figure 4 and
Figure 5, each measure has a different spatial pattern of distribution. Except for closeness centrality, the others present distinct patterns of distribution depending on the descriptive system.
5.2. Statistical Distribution
The histograms (
Figure 6) show the statistical distribution patterns of the centrality measures. Betweenness and information centrality are more likely to have a heavy tail distribution, while closeness centrality is more likely to have a normal distribution, no matter the descriptive system. The characteristic distribution of the values of betweenness and information centrality suggests exponential or power law distribution. However, using simply a histogram to verify power law histogram is a very poor way to verify a scale-free distribution. Of course, it must be confirmed by more powerful statistical packages in future investigation.
5.3. Centrality Patterns and Alexander’s Geometric Properties
Here we attempt to recognize analogies between the resulting patterns from centrality metrics and some of Alexander’s properties. First, the visualization of the spatial distribution of the results for each centre allows us to recognize strong centres, one of the fifteen properties; although it changes accordingly to the metric which is being used and to the descriptive system. The 10% or 20% of the highest values for each measure could be considered as being the strong centres.
Second, we can see the gradient property since we have different classes of values, represented by features of different sizes. As we can see, closeness centrality is not good to grasp it, since it does not have a strong distinguishing power. By contrast, betweenness and information centrality seem to be promising measures.
As closeness centrality does not have a strong distinguishing power, the better visualization scheme is a colour ramp. In
Figure 7, we use a colour ramp in which results are grouped into six classes. This way we can distinguish
gradients for this centrality measure. Consequently, we adopt the quantile method rather than Natural Breaks, which is better for normal distribution samples. Regarding the visual pattern of distribution, in this type of measure, the highest values tend to converge for the geographic centre of the system since it is distance-based.
Regarding statistical distribution, we can see that distance-based measures, such as closeness centrality, are more likely to have a normal distribution. Measures based on the relative position of vertices, such as betweenness and information centrality, are more likely to have heavy tail distribution. It means that they have stronger differentiation power, which is a good way to identify hierarchical levels in a given configuration. Thus, they can be related to
levels of scale, being an alternative to PR centrality suggested by Jiang [
18,
19].
6. Discussion
In this section, we discuss how to improve the network approach already suggested in the literature. Each of the centrality measures combined with different descriptive systems reveals distinct spatial and statistical distribution. In this case study, closeness, betweenness, and information centrality seem to have potential to be used as methods for operationalizing Alexander’s concepts, since they can be related to some of the geometric properties, especially if we look at the spatial and statistical distribution of the results. Of course, it needs to be more developed.
Adopting an approach similar to Jiang [
18,
19], within a network perspective, instead of using only PR centrality [
18], we can use a set of different centrality measures, or to choose the measures that best fits the design objectives being carried out. For example, information centrality [
33,
34] can show the vulnerability of the system, meanwhile, closeness and betweenness show potential for retail activities [
21,
31]. Fortunately, there are many pieces of evidence in the literature about the relationship between centrality measures and aspects of real life.
Alexander’s theories are too abstract to be applied straightforwardly to urban design. However, the visualization of the resulting patterns obtained through the centrality measures can be connected to some of the fifteen geometric properties. In this sense, a network approach can be seen as a bridge between Alexander’s concepts and practical application to urban design. In the future, it can be explored as a monitoring tool. Such a tool can be thought of as a supporting tool for urban designers, as well as a monitoring tool for city growth. Of course, we still need a lot of research to have a better understanding of the potential of the fifteen properties and wholeness to indicate quality to the built environment.
We are aware that some of Alexander’s core ideas remain unaddressed. Thus, we highlight some of them, for future research. The first one relates to the approach used to build the urban graph and the components considered as centres. The three methods used in the current paper deal mainly with the street network. However, it is a poor approach, since urban design deals with many other crucial aspects, such as built forms and activities. Thus, we need to find out how to incorporate them in the urban graph, overcoming the strict street network view, commonly used in urban configurational studies. The next step of this research is to study more detailed descriptive systems, which include the built forms, for example.
There is another worrying issue regarding the urban graph. Some of the descriptive methods tested in this paper are regular networks, which means that they have a uniform degree of connectivity. However, the best way to grasp wholeness and scaling hierarchy is using a complex network perspective, as suggested by Jiang [
12,
13]. Regarding this issue, axial lines seem to have some advantage. Nevertheless, a small-world network could also be achieved by incorporating built forms as components of the graph.
Finally, another issue that remains unaddressed is the notion of the properties as transformations, namely being part of a harmony-seeking process. We could gain more insights if we consider centrality as a process rather than static measures. It could be done by running the centrality measures at various time snapshots. Such a procedure could be used as a tool for monitoring the design process and urban development of a city.
7. Conclusions
This article took a network approach to Alexander’s findings. The focus was to bring Alexander’s abstract theories into the urban design realm, specifically addressing configurational issues. Since the aim was contributing to the operationalization of Alexander’s concepts through a network perspective, we attempt to discuss how to improve the network approach already suggested in the literature.
The approach adopted enhances the idea that we can address the notions of wholeness and centres from a network perspective, as previously suggested [
18,
19]. Nevertheless, we observe that a more careful selection of descriptive systems and measuring methods should be done considering the variety of methods available. In this paper, we attempt to identify existing network techniques that seen to be suitable for the task established by Alexander, beyond Jiang’s suggestion. A key point to move forward is deeper investigation of how to describe the urban elements, how to build the graph, how to identify spatial differentiation, and how to visualize the results.
Therefore, the current paper provided some clues for further studies on the challenging task of operationalizing Alexander’s from a network perspective. It could be supported by spatial network analysis techniques, GIS, and statistical packages. This kind of research is important because it can lead to the development of new tools for supporting urban planning and design. However, we depend on more research addressing network properties of urban behaviour to produce a useful tool derived from Alexander’s theories.