1. Introduction
The introduction of Space Syntax [
1] in urban studies has certainly had the merit of highlighting the importance of urban topology for activities connected with the use of open spaces, and in particular for the movement of pedestrians [
2]. In addition, its reformulation in terms of graph theory has opened new theoretical and use perspectives, linked to the processes of diffusion on dual graphs [
3]. Shifting attention from the Euclidean geometry of urban space to its connectivity has shown that the city is a tool to connect urban phenomena: a given phenomenon, for instance the location of commercial activities, can have different effects when it manifests in differently connected spaces [
4].
Among the many variables that define the behavior of a city, Space Syntax has considered almost exclusively spatial ones. Axial lines or lines of sight are the fundamental element of the model [
2], variables whose topology is conditioned by the shape of the city. In graph formulation, these lines are represented by graph nodes, while where they cross determines the graph’s edges. As made evident in [
5], the axial methods changed the ideas about the structure and the function of a city [
6,
7,
8] dramatically, but also showed the possibility to be generalized [
9,
10,
11]. An exhaustive discussion about the methods to assess the continuity of the axial line can be found in [
3].
Since the choice of this variable is to some extent arbitrary, many proposals have been advanced to make it objective [
6,
7,
12]. In any case, the resulting graph
always consists of open spaces
and connections between them
where
. It is important to note that the graph represents neither the geometry nor the topology of the city, but rather the way in which the city connects the axial lines.
On the basis of this observation, we can imagine that nodes v of the graph are generic urban variables, for example the amount of urban greenery, pollution levels, the income of inhabitants or even the usual Space Syntax axial lines. These quantities are naturally geolocalized, but their connection is conditioned by the structure and shape of the city. It is therefore possible to establish these connections and study how the city of green areas, income or services, and of course also the “classic” city of axial lines, are organized.
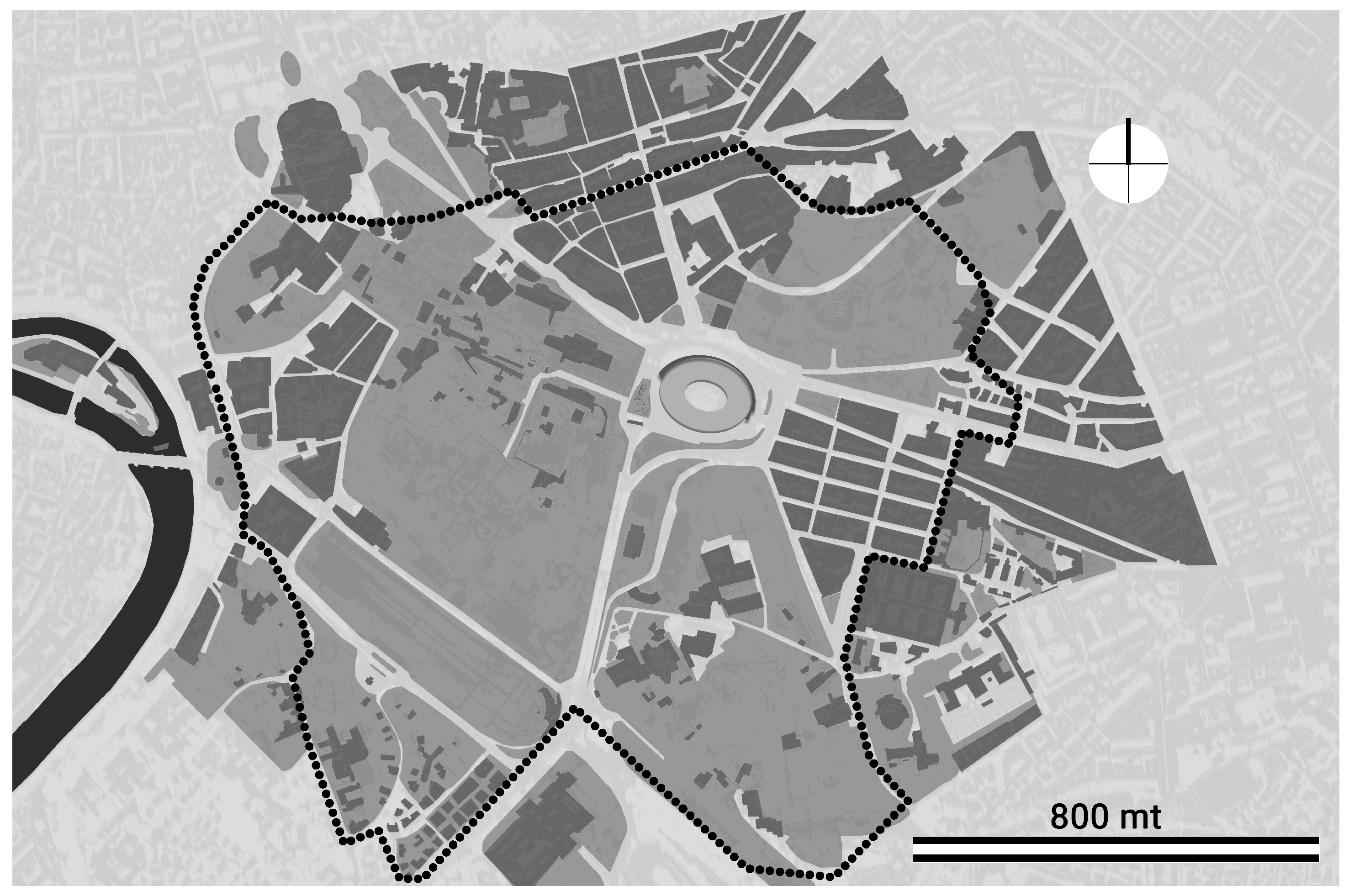
In this paper, we propose a rigorous method to extend Space Syntax to generic variables. As a case study, we investigate the consequences of pedestrianizing a central archaeological area in Rome (Italy).
The paper is organized as follows. In the next section, we illustrate the method to obtain the generalized graph and show how, in the particular case of axial lines, the same results are obtained as with the Space Syntax approach. In
Section 3, we use the method to study pedestrian mobility in the central archaeological area of Rome, comparing the current situation with the layout proposed by Roma Tre University. In
Section 4, we show the results of the proposed technique, and how the method makes it possible to examine an urban project using the characteristic quantities of generalized Space Syntax. Finally, in
Section 5, we discuss the criticalities and future developments of the method.
2. The Model
Basic variables of Space Syntax are the axial lines
, which in their more general definition [
5] belong to a generic
V set. These variables represent a property of the space (the visual lines embraced by the gaze) but are not located in a point. The interaction between two of them
is represented by their intersection: if the corresponding
and
visual lines meet, then
and
, otherwise f
. This property, however, is not defined by
u and
v variables, but by the inner structure of the city that contains them. In many parts of Manhattan, for example, these lines connect two separate sets of a bipartite graph [
13], while, in a medieval city, the nodes are much more interconnected [
5].
In general, consciously or unconsciously, city planners establish a connectivity criterion for these lines [
5]. However, variables
are generic variables and may indicate urban properties different from visual lines. Thus, for instance, nothing precludes us from identifying
v with the use of a street, which is pedestrian, driveable, semi-pedestrian, etc.; the variable therefore measures a property of that street.
There are at least two main reasons that suggest generalizing the space syntax theory. The first is of theoretical nature: the graph theory is so wide and full of deep results that can enlighten many aspects of the city behavior, while the city is represented in terms of generalized graphs. The second one is related to the city viewed as the connecting structure of the urban features.
To give an example, a blindfolded walker detects a different city from the axial one. However, the “acoustic city” is generated by the same topology of the “axial city”. To understand the global urban behavior, a method is needed to deal with the acoustic space syntax as well as the spatial one. We would then like to use the results and techniques of Space Syntax to understand how the structure of the city affects the interaction between these uses. To do so, we introduce a rigorous process of constructing the corresponding graph.
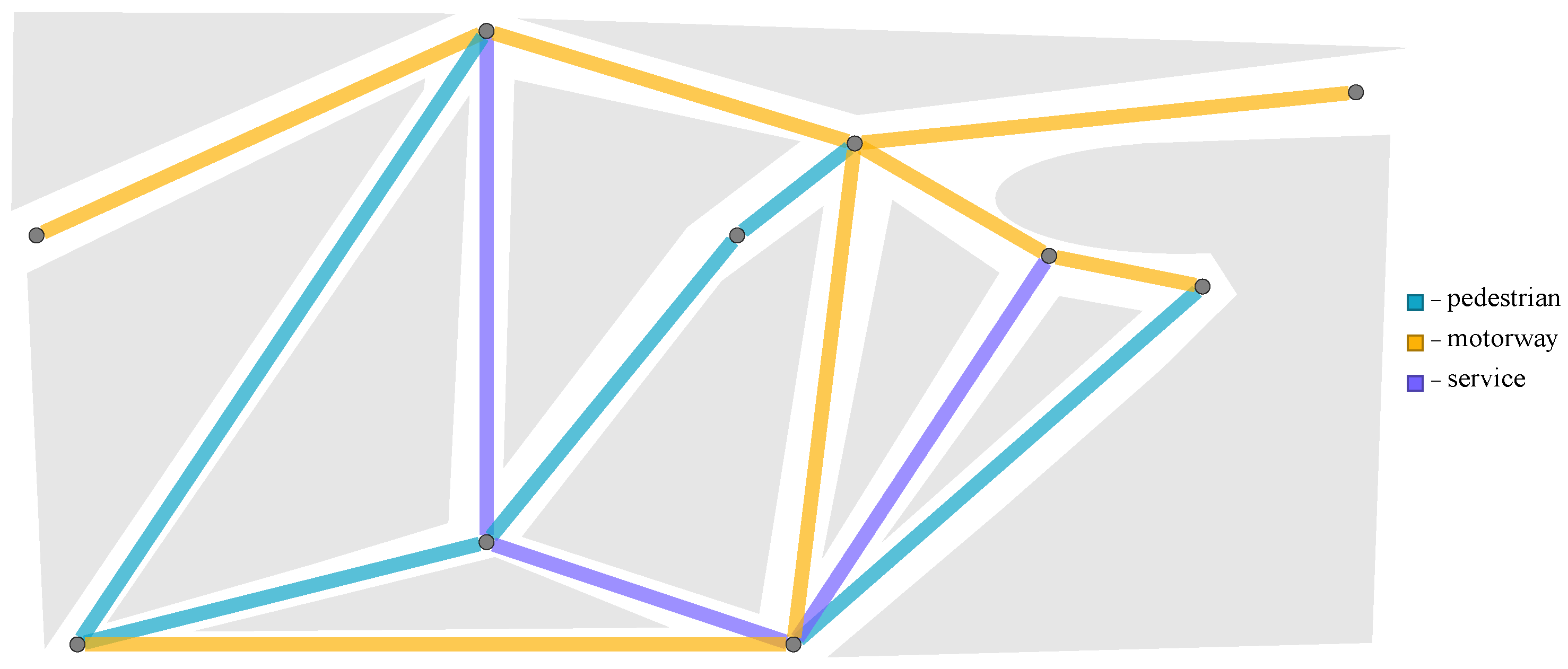
Consider a generic road graph
, where the vertices are the intersections or other road-spots and the edges are their connections, and superimpose it on a map of the city as in
Figure 1. At the end of this section, we show that, if the nodes are sufficiently dense, all the results are insensitive to the choice of this graph.
Different colors indicate different uses of the streets: pedestrian, driveable and service, while grey areas represent inaccessible spaces. Each color is therefore a property of space. In the particular case of Space Syntax, properties are the axial lines.
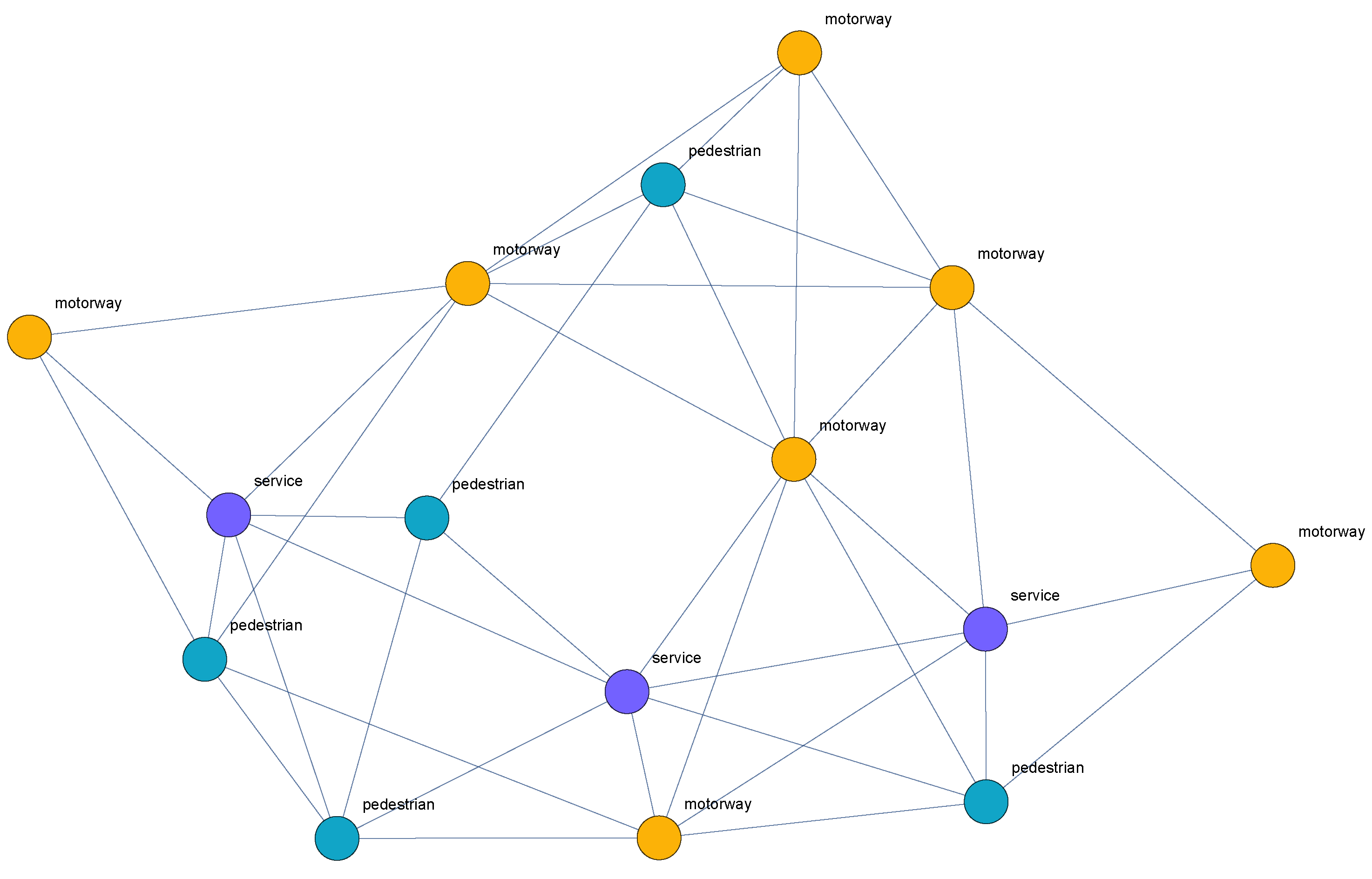
From graph
G of
Figure 1, we can construct the line graph
, the nodes of which derive from the edges of
G. If two nodes of
, that is two edges of
G, have a node in common, then they are connected in
. In substance, the edges of
G become nodes of
, and are only connected when the two starting edges cross each other. The line graph of
Figure 1 is shown in
Figure 2.
We can immediately see that the properties of the
G edges become properties of the vertices of
, which is a colored (non-proper vertex coloring) non geolocalized graph. Graph
then describes the topology of the city in relation to the property we chose to study. We recall that, in the language of graph theory, a proper colored graph is a graph where two adjacent nodes always have different colors [
14]. We also remark that in the proposed model the resulting graph describing the connectivity among the urban variables is alway a proper colored graph.
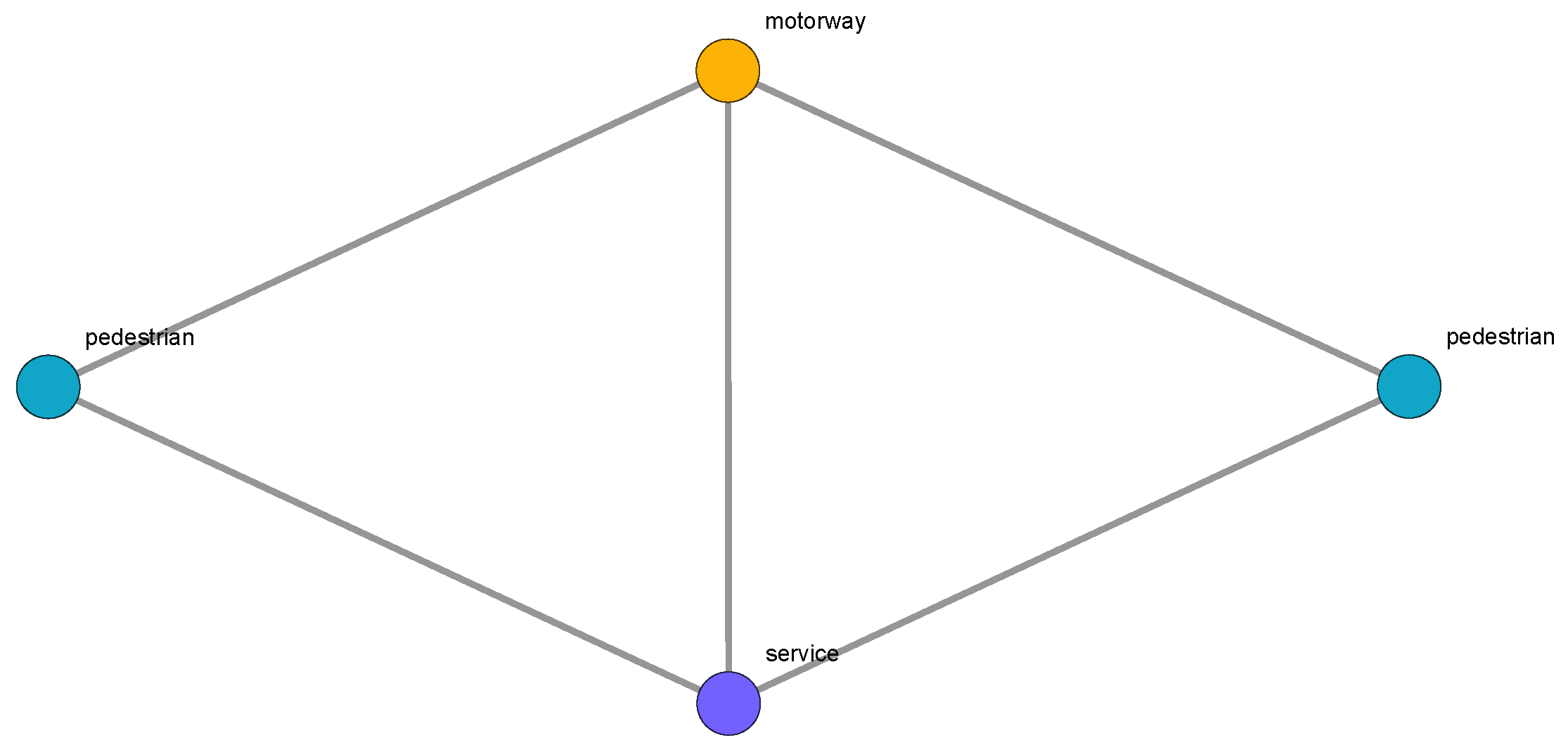
The next step is to contract the nodes of
that are connected and have the same color. A set of nodes connected with the same property can be represented by a single node, but only if in the contraction process all the nodes maintain the original connections with the nodes of different color. We thus obtain the contracted line graph
. The result of our example is shown in
Figure 3.
We observe that in
Figure 3 pedestrian zones are separated from motorway and service areas, which was also evident when looking at graph
G. However, when analyzing a large space with thousands of connections, the connective structure is not immediately evident. Moreover, as we see in the following section, in the contracted graph
it is possible to measure all the parameters of Space Syntax (and not only), such as relative asymmetry, centrality, degree distribution or spectral gap. In this case, however, these measurements do not refer to axial or visual lines, but to the property we have chosen to label the
G edges.
We emphasize that the line graph and the contraction procedures can not be inverted [
5]. In fact, if we contract the edges before computing the line graph, we obtain different and inconsistent results. For example, if we invert the two procedures for the graph in
Figure 1 we have a connection between the two pedestrian nodes that does not exist. We also note that if we had chosen visual lines as labels, we would have obtained exactly the same results as with the Space Syntax approach.
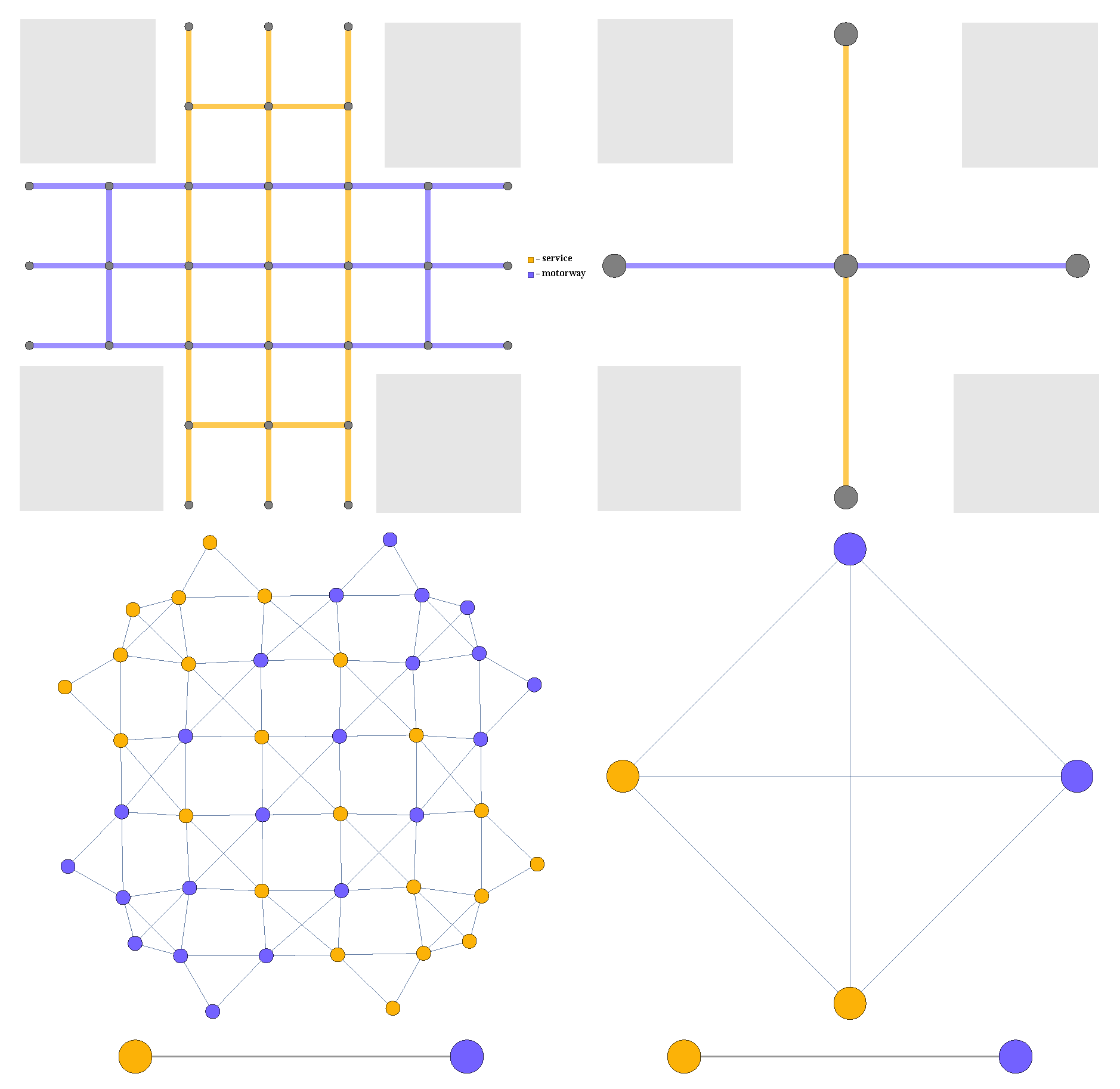
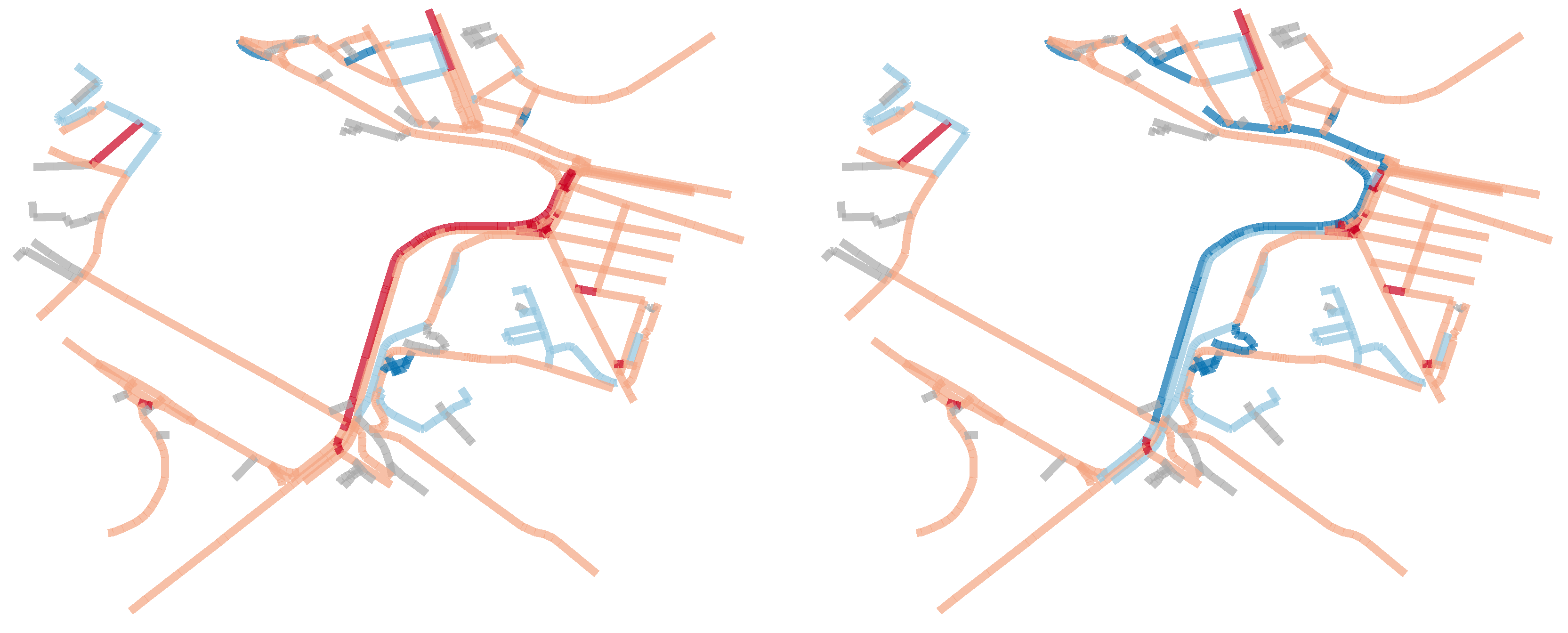
Finally, we notice that as long as the primary graph is sufficiently dense and the labels are properly chosen, all the results are insensitive to the choice of the primary graph. Consider for example the crossroad of
Figure 4. The two contracted line graphs are identical, but the first primary graph is more dense and detailed than the second one. In general, it is possible to replace the primary graph with a regular lattice with suitable labels and with the edge length shorter than the width of the street.
4. Results
We can examine the graph in
Figure 8, obtained in the previous section with Space Syntax methods, bearing in mind that the measurements do not refer to spaces and their connections, but to road uses and their connections.
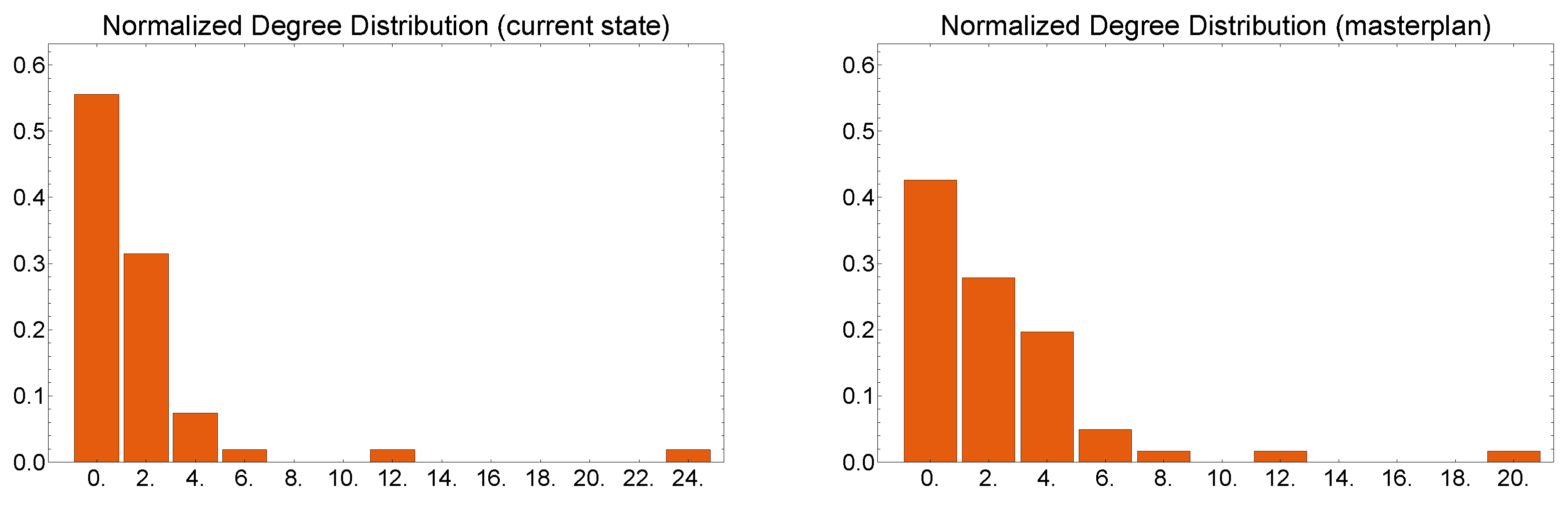
The degree distribution shows the first difference between the status quo and the Master plan (
Figure 9). Currently, there are few hubs connecting different road uses, while in the project some of these hubs are transformed into nodes with a low degree of connectivity, making the graph more entangled and therefore inherently more fluid. The hub with 24 edges decreases in degree to 20 and the grid is more connected, as shown in
Figure 8.
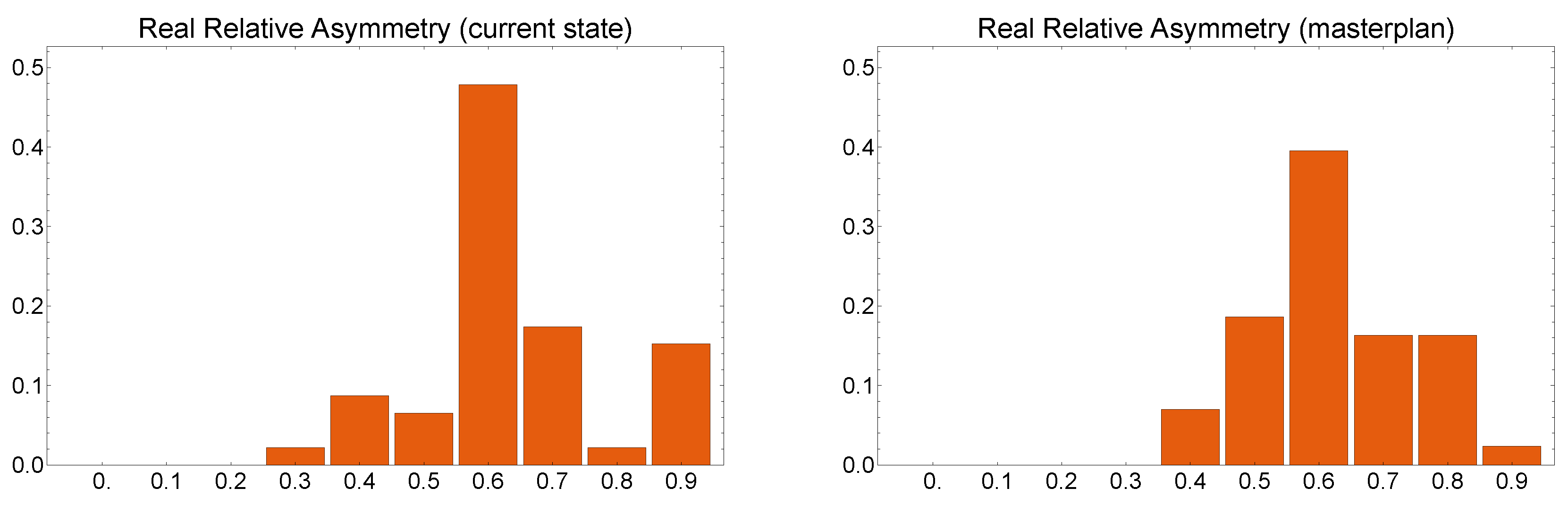
Real Relative Asymmetry (RRA) provides a measure of the integration or segregation of the city [
1]. In the case of Space Syntax, the city integrates or separates the axial lines in a generic sense; in our case, it integrates or separates the uses of roads. The distribution of this quantity shows that the histogram of
Figure 10 moves a little to the left, towards a topology that is less segregated in the Master plan than in the current situation. The pedestrianization of Via di San Gregorio does not in fact eliminate the carriageways, but widens and improves the parallel pedestrian route. This layout makes it possible to maintain the connectivity of motor traffic, but at the same time connects different footpaths and reduces pedestrian segregation.
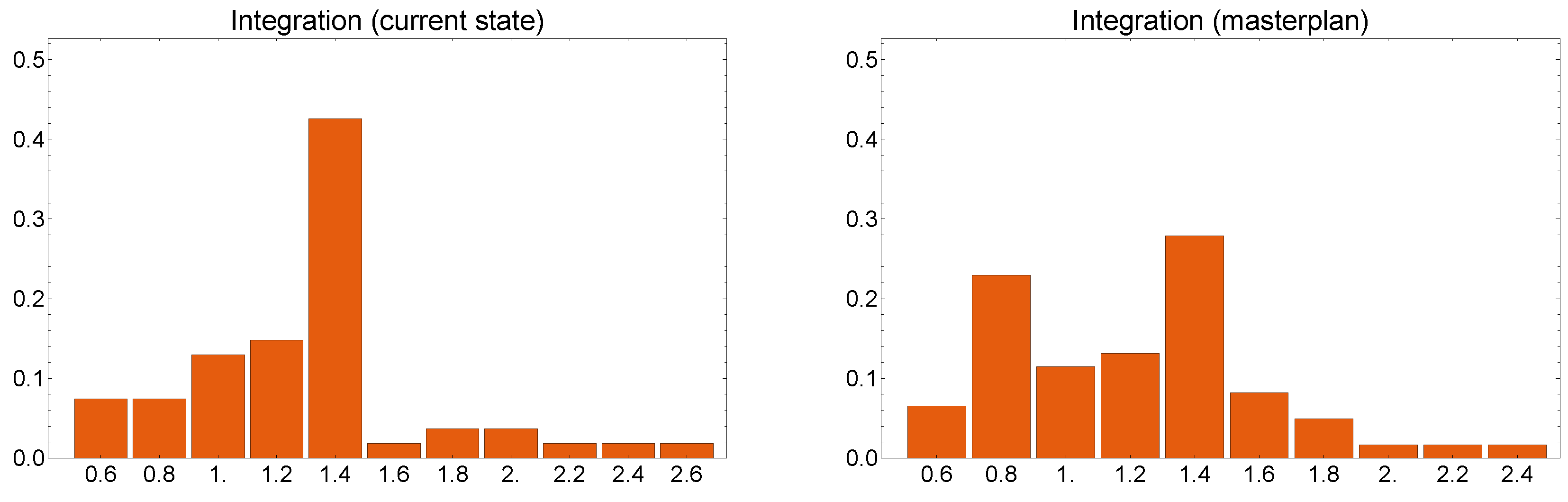
The distribution of Integration [
1], shown in
Figure 11, clarifies the proposed method and the efficiency of the measures suggested by the Master plan. In our case, contrary to what happens in classic Space Syntax theory, it does not measure the number of (normalized) steps needed to move from one space to another, but the number of different (normalized) road-uses that need to be changed. The difference with respect to the space syntax of the axial lines is not large. In our case, spaces are characterized by the use in terms of mobility and interactions between different uses; in the “classic” case, by their visibility and interaction of views.
In both cases, the information we obtain is related to topological character and we have no information about the size of the spaces or the time it takes to travel the roads. However, metric information can be used as a primary graph label
and become an additional parameter of the topological description. From
Figure 10, we can see that the Master plan distributes the integration in a more uniform way, moving it towards greater connectivity.
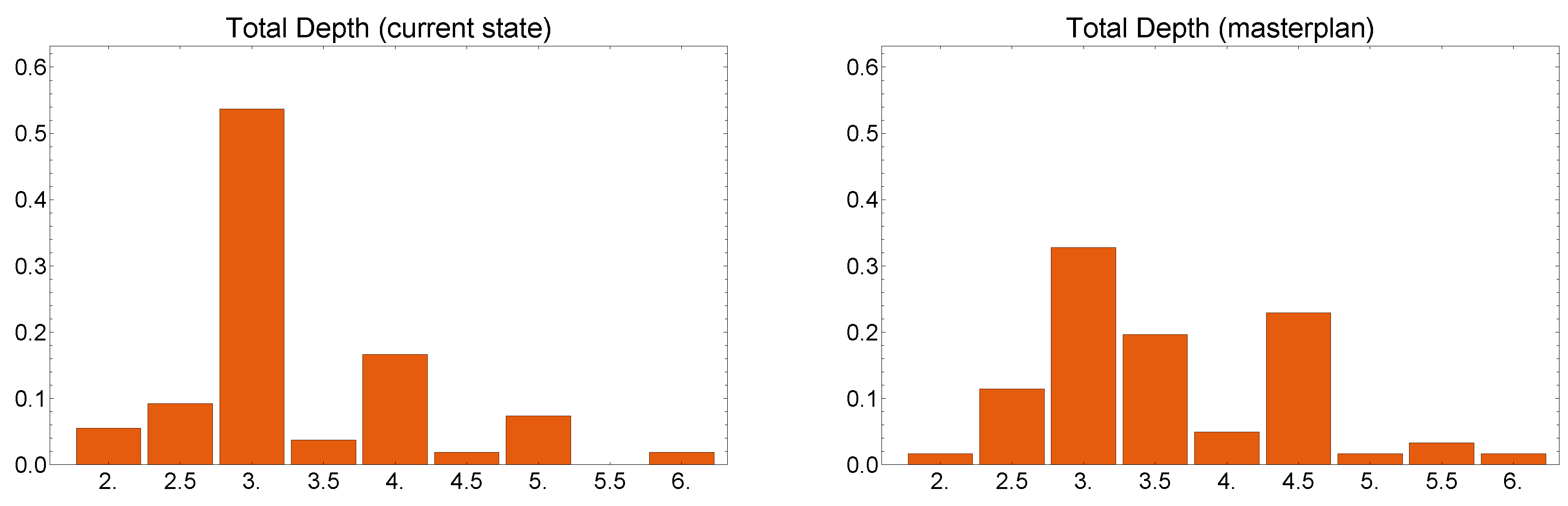
Finally, in
Figure 12, the last measure of Space Syntax we consider is Total Depth, which indicates the sum of depths from a root line to all others, depth meaning the fewest number of changes of lines intervening between the root and another [
1]. Here, too, we represent its distribution because the aim of the Master plan is to make these quantities more uniform. In fact, the plan for Via di San Gregorio amplifies the histogram, making the probability of crossing a road use, passing from one use to another, more uniform.
In this section, we indicated the urbanistic quantities that are most relevant for evaluating the effects of the Master plan with respect to the status quo, but all the characteristic variables of space syntax can be calculated on the graph of
Figure 8.
The tool developed makes it extremely easy to compare qualitatively and quantitatively. Analyzing the project, it is evident that a minor pedestrianization intervention has a very significant effect on the general connectivity of the area and on the interchange between different mobility criteria. However, we underline that, as with Space Syntax, the method is not used to design, but only to objectively evaluate the effects of a plan.
5. Discussion
We introduced a generalization of Space Syntax to extend the quantities that describe axial lines to generic urban variables. The method is based on the construction of a primary graph whose edges are labeled and categorized by the values of selected variables. The choice of the primary network can be absolutely generic, as long as it is sufficiently dense. For simplicity, we chose to identify the edges with road sections, but we could have superimposed any grid on the map of the city. Superimposing a dense square grid or random network on the city and coloring the edges with the values of the corresponding variables, we obtain a graph that, once transformed into a line graph and then contracted, always produces the same result.
In fact, it is the city itself that connects urban properties: relationships do not change when we modify the method of measuring them. We also observe that use of the proposed method clarifies some aspects of Space Syntax that are not evident in the original formulation, in particular the statistical nature of many urban quantities. In this sense, greater reliability of the results is obtained when dealing with very large graphs. However, this does not mean that Space Syntax is more reliable for studying a large city than a building, but rather that, in the analysis of small spaces, it is necessary to superimpose a denser network, or equivalently to measure the quantities that interest us in a very detailed way.
In fact, if we model the primary graph of a building by means of a dense regular lattice, we can take into account the micro accessibility of the space, which could be determined for example by furniture, information sources, illumination or possible services. The continuous limit for the space syntax quantities when the lattice edges size goes to zero gives the effective quantities of interest. If a simple graph gives the same result of a dense one, we say that the simple model is reliable.
Finally, let us point out that the proposed method makes it possible to compare different variables. For example, we could have measured noise pollution currently and under the Master plan, and compared the corresponding graphs and corresponding quantities of the generalized Space Syntax. The model of interaction between different graphs will be discussed in a later paper.