Spatial Heterogeneity of Sustainable Transportation Offer Values: A Comparative Analysis of Nantes Urban and Periurban/Rural Areas (France)
Abstract
:1. Introduction
- it evaluates the value of alternatives to single-occupant car use in both urban and periurban/rural areas;
- it looks at the spatial heterogeneity of these values within each subarea;
- it considers original transport infrastructures in such types of analyses (hedonic price method), namely carpool areas in periurban/rural areas and a bike-sharing system in an urban area.
2. Literature Review
3. Presentation of the Econometric Models
3.1. Hedonic Price Model
3.2. Spatial Models
- (1)
- Spatial AutoRegressive Model (SAR) [37]:where Y is the variable explained, X is the matrix of the exogenous variables, is an error term, and β is the vector of regression coefficients. The SAR model accounts for a spatial dependence on the endogenous variable: the price of the house sold (Y) depends on the prices of neighboring houses, being the spatial parameter to be estimated.Y = ρWY + Xβ + ε
- (2)
- Spatial Error Model (SEM) [37]:where Y is the variable explained, X is the matrix of the exogenous variables, is an error term, and β is the vector of regression coefficients. The SEM model is specified with an autoregressive structure of the error term, where λ is the spatial parameter to be estimated.Y = Xβ + ε with ε = λWε + µ
- (3)
- Spatial Durbin Model (SDM) [37]:The SDM model combines the dependence effects on the explanatory variables and on the endogenous variable. The spatial autoregressive process is applied to both the explained and explanatory variables. and γ are the spatial parameters to be estimated. This model can potentially remove the bias caused by the omitted variables.
- (4)
- Geographically Weighted Regression (GWR) [38]:where (ui,vi) represents the geographical coordinates of location i. The GWR model aims to detect the spatial heterogeneity of statistical relationships by exhibiting the spatial patterning of local regression coefficients. It extends the traditional regression framework by allowing coefficients to vary throughout space. One weighted regression is performed per data point, according to a spatial weighting scheme giving more importance to nearer neighbors than farther ones. A key point of the GWR model is therefore to calibrate an appropriate kernel function (see Section 5).
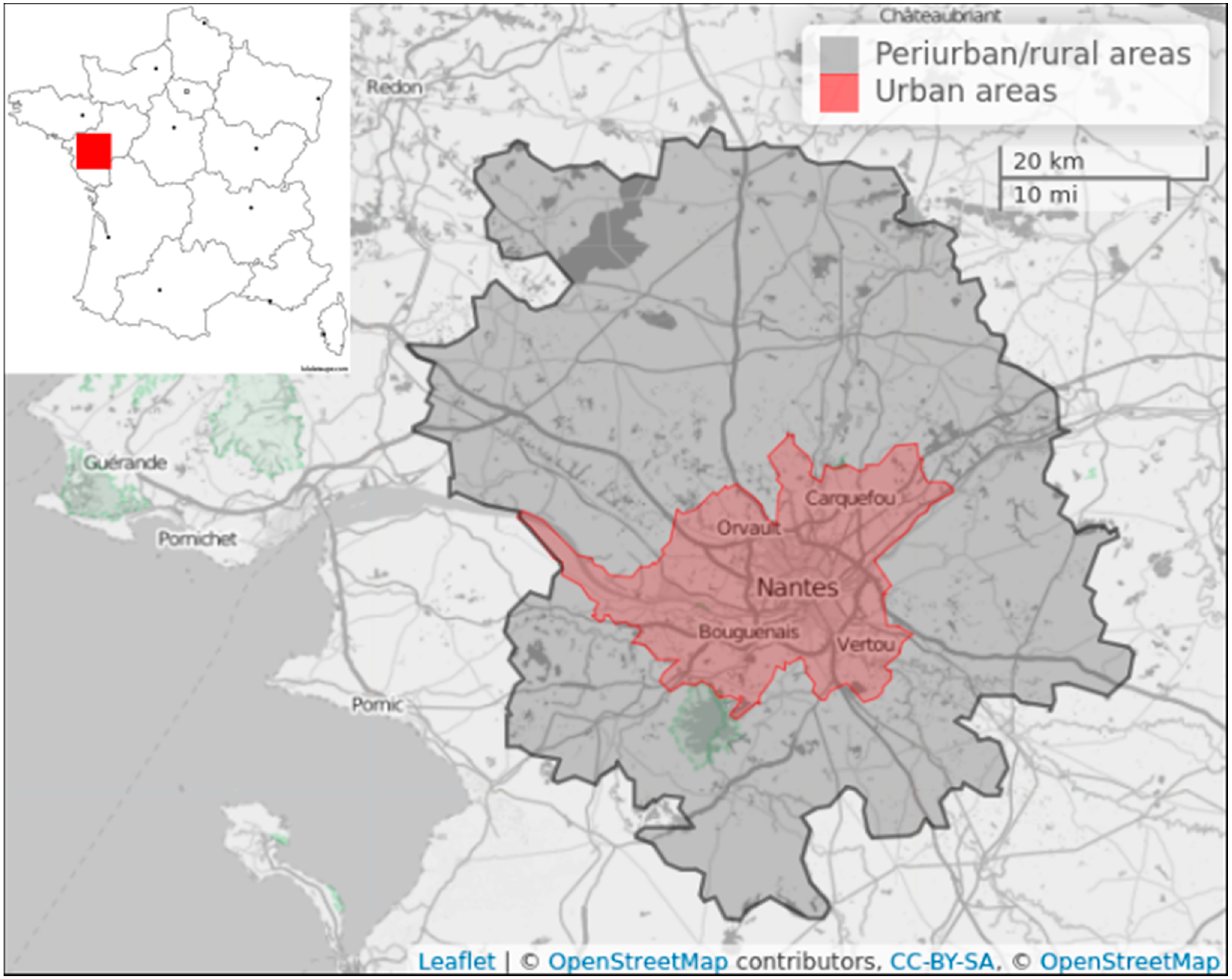
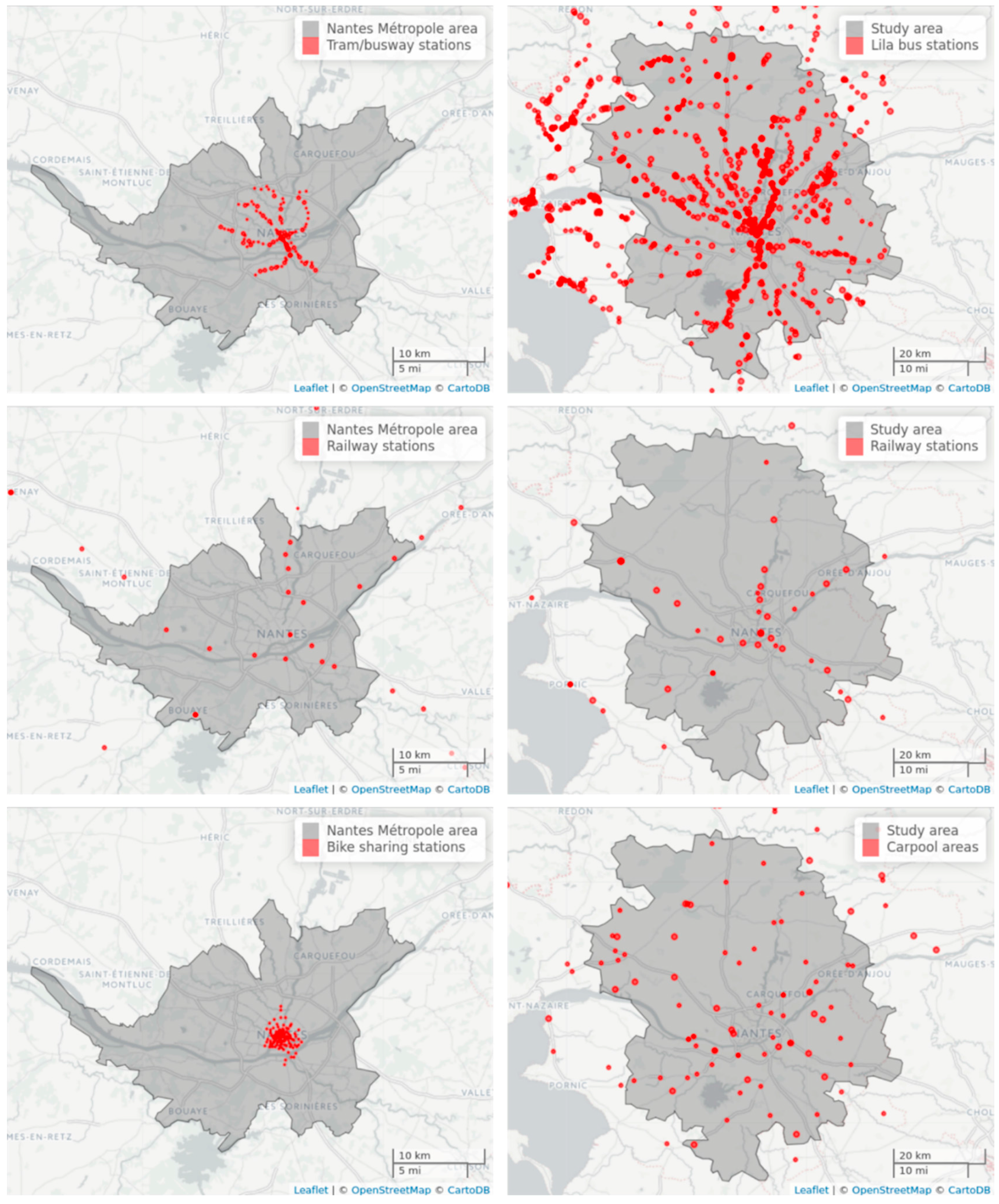
4. Study Area and Database
4.1. Nantes Urban and Periurban/Rural Areas
4.2. House-Related Variables
4.3. Spatial Variables
4.4. Descriptive Statistics
5. Model Calibration and Selection
6. Results
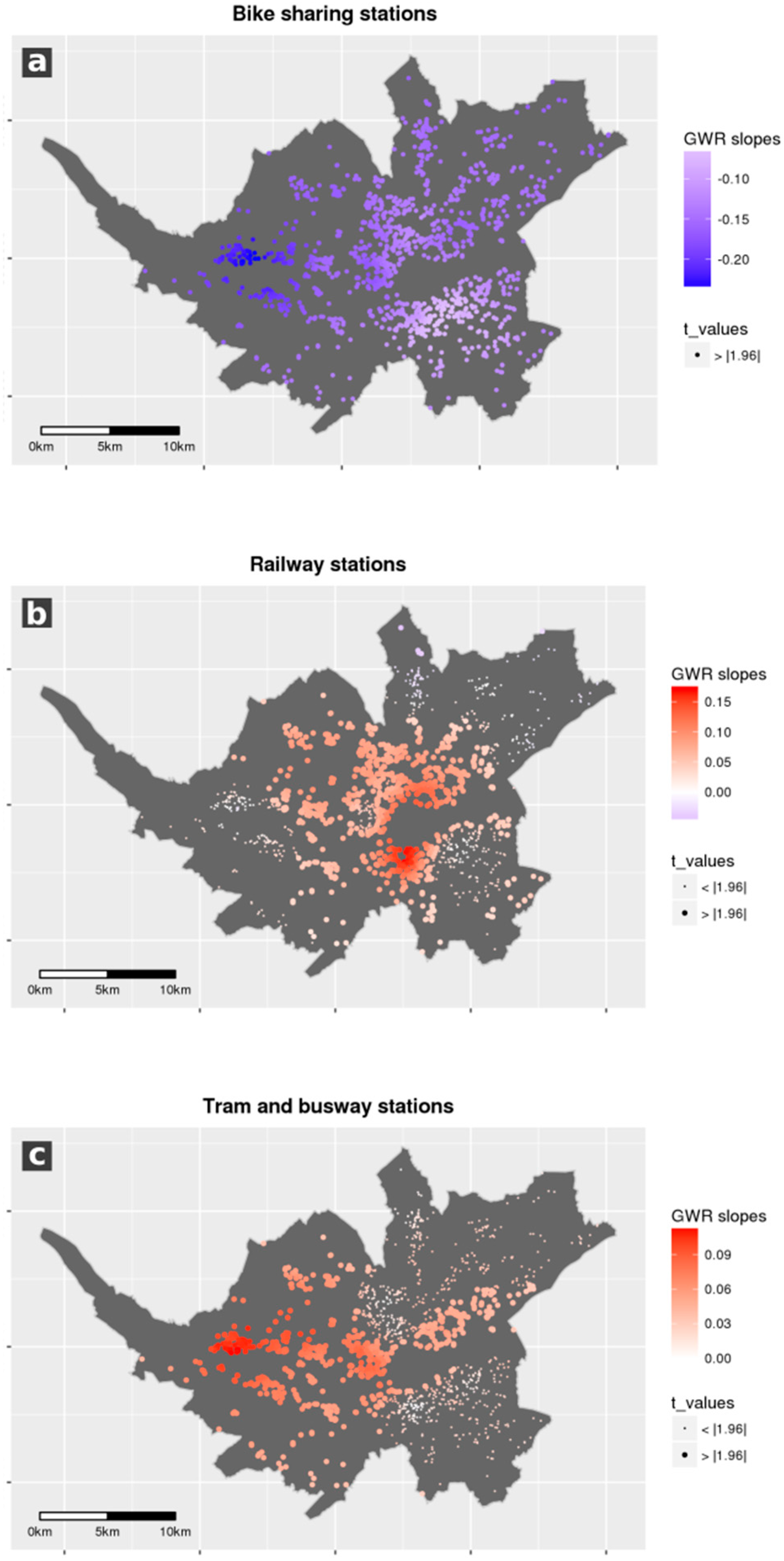
6.1. Model Results for the Urban Area (Nantes Métropole)
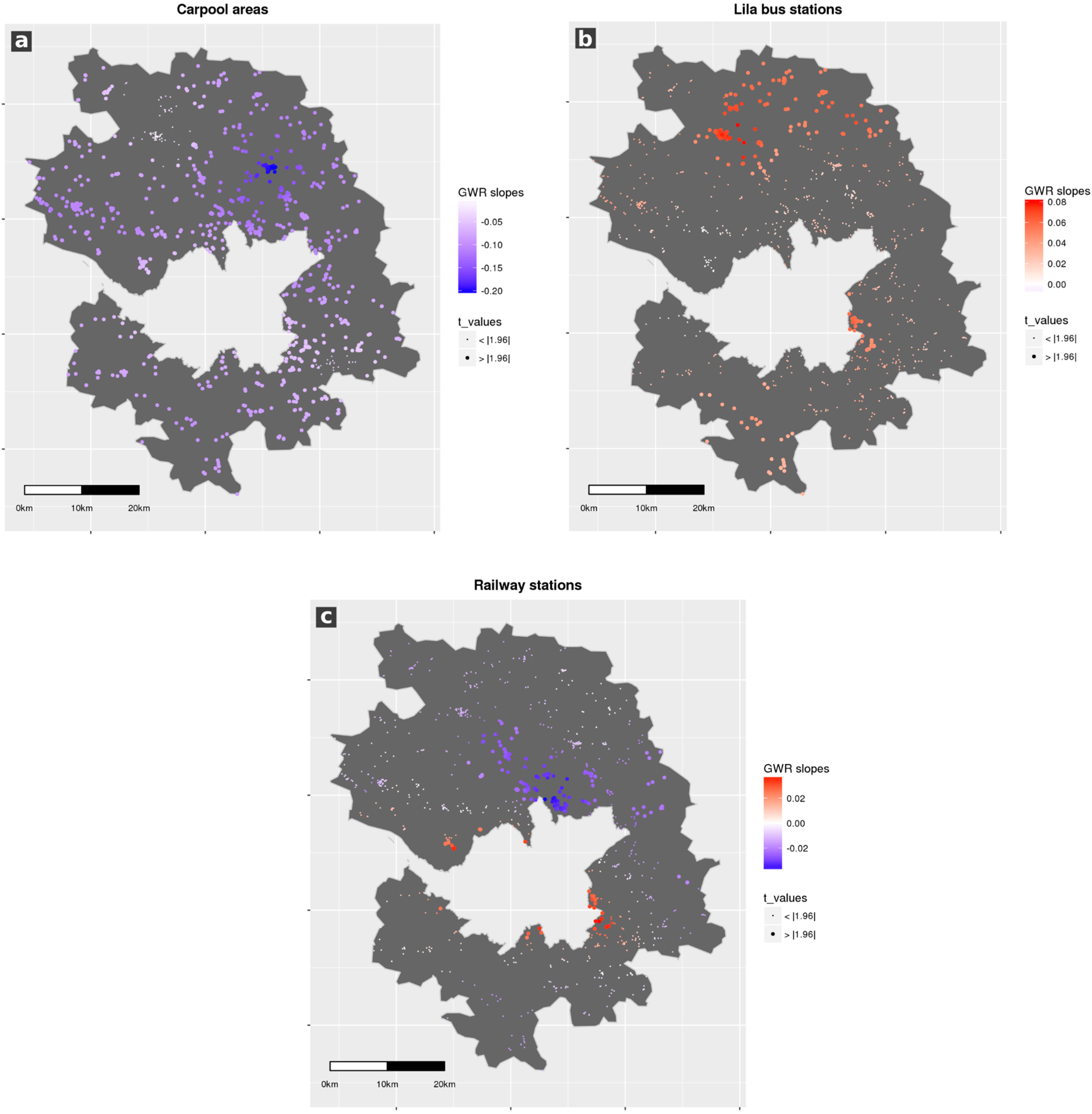
6.2. Model Results for the Periurban and Rural Areas
7. Discussion
7.1. Urban Area (Nantes Métropole)
7.2. Periurban and Rural Areas
8. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- European Environment Agency. Climate Change, Impacts and Vulnerability in Europe 2016; European Environment Agency: Copenhagen, Denmark, 2017. [Google Scholar]
- French Ministry of Ecological and Inclusive Transition. Les Comptes des Transports en 2015; French Ministry of Ecological and Inclusive Transition: La Défense, France, 2016; p. 184. [Google Scholar]
- Commissariat Général au Développement Durable. Chiffres clés de l’Environnement; Commissariat Général au Développement Durable: La Défense, France, 2016; p. 72. [Google Scholar]
- Bulteau, J. Tradable emission permit system for urban motorists: The neo-classical standard model revisited. Res. Transp. Econ. 2012, 36, 101–109. [Google Scholar] [CrossRef]
- Cohen, J.P.; Paul, C.M. The impacts of transportation infrastructure on property values: A higher-order spatial econometrics approach. J. Reg. Sci. 2007, 47, 457–478. [Google Scholar] [CrossRef]
- Billings, S.B. Estimating the value of a new transit option. Reg. Sci. Urban Econ. 2011, 41, 525–536. [Google Scholar] [CrossRef]
- Efthymiou, D.; Antoniou, C. How do transport infrastructure and policies affect house prices and rents? Evidence from Athens, Greece. Transp. Res. Part Policy Pract. 2013, 52, 1–22. [Google Scholar] [CrossRef]
- Diao, M.; Leonard, D.; Sing, T.F. Spatial-difference-in-differences models for impact of new mass rapid transit line on private housing values. Reg. Sci. Urban Econ. 2017, 67, 64–77. [Google Scholar] [CrossRef]
- Le Boennec, R.; Salladarré, F. The impact of air pollution and noise on the real estate market. The case of the 2013 European Green Capital: Nantes, France. Ecol. Econ. 2017, 138, 82–89. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Beckerich, C. Biens Publics et Valeurs Immobilières; ADEF: Paris, France, 2001. [Google Scholar]
- Fritsch, B. Tramway et prix des logements à Nantes. Espace Géogr. 2007, 36, 97. [Google Scholar] [CrossRef]
- Boucq, E.; Papon, F. Assessment of the Real Estate Benefits Due to Accessibility Gains Brought by a Transport Project: The Impacts of a Light Rail Infrastructure Improvement in the Hauts-de-Seine Department; ISTIEE Istituto per lo Studio dei Trasporti Nell’Integrazione Economica Europea: Trieste, Italy, 2008. [Google Scholar]
- Nguyen-Luong, D.; Boucq, E. Evaluation de l’Impact du T3 sur les Prix de l’Immobilier Résidentiel; Institut d’Aménagement et d’Urbanisme: Paris, France, 2011. [Google Scholar]
- Martínez, L.; Viegas, J. Effects of transportation accessibility on residential property values. Transp. Res. Rec. J. Transp. Res. Board 2009, 2115, 127–137. [Google Scholar] [CrossRef]
- Bowes, D.R.; Ihlanfeldt, K.R. Identifying the impacts of rail transit stations on residential property values. J. Urban Econ. 2001, 50, 1–25. [Google Scholar] [CrossRef]
- Weinberger, R. Light rail proximity: Benefit or detriment in the case of Santa Clara County, California? Transp. Res. Rec. J. Transp. Res. Board 2001, 1747, 104–113. [Google Scholar] [CrossRef]
- Cervero, R.; Duncan, M. Transit’s value-added effects: Light and commuter rail services and commercial land values. Transp. Res. Rec. J. Transp. Res. Board 2002, 1805, 8–15. [Google Scholar] [CrossRef]
- Hess, D.B.; Almeida, T.M. Impact of Proximity to Light Rail Rapid Transit on Station-area Property Values in Buffalo, New York. Urban Stud. 2007, 44, 1041–1068. [Google Scholar] [CrossRef]
- Clower, T.L.; Weinstein, B.L. The impact of Dallas (Texas) area rapid transit light rail stations on taxable property valuations. Australas. J. Reg. Stud. 2002, 8, 389–400. [Google Scholar]
- Welch, T.F.; Gehrke, S.R.; Wang, F. Long-term impact of network access to bike facilities and public transit stations on housing sales prices in Portland, Oregon. J. Transp. Geogr. 2016, 54, 264–272. [Google Scholar] [CrossRef]
- Seo, K.; Golub, A.; Kuby, M. Combined impacts of highways and light rail transit on residential property values: A spatial hedonic price model for Phoenix, Arizona. J. Transp. Geogr. 2014, 41, 53–62. [Google Scholar] [CrossRef]
- Mulley, C.; Ma, L.; Clifton, G.; Yen, B.; Burke, M. Residential property value impacts of proximity to transport infrastructure: An investigation of bus rapid transit and heavy rail networks in Brisbane, Australia. J. Transp. Geogr. 2016, 54, 41–52. [Google Scholar] [CrossRef]
- Pan, H.; Zhang, M. Rail transit impacts on land use: Evidence from Shanghai, China. Transp. Res. Rec. J. Transp. Res. Board 2008, 2048, 16–25. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Qin, P.; Chonabayashi, S. Wheels of fortune: Subway expansion and property values in Beijing. J. Reg. Sci. 2016, 56, 792–813. [Google Scholar] [CrossRef]
- Chen, Z.; Haynes, K.E. Impact of high speed rail on housing values: An observation from the Beijing–Shanghai line. J. Transp. Geogr. 2015, 43, 91–100. [Google Scholar] [CrossRef]
- Liu, J.H.; Shi, W. Impact of Bike Facilities on Residential Property Prices. Transp. Res. Rec. J. Transp. Res. Board 2017, 2662, 50–58. [Google Scholar] [CrossRef]
- El-Geneidy, A.; van Lierop, D.; Wasfi, R. Do people value bicycle sharing? A multilevel longitudinal analysis capturing the impact of bicycle sharing on residential sales in Montreal, Canada. Transp. Policy 2016, 51, 174–181. [Google Scholar] [CrossRef]
- Lancaster, K.J. A new approach to consumer theory. J. Political Econ. 1966, 74, 132–157. [Google Scholar] [CrossRef]
- Freeman, A.M., III. The Benefits of Environmental Improvement: Theory and Practice; Published for Resources for the Future; Johns Hopkins University Press: Baltimore, MD, USA, 1979; ISBN 978-0-8018-2163-9. [Google Scholar]
- Bartik, T.J. The estimation of demand parameters in hedonic price models. J. Political Econ. 1987, 95, 81–88. [Google Scholar] [CrossRef]
- Cheshire, P.; Sheppard, S. The welfare economics of land use planning. J. Urban Econ. 2002, 52, 242–269. [Google Scholar] [CrossRef]
- Anselin, L. Spatial econometrics. In A Companion to Theoretical Econometrics; Baltagi, B.H., Ed.; Blackwell Publishing Ltd.: Malden, MA, USA, 2003; pp. 310–330. ISBN 978-0-470-99624-9. [Google Scholar]
- Le Gallo, J.; Thomas, I. Statistique, économétrie et espace : Progrès et défis en science régionale. Rev. d’Économie Régionale Urbaine 2015. [Google Scholar] [CrossRef]
- Jayet, H. Econométrie et données spatiales—Une introduction à la pratique. Cah. Econ. Sociol. Rural. 2001, 58–59, 105–129. [Google Scholar]
- Ermagun, A.; Levinson, D. An Introduction to the Network Weight Matrix. Geogr. Anal. 2017, 50, 76–96. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008; ISBN 978-1-4200-6424-7. [Google Scholar]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Bae, C.-H.C.; Jun, M.-J.; Park, H. The impact of Seoul’s subway Line 5 on residential property values. Transp. Policy 2003, 10, 85–94. [Google Scholar] [CrossRef]
- Florax, R.J.G.M.; Folmer, H.; Rey, S.J. Specification searches in spatial econometrics: The relevance of Hendry’s methodology. Reg. Sci. Urban Econ. 2003, 33, 557–579. [Google Scholar] [CrossRef]
- Elhorst, J.P. Applied Spatial Econometrics: Raising the Bar. Spat. Econ. Anal. 2010, 5, 9–28. [Google Scholar] [CrossRef]
- Lee, L.-F. Asymptotic Distributions of Quasi-Maximum Likelihood Estimators for Spatial Autoregressive Models. Econometrica 2004, 72, 1899–1925. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships, 1st ed.; Wiley: Chichester, UK; Hoboken, NJ, USA, 2002; ISBN 978-0-471-49616-8. [Google Scholar]
- Feuillet, T.; Charreire, H.; Menai, M.; Salze, P.; Simon, C.; Dugas, J.; Hercberg, S.; Andreeva, V.A.; Enaux, C.; Weber, C.; et al. Spatial heterogeneity of the relationships between environmental characteristics and active commuting: Towards a locally varying social ecological model. Int. J. Health Geogr. 2015, 14. [Google Scholar] [CrossRef] [PubMed]
- European Commission. 2013. Available online: http://ec.europa.eu/environment/europeangreencapital/winning-cities/2013-nantes/ (accessed on 10 September 2017).
- Bureau, B.; Glachant, M. Évaluation de l’impact des politiques, assessing the Impact of “Green Neighborhood” and “Quiet Neighborhood” Policies on Paris Property Values. Econ. Prévis. 2010, 1, 27–44. [Google Scholar]
- Saulnier, J. Une Application des Prix Hédonistes : Influence de la Qualité de l’Air sur le Prix des Logements ? Available online: http://prodinra.inra.fr/?locale=fr#!ConsultNotice:150792 (accessed on 1 November 2017).
- Wagner, G.A.; Komarek, T.; Martin, J. Is the light rail “Tide” lifting property values? Evidence from Hampton Roads, VA. Reg. Sci. Urban Econ. 2017, 65, 25–37. [Google Scholar] [CrossRef]
| Variables | Definition | URBAN Area Mean or % (Std.) | Periurban/Rural Area Mean or % (Std.) |
|---|---|---|---|
| House price in € | Dependent variable | 272,031 (122,070) | 188,566 (85,865) |
| Intrinsic Variables | |||
| Living surface area (m2) | Living space in square meters entered in the deed | 104.96 (27.7) | 104.46 (26.5) |
| Land surface area (m2) | Total area of land in square meters, corresponding to the cadastral area | 1143.9 (4057.6) | 1583.33 (4260.3) |
| Construction period | When the house was built, with 7 different classes: | ||
| A: <1913 | 5.1 | 11.2 | |
| B: 1914–1947 | 15.4 | 20.2 | |
| C: 1948–1969 | 19.4 | 11.2 | |
| D: 1970–1980 | 24.2 | 18.4 | |
| E: 1981–1991 | 14.2 | 8.3 | |
| F: 1992–2000 | 8.7 | 6.7 | |
| G: 2001–2012: the reference variable | 13.0 | 24.0 | |
| Neighborhood Variables | |||
| Population density (inhabitants/km2) | Population density (inhabitants/km²) at the IRIS scale | 3003.9 (2553.0) | 196.6 (257.8) |
| Unemployment rate (%) | Unemployment rate at the IRIS scale | 9.9 (3.8) | 7.8 (1.8) |
| Social diversity index | Diversity index (from 0 to 1) at the IRIS scale based on 6 socio-professional classes. A value of 1 indicates an identical distribution of the 6 classes in the IRIS. | 0.82 (0.03) | 0.86 (0.03) |
| School | Distance to the nearest primary or high school | 540.4 (537.8) | 1150.1 (1054.1) |
| Parks | Distance to the nearest park | 398.8 (300.5) | 1270.8 (1240.9) |
| Shopping center | Distance to the nearest shopping center | 994.5 (749.8) | 2953.6 (2337.5) |
| Transport Infrastructure Variables | |||
| Railway station | Distance to the nearest railway station | 2288 (1397) | 6984 (5304) |
| Tram or busway station | Distance to the nearest tram or busway station | 2358 (2353) | n/a |
| Bike-sharing station | Distance to the nearest bike-sharing station | 4363 (3435) | n/a |
| “Lila” bus station | At least one “Lila” bus station in a buffer of 500 m radius near the house. It is a dummy variable, 1 if <500 | n/a | 0.45 (0.5) |
| Carpool area | At least one carpool area in a buffer of 1500 m radius near the house. It is a dummy variable, 1 if <1500 m | n/a | 0.34 (0.48) |
| Statistics | Urban Area | Periurban/Rural Areas | ||||||
|---|---|---|---|---|---|---|---|---|
| OLS | SAR | SEM | SDM | OLS | SAR | SEM | SDM | |
| n | 1353 | 1353 | 1353 | 1353 | 909 | 909 | 909 | 909 |
| Moran’s I | 0.11 *** | −0.02 | −0.00 | −0.00 | 0.12 *** | 0.02 | −0.00 | −0.00 |
| n/a | 0.42 *** | n/a | 0.31 *** | n/a | 0.19 *** | n/a | 0.31 *** | |
| λ | n/a | n/a | 0.54 *** | n/a | n/a | n/a | 0.54 *** | n/a |
| Robust LMlag | n/a | 67.1 *** | n/a | n/a | n/a | 6.2 * | n/a | n/a |
| Robust LMerr | n/a | n/a | 10.2 *** | n/a | n/a | n/a | 4.5 * | n/a |
| Variable | OLS (t-Values) | SAR (t-Values) | GWR (Min) | GWR (Median) | GWR (Max) |
|---|---|---|---|---|---|
| (Intercept) | 8.320 *** (19.98) | 3.326 *** (5.46) | 4.91 | 8.16 | 11.29 |
| Intrinsic characteristics | |||||
| Log(Living surface area) | 0.891 *** (28.28) | 0.828 *** (29.08) | 0.70 | 0.86 | 1.03 |
| Log(Land surface area) | 0.075 *** (6.38) | 0.079 *** (9.91) | 0.01 | 0.08 | 0.13 |
| cod_constA | −0.185 *** (−4.00) | −0.172 *** (−4.55) | −0.41 | −0.21 | 0.00 |
| cod_constB | −0.227 *** (−7.75) | −0.220 *** (−7.72) | −0.34 | −0.23 | −0.12 |
| cod_constC | −0.248 *** (−9.31) | −0.238 *** (−8.98) | −0.35 | −0.24 | −0.11 |
| cod_constD | −0.183 *** (−7.42) | −0.176 *** (−7.72) | −0.36 | −0.19 | −0.11 |
| cod_constE | −0.154 *** (−5.60) | −0.140 *** (−8.98) | −0.28 | −0.14 | −0.05 |
| cod_constF | −0.012 (−0.39) | −0.009 (−7.09) | −0.12 | −0.02 | 0.09 |
| Neighborhood characteristics | |||||
| Log(DensPop) | 0.040 ** (3.23) | 0.024 * (2.22) | −0.02 | 0.04 | 0.13 |
| Unemployment rate | −0.005 ° (−1.93) | −0.002 (−1.01) | −0.02 | −0.01 | 0.01 |
| Social diversity index | −0.469 (−1.40) | −0.082 (−0.26) | −1.69 | −0.18 | 3.05 |
| log(dist_school) | −0.030 ** (−2.86) | −0.033 *** (−3.22) | −0.07 | −0.03 | 0.03 |
| log(dist_park) | 0.017 (1.45) | 0.009 (0.78) | −0.05 | 0 | 0.10 |
| log(dist_shop) | 0.017 (1.37) | 0.005 (0.49) | −0.04 | 0.01 | 0.08 |
| Sustainable transport attributes | |||||
| log(dist_tram) | 0.05 *** (4.58) | 0.035 ** (3.23) | 0.00 | 0.04 | 0.12 |
| log(dist_railway station) | 0.063 *** (5.46) | 0.034 ** (3.05) | −0.04 | 0.07 | 0.19 |
| log(dist_bike-sharing station) | −0.134 *** (−9.83) | −0.094 *** (−7.27) | −0.23 | −0.15 | −0.06 |
| Rho | 0.423 *** | ||||
| Model diagnostics | |||||
| AICc | 375.284 | 264.620 | 251.526 | ||
| Nagelkerke R2 | - | 0.592 | - | ||
| Adjusted R2 | 0.551 | - | 0.617 | ||
| Moran’s I (p-value) | 0.001 | 0.961 | 0.080 | ||
| Variable | OLS (t-Values) | SAR (t-Values) | GWR (Min) | GWR (Median) | GWR (Max) |
|---|---|---|---|---|---|
| (Intercept) | 7.678 *** (15.47) | 5.540 *** (8.94) | 4.56 | 7.56 | 9.30 |
| Intrinsic characteristics | |||||
| Log(Living surface area) | 0.738 *** (16.84) | 0.732 *** (16.62) | 0.66 | 0.87 | 0.95 |
| Log(Land surface area) | 0.155 *** (7.83) | 0.152 *** (12.47) | 0.06 | 0.1 | 0.16 |
| cod_constA | −0.403 *** (−8.89) | −0.402 *** (−11.00) | −0.48 | −0.32 | −0.16 |
| cod_constB | −0.343 *** (−11.31) | −0.342 *** (−10.93) | −0.46 | −0.27 | −0.10 |
| cod_constC | −0.256 *** (−6.53) | −0.255 *** (−6.99) | −0.41 | −0.25 | −0.16 |
| cod_constD | −0.239 *** (−9.06) | −0.244 *** (−7.80) | −0.31 | −0.19 | −0.14 |
| cod_constE | −0.145 *** (−4.57) | −0.145 *** (−3.60) | −0.20 | −0.16 | −0.08 |
| cod_constF | −0.026 (−0.83) | −0.034 (−0.79) | −0.06 | −0.02 | 0.02 |
| Neighborhood characteristics | |||||
| Log(DensPop) | 0.071 *** (4.09) | 0.055 *** (3.33) | 0.05 | 0.13 | 0.18 |
| Unemployment rate | −0.027 *** (−4.71) | −0.018 ** (−2.92) | −0.02 | 0.00 | 0.00 |
| Social diversity index | −0.766 ° (1.88) | 0.542 (1.36) | −1.88 | −0.19 | 3.52 |
| log(dist_school) | 0.003 (0.20) | −0.002 (−0.13) | −0.03 | −0.00 | 0.02 |
| log(dist_park) | −0.025 * (−2.32) | −0.025 * (−2.09) | −0.06 | 0.00 | 0.03 |
| log(dist_shop) | −0.024 * (−2.42) | −0.21 * (−1.85) | −0.05 | −0.02 | 0.03 |
| Sustainable transport attributes | |||||
| Carpool area-1500_01 | −0.087 *** (−3.93) | −0.064 ** (−2.59) | −0.22 | −0.10 | −0.04 |
| nb_lila500_01 | 0.063 ** (2.77) | 0.041 ° (1.75) | −0.02 | 0.02 | 0.06 |
| log(dist_railway station) | −0.040 *** (−3.67) | −0.033 ** (−3.05) | −0.04 | −0.01 | 0.04 |
| Rho | 0.193 *** | ||||
| Model diagnostics | |||||
| AICc | 446.589 | 420.329 | 398.347 | ||
| Nagelkerke R2 | - | 0.611 | - | ||
| Adjusted R2 | 0.591 | - | 0.640 | ||
| Moran’s I | 0.001 | 0.144 | 0.147 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulteau, J.; Feuillet, T.; Le Boennec, R. Spatial Heterogeneity of Sustainable Transportation Offer Values: A Comparative Analysis of Nantes Urban and Periurban/Rural Areas (France). Urban Sci. 2018, 2, 14. https://doi.org/10.3390/urbansci2010014
Bulteau J, Feuillet T, Le Boennec R. Spatial Heterogeneity of Sustainable Transportation Offer Values: A Comparative Analysis of Nantes Urban and Periurban/Rural Areas (France). Urban Science. 2018; 2(1):14. https://doi.org/10.3390/urbansci2010014
Chicago/Turabian StyleBulteau, Julie, Thierry Feuillet, and Rémy Le Boennec. 2018. "Spatial Heterogeneity of Sustainable Transportation Offer Values: A Comparative Analysis of Nantes Urban and Periurban/Rural Areas (France)" Urban Science 2, no. 1: 14. https://doi.org/10.3390/urbansci2010014
APA StyleBulteau, J., Feuillet, T., & Le Boennec, R. (2018). Spatial Heterogeneity of Sustainable Transportation Offer Values: A Comparative Analysis of Nantes Urban and Periurban/Rural Areas (France). Urban Science, 2(1), 14. https://doi.org/10.3390/urbansci2010014




