U.S. Metropolitan Spatial Structure Evolution: Investigating Spatial Patterns of Employment Growth from 2000 to 2010
Abstract
:1. Introduction
2. Data and Method
2.1. Data
2.2. Method
2.2.1. Defining Five Submetro Sections
2.2.2. Delimiting Urban and Rural Areas
2.2.3. Identifying Employment Clusters
3. Results
3.1. A Metro’s Five Submetro Sections
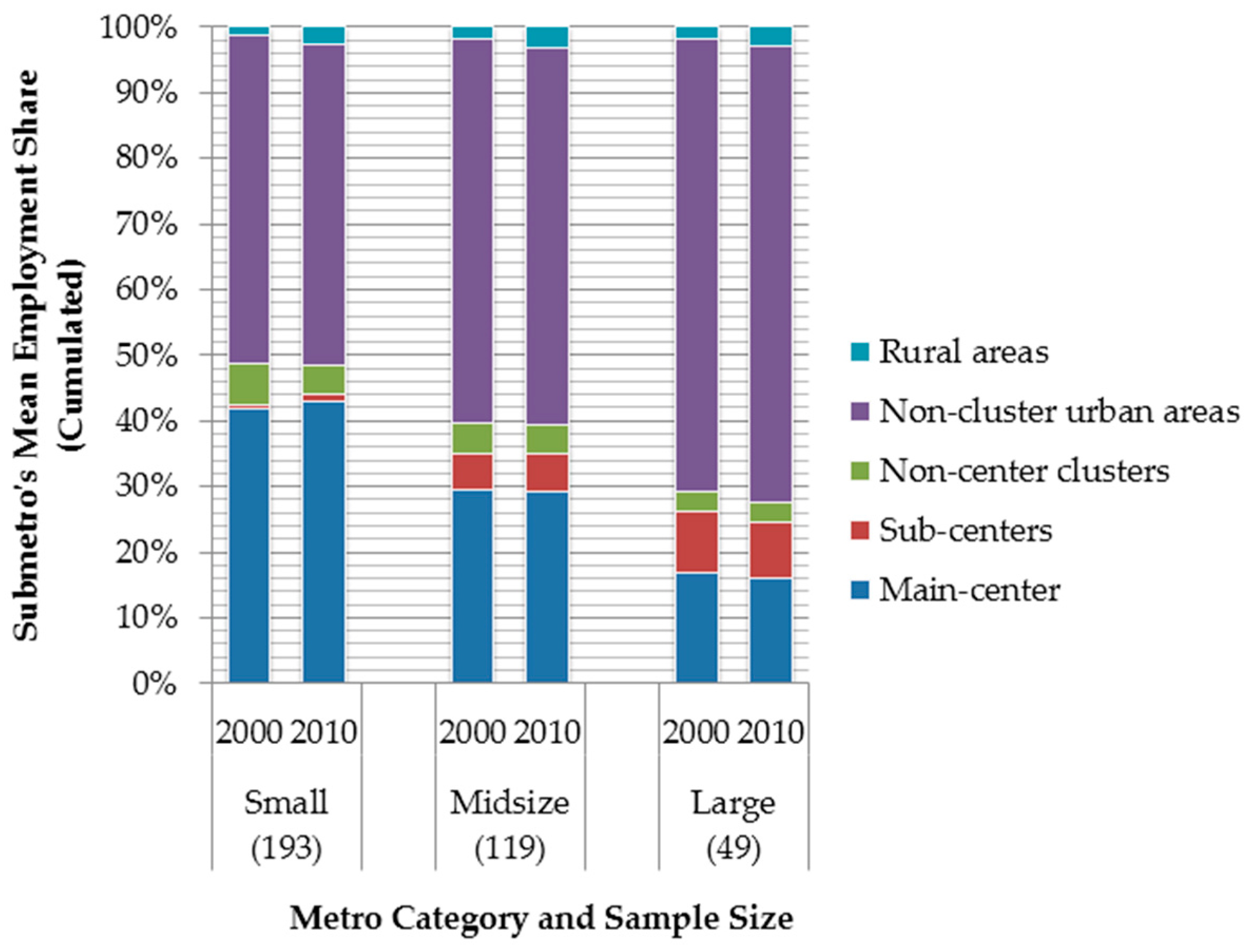
3.2. Spatial Structure Charateristics
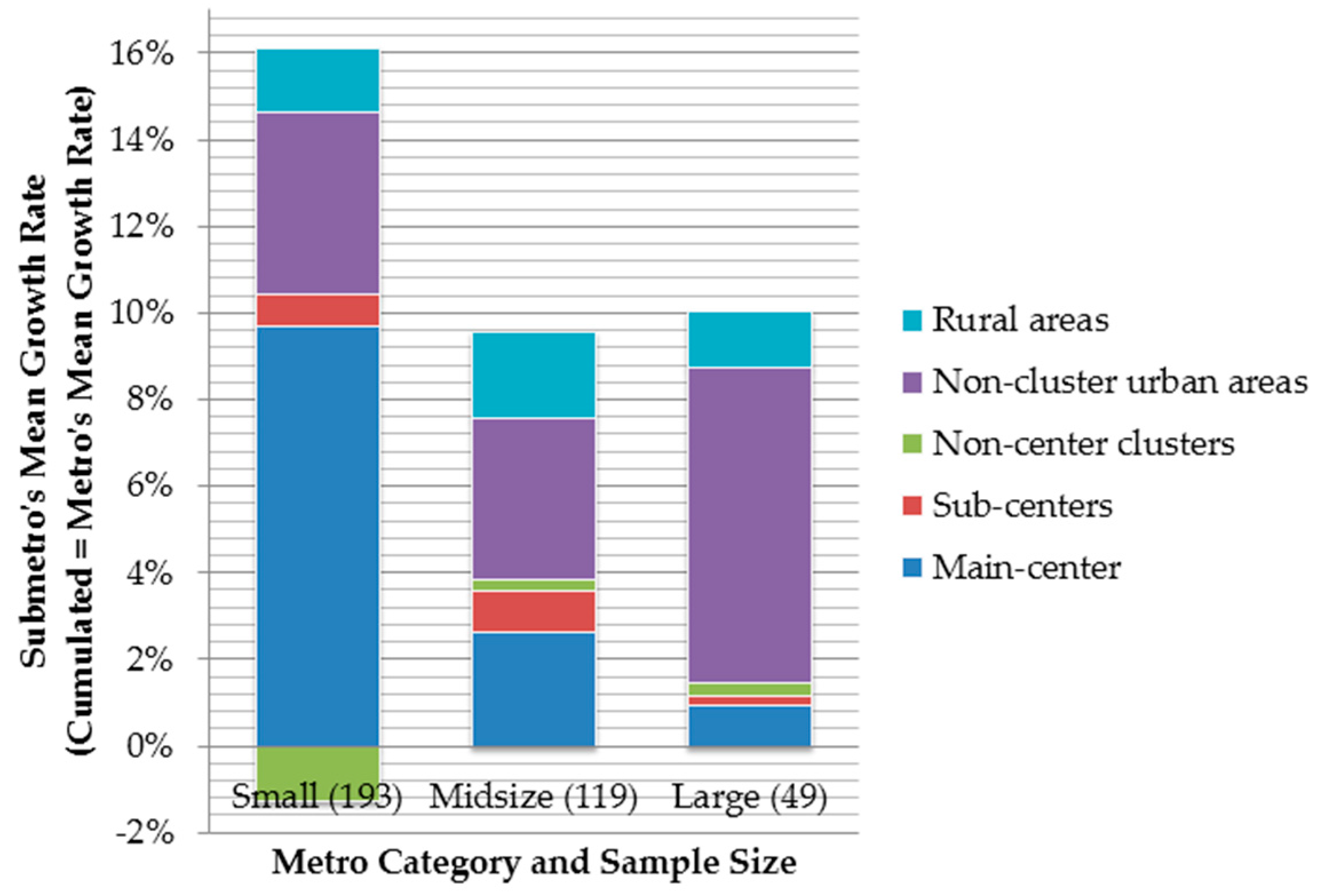
3.3. The Distribution of Employment Growth
3.4. The Correlations of Submetro Growth
4. Discussion and Conclusions
Author Contributions
Conflicts of Interest
References
- O’Sullivan, J.L. The great nation of futurity. U.S. Democr. Rev. 1839, 6, 426–430. [Google Scholar]
- Duany, A.; Plater-Zyberk, E.; Speck, J. Suburban Nation: The Rise of Sprawl and the Decline of the American Dream; Farrar, Straus and Giroux: New York, NY, USA, 2001. [Google Scholar]
- Lopez, R.; Hynes, H.P. Sprawl in the 1990s measurement, distribution, and trends. Urban Aff. Rev. 2003, 38, 325–355. [Google Scholar] [CrossRef] [PubMed]
- O’sullivan, A. Urban Economics; McGraw-Hill/Irwin: New York, NY, USA, 2007. [Google Scholar]
- Garreau, J. Edge City: Life on the New Frontier; Doubleday: New York, NY, USA, 1991. [Google Scholar]
- Krugman, P.R.; Venables, A.J. Globalization and inequality of nations. Q. J. Econ. 1995, 110, 857–880. [Google Scholar] [CrossRef]
- Cervero, R.; Wu, K.L. Polycentrism, commuting, and residential location in the San Francisco Bay area. Environ. Plan. A 1997, 29, 865–886. [Google Scholar] [CrossRef] [PubMed]
- Lang, R.E. Edgeless Cities: Exploring the Elusive Metropolis; Brookings Institution Press: Washington, DC, USA, 2003. [Google Scholar]
- Giuliano, G.; Small, K.A. The determinants of growth of employment subcenters. J. Transp. Geogr. 1999, 7, 189–201. [Google Scholar] [CrossRef]
- McMillen, D.P.; Lester, T.W. Evolving subcenters: Employment and population densities in Chicago, 1970–2020. J. Hous. Econ. 2003, 12, 60–81. [Google Scholar] [CrossRef]
- Lee, B. Edge or edgeless cities? Urban spatial structure in U.S. metropolitan areas, 1980 to 2000. J. Reg. Sci. 2007, 47, 479–515. [Google Scholar] [CrossRef]
- Giuliano, G.; Agarwal, A.; Redfearn, C.; Traveled, V.M. Metropolitan Spatial Trends in Employment and Housing. Available online: http://onlinepubs.trb.org/Onlinepubs/sr/sr298giuliano.pdf (accessed on 14 August 2017).
- Redfearn, C.L. Persistence in urban form: The long-run durability of employment centers in metros. Reg. Sci. Urban Econ. 2009, 39, 224–232. [Google Scholar] [CrossRef]
- Cervero, R.; Komada, Y.; Krueger, A. Suburban Transformations: From Employment Centers to Mixed-Use Activity Centers. Available online: http://escholarship.org/uc/item/9h8387sz (accessed on 1 August 2017).
- Anas, A.; Arnott, R.; Small, K.A. Urban spatial structure. J. Econ. Lit. 1998, 36, 1426–1464. [Google Scholar]
- Batty, M. Building a science of cities. Cities 2012, 29, S9–S16. [Google Scholar] [CrossRef]
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Bettencourt, L.M.A. The origins of scaling in cities. Science 2013, 340, 1438–1441. [Google Scholar] [CrossRef] [PubMed]
- Gordon, P.; Richardson, H.W. Beyond polycentricity: The dispersed metropolis, Los Angeles, 1970–1990. J. Am. Plan. Assoc. 1996, 62, 289–295. [Google Scholar] [CrossRef]
- Bogart, W.T. Don’t Call It Sprawl: Metropolitan Structure in the Twenty-First Century; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Yang, J.; French, S.; Holt, J.; Zhang, X. Measuring the Structure of U.S. Metropolitan Areas, 1970–2000: Spatial Statistical Metrics and an Application to Commuting Behavior. J. Am. Plan. Assoc. 2012, 78, 197–209. [Google Scholar] [CrossRef]
- Wheaton, W.C. Commuting, congestion, and employment dispersal in cities with mixed land use. J. Urban Econ. 2004, 55, 417–438. [Google Scholar] [CrossRef]
- Giuliano, G.; Small, K.A. Subcenters in the Los Angeles region. Reg. Sci. Urban Econ. 1991, 21, 163–182. [Google Scholar] [CrossRef]
- McMillen, D.P.; Smith, S.C. The number of subcenters in large urban areas. J. Urban Econ. 2003, 53, 321–338. [Google Scholar] [CrossRef]
- Pan, Q.; Ma, L. Employment subcenter identification: A GIS-based method. Tex. South. Univ. Sci. Urban Econ. 2006, 21, 63–82. [Google Scholar]
- Matsuo, M. Metropolitan Form, Transportation, And Labor Accessibility—Empirical Evidence from Four US Metropolitan Areas. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 2008. [Google Scholar]
- Fujita, M.; Ogawa, H. Multiple Equilibria and Structural Transition of Non-Monocentric Urban Configurations. Reg. Sci. Urban Econ. 1982, 12, 161–196. [Google Scholar] [CrossRef]
- Thompson, W.R. A Preface to Urban Economics; Resources for the Future: Washington, DC, USA, 1965; Volume 43. [Google Scholar]
- Lee, B.; Gordon, P. Urban spatial structure and economic growth in us metropolitan areas. In Proceedings of the 46th Annual Meeting of the Western Regional Science Association, Newport Beach, CA, USA, 21–24 February 2007. [Google Scholar]
- U.S. Department of Health & Human Services (National Center for Health Statistics). NCHS Urban-Rural Classification Scheme for Counties. Available online: https://www.cdc.gov/nchs/data_access/urban_rural.htm (accessed on 7 August 2017).
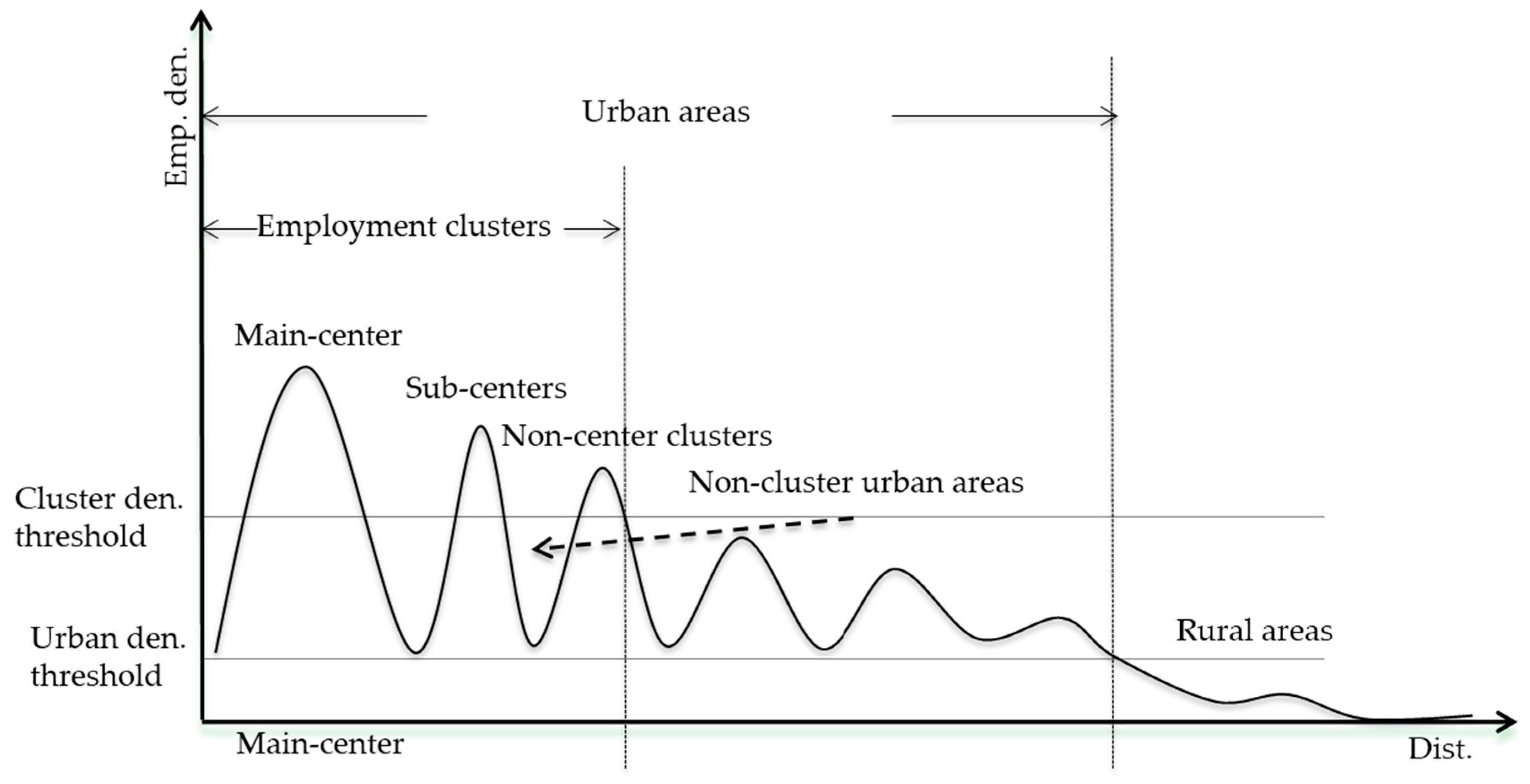
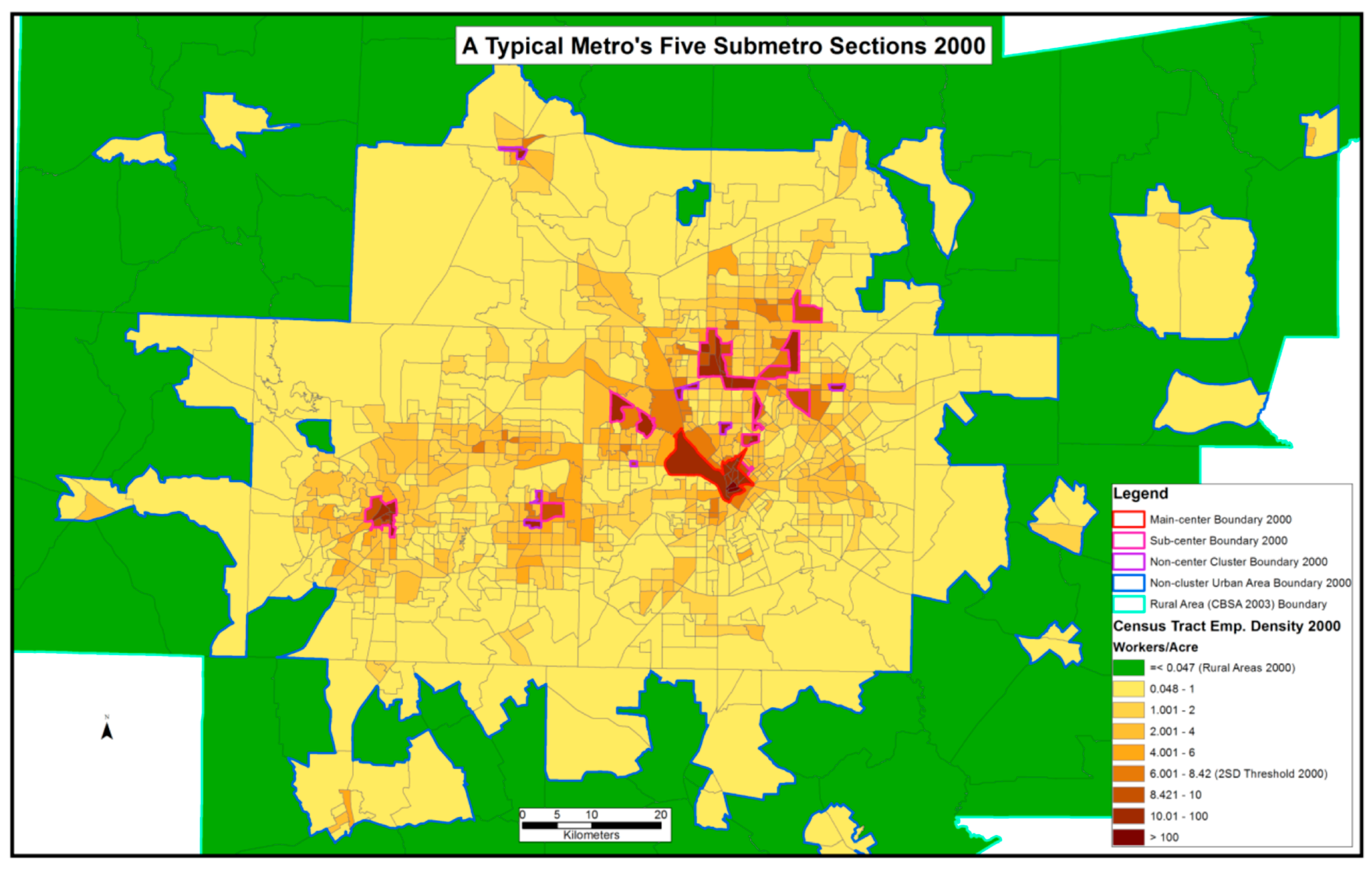
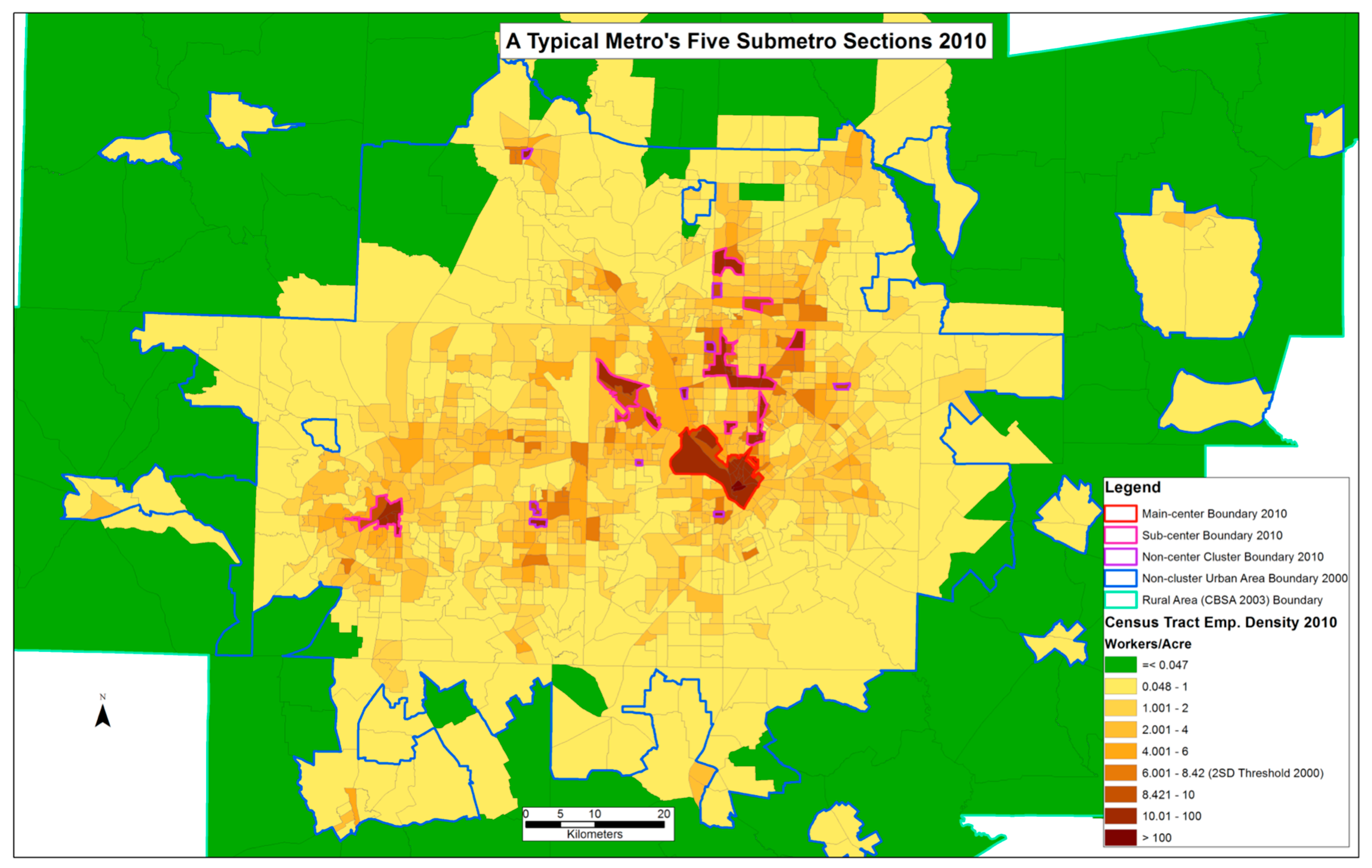
| Thresholds | Main-Center | Sub-Centers | Non-Center Clusters | Non-Cluster Urban Areas | Rural Areas |
|---|---|---|---|---|---|
| Urban Density | √ | √ | √ | √ | |
| Cluster Density | √ | √ | √ | ||
| Center Size | √√ | √ |
| Section of Growth | Section No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Main-center | 1 | 1 | |||||
| Sub-centers | 2 | −0.25 * | 1 | ||||
| Non-center clusters | 3 | −0.22 * | −0.03 | 1 | |||
| Non-cluster urban areas | 4 | −0.17 * | −0.02 | −0.14 * | 1 | ||
| Rural areas | 5 | −0.14 | 0.04 | 0 | 0.02 | 1 | |
| Metro | 6 | 0.67 * | 0.10 | 0.08 | 0.40 * | 0.12 | 1 |
| Section of Growth | Section No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Main-center | 1 | 1 | |||||
| Sub-centers | 2 | 0 | 1 | ||||
| Non-center clusters | 3 | −0.1 | −0.28 * | 1 | |||
| Non-cluster urban areas | 4 | −0.1 | −0.14 | −0.04 | 1 | ||
| Rural areas | 5 | −0.14 | −0.22 * | −0.15 | 0.16 | 1 | |
| Metro | 6 | 0.54 * | 0.27 * | 0.04 | 0.59 * | 0.18 | 1 |
| Section of Growth | Section No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| Main-center | 1 | 1 | |||||
| Sub-centers | 2 | −0.22 | 1 | ||||
| Non-center clusters | 3 | 0.04 | 0.29 * | 1 | |||
| Non-cluster urban areas | 4 | 0.16 | 0.24 | 0.27 | 1 | ||
| Rural areas | 5 | 0.19 | −0.02 | 0.27 | 0.54 * | 1 | |
| Metro | 6 | 0.41 * | 0.41 * | 0.41 * | 0.89 * | 0.66 * | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yang, J.; Güneralp, B.; Burris, M. U.S. Metropolitan Spatial Structure Evolution: Investigating Spatial Patterns of Employment Growth from 2000 to 2010. Urban Sci. 2017, 1, 28. https://doi.org/10.3390/urbansci1030028
Huang X, Yang J, Güneralp B, Burris M. U.S. Metropolitan Spatial Structure Evolution: Investigating Spatial Patterns of Employment Growth from 2000 to 2010. Urban Science. 2017; 1(3):28. https://doi.org/10.3390/urbansci1030028
Chicago/Turabian StyleHuang, Xiaoyan, Jiawen Yang, Burak Güneralp, and Mark Burris. 2017. "U.S. Metropolitan Spatial Structure Evolution: Investigating Spatial Patterns of Employment Growth from 2000 to 2010" Urban Science 1, no. 3: 28. https://doi.org/10.3390/urbansci1030028
APA StyleHuang, X., Yang, J., Güneralp, B., & Burris, M. (2017). U.S. Metropolitan Spatial Structure Evolution: Investigating Spatial Patterns of Employment Growth from 2000 to 2010. Urban Science, 1(3), 28. https://doi.org/10.3390/urbansci1030028




