Abstract
This paper addresses the simultaneous feeder routing and conductor sizing problem in unbalanced three-phase distribution systems, formulated as a nonconvex mixed-integer nonlinear program (MINLP) that minimizes the equivalent annualized expansion cost—combining investment and loss costs—under voltage, ampacity, and radiality constraints. The model captures nonconvex voltage–current–power couplings, load asymmetries, and discrete conductor selections, creating a large combinatorial design space that challenges heuristic methods. An exact MINLP formulation in complex variables is implemented in Julia/JuMP and solved with the Basic Open-source Nonlinear Mixed Integer programming (BONMIN) solver, which integrates branch-and-bound for discrete variables and interior-point methods for nonlinear subproblems. The main contributions are: (i) a rigorous, reproducible formulation that jointly optimizes routing and conductor sizing; (ii) a transparent, replicable implementation; and (iii) a benchmark against minimum spanning tree (MST)-based and metaheuristic approaches, clarifying the trade-off between computational time and global optimality. Tests on 10- and 30-node rural feeders show that, although metaheuristics converge faster, they often yield suboptimal solutions. The proposed MINLP achieves globally optimal, technically feasible results, reducing annualized cost by 14.6% versus MST and 2.1% versus metaheuristics in the 10-node system, and by 17.2% and 2.5%, respectively, in the 30-node system. These results highlight the advantages of exact optimization for rural network planning, providing reproducible and verifiable decisions in investment-intensive scenarios.
1. Introduction
1.1. General Context
The management of electrical distribution systems is a fundamental aspect of power system operation, ensuring reliable and efficient delivery of electricity to end-users [1]. As modern societies experience rapid urbanization, industrial growth, and increasing electrification, the demand for electricity continues to rise significantly [2]. This growth exerts considerable pressure on existing distribution infrastructure, compelling utilities to invest in upgrading and expanding networks to meet future load requirements sustainably [3].
Unbalanced three-phase distribution networks are prevalent in numerous applications, particularly in rural and developing regions where the load profiles tend to be highly asymmetric [4]. Managing these unbalances is critical since they can result in increased energy losses, reduced equipment lifespan, and compromised voltage quality [5]. These challenges are exacerbated in networks with long feeders or dispersed load centers, where phase imbalances and load dynamics have a more pronounced impact on system stability and efficiency [6].
Furthermore, the complexity of unbalanced systems necessitates sophisticated modeling and control strategies. Modern techniques employ advanced thematics such as smart grid technologies, distributed energy resources, and automation to enhance operational flexibility [7]. These developments aim to reduce losses, improve voltage regulation, and facilitate optimal use of network assets. Consequently, innovative optimization and control methodologies have gained prominence as essential tools for effective distribution system management, especially in the context of integrating renewable energy sources and ensuring resilience against outages [7,8].
Overall, the continuous evolution of distribution networks underscores the importance of analytical tools and solution frameworks capable of addressing unbalance, uncertainty, and complexity [9,10]. This paper positions itself within this context, contributing to the development of advanced optimization methodologies for distribution system planning and operation.
1.2. Motivation
The planning of distribution networks involves complex decision-making processes that must account for multiple technical, economic, and operational factors. Efficient optimization methodologies are vital because they enable system operators and planners to identify the most cost-effective and reliable configurations for infrastructure deployment, equipment sizing, and network configuration [11,12]. These advanced techniques facilitate the evaluation of various scenarios, helping to determine optimal locations for distributed energy resources, capacitor placement, and load management strategies. By providing a comprehensive understanding of the trade-offs involved, such methodologies ensure that future network expansions are both economically sustainable and capable of accommodating the evolving demands of modern power systems [13,14].
Moreover, as power systems integrate increasing shares of renewable energy sources and smart grid technologies, the complexity of distribution planning intensifies. Efficient optimization frameworks are essential for managing this complexity in a dynamic and uncertain environment [15]. They support proactive decision-making, improve system resilience, and help maintain voltage stability and power quality under varying load and generation conditions [16]. Ultimately, these methodologies contribute to the development of flexible, adaptive, and resilient distribution networks capable of meeting the challenges of the energy transition, ensuring long-term reliability and sustainability of electrical delivery systems [17].
1.3. Literature Review
The evolution of power system optimization techniques has seen a shift from deterministic approaches to more dynamic and integrated methodologies. Historically, models were simplistic, focusing on either routing or conductor selection with limited consideration for the complex interactions between electrical and economic factors. Recent literature highlights the use of mixed integer nonlinear programming (MINLP) models [18,19], which attempt to address these complexities by considering both continuous and discrete decision variables [20]. While heuristic and metaheuristic algorithms [21,22] have been extensively applied due to their computational efficiency, they often lack guarantees of global optimality, leading to potentially suboptimal solutions.
Authors of [13] applied a tabu search algorithm to optimize conductor selection in three-phase distribution networks. Their approach assumes that the grid topology has already been determined using the minimum spanning tree concept, focusing specifically on refining the selection of conductor calibers to minimize total costs. This methodology highlights the importance of effective initial solutions and demonstrates how metaheuristic algorithms, such as tabu search, can be leveraged to enhance planning outcomes when integrated with power flow simulations under different load conditions. In [23], a network reconfiguration algorithm was proposed to assist in the operation and expansion planning of three-phase distribution systems. The study recognized that power losses reduced utility benefits and that unbalanced three-phase voltages could damage electrical machinery. Consequently, the authors formulated the problem as a multi-objective optimization using Evolutionary Algorithms, aiming to simultaneously minimize power losses and voltage unbalance. To validate the effectiveness of the proposed algorithm, a large-scale radial distribution system operated under maximum load conditions was considered for operational planning. Additionally, multiple scenarios were tested to assess the algorithm’s potential as an expansion planning tool. The results demonstrated that the algorithm maximized utility profits while improving system performance through reduced power losses and voltage unbalance. The authors of [24] proposed a methodology for planning active distribution networks in smart grids, focusing on cost-efficiency and reliability. Their approach integrated the capabilities of distributed energy resources (DER) into asset reinforcement, operational decisions, and data utilization, supporting time-variable operational services. The methodology was validated through testing on a real network with 450,000 delivery points over 5000 km2. In Ref. [25], the authors presented a novel MINLP model aimed at increasing the photovoltaic hosting capacity in unbalanced three-phase distribution systems. The problem integrated the optimal operation of capacitor banks and network reconfiguration under both radial and closed-loop topologies. To ensure solvability with existing optimization tools, the authors employed linearization strategies to convert the MINLP into a mixed-integer linear programming formulation, guaranteeing optimality with off-the-shelf solvers. The approach was validated through several tests on a 25-node unbalanced three-phase distribution system, demonstrating its effectiveness in enhancing PV penetration when considering different network reconfiguration strategies.
The authors of [26] proposed an optimization model for day-ahead operation of unbalanced distribution systems with photovoltaic integration, incorporating conservation voltage reduction techniques. Their approach considered deterministic, stochastic, and robust methods to account for load uncertainties, aiming to minimize energy consumption at the substation by coordinating traditional (online tap changers, capacitor banks) and modern (smart photovoltaic inverters) elements. The original MINLP problem was transformed into a continuous linear programming model, and results on a modified IEEE 123-bus system demonstrated energy savings and demand reduction across all approaches. Notably, the robust approach provided better voltage stability and lower computational effort, highlighting its potential for utility applications. Ref. [27] proposed an optimization approach based on Particle Swarm Optimization to minimize voltage unbalance in Three-Phase-Two-Wire rural networks. Their method addressed the inherent voltage unbalance caused by uneven load distribution, a key challenge in this emerging technology recently implemented in Brazil. Additionally, a standardized phase distribution strategy was introduced to reduce computational complexity. Validation through statistical analysis confirmed that the optimized particle swarm approach consistently yielded the best solutions, while the simplified method maintained voltage unbalance within regulatory limits in most cases, demonstrating its practical effectiveness. The authors of [28] proposed a multi-stage model based on MINLP to determine the optimal expansion planning of sub-transmission systems. Their approach included the strategic placement and reinforcement of distributed generation units in distribution networks over the planning horizon, ensuring service demand was met at minimum cost while satisfying operational constraints such as voltage drop limits and capacity of substations, medium voltage feeders, and distributed generation units. The model also optimized the planning of existing and new substations, medium voltage feeder routes, and the operational scheduling of distributed generation units. Furthermore, expansion limitations of existing and candidate substations and distributed generation units were incorporated as constraints. The effectiveness of the proposed model was validated through several case studies, demonstrating its potential for comprehensive system expansion planning. In [29], the authors proposed a tabu search algorithm for optimizing conductor selection in electrical distribution networks, with the goal of minimizing investment and operational costs. The algorithm was implemented using the DIgSILENT Power Factory programming language, enabling a comprehensive consideration of loadability limits, voltage levels, and various operational constraints. Experiments performed on 27- and 33-node systems with balanced loads demonstrated that the approach effectively balanced investment and operating costs, outperforming metaheuristic strategies reported in the literature. This method provides a valuable tool for network operators aiming to improve efficiency through informed conductor selection decisions.
Table 1 synthesizes the literature into three lines—(A) cascaded heuristics/metaheuristics, (B) reconfiguration/operation models (deterministic, stochastic, or robust), and (C) MINLP planning formulations—summarizing typical approaches, strengths, and specific limitations. By mapping each line of work to the corresponding methodological gap, the table makes explicit how prevailing strategies either decouple routing from conductor sizing, rely on simplified surrogates that underrepresent three-phase couplings, or only partially cover the joint decision space. This structured comparison provides a transparent basis for positioning the present study within the state of the art.

Table 1.
Comparative synthesis of prior studies and advances of the present work.
As the table indicates, lines (A) and (B) prioritize computational expediency and operational tractability but lack verifiable global optimality and integrated investment decisions, while line (C) offers unified modeling at the expense of physical fidelity or scope (e.g., linearizations or single-phase equivalents, or omission of routing). In response, the proposed framework advances the field by formulating an exact MINLP in the complex domain that co-optimizes feeder routing and conductor sizing under radiality, voltage, and ampacity limits, preserves three-phase couplings via current-injection power flow, and is solved with BONMIN to deliver reproducible, globally optimal solutions on representative rural feeders. This closes the identified gaps and clarifies the time–optimality trade-off against cascaded and metaheuristic baselines.
The literature review reveals a progressive shift toward integrated formulations for distribution network planning; however, several gaps still limit realism and optimality under unbalanced operating conditions: (i) the widespread use of single-phase equivalents or linearized models that obscure couplings and phase asymmetries; (ii) the sequential treatment of feeder routing and conductor sizing, which often fixes suboptimal topologies; (iii) the inherently nonconvex and mixed-integer nature of the problem, with radiality, voltage, and ampacity constraints that hinder global optimality guarantees; and (iv) the combinatorial growth arising from discrete conductor catalogs and multiple candidate topologies. Collectively, these limitations explain why heuristic and metaheuristic approaches, although computationally fast, yield solutions with no global optimality assurance and limited scalability—particularly in rural three-phase networks, where investment decisions require technical traceability and reproducibility.
Accordingly, the research problem is explicitly formulated as follows: to design an exact optimization framework that simultaneously determines feeder routing and conductor selection in unbalanced three-phase distribution systems, accurately modeling couplings in the complex domain, enforcing radiality and operational limits (voltage and ampacity), and minimizing the equivalent annual expansion cost. The proposed framework must ensure global optimality and demonstrate computational scalability in realistic rural feeders, while providing a transparent and reproducible implementation for fair comparison against cascaded and metaheuristic approaches. This formulation aims to clearly establish both the scientific contribution and the practical relevance of the study.
1.4. Contribution, Scope, and Limitations
This paper introduces an exact optimization framework that jointly determines the routing and conductor sizing in unbalanced three-phase distribution systems, formulated as an MINLP model [30]. Unlike traditional layered or heuristic approaches, the proposed method fully integrates the physics of three-phase power flow with economic considerations, ensuring globally optimal and technically consistent solutions. Major contributions include: developing a comprehensive, physics-based MINLP model that minimizes long-term costs associated with network investments and energy losses; enforcing operational constraints such as voltage regulation, current ampacity, and radial topology; and demonstrating the effectiveness of the approach through benchmark case studies on 10- and 30-node networks, showing significant improvements over heuristic and metaheuristic methods in terms of cost, optimality, and solution reproducibility.
Despite these strengths, the framework has certain limitations. The combined nonconvex power flow and combinatorial topology design make the problem NP-hard, which restricts its applicability to medium-scale networks—typically those with up to a few dozen nodes—due to high computational times, often several hours. Additionally, the current model assumes static worst-case demand profiles, limiting its ability to capture load variability and stochastic operational conditions. Furthermore, it does not yet incorporate active elements such as distributed generation, reactive power compensation devices, or demand-side management, which are increasingly important in modern distribution systems. Addressing these limitations through model extensions, decomposition techniques, or hybrid solution approaches remains a promising direction for future research.
1.5. Document Structure
The paper is structured as follows: Section 2 details the problem formulation and modeling, including the mathematical representation of the optimization challenge. Section 3 describes the methodological framework and computational techniques employed in this study. In Section 4, we present case studies that illustrate the application of our model to real-world scenarios. The results and analysis are discussed in Section 5, highlighting the efficiency and advantages of the proposed method. Finally, Section 6 offers conclusions and suggests directions for future research, focusing on potential model extensions and applications.
2. Problem Formulation and Modeling
The problem of simultaneous routing and conductor selection in unbalanced three-phase distribution networks can be formulated as a mixed-integer nonlinear programming model (MINLP) [31,32]. This formulation incorporates both the physical laws governing power flow in asymmetric multiconductor systems and the investment decisions associated with the construction of candidate routes and the selection of conductor types. The objective is to minimize the long-term economic cost of network expansion, which includes the annualized investment in conductors and the operational costs arising from power losses, while ensuring compliance with operational constraints (voltage regulation and ampacity limits) as well as topological constraints (radial configuration and connectivity) [33].
The proposed model is expressed in complex variables to explicitly account for phase couplings and load unbalance effects, thereby avoiding simplifications that could distort the actual performance of the distribution system. The following sections present, first, the objective function (Section 2.1) and, subsequently, the set of constraints (Section 2.2), which together guarantee both the technical feasibility and the economic optimality of the expansion plan.
2.1. Objective Function
The formulation explicitly integrates the technical and economic dimensions of the problem by combining the cost of electrical losses with the investment required for conductor installation. Both components are annualized through financial factors, ensuring that the optimization criterion accurately reflects the long-term economic performance of the distribution system. The following equations are original derivations in the complex domain for unbalanced three-phase planning. Their conceptual foundation draws on the single-phase modeling insights of [33], while extending them to explicitly capture couplings, phase asymmetry, and the joint routing–sizing decision space.
The Equations (1)–(3) detail the modeling of these costs and illustrate how the decision variables, electrical quantities, and economic parameters interact within the optimization process.
Being,
In Equation (1), represents the equivalent annual total cost of the distribution system under study. This cost consists of two components: , which corresponds to the cost associated with energy losses in the conductors, and , which represents the investment cost of installing the selected conductors. Both terms are weighted through financial factors: , known as the capital recovery factor, which converts a present investment into a uniform annual payment considering the annual interest rate and the planning horizon of N years; and , a cost update factor that reflects the variation in energy tariffs over the time horizon , accounting for the growth rate of energy prices relative to the discount rate .
Equation (2) represents the cost associated with energy losses.
Here, denotes the phase voltage drop in branch l, while represents the current flowing through branch l. The factor converts the power losses into the corresponding annual energy cost, where T denotes either the total hours per year or the duration of the representative period. This matrix/complex formulation is equivalent to the familiar (Joulse effect), while remaining valid for unbalanced three-phase operation and any feasible choice of conductor type.
In the proposed model, ohmic losses on each branch are evaluated using the complex-domain expression in (2). Under unbalanced operation, phase currents become unequal and, through the line impedances, induce unequal voltage drops; both phenomena are captured by (2) because losses scale with the square of the phase-current magnitudes. Hence, greater current unbalance leads to higher aggregate losses and typically exacerbates voltage deviations at downstream nodes. Conversely, design actions that reduce current unbalance—route adjustments, or conductor resizing—mitigate voltage unbalance and decrease the loss component accounted for in (2).
Remark 1.
It is important to note that the subscript denotes the three-phase condition of the electrical variables, representing them as a three-dimensional vector . In the case of impedance, it is expressed as a matrix [34].
Finally, Equation (3) represents the investment cost corresponding to the installation of the selected conductors.
where, denotes the unit cost of conductor type c per phase (e.g., USD/km–phase). It is multiplied by the branch length and the binary selection variable . The binary variable indicates whether conductor c is selected for branch l, ensuring that only one conductor size is chosen when the branch is built.
2.2. Set of Constraints
The formulation of the MINLP model incorporates four complementary groups of conditions: (i) the physical laws governing current balance, power–current relationships, and Ohm’s law in unbalanced three-phase systems; (ii) the operational limits on voltage magnitudes and conductor ampacity; (iii) the design constraints that enforce radial topology and unique conductor selection; and (iv) the reference conditions that define the slack node and guarantee system equilibrium.
2.2.1. Physics of Unbalanced Three-Phase Networks
Equation (4) presents the extension of Kirchhoff’s current laws to the nodes of the distribution system, ensuring current balance in unbalanced three-phase operation.
This equation establishes that corresponds to the vector of three-phase currents injected by the source at node i, while and represent the currents absorbed by loads connected in wye and delta configurations, respectively. denotes the three-phase incidence matrix that relates node i to its incident branches. In this way, the constraint ensures that Kirchhoff’s current law is satisfied at each node i; that is, the algebraic sum of net injections equals the current flowing into the lines connected to the node.
The term allows the conversion of line currents of the load into their phase equivalents. The corresponding transformation matrix is defined as:
Equations (5) and (6) show the power–current relationships of the loads, which may be connected either in wye or in delta configuration.
In these expressions, and represent the vectors of the complex power demanded at node i for each type of connection. The term corresponds to the vector of phase voltages at node i, and the operator builds a diagonal matrix that allows each voltage to be multiplied by its associated current. In the case of the delta connection, the matrix transforms phase voltages into line voltages to calculate the power associated with each branch of the connection.
Finally, Equation (7) defines the voltage drop in the network branches.
In this expression, is a binary variable that indicates whether the branch l is built (1) or not (0), and is the three-phase impedance matrix associated with the conductor type c.
The equality on the left expresses the branch voltage drop l as the ordered difference of the nodal voltages (only if ), while the equality on the right imposes Ohm’s law with the full sequence coupled impedance matrix , scaled by branch length and selected conductor size c by binary variable (). In this way, the equality links the difference of nodal voltages with the voltage drop obtained from Ohm’s law, ensuring electrical consistency among branch construction decisions, conductor selection, and operational variables.
For modeling consistency, line impedances are expressed in a compact complex matrix that represents the three phase conductors and captures interphase coupling; voltages, currents, and complex powers are defined accordingly, ensuring a well-posed three-wire formulation. Four-wire segments can be incorporated by applying a Kron reduction to eliminate the neutral and obtain an equivalent representation, whereas two-phase or single-phase sections are handled by suppressing the absent phases within the same notation (no mutual coupling with non-existent conductors) [34]. Conductor investment costs are computed under the three-conductor convention and can be proportionally adjusted when a segment includes a different number of conductors.
2.2.2. Operational Limits
Equation (8) establishes the service voltage limits of the distribution system, ensuring that the nodal voltages remain within the permissible range defined by regulatory and operational standards.
The parameter defines the minimum allowable per-phase voltage (usually expressed as a percentage of the nominal voltage), while sets the maximum acceptable voltage limit. The vector is a three-dimensional column vector of ones, which replicates the reference values and across all phases of the system.
Finally, Equation (9) establishes the thermal current limits that the selected conductor c can withstand per phase, ensuring that the operating currents do not exceed the ampacity of the conductor.
The parameter represents the maximum thermal capacity of conductor type c, that is, the current limit it can carry without overheating. In this case, the binary variable activates conductor type c in branch l, so that only the ampacity of the selected conductor contributes to the inequality. Finally, the vector replicates this limit across the three phases.
2.2.3. Radial Topology and Design Consistency
Equation (10) ensures the minimum connectivity per node.
This condition requires that each node be incident to at least one constructed branch, and that at least one node has an incoming or outgoing connection, thereby avoiding isolated nodes.
On the other hand, Equation (11) guarantees that the resulting system is radial.
Together with Equation (10), this condition enforces an arborescence (i.e., cycle-free structure) that connects all nodes of the system with exactly branches, which characterizes a radial network [35]. The equality condition makes the existence of cycles incompatible.
Finally, Equation (10) enforces the assignment of a single conductor size to each constructed branch of the network.
From this equation, it can be observed that if branch l is not constructed (), no conductor size is assigned (); whereas if the branch is built, the exclusive selection of exactly one conductor is enforced.
2.2.4. Reference Conditions
Equation (13) states that, for all nodes in the network except the reference node (i.e., substation or slack node), the current injection is zero. This implies that these nodes behave exclusively as demand nodes, without the capability of supplying energy to the system.
In the absence of any other generation source in the system, the power balance is concentrated at the slack node, which acts as the main substation responsible for supplying both the loads and the network losses.
Finally, Equation (14) defines the reference voltage at the substation node.
It fixes both the magnitude and the phasor angle at the slack node, thereby closing the system of equations and establishing the voltage reference framework. This condition ensures the convergence of the power flow to a unique solution [36].
2.3. Computational Complexity Analysis
As discussed above, the simultaneous routing and conductor selection model can be classified as a nonconvex MINLP problem. Its complexity arises from the interaction between discrete expansion decisions and the nonlinear power flow equations.
Let denote the number of nodes, the number of candidate branches, and the number of available conductor types. The size of the optimization problem can then be characterized as shown in Table 2 and Table 3.

Table 2.
Model characterization regarding the number of variables.

Table 3.
Model characterization regarding the number of equations, inequalities, and objective functions.
It is important to note that the objective function is not a decision variable itself but rather a scalar expression that depends on the other decision variables of the model (investment and losses).
- Binary variables: The model includes m variables that determine branch construction and variables that enforce exclusive conductor selection. Hence, the discrete component of the problem grows on the order of .
- Continuous variables: As shown in the Table 2, most of the equations are complex and contribute approximately variables. Therefore, the continuous space is of order .
- Constraints: The formulation includes: (i) Kirchhoff’s current laws at every node, (ii) Ohm’s law for each branch, (iii) voltage magnitude limits, (iv) ampacity constraints, and (v) radiality and selection constraints. Therefore, the number of constraints grows linearly with the number of nodes, candidate lines, and available conductor sizes, i.e., .
Despite the linear scaling of variables and constraints in terms of n, m, and k, the model is intrinsically NP-hard due to two structural properties:
- Power flow equations: These introduce nonlinear and nonconvex couplings between voltages, currents, and impedance matrices. Bilinear terms and absolute values constraints make the continuous relaxation nonconvex, thereby eliminating polynomial-time solution guarantees [39].
Therefore, the search space comprises all possible configurations of branches and conductor assignments, as illustrated in the following formula. It corresponds to the product between the possible combinations of selecting lines from the m available candidates (i.e., ), and the possible combinations of assigning k conductor types to the selected lines (i.e., ).
Each possible solution requires solving a nonconvex power flow problem. For example, in a system with 10 nodes, 17 candidate lines, and 6 possible conductor types, there are approximately possible combinations. This exponential growth with respect to the discrete variables explains the computational intractability of the model under brute-force enumeration.
This analysis illustrates why heuristic and metaheuristic approaches have often been employed in the literature [40]. However, such methods cannot provide guarantees of optimality or feasibility [41]. By contrast, exact global optimization techniques—such as branch-and-bound combined with convex relaxations, outer approximation, and physics-based cutting planes—are capable of delivering certified solutions [42,43]. Within this framework, the nonlinear programming (NLP) subproblems arising in the branch-and-bound process are solved using the interior-point method, which is particularly well-suited for large-scale nonlinear systems with inequality constraints [44].
These methods ensure that the final network design (i) satisfies all technical limits on voltages and currents, (ii) preserves the required radial topology, and (iii) minimizes the equivalent annual economic cost. Such guarantees are essential in distribution system planning, where the capital-intensive nature of investment decisions demands rigorous mathematical justification.
3. Methodological Framework
This section presents the procedure actually applied in the study, organized as a step-by-step pipeline that connects data preparation, model assembly, and the MINLP solution process. The methodology is based on solving the MINLP model that simultaneously determines the routing and conductor sizing of unbalanced three-phase distribution systems. Its implementation requires advanced computational tools capable of representing nonlinear power system equations and addressing optimization problems that combine discrete and continuous decision variables.
The implementation was carried out in the Julia programming language (v1.11.6), which provides a high-performance environment with flexible syntax and a rich ecosystem for scientific computing [45]. For mathematical modeling, the JuMP package (v1.29.0) was employed, offering a user-friendly algebraic interface that enables the compact and structured representation of large-scale MINLP models [46]. Its support for vectorized notation is particularly well suited to the multiconductor and multiphase formulation adopted in this study. To solve the optimization problem, the BONMIN solver (v1.8.9) was selected [47].
BONMIN integrates branch-and-bound (B&B) with outer approximation techniques, allowing global exploration of the discrete search space while efficiently handling nonlinear continuous relaxations [48]. Nonlinear subproblems are solved using the interior-point method, which provides numerical stability in the presence of nonconvexities such as bilinear voltage–current relationships and absolute-value constraints in ampacity and voltage limits [49]. This combination of tools enables the proposed methodology to deliver globally optimal and technically consistent solutions, ensuring reliability in distribution system planning.
3.1. Interior-Point Method
The interior-point method is an iterative algorithm designed to solve NLP problems with continuous variables and constraints [48]. Unlike boundary-based methods such as the simplex algorithm, interior-point methods traverse the feasible region from within, introducing barrier functions that penalize proximity to the constraint boundaries [48]. At each iteration, a system of linearized equations derived from the Karush–Kuhn–Tucker conditions is solved, progressively guiding the solution toward feasibility and optimality. By following a central trajectory inside the feasible region, the method avoids the combinatorial complexity of boundary exploration and efficiently handles problems with a large number of variables and constraints [48].
This approach is particularly effective for large-scale, nonlinear, and constrained problems, offering polynomial-time complexity for nonconvex cases and strong convergence properties in practice. Its robustness in managing nonlinearities and inequality constraints makes it especially suitable for power system applications, where voltage regulation limits, current ampacity restrictions, and bilinear voltage–current relations lead to highly nonconvex feasible regions.
3.2. Interaction of Branch & Bound and Interior-Point Method in MINLP
In the context of this paper, B&B and the interior-point method interact in a complementary manner, as illustrated in Figure 1.
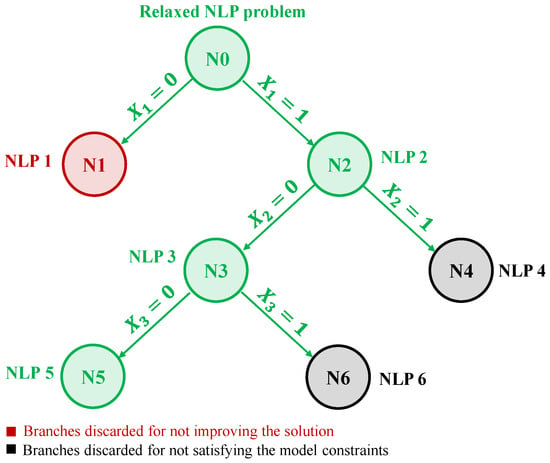
Figure 1.
Illustration of the Branch-and-Bound process for solving the proposed MINLP problem.
The B&B framework manages the discrete decisions by generating subproblems associated with specific combinations of binary variables, such as route construction and conductor type assignment. Each subproblem is formulated as a NLP relaxation, which is then solved using the interior-point method. The NLP solutions provide lower bounds that guide the branching and pruning process within the B&B tree. This interaction ensures that while B&B systematically explores the combinatorial search space, the interior-point method delivers accurate and efficient solutions for the continuous part of the model. Together, they enable the solver to address both discrete design choices and continuous electrical equations, converging to a globally optimal and technically feasible solution.
The framework solves, in an integrated manner, feeder routing and conductor sizing for unbalanced three-phase distribution systems. Figure 2 summarizes the workflow of the proposed methodology.
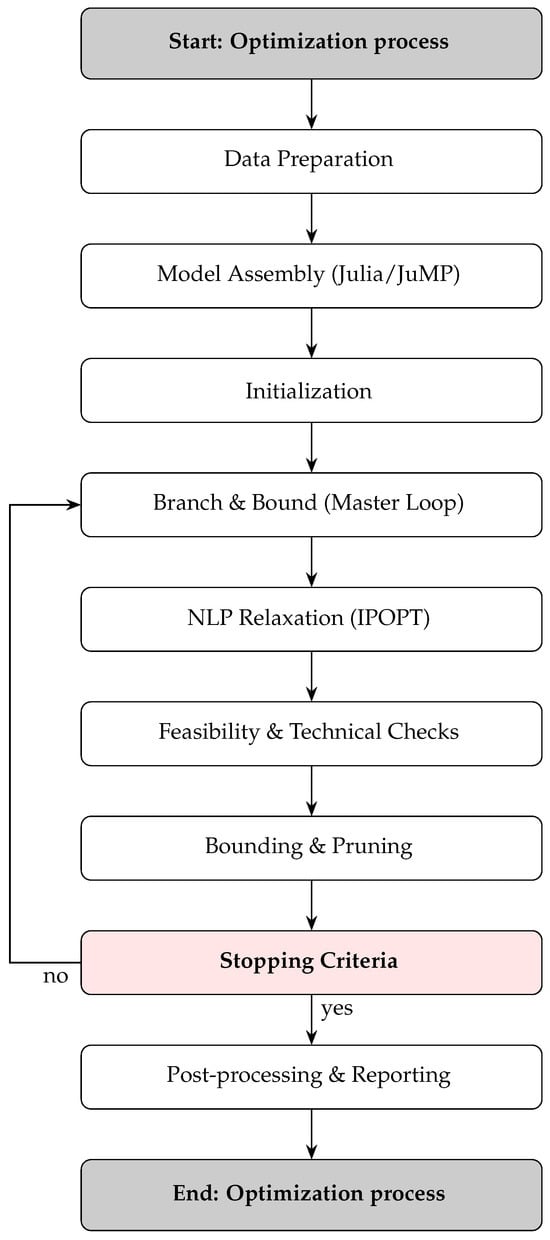
Figure 2.
Methodological framework: step-by-step pipeline and interaction between Branch & Bound and IPOPT.
3.3. Inputs and Data Preparation
The inputs comprise: (i) network data (set of buses, candidate rights-of-way/edges, per-edge impedances, and admissible conductor catalog—AAAC/ACSR); (ii) load models per phase with explicit /Y connections; and (iii) economic and planning parameters (investment costs, loss valuation, discount rate). These data are validated for topological consistency and bounds (voltage and ampacity) before model assembly.
3.4. Model Assembly in Julia/JuMP
The optimization model is written in Julia (v1.11.6) with JuMP (v1.29.0) [45,46]. The formulation is a nonconvex MINLP in the complex domain that: (i) embeds current-injection power-flow equations for three-phase unbalanced operation; (ii) enforces radiality and connectivity; (iii) respects voltage and ampacity constraints per phase; and (iv) minimizes the equivalent annual cost (investment in conductors + energy losses). Vectorized expressions are used to compactly encode multiconductor/multiphase relations. Binary variables represent route activation and conductor-type decisions; continuous variables represent nodal voltages and branch currents.
3.5. Solution Procedure (B&B + Interior-Point)
The model is solved with BONMIN (v1.8.9) [47], which combines B&B with outer-approximation machinery for MINLP [48]. Nonlinear subproblems are handled by an interior-point method (IPOPT), well-suited to the nonconvexities induced by bilinear voltage–current couplings and absolute-value constraints in ampacity/voltage limits [49]. The procedure applied in this study is:
- Initialization. Set variable domains (binary routing/conductor choices; complex ), default bounds, and solver tolerances (optimality gap, feasibility). If an incumbent is available, initialize it.
- Master loop (B&B). Iteratively branch on binary decisions (build/not build a route; select conductor type) to generate a search tree. At each node, form an NLP relaxation by fixing/relaxing the relevant binaries.
- NLP relaxation (Interior-Point). Solve the continuous subproblem with interior-point: compute a primal solution and a valid lower bound (from the relaxation). Enforce numerical safeguards (scaling, barrier updates).
- Feasibility and technical checks. Verify that the primal solution satisfies per-phase voltage limits, ampacity constraints, and radiality/connectivity. If feasible and better than the incumbent, update the incumbent.
- Bounding and pruning. Compare node lower bounds with the incumbent objective. Fathom nodes that cannot improve the incumbent. Continue branching on promising nodes according to the node-selection policy.
- Termination. Stop when the optimality gap meets the tolerance or when the node list is exhausted. Return the best feasible solution (topology and conductor assignments) with the associated objective value.
Figure 2 (“Methodological Framework—Flowchart”) depicts these steps and the information exchanged between the B&B layer (discrete decisions and bounds) and the interior-point layer (continuous relaxations and primal solutions).
3.6. Stopping Criteria, Outputs, and Post-Processing
The algorithm terminates when the relative optimality gap falls below the prescribed tolerance or when the exploration budget is exhausted. The outputs include: (i) the final radial topology and per-branch conductor types; (ii) the cost breakdown (investment and losses) and electrical profiles (voltages, currents); and (iii) sensitivity analyses with respect to conductor catalog and energy price. All experiments are executed with fixed software versions (Julia, JuMP, BONMIN/IPOPT) and documented solver options to ensure reproducibility.
4. Case Study Systems
To evaluate the performance of the proposed MINLP formulation, two rural distribution test systems were considered. These systems were generated randomly following the guidelines established by Enel Colombia in its Generalidades. Normas de construcción de redes aéreas rurales de distribución [50]. Such networks typically operate at medium voltage levels ranging between 11.4 kV and 13.2 kV, are characterized by long feeder sections due to the dispersed location of consumers, and generally supply low load demand. For this study, two representative cases are analyzed: a 10-node system and a 30-node system, which serve to validate the formulation under different scales of network complexity.
4.1. 10-Node Distribution System
The 10-node distribution network operates at a line-to-line voltage of 11.4 kV at the substation node (node 1, shown in blue) and comprises 10 nodes, including 9 demand points. The total installed three-phase load is 1111 kW and 444 kVAr. For the route selection analysis, 17 potential construction routes (line segments) are considered, as illustrated in Figure 3.
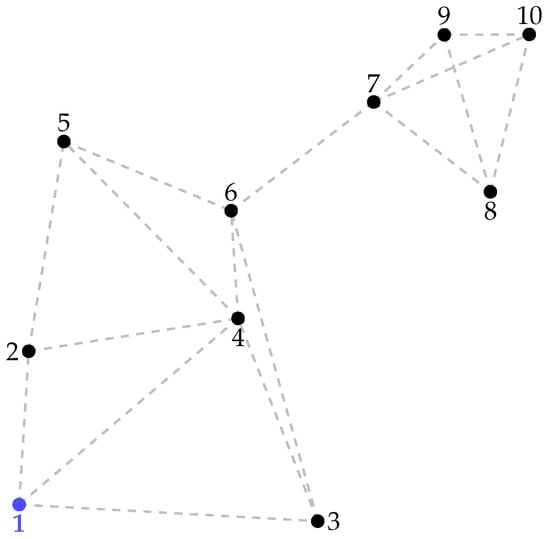
Figure 3.
10-node distribution systems with all possible routing options.
Table 4 and Table 5 compile the parametric data of the 30-node system, detailing the load at each node along with the set of lines available for construction.

Table 4.
Nodal three-phase load demand profile for the 10-node distribution system.

Table 5.
Candidate distribution routes in the 10-node system.
4.2. 30-Node Distribution System
The 30-node distribution network operates at a line-to-line voltage of 11.4 kV at the substation node (node 1, shown in blue) and consists of 30 nodes and 29 demand points. The total installed three-phase power is 2374 kW and 978 kVAr. For the route selection analysis, 55 potential construction routes are considered, as illustrated in Figure 4.
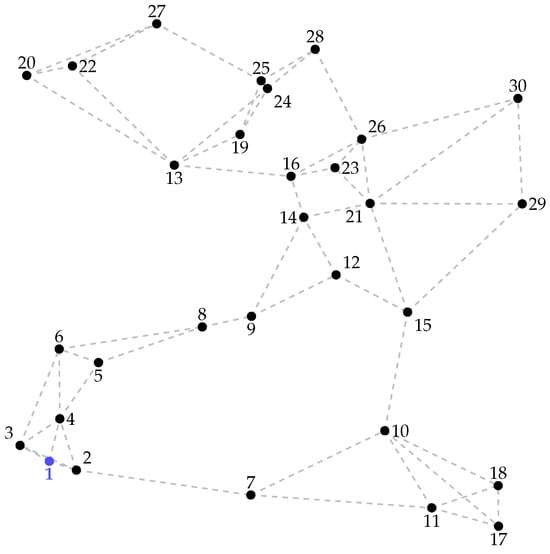
Figure 4.
30-node distribution systems with all possible routing options.
Table 6 and Table 7 compile the parametric data of the 30-node system, detailing the load at each node along with the set of lines available for construction.

Table 6.
Nodal three-phase load demand profile for the 30-node distribution system.

Table 7.
Candidate distribution routes in the 30-node system.
4.3. Available Conductors for Selection
Following the technical specifications of Enel Colombia for medium-voltage rural overhead networks, All-Aluminum Alloy Conductor (AAAC) is adopted as the standard, with Aluminum Conductor Steel-Reinforced (ACSR) used only in specific cases [50]. In three-phase configurations, the neutral conductor is sized with a smaller caliber than the phase conductors [50]. For this study, six conductor types recommended by Enel Colombia for rural applications are considered as discrete options in the optimization process. Each conductor is characterized by its electrical and economic parameters, including size, geometric mean radius (), resistance (), ampacity (), and unit investment cost (). These data, summarized in Table 8, provide the basis for the thermal constraints of the mathematical model and enable the assessment of trade-offs between investment cost and energy transport capacity.

Table 8.
Calibers considered for solving the conductor selection problem [50].
With respect to the geometric configuration of distribution lines, the technical specifications of Enel Colombia indicate that in medium-voltage four-wire systems with a shield wire, this element serves as the neutral conductor and is positioned at the top of the structure. In rural areas, tangential configurations are most commonly adopted, as illustrated in Figure 5 [51].
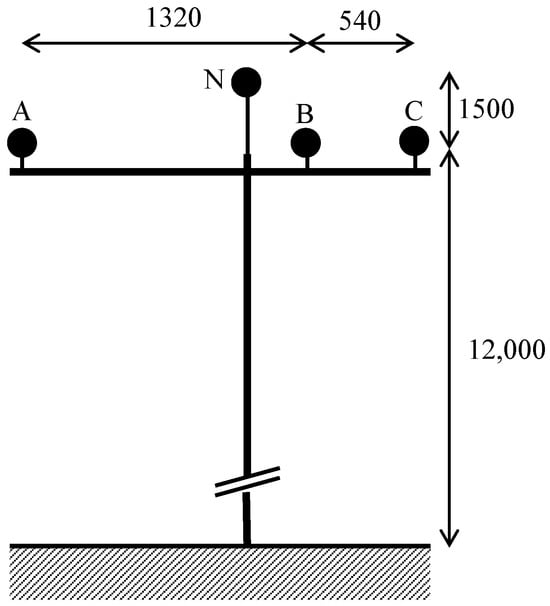
Figure 5.
Rural overhead distribution line with tangential configuration (all distances are given in mm).
Based on this geometric arrangement and the electrical parameters of the conductors listed in Table 8, the modified Carson equations are applied to compute the impedance matrix for each conductor type [34]. These calculations are fundamental to the evaluation of the mathematical model, as they provide an accurate representation of coupling effects and line electrical characteristics. The resulting impedance matrices are summarized in Table 9.

Table 9.
Impedance matrix corresponding to available conductor type.
For the development of the model and the evaluation of the proposed solutions, additional technical and economic parameters were incorporated, following the specifications reported in [33]. The energy cost was set at USD/kWh. To account for future conditions, an annual demand growth rate of and an energy price growth rate of were considered. Voltage regulation limits were established at and relative to the nominal value. The planning horizon was defined as years, with a total of h per year used to compute energy losses and operating costs. Together, these parameters provide a consistent reference framework for evaluating the technical and economic performance of the distribution network under alternative expansion configurations.
Remark 2.
The planning problem was evaluated under a worst-case scenario, assuming all loads operate at 100% of their nominal power for 8760 h per year. This conservative assumption captures maximum losses and voltage stress, ensuring that the proposed expansion plans remain technically feasible and robust against demand underestimation, while providing reliable strategies for safe long-term operation.
5. Simulation Results and Analysis
The computational experiments were conducted on a workstation equipped with a 12th-generation Intel Core i7-12700T processor @ 1.40 GHz, 32 GB of RAM, and a 64-bit Windows 11 Pro operating system. With respect to the software environment, the model was implemented in Julia v1.11.6 using the JuMP v1.29.0 optimization framework for model specification. The MINLP problems were solved with the BONMIN v1.8.9 solver, which integrates branch-and-bound and outer approximation techniques, while the nonlinear programming subproblems were addressed through the interior-point method, ensuring convergence in the presence of nonlinear and nonconvex constraints.
To validate the effectiveness of the proposed exact formulation, the results were compared against cascaded approaches commonly reported in the literature. In the first stage, network topologies were generated: (i) based on distance minimization, using minimum spanning tree (MST) heuristics [13], and (ii) based on energy loss minimization, using Grey Wolf Optimizer (GWO) [52], Vector Search Algorithm (VSA) [53], Salp Swarm Algorithm (SSA) [54], and Equilibrium Optimizer (EO) [55]. This stage enabled the construction of feasible trees to feed into the subsequent step. In the second stage, the conductor selection problem was addressed independently, again relying on the aforementioned metaheuristics to determine the conductor types assigned to each branch of the candidate topology. It is important to emphasize that the general configuration parameters, such as the number of iterations and the population size, were established uniformly for all the metaheuristic algorithms evaluated (i.e., 20 individuals and a maximum of 1000 iterations). This decision was made to ensure a fair comparison scenario, avoiding the possibility that differences in the allocation of computational resources could influence the observed performance.
This comparison provides a comprehensive benchmark, allowing the evaluation of the advantages of the proposed exact approach not only in terms of optimality and feasibility guarantees but also with respect to economic performance and network efficiency when contrasted with heuristic and metaheuristic cascaded strategies.
5.1. Results in the 10-Node Distribution System
Figure presents the results of the route selection process for the 10-node test system. Three different topologies are compared: the radial network obtained by the MST approach, the best radial configuration identified by the EO metaheuristic algorithm, and the exact MINLP solution proposed in this work. The total lengths of the resulting networks are 17,268.56 m, 17,704.87 m, and 21,192.93 m, respectively.
Figure 6 presents the results of the route selection process for the 10-node test system, comparing three topologies: the radial network obtained by the MST approach, the best radial configuration identified by the EO metaheuristic algorithm, and the exact MINLP solution proposed in this work.
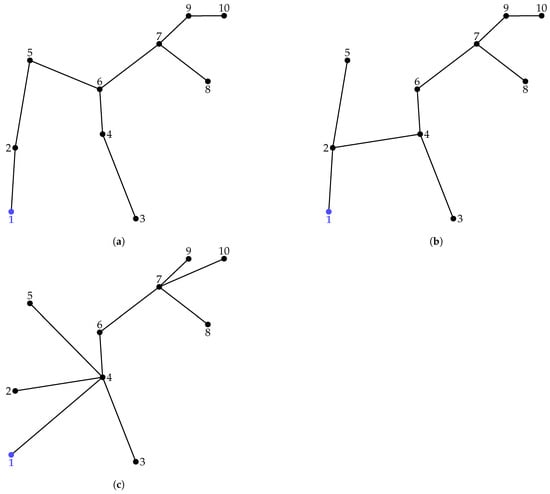
Figure 6.
Comparison of radial topologies for the 10-node system: (a) MST-based solution (17,268.56 m), (b) best metaheuristic solution (17,704.87 m), and (c) exact MINLP solution (21,192.93 m).
The MST topology prioritizes the shortest connections between nodes, resulting in a total length of 17,268.56 m. The metaheuristic-based configuration slightly increases the length to 17,704.87 m (about 2.5% longer than the MST) by incorporating marginally more infrastructure to achieve lower energy losses and improved operational performance. In contrast, the MINLP design requires a significantly longer network of 21,192.93 m, representing an increase of approximately 22.7% compared to the MST and 19.7% relative to the best metaheuristic solution. This additional distance arises because the MINLP formulation does not aim to minimize length alone; rather, it balances investment and operational costs by simultaneously optimizing route selection and conductor sizing under both economic and electrical constraints. Consequently, the longer routes in the exact solution enable improved current distribution, enhanced voltage profiles, and reduced losses once conductor selection is considered. Overall, the comparison shows that while minimizing distance is efficient from a purely geometric perspective, a comprehensive optimization approach may justify additional infrastructure if it delivers superior long-term technical and economic performance.
This behavior is confirmed by the results summarized in Table 10, which presents the outcomes of the conductor selection stage under different optimization approaches. The first column identifies the method employed, followed by the selected conductor configuration for each branch. The next three columns report the economic indicators: total annualized cost, annualized energy loss cost, and annualized investment cost. The last two columns show the percentage standard deviation and the average computational time.

Table 10.
Optimization results for conductor selection in the 10-node distribution network.
The cascaded MST–metaheuristic solutions yield identical results, with an annualized total cost of approximately USD 84,010.53. When metaheuristics are applied directly, a different conductor configuration is obtained, reducing the annualized cost to USD 73,338.90. This improvement stems mainly from a lower investment cost, with a reduction of approximately 11% compared to the MST-based solutions, while also slightly decreasing the cost of losses. The exact MINLP formulation achieves the best performance, with an annualized total cost of USD 71,796.49, resulting from a more efficient selection of conductors that reduces investment by approximately 16.8% compared to the MST-based solutions and balances loss costs at USD 25,312.65. In terms of overall savings, the MINLP approach reduces the total annualized cost by 14.6% compared to the MST-based solutions and by 2.1% relative to the direct application of metaheuristics.
In the other hand, Figure 7 presents the profiles of the main electrical variables obtained for the 10-node distribution system. Figure 7a shows the nodal voltages of phases A, B, and C in per-unit values, while Figure 7b illustrates the branch currents along the network lines.
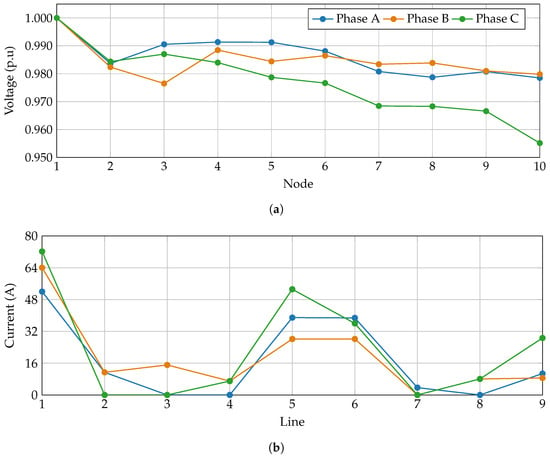
Figure 7.
Electrical variables in the 10-node distribution system: (a) nodal voltages, and (b) branch currents.
In Figure 7a, the voltage profiles remain close to the nominal value, but phase differences highlight the effect of load unbalance. The minimum voltage is approximately 0.953 p.u. at node 10 in phase C, which is about 4.7% below the reference and represents the most critical operating point. By contrast, phases A and B maintain slightly higher levels, with values above 0.98 p.u. across the network. Figure 7b shows the branch currents for each phase. The highest current occurs in line 1, with a peak of about 74 A in phase A, corresponding to the main feeder directly supplied by the substation. Beyond this point, current magnitudes decrease substantially, with most branches operating below 50 A and several below 10 A. This behavior is consistent with the low load density that characterizes rural distribution systems.
The 10-node network operates with relatively low current levels due to its rural nature. Nevertheless, the presence of significant voltage drops—particularly in phase C, caused by long line lengths—indicates the need for larger conductor sizes to preserve voltage regulation across the system. This finding confirms that, in rural grids, the limiting factor is not the thermal capacity of the conductors but rather the ability to maintain acceptable voltage levels at remote nodes.
The analysis of the 10-node system demonstrates that the proposed MINLP approach outperforms cascaded strategies. MST-based solutions, while efficient in terms of distance minimization, incur higher investment costs and overlook key operational aspects. Metaheuristic approaches partially address these limitations by incorporating electrical objectives, providing faster solutions with limited variability—an effect amplified by the relatively small size of the test system—but they lack global guarantees and may yield suboptimal configurations. In contrast, the MINLP formulation jointly optimizes route selection and conductor sizing under both economic and electrical constraints, delivering a unique, globally optimal, and technically consistent solution. Although this exact method requires a longer total route and significantly higher computational effort, it ensures that the expansion plan simultaneously meets topological, operational, and economic requirements. These results underscore the relevance of exact optimization methods in distribution system planning, where capital-intensive investment decisions must be supported by rigorous, verifiable, and globally optimal solutions.
5.2. Results in the 30-Node Distribution System
Figure 8 presents the results of the route selection process for the 30-node test system, comparing the three topologies. The total network lengths are 39,178.56 m for the MST approach, 42,889.18 m for the metaheuristic-based approach, and 47,041.03 m for the MINLP solution.
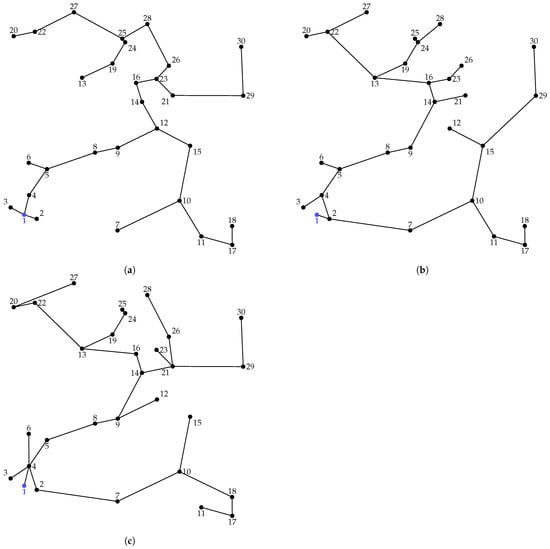
Figure 8.
Comparison of radial topologies for the 30-node system: (a) MST-based solution (39,178.56 m), (b) best metaheuristic solution (42,889.18 m), and (c) exact MINLP solution (47,041.0342 m).
The MST topology minimizes the total distance, yielding the shortest overall length of 39,178.56 m by prioritizing purely geometric efficiency and establishing the shortest possible connections between nodes. The metaheuristic-based solution extends the network length to 42,889.18 m, about 9.5% longer than the MST, as it seeks to reduce electrical losses through adjustments in route selection beyond distance minimization. The exact MINLP design produces the longest network, with a total length of 47,041.03 m—an increase of 20.1% compared to the MST and 9.7% relative to the best metaheuristic solution. This additional distance reflects the broader optimization perspective of the MINLP formulation, which balances investment and operational costs by jointly optimizing route selection and conductor sizing under both economic and electrical constraints. As a result, the model may favor longer connections when they improve current distribution, voltage drops, and overall system efficiency once conductor capacities and loss costs are taken into account.
Additionally, Table 11 presents the results of conductor selection for the 30-node system, containing the same type of information reported in Table 10.

Table 11.
Optimization results for conductor selection in the 30-node distribution network.
The MST–metaheuristic cascaded strategies yield annualized total costs in the range of USD 208,560.84 to USD 210,964.57, significantly higher than those obtained with either direct metaheuristic application or the MINLP solution. These elevated costs are mainly driven by high investment requirements (USD 799,970.40–810,480.24), since the topology enforced by the MST restricts flexibility in conductor allocation. Energy losses also remain substantial, around USD 98,000–99,000.
Direct application of metaheuristics provides considerable improvements. The best-performing method (EO) achieves an annualized cost of USD 183,771.61, with investment costs of USD 857,636.23 and energy loss costs of USD 71,162.44. Compared to MST-based strategies, this represents a reduction of approximately 12% in total annualized cost, primarily achieved by lowering both investment and loss components. Other metaheuristics (VSA, SSA, GWO) yield similar gains, with annualized costs ranging between USD 184,124.27 and USD 193,927.13.
The exact MINLP formulation delivers the best performance, with an annualized total cost of USD 180,902.80. This corresponds to a reduction of about 14.2% relative to the average MST-based solutions and 1.6–2.5% compared to the best metaheuristics. Importantly, the MINLP reduces investment costs to USD 793,060.13—2–3% lower than metaheuristic-based designs—while maintaining losses at USD 75,204.42. Although this loss value is slightly higher than that obtained with EO, it is offset by the lower investment. In terms of robustness, the MINLP provides zero variability (SD = 0%), whereas metaheuristics show SD values between 0.14% and 1.6%.
A key trade-off emerges in computational time: metaheuristics solve the problem in approximately 120–200 s, while the MINLP requires around 39,562 s (over 10 h). Despite this, the MINLP guarantees a globally optimal and technically consistent solution, which is crucial in practical planning contexts where capital-intensive investment decisions must be supported by verifiable optimality guarantees.
For the 30-node system the MINLP formulation once again outperforms both cascaded approaches, confirming that the simultaneous optimization of routes and conductors under exact methods leads to superior long-term economic performance and strict compliance with operational constraints.
On the other side, Figure 9 presents the electrical variables for the 30-node distribution system.
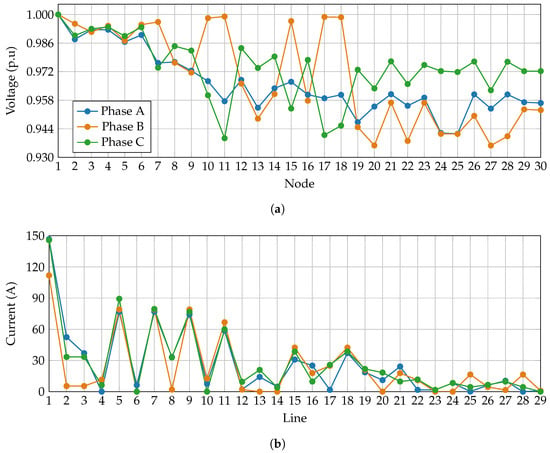
Figure 9.
Electrical variables in the 30-node distribution system: (a) nodal voltages, and (b) branch currents.
In Figure 9a, the voltages progressively decrease with distance from the substation, reflecting the long feeder sections typical of rural systems. The most critical condition occurs in phase B at node 20, where the minimum voltage reaches approximately 0.9358 p.u., representing a deviation of nearly 7% below nominal. Phases A and C exhibit slightly better regulation, remaining mostly above 0.94 p.u., but still show clear unbalance and significant dispersion across the network. Figure 9b illustrates the branch current profiles. The highest current is recorded in the main feeder, specifically in line 1 with a peak of about 150 A in phase C. Beyond this section, currents decrease sharply, with most branches carrying less than 50 A and many below 20 A, which is consistent with the low load density characteristic of rural distribution systems.
Although branch currents remain relatively low, the main challenge in rural networks is voltage regulation. The substantial drop observed in phase B at remote nodes underscores the need for larger conductor sizes, not to address thermal limits but to maintain acceptable service voltages. This analysis confirms that, in rural systems, conductor sizing is primarily dictated by voltage quality requirements rather than ampacity constraints.
The results from the 10-node and 30-node test systems consistently show that the exact MINLP formulation outperforms heuristic ans metaheuristic strategies. While MST-based approaches minimize geometric distance, they incur higher investment costs and energy losses due to their restrictive topology. Metaheuristics achieve partial improvements by embedding electrical objectives, lowering total annualized costs and losses, but they exhibit variability and lack guarantees of global optimality. In contrast, the MINLP approach provides the lowest annualized costs by jointly optimizing routes and conductor sizes under both economic and electrical constraints, delivering reproducible and globally optimal solutions.
As system size increases, the advantages of the MINLP formulation become more evident. This approach achieves greater cost savings relative to MST-based solutions and consistently outperforms metaheuristics by providing globally optimal results that are both technically consistent and economically efficient. While the computational burden grows with network complexity, the method remains tractable for medium-scale systems and proves particularly valuable for strategic distribution planning, where capital-intensive decisions demand solutions that are robust, reproducible, and mathematically verifiable.
6. Conclusions and Future Works
This paper presented an exact optimization methodology for the simultaneous selection of routes and conductors in unbalanced three-phase distribution systems, formulated as a MINLP problem. The model integrates the physical laws of three-phase power flow with the minimization of investment and operational costs, while ensuring radial topology, compliance with voltage and ampacity limits, and globally optimal network designs. The formulation was implemented in Julia using JuMP optimization environment and solved with BONMIN, with results benchmarked against cascaded strategies based on MST and metaheuristic approaches.
Numerical results on 10-node and 30-node test systems confirmed the superiority of the proposed MINLP formulation. For the 10-node system, the MINLP achieved an annualized cost of USD 71,796.49, reducing costs by 14.6% compared to MST-based solutions (USD 84,010.53) and 2.1% relative to metaheuristics (USD 73,338.90). Investment decreased by 16.8% with respect to MST while maintaining balanced loss costs at USD 25,312.65. For the 30-node case, the MINLP yielded the lowest annualized cost of USD 180,902.80, improving results by approximately 14.2% relative to MST-based solutions (above USD 210,000) and 1.6–2.5% compared to the best-performing metaheuristics (USD 183,771.61–184,124.27). The investment component was reduced to USD 793,060.13, about 2–3% below metaheuristic solutions, while ensuring technical feasibility and zero variability (standard deviation = 0%). Although computational times were higher (approximately 39,562 s), the method consistently provided globally optimal and reproducible results, demonstrating its relevance for planning contexts where investment decisions are capital intensive.
Future research directions include extending the MINLP formulation to account for time-varying and stochastic demand profiles, thereby capturing the impact of load uncertainty on planning decisions; incorporating distributed generation units, such as photovoltaic systems, and assessing their influence on conductor sizing and route selection; and evaluating the combined deployment of reactive power compensators (e.g., D-STATCOMs) to improve voltage regulation and reduce system losses. In addition, scaling the methodology to large-scale, realistic distribution networks through decomposition techniques and advanced global optimization strategies is a promising avenue. Finally, developing hybrid exact–metaheuristic approaches that combine the global guarantees of MINLP with the computational efficiency of heuristics could further enhance scalability for very large systems.
Author Contributions
Conceptualization, methodology, software, and writing (review and editing): B.C.-C., O.D.M., L.F.G.-N., S.B.-M. and C.A.T.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Institución Universitaria Pascual Bravo, Research Project: Regulación de frecuencia eléctrica empleando resortes eléctricos en sistemas con alta penetración de energías renovables, code PCT00036.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the financial support provided by the Institución Universitaria Pascual Bravo, Research Project: Regulación de frecuencia eléctrica empleando resortes eléctricos en sistemas con alta penetración de energías renovables, code PCT00036. The second author acknowledges the support provided by Thematic Network 723RT0150, i.e., Red para la integración a gran escala de energías renovables en sistemas eléctricos (RIBIERSE-CYTED), funded through the 2022 call for thematic networks of the CYTED (Ibero-American Program of Science and Technology for Development).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Villarreal, M.I.Z.; Téllez, A.A.; Krishnan, N.; García, M. Expansion Planning of Electrical Distribution Systems Considering Voltage Quality and Reliability Criteria. Energies 2025, 18, 2822. [Google Scholar] [CrossRef]
- Firoozi, A.A.; Firoozi, A.A.; Oyejobi, D.; Avudaiappan, S.; Flores, E.S. Emerging trends in sustainable building materials: Technological innovations, enhanced performance, and future directions. Results Eng. 2024, 24, 103521. [Google Scholar] [CrossRef]
- Firoozi, A.A.; Firoozi, A.A.; Maghami, M.R. Harnessing photovoltaic innovation: Advancements, challenges, and strategic pathways for sustainable global development. Energy Convers. Manag. X 2025, 27, 101058. [Google Scholar] [CrossRef]
- Montoya, O.D.; Cortés-Caicedo, B.; Florez-Cediel, O.D. On the Exact Formulation of the Optimal Phase-Balancing Problem in Three-Phase Unbalanced Networks: Two Alternative Mixed-Integer Nonlinear Programming Models. Electricity 2025, 6, 9. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, X. Comprehensive analysis on three-phase imbalance management technology of low-voltage distribution network. Appl. Comput. Eng. 2024, 62, 309–314. [Google Scholar] [CrossRef]
- Dobrzynski, K.; Czapp, S. Voltage and Current Unbalance Reduction in Power Networks with Distributed Generation and Electric Vehicles. Energies 2024, 17, 2780. [Google Scholar] [CrossRef]
- Fose, N.; Singh, A.R.; Krishnamurthy, S.; Ratshitanga, M.; Moodley, P. Empowering distribution system operators: A review of distributed energy resource forecasting techniques. Heliyon 2024, 10, e34800. [Google Scholar] [CrossRef] [PubMed]
- Yaghoubi, E.; Yaghoubi, E.; Maghami, M.R.; Rahebi, J.; Zareian Jahromi, M.; Ghadami, R.; Yusupov, Z. A Systematic Review and Meta-Analysis of Model Predictive Control in Microgrids: Moving Beyond Traditional Methods. Processes 2025, 13, 2197. [Google Scholar] [CrossRef]
- Nabian Dehaghani, M.; Korõtko, T.; Rosin, A. Power quality improvement in DG based distribution systems: A review. Renew. Sustain. Energy Rev. 2026, 225, 116184. [Google Scholar] [CrossRef]
- Alqahtani, M.; Alghamdi, A.S. Optimized Coordination of Distributed Energy Resources in Modern Distribution Networks Using a Hybrid Metaheuristic Approach. Processes 2025, 13, 1350. [Google Scholar] [CrossRef]
- Saldaña-González, A.E.; Aragüés-Peñalba, M.; Sumper, A. Distribution network planning method: Integration of a recurrent neural network model for the prediction of scenarios. Electr. Power Syst. Res. 2024, 229, 110125. [Google Scholar] [CrossRef]
- Burmeister, S.C.; Schryen, G. Distribution network optimization: Predicting computation times to design scenario analysis for network operators. Energy Syst. 2023, 16, 227–254. [Google Scholar] [CrossRef]
- Montoya, O.D.; Serra, F.M.; De Angelo, C.H.; Chamorro, H.R.; Alvarado-Barrios, L. Heuristic Methodology for Planning AC Rural Medium-Voltage Distribution Grids. Energies 2021, 14, 5141. [Google Scholar] [CrossRef]
- Bolaños, R.I.; Guzmán-Henao, J.A.; Grisales-Noreña, L.F.; Montoya, O.D.; Hernández, J.C. Hierarchical Optimization of DGs, BESSs, and D-STATCOMs for Reducing Energy Losses and CO2 Emissions in Unbalanced Off-Grid Networks. Results Eng. 2025, 28, 107098. [Google Scholar] [CrossRef]
- Barrera-Singaña, C.; Comech, M.P.; Arcos, H. A Comprehensive Review on the Integration of Renewable Energy Through Advanced Planning and Optimization Techniques. Energies 2025, 18, 2961. [Google Scholar] [CrossRef]
- Bambaravanage, T.; Perera, C.; Rodrigo, A. An effective stability solution for small power systems with high distributed generation. Discov. Energy 2025, 5, 17. [Google Scholar] [CrossRef]
- Riaño-Enciso, L.M.; Cortés-Caicedo, B.; Montoya, O.D.; Grisales-Noreña, L.F.; Hernández, J.C. Sustainable Metaheuristic-Based Planning of Rural Medium- Voltage Grids: A Comparative Study of Spanning and Steiner Tree Topologies for Cost-Efficient Electrification. Sustainability 2025, 17, 8145. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Florez-Cediel, O.D. Exact Mixed-Integer Nonlinear Programming Formulation for Conductor Size Selection in Balanced Distribution Networks: Single and Multi-Objective Analyses. Electricity 2025, 6, 14. [Google Scholar] [CrossRef]
- Marcelo, J.A.; Muñoz-Delgado, G.; Contreras, J.; Sanches Mantovani, J.R. A Novel Solution Technique for the Expansion Planning of Modern Distribution Systems: A Feasibility-Driven Approach. IEEE Access 2025, 13, 120632–120647. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing Radiality Constraints in Distribution System Optimization Problems. IEEE Trans. Power Syst. 2012, 27, 172–180. [Google Scholar] [CrossRef]
- Valencia, D.A.; Hincapie, I.R.A.; Gallego, R.R.A. Expansion planning of joint medium- and low-voltage three-phase distribution networks considering the optimal integration of distributed energy resources. Energy Rep. 2023, 9, 1183–1200. [Google Scholar] [CrossRef]
- Lavorato, M.; Rider, M.J.; Garcia, A.V.; Romero, R. Distribution network planning using a constructive heuristic algorithm. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Benitez Cattani, I.; Chaparro, E.; Barán, B. Distribution System Operation and Expansion Planning using Network Reconfiguration. IEEE Lat. Am. Trans. 2020, 18, 845–852. [Google Scholar] [CrossRef]
- Picard, J.L.; Aguado, I.; Cobos, N.G.; Fuster-Roig, V.; Quijano-López, A. Electric Distribution System Planning Methodology Considering Distributed Energy Resources: A Contribution towards Real Smart Grid Deployment. Energies 2021, 14, 1924. [Google Scholar] [CrossRef]
- Macedo, L.H.; Vargas, R.; Home-Ortiz, J.M.; Mantovani, J.R.S.; Romero, R.; Catalao, J.P.S. Increasing the PV Hosting Capacity in Unbalanced Three-Phase Distribution Networks Through Reconfiguration with Closed-Loop Operation. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Noel da Silva, M.S.; Lima, D.A. Optimal operation planning of distribution systems under uncertainty in load modeling by using decentralized energy resources. Electr. Power Syst. Res. 2021, 196, 107269. [Google Scholar] [CrossRef]
- Martins, R.M.; Cardoso, G.; Marchesan, G. Three-Phase-Two-Wire Rural Distribution System Planning: Load Phase Distribution for Minimum Voltage Unbalance. IEEE Trans. Power Deliv. 2025, 40, 2131–2141. [Google Scholar] [CrossRef]
- Jalali, M.; Zare, K.; Hagh, M.T. A multi-stage MINLP-based model for sub-transmission system expansion planning considering the placement of DG units. Int. J. Electr. Power Energy Syst. 2014, 63, 8–16. [Google Scholar] [CrossRef]
- Vélez-Marín, V.M.; Montoya, O.D.; Hernández, J.C. A DIgSILENT Programming-Based Approach for Selecting Conductors in Distribution Networks via the Tabu Search Algorithm. In Proceedings of the 2024 IEEE Colombian Conference on Applications of Computational Intelligence (ColCACI), Pamplona, Colombia, 17–19 July 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Cortés-Caicedo, B.; Montoya, O.D. An accurate MINLP formulation for selecting conductors in three-phase asymmetric networks: A computational implementation in the Julia software. Results Control Optim. 2025, 20, 100596. [Google Scholar] [CrossRef]
- Gallego Pareja, L.A.; López-Lezama, J.M.; Gómez Carmona, O. Optimal integration of distribution network reconfiguration and conductor selection in power distribution systems via MILP. Energies 2023, 16, 6998. [Google Scholar] [CrossRef]
- Bosisio, A.; Berizzi, A.; Amaldi, E.; Bovo, C.; Sun, X.A. Optimal feeder routing in urban distribution networks planning with layout constraints and losses. J. Mod. Power Syst. Clean Energy 2020, 8, 1005–1014. [Google Scholar] [CrossRef]
- Cortés-Caicedo, B.; Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W.; Ardila-Rey, J.A. Simultaneous Feeder Routing and Conductor Selection in Rural Distribution Networks Using an Exact MINLP Approach. Smart Cities 2025, 8, 68. [Google Scholar] [CrossRef]
- Kersting, W.H. Distribution system modeling and analysis. In Electric Power Generation, Transmission, and Distribution; CRC Press: Boca Raton, FL, USA, 2018; pp. 26-1–26-58. [Google Scholar] [CrossRef]
- Kamal, M.M.; Ashraf, I.; Fernandez, E. Planning and optimization of microgrid for rural electrification with integration of renewable energy resources. J. Energy Storage 2022, 52, 104782. [Google Scholar] [CrossRef]
- Geth, F.; Chapman, A.C.; Heidari, R.; Clark, J. Considerations and design goals for unbalanced optimal power flow benchmarks. Electr. Power Syst. Res. 2024, 235, 110646. [Google Scholar] [CrossRef]
- Ljubić, I. Solving Steiner trees: Recent advances, challenges, and perspectives. Networks 2021, 77, 177–204. [Google Scholar] [CrossRef]
- Yang, B.; Zheng, W. Near-optimal Steiner tree computation powered by node embeddings. Knowl. Inf. Syst. 2023, 65, 4563–4583. [Google Scholar] [CrossRef]
- Bienstock, D.; Verma, A. Strong NP-hardness of AC power flows feasibility. Oper. Res. Lett. 2019, 47, 494–501. [Google Scholar] [CrossRef]
- Zhadan, A.; Martemyanov, A.; Allahverdyan, A.; Petrosian, O.; Gao, H. Linearization method for MINLP energy optimization problems. Sci. Rep. 2025, 15, 27853. [Google Scholar] [CrossRef]
- Tahami, H.; Fakhravar, H. A literature review on combining heuristics and exact algorithms in combinatorial optimization. Eur. J. Inf. Technol. Comput. Sci. 2022, 2, 6–12. [Google Scholar] [CrossRef]
- Kuchlbauer, M.; Liers, F.; Stingl, M. Outer approximation for mixed-integer nonlinear robust optimization. J. Optim. Theory Appl. 2022, 195, 1056–1086. [Google Scholar] [CrossRef]
- Oustry, A. AC Optimal Power Flow: A strengthened SDP relaxation and an iterative MILP scheme for global optimization. Open J. Math. Optim. 2022, 3, 19. [Google Scholar] [CrossRef]
- Östermark, R. Solving difficult mixed integer and disjunctive non-linear problems on single and parallel processors. Appl. Soft Comput. 2014, 24, 385–405. [Google Scholar] [CrossRef]
- Datseris, G. DynamicalSystems. jl: A Julia software library for chaos and nonlinear dynamics. J. Open Source Softw. 2018, 3, 598. [Google Scholar] [CrossRef]
- Lubin, M.; Dowson, O.; Dias Garcia, J.; Huchette, J.; Legat, B.; Vielma, J.P. JuMP 1.0: Recent improvements to a modeling language for mathematical optimization. Math. Program. Comput. 2023, 15, 581–589. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Rakočević, S.; Ćalasan, M.; Ali, Z.M.; Hasanien, H.M.; Turky, R.A.; Aleem, S.H.A. BONMIN solver-based coordination of distributed FACTS compensators and distributed generation units in modern distribution networks. Ain Shams Eng. J. 2022, 13, 101664. [Google Scholar] [CrossRef]
- Grossmann, I.E. Review of nonlinear mixed-integer and disjunctive programming techniques. Optim. Eng. 2002, 3, 227–252. [Google Scholar] [CrossRef]
- Potra, F.A.; Wright, S.J. Interior-point methods. J. Comput. Appl. Math. 2000, 124, 281–302. [Google Scholar] [CrossRef]
- Enel Colombia. Normas de Construcción: Líneas Aéreas Rurales de Distribución. 2025. Available online: https://likinormas.enelcol.com.co/normas/lineas-aereas-rurales-de-distribucion/generalidades-lineas-aereas-rurales-lar/generalidades-normas-de-construccion-redes-aereas-rurales-de-distribucion#2.1.4consideracionespreliminares (accessed on 12 September 2025).
- Enel Colombia. Normas de Construcción: Líneas Aéreas Urbanas de Distribución—LA202 Circuito Primario Sencillo Construcción Tangencial (11.4–13.2 kV). 2025. Available online: https://likinormas.enelcol.com.co/normas/lineas-aereas-urbanas-de-distribucion/lineas-aereas-114-132-kv/la202-circuito-primario-sencillo-construccion-tangencial (accessed on 12 September 2025).
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A new metaheuristic for numerical function optimization: Vortex Search algorithm. Inf. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl.-Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).