Optimal Planning and Dynamic Operation of Thyristor-Switched Capacitors in Distribution Networks Using the Atan-Sinc Optimization Algorithm with IPOPT Refinement

Abstract

This paper proposes an innovative hybrid optimization framework for the optimal installation and operation of thyristor-switched capacitors (TSCs) within medium-voltage distribution networks, targeting both energy losses reduction and cost efficiency. The core of the approach combines the exploratory capabilities of the atan-sinc optimization algorithm (ASOA), a recent metaheuristic inspired by mathematical functions, with the local refinement power of the IPOPT solver within a master–slave architecture. This integrated method addresses the inherent complexity of a multi-objective, mixed-integer nonlinear programming problem that seeks to balance conflicting goals: minimizing annual system losses and investment costs. Extensive testing on IEEE 33- and 69-bus systems under fixed and dynamic reactive power injection scenarios demonstrates that our framework consistently delivers superior solutions when compared to traditional and state-of-the-art algorithms. Notably, the variable operation case yields energy savings of up to 12%, translating into annual monetary gains exceeding USD 1000 in comparison with the fixed support scenario.The solutions produce well-distributed Pareto fronts that illustrate valuable trade-offs, allowing system planners to make informed decisions. The findings confirm that the proposed strategy constitutes a scalable, and robust tool for reactive power planning, supporting the deployment of smarter and more resilient distribution systems.

1. Introduction

The increasing integration of distributed energy resources (DERs), the rising demands for power quality, and the urgent need for energy efficiency have substantially reshaped the operation of modern distribution networks [1,2]. The proliferation of renewables such as photovoltaic (PV) systems, wind turbines, and energy storage units has introduced a high level of variability and uncertainty, making real-time grid management more complex and demanding sophisticated control and optimization strategies [3,4]. In particular, medium-voltage distribution networks (MVDNs) confront escalating challenges in maintaining voltage stability, reducing technical losses, and ensuring operational reliability amid highly fluctuating loads and decentralized power injections [5,6]. This evolving landscape necessitates innovative solutions that can dynamically adapt to changing grid conditions while minimizing operating costs and environmental impacts.

In addressing these issues, advanced reactive power compensation devices such as thyristor-switched capacitors (TSCs) have gained prominence due to their fast switching capability, modularity, and controllability [7,8]. Their ability to rapidly respond to load fluctuations makes them suitable for deployment in highly dynamic environments, facilitating real-time voltage regulation and enabling power quality improvement [7]. When optimally located and correctly sized, TSCs can significantly improve voltage profiles, minimize line losses, and enhance the overall energy efficiency [9]. Nevertheless, the optimal siting and sizing of these devices—especially under varying load profiles and renewable generation patterns—represents a complex, nonlinear mixed-integer optimization problem [10,11]. This challenge is further intensified by the combinatorial nature of discrete device placements coupled with continuous control variables, as well as by the nonlinear power flow constraints that characterize realistic distribution systems.

Adding to this complexity, decision-makers often aim to balance conflicting objectives such as total energy losses minimization and reduction in investment and operating costs of reactive power compensators. This naturally implies a multi-objective optimization (MOO) problem, for which there is no single optimum, but rather a set of Pareto-optimal solutions representing the optimal trade-offs between competing criteria [12,13]. Multi-objective solution generation allows utilities and system operators to evaluate different strategies based on economic, environmental, and reliability considerations, thus supporting more informed and balanced decision-making.

Recent research has explored various solution strategies, from deterministic solvers like BONMIN and COUENNE for small-scale problems [14] to metaheuristic techniques, including genetic algorithms, particle swarm optimization, and the artificial hummingbird algorithm [8,15,16]. Hybrid approaches that combine global search heuristics with local optimization techniques have demonstrated the capacity to efficiently navigate high-dimensional and non-convex search spaces, often outperforming purely heuristic or deterministic methods in terms of solution quality and convergence speed [11]. Despite these advances, existing metaheuristic methods often face difficulties in sustaining solution diversity, avoiding premature convergence, and efficiently handling the large-scale, mixed-integer nature of problems dealing with real distribution systems, particularly when computational resources and real-time operational constraints are considered.

Motivated by these gaps, this paper proposes a novel hybrid framework that combines the exploratory capabilities of the atan-sinc optimization algorithm (ASOA)—a recent math-inspired metaheuristic technique—paired with a high-precision local optimization tool called IPOPT. The ASOA leverages the mathematical properties of arctangent and sinc functions to enable oscillatory and adaptive search behaviors that effectively explore high-dimensional, non-convex landscapes [17]. The overall architecture employs a master–slave approach that efficiently handles the studied mixed-integer, multi-objective problem, generating a well-distributed Pareto front for the siting, sizing, and dispatch of TSCs under realistic load scenarios.

The main contributions of this work are presented below:

• The development of a novel multi-objective mixed-integer nonlinear programming (MINLP) formulation that explicitly incorporates time-varying load profiles and dynamic reactive power support strategies, enabling a comprehensive optimization of TSC siting, sizing, and operation in distribution networks.
• The introduction of a hybrid framework that combines ASOA with IPOPT, providing an efficient and robust solution approach capable of handling the high-dimensional, large-scale, and complex nature of the studied problem, with demonstrated performance on standard benchmarks.

This study primarily focuses on developing and validating the proposed hybrid optimization framework using standard small-scale IEEE test systems (33 and 69 nodes). While the approach yields promising results in terms of solution quality, convergence, and cost reduction, this analysis does not explicitly account for load variability or the stochastic nature of renewable energy sources (RES). Incorporating such uncertainties is essential for a comprehensive validation of the strategy’s robustness under realistic operating conditions. Addressing these factors remains part of our future research direction; a more detailed assessment on larger-scale, real-world distribution networks will be performed to evaluate the practical applicability of the proposed methodology.

The remainder of this paper is organized as follows. Section 2 introduces the mathematical formulation of the multi-objective optimization problem. Section 3 describes the proposed hybrid solution methodology, including the ASOA and its integration with IPOPT. Section 4 presents the characteristics of the test systems and the simulation setup, and Section 5 discusses the numerical results obtained under various operating scenarios. Finally, Section 7 summarizes the main conclusions and proposes some directions for future work.

2. Multi-Objective Formulation of the Optimization Problem

This section presents the multi-objective mathematical formulation for the optimal siting and sizing of TSCs in MVDNs. The problem is formulated as a MINLP model involving both discrete and continuous decision variables [9]. The optimization process considers two conflicting objectives: the minimization of both the technical energy losses and the annualized investment costs associated with TSC deployment [18]. These objectives form a vector-valued cost function subject to nonlinear power flow equations, thermal and voltage limits, and operational constraints.

2.1. Multi-Objective Problem Statement

Let $\mathbf{x}$ denote the vector of decision variables, including the siting indicators $x_k\in \{0,1\}$, the sizing variables $q_k^{\mathrm{TSC}}$, and the network voltage variables $\{v_{kh},{\theta }_{kh}\}$. The multi-objective optimization problem is formally expressed as follows [19]:

$$\underset{\mathbf{x}}{min}\mathbf{f}\left(\mathbf{x}\right)=\left[\begin{array}{c}{f}_1\left(\mathbf{x}\right)\\ f_2\left(\mathbf{x}\right)\end{array}\right],$$

(1)

subject to:

• The Power Balance Constraints (4) and (5),
• The Branch Current Constraints (6)–(8),
• The Voltage Regulation Constraints (9) and (10),
• The TSC Siting and Operation Constraints (11)–(13),
• The Optional Fixed Injection Constraint (14).

The components of the Objective Function (1) are defined below [8]:

Objective 1:

minimization of technical energy losses

$$f_1\left(\mathbf{x}\right)=C_{\mathrm{kWh}}T\sum _{h\in \mathcal{H}}\sum _{k\in \mathcal{N}}\sum _{m\in \mathcal{N}}{v}_{kh}{v}_{mh}{Y}_{km}cos({\theta }_{kh}-{\theta }_{mh}-{\varphi }_{km}){\Delta }_h,$$

(2)

where $C_{\mathrm{kWh}}$ is the cost of energy per kWh, T is the number of days of operation in a year, and ${\Delta }_h$ is the duration of the time interval h. The sets $\mathcal{N}$ and $\mathcal{H}$ represent the network buses and time periods, respectively.

Objective 2:

minimization of the annualized investment cost

$$f_2\left(\mathbf{x}\right)=T\left({\displaystyle \frac{k_1}{k_2}}\right)\sum _{k\in \mathcal{N}}{q}_k^{\mathrm{TSC}}\left({\omega }_1{\left(q_k^{\mathrm{TSC}}\right)}^2+{\omega }_2{q}_k^{\mathrm{TSC}}+{\omega }_3\right),$$

(3)

where ${\omega }_1$, ${\omega }_2$, and ${\omega }_3$ are cost coefficients, and $k_1/k_2$ denotes the annuitization factor used to account for the time value of money over the planning horizon.

2.2. Power Flow Constraints

The power balance at each bus and time period is maintained through the nonlinear active and reactive power equations [10]:

$$\begin{array}{cccc}\hfill p_{kh}^g-p_{kh}^d& =\sum _{m\in \mathcal{N}}{v}_{kh}{v}_{mh}{Y}_{km}cos({\theta }_{kh}-{\theta }_{mh}-{\varphi }_{km}){\Delta }_h,\hfill & \hfill & \forall k\in \mathcal{N},\forall h\in \mathcal{H},\hfill \end{array}$$

(4)

$$\begin{array}{cccc}\hfill q_{kh}^g-q_{kh}^d+q_{kh}^{\mathrm{TSC}}& =\sum _{m\in \mathcal{N}}{v}_{kh}{v}_{mh}{Y}_{km}sin({\theta }_{kh}-{\theta }_{mh}-{\varphi }_{km}){\Delta }_h,\hfill & \hfill & \forall k\in \mathcal{N},\forall h\in \mathcal{H}.\hfill \end{array}$$

(5)

2.3. Thermal and Voltage Constraints

2.3.1. Branch Current Flow Limits

The current flowing from buses k to m during the time period h is given by its real and imaginary components [20]:

$$\begin{array}{cc}\hfill i_{kmh}^r& =y_{km}\left(v_{kh}cos({\theta }_{kh}-{\varphi }_{km})-v_{mh}cos({\theta }_{mh}-{\varphi }_{km})\right),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill i_{kmh}^i& =y_{km}\left(v_{kh}sin({\theta }_{kh}-{\varphi }_{km})-v_{mh}sin({\theta }_{mh}-{\varphi }_{km})\right),\hfill \end{array}$$

(7)

which must satisfy the following thermal limit:

$$\sqrt{{\left(i_{kmh}^r\right)}^2+{\left(i_{kmh}^i\right)}^2}\le I_{km}^{max},\forall (k,m)\in \mathcal{L},\forall h\in \mathcal{H}.$$

(8)

2.3.2. Voltage Magnitude Constraints

Voltage levels are maintained within the regulatory limits as follows [21]:

$$\begin{array}{cccc}\hfill v_{sh}& =V_{\mathrm{nom}},{\theta }_{sh}=0,\hfill & \hfill & \forall h\in \mathcal{H},\hfill \end{array}$$

(9)

$$\begin{array}{cccc}\hfill V_{min}& \le v_{kh}\le V_{max},\hfill & \hfill & \forall k\in \mathcal{N},\forall h\in \mathcal{H}.\hfill \end{array}$$

(10)

2.4. TSC Siting and Sizing Constraints

TSC deployment is modeled via binary siting and sizing variables ($x_k$ and $q_k^{\mathrm{TSC}}$, respectively), which is subject to [11]:

$$\begin{array}{cccc}\hfill 0\le q_k^{\mathrm{TSC}}& \le x_k{q}_{max}^{\mathrm{TSC}},\hfill & \hfill & \forall k\in \mathcal{N},\hfill \end{array}$$

(11)

$$\begin{array}{cccc}\hfill -q_k^{\mathrm{TSC}}\le q_{kh}^{\mathrm{TSC}}& \le q_k^{\mathrm{TSC}},\hfill & \hfill & \forall k\in \mathcal{N},\forall h\in \mathcal{H},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \sum _{k\in \mathcal{N}}{x}_k& \le x_{max}^{\mathrm{TSC}}.\hfill \end{array}$$

(13)

For fixed reactive power injection scenarios, Constraint (12) is replaced by

$$q_{kh}^{\mathrm{TSC}}=q_k^{\mathrm{TSC}},\forall k\in \mathcal{N},\forall h\in \mathcal{H}.$$

(14)

2.5. Solution Strategy

The multi-objective MINLP problem formulated in (1) and constrained by (4)–(14) poses substantial computational challenges due to its nonlinear, non-convex nature, as well as to the presence of both discrete and continuous decision variables [11]. To address this complexity, a hybrid mataheuristic optimization framework is employed which combines global exploration and local refinement.

Specifically, this work adopted the ASOA, a recently proposed math-inspired metaheuristic method, in order to generate candidate configurations for the placement of TSCs [17]. ASOA effectively explores the high-dimensional decision space and constructs a representative Pareto front, capturing the trade-offs between conflicting objectives, such as energy losses minimization and investment costs reduction.

For each candidate solution generated by ASOA, the corresponding TSC size and hourly reactive power dispatch are computed by solving an optimal power flow (OPF) subproblem using the JuMP modeling language and the IPOPT solver in Julia [22]. This ensures that each configuration is not only optimal in terms of the objective functions, but also feasible with respect to the operational constraints.

The proposed hybrid strategy allows efficiently navigating the search space while accurately satisfying the problem constraints. In this work, simulation results obtained on benchmark 33- and 69-bus distribution networks demonstrated the framework’s capability to significantly reduce both technical losses and annualized investment costs when compared to conventional fixed compensation approaches. Moreover, the solution methodology exhibited strong scalability properties and practical relevance for real-world distribution system planning.

3. Multi-Objective Optimization Methodology

Multi-objective optimization (MOO) involves simultaneously minimizing or maximizing multiple conflicting objective functions subject to a given set of constraints. In the context of this study, the goal was to minimize two competing criteria: the technical energy losses ($f_1$) and the annualized investment cost associated with TSC deployment ($f_2$), as defined in Equations (2) and (3), respectively. This implies a MIN–MIN optimization problem over the feasible space $\mathcal{X}$ defined by the constraints in Equations (4)–(14).

3.1. Pareto Optimality and Dominance

In MOO problems, a solution ${\mathbf{x}}^{*}\in \mathcal{X}$ is said to be Pareto optimal if there is no other feasible solution $\mathbf{x}\in \mathcal{X}$, such that [23]

$$f_j\left(\mathbf{x}\right)\le f_j\left({\mathbf{x}}^{*}\right)\forall j\in \{1,2\}\mathrm{and}{f}_k\left(\mathbf{x}\right)<f_k\left({\mathbf{x}}^{*}\right)\mathrm{for}\mathrm{at}\mathrm{least}\mathrm{one}k.$$

(15)

The set of all non-dominated solutions constitutes the Pareto front, which characterizes the trade-off boundary between the competing objectives [24].

3.2. Pareto Front Construction for MIN–MIN Problems

When simultaneously minimizing energy losses and investment costs (MIN–MIN), the Pareto front is located in the lower-left region of the objective space ${\mathbb{R}}^2$. Each solution on the front represents a non-dominated trade-off, where an improvement in one objective implies a compromise in the other. Therefore, the final decision depends on application-specific operational and economic priorities [25].

To generate this Pareto front, a hybrid matheuristic framework based exclusively on the ASOA was adopted. This algorithm employs the combined properties of the arctangent and sinc functions to produce oscillatory, bounded, and adaptive update dynamics [17]. This behavior allows balancing global exploration with fine-grained local exploitation, which is particularly effective for identifying well-distributed non-dominated solutions in non-convex and mixed-integer spaces.

The procedure consists of the following steps:

• Metaheuristic exploration via ASOA. The candidate solutions $\mathbf{x}$, including siting decisions for TSCs, are generated using ASOA, whose update mechanism encourages a wide search while maintaining convergence pressure near complex Pareto-optimal regions.
• Local refinement using IPOPT. For each candidate solution, the associated continuous variables—specifically TSC size and hourly reactive power dispatch—are optimized by solving a constrained nonlinear OPF problem using the IPOPT in the Julia environment. This step ensures both solution feasibility and an accurate evaluation of the objective functions.
• Non-dominated sorting. Th evaluated solutions are subjected to fast non-dominated sorting in order to identify and retain those on the current Pareto front approximation. This classification ensures that only efficient trade-offs are maintained throughout the optimization process.

By integrating ASOA’s exploratory power with IPOPT’s local accuracy, the proposed framework provides a reliable and computationally efficient approach for Pareto front construction in MIN–MIN multi-objective scenarios. This methodology is effective for solving large-scale, mixed-integer, and nonlinear planning problems in distribution networks.

3.3. Implementing the Algorithm

ASOA is a math-inspired metaheuristic designed to address nonlinear, non-convex, and mixed-integer optimization problems. Its update mechanism leverages the oscillatory nature of the sinc function and the bounded, smooth transitions of the arctangent function. These mathematical properties allow maintaining a robust balance between global exploration and local exploitation across the decision space.

The algorithmic structure of the ASOA presented in Algorithm 1 facilitates the integration of ASOA into multi-objective optimization frameworks and hybrid procedures involving local solvers such as IPOPT. Its flexibility enables the dynamic adjustment of control parameters and modular replacement mechanisms, enhancing adaptability across diverse engineering applications.

Remark 1.

In MOO, the best solution ${\mathbf{x}}^{★}$ corresponds to any member of the current Pareto front. Since all Pareto-optimal points are non-dominated, ${\mathbf{x}}^{★}$ is typically selected from the current approximation of the front, either randomly or using a preference-based criterion.

3.4. Visualization and Decision-Making

The resulting Pareto front can be visualized in the two-dimensional objective space $(f_1,f_2)$, allowing for a clear understanding of the trade-offs involved. In particular, convex regions indicate favorable compromise zones, whereas discontinuities or sharp corners may suggest conflicting design priorities. Decision-makers can apply additional selection criteria—such as the identification of knee points, the evaluation of cost-benefit ratios, or adherence to regulatory thresholds—to select the most appropriate solution for practical implementation.

Algorithm 1 Atan-sinc optimization algorithm.

1: Input: Objective function $f\left(\mathbf{x}\right)$, decision space bounds $[\mathbf{l},\mathbf{u}]$, maximum number of iterations T, population size N 2: Randomly initialize a population of N candidate solutions ${\left\{{\mathbf{x}}_i\right\}}_{i=1}^N$ within $[\mathbf{l},\mathbf{u}]$ 3: Evaluate each candidate using the objective function(s) $f_j\left({\mathbf{x}}_i\right)$ 4: Identify the best solution ${\mathbf{x}}^{★}$ via non-dominated sorting 5: for $t=1$ to T do 6:       for each candidate solution ${\mathbf{x}}_i$ do 7:           Generate the control parameters $r_1,r_2,r_3\in [0,1]$ 8:           Update the solution using one of ASOA’s mathematical operators: Arctangent-based update: ${\mathbf{x}}_i^{t+1}={\mathbf{x}}_i^t+{\displaystyle \frac{2r_1}{\pi }}{tan}^{-1}\left(\pi r_2\right)·\left|r_3{\mathbf{x}}^{★}-(1-r_3){\mathbf{x}}_i^t\right|$ Sinc-based update: ${\mathbf{x}}_i^{t+1}={\mathbf{x}}_i^t+{\displaystyle \frac{r_1}{\pi }}·{\displaystyle \frac{sin\left(\pi r_2\right)}{r_2+ϵ}}·\left|r_3{\mathbf{x}}^{★}-(1-r_3){\mathbf{x}}_i^t\right|$ 9:           Apply boundary control to ensure ${\mathbf{x}}_i^{t+1}\in [\mathbf{l},\mathbf{u}]$ 10:         Evaluate $f\left({\mathbf{x}}_i^{t+1}\right)$ and update the population if improved or non-dominated 11:     end for 12:     Update the best solution(s) ${\mathbf{x}}^{★}$ or Pareto set $\mathcal{P}$ 13: end for 14: Return: Pareto front $\mathcal{P}$ (for MOO)

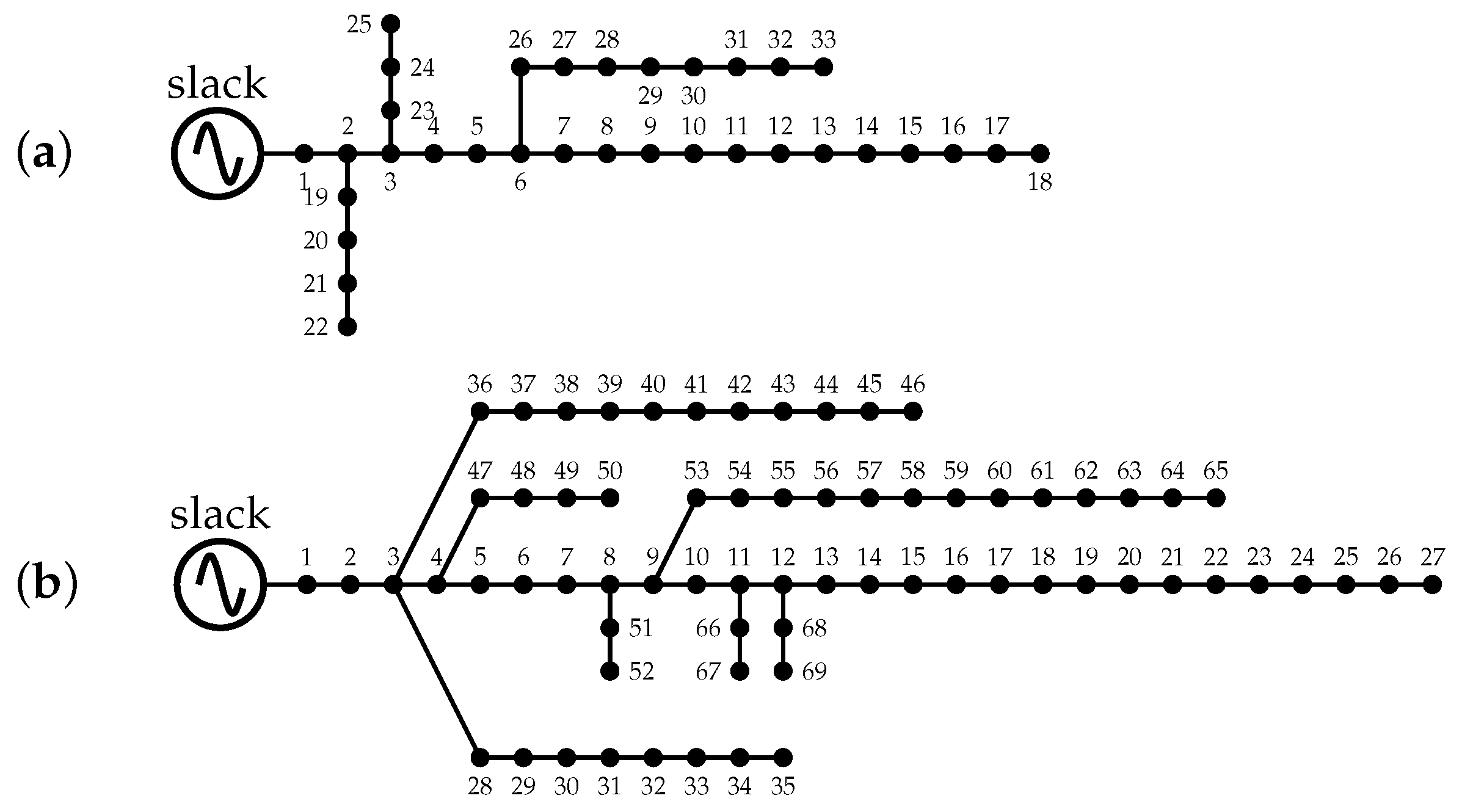
4. Test Systems Used

To assess the performance of the proposed solution methodology, two standard radial distribution test systems comprising 33 and 69 nodes were utilized [9]. The topological layout of each feeder is shown in Figure 1, and the corresponding electrical parameters, including line impedances and peak load demands, are provided in

Table 1. Main parameters for the 33-node test system.

Node i–j	${\mathit{R}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{X}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)	Node i–j	${\mathit{R}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{X}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)
1–2	0.0922	0.0477	100	60	17–18	0.7320	0.5740	90	40
2–3	0.4930	0.2511	90	40	2–19	0.1640	0.1565	90	40
3–4	0.3660	0.1864	120	80	19–20	1.5042	1.3554	90	40
4–5	0.3811	0.1941	60	30	20–21	0.4095	0.4784	90	40
5–6	0.8190	0.7070	60	20	21–22	0.7089	0.9373	90	40
6–7	0.1872	0.6188	200	100	3–23	0.4512	0.3083	90	50
7–8	1.7114	1.2351	200	100	23–24	0.8980	0.7091	420	200
8–9	1.0300	0.7400	60	20	24–25	0.8960	0.7011	420	200
9–10	1.0400	0.7400	60	20	6–26	0.2030	0.1034	60	25
10–11	0.1966	0.0650	45	30	26–27	0.2842	0.1447	60	25
11–12	0.3744	0.1238	60	35	27–28	1.0590	0.9337	60	20
12–13	1.4680	1.1550	60	35	28–29	0.8042	0.7006	120	70
13–14	0.5416	0.7129	120	80	29–30	0.5075	0.2585	200	600
14–15	0.5910	0.5260	60	10	30–31	0.9744	0.9630	150	70
15–16	0.7463	0.5450	60	20	31–32	0.3105	0.3619	210	100
16–17	1.2860	1.7210	60	20	32–33	0.3410	0.5302	60	40

and 

Table 2. Main parameters for the 69-node test system.

Node i–j	${\mathit{R}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{X}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)	Node i–j	${\mathit{R}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{X}}_{\mathit{i}\mathit{j}}$ ($\mathbf{\Omega }$)	${\mathit{P}}_{\mathit{j}}$ (kW)	${\mathit{Q}}_{\mathit{j}}$ (kvar)
1–2	0.0005	000012	0.00	0.00	3–36	0.0044	0.0108	26.00	18.55
2–3	0.0005	0.0012	0.00	0.00	36–37	0.0640	0.1565	26.00	18.55
3–4	0.0015	0.0036	0.00	0.00	37–38	0.1053	0.1230	0.00	0.00
4–5	0.0251	0.0294	0.00	0.00	38–39	0.0304	0.0355	24.00	17.00
5–6	0.3660	0.1864	2.60	2.20	39–40	0.0018	0.0021	24.00	17.00
6–7	0.3810	0.1941	40.40	30.00	40–41	0.7283	0.8509	1.20	1.00
7–8	0.0922	0.0470	75.00	54.00	41–42	0.3100	0.3623	0.00	0.00
8–9	0.0493	0.0251	30.00	22.00	42–43	0.0410	0.0478	6.00	4.30
9–10	0.8190	0.2707	28.00	19.00	43–44	0.0092	0.0116	0.00	0.00
10–11	0.1872	0.0619	145.00	104.00	44–45	0.1089	0.1373	39.22	26.30
11–12	0.7114	0.2351	145.00	104.00	45–46	0.0009	0.0012	29.22	26.30
12–13	1.0300	0.3400	8.00	5.00	4–47	0.0034	0.0084	0.00	0.00
13–14	1.0440	0.3450	8.00	5.50	47–48	0.0851	0.2083	79.00	56.40
14–15	1.0580	0.3496	0.00	0.00	48–49	0.2898	0.7091	384.70	274.50
15–16	0.1966	0.0650	45.50	30.00	49–50	0.0822	0.2011	384.70	274.50
16–17	0.3744	0.1238	60.00	35.00	8–51	0.0928	0.0473	40.50	28.30
17–18	0.0047	0.0016	60.00	35.00	51–52	0.3319	0.1114	3.60	2.70
18–19	0.3276	0.1083	0.00	0.00	9–53	0.1740	0.0886	4.35	3.50
19–20	0.2106	0.0690	1.00	0.60	53–54	0.2030	0.1034	26.40	19.00
20–21	0.3416	0.1129	114.00	81.00	54–55	0.2842	0.1447	24.00	17.20
21–22	0.0140	0.0046	5.00	3.50	55–56	0.2813	0.1433	0.00	0.00
22–23	0.1591	0.0526	0.00	0.00	56–57	1.5900	0.5337	0.00	0.00
23–24	0.3463	0.1145	28.00	20.00	57–58	0.7837	0.2630	0.00	0.00
24–25	0.7488	0.2475	0.00	0.00	58–59	0.3042	0.1006	100.00	72.00
25–26	0.3089	0.1021	14.00	10.00	59–60	0.3861	0.1172	0.00	0.00
26–27	0.1732	0.0572	14.00	10.00	60–61	0.5075	0.2585	1244.00	888.00
3–28	0.0044	0.0108	26.00	18.60	61–62	0.0974	0.0496	32.00	23.00
28–29	0.0640	0.1565	26.00	18.60	62–63	0.1450	0.0738	0.00	0.00
29–30	0.3978	0.1315	0.00	0.00	63–64	0.7105	0.3619	227.00	162.00
30–31	0.0702	0.0232	0.00	0.00	64–65	1.0410	0.5302	59.00	42.00
31–32	0.3510	0.1160	0.00	0.00	11–66	0.2012	0.0611	18.00	13.00
32–33	0.8390	0.2816	14.00	10.00	66–67	0.0470	0.0140	18.00	13.00
33–34	1.7080	0.5646	19.50	14.00	12–68	0.7394	0.2444	28.00	20.00
34–35	1.4740	0.4873	6.00	4.00	68–69	0.0047	0.0016	28.00	20.00

. Both networks operate at a nominal line-to-ground voltage of 12.66 kV, with voltage limits set between 0.90 and 1.10 p.u., in accordance with conventional utility standards [26]. These test systems were selected due to their extensive use in the literature as benchmarking platforms for validating power flow models and optimization algorithms in problems involving distribution networks. This allows for consistent comparisons with prior studies such as that by [8].

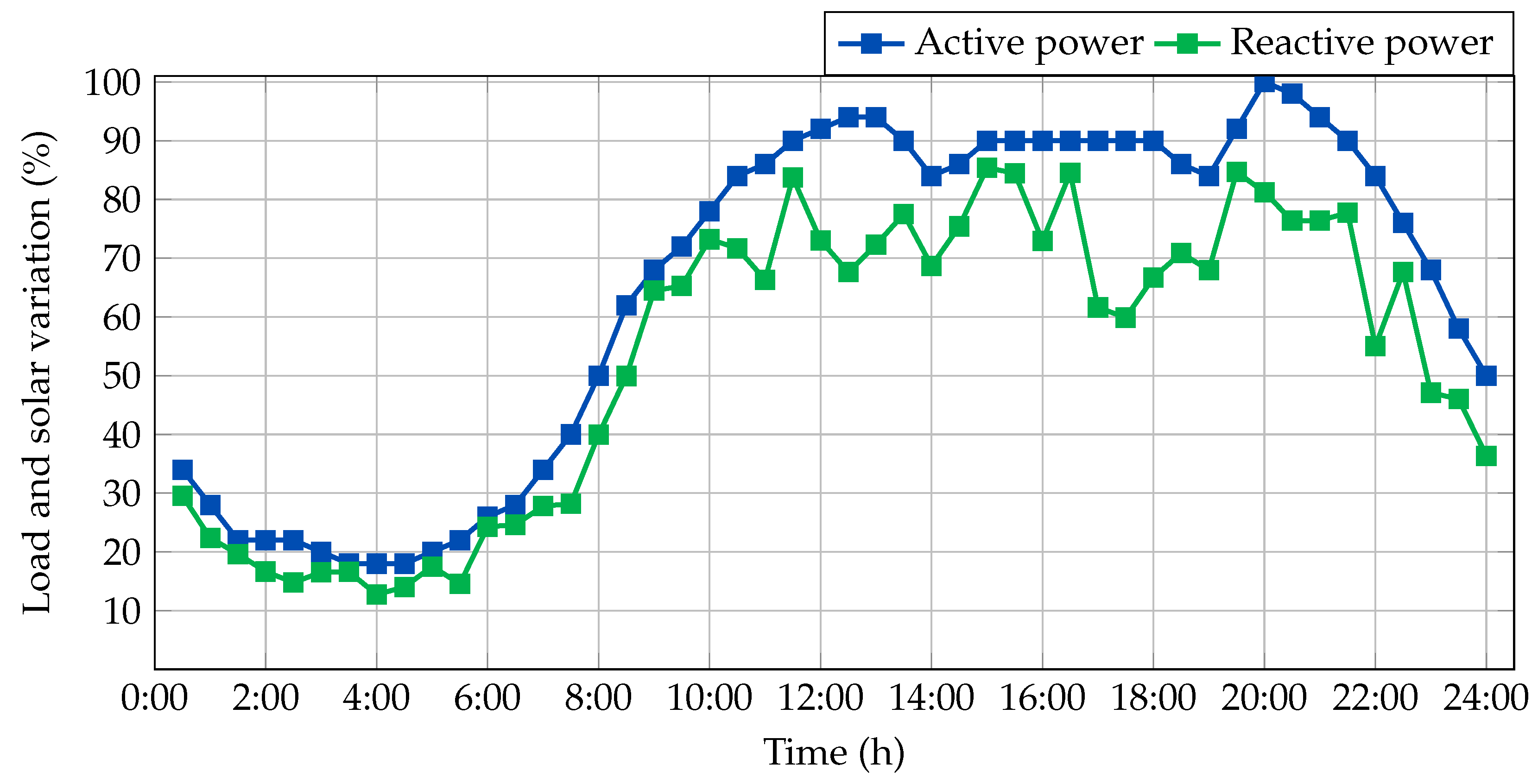
To evaluate the dynamic behavior of TSC devices in these 33- and 69-bus test feeders, a time-dependent load profile was employed to emulate realistic daily demand fluctuations. The baseline power demand at each node—derived from the peak values listed in Table 1 and Table 2—was scaled across time intervals using the hourly load variation factors illustrated in Figure 2. These scaling factors represent the percentage changes in demand over a typical day, allowing the simulation to capture operational variability. This methodology supports a more representative assessment of the TSCs’ effectiveness in adapting to load dynamics, aligning with the practical requirements and challenges faced by modern distribution network management.

Note that the y-axis depicts the daily variations in active and reactive power, expressed as percentages relative to their corresponding peak values at the substation terminal. This normalization follows standard practices in power system analysis to facilitate comparisons across different systems and scenarios.

Furthermore,

Table 3. Technical and economic parameters for computing the objective function $f_2$ (TSC investment costs).

Parameter	Value	Unit	Parameter	Value	Unit
${\omega }_1$	1.50	USD/Mvar3	${\omega }_2$	−713.00	USD/Mvar2
${\omega }_3$	153,750	USD/Mvar	T	365	days
$k_1$	${\displaystyle \frac{6}{2190}}$	1/day	$k_2$	10	years
${\Delta }_h$	${\displaystyle \frac{1}{2}}$	hour	$C_{\mathrm{kWh}}$	0.1390	USD/kWh

summarizes the technical and economic parameters employed to estimate the operating costs associated with TSC implementation. These values, adapted from [9], provide the necessary inputs for conducting a cost-based assessment of TSC performance. The presented data lay the foundation for evaluating the economic implications of TSC integration within the analyzed distribution systems.

5. Simulation Results

The proposed methodology was implemented using the Julia programming language (version 1.9.2) [27]. All simulations were conducted on a personal computer featuring an AMD Ryzen 7 3700 processor (2.3 GHz), 16 GB of RAM, and 64-bit Microsoft Windows 10 Single Language. Julia was chosen for its ability to deliver high computational performance, offering execution speeds comparable to low-level languages while retaining the readability and ease of use of high-level ones. This makes it particularly well suited for solving complex and resource-intensive optimization problems.

For the mathematical modeling and solution of the optimization problem, Julia’s JuMP package was chosen due to its expressive syntax and compatibility with various solvers [27]. The nonlinear programming subproblems related to the continuous decision variables—such as the sizing and dispatch of the TSCs—were addressed using the IPOPT solver, which is well suited for handling large-scale, sparse, and non-convex problems. To explore the global solution space, the ASOA-IPOPT approach was implemented in the Julia environment. These algorithms were responsible for generating candidate solutions regarding TSC siting and configuration. For each candidate, IPOPT was invoked to refine the continuous variables, thus forming a hybrid metaheuristic-local optimization approach tailored to the complexity of the studied MINLP problem [11].

The study analyzed the following scenarios in order to evaluate the impact of the proposed reactive power compensation strategy:

• Benchmark comparison: A baseline case inspired by conventional approaches from the literature, where TSCs are optimally located and sized using a classical single-objective formulation. In this scenario, reactive power injection remains fixed throughout the 24 h period.
• Single-objective with time-varying injection: An intermediate approach in which the optimization process still considers a single objective, but the reactive power output of TSCs is adjusted on an hourly basis. This case aimed to explore the potential performance gains introduced by incorporating load variability while maintaining a simple optimization structure.
• Multi-objective with time-varying injection: A comprehensive formulation where both objectives—energy losses minimization and investment costs reduction—are considered simultaneously. In this scenario, TSCs dynamically adjust their reactive power output on an hourly basis, enabling a more flexible and realistic compensation strategy aligned with the time-varying nature of electrical demand.

5.1. Parameterization of the ASOA-IPOPT Approach

To determine the optimal population size and number of iterations, a search grid approach was employed. This method explores various combinations of population sizes and iteration counts to identify the parameters that ensure both convergence and a comprehensive exploration of the solution space. Population sizes ranging from 10 to 50 and iteration counts from 50 to 200 were evaluated. The results for the tested systems are detailed in

Table 4. Average processing times (in seconds) for the 33-bus grid.

	No. of Iterations
No. of Solutions	50	100	150	200
10	896.45 (✗)	1795.85 (✗)	2680.50 (✗)	3404.70 (✓)
20	1726.55 (✗)	3460.31 (✗)	5170.50 (✓)	6825.78 (✓)
30	2477.05 (✗)	4948.66 (✗)	7474.65 (✓)	9862.50 (✓)
40	3194.55 (✗)	6387.69 (✓)	9518.40 (✓)	12,601.56 (✓)
50	4192.40 (✓)	8396.30 (✓)	12,602.25 (✓)	16,619.20 (✓)

and

Table 5. Average processing times (in seconds) for the 69-bus grid.

	No. of Iterations
No. of Solutions	50	100	150	200
10	5962.30 (✗)	11,836.25 (✗)	17,919.32 (✗)	23,599.80 (✗)
20	11,570.95 (✗)	23,221.58 (✗)	34,468.44 (✗)	45,557.78 (✗)
30	16,553.35 (✗)	32,806.69 (✗)	49,960.04 (✗)	65,533.38 (✗)
40	24,741.29 (✗)	49,496.77 (✗)	74,003.52 (✓)	99,471.36 (✓)
50	28,278.00 (✗)	56,378.98 (✓)	85,184.97 (✓)	112,179.34 (✓)

.

As anticipated, processing times increase with both the number of solution individuals and the number of iterations (see Table 4 and Table 5). This behavior aligns with the expectation that larger populations and more iterations provide more comprehensive exploration of the solution space, albeit at the cost of increased computational resources. Notably, a configuration utilizing 40 individuals and 100 iterations successfully reaches the optimal solution—this is indicated by the checkmark (✓) in the tables. This specific configuration strikes a balance between computational efficiency and solution accuracy, making it a practical choice for effective optimization.

In contrast, the configurations marked with a cross (✗) failed to reach an optimal solution, often due to insufficient exploration capabilities resulting from smaller population sizes or fewer iterations. Such setups might not provide enough diversity or computational effort to thoroughly explore and converge on the optimal regions of the solution space. These findings reinforce the importance of selecting appropriate parameter settings to ensure that optimization can be both efficient and effective across varying system complexities.

It is important to note that, for both the 33- and 69-bus feeders, the total number of possible TSC locations is determined by (16) [28]. Specifically,

$$\begin{array}{c}\hfill d=C(n-1,k)={\displaystyle \frac{(n-1)!}{(n-1-k)!k!}}\end{array}$$

(16)

where d represents the total number of potential solutions, n is the number of nodes in the network, and k is the number of devices to be installed.

For instance, with $k=3$, the 33-bus grid has 4960 possible solutions, while the 69-bus grid has 50,116. Given that our approach evaluates approximately 40 potential solutions in 100 iterations, this corresponds to exploring about 80.65% of the solution space for the 33-bus system, as well as roughly 7.98% for the 69-bus system. These results suggest that, even when exploring a relatively small portion of the total search space, our methodology is effective for reaching high-quality solutions. This highlights the efficiency of our approach in balancing computational effort with solution quality, demonstrating that selecting a limited set of candidate solutions and performing iterative refinement can yield reliable results in complex and large solution spaces.

5.2. Comparative Analysis Under Fixed Operation Scenario

To assess the performance of the proposed ASOA-IPOPT approach in the fixed operation scenario, a comparative study was conducted using both deterministic and metaheuristic optimization techniques. The selected methods included BONMIN (a classical MINLP solver), the Chu and Beasley genetic algorithm (CBGA), particle swarm optimization (PSO), the black widow optimizer (BWO), and the artificial hummingbird algorithm (AHA). These algorithms were applied to the IEEE 33- and 69-bus radial distribution systems to determine the optimal siting and sizing of TSCs devices.

Table 6. Numerical results for the 33- and 69-bus grids in the fixed operation case.

The 33-Bus Grid
Method	Location (Node)	Size (Mvar)	Objective Function (USD/Year)	Expected Reduction (%)
BONMIN	[6, 18, 30]	[0.0000, 0.1138, 0.4551]	100,221.38	11.10
CBGA	[13, 30, 31]	[0.1528, 0.3227, 0.1157]	100,139.21	11.18
PSO	[14, 30, 31]	[0.1486, 0.3244, 0.1157]	100,107.24	11.21
BWO	[14, 30, 32]	[0.1486, 0.3337, 0.1064]	100,093.29	11.22
AHA	[14, 30, 32]	[0.1486, 0.3337, 0.1064]	100,093.29	11.22
ASOA-IPOPT	[14, 30, 32]	[0.1486, 0.3337, 0.1064]	100,093.29	11.22
The 69-bus grid
BONMIN	Does not converge
CBGA	[21, 61, 65]	[0.0662, 0.4840, 0.0635]	104,695.69	12.55
PSO	[23, 61, 64]	[0.0526, 0.4009, 0.1504]	104,679.61	12.56
BWO	[21, 61, 64]	[0.0647, 0.4363, 0.1125]	104,658.03	12.58
AHA	[21, 61, 64]	[0.0647, 0.4363, 0.1125]	104,658.03	12.58
ASOA-IPOPT	[21, 61, 64]	[0.0647, 0.4363, 0.1125]	104,658.03	12.58

summarizes the results in terms of the selected nodal locations, the corresponding reactive power capacities (in Mvar), the resulting annualized cost (USD/year), and the percent reduction in the objective function value relative to the base case.

The results in Table 6 reveal that the proposed ASOA-IPOPT achieves identical or superior performance compared to the benchmark metaheuristics in both test cases. For the 33-bus system, ASOA-IPOPT achieves an annualized cost of USD 100,093.29 with an 11.22% reduction—matching the best results obtained by BWO and AHA and outperforming PSO (11.21%) and CBGA (11.18%). BONMIN, although a deterministic solver, yields a slightly worse result (11.10% reduction), indicating its limitations in handling this type of complex MINLP problem.

In the 69-bus case, BONMIN fails to converge, likely due to the increased dimensionality and the nonlinearities in the system. All metaheuristic-based methods succeed in finding feasible and competitive solutions. ASOA-IPOPT once again exhibits the best performance, with a cost reduction of 12.58%—equal to that of BWO and AHA, and slightly better than CBGA (12.55%) and PSO (12.56%). The selected locations and sizes for the TSCs demonstrate consistency in the metaheuristic solutions, reflecting convergence towards optimal configurations.

In light of the above, the following can be stated:

• The ASOA-IPOPT method achieves the best objective function values in both test feeders, demonstrating its effectiveness and robustness.
• For the 33-bus system, ASOA-IPOPT reduces the cost by 11.22%, outperforming BONMIN, CBGA, and PSO.
• In the 69-bus case, deterministic methods fail, but ASOA-IPOPT provides a 12.58% reduction—the highest among all methods.
• ASOA-IPOPT consistently identifies the same optimal locations and sizes as BWO and AHA, suggesting convergence to a high-quality Pareto-optimal solution.
• These results confirm the suitability of the ASOA-IPOPT framework for large-scale, mixed-integer, and nonlinear optimization in distribution network planning.

A further examination of the results reveals that certain bus locations are repeatedly selected as optimal points for TSC placement across different scenarios and test cases. This recurring selection is primarily due to their strategic positions within the network topology, which enable more effective voltage regulation and losses reduction. Typically, these buses are located near the feeders’ midpoints or at nodes where load concentrations significantly influence voltage drops and power flow patterns. By placing TSCs at these critical points, the system can better mitigate voltage deviations and reduce reactive power losses, thus achieving a more efficient and stable operation. These locations often serve as control hubs, where reactive power support has the most substantial impact on overall system performance. This explains their consistent selection across multiple test cases during the optimization process.

5.3. Performance of ASOA-IPOPT Under Variable Reactive Power Injection

To further evaluate the benefits of temporal flexibility in reactive power support,

Table 7. Performance of ASOA-IPOPT under variable reactive power injection.

Test System	TSC Location (Nodes)	TSC Size (Mvar)	Objective Function (USD/Year)	Reduction (%)
33-bus system	[14, 30, 32]	[0.1786, 0.4022, 0.1365]	98,729.21	12.43
69-bus system	[21, 61, 64]	[0.0683, 0.5380, 0.1450]	102,861.83	14.08

summarizes the numerical results obtained using the ASOA-IPOPT approach under a variable reactive power injection strategy. In this scenario, the TSCs are allowed to adjust their output on an hourly basis, offering improved adaptability to demand fluctuations throughout the day. The comparison reveals notable cost reductions and improved system efficiency over the fixed compensation case.

As shown in Table 7, with variable reactive power injection, the ASOA-IPOPT framework yields superior results compared to its fixed counterpart and other benchmark metaheuristics. In the 33-bus system, dynamic operation leads to a cost reduction of 12.43%, improving upon the 11.22% reduction observed under fixed injection. Likewise, in the 69-bus system, the variable injection strategy yields a cost reduction of 14.08%, outperforming the fixed case (12.58%).

These results demonstrate that ASOA-IPOPT not only identifies the optimal siting and sizing configurations but also effectively exploits temporal flexibility to enhance voltage regulation and minimize energy losses. The improved performance confirms the robustness of this master–slave optimization architecture, where ASOA handles discrete placement decisions and IPOPT solves the continuous sizing and dispatch problem across time. This synergy makes the proposed method a valuable and scalable solution for planning dynamic reactive power compensation in real-world distribution networks.

5.4. Multi-Objective Analysis

5.4.1. Results in the 33-Bus Grid

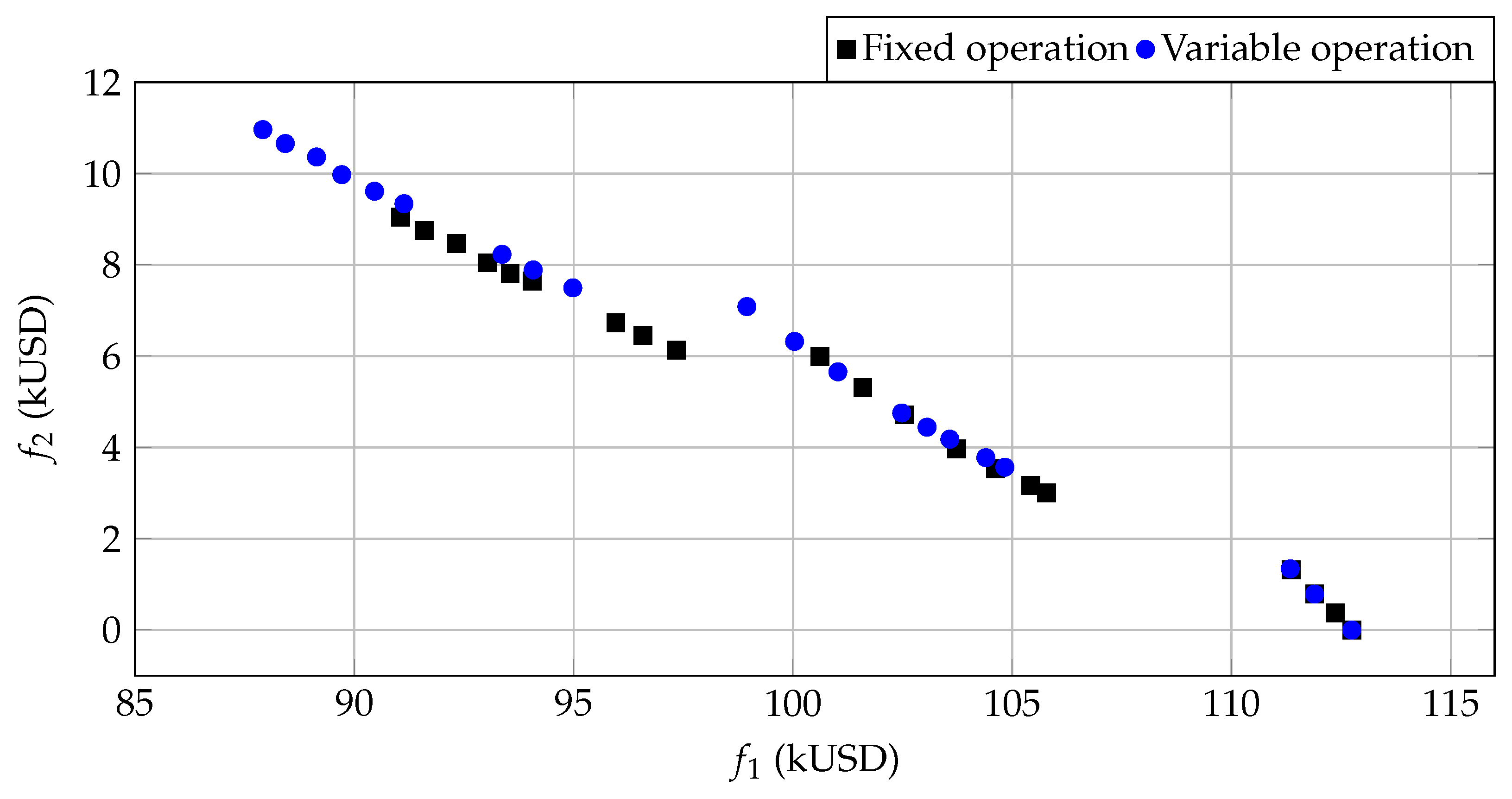
The Pareto front presented in

Table 8. Pareto optimal front for the 33-bus grid.

No.	Fixed Operation			Variable Operation
	${\mathit{f}}_{\mathbf{1}}$ (USD)	${\mathit{f}}_{\mathbf{2}}$ (USD)	${\mathit{f}}_{\mathbf{1}}+{\mathit{f}}_{\mathbf{2}}$ (USD)	${\mathit{f}}_{\mathbf{1}}$ (USD)	${\mathit{f}}_{\mathbf{2}}$ (USD)	${\mathit{f}}_{\mathbf{1}}+{\mathit{f}}_{\mathbf{2}}$ (USD)
1	112,740.88	0.00	112,740.88	112,740.88	0.00	112,740.88
2	112,361.39	370.49	112,731.89	111,561.33	1118.99	112,680.32
3	111,894.54	786.51	112,681.05	104,865.58	3533.53	108,399.12
4	111,361.09	1321.34	112,682.43	104,439.72	3766.80	108,206.51
5	105,578.79	3097.13	108,675.93	103,578.06	4180.40	107,758.46
6	104,735.61	3475.63	108,211.24	103,058.99	4442.85	107,501.84
7	104,015.02	3816.34	107,831.36	102,593.08	4687.03	107,280.11
8	103,573.65	4059.25	107,632.91	102,261.72	4886.10	107,147.82
9	102,545.77	4713.96	107,259.73	101,026.00	5655.99	106,681.98
10	101,593.85	5306.27	106,900.11	100,039.69	6321.73	106,361.42
11	100,614.59	5987.63	106,602.22	98,951.25	7086.04	106,037.28
12	97,354.79	6133.73	103,488.53	94,982.23	7495.94	102,478.17
13	96,576.80	6453.06	103,029.86	94,078.67	7888.02	101,966.70
14	95,963.60	6733.43	102,697.04	93,367.91	8229.46	101,597.37
15	94,055.33	7645.49	101,700.81	91,132.83	9339.99	100,472.82
16	93,554.15	7803.04	101,357.19	90,463.08	9612.27	100,075.35
17	93,027.38	8044.14	101,071.52	89,714.71	9975.18	99,689.89
18	92,330.23	8467.22	100,797.45	89,139.95	10,361.59	99,501.53
19	91,597.28	8746.85	100,344.13	88,426.70	10,656.49	99,083.19
20	91,052.01	9041.29	100,093.30	87,915.08	10,961.39	98,876.47

and depicted in Figure 3 illustrates the inherent trade-offs between $f_1$ and $f_2$ functions.

As expected, the solutions point towards a typical Pareto trade-off, where reducing the total system losses involves higher capital expenses associated with reactive devices. The fixed operation solutions, which do not utilize dynamic reactive support, are clustered at higher loss values (USD 112,740) with zero reactive device costs. Introducing flexible reactive support (variable operation) shifts solutions lower on the loss axis, with reductions of approximately 11% to 13%, at the expense of increased investment. Note that:

• The solutions around indices 10–20 represent balanced trade-offs, with moderate loss reductions (USD 91,000–USD 102,000) and relatively low additional costs (USD 8800–USD 11,000). These can be regarded as optimal points for practical decision-making.
• The convex shape of the Pareto front indicates that, beyond certain investment thresholds, additional reactive support yields marginal benefits in reducing losses, which underscores the importance of selecting an appropriate trade-off point.
• The solutions with adaptive reactive power support almost always outperform their fixed-case counterparts, underlining the value of operational flexibility in achieving energy efficiency.

The Pareto analysis reveals that modest investments in TSCs can substantially decrease energy losses, achieving efficiency gains of over 11%. Decision-makers should identify the knee point of the Pareto front at which additional costs result in diminishing returns. This provides a rational basis for the planning of reactive compensation strategies, balancing capital expenditure and operational savings in distribution system enhancement projects.

5.4.2. Results in the 69-Bus Grid

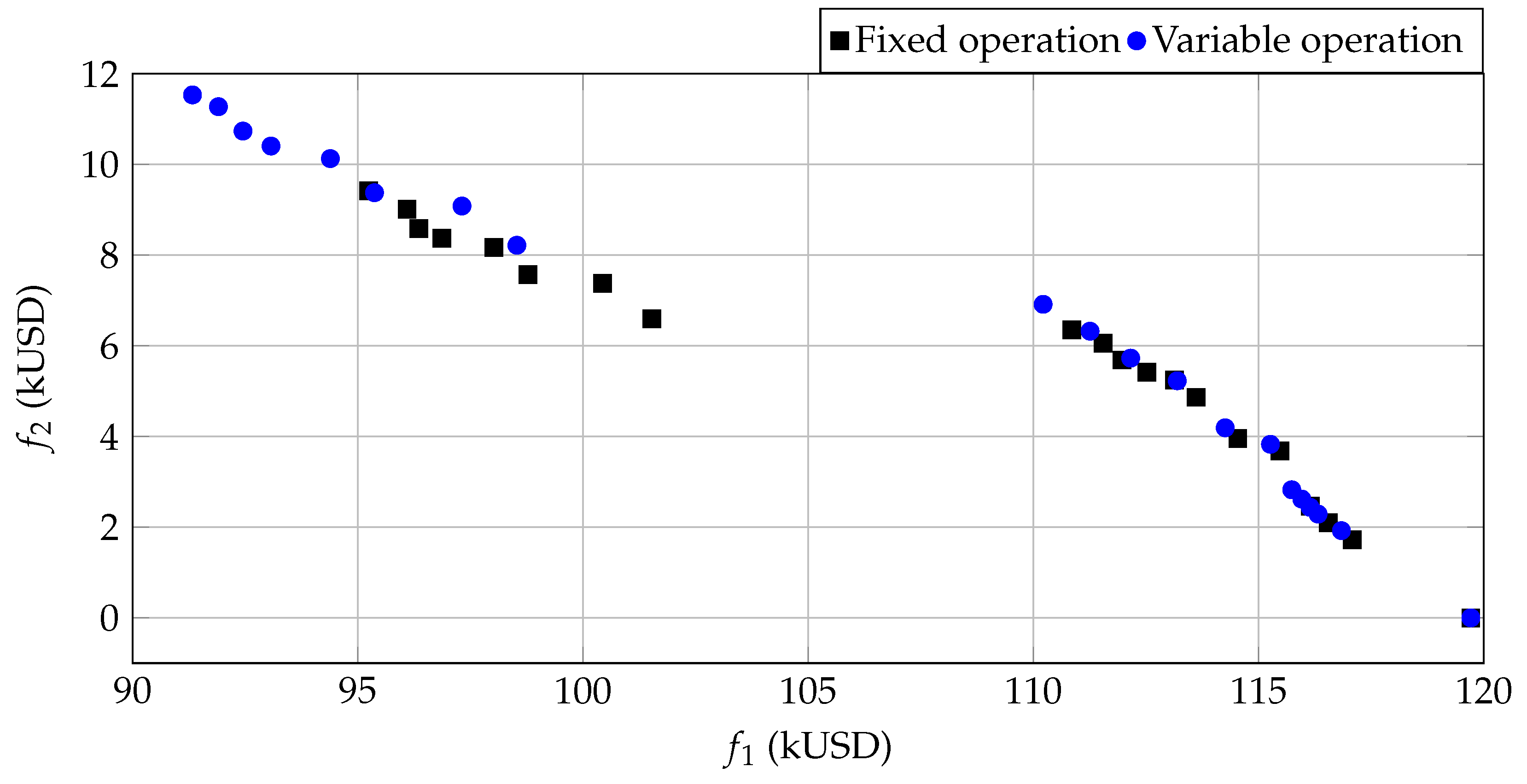
The Pareto front presented in

Table 9. Pareto optimal front for the 69-bus grid.

No.	Fixed Operation			Variable Operation
	${\mathit{f}}_{\mathbf{1}}$ (USD)	${\mathit{f}}_{\mathbf{2}}$ (USD)	${\mathit{f}}_{\mathbf{1}}+{\mathit{f}}_{\mathbf{2}}$ (USD)	${\mathit{f}}_{\mathbf{1}}$ (USD)	${\mathit{f}}_{\mathbf{2}}$ (USD)	${\mathit{f}}_{\mathbf{1}}+{\mathit{f}}_{\mathbf{2}}$ (USD)
1	119,715.63	0.00	119,715.63	119,715.63	0.00	119,715.63
2	117,078.46	1724.58	118,803.05	116,842.28	1922.71	118,765.00
3	116,550.22	2099.20	118,649.42	116,324.04	2288.17	118,612.22
4	116,154.73	2465.79	118,620.52	116,148.32	2436.45	118,584.77
5	115,473.21	3681.92	119,155.13	115,962.50	2617.99	118,580.49
6	114,541.33	3952.74	118,494.07	115,739.87	2823.99	118,563.86
7	113,616.42	4863.55	118,479.97	115,266.35	3826.52	119,092.87
8	113,140.25	5241.25	118,381.50	114,261.23	4189.61	118,450.83
9	112,526.71	5413.32	117,940.03	113,197.18	5226.90	118,424.08
10	111,973.85	5685.33	117,659.18	112,162.74	5726.45	117,889.19
11	111,554.47	6056.07	117,610.54	111,261.21	6320.20	117,581.40
12	110,854.62	6352.80	117,207.42	110,219.52	6912.95	117,132.47
13	101,529.52	6595.48	108,125.00	98,534.74	8215.90	106,750.64
14	100,439.64	7378.50	107,818.14	97,315.74	9079.96	106,395.70
15	98,783.77	7567.70	106,351.47	95,373.28	9373.79	104,747.08
16	98,024.75	8163.95	106,188.70	94,393.37	10,126.15	104,519.51
17	96,864.68	8371.92	105,236.60	93,075.13	10,403.07	103,478.20
18	96,356.11	8578.79	104,934.90	92,453.20	10,732.50	103,185.70
19	96,096.71	9006.48	105,103.19	91,908.04	11,270.75	103,178.79
20	95,240.70	9417.33	104,658.0	91,331.76	11,530.05	102,861.83

and depicted in Figure 4 illustrates the inherent trade-offs between $f_1$ and $f_2$ functions.

In the fixed operation scenario, the Pareto solutions are concentrated at higher energy loss values, around USD 119,716, with no reactive compensation cost ($f_2=0$). This corresponds to the baseline case, where reactive power support is not employed. When adopting a variable reactive support strategy, the solutions shift toward lower $f_1$ values, achieving reductions of approximately 12%. For example, the best solutions in this category lower the energy losses to around USD 104,659 while incurring increased costs (exceeding USD 11,500).

The shape of the Pareto front (Figure 4) indicates a convex trade-off, where initial investments in reactive support substantially reduce energy losses, but further increases result in diminishing gains. This suggests that, beyond a certain investment threshold, additional reactive device capacity provides limited benefits in reducing operational losses.

The solutions around indices 10–15 in the Pareto front offer a practical compromise, with energy losses reduced to about USD 105,000 and costs in the vicinity of USD 9000 to USD 10,000. These ‘knee solutions’ are suitable for stakeholders seeking an optimal balance between performance and expenditure.

This analysis demonstrates that implementing adaptive reactive support can lead to energy savings exceeding 12%, with a proportional increase in capital investment. The shape of the Pareto front emphasizes the importance of strategic decision-making—i.e., selecting a solution on the front that aligns with economic constraints while maximizing operational benefits.

Overall, the results confirm that a flexible, dynamic reactive power strategy significantly enhances system efficiency. However, the returns diminish beyond a certain point, underscoring the importance of Pareto-based trade-off analysis in distribution system planning.

6. Discussion and Limitations

The proposed hybrid ASOA-IPOPT framework demonstrated an effective performance on small to medium-sized IEEE test systems. However, scaling this methodology to larger and more complex distribution networks poses several notable challenges and implies some potential limitations, especially when implementing variable reactive power strategies in operational settings. Such strategies require seamless coordination between network components and control centers, necessitating sophisticated control systems capable of real-time decision-making. Additionally, an effective implementation relies heavily on a robust communication infrastructure to transmit real-time data and control signals—upgrading existing systems may involve technical and financial hurdles. Moreover, the deployment of variable reactive power support may necessitate adjustments to current regulatory frameworks, requiring active engagement with regulatory bodies to ensure compliance and alignment with operational standards.

Addressing these implementation challenges involves the development and integration of advanced control algorithms that can process data and make decisions dynamically, as well as investments in enhanced communication infrastructure to support rapid data exchange and control actions. Collaboration with regulators is also essential for establishing standards that accommodate the operational complexities and benefits of such strategies. Beyond operational considerations, the computational demands and scalability of the framework pose significant challenges. As the network size increases, the decision space expands exponentially, leading to longer computational times and higher memory requirements due to the proliferation of potential TSC siting and sizing options. Furthermore, the nonlinear and non-convex nature of the optimization problem complicates the search for global Pareto-optimal solutions, especially in larger networks with multiple local minima.

To mitigate these issues, the implementation of parallel processing techniques can significantly reduce evaluation times by enabling the simultaneous processing of multiple candidate solutions. Decomposition approaches, such as split-horizon or multi-level decomposition, can improve scalability by dividing the large problem into smaller, more manageable subproblems that are easier to solve independently or iteratively. Additionally, adaptive parameter tuning—e.g., dynamically adjusting population sizes, iteration limits, or exploration–exploitation strategies—can enhance convergence efficiency and solution robustness. Overall, while the current framework offers promising results for small to medium-sized networks, extending its applicability to larger systems necessitates advanced computational strategies to effectively manage the increased complexity. These enhancements will help maintain solution quality while making the methodology more practical for large-scale distribution system planning and operation.

7. Conclusions and Future Work

This study presented a hybrid optimization framework for the optimal placement and sizing of TSCs in medium-voltage distribution networks. The methodology combines the exploratory capabilities of the ASOA with the precise local refinement of the IPOPT solver within a master–slave architecture. Our approach effectively handles the challenging multi-objective MINLP formulation of the studied problem, balancing the minimization of energy losses and investment costs. Extensive validation on the 33- and 69-bus IEEE test systems demonstrated that the proposed approach consistently outperforms benchmark techniques, achieving significant energy savings (up to 12%) and providing valuable Pareto front insights for decision-makers.

The results highlight the effectiveness and robustness of the hybrid ASOA-IPOPT framework in large-scale, complex distribution system planning. The solutions obtained demonstrate good stability, convergence, and solution quality, and the Pareto fronts clearly illustrate the trade-offs between costs and operational benefits. Furthermore, the framework’s flexibility in addressing both fixed and time-varying reactive power injection strategies makes it a practical and adaptable tool for modern distribution system management, providing a solid foundation for future smart grid applications and reactive power compensation strategies.

However, it is important to acknowledge that the validations conducted in this study were limited to small IEEE test systems. To obtain a more comprehensive understanding of the framework’s practical applicability, future research should evaluate its performance on larger, real-world distribution networks—such as 118- or 300-bus systems—and assess its scalability and robustness under more realistic operational conditions. Additionally, incorporating uncertainty modeling (e.g., load variability and renewable generation fluctuations) would further enhance system resilience and planning robustness. The development of real-time or adaptive strategies capable of dynamically updating capacitor placement and sizing in response to operational changes could markedly improve system flexibility and responsiveness.

Finally, advancing towards experimental validation—through hardware-in-the-loop (HIL) setups or actual distribution network deployments—would provide critical insights into the real-world performance and feasibility of the proposed framework. Such efforts are essential for demonstrating its practical applicability and facilitating its transition from simulation-based assessments to field-ready solutions suitable for future smart grid environments.