Abstract
This paper introduces a novel fractional-order fuzzy logic controller (FOFLC) designed for stator voltage control in standalone doubly fed induction generator (DFIG) systems used in wind energy applications. Unlike traditional fuzzy logic controllers (FLCs), which are limited by integer-order dynamics, the FOFLC leverages the advanced principles of fractional-order (FO) calculus. By integrating fuzzy logic with fractional-order operators, the FOFLC enhances system precision, adaptability, and interpretability while addressing the inherent limitations of conventional proportional-integral (PI) controllers and integer-order FLCs. A key innovation of the FOFLC is its dual-mode architecture, enabling it to operate seamlessly as either a traditional FLC or a fractional-order FOFLC controller. This versatility allows for independent tuning of fractional parameters, optimizing the system’s response to transients, steady-state errors, and disturbances. The controller’s flexibility makes it particularly well-suited for nonlinear and dynamically complex stand-alone renewable energy systems. The FOFLC is experimentally validated on a 3-kW DFIG test bench using the dSPACE-1104 platform under various operating conditions. Compared to a conventional PI controller, the FOFLC demonstrated superior performance, achieving 80% reduction in response time, eliminating voltage overshoot and undershoot, reducing stator power and torque ripples by over 46%, and decreasing total harmonic distortion (THD) of both stator voltage and current by more than 50%. These results confirm the FOFLC’s potential as a robust and adaptive control solution for stand-alone renewable energy systems, ensuring high-quality power output and reliable operation.
1. Introduction
The increased need for electrical power, alongside global warming and other environmental issues, has compelled people to look into new ways for green and renewable energy production [1]. In 2023, the global wind power generation installed was about 117 GW, which is 50% higher than in 2022 [2]. In wind power systems, doubly fed induction generators (DFIGs) are among the most widely utilized technologies thanks to their benefits. These generators can operate with rotor speeds of ±30% of synchronous speed [3]. Moreover, DFIGs are equipped with back-to-back converters, which are used on the generator and are downsized to only 25–30% of the total power output of the generator set [4].
Most of the research on DFIGs has been done on systems with grid connection [5,6], but unconstrained DFIG systems are increasingly acknowledged for their usefulness in remote, off-grid locations and in improving the reliability of power supply during outages of the grid system [7,8]. As is the case with most stand-alone systems, controlling these stand-alone DFIG systems presents huge challenges. Unlike grid-connected systems, stand-alone systems have to maintain fixed stator voltage and frequency; therefore, they need to independently control the frequency and voltage at the stator terminals regardless of the wind speed or load conditions, which is very difficult to achieve [9,10]. In order to meet these requirements, controllers must provide tighter control, greater flexibility, and orthogonal structures (decoupled variables) to guarantee stability and performance under all operating conditions [11,12].
Most control strategies used to supervise DFIGs are based on field-oriented control (FOC) [13]. This traditional control strategy typically employs standard proportional–integral (PI) or proportional–integral–derivative (PID) controllers due to their simplicity, ease of implementation, and effectiveness in linear systems. They are particularly well-suited for applications with well-known and constant parameters. However, in wind energy applications, the system is inherently nonlinear, and operating conditions can vary significantly due to changes in wind speed and load [14]. As a result, the performance of PI/PID controllers deteriorates under such condition changes, leading to poor dynamic response, larger torque ripple effects, and increased total harmonic distortion (THD) [15].
Sliding mode control (SMC) [16], backstepping [17], H∞ control [18], passive-based control (PBC) [19], and model reference adaptive control (MRAC) [20] are some adaptive approaches that researchers have tried in dealing with these challenges [21]. While great improvements in the accuracy and robustness of these methods are observed, many of them are dependent on the mathematical model of the machine, which has its disadvantages.
To deal with system nonlinearity and uncertainty without the need for an accurate mathematical model, fuzzy logic controllers (FLCs) offer an elegant solution [22,23]. Structurally based on linguistic IF–THEN rules, FLCs have been designed and implemented in DFIG systems and evaluated against PI controllers, showing better results in a variety of situations [15]. The ability to alter internal components, such as fuzzification [24], rule sets [25], defuzzification [26], and input-output gains [27,28], is what makes FLCs flexible [27]. However, those FLCs, which do not use fractional-order integral and derivative operators and rely on classical FLCs, have difficulties optimizing transience and steady-state performance. Table 1 summarizes the key features of state-of-the-art DFIG control methods, highlighting their advantages and limitations.
In recent years, efforts have been made to develop fuzzy logic controllers (FOFLC) that incorporate fractional-order operators in their structures [29,30]. The addition of tunable parameters (λ and μ) offers finer control dynamics and additional capabilities of adaptability [31]. Fractional calculus has demonstrated remarkable efficacy in theoretical and practical contexts, particularly in the design of advanced control systems, owing to the flexibility provided by the fractional operator, as studied in the works of [32,33]. Its use has been effective in a number of technical domains [32,34,35,36]. A PI controller was optimized in Ref. [36] for the control of asynchronous generators using the fractional-order method. In comparison to the FOC approach, the simulation results showed a decrease in torque ripples, a drop in THD, and an increase in system durability. In Ref. [33], a fuzzy fractional-order PI controller for motor speed regulation was proposed, demonstrating improved dynamic performance and faster recovery characteristics compared to conventional methods. These outcomes confirm the aspect of fractional calculus in enhancing the control system properties, making them more efficient and performing better. Such is the potential of FOFLCs; their application for stand-alone DFIG systems has not been attempted. More precisely, no previous research has dealt with the standalone mode of operation or the practical realization of FOFLCs, which means there is none in the literature.

Table 1.
Examples of DFIG control methods.
Table 1.
Examples of DFIG control methods.
| Control Method | Pros | Cons | Related Work |
|---|---|---|---|
| PI Controller | -Simple, widely used, easy to implement |
-Not suitable for nonlinear processes -Sensitive to operating conditions and parameter variations -Poor dynamic response | [14] |
| SMC | -Effective for nonlinear systems | -Requires an accurate mathematical model. | [16] |
| MRAC | -Suitable for nonlinear processes and uncertainties |
-Computationally extensive/expensive. -Requires plant model/information | [20] |
| FLC | -Handles nonlinearities and uncertainties. |
-Requires expert knowledge -Expensive hardware implementation -Limited performances (non-adjustable dynamics) | [23] |
| Simplified rule FLC | -Suitable for complex and nonlinear processes | -Affected by external disturbances | [37] |
| Single-input FLC | -Simpler structure | -Reduced dynamic performance | [38] |
| Self-tuning FLC-PI | -High performance with nonlinear systems | -Expensive hardware implementation | [39] |
| Probabilistic fuzzy neural network (PFNN) |
-High performance with nonlinear systems -Computationally efficient | -Difficult development and tuning of neural networks | [40] |
| Takagi–Sugeno FLC (TS-FLC) |
-Suitable for nonlinear systems -Computationally efficient | -Requires expert knowledge | [15] |
| Proposed FOFLC |
-More flexible structure (adjustable dynamics) -Simple tuning without structural changes -High performance with nonlinear systems | -Requires additional computation |
To fill this gap, this work introduces a fuzzy logic controller that utilizes a fractional-order logic controller (FOFLC) for controlling the voltage in the stator of stand-alone DFIG systems, thereby improving control accuracy and performance compared to traditional control methods. This controller integrates the advantages of fuzzy logic and superior tuning of fractional-order calculus, guaranteeing that the controller achieves significant improvements in responsive and steady-state control performance. Further, the controller may operate in dual mode as conventional FLC (λ = 1, μ = 1) or fractional FLC (λ ≠ 1, μ ≠ 1), which provides flexibility and ease of use without altering the structure of the controller. The proposed FOFLC has been subjected to tests in real-time on a 3 kW stand-alone DFIG, with preliminary results revealing perfect transient and steady state performance against changing load and speed parameters. The analysis that was conducted employing a standard PI controller demonstrates more benefits of using FOFLC, such as its less responsive times, avoidance of overshooting and undershooting, and dramatic enhancement in power quality. These results confirm the possibility of considering FOFLC as a competent and highly effective control strategy for stand-alone renewable energy systems.
The structure of this article is as follows: Section 2 describes the configuration of the stand-alone DFIG system. Section 3 details the field-oriented control strategy implemented. Section 4 introduces the fractional-order (FO) control approach, establishing the theoretical foundation for the proposed control. Section 5 presents the development of the fractional-order fuzzy logic-based stator voltage control. Section 6 discusses the experimental setup and the results obtained. Finally, Section 7 concludes the paper by summarizing the main contributions of this research and suggesting potential directions for future work.
2. Configuration of Stand-Alone DFIG System
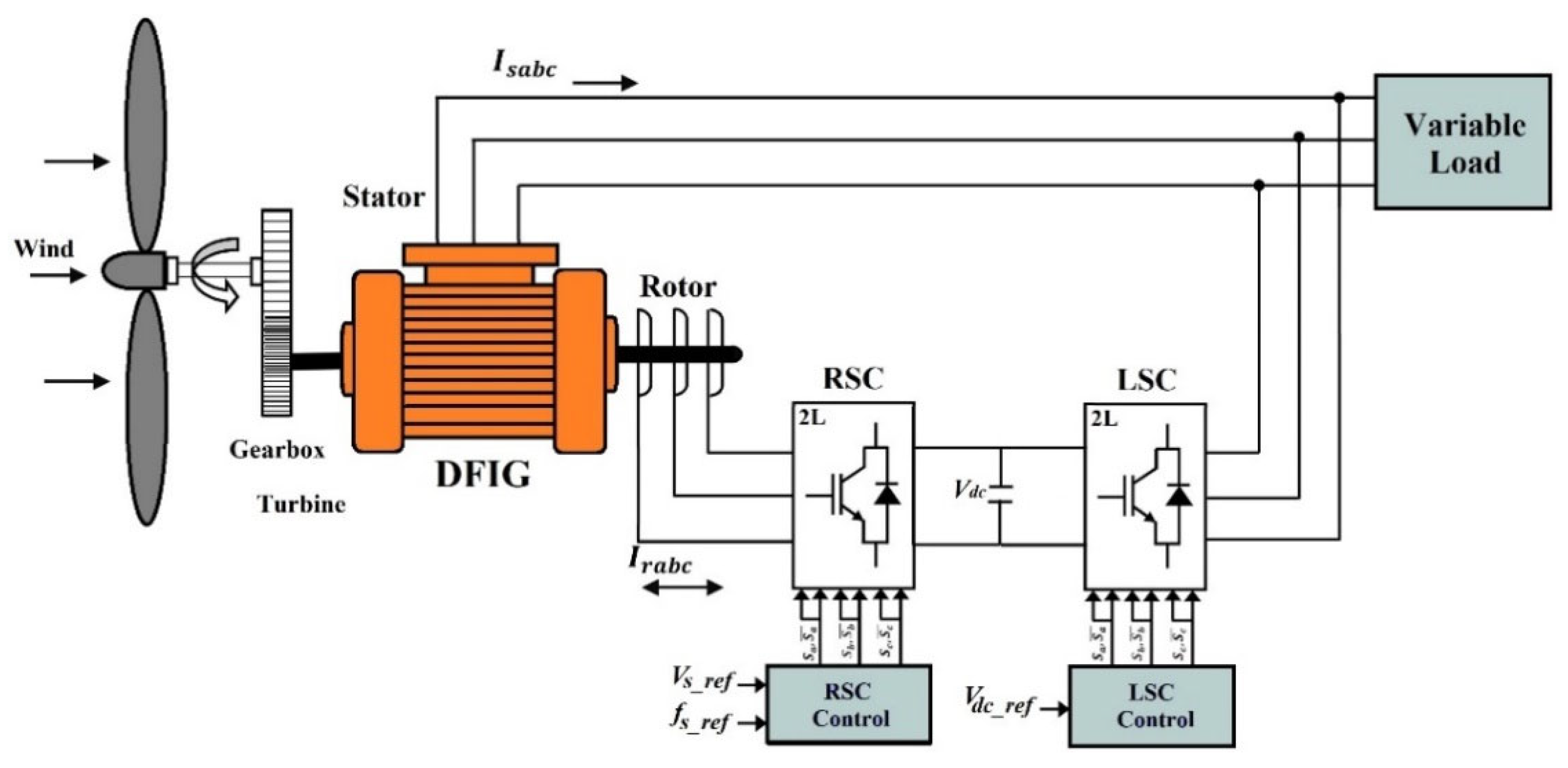
In a wind power generation system (WPGS) utilizing a doubly-fed induction generator (DFIG), two main stator connection configurations are commonly employed. The first is the grid-connected setup, in which the stator is linked to the utility grid and must remain synchronized with it [25]. The second is the stand-alone setup, where the stator is directly coupled to the load, effectively forming a microgrid [15]. This latter configuration removes the need for synchronization between the stator and the load, allowing the DFIG to supply power according to the load demand, without relying on maximum power point tracking (MPPT).
Figure 1 illustrates the configuration of the standalone WPGS using a DFIG. The system is implemented with a back-to-back converter, which comprises two voltage-fed converters using insulated gate bipolar transistor (IGBT) switches: the rotor side converter (RSC) and the load side converter (LSC) [13]. In stand-alone operation, the main goal of the RSC is to maintain a constant stator voltage and frequency, regardless of changes in wind speed or load. Meanwhile, the GSC is responsible for keeping the DC-link voltage stable at a fixed level.
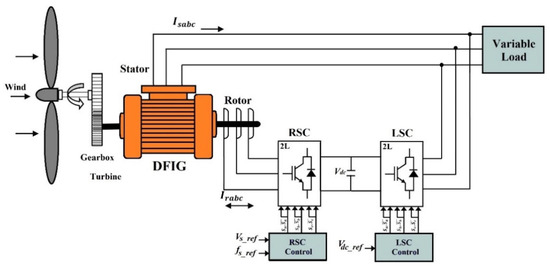
Figure 1.
Wind energy conversion system based on a DFIG stand-alone mode operation.
3. Modeling and Field Oriented Control of Stand-Alone DFIG
3.1. Modeling of DFIG
The DFIG mathematical model can be expressed using the following state equations in the dq synchronous reference frame [4], with the d-axis aligned with the stator flux vector.
- Stator and rotor voltages in d-q frame:
- Stator and rotor fluxes in d-q frame:
- The expression for the electromagnetic torque is:
- The active and reactive stator power equations in the d-q-axis are as follows:
3.2. Field Oriented Control of Stand-Alone DFIG
The RSC control is based on the field oriented control (FOC) to provide decoupling between control currents loops. By applying the FOC principles ( to the DFIG equations in the dq-reference with ( and neglecting the rotor resistance, one can obtain [13,21]:
That is:
Therefore, the reference stator voltage is defined as:
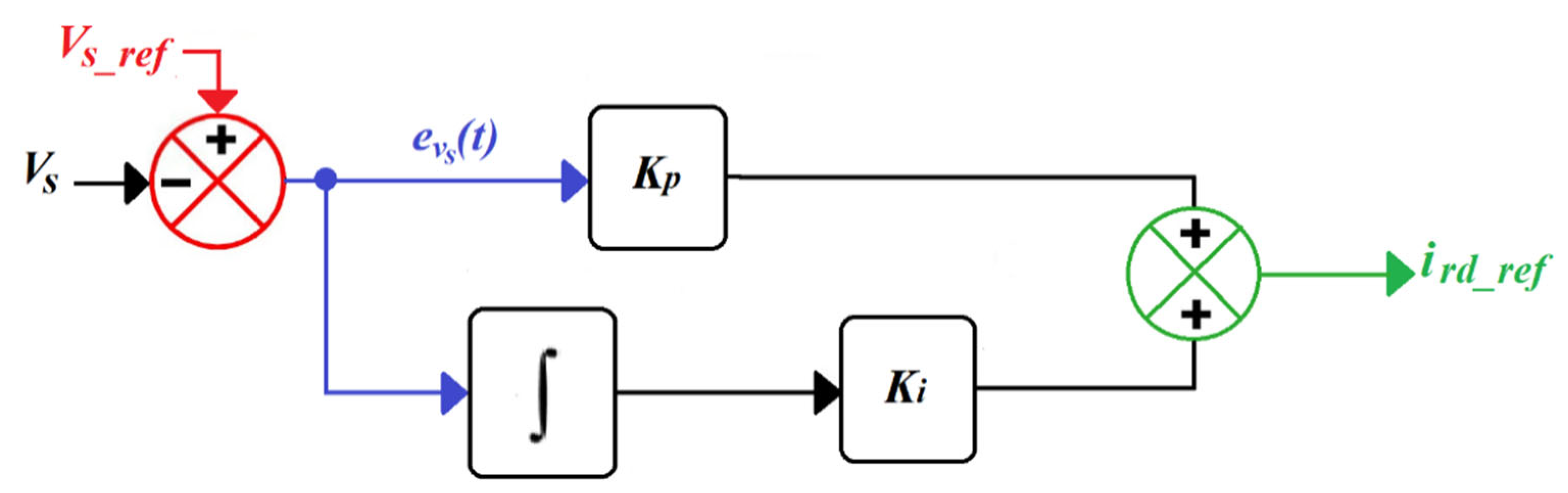
The stator voltage magnitude of the DFIG is regulated by controlling the d-axis rotor current . The reference d-axis rotor current ( is determined by minimizing the error between the desired and actual stator voltage magnitudes ( and ) using a proportional-integral (PI) controller, as illustrated in Figure 2. The dynamic of the PI voltage regulator can be described by:
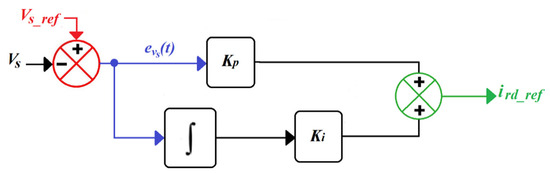
Figure 2.
Conventional PI Controller.
In the stand-alone system, the DFIG generates power according to load demand without operating under MPPT conditions [14]. Consequently, the q-rotor current reference ( is derived from the q-stator current :
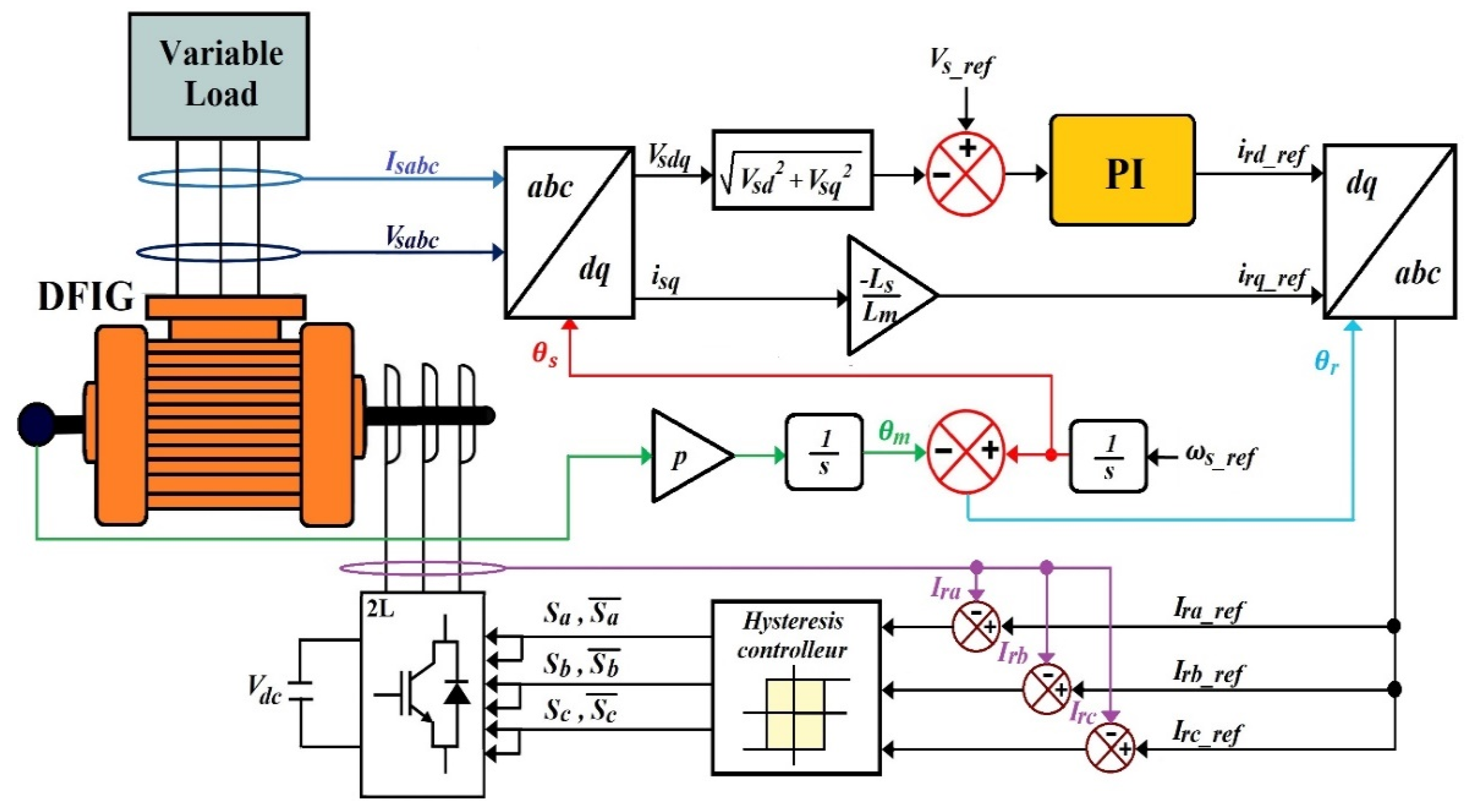
To achieve the desired output stator frequency of 50 Hz, it is essential to synchronize all stator parameters with the dq rotating reference frame. This is accomplished by transforming the three-phase stator voltages and currents into their dq-axis components using the Park transformation with angle (θs). The transformation angle (θs) is determined by integrating the reference stator frequency (ωs = 314 rad/s). Figure 3 shows the global control scheme of stator voltage control based on a conventional PI controller.
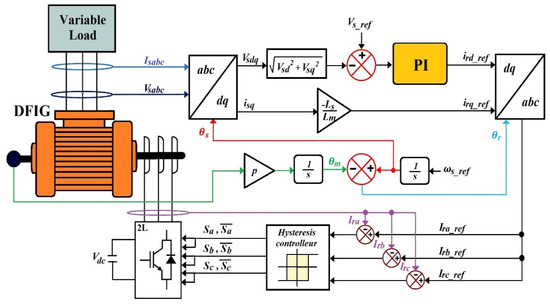
Figure 3.
Conceptual diagram of stator voltage control for stand-alone DFIG using the conventional PI controller.
4. Fractional-Order (FO) Approach
Fractional calculus applies integration and differentiation to the fundamental operator in different order where and t are the operational boundaries and is the fractional order, as defined in Ref. [41].
The Grunwald–Letnikov method [35,42], widely used in fractional-order control, defines λ order calculus for a continuously differentiable function f(t), as shown in Equation (12):
where and Γ is gamma function.
The coefficient can be determined more efficiently through the following recurrence relation:
Equation (12) unified fractional differential and integral operations. Λ > 0 indicates a fractional derivative, and λ < 0 indicates a fractional integral. The expression represents the rounding operation, where h is the step size and t and α are the upper and lower bounds of the integral, respectively.
Assuming the initial time t = 0, the Laplace transform of fractional-order differential equations [42] with constant coefficients can be derived using the classic formula:
where n is the integer such that n−1 < λ ≤ n.
If initial value , then Laplace transform of can be represented as:
5. Fractional-Order Fuzzy Logic-Based Stator Voltage Control
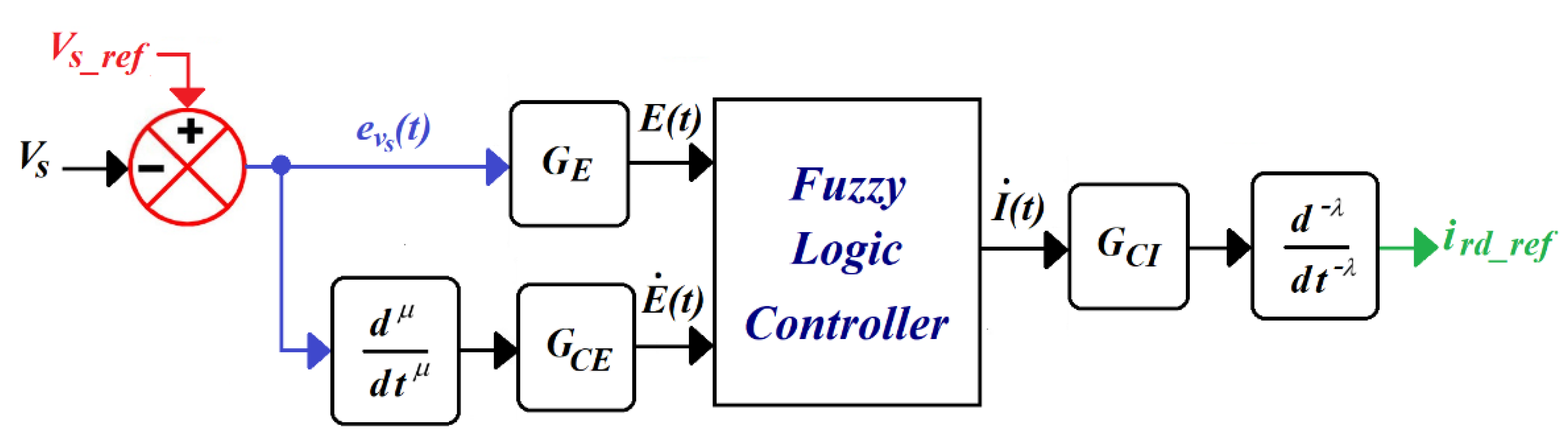
A typical structure of a fuzzy logic controller is depicted in Ref. [43]. If the derivative operator is replaced by the fractional differential and the integral ʃ by the fractional integration , the system transitions to a fractional-order fuzzy logic controller, as shown in Figure 4. Specifically designed for stator voltage control in stand-alone DFIG systems, the proposed FOFLC determines the reference rotor current described by Equation (12):
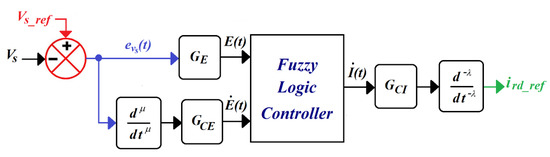
Figure 4.
Proposed fractional-order fuzzy logic controller.
The inputs of the FOFLC are the stator voltage error and its fractional derivative , while the output is the reference current . In this structure, the input scaling factors GE and GCE normalize the controller inputs, transforming them into E and , respectively, while the output scaling factor GCI adjusts the controller output. The parameters λ and µ are the integral and differential order operators, respectively. The stator voltage error is defined as Equation (17):
The transfer function of FOFLC can be shown as Equation (18):
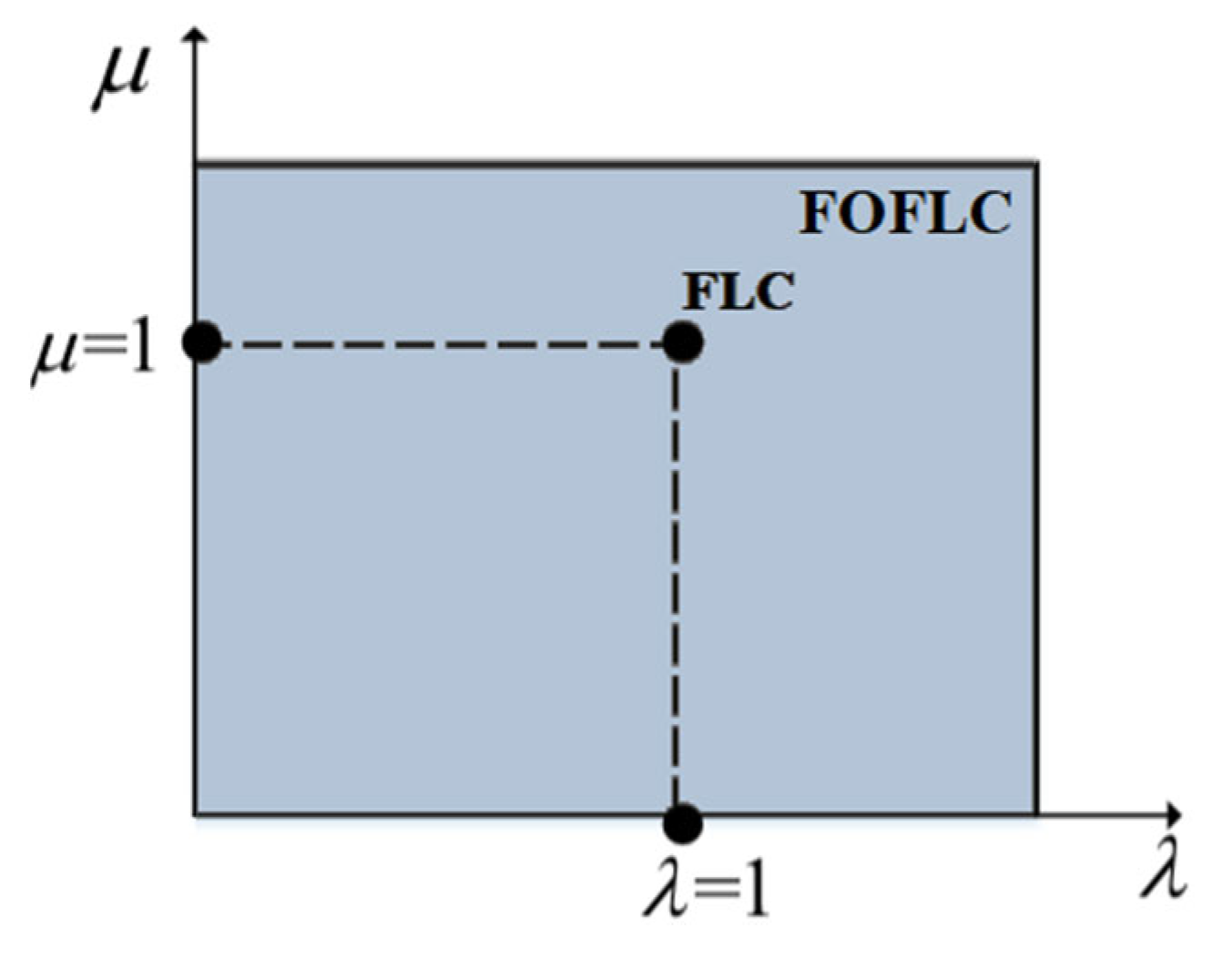
The fractional-order fuzzy logic controller (FOFLC), as shown in Figure 5, has more versatility over classical integer-order controllers. It can be represented as a structure with integrative and differentiating orders on the horizontal and vertical axes, respectively. This enables independent adjustment of fractional orders λ and µ to be made throughout the plane. This significant feature permits the FOFLC to be used in different systems without any structural change, which makes it work as many systems while being decoupled from system parameters. Therefore, the systems do not depend on structural changes. This makes the coordinating of the system performance easier.
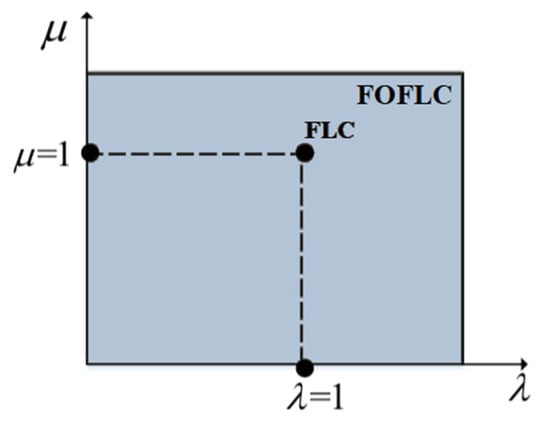
Figure 5.
Representation of the λ-µ plane of fractional-order fuzzy logic control.
Such that λ > 0 and µ ≥ 0, for λ and µ equal to 1, the conventional FLC is obtained.
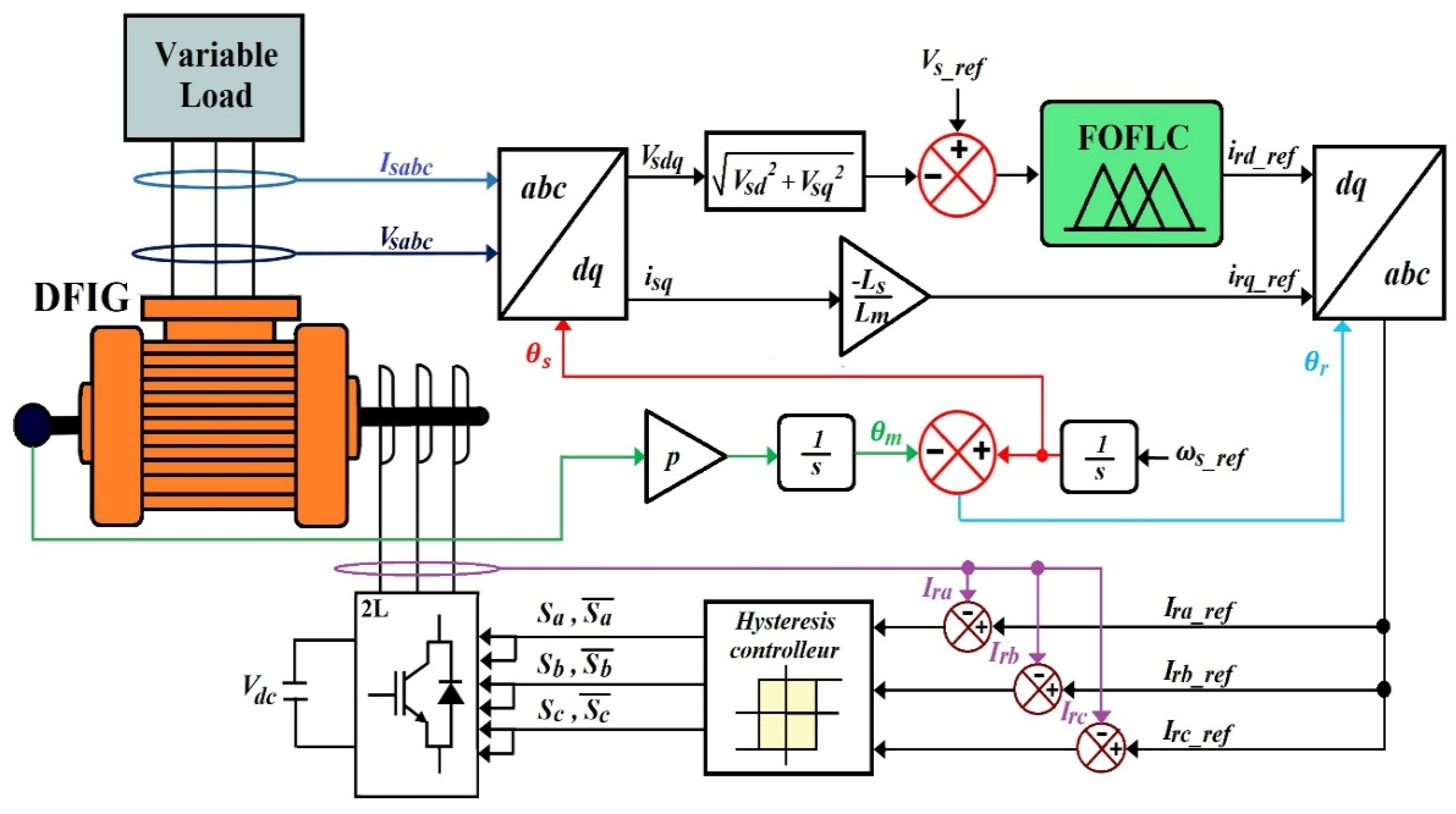
Figure 6 illustrates the global control scheme of the stator voltage control strategy for the stand-alone DFIG, based on the proposed fractional-order fuzzy logic controller.
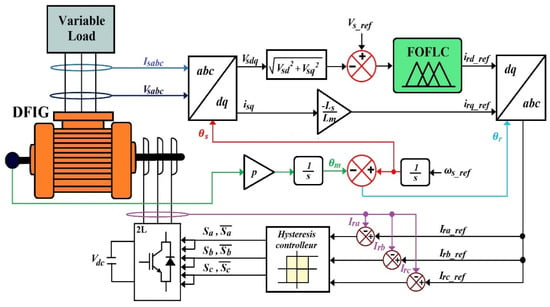
Figure 6.
Conceptual diagram of stator voltage control for stand-alone DFIG using the proposed FOFLC.
5.1. Fuzzy Logic Technique Design
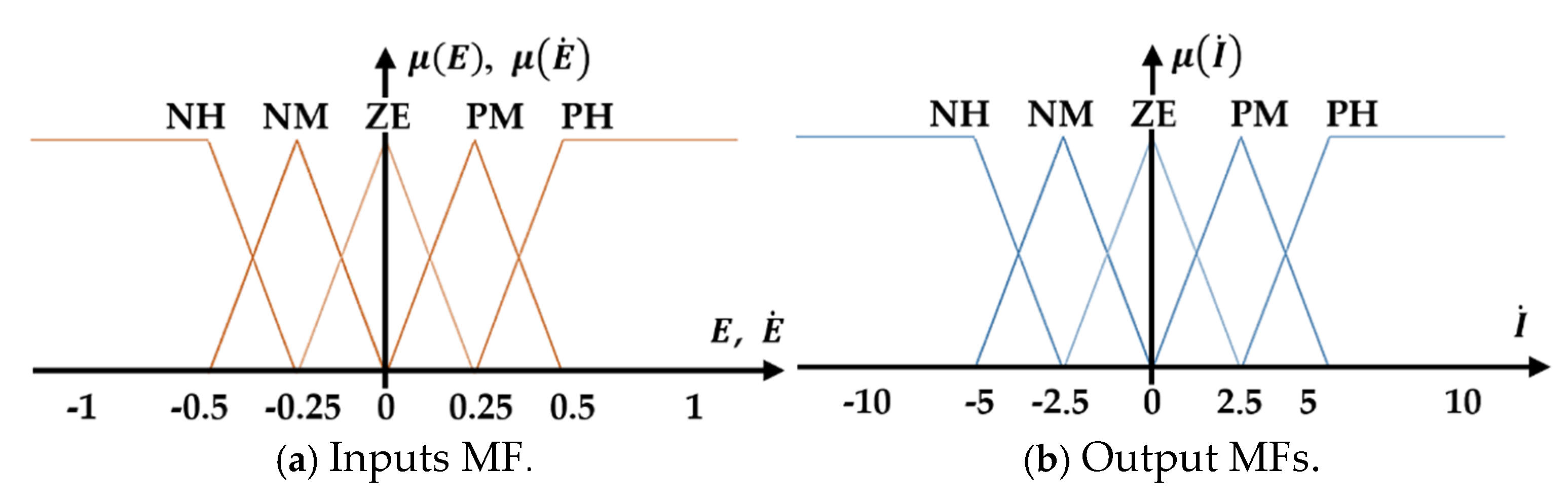
The design and implementation of the fuzzy logic (FL) system in this study involve a systematic selection process aimed at achieving effective control [25]. Specifically, triangular membership functions were selected for both input and output variables due to their simplicity, effectiveness, and ability to capture the essential characteristics of the system. To handle extreme values more robustly, trapezoidal membership functions were employed at the boundaries, as shown in Figure 7. This combination ensures that the controller can effectively address typical operating conditions while maintaining adaptability to edge cases. The fuzzy inference system operates based on a carefully designed set of twenty-five control rules, which are outlined in Table 2. These rules are meticulously crafted to meet an optimal balance between minimizing the predicted error and maintaining manageable complexity in the controller’s structure. By limiting the number of rules to twenty-five, the system avoids unnecessary computational tasks while ensuring comprehensive coverage of key operating scenarios. This approach not only enhances the controller’s responsiveness and accuracy, but also simplifies its tuning and implementation, making it well-suited for real-time applications. Furthermore, the linguistic variables and membership functions are normalized using scaling factors, enabling precise adjustments to the controller’s sensitivity and output range. This normalization ensures consistent performance across varying operating conditions and facilitates fine-tuning of the system’s transient and steady-state behavior. The resulting fuzzy logic system is both efficient and adaptable, providing a robust foundation for the proposed fractional-order fuzzy logic controller (FOFLC). In summary, the integration of triangular and trapezoidal membership functions, along with a well-structured rule base, enables the FL system to deliver accurate and reliable control while addressing the complexities inherent in stand-alone doubly fed induction generator (DFIG) systems.
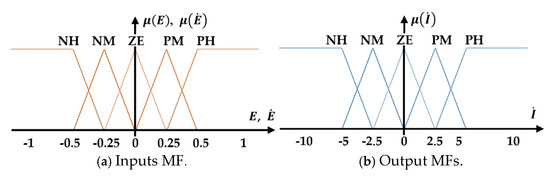
Figure 7.
Membership function of input variables and output variables. With PH: Positive High, PM: Positive Middle, ZE: Zero, NM: Negative Middle, NH: Negative High.

Table 2.
The utilized fuzzy rules table.
In the defuzzification block, linguistic outputs from the inference mechanism are converted into numerical values using the center of gravity method [20].
5.2. Numerical Solution
The fractional-order system inherently possesses infinite-dimensional characteristics, which pose challenges for practical implementation. To address this, finite-dimensional approximations are employed to enable the realization of fractional-order controllers [35]. In this paper, Oustaloup’s approximation method is utilized to approximate fractional-order operators within the frequency band of interest [,] [44]. This approach provides an effective means to represent fractional-order dynamics using rational transfer functions, ensuring compatibility with standard control design and implementation techniques. Specifically, the fractional-order operator is approximated as follows [45]:
The poles , zeros , and the gain K of the above filter can be calculated using:
In this case, N denotes the filter’s order and and are the lower and upper limits of the angular frequency band. In this study, the angular frequency band is defined as [, ] = [10−3, 103] rad/s, and the filter order N is set to 5. This configuration ensures a balance between approximation accuracy and computational efficiency, enabling robust and reliable implementation of the fractional-order fuzzy logic controller (FOFLC) on the experimental platform. The choice of parameters is guided by the need to capture the essential dynamics of the system while maintaining real-time feasibility.
This approximation technique facilitates the practical deployment of fractional-order controllers, bridging the gap between theoretical concepts and real-world applications in stand-alone doubly fed induction generator (DFIG) systems.
6. Experimental Results
To assess the theoretical basis of the fractional-order fuzzy logic controller (FOFLC) for stand-alone DFIG systems, an experimental platform is designed at the LGEB laboratory. A 3 kW AC motor serving as a turbine emulator, a 3 kW doubly fed induction generator (DFIG), and a 4 kW three-phase variable resistive load form the experimental setup. Appendix A Table A1 contains the DFIG parameters.
The components and their interconnections are shown in Figure 8, which illustrates the experimental setup.

Figure 8.
Laboratory experimental prototype for experimental validation.
The control algorithm is executed in MATLAB/Simulink on a dSPACE 1104 platform, providing a sampling rate of 10 kHz for real-time control. For the evaluation of the proposed FOFLC approach, two FOFLC tests are conducted: a reference tracking test and a robustness test for tracking a predetermined setpoint. The efficacy of the FOFLC against a conventional proportional-integral (PI) controller is tested. The Ziegler–Nichols method [14] provided the gains of the PI controller, while empirically optimizing the system response provided the fractional-order parameters λ and µ of the FOFLC [41]. This approach allowed both control strategies to be tested under the same conditions.
The main components used in the setup shown in Figure 8 are: (1) DFIG (3 kW), (2) turbine emulator/induction motor (3 kW), (3) PC with ControlDesk, (4) 4-channel oscilloscope, (5) three-phase autotransformer power supply, (6) three-phase variable resistive load (4 kW–400 V), (7) rotor-side converter (two-level inverter), (8) grid-side converter (two-level rectifier), (9) additional current sensors, (10) dSPACE 1104 real-time interface, (11) 5 V to 15 V signal adaptation circuit, (12) system switch, (13) DC power supply (60 V–3 A or 30 V–6 A), (14) voltage sensors, (15) Hall-effect current sensors, and (16) 1024-pulse encoder.
6.1. Reference Stator Voltage Variation Test
The proposed fractional-order fuzzy logic controller (FOFLC) is used to track the reference stator voltage of the system with a step input change where the reference voltage is increased from 150 V to 250 V with fixed load (35% rated power). Figure 9, Figure 10 and Figure 11 present the voltage regulation and dynamic response of the system, where the performance of the FOFLC is compared to that of the PI controller. The performance indicators for both controllers are outlined in Table 3.
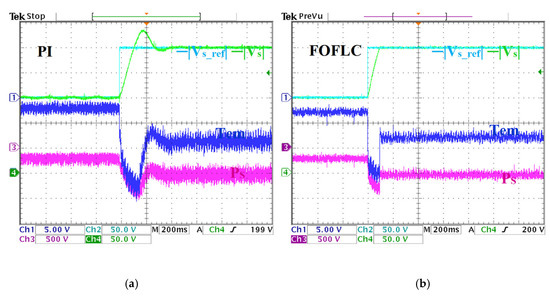
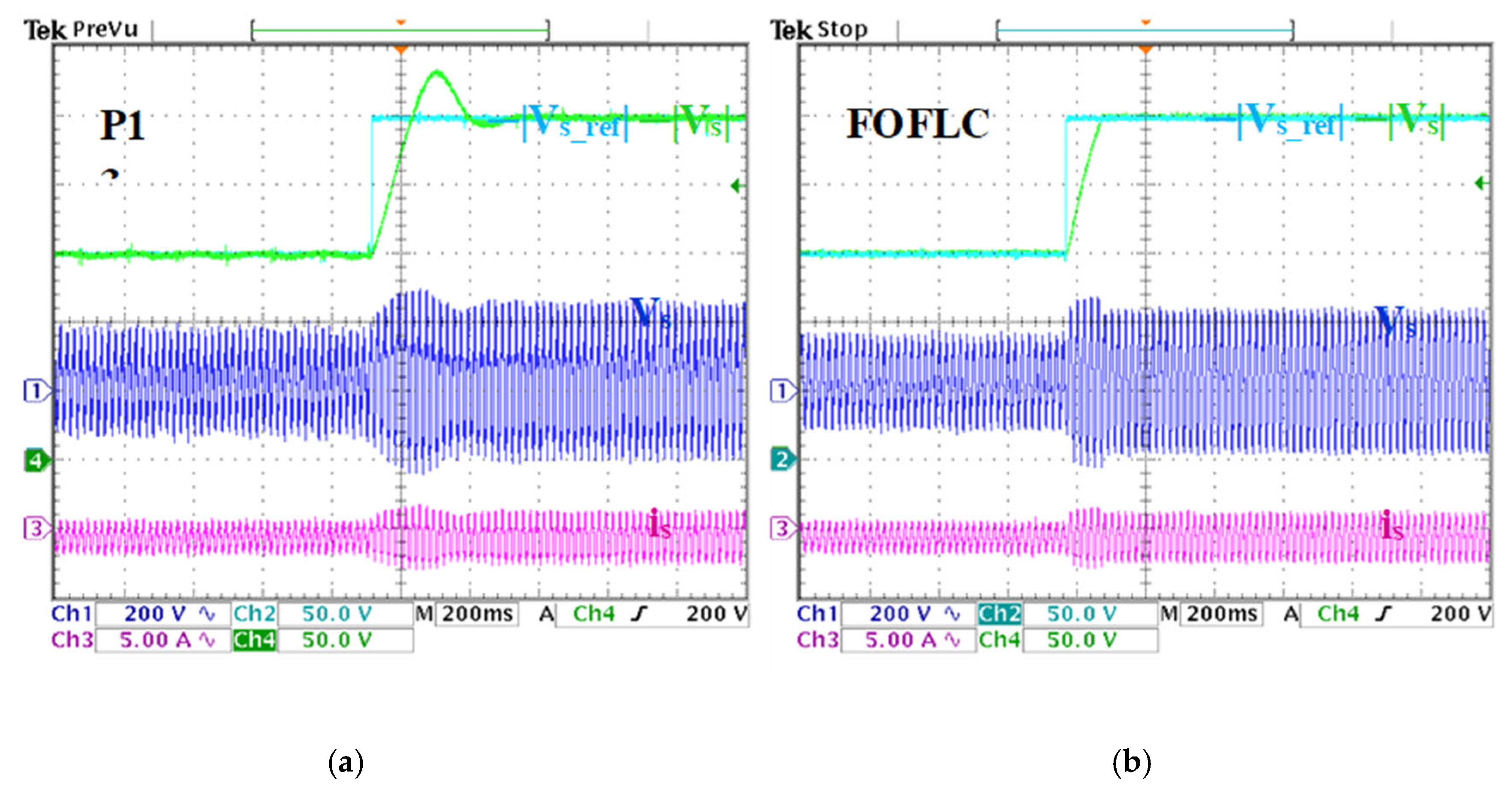
Figure 9.
System response under step variation in the stator voltage magnitude. (a) PI results. (b) FOFLC results. CH1: electromagnetic torque, CH2: reference of stator voltage magnitude, CH3: stator active power, CH4: stator voltage magnitude.
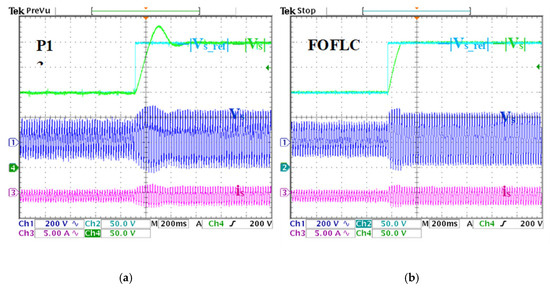
Figure 10.
System response under step variation in the stator voltage magnitude. (a) PI results. (b) FOFLC results. CH1: stator phase voltage, CH2: reference of stator voltage magnitude, CH3: stator phase current, CH4: stator voltage magnitude.
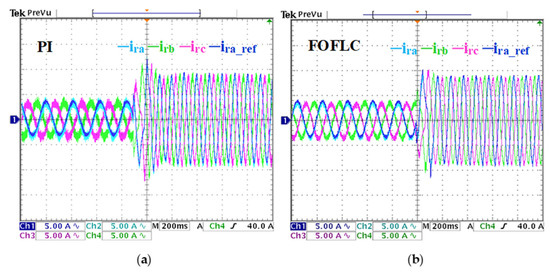
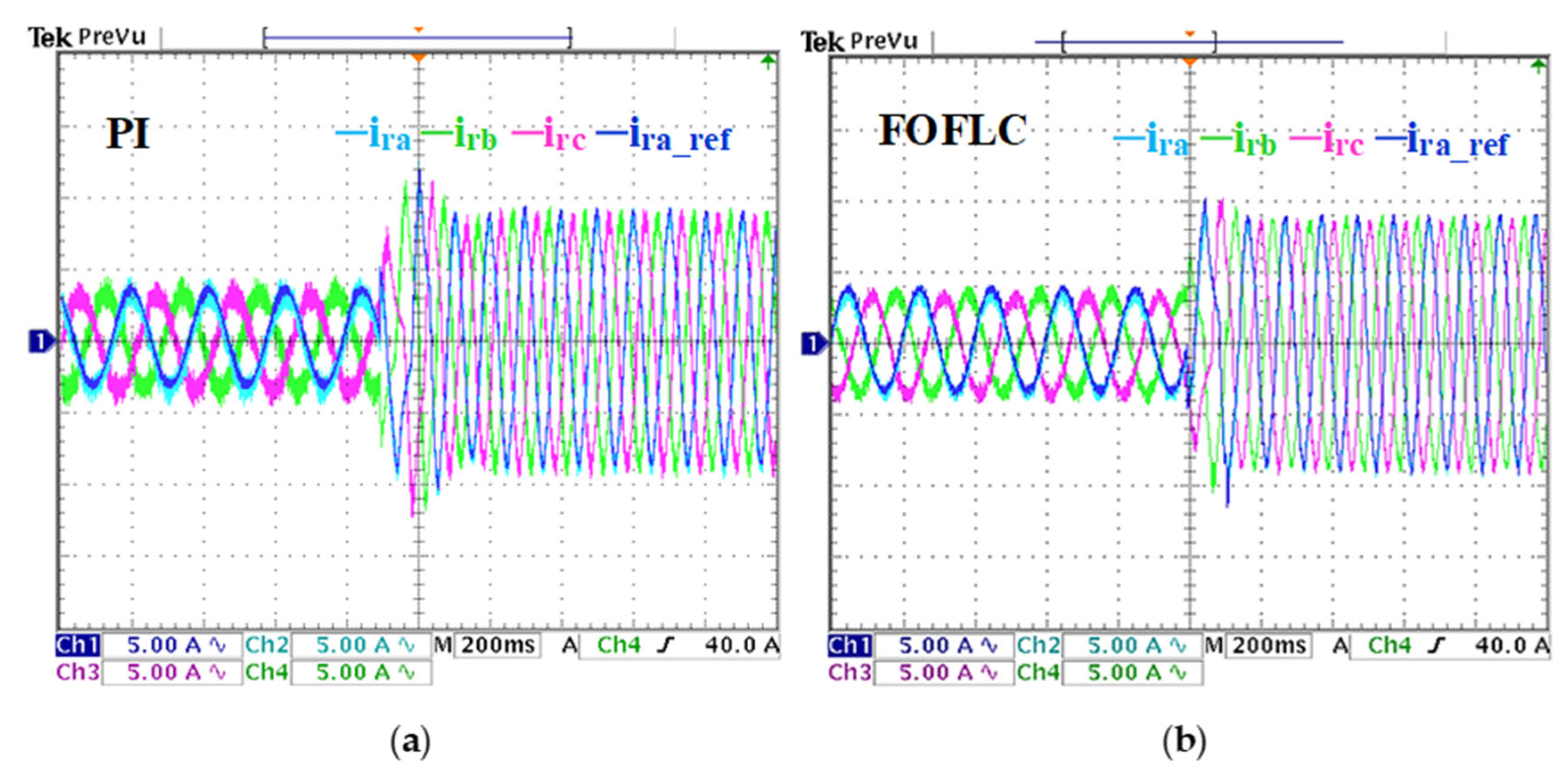
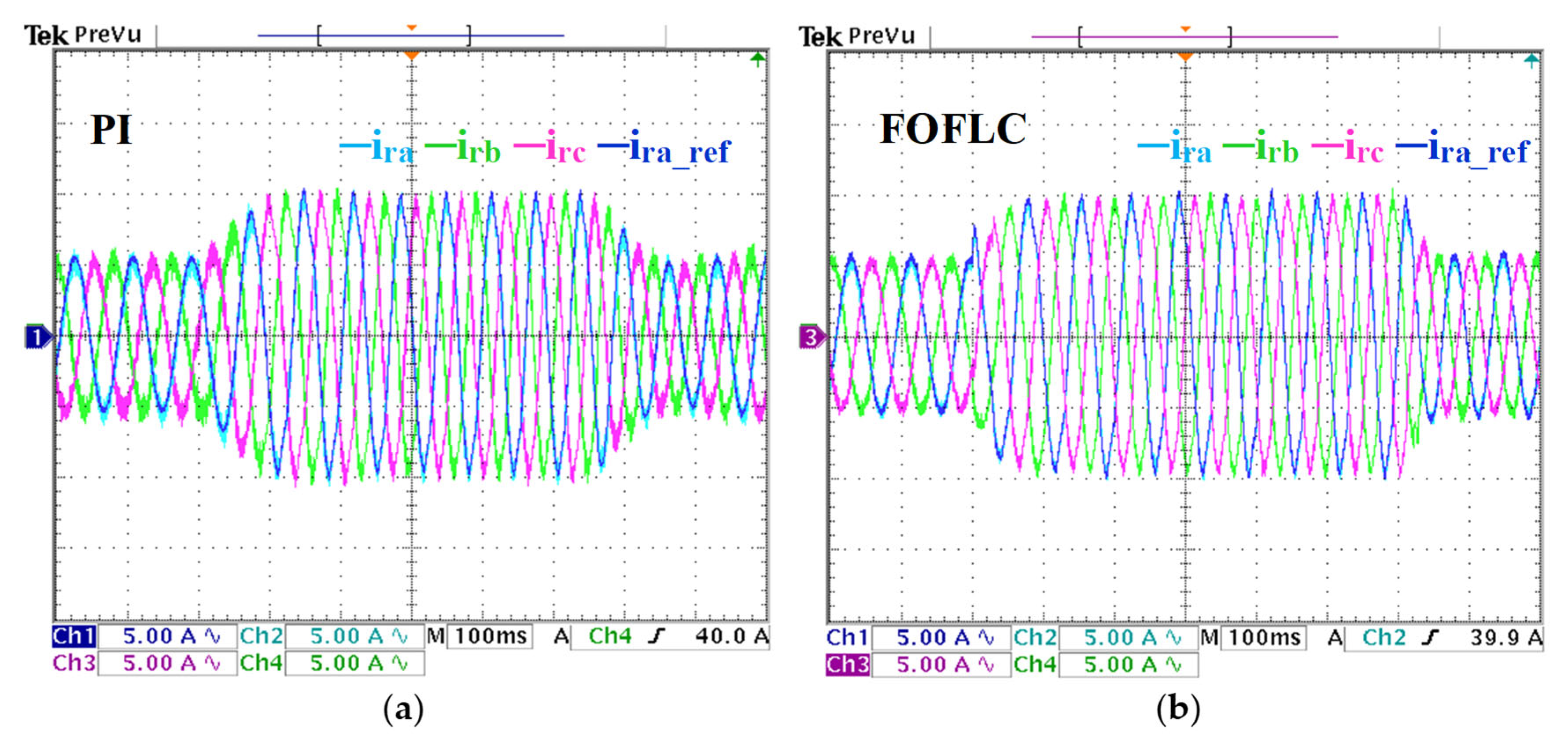
Figure 11.
Rotor current response under step variation in the stator voltage magnitude. (a) PI results. (b) FOFLC results. CH1: reference rotor current phase, CH2, CH3, CH4: three rotor current phases.

Table 3.
Performance comparison of proposed and conventional controls in the reference stator voltage variation test.
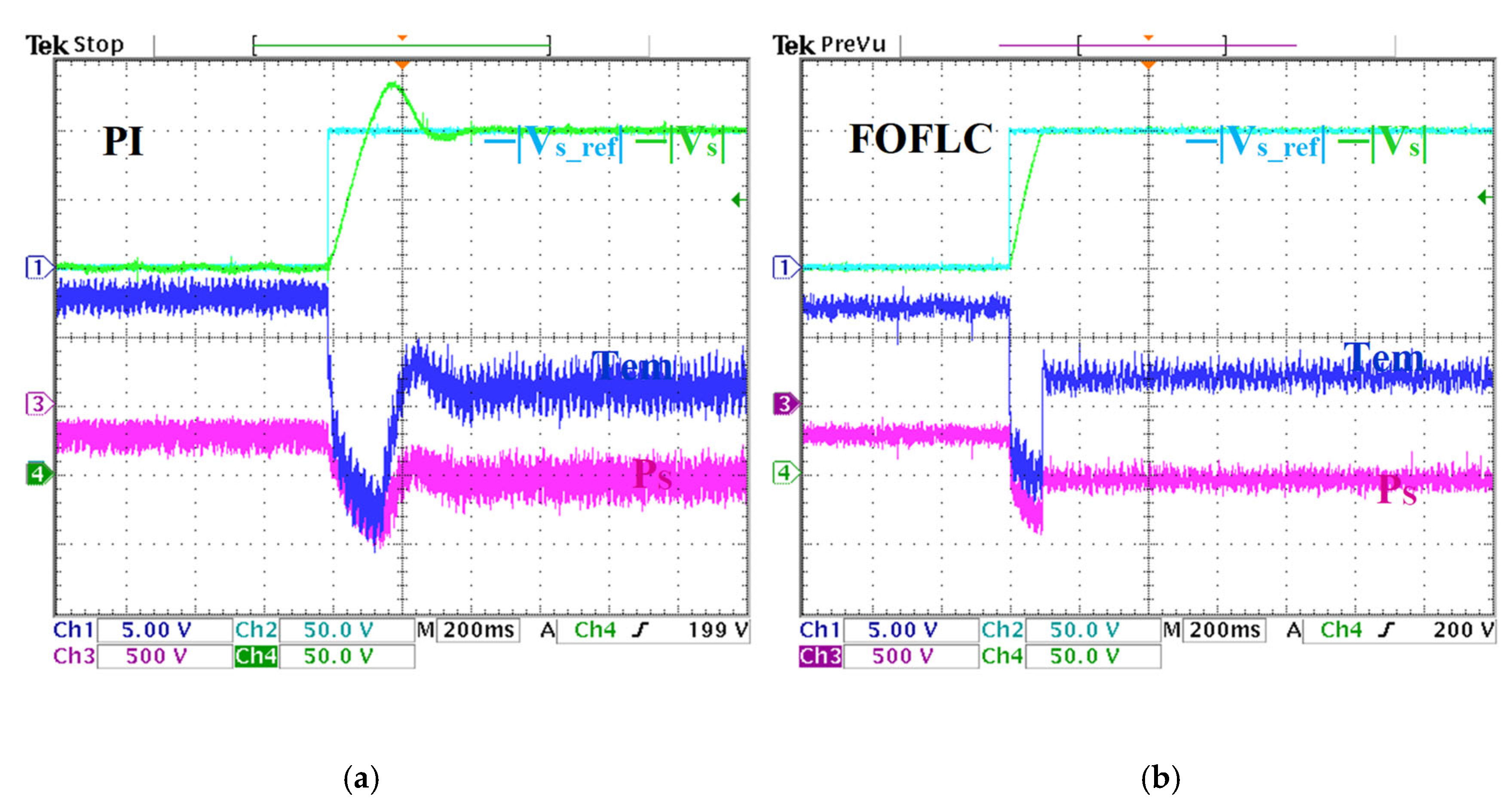
Figure 9a,b illustrates the dynamic response of the stator voltage under a change in the reference voltage. As shown in Figure 9b, the FOFLC eliminates the voltage tracking accuracy regulation overshoot and no undershoot error settings and achieves minimum voltage tracking regulation errors. It achieves this by enabling improved stability and reliability during operations. On the other hand, the PI controller exhibits an overshoot and undershoot of 31 V and 8 V, respectively, out of the scope of transient conditions. Those deviations could severely threaten system reliability in such critical scenarios. In addition, the FOFLC is able to achieve a response time of 0.06 s, which is historically considered fast for such systems, practically achieving 80% faster response time when including the PI controller’s 0.394 s response. This shows the notable FOFLC ability to quickly adapt to rapid system changes and provide responses.
Figure 9a,b depicts also the variations in electromagnetic torque and active power due to the voltage elevation. The torque gradually grew from 2.5 Nm to 8 Nm, while the active power rose from 200 W to 500 W. To quantify the oscillatory content in torque and power, the total waveform oscillation (TWO) factor was employed. This metric serves as a reliable indicator of waveform saliency and dynamic smoothness in DFIG systems [10]. The TWO is defined as: , where and represent the quantities’ RMS and average values, respectively.
Applying this method, the PI controller (Figure 9a) exhibits high ripple content, with TWO values reaching 37.88% for active power and 28.75% for electromagnetic torque, indicating significant oscillations that could compromise system stability and efficiency. In contrast, the FOFLC (Figure 9b) demonstrates a clear reduction in oscillatory content, with TWO values reduced to 19.89% for active power and 13.75% for torque, marking a reduction of nearly 50% compared to the PI controller.
Figure 10a,b reveals the behavior of the stator phase current and voltage in response to the reference voltage change. The PI controller (Figure 10a) introduces observable waveform distortions, whereas the FOFLC (Figure 10b) maintains smooth sinusoidal profiles, even under rapid transitions. This waveform quality preservation translates directly into superior power quality and reduces stress on connected loads.
Figure 11a,b further compares the rotor current control performance. Under PI control, the rotor current exhibits prolonged settling and oscillatory behavior. However, the FOFLC responds with faster convergence and minimal distortion, demonstrating enhanced control and rotor excitation handling.
To quantitatively validate the harmonic suppression capability of the FOFLC, Figure 12 presents the THD measurement results obtained using a PPA500 power analyzer. Figure 12a (PI controller): Stator voltage and current waveforms exhibit notable harmonic content, confirmed by the measured THD values of 2.129% (voltage) and 2.138% (current). Figure 12b (FOFLC): Harmonic distortion is substantially mitigated, with THD reduced to 1.02% (voltage) and 1.038% (current), a more than 50% reduction.

Figure 12.
Visualizing THD for stator current and voltage on the PPA500 power analyzer in the reference voltage variation test. (a) PI results. (b) FOFLC results.
The results show the FOFLC’s ability to operate without distortion, which makes it efficient to use in sensitive loads and applications with high standards of power quality. In summary, the FOFLC outperforms the conventional PI controller in terms of response time, overshoot/undershoot suppression, ripple reduction, and THD mitigation. These findings validate the FOFLC’s robustness and effectiveness in optimizing the performance of stand-alone DFIG systems under dynamic operating conditions.
6.2. Load and Speed Variation Test
The dynamic performance of the proposed fractional-order fuzzy logic controller (FOFLC) is further evaluated under varying load and speed conditions. It is assumed that the generator system as a whole is fully equipped with DFIG loaded with a 30% to 50% rated power spin and afterward stepped back down to 30% unloaded power. In all of the steps, DFIG is operating set to the reference value of stator voltage, which is 150 V. Figure 13, Figure 14 and Figure 15 detail the comparative results between the conventional PI controller and the FOFLC. The statistics for controlling both controllers are summarized in Table 4. One of the greatest complications in conducting this test originates from the fact that the AC motor controlled in an open-loop control leads to minor rotor speed drops when a sudden load is introduced. Unlike normal scenarios of load static changes, this situation adds more difficulty because the rotor speed is changing simultaneously with load changes.
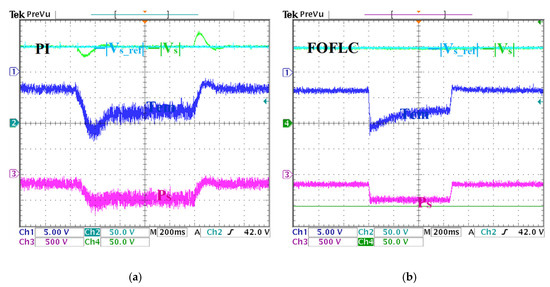
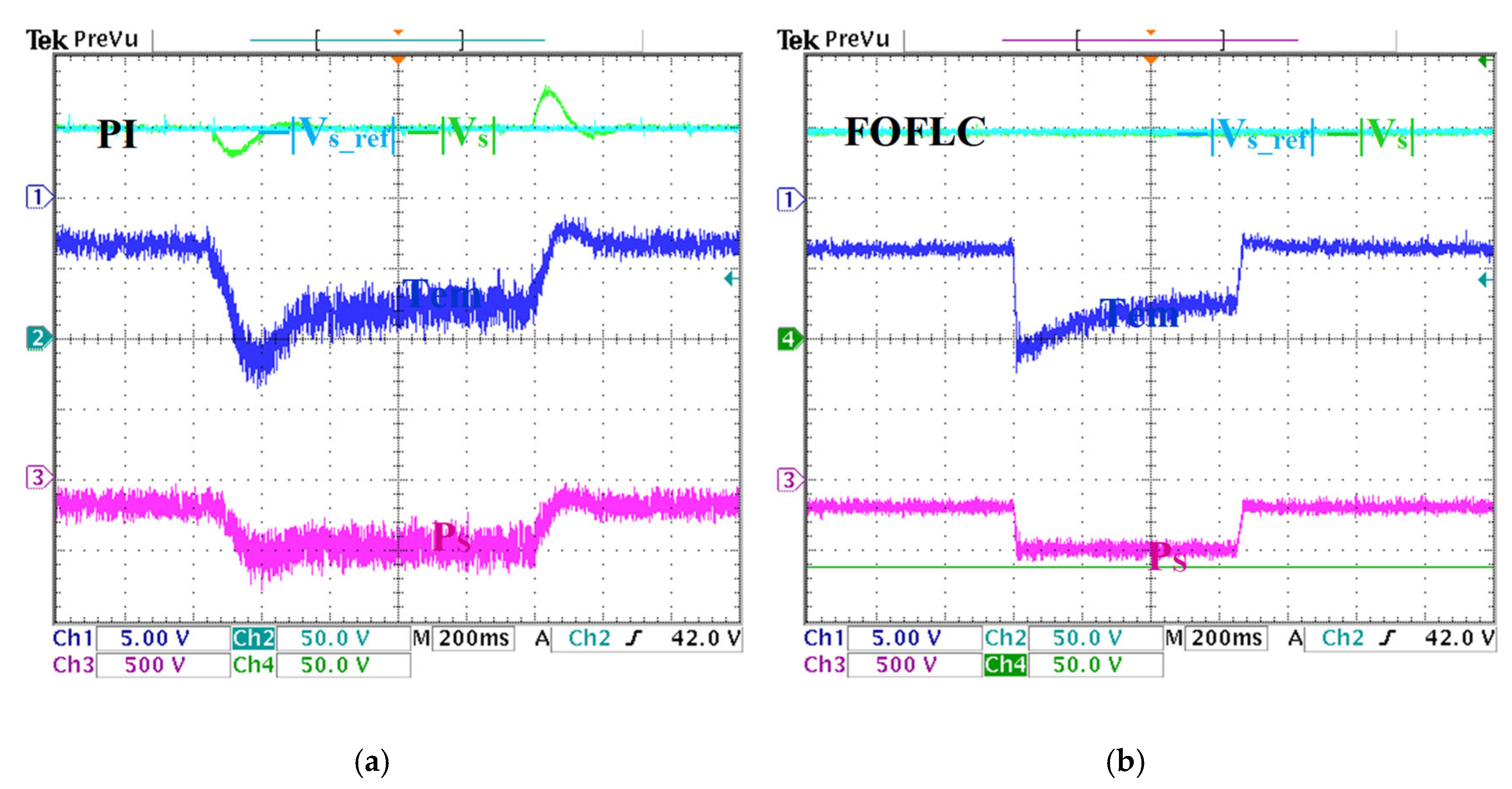
Figure 13.
System response under load and speed variations. (a) PI results. (b) FOFLC results. CH1: electromagnetic torque, CH2: reference of stator voltage magnitude, CH3: stator active power, CH4: stator voltage magnitude.
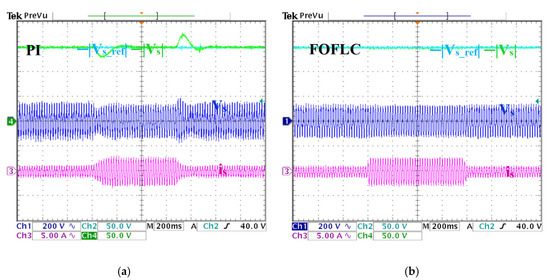
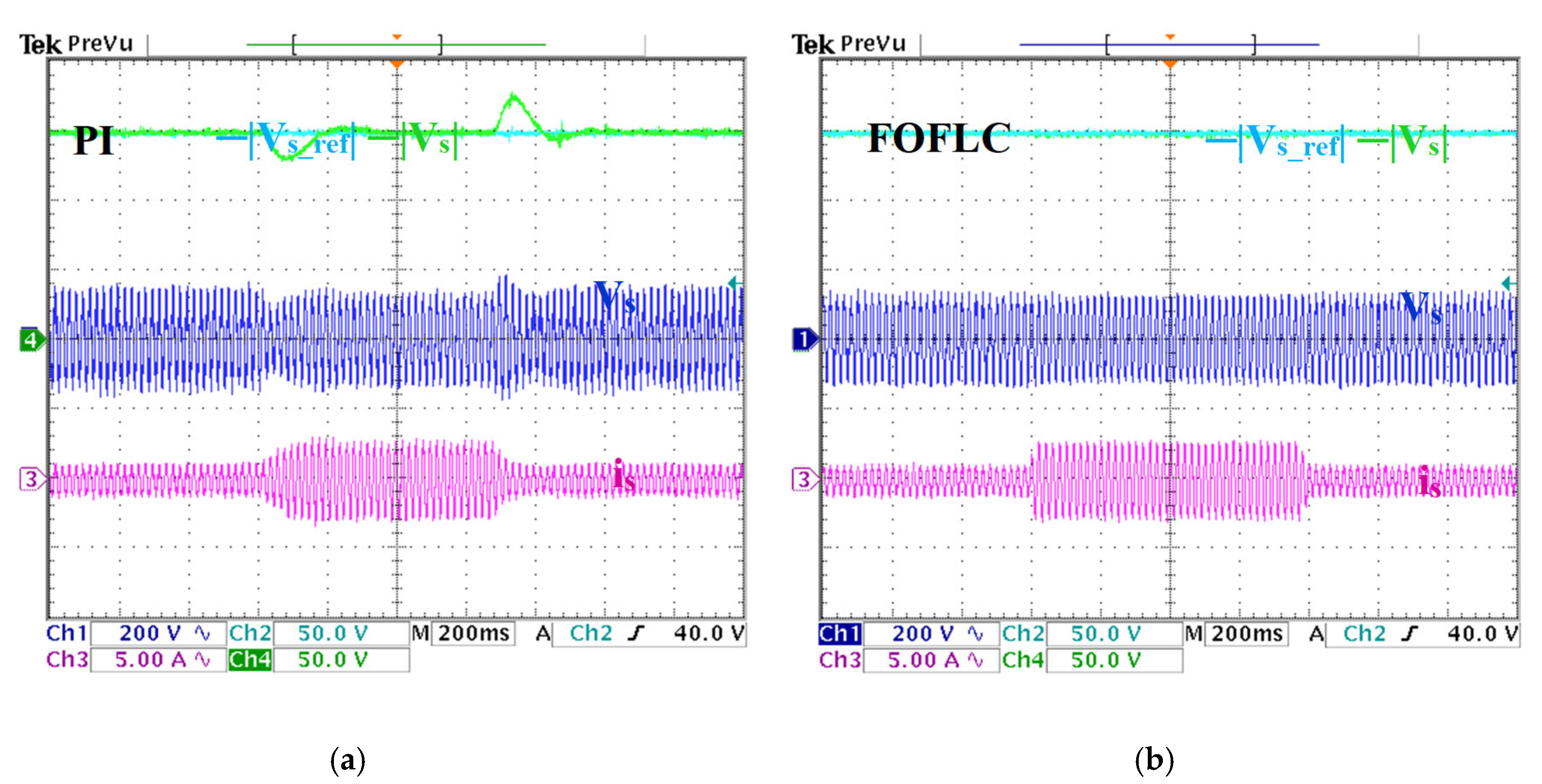
Figure 14.
The phase voltage and current behavior during the load variation test. (a) PI results. (b) FOFLC results. CH1: electromagnetic torque, CH2: reference of stator voltage magnitude, CH3: stator active power, CH4: stator voltage magnitude.
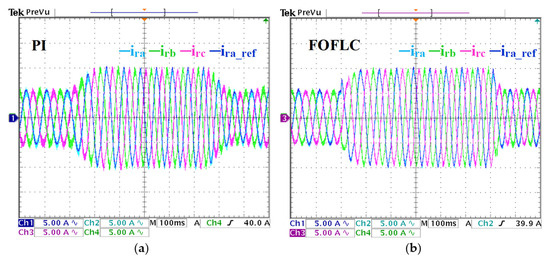
Figure 15.
Rotor current response under load and speed variations. (a) PI results. (b) FOFLC results. CH1: reference rotor current phase, CH2, CH3, CH4: three rotor current phases.

Table 4.
Performance Comparison of the proposed and conventional controls in the load and speed variation test.
Figure 13a presents the system’s response under PI control, where the voltage exhibits considerable deviations due to slow dynamic regulation. The PI controller fails to track the set voltage accurately, with a significant voltage dip down to 29 V and a prolonged recovery time of 0.312 s. This slow response is indicative of the controller’s difficulty in handling rapid changes in load and speed. On the other hand, the FOFLC in Figure 13b demonstrates superior performance, maintaining a precise stator voltage of 150 V throughout the load and speed variations. The FOFLC exhibits fast disturbance rejection, with no overshoot or undershoot, and it was able to adapt seamlessly to load and speed fluctuations without any significant voltage deviations. This underscores the FOFLC’s enhanced voltage regulation capability under dynamic operating conditions.
Figure 13a,b highlight the behavior of electromagnetic torque and active power in response to the changing load. As the load increased, the torque gradually rose from 3.5 Nm to 7.5 Nm, while the active power increased from 200 W to 500 W. To quantify waveform stability, the TWO metrics are again employed. Under PI control, the oscillatory content is significant, with TWO values of 32.11% for active power and 20.89% for electromagnetic torque, indicating pronounced ripples that could lead to mechanical stress and reduced efficiency. In contrast, the FOFLC significantly reduces waveform oscillations, achieving TWO values of 18.32% for power and 14.66% for torque, marking a substantial improvement in dynamic smoothness and system performance.
Figure 14a,b examines the phase voltage and current behavior during the load variation test. As the load increased, the phase current rose linearly from 1 A to 2.7 A, while the phase voltage maintained a clean sinusoidal waveform, even under simultaneous speed and load perturbations, demonstrating the FOFLC’s superior voltage quality and dynamic current modulation capability. To further validate the quality of the electrical output, THD measurements are conducted using a PPA500 power analyzer. The results confirmed the enhanced harmonic suppression of the proposed controller: the PI controller exhibits THD values of 2.365% for voltage and 2.378% for current, whereas the FOFLC achieves significantly lower values of 1.097% and 1.117%, respectively.
Figure 15a,b illustrates the response of the rotor phase current under varying loads and speeds. The FOFLC ensured that the rotor current closely tracked its reference trajectory, demonstrating precise current regulation. The rotor current frequency is modified according to the increased rotational speed, indicating the inherent link between rotor current dynamics and generator speed. Compared to the PI controller, the FOFLC minimized distortions, yielding a clean and stable current waveform even under fluctuating rotor speeds.
The results clearly demonstrate the robustness and adaptability of the FOFLC in providing a stable operation under varying load and wind conditions. The ability to keep the voltage steady, the ripples low, and to reduce harmonic distortion makes it a viable high-performing candidate for assuring high-quality power from stand-alone renewable energy systems, as shown in the Figure 16. The findings underscore the practical applicability of the FOFLC in addressing dynamic challenges and meeting load demands with increased reliability and power quality.

Figure 16.
THD for stator current and voltage on the PPA500 power analyzer in the load and speed variation test. (a) PI results. (b) FOFLC results.
6.3. Brief Comparative Study with Recent Control Techniques
Based on the experimental results, Table 5 presents a comparative analysis between the proposed control strategy and other recent approaches reported in the literature for stand-alone DFIG systems. Among the most notable advantages of the proposed FOFLC is its ability to significantly reduce THD, achieving values close to 1%, which reflects excellent power quality. Additionally, the proposed controller exhibits strong reference tracking and robust disturbance rejection capabilities. For certain performance indicators marked with (-), the corresponding numerical data were unfortunately unavailable. The qualitative ratings used in the table are as follows: (+) indicates medium performance, (++) indicates good performance, and (+++) indicates high performance. For certain performance indicators marked with (-), the corresponding numerical data were unfortunately unavailable.

Table 5.
Comparative analysis based on recent control techniques for stand-alone DFIGs.
This text ios added to explain: The qualitative ratings used in the table are as follows: (+) indicates medium performance, (++) indicates good performance, and (+++) indicates high performance. For certain performance indicators marked with (-), the corresponding numerical data were unfortunately unavailable.
7. Conclusions
The development and experimental verification of a new fractional-order fuzzy logic controller (FOFLC) for self-sufficient DFIG systems and voltage regulation addresses the urgent need for an effective and high-performance control in renewable energy systems. The controller has been developed by introducing a fuzzy logic technique into the fractional-order semantics umbrella. A fuzzy logic controller can now adapt to new situations as well as reach precise operational tuning, and can work as a traditional fuzzy logic controller or a fractional-order fuzzy logic controller. This makes the FOFLC optimal as a controller used in diverse operational conditions.
Real-time experiments on a 3-kW DFIG test bench demonstrated the high superiority of FOFLC over conventional PI controllers. The 80% more rapid response, elimination of overshoot and undershoot, and 60% decrease in ripple amplitudes for stator power and torque are some of the more striking results. Moreover, the FOFLC demonstrated an over 50% decrease in THD of stator voltage and current, ensuring a stable and reliable good power quality output that is needed for sensitive loads. These results illustrate the promise and effectiveness of the FOFLC for stand-alone renewable energy systems. The practical use of FOFLC, through Oustaloup’s approximation for fractional-order operators, allows for the broad use of fractional-order control systems.
While initial comparisons focused on conventional PI controllers, the proposed FOFLC is also evaluated against various advanced control strategies reported in recent literature, including intelligent controllers. Across these comparisons, the FOFLC consistently demonstrated superior dynamic behavior, with one of its most significant advantages being a substantial reduction in THD, achieving levels close to 1%, which reflects excellent power quality.
Despite these promising results, the proposed approach does have certain limitations. The tuning of fractional parameters (λ and μ) currently lacks an automated or optimal strategy, which may limit scalability. Moreover, while the controller performed well in experimental conditions, its robustness under severe disturbances, wide parameter variations, or unbalanced load conditions was not fully evaluated. Also, the reliance on Oustaloup’s approximation introduces computational supplements.
Future research will focus on optimizing the selection of fractional parameters using advanced metaheuristic algorithms, such as genetic algorithms or particle swarm optimization, to improve control performance further. Additionally, sensitivity analyses will be conducted to understand the influence of fractional parameters on system stability and robustness. Another promising direction includes extending the FOFLC to grid-connected DFIG systems and validating its efficacy in power control modes, thereby enhancing its applicability in both standalone and hybrid configurations.
Author Contributions
Conceptualization, F.B. and M.T.B.; methodology, F.B. and M.B.; software, F.B. and M.T.B.; validation, F.B. and M.T.B., M.B., A.B.; formal analysis, F.B. and A.B.; investigation, F.B.; resources, M.T.B. and Amar Golea; writing—original draft preparation, F.B.; writing—review and editing, M.T.B., A.B., M.C., M.B. and M.S.C.; visualization, M.B., M.T.B.; supervision, A.G., M.B. and M.S.C.; funding acquisition, F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data is available.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Stator and rotor voltages | |
| Stator and rotor currents | |
| Stator and rotor resistances | |
| Stator and rotor magnetic fluxes | |
| Stator and rotor inductances | |
| Mutual inductance between stator and rotor | |
| dq stator and rotor voltages | |
| dq stator and rotor currents | |
| dq stator and rotor magnetic fluxes | |
| ,, | Pulses of the stator, slip and the rotor |
| Stator, rotor and mechanical position | |
| p | Number of pole pairs |
| Stator time constant | |
| DC bus voltage | |
| Ps, Qs | Stator active et reactive power |
| Tem | Electromagnetic torque |
| Kp, Ki | Proportional-integral (PI) regulator |
| Input and output scaling factors | |
| Fractional integral and differential operators | |
| DFIG | Doubly-Fed Induction Generators |
| FLCs | Fuzzy Logic Controllers |
| FO | Fractional-Order |
| FOFLC | Fractional-Order Fuzzy Logic Controller |
| FOC | Field Oriented Control |
Appendix A

Table A1.
Parameter of DFIG.
Table A1.
Parameter of DFIG.
| Parameter | Value | Unit |
|---|---|---|
| Power | 3 | KW |
| Rated speed | 1500 | rpm |
| Frequency | 50 | Hz |
| Stator voltage | 380 | V |
| Number of pole pairs | 2 | |
| Torque | 20 | N·m |
| Lm (Magnetizing inductance) | 0.180 | H |
| Ls (Stator inductance) | 0.255 | H |
| Rs (Stator resistance) | 1.6 | Ω |
| Lr (Rotor inductance) | 0.255 | H |
| Rr (Rotor resistance) | 1.8 | Ω |
| Total inertia | 0.03 | Kg·m2 |
References
- Eftekhari, H.; Al-Obaidi, A.S.M.; Eftekhari, S. Aerodynamic Performance of Vertical and Horizontal Axis Wind Turbines: A Comparison Review. Indones. J. Sci. Technol. 2022, 7, 65–88. [Google Scholar] [CrossRef]
- Krishnan, A.; Al-Obaidi, A.S.M.; Hao, L.C. Towards Sustainable Wind Energy: A Systematic Review of Airfoil and Blade Technologies Over the Past 25 Years for Supporting Sustainable Development Goals (SDGs). Indones. J. Sci. Technol. 2024, 9, 623–656. [Google Scholar] [CrossRef]
- Touaiti, B.; Azza, H.B.; Abdelkader, A.; Abbassi, R.; Farah, A.; Jemli, M. Energy control of on-grid hybrid wind/PV power system using doubly fed induction generator-direct current link topology. Energy Sources Part Recovery Util. Environ. Eff. 2025, 47, 8611–8627. [Google Scholar] [CrossRef]
- Abad, G.; López, J.; Rodríguez, M.A.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Patel, K.S.; Makwana, V.H. Modified grid side converter control technique for DFIG connected to nonlinear loads. Energy Sources Part Recovery Util. Environ. Eff. 2024, 46, 15922–15935. [Google Scholar] [CrossRef]
- Dardabi, C.; Álvarez, S.C.; Djebli, A. An Artificial-Neural-Network-Based Direct Power Control Approach for Doubly Fed Induction Generators in Wind Power Systems. Energies 2025, 18, 1989. [Google Scholar] [CrossRef]
- Li, Y.; Sun, W.; Yu, D. RBFNN-based global fast terminal sliding mode control for fully controlled doubly fed induction generator. J. Frankl. Inst. 2024, 361, 107196. [Google Scholar] [CrossRef]
- Misra, H.; Gundavarapu, A.; Jain, A.K. Control Scheme for DC Voltage Regulation of Stand-Alone DFIG-DC System. IEEE Trans. Ind. Electron. 2017, 64, 2700–2708. [Google Scholar] [CrossRef]
- Shukla, R.D.; Tripathi, R.K. Isolated Wind Power Supply System using Double-fed Induction Generator for remote areas. Energy Convers. Manag. 2015, 96, 473–489. [Google Scholar] [CrossRef]
- Chabani, M.S.; Benchouia, M.T.; Golea, A.; Abdealziz, A.Y.; Mossa, M.A. A new sensor-less voltage and frequency control of stand-alone DFIG based dead-beat direct-rotor flux control-experimental validation. ISA Trans. 2025, 158, 715–734. [Google Scholar] [CrossRef]
- Amrane, F.; Francois, B.; Chaiba, A. Experimental investigation of efficient and simple wind-turbine based on DFIG-direct power control using LCL-filter for stand-alone mode. ISA Trans. 2022, 125, 631–664. [Google Scholar] [CrossRef]
- Phan, V.-T.; Nguyen, D.-T.; Trinh, Q.-N.; Nguyen, C.-L.; Logenthiran, T. Harmonics Rejection in Stand-Alone Doubly-Fed Induction Generators With Nonlinear Loads. IEEE Trans. Energy Convers. 2016, 31, 815–817. [Google Scholar] [CrossRef]
- Chabani, M.S.; Benchouia, M.T.; Golea, A.; Becherif, M. Finite-State Predictive Current Control of a Standalone DFIG-Based Wind Power Generation Systems: Simulation and Experimental Analysis. J. Control Autom. Electr. Syst. 2021, 32, 1332–1343. [Google Scholar] [CrossRef]
- Soued, S.; Chabani, M.S.; Becherif, M.; Benchouia, M.T.; Ramadan, H.S.; Betka, A.; Golea, A.; Zouzou, S.E. Experimental behaviour analysis for optimally controlled standalone DFIG system. IET Electr. Power Appl. 2019, 13, 1462–1473. [Google Scholar] [CrossRef]
- Chabani, M.S.; Benchouia, M.T.; Golea, A.; Benmouna, A.; Iqbal, M.; Becherif, M.; Golea, N. Takagi–Sugeno Fuzzy Logic Controller for DFIG Operating in the Stand-Alone Mode: Simulations and Experimental Investigation. Arab. J. Sci. Eng. 2023, 48, 14605–14620. [Google Scholar] [CrossRef]
- Guo, L.; Wang, D.; Peng, Z.; Diao, L. Improved super-twisting sliding mode control of a stand-alone DFIG-DC system with harmonic current suppression. IET Power Electron. 2020, 13, 1311–1320. [Google Scholar] [CrossRef]
- Labdai, S.; Chrifi-Alaoui, L.; Nezli, L.; Hemici, B.; Bussy, P. Implementation of the Adaptive Neural Networks Backstepping Controller for a Stand-Alone DFIG Based WECS. In Proceedings of the 2021 9th International Conference on Systems and Control (ICSC), Caen, France, 24–26 November 2021; pp. 529–535. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Q.; Yang, R.; Tao, G.; Liu, Z. H∞ current damping control of DFIG based wind farm for sub-synchronous control interaction mitigation. Int. J. Electr. Power Energy Syst. 2018, 98, 509–519. [Google Scholar] [CrossRef]
- Wu, W.J.; Xue, H. Passivity-Based Control Strategies of Doubly Fed Induction Wind Power Generator without Speed Sensors. Appl. Mech. Mater. 2013, 380–384, 3124–3128. [Google Scholar] [CrossRef]
- Mebkhouta, T.; Golea, A.; Boumaraf, R.; Benchouia, T.M.; Karboua, D.; Bajaj, M.; Chebaani, M.; Blazek, V. Sensorless finite set predictive current control with MRAS estimation for optimized performance of standalone DFIG in wind energy systems. Results Eng. 2024, 24, 103622. [Google Scholar] [CrossRef]
- Aboub, H.; Mechouma, R.; Azoui, B.; Labiod, C.; Khechekhouche, A. A New Multicarrier Sinusoidal Pulse Width Modulation (SPWM) Strategy based on Rooted Tree Optimization (RTO) Algorithm for Reducing Total Harmonic Distortion (THD) of Switched-Capacitor Nine-level Inverter in Grid-connected PV systems. Indones. J. Sci. Technol. 2022, 7, 19–36. [Google Scholar] [CrossRef]
- Rajendran, S.; Thangavel, V.; Krishnan, N.; Prabaharan, N. DC Link Voltage Enhancement in DC Microgrid Using PV Based High Gain Converter with Cascaded Fuzzy Logic Controller. Energies 2023, 16, 3928. [Google Scholar] [CrossRef]
- Boucetta, F.; Benchouia, M.T.; Bechrif, M.; Chebani, M.; Golea, A.; Boumaaraf, R. Intelligent Controller to Improve Stator Voltage Regulation Performance of a Standalone DFIG: Real-Time Validation. In Proceedings of the 2024 International Conference on Advances in Electrical and Communication Technologies (ICAECOT), Sétif, Algeria, 1–3 October 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Panda, A.K.; Mikkili, S. FLC based shunt active filter (p–q and Id–Iq) control strategies for mitigation of harmonics with different fuzzy MFs using MATLAB and real-time digital simulator. Int. J. Electr. Power Energy Syst. 2013, 47, 313–336. [Google Scholar] [CrossRef]
- Arifin, S.; Uddin, M.N.; Wang, W. Neuro-Fuzzy Adaptive Direct Torque and Flux Control of a Grid-Connected DFIG-WECS With Improved Dynamic Performance. IEEE Trans. Ind. Appl. 2023, 59, 7692–7700. [Google Scholar] [CrossRef]
- da Silva, J.L. Fuzzy Logic Control with PSO Tuning. In Fuzzy Systems—Theory and Applications; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Benchouia, M.T.; Ghadbane, I.; Golea, A.; Srairi, K.; Benbouzid, M.E.H. Implementation of adaptive fuzzy logic and PI controllers to regulate the DC bus voltage of shunt active power filter. Appl. Soft Comput. 2015, 28, 125–131. [Google Scholar] [CrossRef]
- Bao, D.; Liang, X.; Ge, S.S.; Hao, Z.; Hou, B. A framework of adaptive fuzzy control and optimization for nonlinear systems with output constraints. Inf. Sci. 2022, 616, 411–426. [Google Scholar] [CrossRef]
- Anbalagan, P.; Joo, Y.H. Design of memory-based adaptive integral sliding-mode controller for fractional-order T-S fuzzy systems and its applications. J. Frankl. Inst. 2022, 359, 8819–8847. [Google Scholar] [CrossRef]
- Nayak, P.C.; Nayak, B.P.; Prusty, R.C.; Panda, S. Sunflower optimization based fractional order fuzzy PID controller for frequency regulation of solar-wind integrated power system with hydrogen aqua equalizer-fuel cell unit. Energy Sources Part Recovery Util. Environ. Eff. 2021, 47, 9550–9568. [Google Scholar] [CrossRef]
- Huang, S.; Wang, J.; Huang, C.; Zhou, L.; Xiong, L.; Liu, J.; Li, P. A fixed-time fractional-order sliding mode control strategy for power quality enhancement of PMSG wind turbine. Int. J. Electr. Power Energy Syst. 2022, 134, 107354. [Google Scholar] [CrossRef]
- Xie, L.; Wan, D.; Qin, R. Dual-Loop Voltage–Current Control of a Fractional-Order Buck-Boost Converter Using a Fractional-Order PIλ Controller. Fractal Fract. 2023, 7, 256. [Google Scholar] [CrossRef]
- Liu, D.; Han, J.; Chen, G.; Cheng, Y.; Liang, X.; Song, C. Fuzzy self-tuning fractional order PD permanent magnet synchronous motor speed control based on torque compensation. Sci. Rep. 2025, 15, 2141. [Google Scholar] [CrossRef]
- Nako, J.; Psychalinos, C.; Elwakil, A.S. Minimum Active Component Count Design of a PIλDμ Controller and Its Application in a Cardiac Pacemaker System. J. Low Power Electron. Appl. 2023, 13, 13. [Google Scholar] [CrossRef]
- Wase, M.G.; Gebrekirstos, R.F.; Jin, G.-G.; So, G.-B. Fuzzy Gain Scheduling of the Fractional-Order PID Controller for a Continuous Stirred-Tank Reactor Process. Processes 2023, 11, 3275. [Google Scholar] [CrossRef]
- Prabhakaran, A.; Ponnusamy, T.; Thenmozhi; Janarthanan, G. Optimized fractional order PID controller with sensorless speed estimation for torque control in induction motor. Expert Syst. Appl. 2024, 249, 123574. [Google Scholar] [CrossRef]
- Talib, M.; Ibrahim, Z.; Rahim, N.A.; Zulhani, R.; Nordin, N.; Farah, N.; Razali, A. An improved simplified rules Fuzzy Logic Speed Controller method applied for induction motor drive. ISA Trans. 2020, 105, 230–239. [Google Scholar] [CrossRef] [PubMed]
- Puchalapalli, S.; Singh, B. A Single Input Variable FLC for DFIG-Based WPGS in Standalone Mode. IEEE Trans. Sustain. Energy 2020, 11, 595–607. [Google Scholar] [CrossRef]
- Demirbas, S. Self-tuning fuzzy-PI-based current control algorithm for doubly fed induction generator. IET Renew. Power Gener. 2017, 11, 1714–1722. [Google Scholar] [CrossRef]
- Lin, F.-J.; Huang, Y.-S.; Tan, K.-H.; Lu, Z.-H.; Chang, Y.-R. Intelligent-controlled doubly fed induction generator system using PFNN. Neural Comput. Appl. 2013, 22, 1695–1712. [Google Scholar] [CrossRef]
- Dinh, T.N.; Kamal, S.; Pandey, R.K. (Eds.) Fractional-Order System: Control Theory and Applications; MDPI: Basel, Switzerland, 2023. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. In Nonlinear Physical Science; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Khairudin, M.; Refalda, R.; Yatmono, S.; Pramono, H.S.; Triatmaja, A.K.; Shah, A. The Mobile Robot Control in Obstacle Avoidance Using Fuzzy Logic Controller. Indones. J. Sci. Technol. 2020, 5, 334–351. [Google Scholar] [CrossRef]
- AbdelAty, A.M.; Al-Durra, A.; Zeineldin, H.; El-Saadany, E.F. Improving small-signal stability of inverter-based microgrids using fractional-order control. Int. J. Electr. Power Energy Syst. 2024, 156, 109746. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).