Abstract
Estimating the amplitude of a sinewave from a set of data points is a common procedure in various applications. This is typically achieved using a least squares method that provides closed-form estimators. The sampling process itself is often affected by different non-ideal phenomena like additive noise, phase noise, or sampling jitter, for example. Here, the precision of the estimation of a sinewave amplitude when the samples are affected by phase noise or sampling jitter is studied in the case of coherent sampling. The mathematical expression derived is useful in obtaining the confidence intervals for the estimated sinusoidal amplitude. It is also valuable at the time of choosing the proper number of samples to acquire from a signal in order to reach a certain desired level of sinewave amplitude estimation precision. The analytical expression presented is validated using both numerically generated data and experimental data. Various non-ideal factors, such as a fixed, uncontrollable amount of jitter in the setup, additive noise, analog-to-digital converter non-linearity, and limited signal bandwidth, are observed and discussed. Additionally, this work presents an exhaustive overview of the technical aspects involved in the experimental validation, including the implementation of the Monte Carlo type procedure, instrument interface, programming language, and the general development of automated measurement systems, which may be useful to other engineers.
1. Introduction
Estimating the amplitude of a sinewave from a set of data points is a fundamental task in numerous scientific and engineering applications, encompassing fields such as telecommunications, signal processing, and instrumentation. This process is crucial for the accurate analysis and interpretation of various phenomena. For example, in mechanical engineering, monitoring the amplitude of mechanical vibrations is vital for predicting and preventing mechanical failures in engines, turbines, and other machinery [1]. By analyzing vibration amplitudes, engineers can identify early signs of wear and tear, thus implementing timely maintenance to avoid catastrophic failures. In predictive maintenance systems, vibration amplitude analysis is used to monitor the health of rotating machinery, ensuring optimal performance and longevity. In seismology, estimating the amplitude of seismic waves is critical for assessing their magnitude and potential impact. Accurate amplitude measurements enable scientists to evaluate the energy released during an earthquake and predict the likely effects on buildings and infrastructure. This information is essential for designing earthquake-resistant structures, ensuring that they can withstand seismic forces and protect lives and property [2]. Also, in instrumentation and measurement, one often uses sinewaves as a stimulus signal to measure the characteristics of different electronic devices like amplifiers, filters, and analog-to-digital converters (ADCs), among many other devices and systems. One also often uses sinewaves to measure different quantities like temperature [3] or distance [4].
In modern systems, often the signals from the real world are sampled, digitized, and input into computers for storage and processing. It is thus important to have signal processing algorithms that can estimate the various parameters of a sinewave like amplitude, initial phase, offset, and frequency. This estimation is generally made using a least squares procedure that minimizes the average of the squares of the differences between the data points and the sinusoidal modal [5]. Typically, least squares estimation methods offer closed-form solutions that are both efficient and robust in estimating amplitude, initial phase, and offset. In the case of frequency, usually an iterative procedure is employed.
Traditional methods for amplitude estimation include least squares sine fitting [6], Fourier-based approaches [7], and Bayesian estimation techniques [5]. These methods typically assume the presence of additive noise but often neglect the impact of phase noise and jitter, which introduce correlated distortions affecting amplitude precision. Prior research on sine fitting algorithms [8] has primarily focused on reducing bias and improving convergence but does not explicitly account for the degradation caused by phase noise and jitter.
Many measurement techniques rely on sinusoidal signals, where the precision of amplitude estimation directly impacts the overall accuracy of the system. However, real-world measurement systems are subject to noise and imperfections, among which jitter and phase noise are particularly significant. Jitter and phase noise introduce time-domain and frequency-domain distortions, respectively, that can degrade amplitude estimation accuracy. While extensive research has been conducted on the impact of additive noise, the specific contributions of jitter and phase noise to amplitude estimation errors remain less explored. Understanding these effects is critical for designing high-precision measurement systems, improving calibration methods, and mitigating sources of uncertainty in practical applications.
This study systematically investigates the influence of jitter and phase noise on the precision of sinusoidal amplitude estimation, providing both theoretical analysis and empirical validation. By quantifying their impact on residuals in sine fitting, we aim to offer insights that will aid researchers and engineers in improving measurement reliability in metrology, communications, and sensor applications.
In real-world applications, the signals that would ideally be sinusoidal are affected by a myriad of phenomena that distort it in different ways. Examples of these are the non-linear behavior of systems and devices that introduce extra additive sinusoidal components with different frequencies, additive random noise [9], usually normally distributed, quantization error, introduced by the use of analog-to-digital converters with a finite number of bits, phase noise in the signal generators, and uncertainty in the sampling instant, to name just a few. All those non-ideal phenomena affect the metrological characteristics of the sinewave parameter estimation (bias and precision) and of those quantities that are derived from them like gain, bandwidth, total harmonic distortion, and signal-to-noise ratio. The work presented here deals specifically with the estimation of sinewave amplitude obtained from data points sampled from real signals where the sampling process is affected by jitter, which is random, normally distributed with null mean and known standard deviation. Despite extensive research on signal estimation techniques, including the thorough treatment of estimation theory by Kay [5] on the impact of jitter on digital systems [10,11], there remains a need for comprehensive studies that analytically and experimentally address the impact of sampling jitter on sinusoidal amplitude estimation.
As one would expect, such an important estimation has been the subject of previous publications. In 1987, M. F. Wagdy studied the effect of ADC quantization errors on some periodic signal measurements, including sinusoidal amplitude [12]. More specifically, the effect of sampling jitter, which is the subject of this work, has been studied by the same author, together with S. S. Awad in [13]. It derived an approximate analytical expression for the variance of sinusoidal amplitude estimation as a function of jitter variance. Furthermore, it presented the results of numerical simulations intended to validate the analytical derivations. Those results showed a discrepancy between the theoretical and the simulation values, which can be clearly observed in Figure 5 of [13]. The authors acknowledge this discrepancy, which happens also in the case of the estimation of the initial phase of the sinusoid, by saying in the last paragraph before the conclusions: “Both figures show a noticeable systematic deviation between the theoretical results and simulations. The authors could not determine the reason for such deviation”. It is exactly this deviation that was the driving force behind this paper. The author felt that this warranted further investigation to understand the cause of the discrepancy or, at least, confirm that there was one. This was performed here, not only using numerical simulation but also experimental data obtained from actual sampled data points intentionally corrupted by a controllable amount of jitter. Anticipating what comes next in this work, it will be shown that the analytical derivation is correct and that new data from numerical simulation do indeed agree with that expression. Note that this was tried with different numbers of samples and that even with the low number of samples used [10], just 32, there was no discrepancy. Since the original paper [10] did not supply details regarding the numerical simulation procedure used, it is impossible to pinpoint what went wrong there. Furthermore, the experimental data presented here are also in accordance with the analytical expression. Note that, naturally, the author tried to find another publication where the subject of least squares sinusoidal amplitude estimation in the presence of jitter was addressed. Only one such publication was found, namely one from Shize, Cunming, and Shenghe in 1994 [14]. The analytical expression presented is the same as in [13] and as the one presented here later on, specifically in Equation (27). There seems to be agreement between the numerical and analytical results presented in Figure 1 of [14], but a few numbers of points were used, and no error bars were displayed. In this paper, the discrepancy pointed out here earlier was not mentioned.
The analytical expressions derived here are validated in a wide range of signal and data acquisition parameters using numerically generated data and a Monte Carlo type procedure. Even with the numerical validation carried out, there are some important questions that should be posed, namely how well the assumptions introduced in the mathematical derivations cover the range of cases that one might find in practice using data from the real world. One may ask, for example, does the non-linearity of the data acquisition module affect the results obtained? Is the independence between the signal and the type of noise considered valid? Have all the relevant factors been accounted for in the numerical simulations carried out? To answer these questions, it is important to carry out, also, some validation using real data, which is also performed here. Specifically, the voltage samples acquired and digitized with a data acquisition module are going to be used. The values obtained will be used with a least squares fitting procedure to estimate the underlying sinewave amplitude.
The experimental setup used in this research comprises a data acquisition module and two function generators. The primary function generator produces the main sinusoidal signal, while the secondary generator creates a rectangular clock signal that controls the sampling instants. The estimation procedure is repeated many times, and the estimates made, in this case the sinusoidal amplitude, are used to compute their standard deviation. Note that the amplitude values obtained are not equal due to the random phenomena present in the signals generated and the hardware used. The amount of jitter present will be controlled by phase-modulating the clock signal with normally distributed noise produced by a function generator. It will thus be necessary to calibrate the amount of jitter being introduced prior to carrying out the main study.
In addition to validating the theoretical models, this work provides a detailed presentation of the technical aspects involved in the experimental validation. This includes the implementation of the Monte Carlo procedure, instrument interfacing, programming languages used, and the development of automated measurement systems. These insights are intended to assist other engineers and researchers in replicating and extending the findings presented here.
One should note that the bias of this estimator in the presence of jitter has been addressed in [15,16] and that the work presented here complements the work already published by the Journal of the Franklin Institute on the uncertainty of the initial phase estimation of a sinewave [17].
2. Least Squares Sinusoidal Fitting Procedure
Here, the analytical expression for the standard deviation of the sinewave amplitude estimation in the presence of jitter in the sampling instant is derived. We consider the mathematical model of our periodically sampled sinusoidal signal, namely
where denotes the sample voltages and is the sample index that runs from 1 to . Parameters , , , and are the signal amplitude, initial phase, offset, and angular frequency, respectively. The ideal sampling instants are represented by . In this work, these instants will be affected by normally distributed sampling jitter , with null mean and standard deviation given by .
Due to this random phenomenon under study here, the actual sample voltages become, from (1) and replacing with ,
The sinusoidal stimulus signal is also often affected by phase noise due to non-idealities in the signal generator. This phenomenon can be easily added to our mathematical model using the random variable :
It is thus easy to consider the effect of sampling jitter and stimulus signal phase noise together by using the random variable
Note that in the current work, it is assumed that the phase noise and the sampling jitter are statistically independent. It is considered here that this random variable is normally distributed with null mean and standard deviation . Furthermore, assuming homoscedasticity, that is, the spread of residuals is uniform across the range of values of jitter and phase noise, the standard deviation can be easily obtained from the standard deviation of the jitter and the phase noise using
The samples are then used to estimate the sinusoidal amplitude using a least squares procedure, commonly known as “sine fitting”. The estimated value of the amplitude is designated here with a hat over the symbol: . This estimated amplitude is thus a random variable due to the randomness of and . This mathematical procedure consists of building a matrix given by
and then using it together with the samples to estimate the sinewave parameters using
Note that from the estimated in-phase amplitude, , and the estimated in-quadrature amplitude, , it is possible to obtain the estimated sinusoidal amplitude using
The matrix product in (7) is equal to (9). Considering that the sinusoidal frequency is known, one can use coherent sampling and acquire the signal samples, which cover exactly an integer number of signal periods. Some of the terms in (9) vanish, which results in a diagonal matrix:
Inserting this into (7) leads to
and the estimated sinusoidal amplitude, given by (8), becomes
The standard deviation of this estimated amplitude as a function of the jitter/phase noise standard deviation and number of acquired samples is derived in the next section.
3. Estimated Amplitude Standard Deviation
Having presented the analytical expression used to obtain an estimate of the sinusoidal amplitude, , from the acquired samples , one can proceed to determine the standard deviation of that estimate. To begin, one first determines the variance of the estimative of the square amplitude. Using Equation (7.21) in [18], which makes use of a first-order Taylor series approximation, leads to
where the derivatives are to be evaluated at and . The variances of the in-phase and in-quadrature amplitudes have been determined in [18] and Equations (74) and (75), respectively:
so has the covariance between these two amplitudes, which can be found in Equation (80) of [18]:
It is also necessary to determine the partial derivatives in (13):
and
The expected values can also be obtained from [18] and Equations (20) and (21):
and
The partial derivatives then simply become
and
Inserting these two partial derivatives into (13) leads to
Finally, inserting in (12) the variances given by (14), (15), and the covariance given by (16) leads to
Simplifying this leads to
Combining the trigonometric terms leads to
Further simplification results in
This is the main analytical result of this paper. Note that for small values of jitter and phase noise standard deviation, this expression can be reasonably well approximated by
These derivations allow one to compute the standard deviation of the estimated sinusoidal amplitude given the actual amplitude, the number of samples, and the jitter/phase noise standard deviation.
4. Numerical Simulation
To validate the analytical expressions derived here, and which can be used to determine the standard deviation of the estimated amplitude of a sinusoidal signal from a set of data points corrupted by jitter or phase noise, several numerical simulations have been carried out. These simulations consisted of numerically creating a sinusoidal signal with the desired parameters, extracting a set of data points affected by jitter and/or phase noise with the desired statistics, and fitting, in a least square sense, a sinusoidal model to estimate the signal amplitude, offset, and initial phase. In this work, it is considered that the frequency of the signal is known, and thus it does not have to be estimated from the data points.
In Figure 1, one can see an example with 100 data points obtained from a sinusoid corrupted by phase noise with a standard deviation of 0.1 rad.
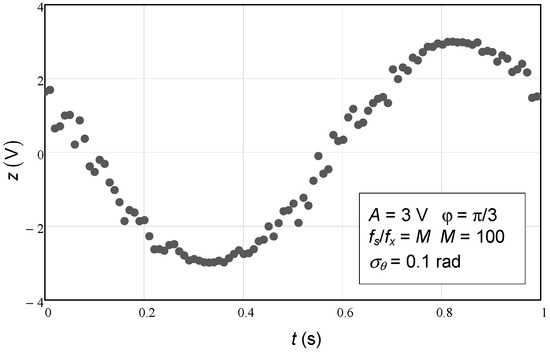
Figure 1.
Simulated data points (100 points) for a sinewave with an amplitude of 3 V, an initial phase of π/3 rad, and a frequency of 1 Hz (fx), corrupted with phase noise/jitter, normally distributed, with null means and a standard deviation of 0.1 rad. The sampling frequency is fs.
By repeating this procedure many times, one obtains several estimates for the sinusoidal parameters. The focus here is on its amplitude. With all those values, one is able to compute their standard deviation and study how it varies with different settings like the number of samples used or the jitter/phase noise standard deviation, for example. In the following, the obtained results are shown.
Figure 2 shows the standard deviation of the estimated amplitude as a function of jitter/phase noise standard deviation. The range of values of the injected phase noise goes from 0 (no phase noise created) to 1 rad. The average of the 2000 values obtained for the sinusoidal amplitude standard deviation, for each value of phase noise standard deviation, is plotted using solid filled circles. The vertical bars represent the confidence intervals for the estimated standard deviation considering a 99.9% confidence level and the case of a chi-squared distribution. The solid line depicts the analytical values given by (27). As observed, these values agree very well with the numerically simulated data, validating the analytical derivations presented here. There is a small discrepancy for higher values of jitter/phase noise standard deviation that deserves further study. This is carried out next.
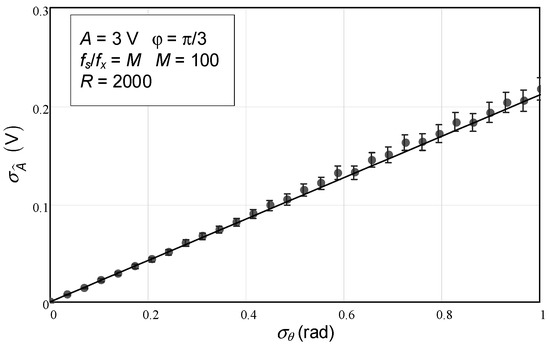
Figure 2.
Standard deviation of the estimated sinewave amplitude as a function of phase noise standard deviation. The circles represent the values obtained with the Monte Carlo analysis. The confidence intervals for a confidence level of 99.9% are represented by the vertical bars. The solid line represents the value given by the theoretical expression (27). The number of repetitions carried out (R) was 2000.
As seen with the numerical simulations presented, the approximations used are quite good if the phase noise standard deviation is lower than 1 rad. In order to justify the applicability of the current work to everyday applications, despite the approximations made, a short list with some typical values of phase noise encountered is presented here:
- Ethernet (Gigabit Ethernet, 125 MHz): 4 mrad [19].
- PCIe Gen3 (8 GHz): 0.1 rad [20].
- Digital Audio (192 kHz DAC): 0.15 mrad [21].
- High-Speed ADC (500 MHz): 0.5 mrad [22].
- FPGA/ASIC Clock Signals (200 MHz): 40 mrad [23].
- HDMI 2.0 (3.4 GHz): 0.8 rad [24].
As can be seen in these random examples, the values of phase noise standard deviation are lower than 0.8 rad and typically much lower. There are, however, some applications where the amount of phase noise is higher, for example:
- 5G NR Base Stations (3.5 GHz): 7 rad [25].
- PLL in RF Transceivers (2.4 GHz): 5 rad [26].
Evidently, the current study is not applicable to these two example applications.
Finally, the number of samples was varied, and the result is presented in Figure 3. One can observe that expression (27) is not so good when the number of samples used is very low (less than 10). In practice, however, the number of samples is generally much higher than this.
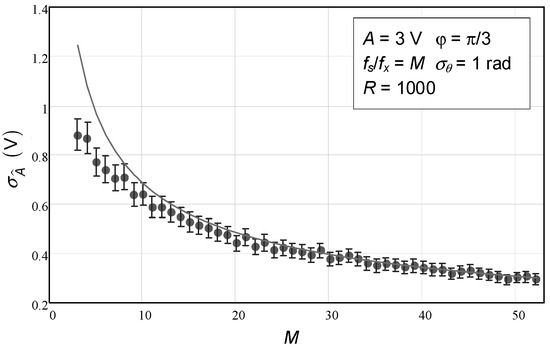
Figure 3.
Standard deviation of the estimated sinewave amplitude as a function of the number of samples. The circles represent the values obtained with the Monte Carlo analysis. The confidence intervals for a confidence level of 99.9% are represented by the vertical bars. The solid line represents the value given by the approximate expression (27).
The results of the Monte Carlo type analysis using numerically simulated data justify the correctness of the analytical expressions derived and give confidence to the user that they can be used in real-life settings. Furthermore, they are valuable to the engineer designing a given acquisition system since they allow one to easily estimate the number of samples that should be acquired to attain a specified confidence in the sinusoidal amplitude estimation.
In the next sections, the analytical expression derived is also validated using experimental data. Calibration of the amount of jitter/phase noise which is injected is carried out.
5. Note on Incoherent Sampling and Different Estimators
Recall that the least squares estimator given in (11) is not the only estimator that can be used to estimate the amplitude of a sinewave from a set of data points. The most rudimentary one would be to find in the data points the highest and the lowest ones and subtract their values:
One can also compute the root-mean-square value of the data points and multiply by the square root of 2:
Another one would be to compute the Discrete Fourier Transform of the data points, , and look for the highest coefficient in the absolute value, :
There are also other possibilities like estimating the envelope of the Hilbert Transform, which is good for modulated signals but computationally complex, or looking for the slope of the data points at zero crossings, which is very sensitive to noise. In cases where the frequency is unknown, one can also use a least squares estimation (four-parameter sine fitting), but in this case it has to be an iterative procedure that tries different possible frequencies, so it is not a closed-form estimator like the three-parameter estimator. This estimator, which is the subject of this work, has the advantages of being simple to compute and uses information from all data points, which reduces estimation uncertainty. It is thus a commonly used estimator in applications where the signal frequency can be assumed to be known, for example, in testing and characterizing systems and devices. In those situations, one typically creates a sinusoidal stimulus signal with known parameters, including frequency, that is applied to the circuit under test. The response from the circuit or system is then sampled and often quantized, leading to a set of samples from which different parameters and figures of merit can be extracted using, among others, least square types of estimations.
The user must therefore choose the number of samples to acquire from the signal, and that is achieved in a way that those samples cover an integer number of periods of the sinewave, which is called “coherent sampling”. To illustrate what happens when this condition is not met, a simple numerical simulation was carried out, whose results can be seen next. In Figure 4, one can see a ser of 100 data points (circles), obtained at a rate of 100 Hz, that came from a sinewave with a frequency of 1.1 Hz. The data points hence do not cover an integer number of periods of the sinewave. The sinewave fitted to the data points using the three-parameter least squares algorithm led to the solid line in the figure, which clearly does not fit well to the data points. This illustrates how inadequate the procedure is when the signal frequency is not known. Recall, however, that the purpose of this work is to study the uncertainty of the sinusoidal amplitude estimation in the presence of phase noise or jitter when the three-parameter sine fitting is used; the purpose is not to compare which procedure is best, nor is it to study what happens when the frequency used in the sine fitting is in error.
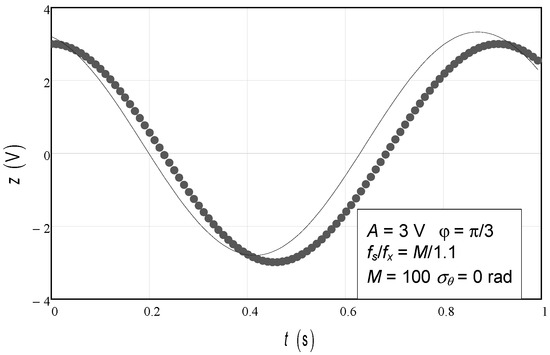
Figure 4.
Simulated data points (100 points) for a sinewave with an amplitude of 3 V, an initial phase of π/3 rad, and a frequency of 1.1 Hz (fx). The sampling frequency (fs) is 100 Hz, and the signal frequency (fx) is 1.1 Hz. There is no phase noise added.
In Figure 5, one can observe the expected value of the sinewave amplitude when the data points cover one to three periods of the sinewave. It is easily observed how severely biased the estimator is in these extreme conditions. The correct value that should be estimated is represented by the solid line (3 V). Once again, one can see how poorly the three-parameter behaves when the chosen frequency is in error. Note that the bias of the estimator has been addressed by the author in [15,16].
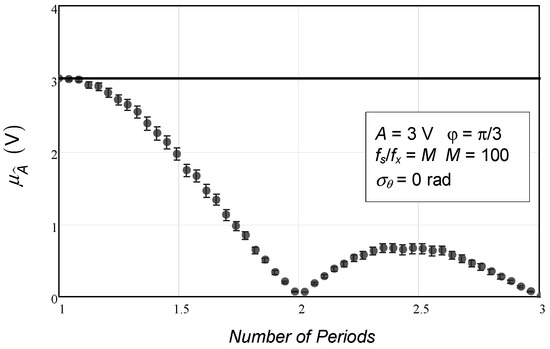
Figure 5.
Expected value of the estimated sinewave amplitude as a function of the number of periods of the sinusoidal signal. The circles represent the values obtained with the Monte Carlo analysis. The confidence intervals for a confidence level of 99.9% are represented by the vertical bars. The solid line represents the value given by the correct value of estimated amplitude (3 V). The number of repetitions made (R) was 100.
The same can be observed in Figure 6, where the standard deviation of the estimated amplitude is plotted as a function of the number of periods covered by the data points. In this situation of the absence of phase noise or jitter (), the correct value would be null, as per Equation (27). This is represented by the solid line at the bottom of the figure.
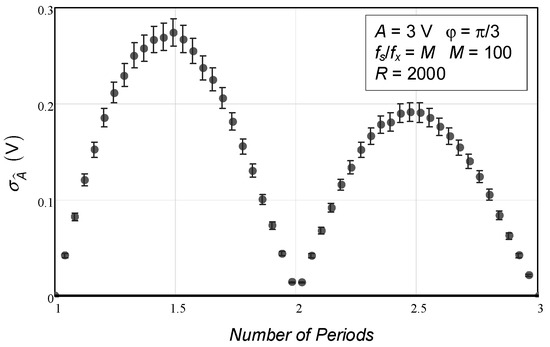
Figure 6.
Standard deviation of the estimated sinewave amplitude as a function of the number of periods of the sinusoid covered by the data points (incoherent sampling). The circles represent the values obtained with the Monte Carlo analysis. The confidence intervals for a confidence level of 99.9% are represented by the vertical bars. The solid line represents the value given by the theoretical expression (27), which in this case is null since there is no phase noise present. The number of repetitions made (R) was 2000.
The conclusion of this section is that the three-parameter least squares procedure is not meant to be used when the signal frequency is not known since it leads to biased estimations and an increase in estimation uncertainty. There are many other estimators that can be used, some which are more simple and some which are more complex. It is worth repeating, however, that this estimator is still of use in many situations, and the study of its estimation uncertainty in the presence of phase noise or jitter is still valid and has produced an analytical expression, namely Equation (27), that can be used to compute the confidence interval of the estimations of sinewave amplitude made with the three-parameter least squares procedure. Undoubtedly, in the future, a similar study could be made regarding the other estimators mentioned above.
6. Experimental Setup
The hardware setup used in this work is composed of three devices and a personal computer: a data acquisition module from National Instruments, model NI USB 6218 connected through a USB interface with the personal computer. This module has an analog-to-digital converter with 16 bits. Although it can operate at different sampling rates, the value used throughout this work was 100 kHz. It also has many input ranges, but here the bipolar ±1 V range was used. Two general purpose function generators were used, one, from Stanford Research, model DS360, was used here to produce a sinusoidal signal, which is applied to channel ai0 of the data acquisition module. The other function generator is an Agilent 33220A general purpose function generator which was configured to produce a rectangular signal that is input into the acquisition module to determine the sampling instants (clock signal). This is connected to the data acquisition module inputs PFI3 and GND (Figure 7). The rectangular signal produced is phase-modulated by an internally generated signal, which is random noise with a normal distribution, and whose peak-to-peak value can be adjusted by the user.
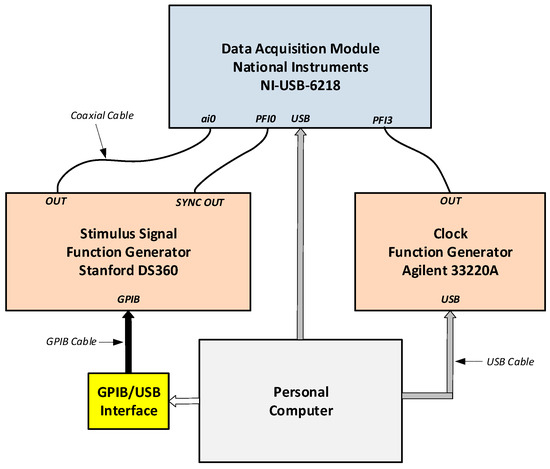
Figure 7.
Block diagram of the test setup where one can observe the personal computer, the data acquisition module, and the two general purpose function generators: one of them (the right one) creates a rectangular signal that controls the instants that the input voltage of the data acquisition module is sampled and which introduces the phase noise, whose effect one wants to study; the other one (the left one) creates a sinusoidal signal that goes to the input of the data acquisition module and creates the sinusoid, whose data points are going to be fit to the sinusoidal model. Those two function generators are controlled by a personal computer using a USB interface or a GPIB interface through a proper USB/GPIB interface module.
A block diagram of the test setup can be observed in Figure 7. There, a personal computer, the data acquisition module, the two function generators, and the connections between the different modules with an indication of the terminal names and pin numbers are shown.
The personal computer is able to control the two function generators. In the case of the function generator producing the clock signal, a USB interface is used. In the case of the other function generator, which produced the sinusoidal stimulus signal, it does not have a USB interface. It only has a general purpose interface bus. It is thus connected to the personal computer using an interface module from Keysight (Santa Rosa, CA, USA).
The hardware setup shown here can create a sinusoidal voltage signal, which is sampled and converted from analog to digital by a data acquisition module that times the sample using a rectangular voltage signal produced by a second function generator. The data points acquired are sent to the personal computer, where software developed using the National Instruments LabVIEW programming language is running, as described in the next section.
7. Software Development
The goal of this work was to create an automated measurement system to study the uncertainty of the least squares sine fitting procedure. In order to achieve this, a personal computer was used which is able to run an application which controls, without user intervention, two function generators. It is able to setup automatically the waveform shapes (sinusoidal and rectangular) as well as their parameters (amplitude, frequency, and DC component). Furthermore, it configures the data acquisition module to acquire a specified number of samples at a chosen rate and send them to the personal computer for storage and processing.
This application was developed entirely by the author and written in National Instruments LabVIEW graphical language. This application is made of several “virtual instruments”, which is the name it is given in this language to the traditionally named “function”. Besides controlling the function generators and gathering the samples, the application is also responsible for the data processing necessary for this study. This includes computing the statistics of the acquired data points, like averages and standard deviations, as well as computing the theoretical expected values and depicting them in a graphical way. This application is also responsible for storing the data and computation results made in text files, which were used to build the charts presented in this paper.
It is too cumbersome and unnecessary, from a scientific perspective, to present and describe all the virtual instruments (VIs) developed, which are more than 100. Instead, only a couple of them will be presented.
Each VI has two parts, namely a “front panel” through which the user interacts with the application, and a “block diagram”, which contains the source code. The application developed has been used by the author to study the uncertainty of several signal processing algorithms and analog-to-digital characterization methods. There are thus many parts which are not relevant to the study at hand. For this reason, the author chose to present here just some cut-outs of the front panels and block diagrams. It serves just for illustration purposes since this paper is not about software development. It is about the precision of sinusoidal amplitude estimation in the presence of phase noise and sampling jitter.
In Figure 8 is the block diagram of the virtual instrument responsible for carrying out the sinewave test where least squares fit of the data points to a sinusoidal model is shown. It starts by computing the setup parameters to use in the subVI named the “Prepare Sinewave Test”. Those parameters are then used to program the function generators in the “Control FGs” subVI. The data acquisition samples are then acquired in the “Acquire or Simulate” subVI, and finally the data points gathered are used to estimate different parameters like sinewave amplitude and initial phase, for example.
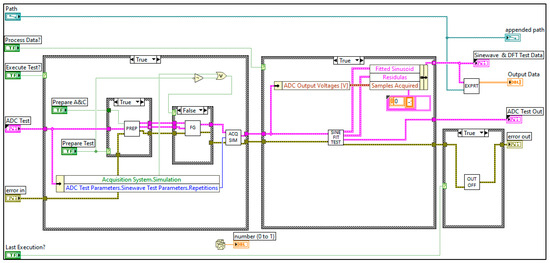
Figure 8.
Image of the block diagram of the virtual instrument that carries out the sinewave test. It starts by computing the setup parameters to be used (left part) in the subVI “Prepare Sinewave Test”, which are then used to program the function generators in the “Control FGs” subVI. The data acquisition samples are then acquired in the “Acquire or Simulate” subVI, and finally the data points gathered are used to estimate different parameters like sinewave amplitude and initial phase.
This VI that was shown in Figure 8 is called inside another VI, which is responsible for repeating the sinewave test a certain number of times, and then the statistics of the results are computed. The block diagram of this VI is shown in Figure 9. One can see a for-loop where the number of iterations is controlled by the input parameter called “Repetitions (N)”. Outside the loop, on the right side of the image, we can see that three subVIs are called to compute the statistics of three parameters that were estimated. In this case, they are the estimated offset, estimated initial phase, and estimated amplitude. Each of these point estimates comes out of the for-loop and becomes an array which is fed into three separate, but identical, copies of the subVI called “Compute Stats & Update”.
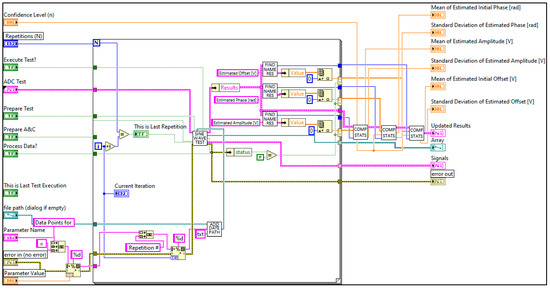
Figure 9.
Image of the block diagram responsible for repeating the test a certain number of times in order to compute the mean and standard deviation of the estimated values of sinewave amplitude, initial phase, and offset.
There is another top-level VI which repeats the sinewave test for different values of clock generator phase noise which is not shown here. It just has a for-loop that changes a parameter, in this case the phase noise amount, and then calls the VI represented in Figure 8. The sinewave amplitude is estimated several times for each value of clock generator phase noise, and the mean and standard deviation of the estimated amplitudes are computed. They are then graphically represented using error bars, as can be seen in Figure 10. Each data point is represented by a circle and an error bar. The more the test is repeated, the shorter the error bars become, but the longer the execution takes. The theoretical expected values are shown with a solid line.
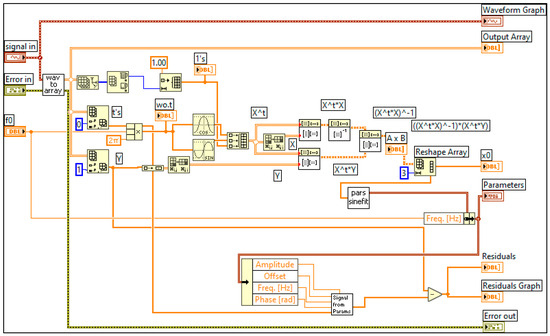
Figure 10.
Image of the block diagram responsible for estimating the sinewave amplitude, initial phase, and DC value given the data points and the sinewave frequency.
The image of the block diagram of the VI that carries out this repetition is presented in Figure 8. It has a for-loop with N iterations inside, which the sinewave test subVI is called. The value of the desired estimates is obtained from the test results. In this case, it is the amplitude, initial phase, and offset. The set of values obtained is then input the subVIs named “Compute Stats & Update Results” in order to compute the means and standard deviations of the estimates, and from there, the error bars of the different estimates.
Figure 10 shows the block diagram of the virtual instruments that compute the sinewave amplitude, initial phase, and DC offset (3-parameter sine fitting) given the data points and the sinusoid frequency. In essence, it implements in LabVIEW the computations described in Equation (7).
Each data point represented in Figure 11, including the error bars, is obtained by repeating the least square sine fitting test many times. The horizontal axis, labeled “Phase noise [º]”, is the phase noise standard deviation , as seen in Equation (27), for example.
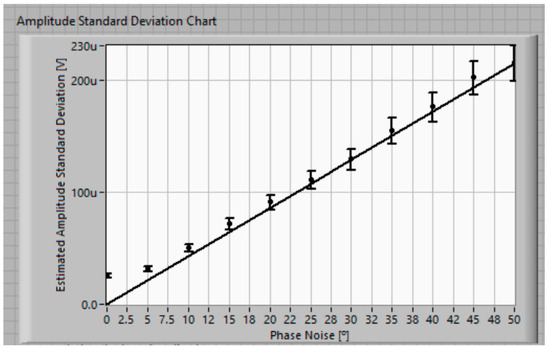
Figure 11.
Image of the front panel portion that shows the result of amplitude estimation as a function of the clock generator phase noise. Each data point is represented by a circle and an error bar. The theoretical expected values are shown with a solid line.
This section is just meant as a quick illustration of the software developed in the context of this research work. Many of the VIs created and used are not covered here. This is not meant to be an exhaustive description of the software created.
The next section presents the experimental data results and compares them with the analytical expressions derived previously.
In the following (Figure 12), a compact pseudocode listing is presented that illustrates the operation of the application developed.

Figure 12.
Pseudocode of the application developed using LabVIEW.
8. Experimental Results
The goal of the present study was to experimentally validate the analytical expression that relates to the standard deviation of the estimate of sinusoidal amplitude obtained by fitting a set of data points to the amount of jitter present in the sampling instants.
The experimental setup described earlier was used to determine the precision of the amplitude estimation for different amounts of jitter. The standard deviation of the sampling jitter was controlled by phase-modulating the sampling clock with normally distributed random noise. This was achieved by using the functionality of the Agilent 33220A function generator, which has the capability to produce a rectangular signal with chosen frequency and amplitude. In the present work, a rectangular signal with 100 kHz frequency and an amplitude from 0 to 5 V was used. Furthermore, this generator has the capability of modulating several parameters of the main signal (like amplitude and phase) using a second internal generator. This secondary generator can produce a periodic signal with different shapes (sinusoidal, triangular, rectangular, etc.) as well as random noise. In the present study, random noise with a normal distribution was used. The phase of the main rectangular signal was thus phase-modulated by a second normally distributed random signal. This rectangular signal was then used in the data acquisition module to control the timing of the sample acquisition.
The clock signal used was a rectangular wave phase-modulated by normally distributed random noise with a range of peak-to-peak values from 0 to 50º in order to control the amount of jitter present. For each value of jitter, the sine fitting test was carried out using a set of 100 points sampled from a sinewave produced by another function generator (Stanford Research DS 360) with an amplitude of 900 mV and a frequency of 5 kHz. For each value of phase noise setting, the sine fitting test was repeated 500 times, and the confidence interval for the estimated amplitude was computed.
The estimate of the standard deviation was obtained from the square root of the sample variance using
as per [13], Equations (9)–(13). Note that the variance of the population is unknown. The confidence interval for the standard deviation estimation is thus
where the confidence level used (γ) was 99.9% and . The number of data points (n) was 500. These confidence intervals were used to represent the error bars in the experimental data obtained, which are depicted in Figure 13, Figure 14 and Figure 15.
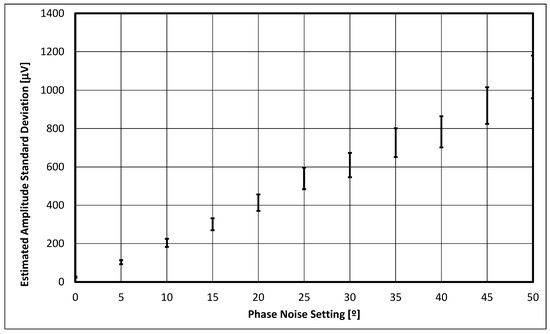
Figure 13.
Chart containing the experimentally estimated sinewave standard deviation as a function of the injected amount of phase noise. The number of data points used was 500, and the confidence level used was 99.9%.
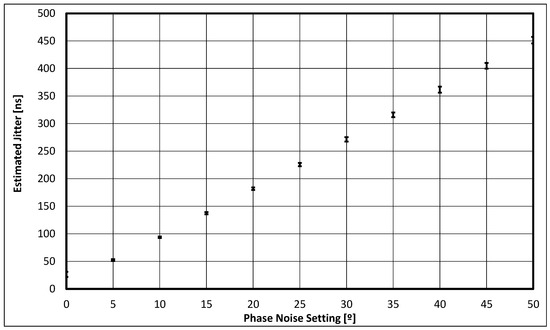
Figure 14.
Representation of the relation between the measured values of phase noise standard deviation and the configured values of phase noise standard deviation. The number of data points used was 50, and the confidence level used was 99.9%. The low-frequency value used was 10 Hz, and the high-frequency value used was 10 kHz.
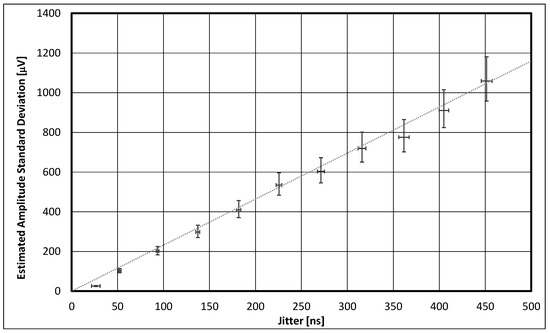
Figure 15.
Experimental estimated amplitude standard deviation as a function of sampling jitter present. The error bars represent the confidence intervals for the estimation of both the amplitude estimation carried out with the least squares sine fitting method and the estimated amount of jitter present. The dashed line represents the straight line that best fits the data points. The number of data points used was 500, and the confidence level used was 99.9%.
Note that the “Phase Noise Setting [º]” is not the same as the jitter (or phase noise) standard deviation. The relationship between the two has to be determined. That is what is experimentally carried out next.
To estimate the amount of jitter present, the test recommended in the IEEE Std. 1057-2017–IEEE Standard for Digitizing Waveform Recorders [27], namely the one in Section 4.9.2.2, was used. In this test, one applies a low frequency () sinewave to the waveform digitizer and computes the root-mean-square error from the residuals obtained from subtracting the data points from the least squares fitted sinewave, obtaining . One then repeats the data acquisition for a high frequency compared to the waveform digitizer bandwidth () and computes a second value of root-mean-square error, obtaining . The amount of jitter that is present is then estimated using
where A is the sinusoid amplitude.
The values obtained for the different function generator settings of phase noise modulation are the ones represented in Figure 14 using, again, error bars to represent the confidence intervals for the same 99.9% confidence level and 50 repetitions (). The low-frequency value used was 10 Hz, and the high-frequency value used was 10 kHz. The amplitude was 900 mV, and the number of acquired samples was 100 at a rate of 100 kHz.
We are thus now able to represent the estimated amplitude standard deviation as a function of jitter. This can be seen in Figure 15. The vertical and horizontal error bars represent the confidence intervals for the estimated sinusoidal amplitude and jitter, as shown in the previous two figures. One can observe a linear relationship between the two variables, as expected from Equation (28).
A straight line was fitted, in a least squares sense, to the data points, and the following relation was obtained:
Comparing this with the expected relation given in (28), one obtains
with
This straight line is depicted in Figure 15 using the dotted trace. A discrepancy was found between the slopes of the analytical and experimental relationships. This discrepancy is given by the coefficient , which was expected to be .
This 16% discrepancy may be due to several phenomena. The method used to measure the amount of jitter introduced was the one suggested in the standard IEEE 1057. This method assumes that when the stimulus signal frequency changes (10 Hz and 10 kHz were used), the sinewave generated has all the same properties, apart from frequency. It assumes that the sinewave amplitude remained the same, which is not guaranteed. Furthermore, the stimulus signal is “filtered” by the frequency response of the data acquisition board. This response might not be perfectly flat for those frequencies. Another problem is that the sinewave generated might have some harmonic distortion, and thus the energy inside the bandwidth of the data acquisition board might be different for the two frequencies. This discrepancy should be the subject of future research to better understand its origin.
9. Conclusions
In this study, a straightforward analytical expression was developed to determine the standard deviation of the estimated amplitude of a sinewave using the least squares method in the presence of jitter or phase noise. The derivation employed a first-order Taylor series approximation, which was validated through both numerical simulations and experimental data using a Monte Carlo approach. The resulting expression not only facilitates the calculation of confidence intervals for sinusoidal amplitude estimation but also aids in determining the number of signal samples required to achieve the desired level of estimation precision.
The experimental setup was described in detail, comprising two function generators and a data acquisition module. The software, developed using National Instruments LabVIEW, was briefly outlined, though its complexity limited a thorough explanation. The level of jitter/phase noise was controlled by phase-modulating the clock signal that times the sample acquisition in the data acquisition module. The injected jitter/phase noise followed a zero-mean normal distribution with an adjustable standard deviation.
The Monte Carlo method was utilized to estimate the standard deviation of the amplitude, repeated across various levels of injected jitter/phase noise. The results revealed a nearly linear relationship between the estimated sinusoidal amplitude and the standard deviation of jitter. However, a 16% discrepancy in the slope of this relationship was observed, the cause of which remains unexplained. It is important to note that several non-ideal factors were present in the experimental setup, including additive voltage noise, quantization error, intrinsic jitter in the sampling module, phase noise in the stimulus signal and clock generators, and limited noise bandwidth in both the function generator and data acquisition module. These factors are believed to be independent of the injected jitter/phase noise, contributing a constant offset to the experimental results rather than an error proportional to the jitter/phase noise standard deviation. Additionally, these factors affect both the sinewave amplitude estimation and the jitter/phase noise estimation processes. The unaccounted-for non-ideal phenomena must be proportional to the amount of jitter/phase noise introduced. Notably, no discrepancies were observed in the numerical simulations, reinforcing the validity of the analytical derivations and the developed software. This suggests that the discrepancy is likely due to an unaccounted hardware-related phenomenon not addressed in this work.
The main result of this work is the derivation of the analytical relationship between phase noise/jitter standard deviation and sinusoidal amplitude estimation precision. A more complex but more accurate analytical expression was obtained, namely Equation (26). A simpler but approximate expression was obtained for the case of low phase noise/jitter standard deviation. This expression, namely Equation (27), shows a linear relationship between phase noise and jitter standard deviation and sinusoid amplitude estimation standard deviation. Furthermore, the current document explained in detail the experimental setup used and the steps taken to calibrate the amount of phase noise present. This can certainly be used by other researchers performing similar experiments involving the use of phase noise or jitter in the test setups.
In the future, one might continue the work presented here by considering, for example, the uncertainty in both amplitude and initial phase in the presence of jitter or phase noise when using the four-parameter sine fitting algorithm where the signal frequency is not known and must be estimated using an iterative procedure. The same goes for the other estimators mentioned in Section 5. Other endeavors that one might pursue, making use of this work, include the uncertainty of the estimation of other signal parameters like signal-to-noise ratio (SNR) or signal-to-noise and distortion (SINAD), or even the uncertainty of parameters associated with devices or circuits that are inferred from the sine fitting of data points, for example, total harmonic distortion (THD) or amplifier gain.
One hopes that this work might be useful to others involved in experimental applications of the sine fitting procedure and also in the experimental validation of the uncertainty of sine fitting parameters and derived quantities and their dependence on non-ideal factors.
Funding
This work is funded by FCT/MECI through national funds and when applicable co-funded EU funds under UID/50008: Instituto de Telecomunicações.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
There are no data available beyond what are presented in this document.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Rao, S.S. Mechanical Vibrations, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004; ISBN 978-0130489876. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996; ISBN 0-13-374943-6. [Google Scholar]
- Dally, J.W.; Riley, W.F.; McConnell, K.G. Instrumentation for Engineering Measurements, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1993; ISBN 978 0471551928. [Google Scholar]
- Queirós, R.; Alegria, F.C.; Girão, P.; Cruz Serra, A. A Multi-Frequency Method for Ultrasonic Ranging. Ultrasonics 2015, 63, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Volume I: Estimation, 1st ed.; Pearson: London, UK, 1993; ISBN 978-0133457117. [Google Scholar]
- Carbone, P.; Schoukens, J. A Rigorous Analysis of Least Squares Sine Fitting Using Quantized Data: The Random Phase Case. IEEE Trans. Instrum. Meas. 2014, 63, 512–530. [Google Scholar] [CrossRef][Green Version]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Händel, P. Properties of the IEEE-STD-1057 four-parameter sine wave fit algorithm. IEEE Trans. Instrum. Meas. 2001, 49, 1189–1193. [Google Scholar] [CrossRef]
- Martino, M.; Losito, R.; Masi, A. Analytical Metrological Characterization of the Three-Parameter Sine Fit Algorithm. ISA Trans. 2012, 51, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Balestrieri, E.; Picariello, F.; Rapuano, S.; Tudosa, I. Review on jitter terminology and definitions. Measurement 2019, 145, 264–273. [Google Scholar] [CrossRef]
- Reinhardt, V.S. A Review of Time Jitter and Digital Systems. In Proceedings of the 2005 IEEE International Frequency and Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005; pp. 38–45. [Google Scholar] [CrossRef]
- Wagdy, M.F. Effect of Quantization Errors on Some Periodic Signal Measurements. IEEE Trans. Instrum. Meas. 1987, 36, 983–989. [Google Scholar] [CrossRef]
- Wagdy, M.F.; Awad, S.S. Effect of Sampling Jitter on Some Sine Wave Measurements. IEEE Trans. Instrum. Meas. 1990, 39, 86–89. [Google Scholar] [CrossRef]
- Shize, G.; Chunming, L.; Shenghe, S. The Effect of Sampling Noise on Band limited Periodic Signal Measurement. In Proceedings of the Instrumentation and Measurement Technology Conference, Hamamatsu, Japan, 10–12 May 1994. [Google Scholar] [CrossRef]
- Alegria, F.C. Contribution of Jitter to the Error of Amplitude Estimation of a Sinusoidal Signal. Metrol. Meas. Syst. 2009, XVI, 465–478. [Google Scholar]
- Alegria, F.C.; Serra, A.C. Gaussian Jitter-Induced Bias of Sine Wave Amplitude Estimation Using Three-Parameter Sine Fitting. IEEE Trans. Instrum. Meas. 2010, 59, 2328–2333. [Google Scholar] [CrossRef]
- Alegria, F.C. Uncertainty of the initial phase estimation of a sinewave in the presence of phase noise, additive noise or jitter. J. Frankl. Inst. 2024, 361, 107116. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991; p. 156. ISBN 978-0070484771. [Google Scholar]
- Alegria, F.C.; Xie, L.; Pasadas, D. Study of the Bias of the Initial Phase Estimation of a Sinewave of Known Frequency in the Presence of Phase Noise. Sensors 2024, 24, 3730. [Google Scholar] [CrossRef] [PubMed]
- IEEE Standard 802.3-2018; EEE Standard for Ethernet. IEEE: Piscataway, NJ, USA, 2018; ISBN 978-1504450904.
- PCI-SIG. PCI Express Base Specification Revision 3.0; PCI-SIG: Beaverton, OR, USA, 2002. [Google Scholar]
- Pohlmann, K.C. Principles of Digital Audio, 6th ed.; McGraw-Hill: New York, NY, USA, 2010; ISBN 978-0071663465. [Google Scholar]
- Razavi, B. Principles of Data Conversion System Design; Wiley-IEEE Press: Hoboken, NJ, USA, 1995; ISBN 978-0780310933. [Google Scholar]
- Pratap, M.; Enge, P. Global Positioning System: Signals, Measurements, and Performance; Ganga-Jamuna Press: Singapore, 2006. [Google Scholar]
- HDMI 2.0 Specification; HDMI Forum Technical Working Group; HDMI Forum, Inc.: Beaverton, OR, USA, 2013.
- 3GPP TS 38.104, NR; Base Station (BS) Radio Transmission and Reception. ETSI: Sophia Antipolis, France, 2018.
- IEEE Std 1057-2017; IEEE Standard for Digitizing Waveform Recorders in IEEE Std 1057-2017 (Revision of IEEE Std 1057-2007). IEEE: Piscataway, NJ, USA, 2018. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).