1. Introduction and Background
Atmospheric dispersion (or transport) models are mathematical equations that are used for the prediction of movement, i.e., advection, and spread, i.e., dispersion, of pollutants in ambient air. Such models are used to study the transport of various pollutants, e.g., trace gases, and airborne particles (aerosols). One major application of atmospheric dispersion models is the evaluation of the impact of emissions from industrial sources, e.g., chimneys, how such emissions are diluted in the atmosphere, as well as how they spread, to assess the risk of exposure in the case of hazardous releases. Another application of such models is to assess pollution within street canyons, arising from the emissions of motor vehicles.
There are several different types of atmospheric dispersion models. Holmes and Morawska [
1] reviewed those models that are specifically valid for airborne particles. More recently, Khan and Hassan [
2], and Johnson [
3] gave a detailed review of developments in air quality modeling, in general. In their reviews, they discussed the various types of modeling approaches, including steady-state Gaussian plume models, which are core to the current study. Snoun et al. [
4] focused their review on Gaussian atmospheric dispersion models and their applications. Woodward et al. [
5] investigated specifically the applicability of Gaussian models to near-field dispersion. Gaussian models are the ones that utilize, in their calculations, the plume model equation discussed in this work.
Gaussian models are commonly used to simulate atmospheric pollutant dispersion near sources because they provide an efficient compromise between reasonable accuracy and manageable computational time [
6]. Such models estimate the concentration of a pollutant at any point in three-dimensional space from knowledge of the emission rate of the pollutant, meteorological conditions, and the distance from the source of emission. These models are commonly used primarily because they are easy to implement and predict concentrations over a wide range of distances from the source.
Two advantages of the Gaussian plume model for the dispersal of air pollutants are its computational simplicity and the fact that phenomena such as reflection of the plume at boundaries, and plume depletion by dry deposition and gravitational settling can be incorporated with ease. These phenomena are particularly important in the case of the dispersal of airborne particles (see, for example, [
7]).
When a Gaussian plume is confined between two parallel boundaries, multiple reflections take place. The latter process gives rise to a modified concentration field as compared to that without boundaries. The effluent associated with a Gaussian plume that is caught up between a pair of parallel reflecting boundaries will undergo multiple reflections, which will enhance the concentration due to restrictive dispersal. Gaussian models that do not consider multiple reflections at boundaries, tend to underestimate the airborne concentration of the pollutant being emitted, especially beyond a certain downwind distance from the source of pollution.
One typical example is when the pollution source lies between an inversion cap or lid, i.e., the bottom of an atmospheric stable layer aloft, associated with an elevated temperature inversion, and the ground. In this case, the two horizontal parallel boundaries define the atmospheric mixing zone. It is worth noting that, one of the boundaries, i.e., the inversion cap or lid, is not always well defined (except for an abrupt temperature inversion) and, hence, the effect of multiple reflections of the plume is not always evident. In this case, reflections are nowhere near complete due to the diffusive nature of the upper boundary, i.e., the inversion cap or lid. The situation can give rise to overprediction of the calculated concentrations, so that the effect of reflections on the concentration field should be implemented with caution. This is an example of horizontal parallel reflecting boundaries. The subject was treated in some detail by Pasquill [
8].
An example of vertical parallel reflecting boundaries is the facades of buildings confining a roadway on either side, making up the geometry of a street canyon or urban notch. In this case, reflections are more well-defined due to the rigid nature of the boundaries, i.e., building facades that confine the roadway. Given the restrictive environment, i.e., short width of the street canyon (especially, in comparison to building height), multiple reflections take place in a relatively short period of time. This is in contrast with the previous case where the two boundaries are the ground and the inversion cap or lid, which are separated by a (mixing) length or height, of the order of hundreds of meters.
There are many published roadway-type, or more specifically, street canyon air quality models that simulate dispersion of pollution through the application of the Gaussian dispersion model equation. Some classical examples include the Canyon Plume Box (CPB) model [
9], the Operational Street Pollution model (OSPM) [
10], and the Street Level Air Quality (SLAQ) model by Micallef and Colls [
11]. Vardoulakis et al. [
12] provided a detailed review of street canyon air quality models, some of which utilize the Gaussian plume dispersion model equation.
There are various methods that one can employ to correct for multiple reflections. One way is to utilize the concept of image sources. In this work, the Gaussian plume model equation corrected for multiple reflections at parallel boundaries, is rewritten by utilizing knowledge and properties of the Jacobi theta functions, which are discussed in the following section.
2. Two Preliminary Mathematical Results with Proofs
Jacobi theta functions are discussed in textbooks on modern analysis, functional analysis, and special functions (see, for example, [
13,
14,
15]). There are four Jacobi theta functions. These are
,
,
, and
, functions of parameters
and
, which can be real or complex numbers. They are defined by infinite series as given in the following equations:
where
is an integer and a dummy variable. It is worth noting that
governs the periodicity, while
is related to the size of the amplitude of the resulting function.
Schiefermayr [
16] and Singh et al. [
17] discussed some very interesting properties of such functions, which go beyond what is normally found in textbooks of mathematical analysis.
The Jacobi theta function of the third kind, i.e., , is the one which will be encountered most in the following discussion. Before embarking on the main derivation in this work, two useful results (lemmas) are first derived. The following are the derivations of these two preliminary results needed in the main discussion here (and in the subsequent section).
The first preliminary result states that the Jacobi theta function of the third kind can be written as
where
.
The following is proof of this result.
But,
, and since the sine and cosine functions are odd and even functions, respectively, we have,
and
. Therefore, for
, one obtains
and for
, the following result holds
Substituting Equations (7) and (8), in Equation (6) gives
By using the standard definition of the Jacobi theta function of the third kind, given in Equation (3), simple algebra leads to the following equation
The second preliminary result is the following:
where the
-function is defined as hereunder,
and
where
is an integer and a dummy variable.
The following is proof of this result.
Consider the
th term of the series given by Equation (12), i.e.,
Expanding the right-hand side of the equation gives
which leads to
Summing over
from
to
gives
where
. From Equation (5),
Comparing the right-hand side of Equation (15) with
, gives
and
. Substituting for
and
in Equation (15) gives
Substituting in Equation (14) gives
as required.
By similar arguments, one can prove that
Hitherto, no physical meaning has been ascribed to the various parameters used in the above derivations, but the symbols were chosen keeping in mind that in what follows, the obtained mathematical results are applied to the Gaussian plume model equation for atmospheric dispersion.
3. Mathematical Derivation of the Main Result, and Discussion of Its Limitations
The following is a derivation of an expression for the summation of concentrations from multiple reflections of a Gaussian plume confined by a pair of horizontal parallel (reflecting) boundaries at (ground) and (atmospheric temperature inversion cap or lid). Consequently, defines the atmospheric mixing height (or depth). The emission source is assumed to be located at Cartesian coordinates, , and, hence, at a height above ground, where . The source is assumed to be continuous and time-independent (state–state scenario). This framework is used when calculating the contribution from point sources such as stacks/chimneys. It is worth noting that the derivation for the case of a vertical pair of reflecting boundaries, as in the case of a street canyon, is mathematically analogous to the following.
In defining the boundaries and source location, the Cartesian reference frame is used so that the Gaussian plume model, with no reflections and with advection in the y-direction, is consistently given by
where
is the concentration (mass per unit volume) at the location having Cartesian coordinates
,
is the emission rate (mass per unit time),
is the advection speed (length per unit time), which is the average over the considered height, and
and
are the horizontal and vertical dispersion parameters (length), respectively. The latter two parameters define the width of the (Gaussian) concentration distribution as a function of distance in the x- and z-directions, respectively, and orthogonal to advective flow (the latter, in the y-direction). The model is only valid for certain conditions, which are discussed in detail by Lyons and Scott [
18].
Note that, if the origin of the reference frame coincides with the source, then the expression on the right-hand of Equation (19) would simplify to the following:
This is equivalent to having the source located at the ground level. To account for (single) reflection at the ground, the method of images is generally used. In this case, ground level reflection is modeled by a virtual image source at a distance
below the ground surface. Equation (19) is then modified to
Note that an extra term is introduced in Equation (19) to give Equation (21). This term accounts for the virtual image source. To account for reflections at the inversion cap, i.e., to account for multiple reflections, Equation (21) is modified to the following (see, for example, [
19]):
where
is an integer and a dummy variable.
The model equation now involves two infinite series that account for multiple reflections at the two reflecting boundaries confining the Gaussian plume within the bottom-most layer of the atmosphere, defined by the ground and the atmospheric temperature inversion cap or lid. For computational purposes, a definite summation expression is preferred, as it makes it easy to translate into computer code.
Using Equation (12), Equation (22) can be rewritten using the
-function,
This can be rewritten in terms of the Jacobi theta function of the third kind, using Equations (17) and (18) to give
where
has been defined previously.
In the following, a definite expression will be derived for the
-function. If the
parameter in the Jacobi theta function of the third kind,
, can be expressed as
where
is a (constant) complex number whose imaginary part is positive, then by Landberg’s transformation [
13] gives
The prime (′) merely indicates that
is not replacing the
parameter but that Equation (27) defines
. Hence,
In anticipation of what follows, and considering Equation (13), let
Equating the right-hand sides of Equations (25) and (28) gives
Once again, in anticipation of what follows, let
Substituting Equations (29) and (30), in Equation (26) gives
Using Equations (25), (27)–(30) to transform from
to
on the left-hand side of Equation (31), and Equations (25), (27) and (32) to transform
to
on the right-hand side of Equation (31),
which leads to the following:
Replacing the left-hand side of Equation (33) by that of Equation (17), one obtains
Similarly, one obtains the following:
The next step in the derivation is to expand the following two functions: and .
Consider Neville’s theta function,
, corresponding to the Jacobi theta function of the third kind [
20], namely,
Expressing
as an infinite product [
20] gives
where
and
are complementary real numbers such that
and
. Putting (
z + H) = 0 in Equations (36) and (37) gives
and
respectively. Equations (38) and (39) imply that
Substituting Equation (40) in Equation (37) gives
From Equations (36) and (41) one obtains
From the definition of the Jacobi theta function of the third kind, i.e., Equation (3),
and for
, this equation reduces to
Equations (42) and (43) yield
Adding Equations (45) and (46) gives
Now,
. Hence,
Substituting in Equation (47) gives
Adding Equations (34) and (35) gives
Substituting the left-hand part of Equation (49) in Equation (50) gives
where from Equation (32),
. Substituting Equation (51) in Equation (23) gives
Equation (52) is the Gaussian plume model equation for atmospheric dispersion corrected for multiple reflections at parallel boundaries, which avoids the use of infinite series, and, hence, facilitates computation and coding, in general. It is worth noting that, by avoiding the infinite series, the issue of divergence (or lack of convergence) is eliminated.
4. Numerical Testing and Comparison of the Gaussian Plume Model Equations
Inevitably, any form (with or without reflection, etc.), of the Gaussian plume model equation will involve the relevant dispersion parameters. Pursuing the case discussed in the previous two sections, let the Gaussian plume be confined by a pair of horizontal parallel (reflecting) boundaries at (ground) and (atmospheric temperature inversion cap or lid). Consequently, defines the atmospheric mixing height (or depth).
If advective flow is in the y-direction, then the dispersion parameters of relevance would be and , each having units of length. These two parameters define the width of the (Gaussian) concentration distribution in the x- and z-directions. The dispersion parameters are a function of downwind distance (in the y-direction) from the source of pollution. Consequently, each of the dispersion parameters is orthogonal to advective flow (in the y-direction).
Gaussian dispersion parameters are very important and necessary in the calculation of the concentration field associated with the pollution plume. They are dependent on atmospheric conditions at the dispersion site. These basic ideas are clearly discussed in standard reference books, such as that by Zannetti [
21]. There are various formulae and semi-empirical expressions that can be used for the computation of the dispersion parameters. In this regard, pioneering work was accomplished by Weber [
22] and Pasquill [
23], amongst others. A full discussion on the topic concerning the calculation of the dispersion parameters is beyond the scope of the current study, but the reader is directed to the work by Miller [
24], which examines Gaussian plume dispersion parameters for rough terrain, which is somewhat more complicated than the open (or non-rough) case. Two other important and recent studies that compare various schemes used for the computation of the Gaussian dispersion parameters (also referred to as sigmas) are those of Sharan et al. [
25] and Essa et al. [
26]. The former considers low wind conditions, while the latter includes also moderate wind regimes.
The adopted methodology, in the current study, is the one from McElroys’ correlations and is detailed in [
27], and more recently by Essa et al. [
26]. This suffices for the intents and purposes of the numerical testing being carried out here. Specifically, this class of (power law) formulations for the dispersion parameters is discussed in substantial detail by Fields and Miller [
28]. In the following paragraph, the mathematical equations used in the current numerical testing are explicitly discussed for clarity.
In the numerical testing, Gaussian dispersion parameters,
and
(also referred to as sigma-x and sigma-z, respectively), are given by the mathematical equations:
and
where
,
,
and
take values that are dependent on atmospheric (Pasquill-type) stability, i.e., A (extremely unstable conditions) to F (moderately stable conditions), as given in
Table 1. In
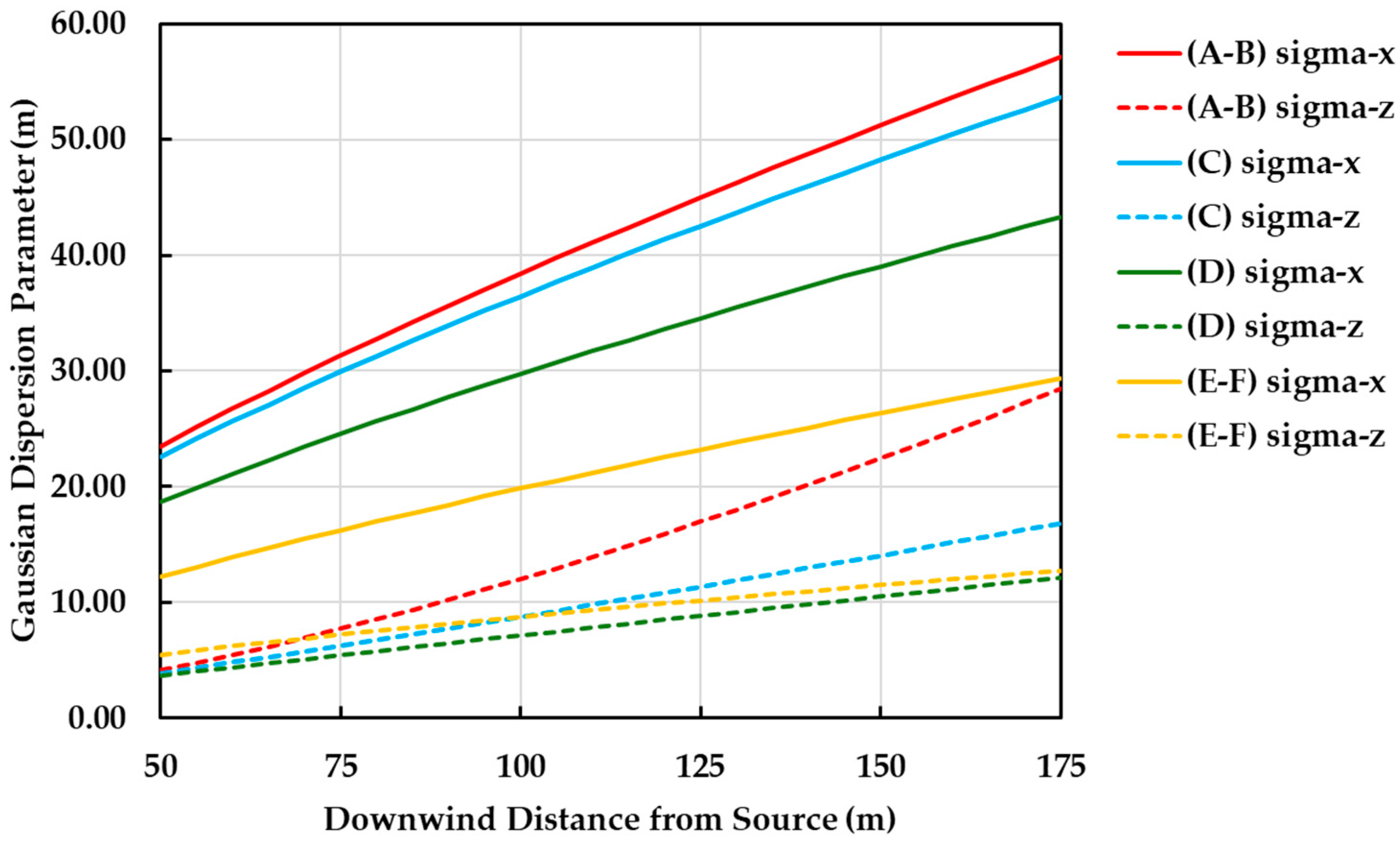
Figure 1, the actual Gaussian dispersion parameters,
and
(also referred to as sigma-x and sigma-z, respectively), are plotted as a function of downwind distance from the source of pollution, for the various atmospheric (Pasquill-type) stability classes.
One observes that the spread or dispersion of the pollutant is more substantial in the z-direction as compared to the x-direction. This is in keeping with the relevant physical processes. In the z-direction, thermal buoyancy plays an important role, especially given that the plume’s temperature tends to be higher than the ambient (surrounding) temperature. Diffusion occurs in both directions. Downwind from the source of pollution, the dispersion parameters are expected to increase given that the spread or dispersion of the pollutant is a continuous process.
Apart from the Gaussian dispersion parameters, the other important and necessary parameter for the determination of the concentration field associated with the Gaussian plume is the atmospheric mixing height, .
There are various techniques and methodologies for the determination of the said parameter. One common relevant experimental method involves the use of a ceilometer. This is a ground-based remote sensing technique. Eresmaa et al. [
29] described in some detail a novel method for estimating the atmospheric mixing height based on ceilometer measurements. They also tested their technique against commonly used methods for determining the atmospheric mixing height. In fact, they carried out a comparison of atmospheric mixing height estimated using ceilometer data and radio soundings. Eresmaa et al. [
30] developed a three-step method for estimating the atmospheric mixing height from vertical profile backscattering coefficient data obtained using ceilometers. Martano [
31] described an algorithm for the calculation of the atmospheric mixing height in coastal areas. The algorithm is simple and uses wind, temperature, momentum flux, and heat flux time series as input data. Wright et al. [
32] discussed in detail the use of satellite observations for the estimation of the atmospheric mixing height in the Western United States. Feng et al. [
33], in developing their methodology, also used satellite data. Specifically, they used atmospheric profiles from the MODerate Resolution Imaging Spectroradiometer (MODIS) instrument onboard the NASA-Aqua satellite, to achieve high spatial resolution.
Most existing parameterizations for the atmospheric mixing height have been developed for homogeneous terrain conditions. It is worth noting that the urban boundary layer exhibits many differences in comparison with the rural homogeneous boundary layer due to the larger surface roughness and increased surface heating, and because of the horizontal inhomogeneity of certain meteorological fields. Baklanov et al. [
34] made recommendations on the applicability and improvement of various pre-processors, schemes, and models for atmospheric mixing height that are specific to urban areas.
Over the years, efforts were made to achieve standardization of the methodology for the determination of the atmospheric mixing height. The work by Fearon et al. [
35] was an effort in this direction, and it also summarizes the main four methods used for estimating the atmospheric mixing height.
For the intents and purposes of the current numerical testing, a fixed, arbitrary but meaningful value of 300 m was adopted for the atmospheric mixing height.
With regard to atmospheric conditions and source emission characteristics that can be adopted for numerical testing, there are an infinite number of possible data sets or combinations. In the current study, only one set was considered, as proof of concept. Further numerical testing and experimental evaluation are beyond the scope of the current study and will constitute the main subject matter of subsequent research projects and articles. Nevertheless, the numerical testing and comparison accomplished here suffice to show that further work is indeed merited. In the following paragraphs, the adopted set of input data are detailed, and the associated output is discussed.
For the numerical testing, the adopted conditions were chosen so as to emulate typical atmospheric daytime conditions encountered in the Mediterranean region. Strong sunshine and a wind speed of 5 ms−1 were assumed. These conditions are associated with atmospheric (Pasquill-type) stability class C. As stated earlier, the atmospheric mixing height was assumed to be equal to 300 m. The height of the point source of emission, e.g., chimney, (also known as stack height) was assumed to be 18 m, and the emission rate was taken to be 100 gs−1. The airborne concentration was calculated at a height of 18 m, i.e., at the same level of release of the effluent, and along the center-line of the plume, at 10 m intervals starting from a downwind distance of 200 m from the source of pollution. The near-field was avoided, knowing that Gaussian plume atmospheric dispersion models are not the ideal choice for regions that are close to the source of pollution.
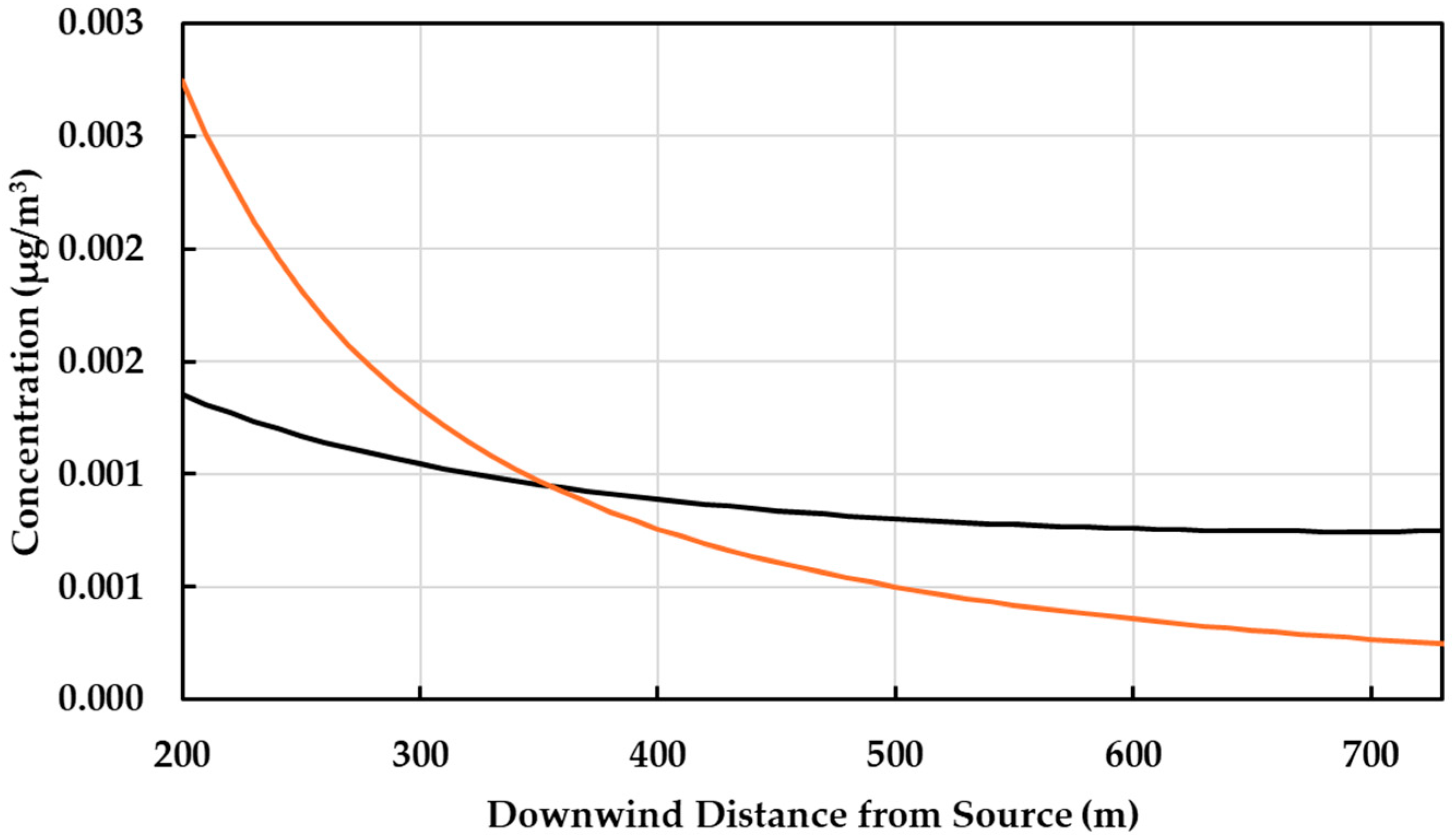
The Gaussian plume model equation for atmospheric dispersion, albeit corrected for multiple reflections at a pair of parallel horizontal boundaries that capture between them the release of the effluent, is given by Equation (52) (reflection model). Calculations made using the latter equation were compared with those obtained using the corresponding (standard) Gaussian plume model equation given by Equation (19) (no-reflection model). The latter does not account for any kind of reflection. The results of the comparison are graphically represented in
Figure 2.
One can observe that there are discrepancies between the two calculation methods, i.e., with and without reflection, as expected. Closer to the pollution source, the no-reflection model overestimates the reflection model. This can be attributed to the way dispersion in the vertical direction is mathematically expressed. Referring to Equation (19), the relevant term in the no-reflection model is given by
whereas in the reflection model, the latter is rewritten (or “replaced”) by
This rewriting is the outcome of taking into account multiple reflections at the horizontal boundaries. In the process, the said rewriting gives rise to a lower concentration in the near-field, along the centerline of the plume (at the stack height).
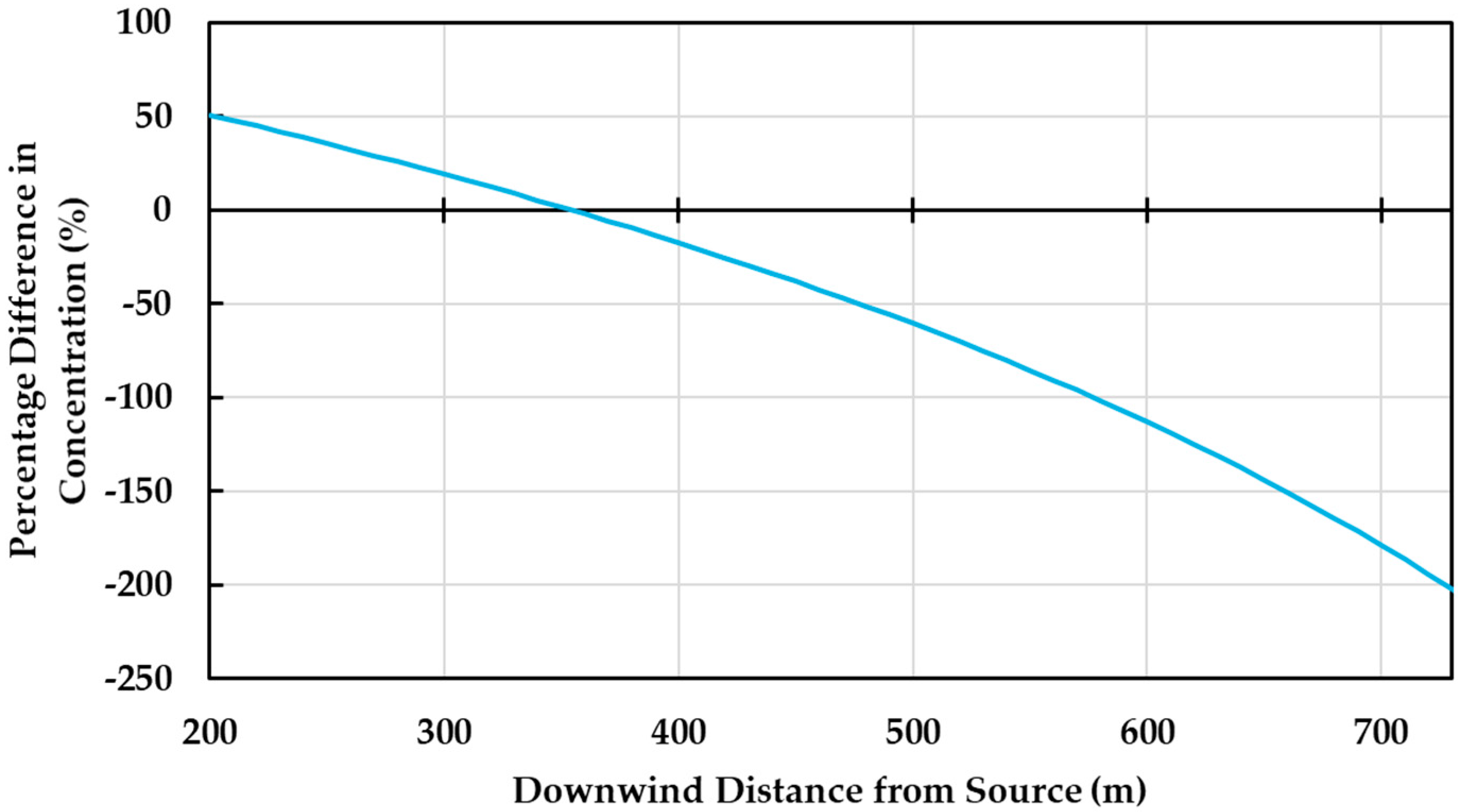
Downwind, approximately at a distance of 350 m from the source of pollution, along the plume centerline (at the stack height), the two models match. Beyond the latter point, and further downwind from the source of pollution, the no-reflection model underestimates the reflection model. These observations are in keeping with the effect of reflections at the horizontal boundaries, i.e., the ground and the atmospheric temperature inversion cap or lid. Multiple reflections of the plume give rise to higher concentrations, but the effectiveness of this stance becomes more evident downwind of the source of pollution, following several reflections. In the near-field, the mass of the effluent within the plume is closer to the centerline and away from the horizontal boundaries, so that reflection is somewhat ineffective. This explains why beyond a certain point downwind from the source of pollution, the reflection model overestimates the no-reflection model. The said discrepancy increases farther away from the source of pollution, as shown in
Figure 3.
5. Conclusions
It has been shown that the Gaussian plume model equation used in atmospheric dispersion can be mathematically represented by Equation (52) for an environment, which is confined by a pair of parallel horizontal reflecting boundaries. In this manner, the model accounts for changes in the distribution of pollution occurring due to multiple reflections at the boundaries. The model is directly applicable for the case where the ground and the atmospheric temperature inversion cap or lid play the role of the horizontal boundaries. An analogous expression is valid when the boundaries are a pair of parallel vertical reflecting planes confining the Gaussian plume. A practical example of the latter is the street canyon environment with the sources of pollution being motor vehicles. In the latter case, the boundaries, i.e., facades of buildings confining the roadway, are rigid and reflections are near complete. In the former case, the upper boundary, i.e., inversion cap or lid, is diffusive and reflections are not complete. Consequently, the said model equation is more suited for the case of the street canyon environment.
Preliminary numerical testing was undertaken to catch a glimpse of the character and behavior of the new mathematical formulation of the Gaussian plume model allowing for multiple reflections at two horizontal parallel boundaries. The calculations made with the latter/new formulation were compared with those obtained using the (standard) Gaussian plume model equation (with no reflections). The outcome of the preliminary numerical testing and comparison indicates that further investigation is warranted.
Beyond a certain downwind distance from the source of pollution, the effect of multiple reflections of the Gaussian plume, on the concentration at the centerline of the plume (at the stack height) was evident. Experimental verification of this and other observed phenomena is necessary and is planned for the near future as part of the current ongoing project.
The new formulation, or rewriting, of the Gaussian plume model equation corrected for multiple reflections at parallel plane boundaries confining the source of pollution (and, hence, the associated plume) provides air quality specialists with an opportunity for easy implementation of the associated phenomenon (referring to multiple reflections). While further (numerical and experimental) investigation is warranted and necessary, preliminary testing has shown that the new formulation is numerically stable and gives realistic outcomes.