Permeability Measurement of Glass-Fiber Textiles Used in Composites Industry Using Radial Flow Experimental Setup and Comparison with Image-Based Numerical Methods

Abstract

Permeability measurement of engineering textiles is a key step in preparing composite manufacturing processes. A radial flow experimental setup was used in this work to measure the unsaturated and saturated in-plane permeabilities of five different types of E-glass textiles and their ratios. In parallel, delayed tow saturation during the oil injection stage was visually observed to identify fabrics that exhibited a significant dual-scale effect. A numerical approach to determine the saturated permeability of a given fabric geometry at the mesoscale was tested and validated against analytical models found in the literature. It was then applied to a realistic geometry acquired from an E-glass plain weave textile using an X-ray microtomography scanner (μCT). Two numerical methods were adopted: the single-scale method, where the tows are considered impermeable, and the dual-scale method, where the permeability of the tows is taken into account. The numerical results from both methods were then compared with the experimental values and showed good agreement, especially with the second method.

1. Introduction

Composite materials are increasingly and widely used in automobile, shipbuilding, aeronautics, and aerospace applications. These materials are manufactured from fibrous reinforcements that can take the form of woven fabrics, non-crimp fabrics, knits, braids, or random mats [1]. The fabrics are transformed into composite parts using different manufacturing processes. One of the most used and developed methods is liquid composite molding (LCM) due to its various advantages, such as being low-cost, clean, and more efficient than other methods. The LCM process is based on the impregnation of dry reinforcement with a low-viscosity resin [2]. During the impregnation step, the liquid resin flows through the reinforcement, which can be considered a porous medium. This flow is a key phenomenon that has a significant effect on the quality of the final part since dry zones (not fully covered by resin) can appear if flow parameters such as the injection pressure and the positions of the injection and vent gates are not well defined [3]. An important parameter to be considered in this step is the permeability of the preform, which is defined as the ability of the porous domain to let fluid flow through it. Permeability influences the resin flow front advancement through the fibrous reinforcement and ultimately controls the mold-filling time. This material property is crucial for composite fabrication optimization and is an important input for mold-filling simulations [4]. These simulations are used to accurately predict the flow front position, fill time, and formation of voids and dry spots. A good characterization of the material properties is important to run them properly.

In order to meet the growing demand for composites, different types of reinforcements are being developed with different properties and architectures. Therefore, an accurate and efficient characterization method, such as permeability measurement, is needed. There exists a large variability in permeability measurement methods, as no standard method has been achieved [4]. Errors in permeability prediction can lead to improper process design and manufacturing of defective parts.

The flow of resin through a fibrous network is usually considered a creeping flow associated with low Reynolds number ($Re$) values. Under these conditions, Darcy’s law (Equation (1)) can be used to model the resin flow by relating the volume-averaged flow velocity u to the volume-averaged pressure P through the reinforcement permeability tensor $K$ and the fluid viscosity μ. This law, based on experimental observations, is a phenomenological model [5] used to characterize fluid flow in porous media at the macro scale.

$$u=-{\displaystyle \frac{K}{\mu }}\nabla P$$

(1)

Darcy’s law was applied in our case to model fluid flow in fibrous textiles. It was originally introduced to model the flow in sands and is a theoretical foundation of groundwater hydrology. It is a phenomenological law that has been used by various researchers in fluid mechanics and reservoir engineering in order to solve complex problems of fluid flow in porous media such as rocks [6]. Several studies have been conducted to review the use of Darcy’s law to model the flow of natural reservoirs [7] and underground fluids [8].

This paper is aimed at characterizing the permeability $K$ of a given textile using experimental and numerical methods. Different permeability determination methods can be found in the literature and can be classified into three main groups: analytical, experimental, and numerical methods. Different analytical models relate the permeability to the fiber volume fraction $V_f$ and are based on simplifying assumptions where the fibers are modeled as parallel cylinders arranged in regularly ordered networks (e.g., quadratic and hexagonal) [9,10]. These models are idealized, valid only for a certain range of fiber volume fractions, and do not accurately represent the complex geometry of real preforms. Alternatively, many researchers have used experimental procedures to measure the permeability of fibrous reinforcements. These experiments can be classified according to the following parameters [11,12,13]:

• Type of fluid: gas or liquid.
• Direction of measurement: in-plane, out-of-plane, or 3D.
• Type of flow: radial or unidirectional.
• Injection boundary conditions: constant pressure or constant flow rate.
• Saturation state of the textile: saturated or unsaturated.

The experiments allow us to take into account the variabilities existing in the textiles, but they have the disadvantage of being labor- and, time-intensive and resource-consuming since they involve many sensors, transducers, and digital cameras [14]. Another drawback is the absence of a standardized approach. Several international benchmark exercises [15,16] were launched in order to study the variation in the experimental measurements on different geometries (non-crimp and woven fabrics) and found a coefficient of variation of more than 20%.

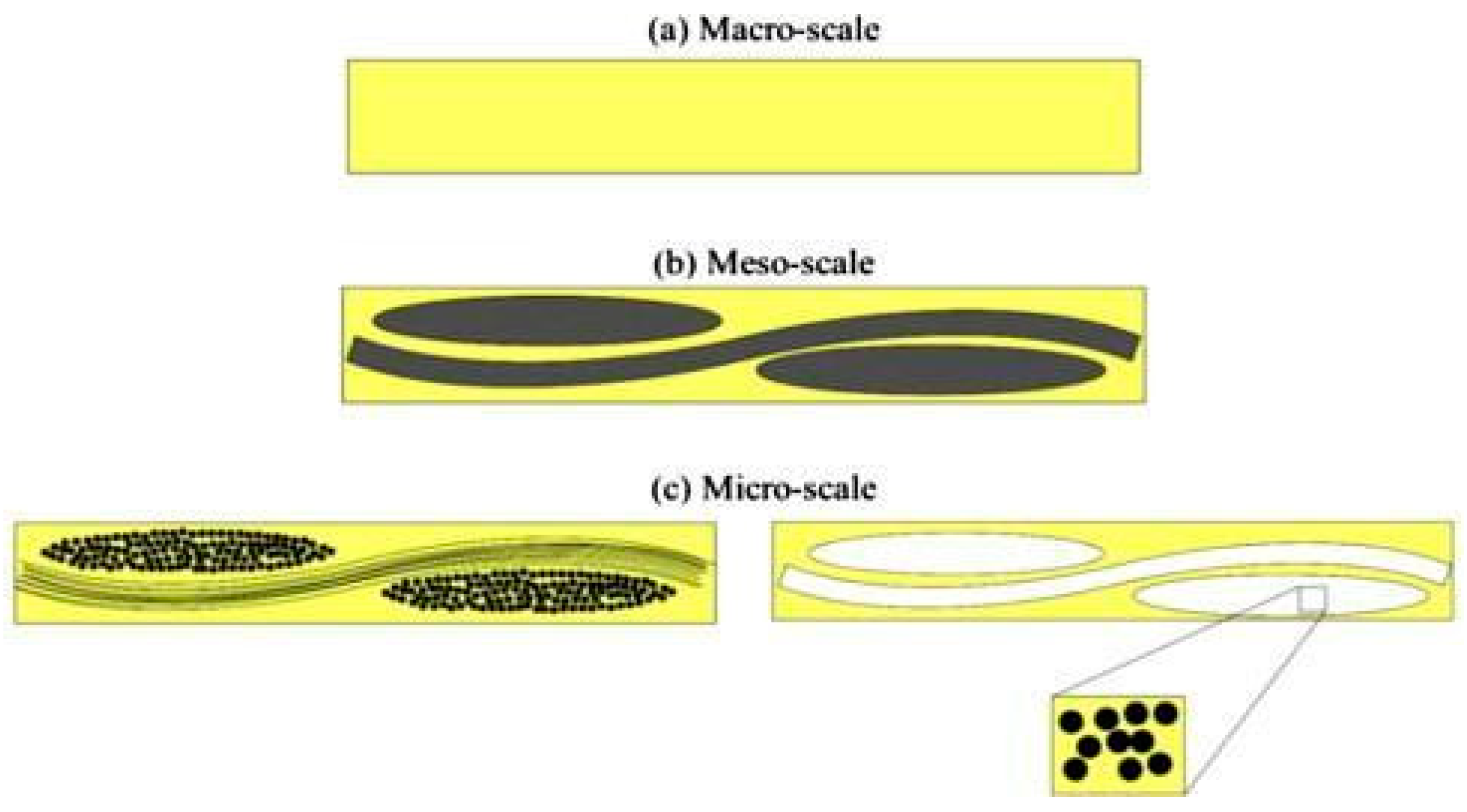
A promising alternative is the use of numerical methods that combine textile modeling and computational fluid dynamics CFD techniques. The potential of numerical methods is increasing with the growth in computing capabilities. Numerical permeability prediction has many advantages, such as the ability to efficiently explore a large range of parameters without the need to resort to experimental measurements. There are, however, modeling challenges associated with the complex structure of reinforcements that include geometrical variability, anisotropic structure, and dual-scale porosity. The latter, in particular, necessitates the use of multiscale approaches in order to predict the virtual permeability accurately. The choice of the modeling scale (Figure 1) is important to optimize the numerical simulation since at the macroscale (i.e., component scale, $\mathrm{m}$-range), the preformed geometrical details are not well represented. In contrast, at the micro-scale (fiber scale, $\mathsf{\mu }\mathrm{m}$ range), the computational cost is prohibitively high [17]. The mesoscale models (tow scale, $\mathrm{m}\mathrm{m}$-range) provide a good compromise between accuracy and efficiency.

In the first section of this paper, a 2D radial flow experimental procedure to determine the in-plane permeability tensor of different textiles is presented. The setup is designed to measure the unsaturated (transient) and saturated (steady-state) permeability in a single experimental run. The tests were carried out on different types of E-glass fabrics with various stitching styles and areal weights. The ratio of the unsaturated to saturated permeability for the different textiles was quantified at three different fiber volume fractions, and the flow front advancement was observed in order to identify the fabrics that exhibited a significant dual-scale effect (the difference in fluid velocity between the inter-tow and intra-tow space).

In the second section, two numerical methods for predicting the saturated permeability of a given textile geometry at the mesoscale are described. The first method is based on solving the Navier–Stokes equations in the inter-tow space while considering the tows as impermeable (i.e., single-scale flow). In the second method, the Brinkman equation is solved over the entire domain, and the flow inside the tows is considered (i.e., dual-scale flow). The numerical approach was first validated against analytical models found in the literature and then used to determine the permeability of a realistic geometry acquired from an E-glass plain weave fabric at three fiber volume fractions using an X-ray μCT scanner. The measured saturated permeabilities of the scanned textiles were compared with their corresponding predicted values. Good agreement was found, especially regarding the dual-scale case.

2. Radial Flow Experimental Setup for the Measurement of the Permeability of Fibrous Textiles

A 2D radial flow in-plane permeability experimental setup was used to measure the unsaturated and saturated permeability of five different E-glass fabrics at different fiber volume fractions: plain weave fabric, 0/90 biaxial stitched fabric, quad axial fabric, unidirectional reinforcement, and twill weave fabric. Examples are given in Figure 2.

The test rig has been developed over the years in the Centre for Advanced Materials Manufacturing and Design (CAMMD) at The University of Auckland in order to efficiently characterize the in-plane permeability of fibrous textiles [18]. Figure 3 shows a schematic representation of this rig that was used by F. Zhang et al. [19] and S. Comas-Cardona [20] to investigate the transient permeability of Chopped Strand Mat (CSM) and other fabrics.

In the first part of this section, the experimental facility, including the different tools used and the steps of the experimental procedure, are presented. In the second part, the results are discussed, and the key findings of these experiments are presented.

In the scope of this paper, the test rig has been used to measure two different permeability values: the unsaturated or transient permeability through the following of the flow front, as will be explained later, and the saturated or steady-state permeability through the injection of an additional quantity of oil after the saturation of sample which enables to compute the steady-state mass flow rate.

The radial flow technique was particularly chosen because of the relative simplicity of the setup compared to other techniques, in addition to its ability to compute the complete in-plane permeability tensor within a single test, which minimizes effort and cost.

2.1. Experimental Facility

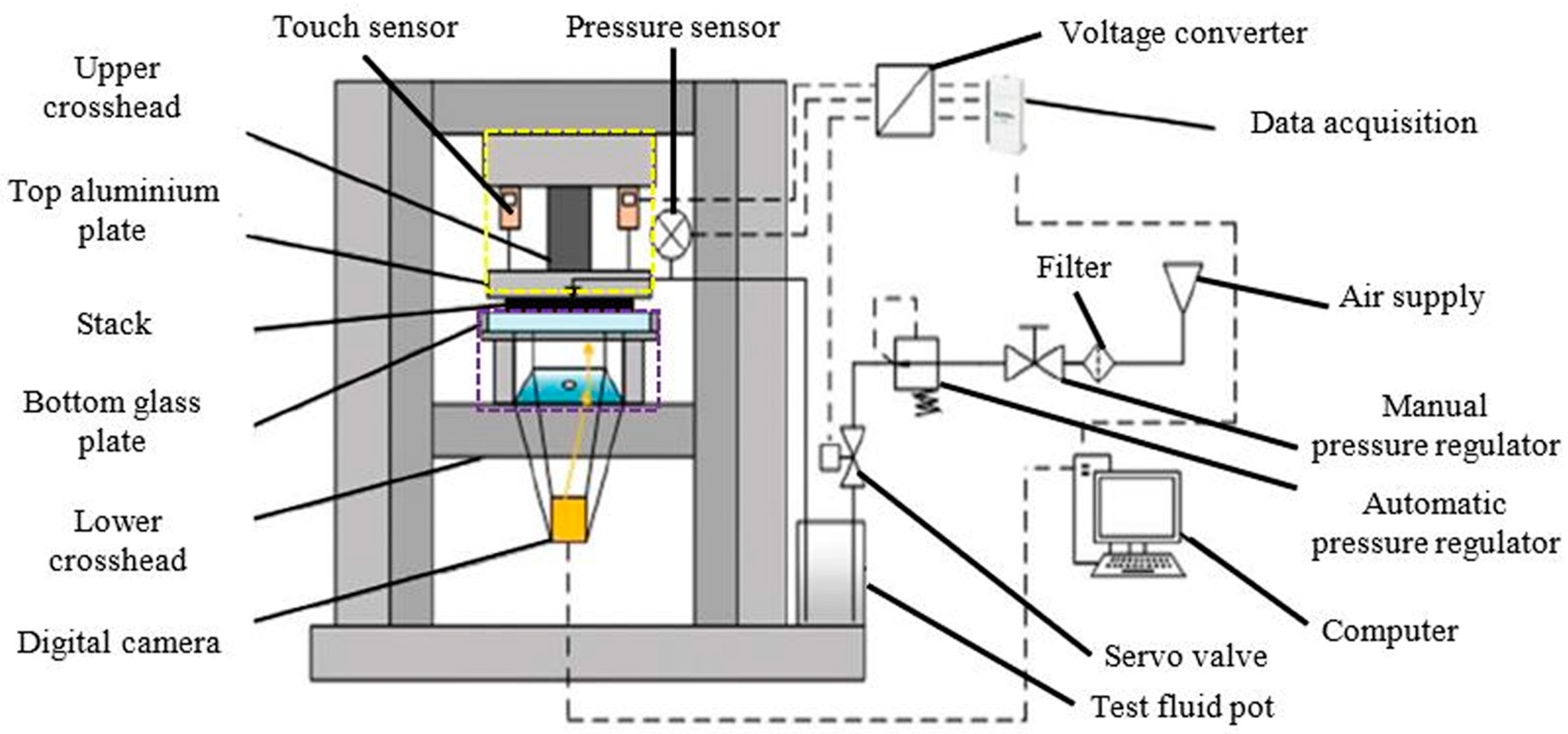
The 2D in-plane testing facility was installed on an Instron 1186 Universal Testing Machine (UTM) to provide accurate control of the cavity thickness and measurement of the total compaction force applied. The whole facility was situated in an environmentally controlled room to obtain consistent measurements (a constant temperature of 22 °C).

Each sample was set between two plates: a transparent lower plate, Figure 4a, made of $55\mathrm{m}\mathrm{m}$ thick glass with a side length of $350\mathrm{m}\mathrm{m}$ that allows flow front detection through optical monitoring and a circular upper plate, Figure 4b, of a diameter of $250\mathrm{m}\mathrm{m}$ and $30\mathrm{m}\mathrm{m}$ thick that was parallelly aligned to the lower plate with a spherical alignment unit and a manufactured strain-gauged compressive alignment specimen. Through these alignment tools, a uniform cavity thickness with a tolerance of $5\mathsf{\mu }\mathrm{m}$ could be achieved. These plates were designed to minimize deflection during the compaction step, allowing a maximum deflection of $0.07\mathrm{m}\mathrm{m}$ under an average compaction pressure of $2\mathrm{M}\mathrm{P}\mathrm{a}$ [20]. The range of target thickness was around 3 mm which adheres to the ISO 4410:2023 [21] recommendations (Test methods for the experimental characterization of in-plane permeability of fibrous reinforcements for liquid composite molding), with target thickness precision being around 2%.

A Navitar SV5C10 0238 digital camera (manufactured by NAVITAR, INC in Rochester, NY, USA) was attached to the setup via an L-bend with its lens pointing to a 45° angled mirror (with respect to the horizontal plate) to capture the flow front evolution during the test fluid infusion. Two Mitutoyo IDU25 touch sensors $1\mathsf{\mu }\mathrm{m}$ resolution were used to measure the distance between the parallel plates; they were attached to the top plate with their probe touching the upper surface of the bottom plate. National Instruments LabVIEW saved the captured data (time, pressure, and oil mass) for post-processing.

The different measurement accuracies of the experimental facility are summarized in the following table (

Table 1. Measurement accuracies.

Measurement	Accuracy
Sample mass	$\pm 0.01 \mathrm{g}$
Injected oil mass	$\pm 0.1 \mathrm{g}$
Cavity thickness	$\pm 5 \mathsf{\mu }\mathrm{m}$
Fluid pressure	$\pm 1\%$
Temperature	$\pm 0.1 °\mathrm{C}$

).

A general overview of the experimental setup is shown in Figure 5.

2.2. Experimental Procedure

Utilizing a hydraulic press machine and a dedicated circular cutting knife, Figure 6a, circular stacks with a diameter of $200\mathrm{m}\mathrm{m}$ of fibrous textiles were prepared.

A hole of 15 mm diameter was punched at the center of each sample to serve as an injection port for the test fluid, Figure 6b. The mass of each sample was measured before starting the experiment using a digital balance (which measures up to $0.01\mathrm{g}$ precision). The sample was then placed on the bottom glass plate, Figure 7, and must be accurately placed at the center to ensure a pure in-plane flow during the injection step. The layers were assembled in a 0/90/0/90 sequence to enforce isotropic in-plane flows and, thus, circular flow fronts.

The position of the bottom plate was controlled by the Instron machine in order to achieve the target fiber volume fraction, $V_f$, as given by Equation (2):

$$V_f={\displaystyle \frac{m}{\rho Ah}}$$

(2)

where $m$ is the mass of the sample, $\rho$ is the fiber density (characteristic of the used fabric), $A$ is the sample’s planar area, and $h$ is the target compaction thickness. In this equation, the term ${\displaystyle \frac{m}{\rho }}$ provides the actual volume of the sample, while the term $A\cdot h$ is the total volume occupied by the sample plus air/oil; thus, their ratio provides the actual fiber volume fraction. The following table (

Table 2. Average sample mass and cavity thickness for different fiber volume fractions.

Textile	${\mathit{V}}_{\mathit{f}}$	Average Sample Mass [g]	Average Cavity Thickness [mm]
Plain Weave fabric	0.5	106.8	2.7
	0.55	107.1	2.43
	0.6	107	2.25
0/90 Biaxial stitched fabric	0.5	114.275	2.86
	0.55	114.33	2.6
	0.6	113.9	2.38
Quad Axial stitched fabric	0.5	109.3	2.74
	0.55	109.33	2.49
	0.6	109.6	2.29
Unidirectional reinforcement fabric	0.5	101.45	2.544
	0.55	101.56	2.315
	0.6	101.375	2.118
Twill Weave fabric	0.5	74.16	1.86
	0.55	74.6	1.69

) summarizes the average sample mass and the average cavity thickness for each fiber volume fraction for the different textiles:

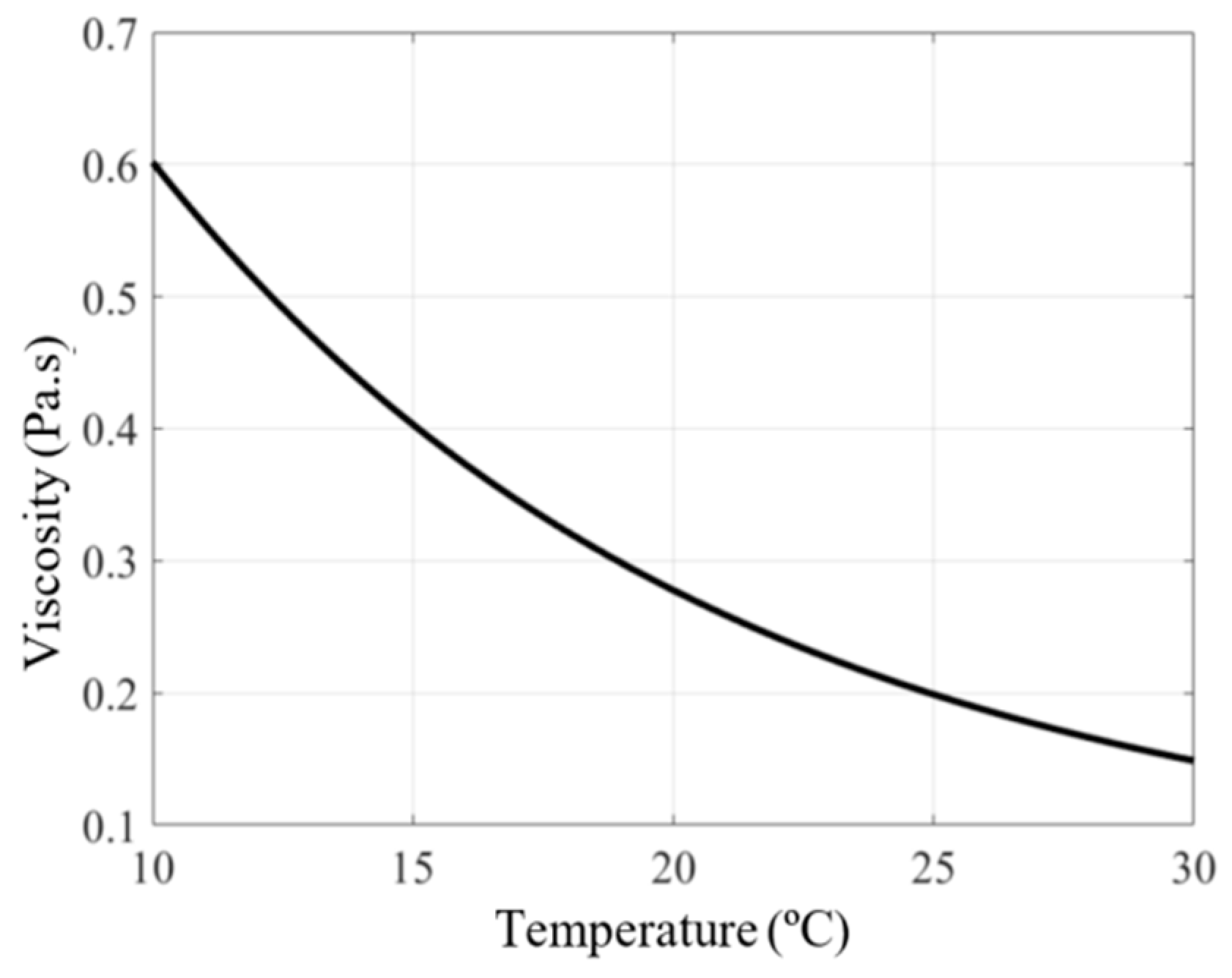
The test fluid was then injected radially from the oil pot into the sample initially filled with air via a circular port of 15 mm in diameter, centered on the top plate. The test fluid used was a Newtonian Mobil DTE series HEAVY mineral oil ISO VG 100, whose temperature-dependent viscosity, Figure 8, was determined using a Parr Physica UDS200 rheometer and is given by the following power-law:

$$\mu =-0.00000000519\cdot T^5+0.00000111\cdot T^4-0.0000969\cdot T^3+0.00448\cdot T^2-0.114\cdot T+1.38$$

(3)

The oil was supplied from an enclosed metallic pot driven by pressurized air regulated by a FESTO proportional pressure controller. During the injection, the fluid flowed through the specimen radially, and the flow front progression was captured and analyzed to determine the in-plane permeability of the sample.

The oil was injected from the sample center at a constant pressure of $50\mathrm{k}\mathrm{P}\mathrm{a},$ and the outlet was placed at atmospheric pressure. The flow front progression was recorded as a series of images at a frequency of $1\mathrm{H}\mathrm{z},$ Figure 9.

In addition to the flow front progression, the static inlet pressure measured by a pressure sensor located near the injection gate and the oil temperature measured by a thermocouple in the pressure pot were also recorded at regular time intervals.

A MATLAB 2023b script developed in CAMMD was used to process the captured flow front images [14]. The algorithm comprises the following steps starting from the initial image captured by the camera, which was converted to grayscale, Figure 10a:

• The possible distortions due to the camera and mirror positioning are corrected using a geometric transformation routine applied to the input images, Figure 10b.
• A binary image is obtained from the subtraction of the transformed image from its corresponding initial image, Figure 10c.
• The boundary pixels of the binary image are fitted with a direct least-square ellipse, from which various geometrical parameters are extracted: major radius a, minor radius b, and major axis orientation $\theta$, Figure 10d.

The unsaturated permeability was computed using the formula given by Weitzenbock et al. [22], derived from Darcy’s law for radial flow in equations (Equations (4) and (5)).

$$K_{11}=(a^2[2ln({\displaystyle \frac{a}{r_i}})-1]+r_i^2){\displaystyle \frac{\mu (1-V_f)}{4t{P}_{inj}}}$$

(4)

$$K_{22}=(b^2[2ln({\displaystyle \frac{b}{r_i}})-1]+r_i^2){\displaystyle \frac{\mu (1-V_f)}{4t{P}_{inj}}}$$

(5)

where $K_{11}$ and $K_{22}$ are the major and minor in-plane principal permeability components, $a$ and $b$ are the major and minor radii of the fitted flow front ellipse, $r_i$ is the radius of the injection hole, μ is the test oil viscosity deduced from the measured oil temperature using the viscosity-temperature curve (Figure 8), $t$ is the time from the start of the injection, and $P_{inj}$ is the inlet injection pressure. In the Weitzenbock formula [22], the pressure used corresponds to the pressure drop, but it is approximated to the injection pressure $P_{inj}$ in our case, we assume that the outlet is at atmospheric pressure (i.e., zero gauge pressure).

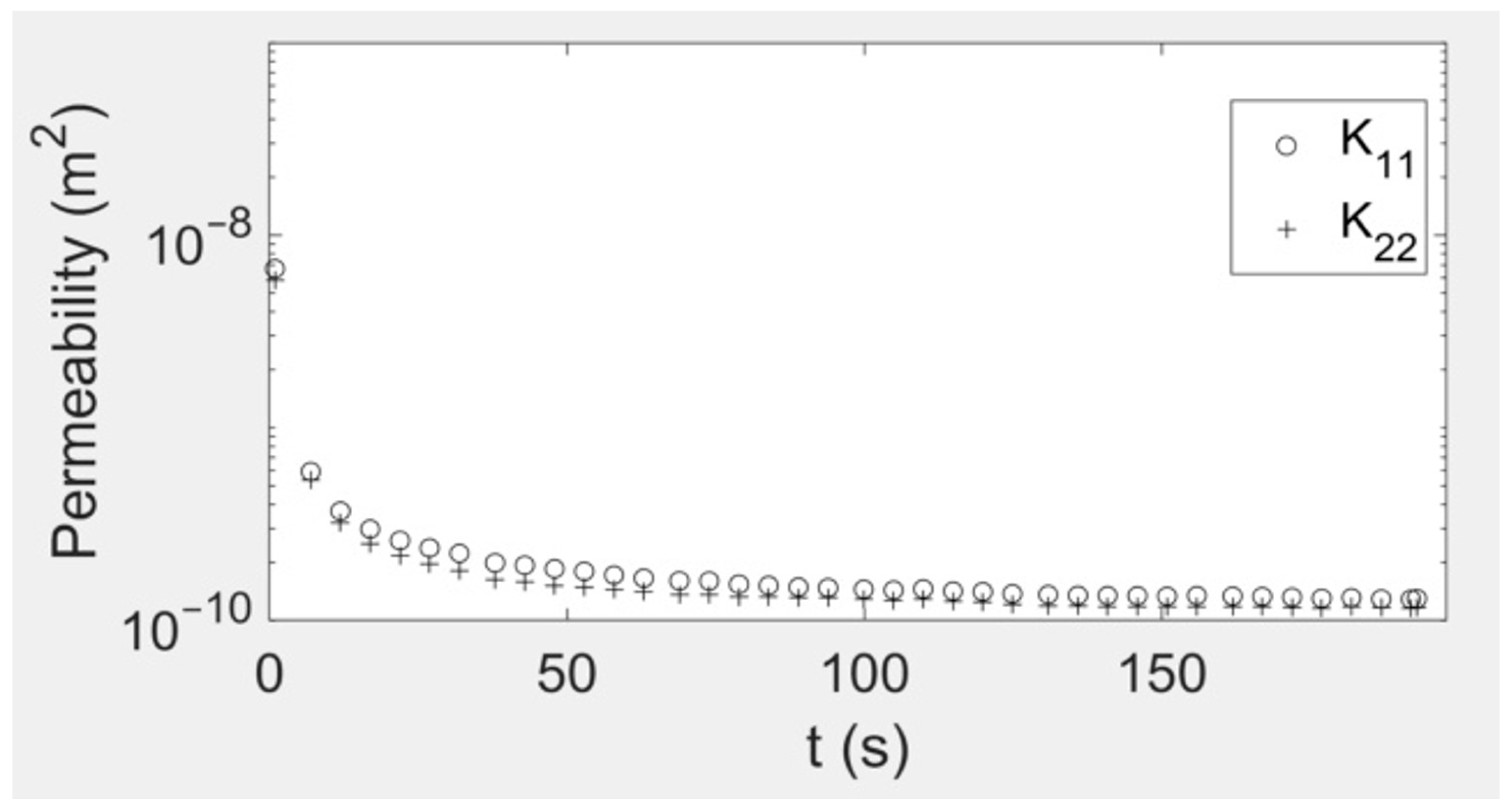
For each test, the permeability tensor is computed for each flow front image and plotted against the time steps. The reported permeability values are given by the average of the final one-third of the computed values to eliminate any flow stabilization effects at the start of the experiment. As can be observed in Figure 11, the measured permeability values become stable after a short initial transient effect.

This setup also allows the measurement of isotropic saturated permeability. After the sample is fully saturated, the oil injection is continued in order to compute the steady-state mass flow rate, which is found by fitting a linear regression to the mass-time curve. The saturated permeability is deduced using Darcy’s law through equation (Equation (6)) [23].

$$K_{saturated}={\displaystyle \frac{Q·\mu ·ln\left(\frac{r_0}{r_i}\right)}{2\pi ·\rho ·h·P_{inj}}}$$

(6)

where $Q$ is the steady-state mass flow rate, $\mu$ is the oil viscosity, $r_0$ is the sample’s outer radius, $r_i$ is the internal radius taken as the radius of the punched hole, $\rho$ is the oil density, $h$ is the cavity thickness, and $P_{inj}$ is the injection pressure.

2.3. Results

These experiments were carried out in order to quantify the difference between the transient and steady-state permeabilities of the tested textiles and to observe the flow front advancement during the injection step. The flow front shape provides an idea of fabrics where the dual-scale effect is significant. Three different fiber volume fractions $V_f$ ($0.5$, $0.55$ and $0.6$) were considered, except for the twill weave fabric, for which 16 layers were used for each sample because of its low linear density; as a result, the quantity of fabric was not sufficient to carry out the tests at three fiber volume fractions. The isotropic unsaturated permeability used for the comparison is the average (geometric mean) of the values found in the principal directions $K_{unsat}=\sqrt{K_{11}·K_{22}}$.

The ratios $K_{unsat}/K_{sat}$ are different from one textile to another and were found to vary between $0.9$ and $1.42$, which is the range found in the literature. Researchers found ratios between $0.25$ and $4$ [2,24], and for most of them [25,26], the ratio was around $1$. The difference in this ratio from one textile to another can be explained by the difference in the size of the inter-tow space, which affects the importance of the capillary effects and their effect on the transient flow and, as a result, on the value of the unsaturated permeability.

Table 3. Summary of the experimental results.

Textile	${\mathit{V}}_{\mathit{f}}$	${\mathit{K}}_{\mathit{s}\mathit{a}\mathit{t}}$ $[{10}^{-10}{\mathbf{m}}^2$]	${\mathit{K}}_{\mathit{u}\mathit{n}\mathit{s}\mathit{a}\mathit{t}}$ $[{10}^{-10}{\mathbf{m}}^2$]	${\mathit{K}}_{\mathit{u}\mathit{n}\mathit{s}\mathit{a}\mathit{t}}/{\mathit{K}}_{\mathit{s}\mathit{a}\mathit{t}}$
E-glass Plain weave ($800\mathrm{g}/{\mathrm{m}}^2)$	$0.5$	$2.916\pm 0.19$	$3.16\pm 0.24$	$1.08$
	$0.55$	$1.12\pm 0.11$	$1.16\pm 0.14$	1.04
	$0.6$	$0.482+0.06$	$0.458\pm 0.054$	0.95
0/90 Biaxial stitched fabric ($825\mathrm{g}/{\mathrm{m}}^2)$	$0.5$	$1.39\pm 0.2$	$1.6\pm 0.3$	$1.15$
	$0.55$	$0.672\pm 0.097$	$0.729\pm 0.11$	$1.08$
	$0.6$	$0.326\pm 0.044$	$0.34\pm 0.011$	$1.04$
Quad Axial Stitched Fabric ($851\mathrm{g}/{\mathrm{m}}^2)$	$0.5$	$0.62\pm 0.026$	$0.649\pm 0.038$	$1.045$
	$0.55$	$0.27\pm 0.012$	$0.286\pm 0.007$	$1.05$
	$0.6$	$0.171\pm 0.016$	$0.177\pm 0.0178$	$1.03$
Unidirectional reinforcement fabrics ($850\mathrm{g}/{\mathrm{m}}^2)$	$0.5$	$3.5\pm 0.22$	$4.97\pm 0.8$	$1.42$
	$0.55$	$1.91\pm 0.057$	$2.47\pm 0.097$	$1.29$
	$0.6$	$1.12\pm 0.16$	$1.33\pm 0.218$	$1.19$
Twill weave ($295\mathrm{g}/{\mathrm{m}}^2$)	$0.5$	$0.398\pm 0.004$	$0.38\pm 0.045$	$0.96$
	$0.55$	$0.2\pm 0.022$	$0.183\pm 0.023$	$0.91$

summarizes the experimental findings. Each test was repeated three to four times, and the relative standard deviation was between 3% and 16%, which is comparable to the standard deviations (around 15%) found in the experimental benchmark [16] and provides confidence in the repeatability of our results. The discrepancy between different repeats can be attributed to the manual preparation and handling of samples, uncertainties in sensor readings, and the effects of ambient conditions.

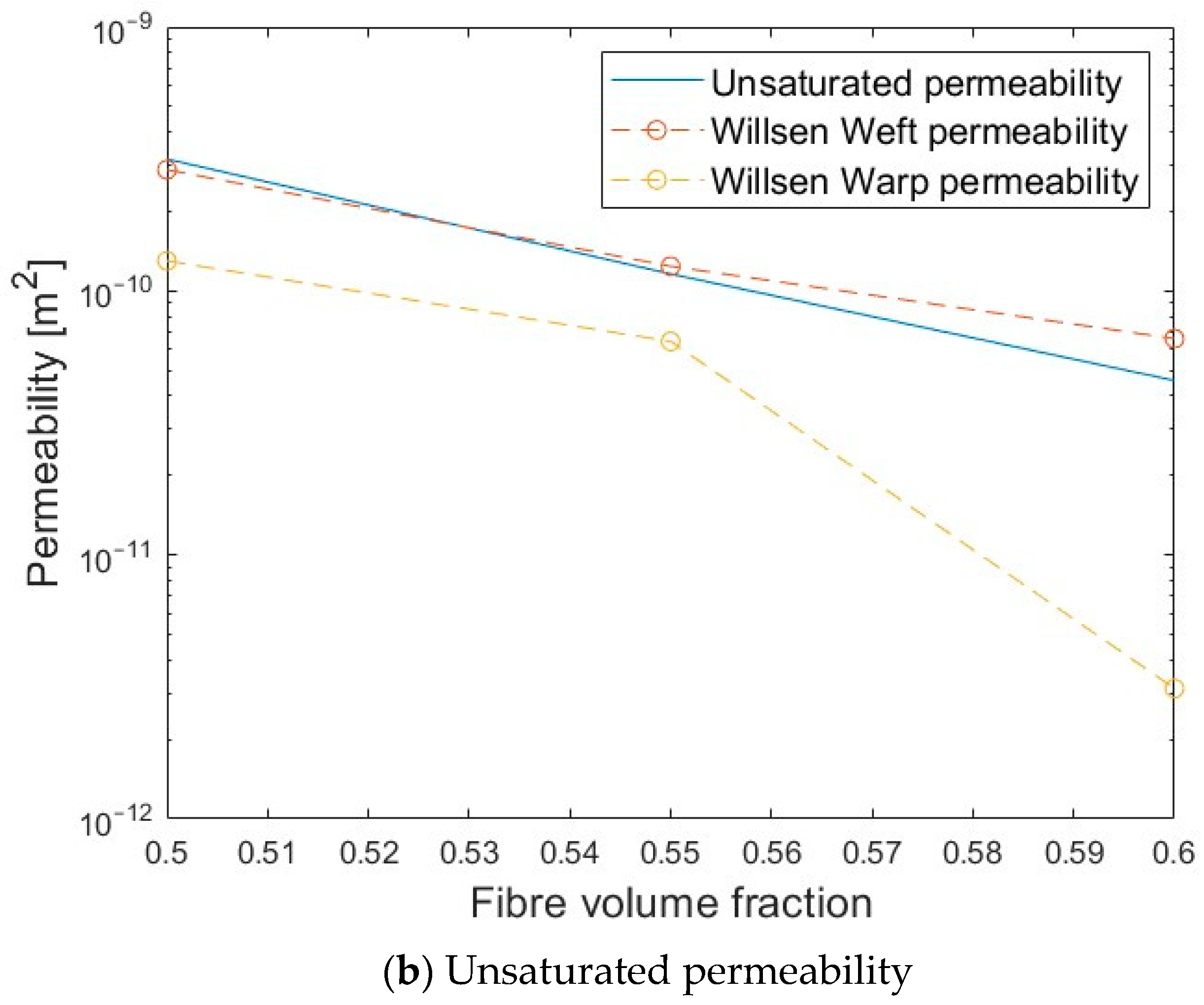
Specific to the E-glass plain weave textile ($800\mathrm{g}/{\mathrm{m}}^2)$, Wijaya [14] performed detailed unsaturated and saturated permeability characterizations of the same fabric in both the warp and weft directions. In the study, no relative change in orientation within a given sample stack was permitted (i.e., the warp and weft tows of all layers were nominally aligned in their respective directions). The results of the said work served as a basis for comparison with our values since the isotropic value that we are measuring should lie more or less between the weft and warp permeability given by his tests. The results plotted in the following Figure 12 confirm the good agreement between both measurements and provide more confidence in the accuracy and repeatability of our results.

Another objective of the experiments was to observe the flow front advancement in the different fabrics in order to identify those where the dual-scale effect, i.e., the difference in flow front progress between the inter-tow and intra-tow space, is stronger. This effect is clearly visible in the unidirectional reinforcement (Figure 13a) and biaxial stitched fabrics (Figure 13b) and less so in the plain weave textile (Figure 13c), whereas the flow front was nearly compact and uniform for the twill weave and quad axial stitched fabrics (Figure 14).

These observations are consistent with the architecture of the textiles since the free space or inter-tow space is larger for the unidirectional, biaxial, and plain weave textiles than for the quad axial and twill weave textiles. The oil flowed faster in the inter-tow spaces than in the intra-tow spaces; such a difference in velocity was evident in these textiles.

3. Permeability Determination Using Numerical Simulation

Numerical simulation is largely used at the component scale to simulate the LCM process; however, its adoption for textile permeability characterization is not well developed despite its increasing potential. It appears as an attractive proposition for theoretical and experimental alternatives because it neither generates large amounts of material waste (test fluid, textiles, etc.) nor uses complex equipment, and it allows it to carry out many parametric studies efficiently [4].

In this section, two numerical methods for saturated permeability determination are presented. The first method, the single-scale approach, is based on solving the Navier–Stokes equations in the inter-tow free space and neglecting the flow inside the fiber tows (i.e., solid impermeable tows). This assumption is justified by the low permeability of the tows (around ${10}^{-13}{\mathrm{m}}^2$), which is around two orders of magnitude lower than the overall textile permeability [27]. The second method, the dual-scale approach, is based on solving the Brinkman equation on the whole domain (including the intra-tow domain) using a specific multiscale OpenFoam solver that allows simulating the inter- and intra-tow flows by considering the computational domain as a porous medium.

Both methods were applied to a scanned 3D geometry acquired from a 4-layer stack E-glass plain weave specimen with an areal weight of $800\mathrm{g}.{\mathrm{m}}^{-2}$ and a tow linear density of $2400\mathrm{g}.{\mathrm{k}\mathrm{m}}^{-1}$. The numerical values are compared to the experimental values obtained with the experimental setup described in the previous section that was used to measure the weft and warp permeabilities of a sample of four layers of the same plain weave textile.

3.1. Numerical Approach

The general procedure for numerically determining the permeability of a given flow geometry is as follows. A pressure gradient $∆P$ is imposed between the inlet and the outlet of a given domain across a flow distance $L_{flow}$. The steady-state volumetric flow rate $Q$ through a cross-sectional area normal to the flow direction $A_{flow}$ is numerically computed by solving the corresponding fluid equations assuming creeping flow (i.e., incompressible and non-inertial characterized by a low Reynolds number).

The flow domain is considered saturated by a fluid of viscosity $\mu$ so that the capillary effects are neglected [28], and the permeability is deduced from Darcy’s law (Equation (1)) for linear flow according to the following relationship:

$$K={\displaystyle \frac{Q·\mu ·L_{flow}}{A_{flow}·∆P}}$$

(7)

The flow through the structure is solved using the computational fluid dynamics CFD open-source software OpenFOAM v7 based on the Finite Volume Method FVM.

3.2. Comparison with Analytical Models

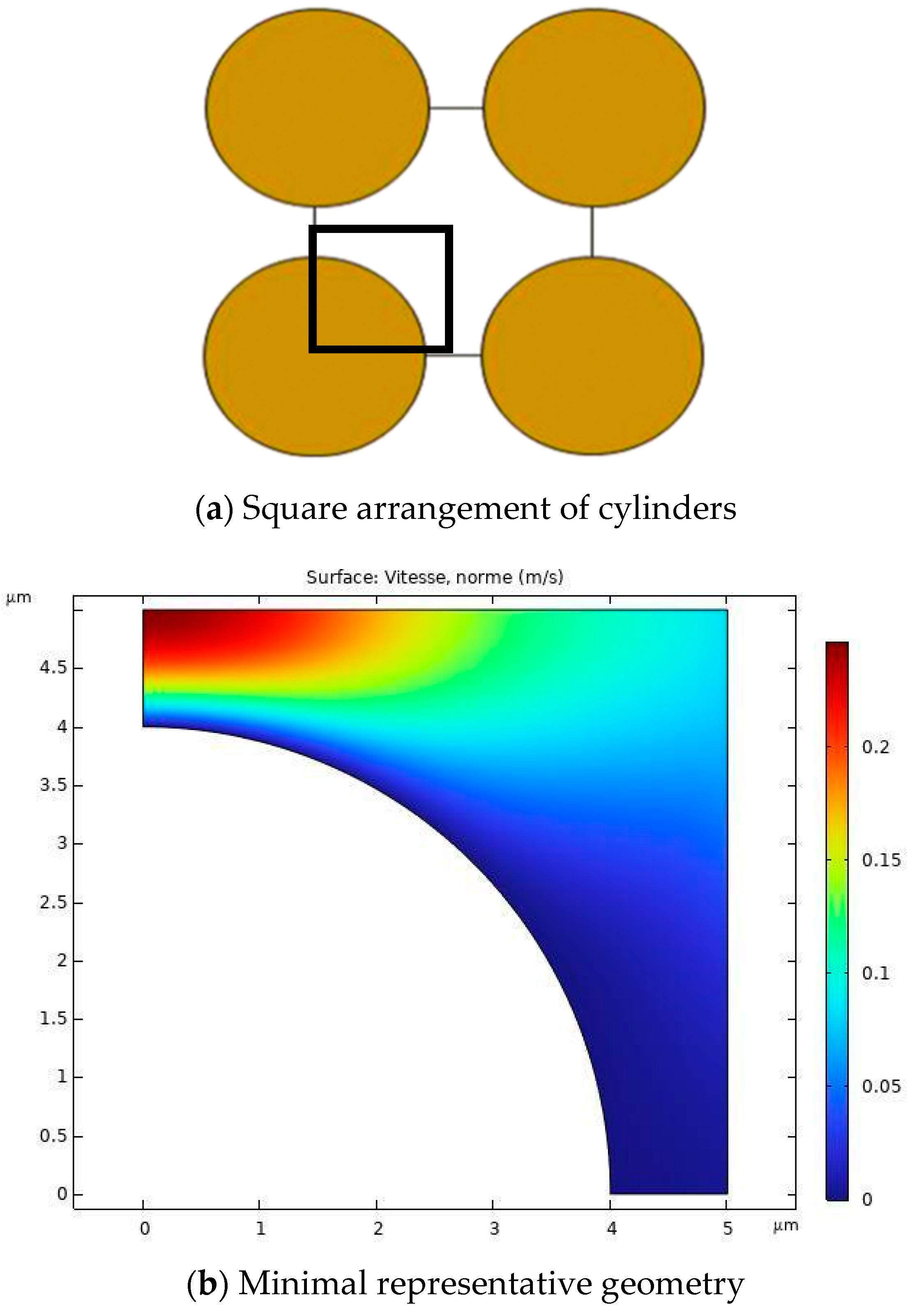
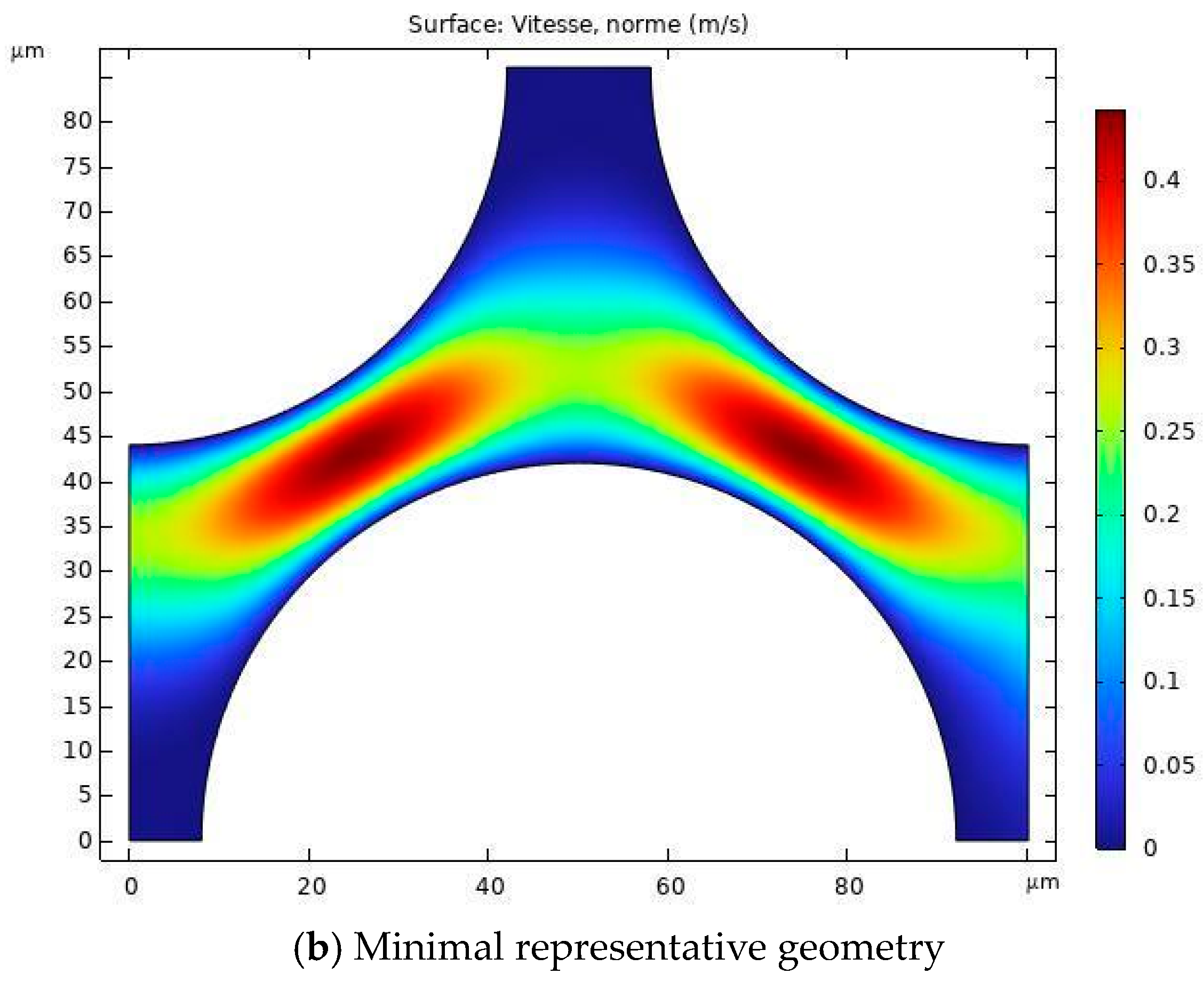
The first test to validate the numerical approach was performed on a square array of impermeable cylinders, Figure 15a, in order to compare the transverse permeability of this configuration with the analytical models found in the literature. Using the symmetry properties of the configuration, a minimal representative geometry, black square in in Figure 15a, was used in the simulations in order to minimize the computing effort.

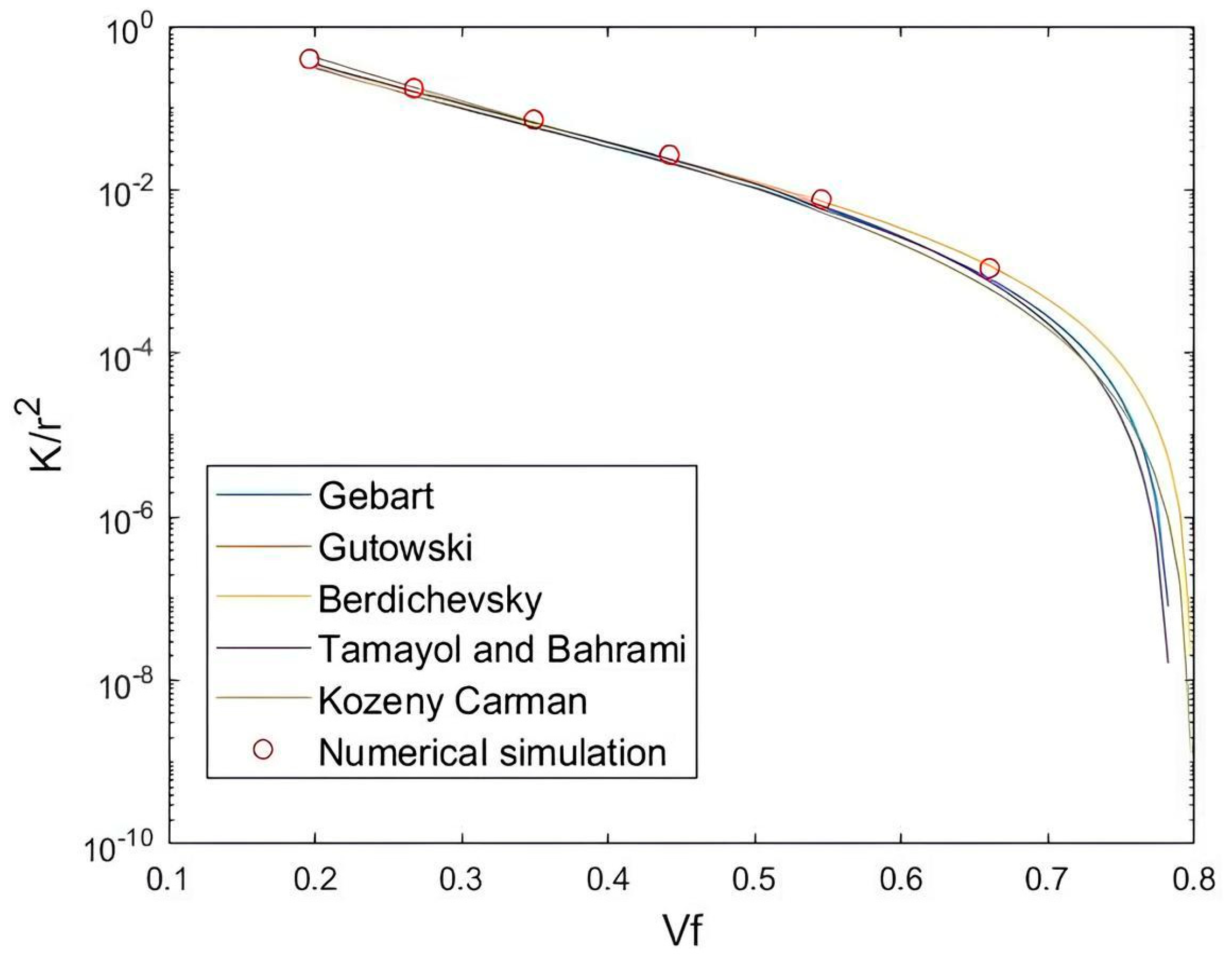
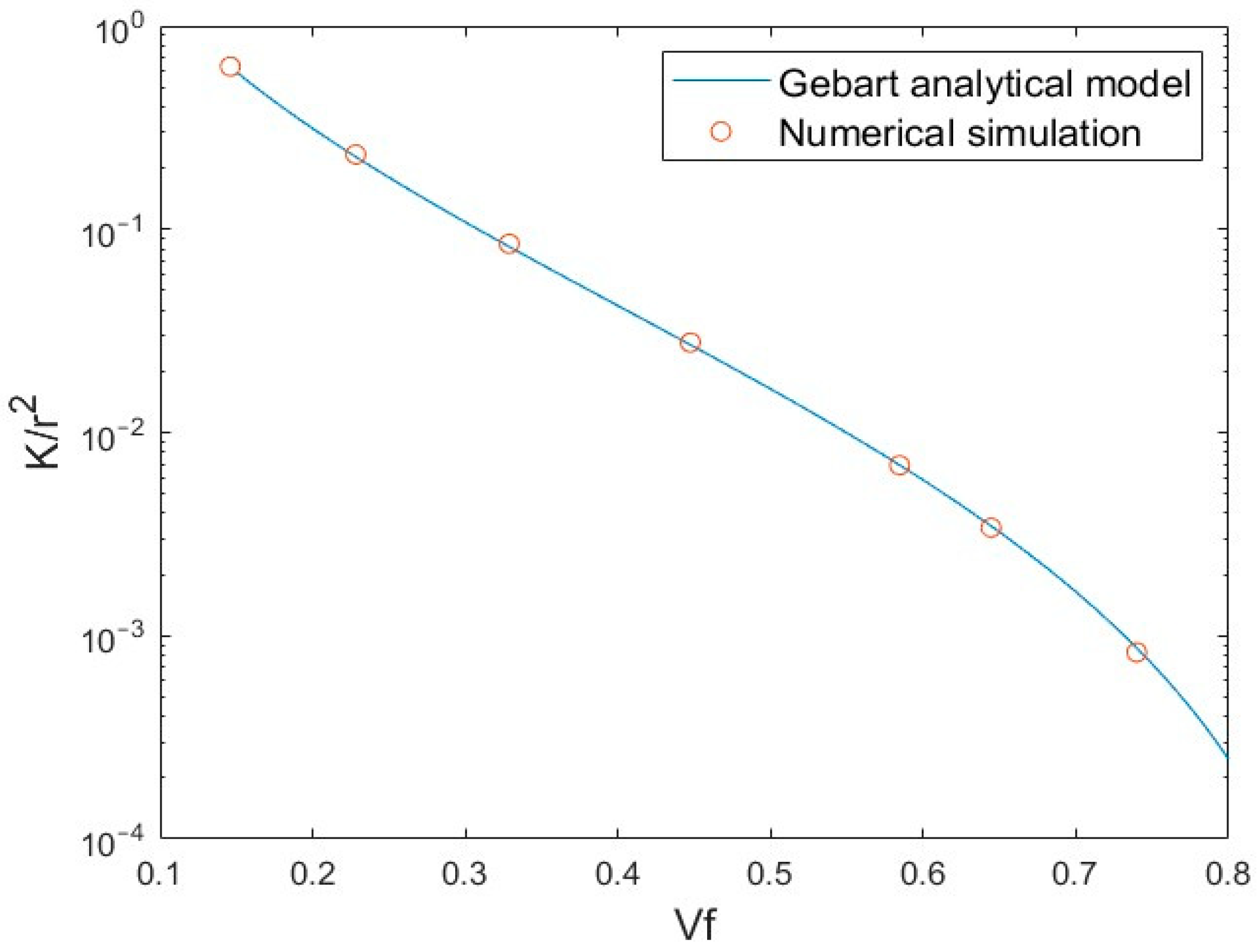
The simulations were carried out at different fiber volume fractions ranging from $0.2$ to $0.7,$ and the computed non-dimensionalized permeability values, ${\displaystyle \frac{K}{r^2}}$, were plotted in Figure 16 as a function of fiber volume fraction. In the same graph, the analytical predictions from models such as Gebart, Gutowski, Kozeny-Carman, etc. [9] have also been plotted for comparison. It can be seen that a good agreement was found between the numerical and analytical values.

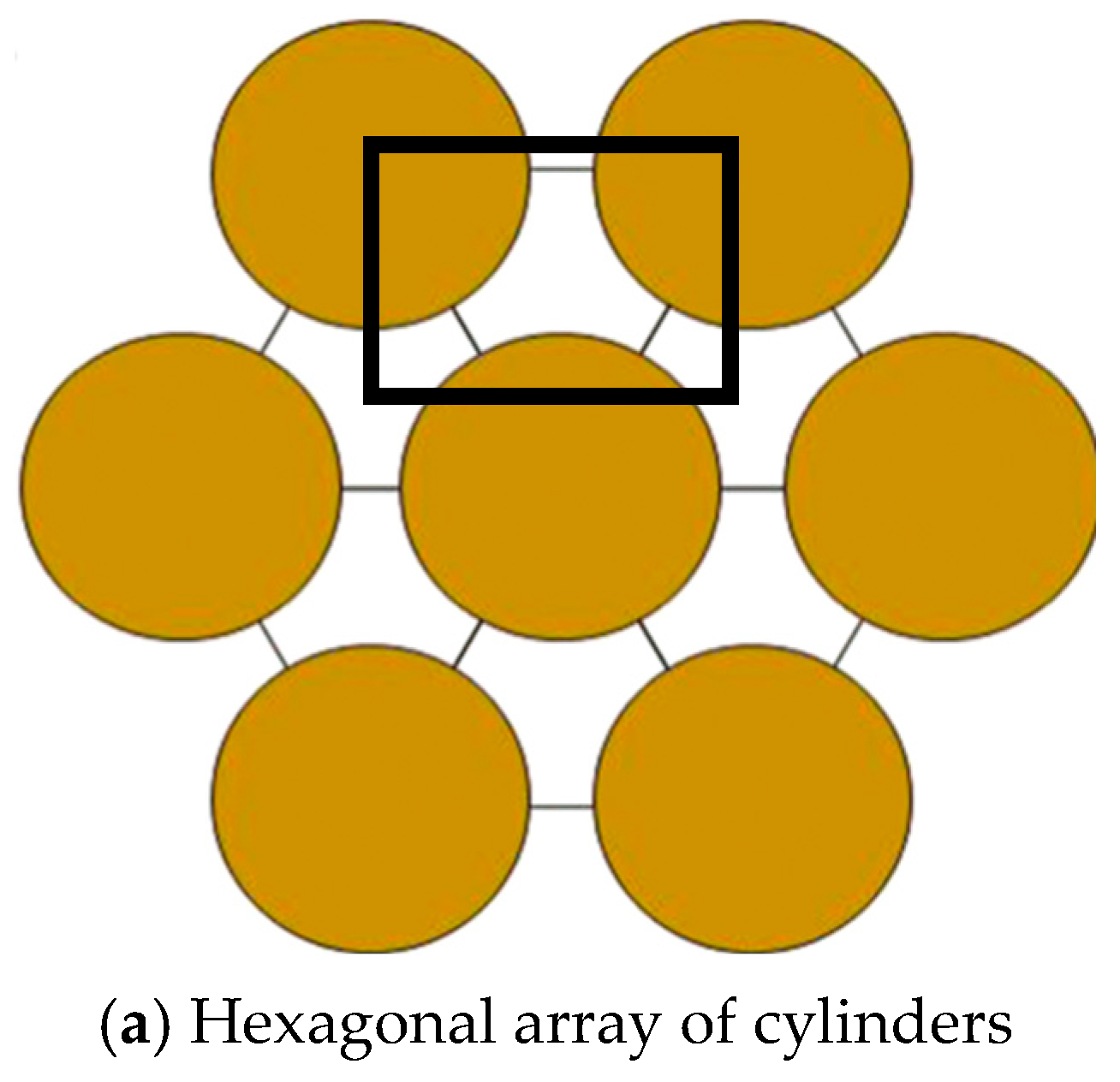
A similar numerical versus analytical investigation was also carried out on the flow around a hexagonal array of fibers. A minimal representative geometric domain (black square in Figure 17a) is also considered in this case, Figure 17b. The results of the simulation, Figure 18, are compared to those of the Gebart model and show very good agreement.

The objective of this section is to validate the numerical approach to simple geometries, solving the Navier–Stokes equations in the free space between the cylinders. In the next section, this method, in addition to the dual-scale method based on the Darcy–Brinkman equations, is described, and the flow simulation was performed in a realistic 3D textile geometry.

3.3. Image-Based Permeability Determination

The 3D representation of the textile meshes was acquired from a 4-layer stack E-glass plain weave specimen. During the stacking process, no relative interlayer change in orientation was allowed. Note that the same textile was experimentally characterized. The plain weave has a nominal areal weight of $800\mathrm{g}.{\mathrm{m}}^{-2}$ and a tow linear density of $2400\mathrm{g}.{\mathrm{k}\mathrm{m}}^{-1}$. The acquisition was realized using an X-ray microtomography ($\mu CT$) scanner, which provided volumetric data of the textile at grayscale, e.g., Figure 19, at three different compaction levels corresponding to fiber volume fractions of $0.5,0.55$, and $0.6$. An image processing algorithm was then used to separate the inter-tow space from the tow data and to obtain the final 3D geometry. The physical dimensions of the scanned specimen were $25.14\mathrm{m}\mathrm{m}\times 26.04\mathrm{m}\mathrm{m}$ with a variable height for each target fiber volume fraction (between $2.18\mathrm{m}\mathrm{m}$ and $3.28\mathrm{m}\mathrm{m}$). The voxel dimensions were $2012\times 2084$ pixels in the weft and warp directions and a variable number of pixels in the through-thickness direction ($175$ for the highest volume fraction $0.6$ and $211$ for the smallest one $0.5$). The acquisition procedure is described in detail in the paper of Wijaya et al. [29].

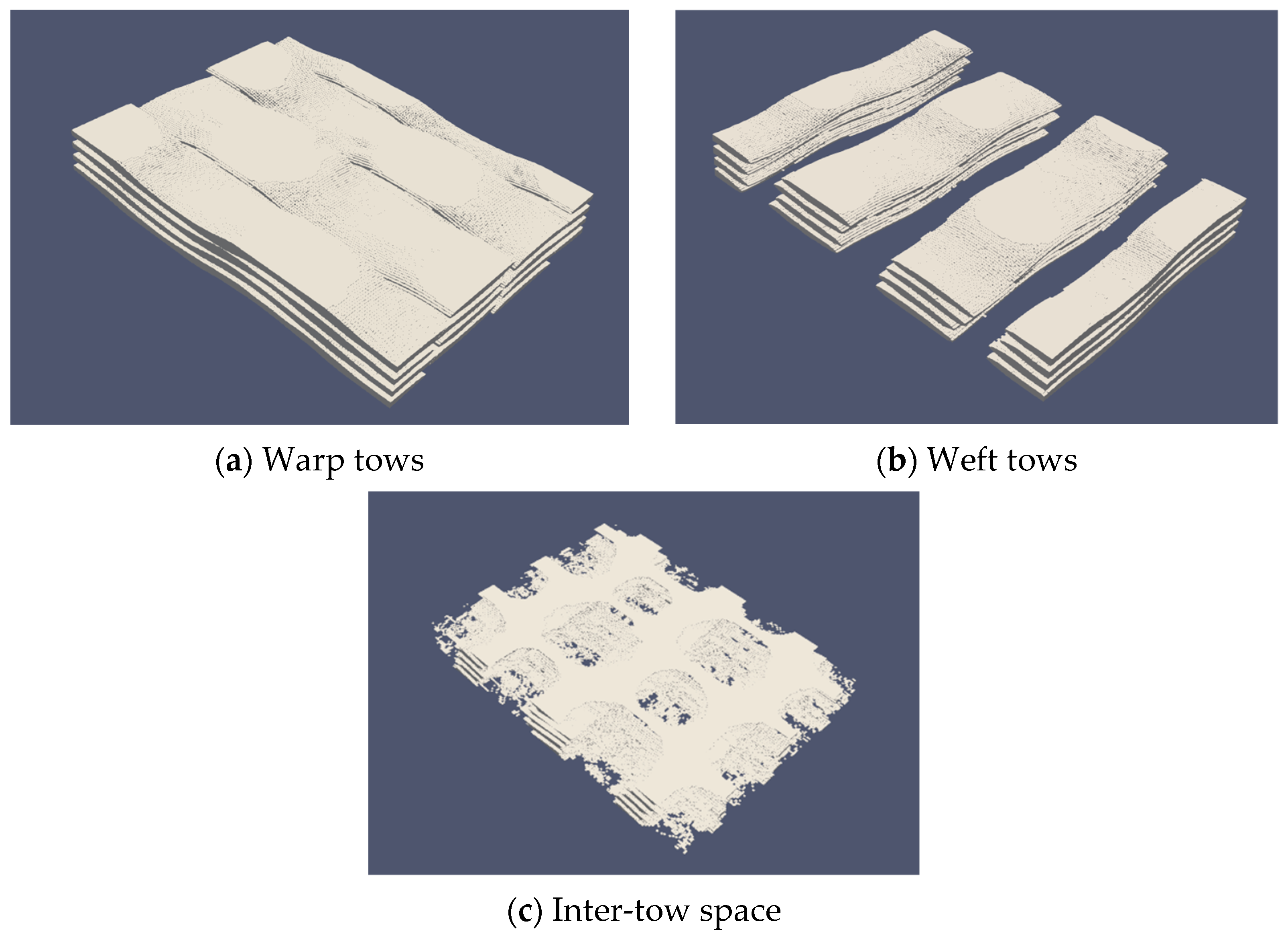
For the given 3D geometry data, three different stereolithography (STL) files suitable for numerical simulation were generated using a MATLAB algorithm. These STL files corresponded to the volume of the warp tows, weft tows, and inter-tow space (Figure 20). The algorithm is based on a 3D image processing methodology developed by Wijaya [29], which allows the segmentation of the reconstructed grayscale data of a woven textile into three groups: weft and warp tows and inter-tow space. Segmentation is a crucial step in the processing of grayscale images and affects the accuracy of numerical simulations. The methodology used separates the different zones with satisfactory quality, but more sophisticated methods using AI, for example, are being developed. Guibert et al. [30] discussed the effects of image processing techniques on phase identification in grayscale scanned geometries in their paper.

3.3.1. Single-Scale Flow

Here, the tows were considered solid impermeable zones (the fluid flows only in the inter-tow free space). In order to optimize the simulation time and allocated computational resources, only the inter-tow space was meshed (Figure 21), and the Navier–Stokes equations were solved in this domain. This approximation allows to reduce the computation resources used and is justified by the low permeability of the tows (${10}^{-13}–{10}^{-14}{\mathrm{m}}^2)$ [27].

The numerical approach described was used to compute the saturated permeability of the flow domain using the boundary conditions described in Figure 22. Note that the permeability values in the weft and warp directions were computed by specifying the axis of the pressure gradient, and, hence, the flow direction.

The viscosity of the simulated test fluid was set to $\mu =1\mathrm{m}\mathrm{P}\mathrm{a}.\mathrm{s}$ (close to the typical viscosity of industrially used resins [31]), and a pressure gradient $∆P=P_{in}-P_{out}=990\mathrm{P}\mathrm{a}$ is imposed between the inlet and the outlet.

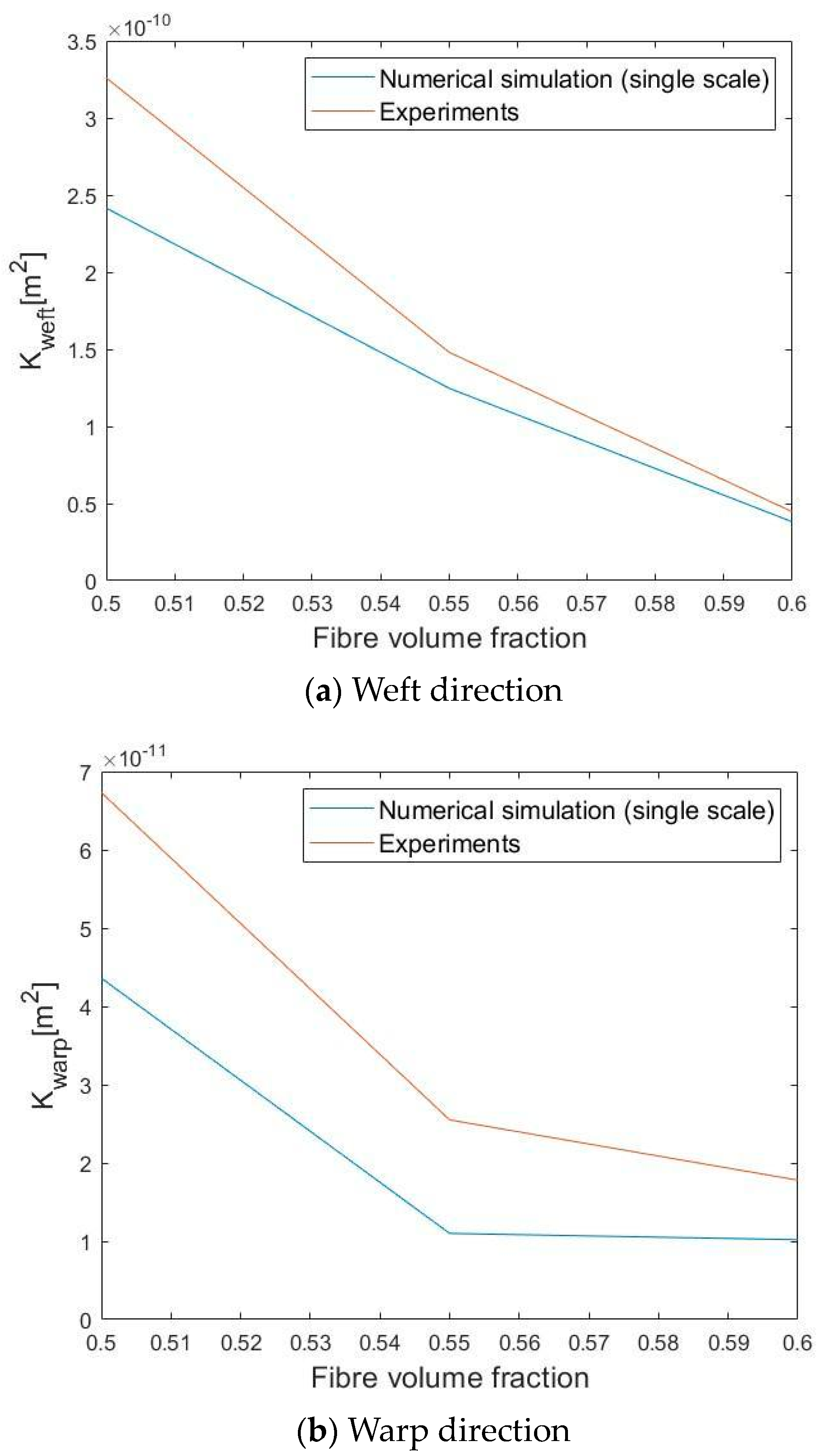
The permeability values in the weft and warp directions were computed using Equation (6). The flow in the meshed domain was simulated using the steady-state solver simpleFoam in OpenFoam v7 [32]. The flow rate was computed by integrating the flow velocity at the outlet surface. The results of the numerical permeability in the weft and warp directions, compared to the corresponding experimental values for different fiber volume fractions, are shown in Figure 23a and Figure 23b, respectively. The numerical method underestimates the experimental values, as expected, since the flow inside the tows was neglected in the simulation. A large scatter between the numerical simulation and the experimental results for the warp direction is observed (up to $56\%$) compared to the weft direction (maximum of $25\%$), which can be attributed to the insufficient scan accuracy and the small size of the flow channels in the warp direction. Therefore, these narrow geometries are more difficult to mesh and can eventually be artificially removed if they are badly shaped, and the permeability in the warp direction is largely underestimated [31]. This problem can be solved if the flow inside the tows is also simulated, as explained in the following section.

3.3.2. Dual-Scale Flow

Here, the tows were considered permeable, and the simulated fluid was allowed to flow between and inside the tow spaces. The Brinkman equation was adapted to solve such a multiscale flow problem. The same boundary conditions used in the single-scale simulations, Figure 22, were again used. The complete domain (i.e., inter-tow space, weft, and warp tows), as depicted in Figure 24, was meshed, and the interface elements between different spaces were chosen depending on the surface orientation of the tows’ geometry using the specific command useSurfaceOrientation in OpenFOAM. This command allows one to select all cells inside a closed surface, the tows in this case, in order to assign them specific properties. The permeability of the tows was computed using the Gebart analytical model, assuming a hexagonal arrangement of fibers. The fiber radius of the used glass fabric, needed as an input for the Gebart model, was measured using microscopy images, and an average of $12.12\mathsf{\mu }\mathrm{m}$ was found [14]. The local values of fiber volume fraction and permeability are given by the scan, whereas in the simulation, average and constant values are computed and assigned to the weft and warp tows, assuming that permeability tensors are diagonal for simplicity reasons since the off-diagonal permeability values do not affect the fluid flow in this case [33]. The values of permeability assigned to the weft and warp tows are given in equations 8 and 9. A geometric average was used to compute these values because of the non-periodic nature of the voxel’s permeability values. This approach was adapted from the averaging method used in random permeability distribution media in reservoir engineering [34].

$$K_{tows,warp}=\begin{array}{ccc}3.69·{10}^{-12}& 0& 0\\ 0& 7.68·{10}^{-13}& 0\\ 0& 0& 7.68·{10}^{-13}\end{array}{\mathrm{m}}^2$$

(8)

$$K_{tows,weft}=\begin{array}{ccc}1.78·{10}^{-12}& 0& 0\\ 0& 3.59·{10}^{-13}& 0\\ 0& 0& 3.59·{10}^{-13}\end{array}{\mathrm{m}}^2$$

(9)

An open-sourced multiscale Darcy–Brinkman solver called hybridPorousInterFoam was used for this simulation. This solver allows the simulation of two-phase flows in hybrid systems containing both porous matrices and solid-free regions [35]. A unique set of partial differential equations is used to represent the flow in both regions using the same mesh without the need to define complex interfacial conditions.

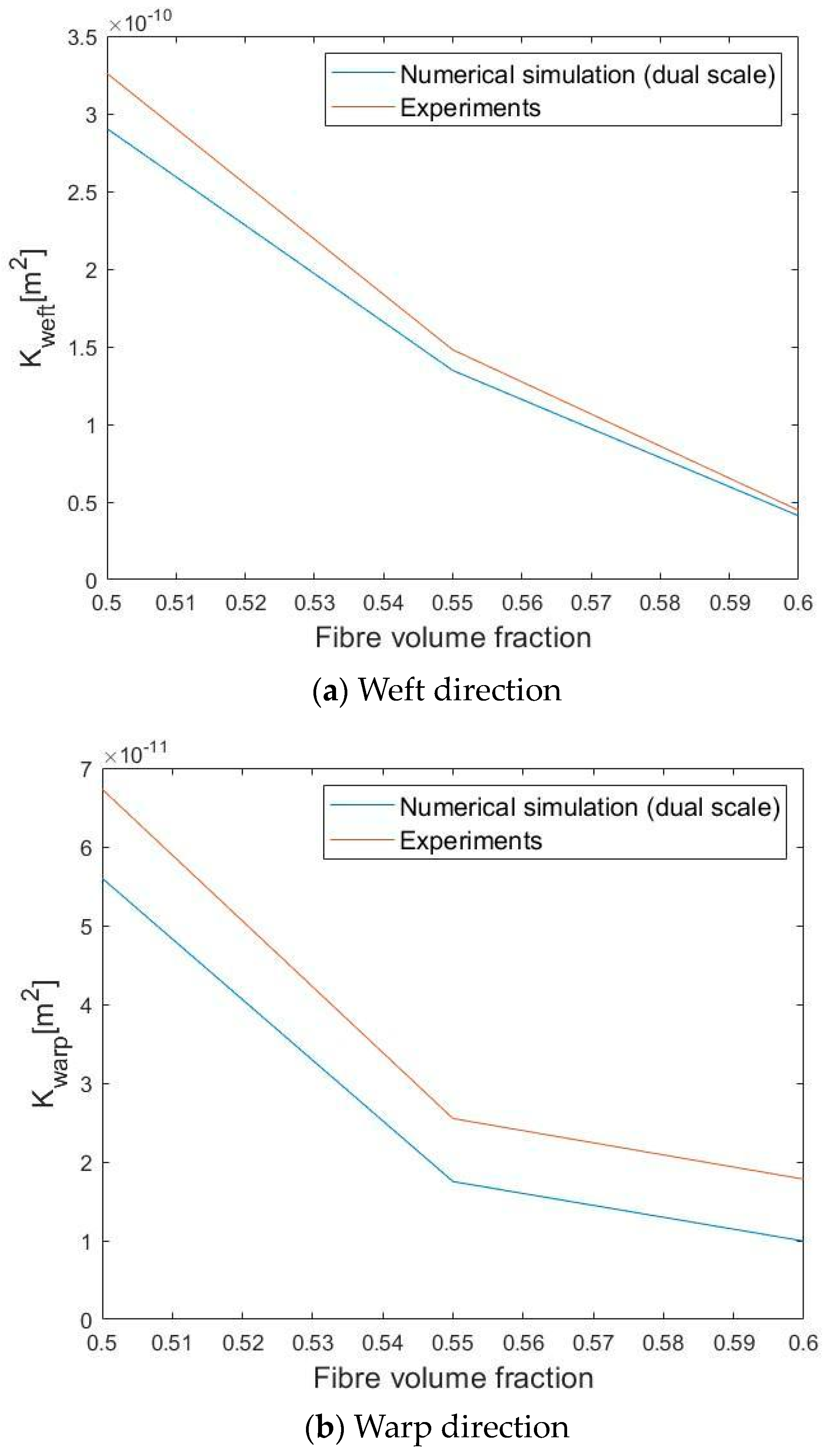
As can be observed in Figure 25, the permeability values obtained by this numerical method are closer to the experimental values than those obtained by the single-scale tests. The deviation from the experimental values is reduced to 11% for $V_f=0.5$ and 8% for $V_f=0.6$ in the weft direction, and it is around 20% in the warp direction; this is a significant improvement in permeability prediction accuracy compared to the single-scale simulation results. Nonetheless, there is still a deviation that can be reduced by refining the mesh of the computational domain further, as demonstrated by Guibert et al. [36]. The experimental/numerical deviations in this case can be explained by the assumption of constant permeability and porosity in the weft and warp directions, neglecting local variations in these parameters.

4. Conclusions

A 2D radial flow experimental setup was used to investigate the discrepancy between the unsaturated and saturated permeabilities and to observe the flow front during the fluid injection of different types of textiles. The experimental setup detailed in this article provides robust and repeatable unsaturated and saturated permeability data with reduced errors. The ratio between both permeabilities was between 0.9 and 1.42, which lay in the range found in the literature and was coherent with the flow front observations; the difference between both permeabilities was higher for the Unidirectional and Biaxial textiles corresponding to higher permeability ratios, for example. It was also confirmed that the flow front shape and the ratio ${\displaystyle \raisebox{1ex}{$K_{unsat}$}\!\left/ \!\raisebox{-1ex}{$K_{sat}$}\right.}$ depend on the properties of the used textiles, such as the stitching style, areal weight, and especially the size of the inter-tow space, which shows the importance of the capillary effects on the fluid flow in porous media.

Two numerical methods for saturated permeability prediction were proposed. The first method is based on solving the Navier–Stokes equations in the inter-tow space and neglecting the permeability of the tows. In the second method, the flow inside the tows was considered using a specific OpenFOAM solver based on solving the Brinkman equations in multiscale domains. Both methods were used to measure the permeability of the scanned textile, and the results were compared with the experimental values given by the previously described setup. The dual-scale method gave results closer to those of the experiments, which shows the importance of using a multiscale approach to model the flow of fibrous reinforcements. The main challenge with these methods is their dependence on the quality of the scanned geometry, segmentation algorithm, and mesh refinement. Permeability determination using numerical simulations is a topic that is under development, as no standard method currently exists. The second part of this article contributes to the standardization efforts of virtual permeability determination, as international benchmark exercises are being launched to identify the different numerical methods that can be used for permeability measurement based on real images. The solver used in the dual-scale numerical method can also be used to simulate the resin flow front advancement during impregnation in order to visualize the filling scenario and to identify the locations of the potential dry spots, which can be the subject of upcoming work.