On Hens, Eggs, Temperatures and CO2: Causal Links in Earth’s Atmosphere
Abstract
:Science is generated by and devoted to free inquiry: the idea that any hypothesis, no matter how strange, deserves to be considered on its merits. The suppression of uncomfortable ideas may be common in religion and politics, but it is not the path to knowledge; it has no place in the endeavor of science. We do not know in advance who will discover fundamental new insights.Carl Sagan [1]
1. Introduction
Clearly, the results […] suggest a (mono-directional) potentially causal system with T as the cause and [CO2] as the effect. Hence the common perception that increasing [CO2] causes increased T can be excluded as it violates the necessary condition for this causality direction.
[…] in other words, it is the increase of temperature that caused increased CO2 concentration. Though this conclusion may sound counterintuitive at first glance, because it contradicts common perception […], in fact it is reasonable. The temperature increase began at the end of the Little Ice Period, in the early nineteenth century, when human CO2 emissions were negligible […].
- To expand the time frame of the investigation backward and forward by exploiting the longest available data series (Section 4).
- To check whether seasonality, as reflected in different phases of [CO2] time series at different latitudes, plays any role that could modify or possibly reverse the detected causality relationship (Section 5).
- To propose and apply a method for investigating the effect of the timescale in causality detection (Section 6).
- To extend the methodology for disambiguating cases in which the type of causality, HOE or unidirectional, is not quite clear (Section 7).
- To exploit the methodology in defining a type of data analysis that, regardless of the detection of causality per se, could shed light on modeling performance by comparing observational data with model results (Section 8).
- To discuss possible extensions of the scope of the methodology, i.e., from detecting possible causality to building a more detailed model of stochastic type (Section 9).
- To provide logical support for the findings by revisiting the carbon balance in the atmosphere (Appendix A.1) and investigating additional processes that may have caused increases in temperature (Appendix A.2, Appendix A.3 and Appendix A.4).
2. Summary of the Stochastic Approach to Causality
- Potentially HOE causal if we have for both some positive and some negative lags j,
- Potentially causal if for all , and
- Potentially anticausal if for all
3. Data and Case Studies
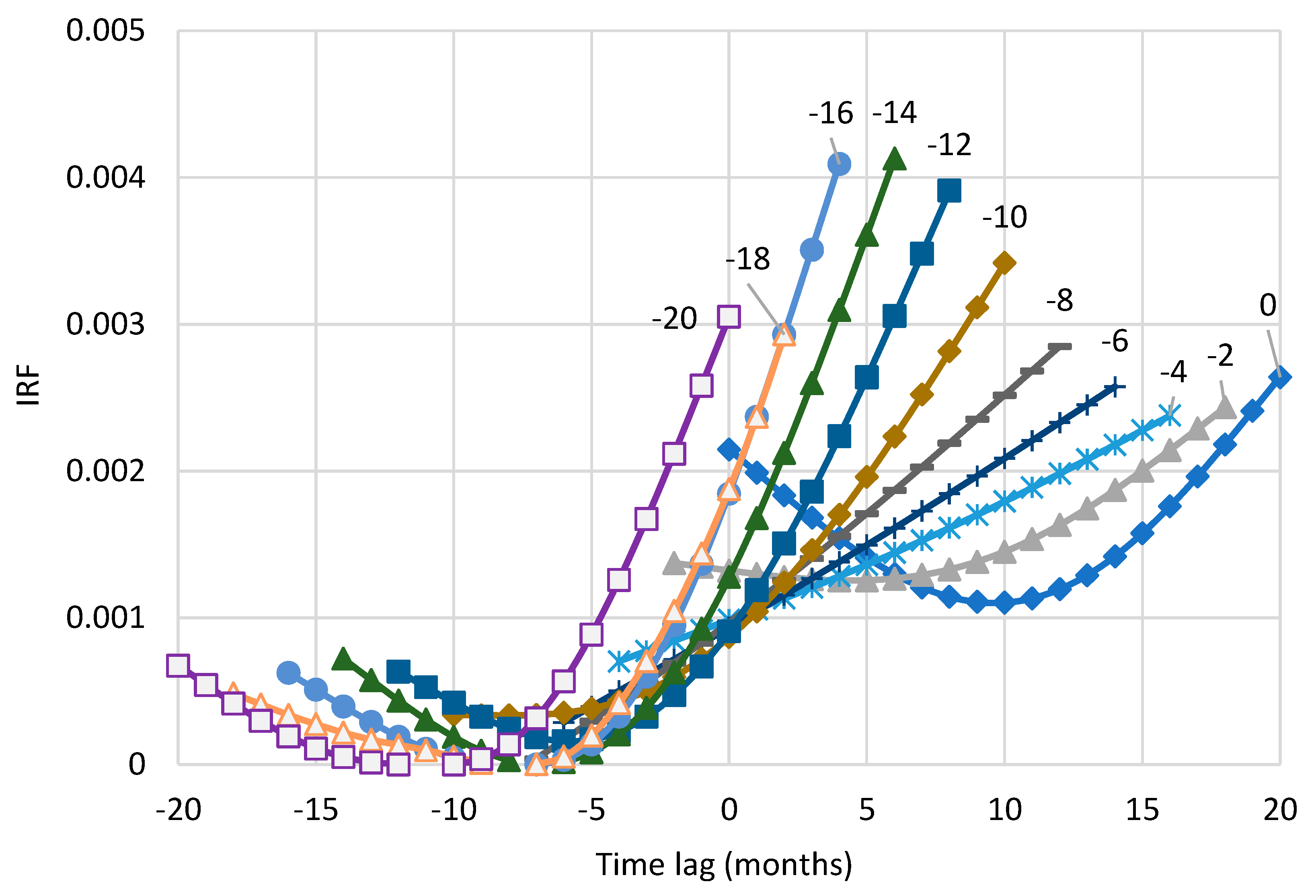
4. Investigating the Maximum Time Span That Modern Data Allow
5. Investigating the Possible Effect of Seasonality
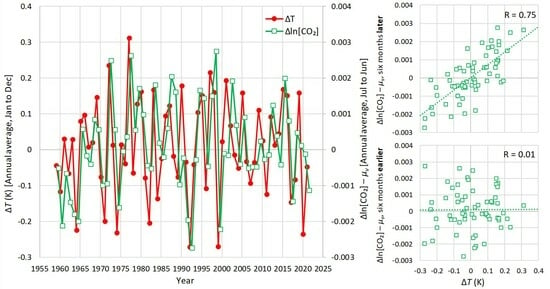
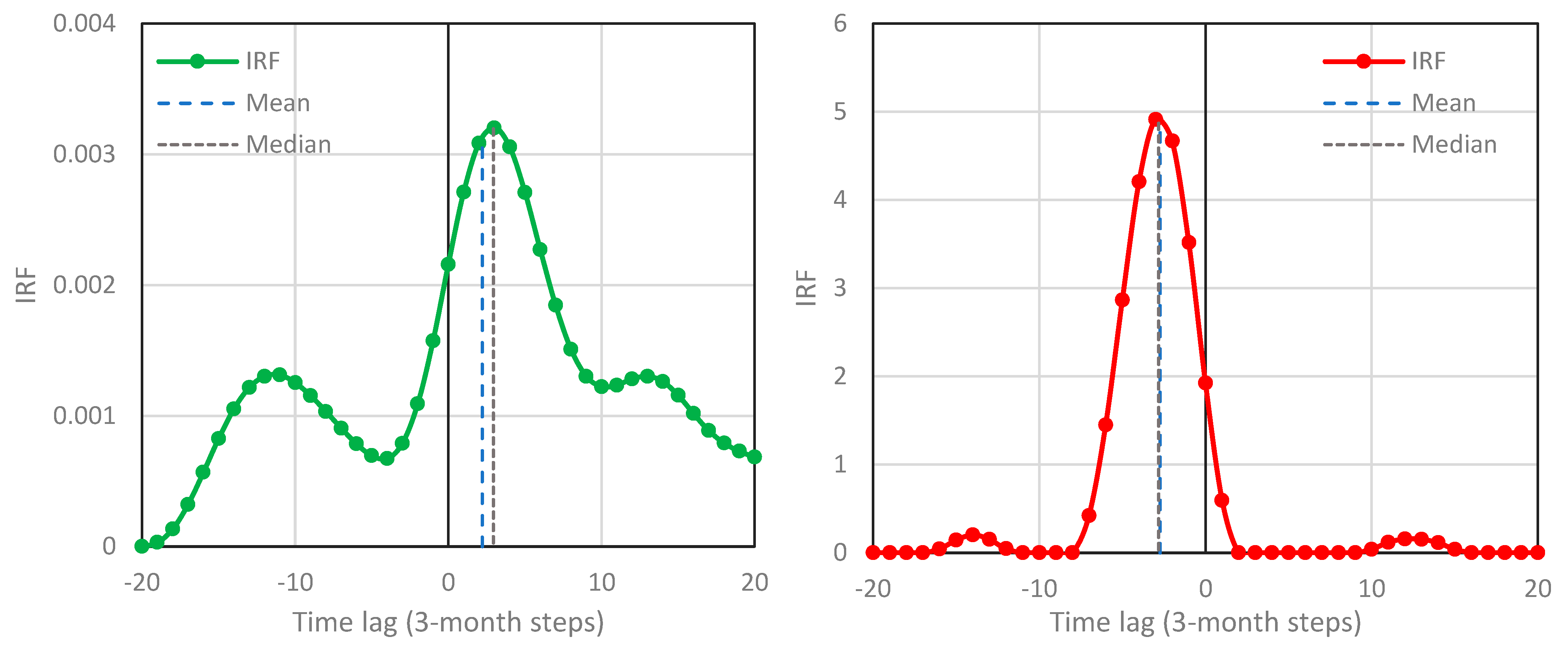
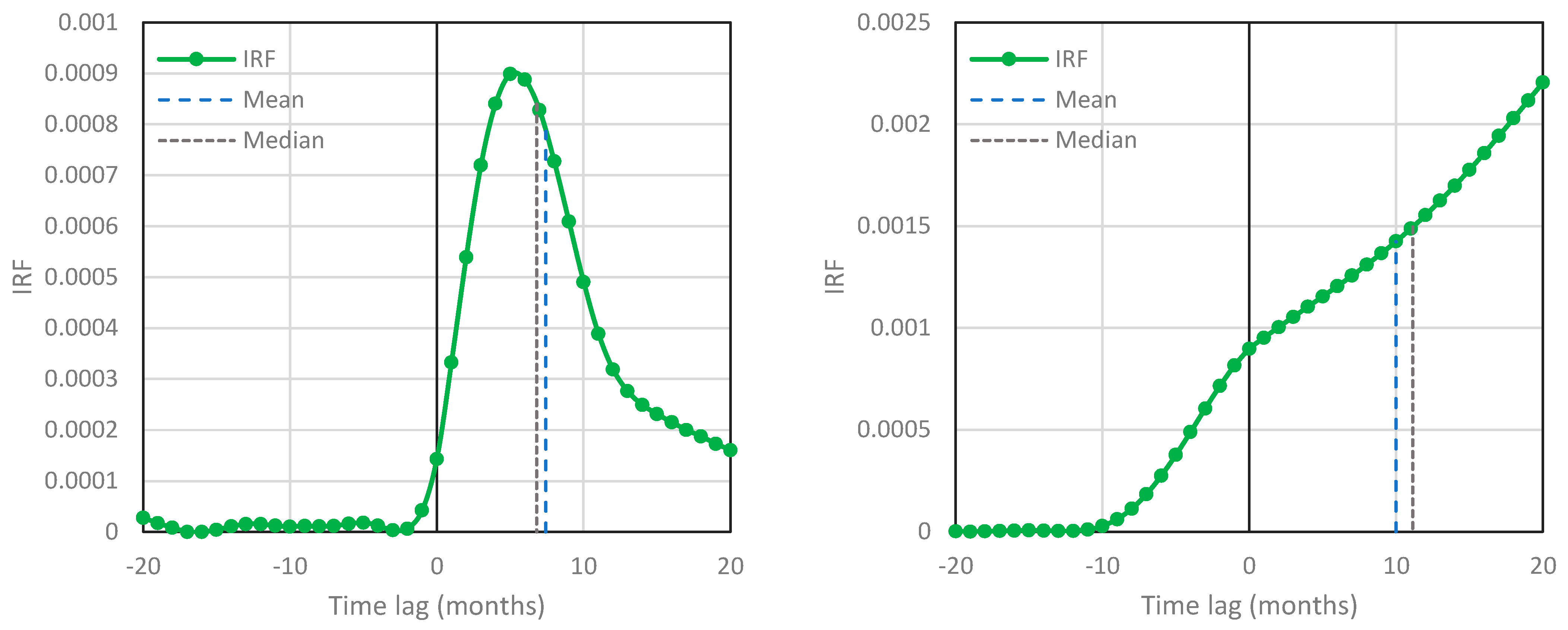
- The system T-[CO2] appears to be potentially causal (unidirectional) in the direction , rather than hen-or-egg causal.
- All characteristic time lags () are positive in the direction (ranging from about 7 to about 10 months), and negative in the direction .
- The explained variance ratio is greater in the direction (about 1/3) than in the direction (around 1/5).
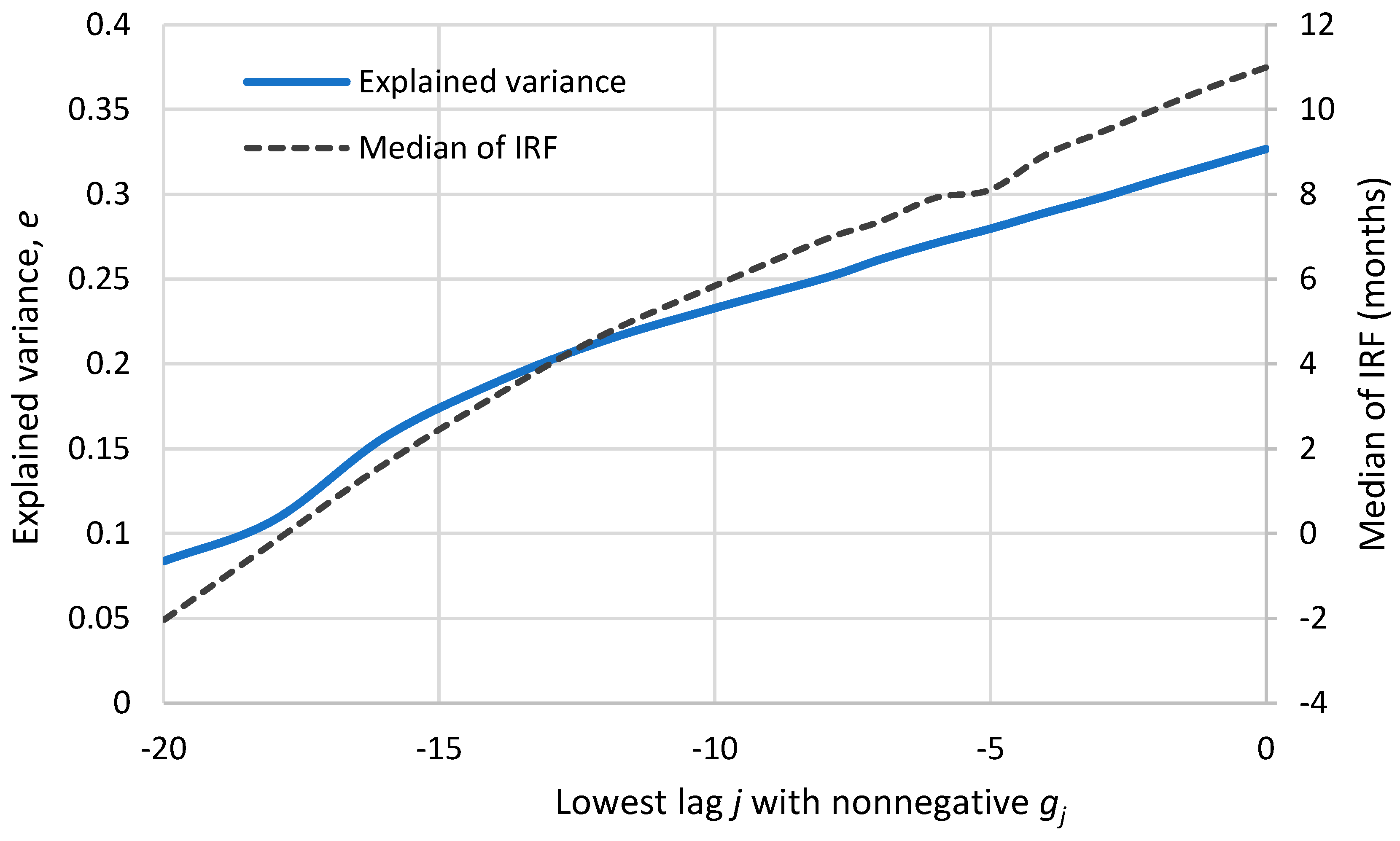
6. On the Timescale of Validity of Results
7. Possible Ambiguities and Disambiguation
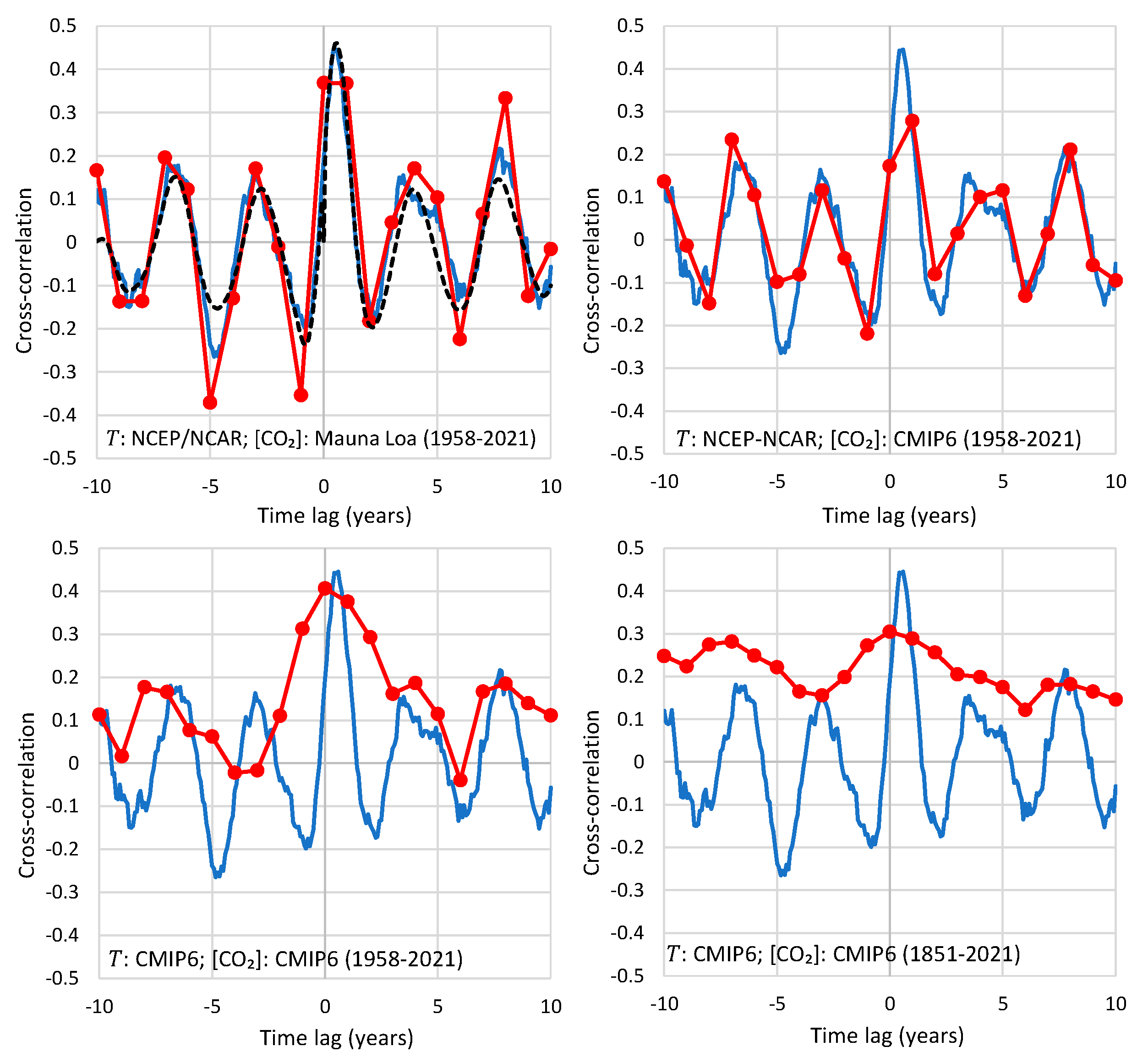
8. Comparing Observational Data with Model Results
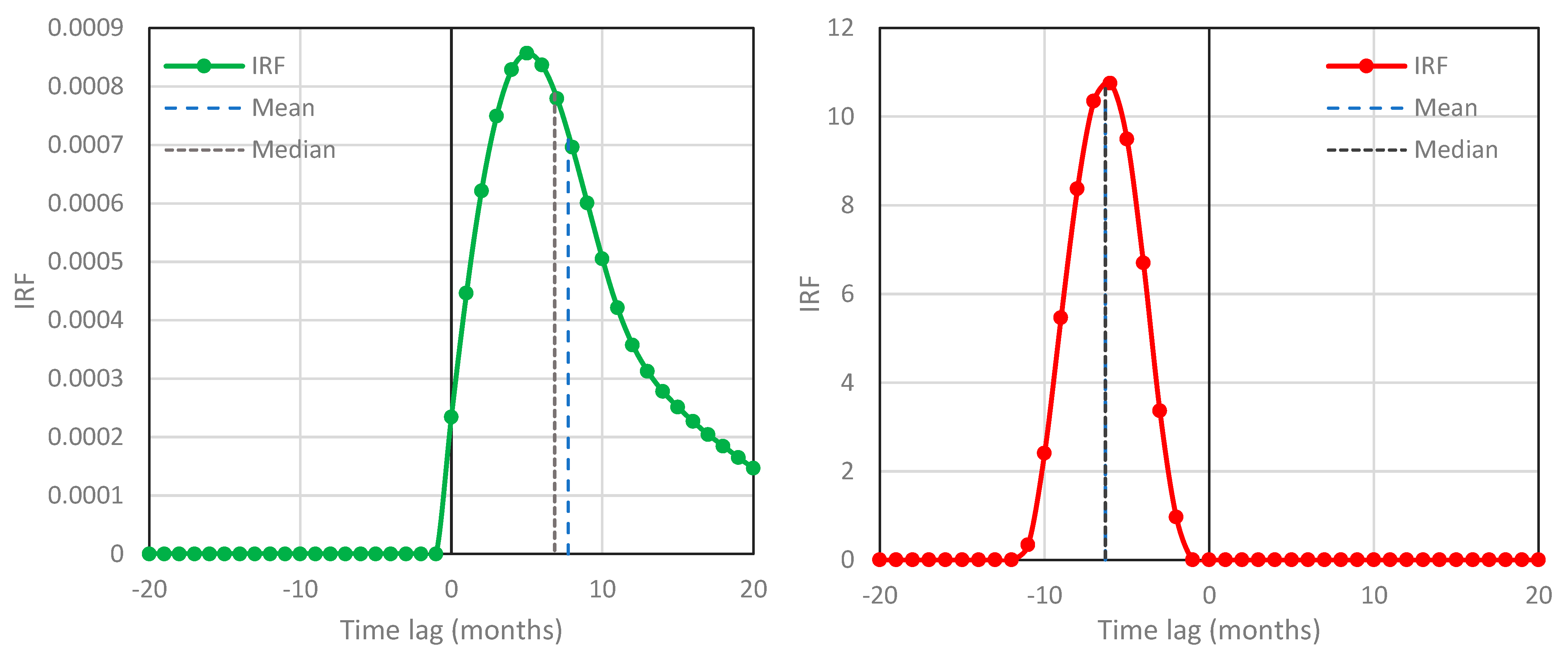
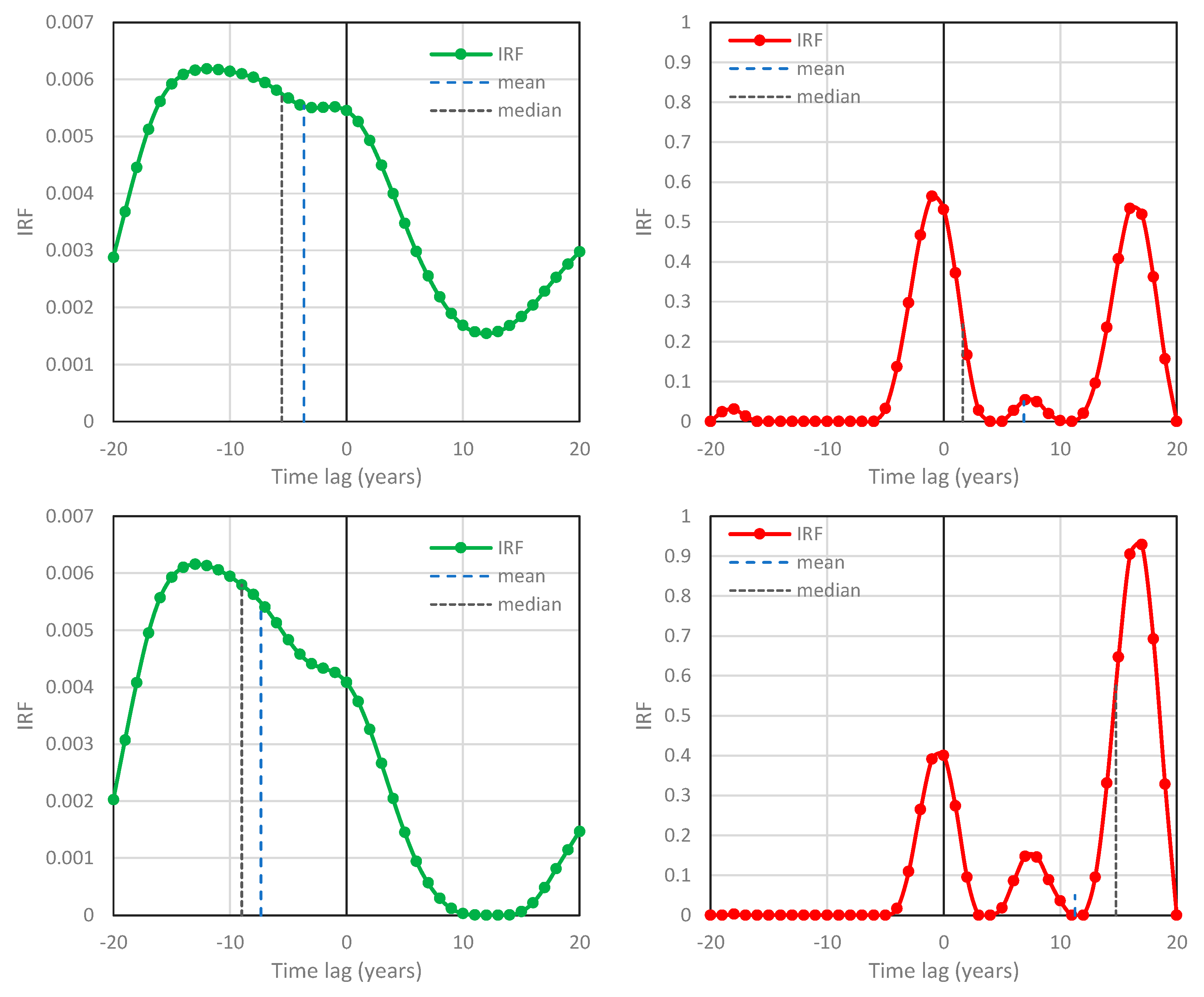
- There is no essential difference between the results for the periods 1850–2100 and 1850–2021.
- While, as expected, the IRFs differ if they are calculated with or without constraining roughness, the characteristic lags are similar in the two cases (with the exception of in cases #17 and #21).
- In all cases, the lags are negative in the direction and positive in the direction , suggesting a HOE causality with principal direction .
- Clearly, the finding in point 3, resulting from climate model outputs, is opposite to the results found when real measurements are used (NCEP/NCAR Reanalysis temperature and Mauna Loa [CO2] time series).
- Oddly, while the principal direction suggested by the models is , the explained variance is impressively low (10–15%) in this direction and impressively high (reaching 90%) in the opposite direction, .
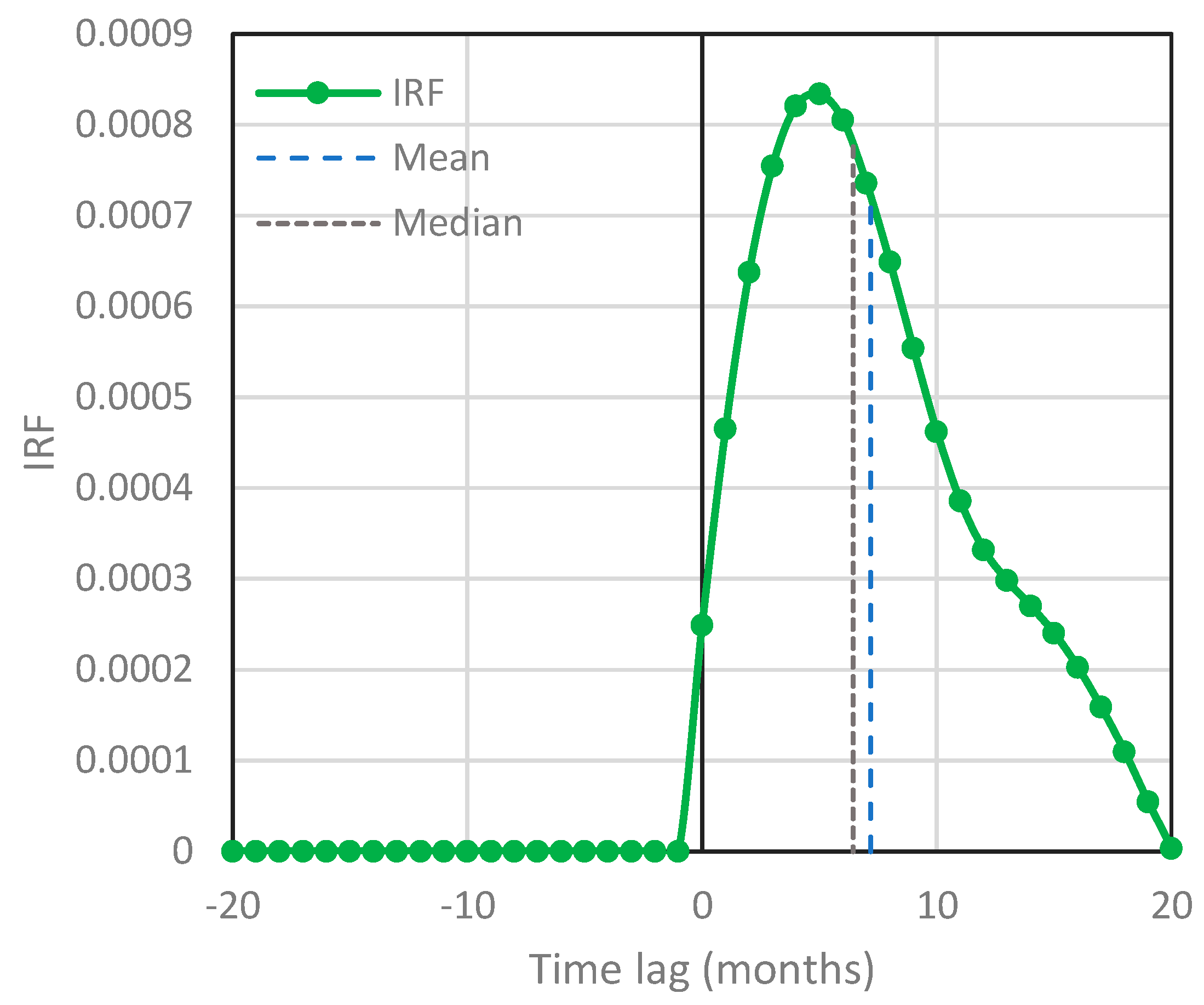
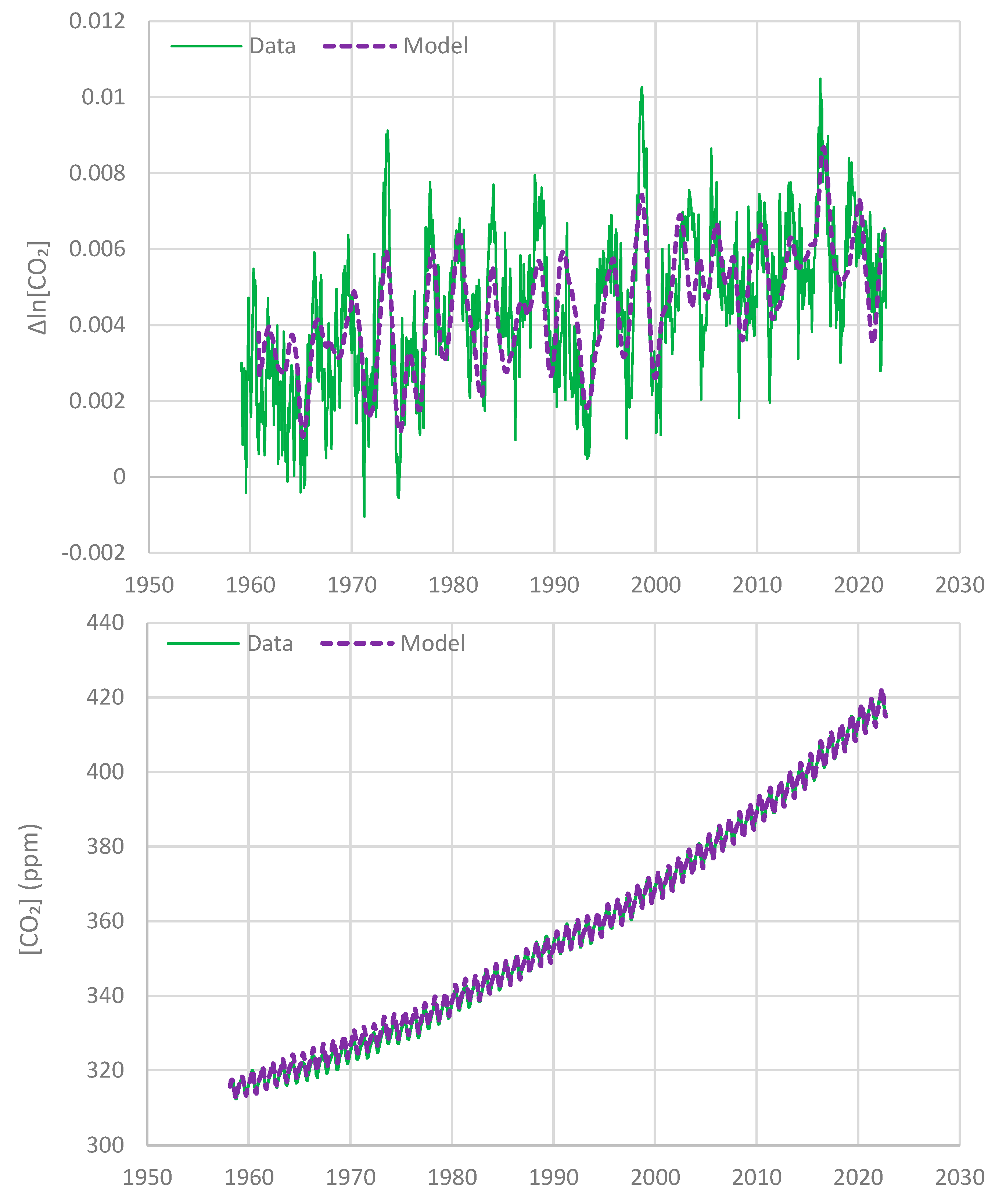
9. Discussion and Further Results
- The dependence of the carbon cycle on temperature is quite strong and indeed major increases of [CO2] can emerge as a result of temperature rise. In other words, we show that the natural [CO2] changes due to temperature rise are far larger (by a factor > 3) than human emissions (Appendix A.1).
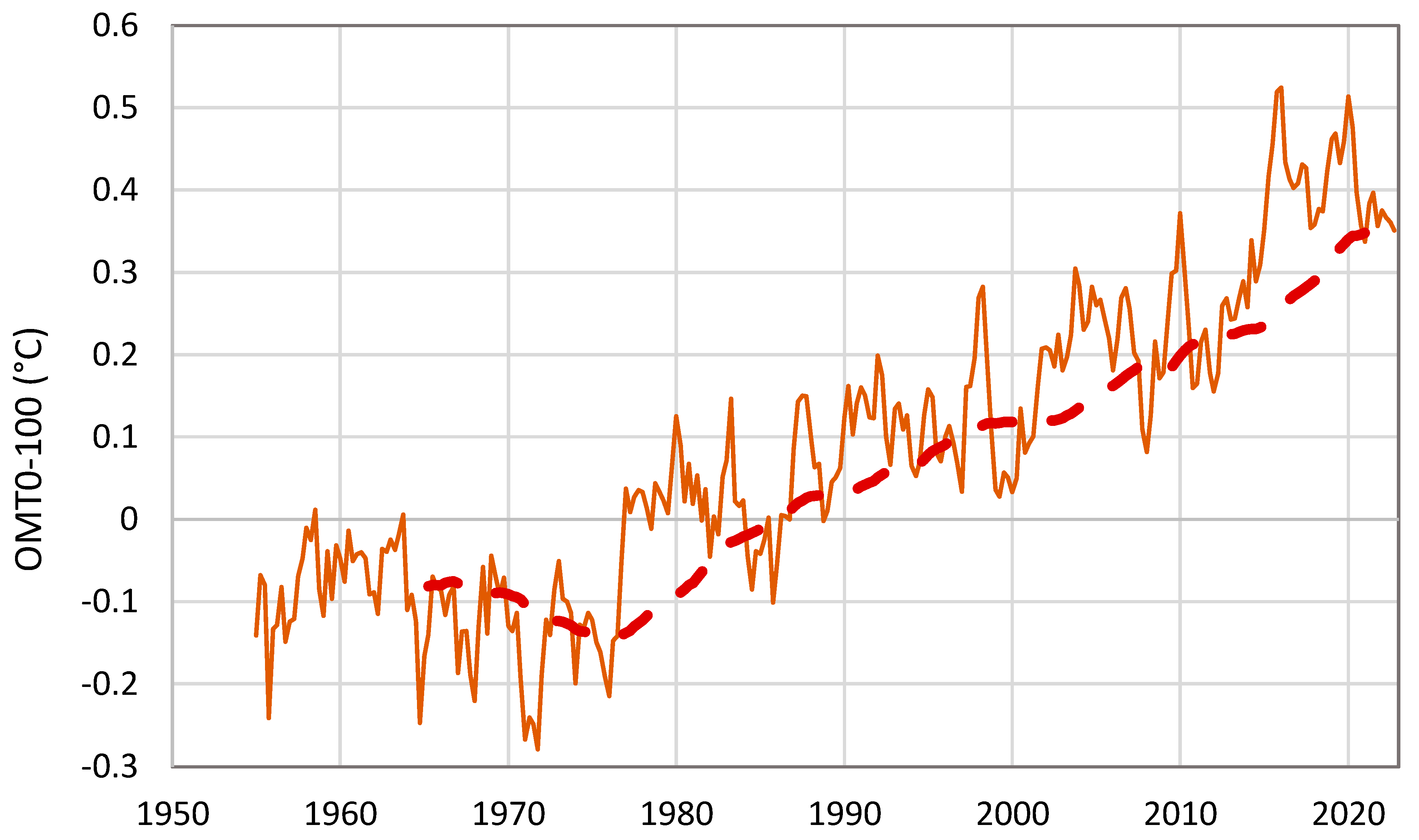
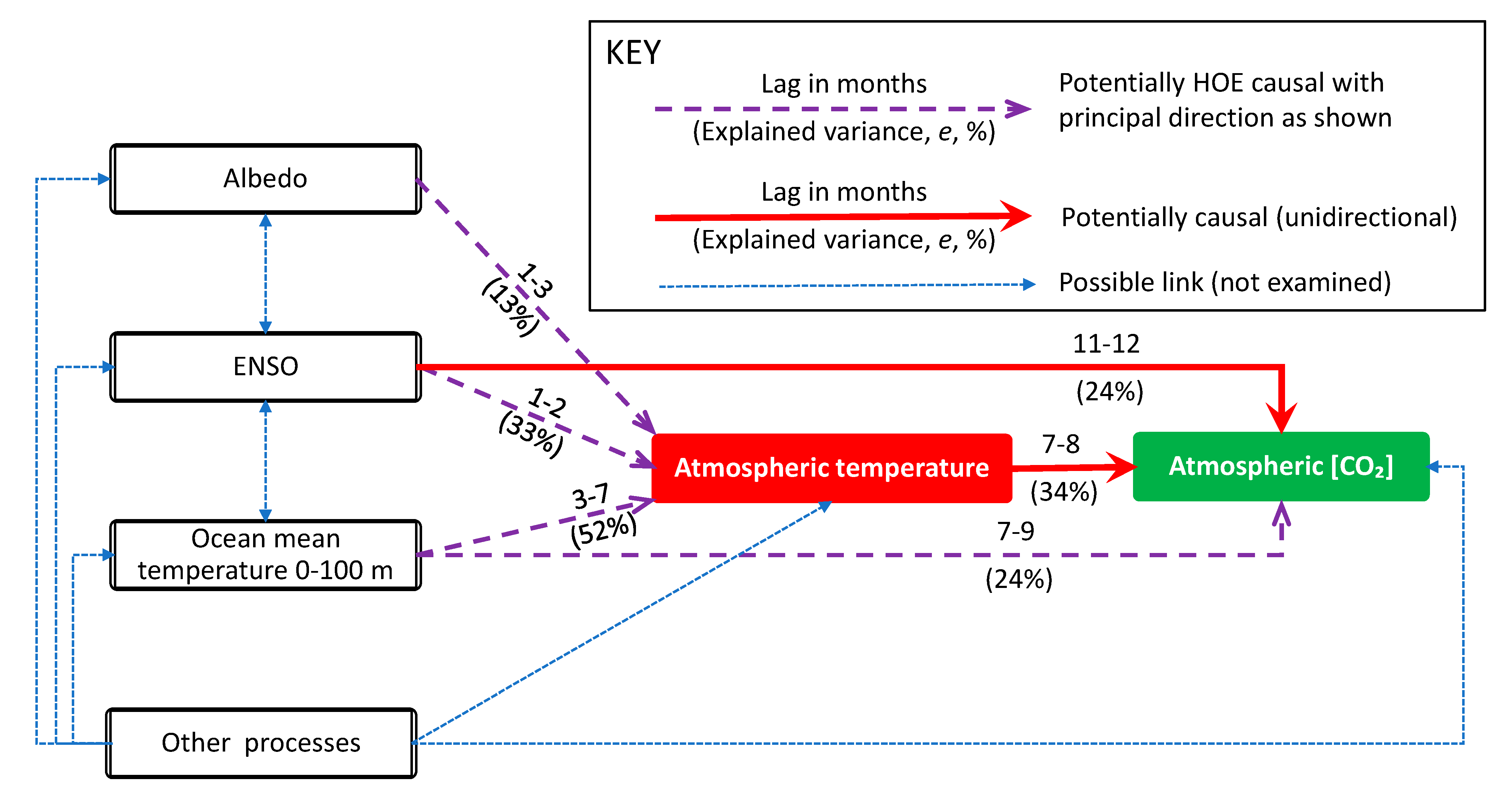
- There are processes, such as the Earth’s albedo (which is changing in time as any other characteristic of the climate system), the El Niño–Southern Oscillation (ENSO) and the ocean heat content in the upper layer (represented by the vertically averaged temperature in the layer 0–100 m), which are potential causes of the temperature increase, unlike what is observed with [CO2], their changes precede those of temperature (Appendix A.2, Appendix A.3 and Appendix A.4).
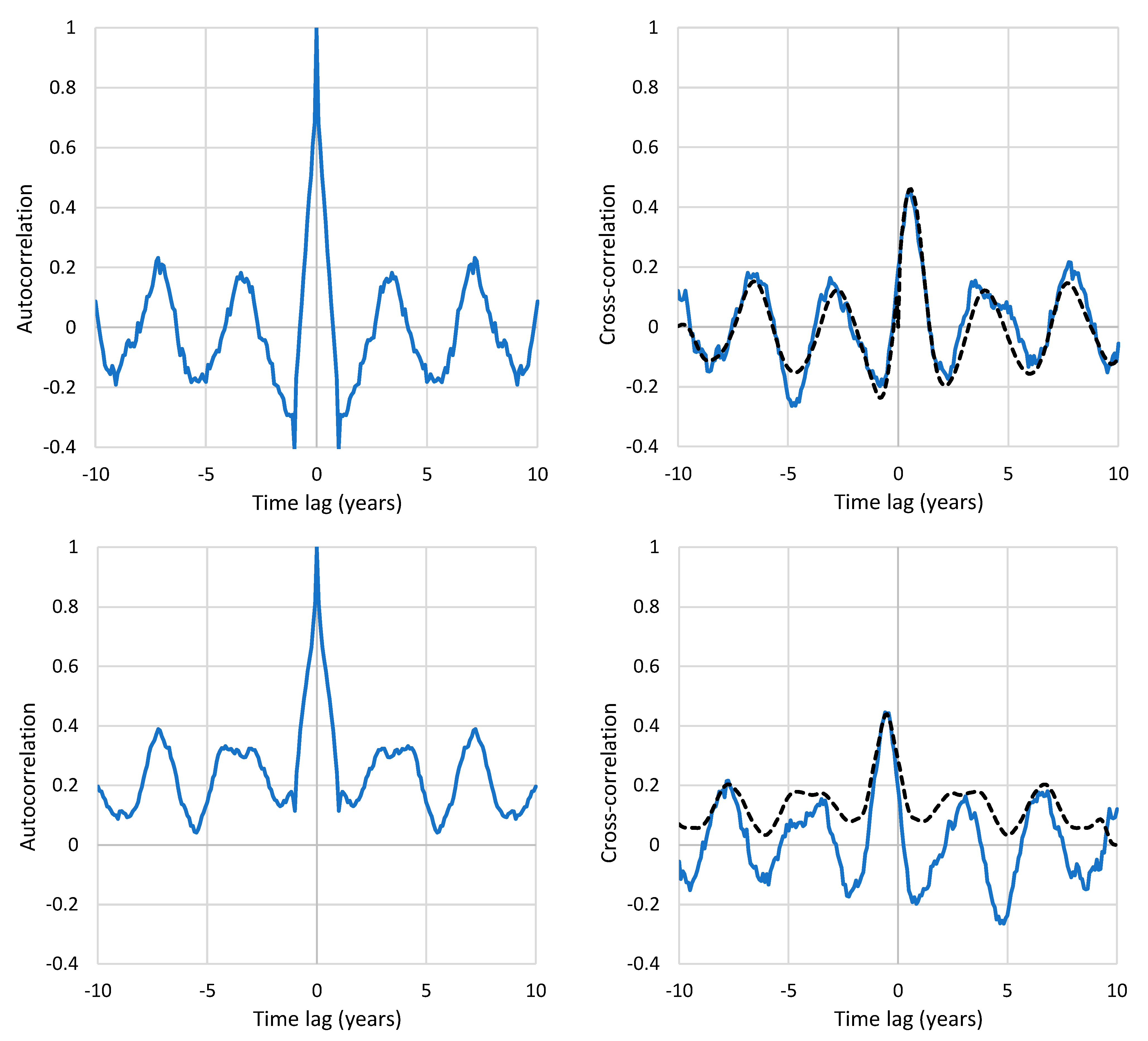
- On a large timescale, the analysis of paleoclimatic data supports the primacy of the causal direction T → [CO2], even though some controversy remains about this issue (Appendix A.5).
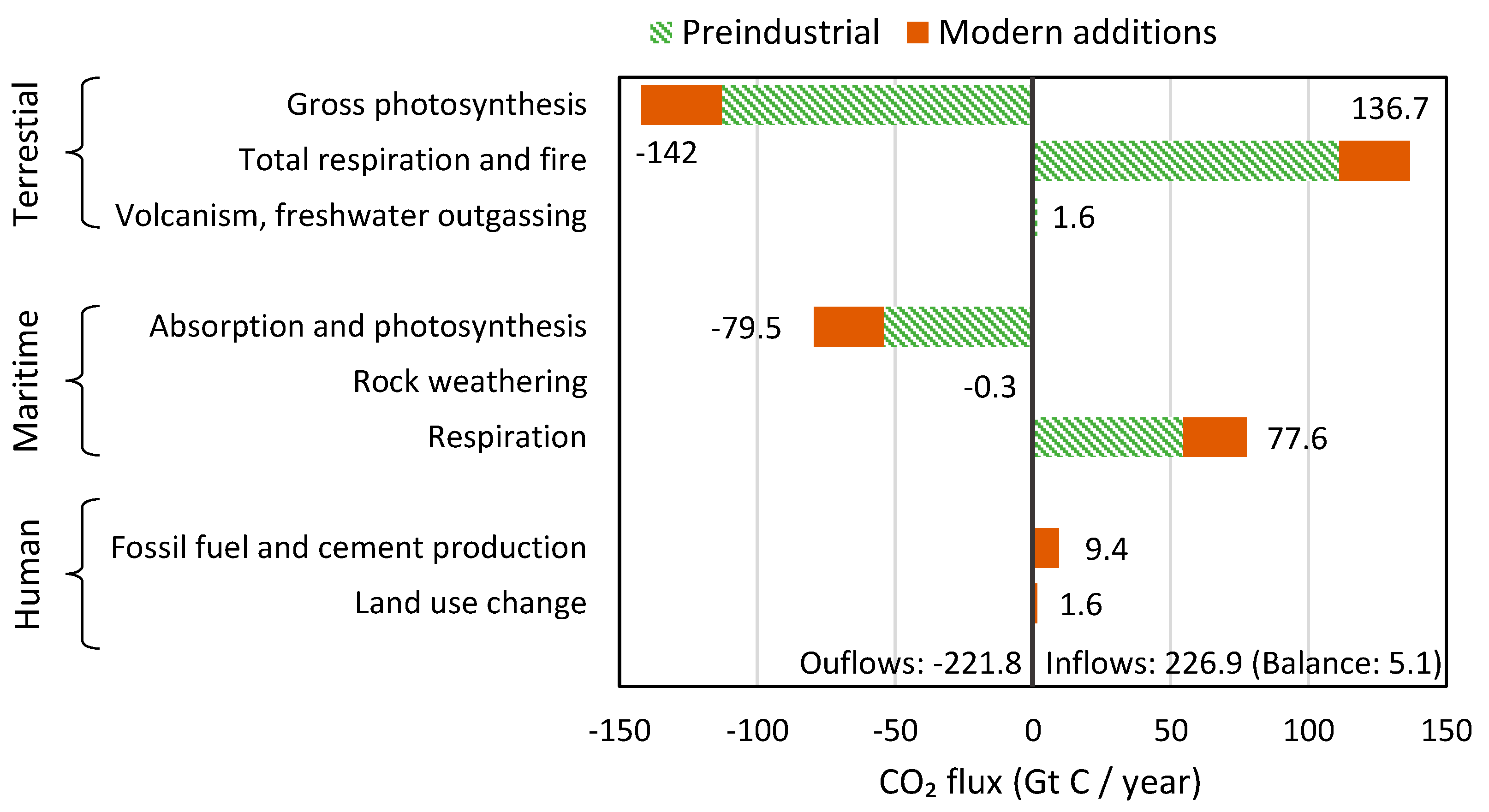
- Terrestrial and maritime respiration and decay are responsible for the vast majority of CO2 emissions [32], Figure 5.12.
- Overall, natural processes of the biosphere contribute 96% to the global carbon cycle, the rest, 4%, being human emissions (which were even lower in the past [33]).
- The biosphere is more productive at higher temperatures, as the rates of biochemical reactions increase with temperature, which leads to increasing natural CO2 emission [2].
- Additionally, a higher atmospheric CO2 concentration makes the biosphere more productive via the so-called carbon fertilization effect, thus resulting in greening of the Earth [34,35], i.e., amplification of the carbon cycle, to which humans also contribute through crops and land-use management [36].
10. Conclusions
- All evidence resulting from the analyses of the longest available modern time series of atmospheric concentration of [CO2] at Mauna Loa, Hawaii, along with that of globally averaged T, suggests a unidirectional, potentially causal link with T as the cause and [CO2] as the effect. This direction of causality holds for the entire period covered by the observations (more than 60 years).
- Seasonality, as reflected in different phases of [CO2] time series at different latitudes, does not play any role in potential causality, as confirmed by replacing the Mauna Loa [CO2] time series with that in South Pole.
- The unidirectional potential causal link applies to all timescales resolved by the available data, from monthly to about two decades.
- The proposed methodology is simple, flexible and effective in disambiguating cases where the type of causality, HOE or unidirectional, is not quite clear.
- Furthermore, the methodology defines a type of data analysis that, regardless of the detection of causality per se, assesses modeling performance by comparing observational data with model results. In particular, the analysis of climate model outputs reveals a misrepresentation of the causal link by these models, which suggest a causality direction opposite to the one found when the real measurements are used.
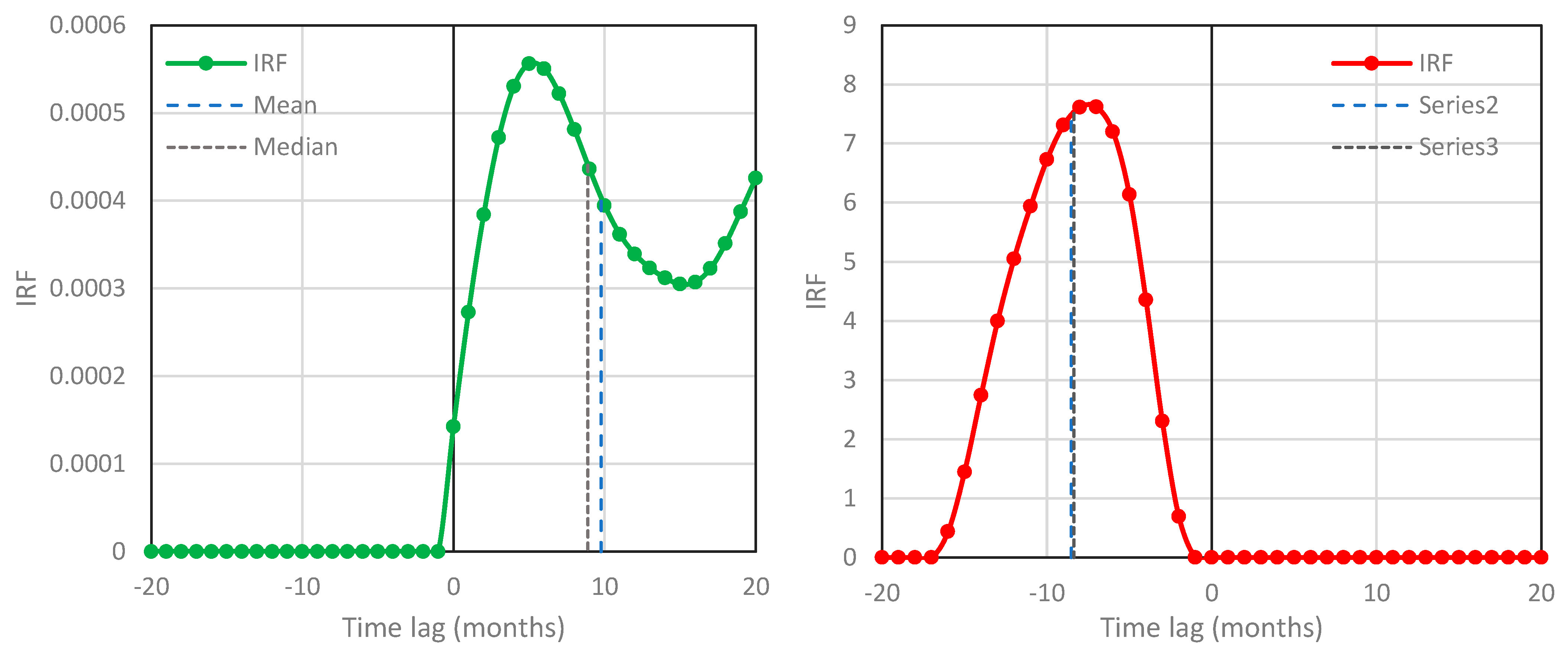
- Extensions of the scope of the methodology, i.e., from detecting possible causality to building a more detailed model of stochastic type, are possible, as illustrated by a toy model for the T-[CO2] system, with explained variance of [CO2] reaching an impressive 99.9%.
- While some of the findings of this study seem counterintuitive or contrary to mainstream opinions, they are logically and computationally supported by arguments and calculations given in the Appendices.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Notes on Carbon Cycle and its Dependence on Temperature

Appendix A.2. Investigation of Causality between Albedo and Atmospheric Temperature

| Case System | # | Direction | ||||||
|---|---|---|---|---|---|---|---|---|
| Albedo, α: CERES, TERRA; T: NCEP/NCAR; period: 2000–2022 | 24 | 3 | 1.08 | 2.90 | 0.24 | 0.13 | 9.1 × 10–4 | |
| 25 | –3 | –0.31 | –2.46 | 0.24 | 0.06 | 3.6 × 10–4 |

Appendix A.3. Investigation of Causality between El Niño, Atmospheric Temperature and CO2

| Case System | # | Direction | ||||||
|---|---|---|---|---|---|---|---|---|
| : NOAA; T: NCEP/NCAR; period: 1951–2022 | 26 | 3 | 4.14 | 3.85 | 0.46 | 0.33 | 8.1 × 10–4 | |
| 27 | 3 | –2.15 | –0.93 | 0.46 | 0.30 | 2.3 × 10–3 | ||
| : NOAA; [CO2]: Mauna Loa, period: 1958–2022 | 28 | 11 | 11.62 | 11.15 | 0.32 | 0.24 | 6.6 × 10–4 | |
| 29 | –11 | −3.73 | –3.84 | 0.32 | 0.08 | 0 |

Appendix A.4. Investigation of Causality between Ocean Heat Content, Atmospheric Temperature and CO2
| Case System | # | Direction | ||||||
|---|---|---|---|---|---|---|---|---|
| OMT0–100: NOAA; T: NCEP/NCAR; period: 1955–2022 | 30 | ΔOMT0–100 | 0 | 2.42 | 0.98 | 0.68 | 0.53 | 7.1 × 10–3 |
| 31 | ΔOMT0–100 | 0 | –2.15 | –0.93 | 0.68 | 0.52 | 3.8 × 10–3 | |
| OMT0–100: NOAA; [CO2]: Mauna Loa; period: 1958–2022 | 32 | ΔOMT0–100 | 2 | 2.22 | 2.93 | 0.46 | 0.35 | 5.8 × 10–4 |
| 33 | ΔOMT0–100 | –2 | −2.73 | –2.82 | 0.46 | 0.21 | 5.6 × 10–3 |

Appendix A.5. Notes on the T-[CO2] Relationship on Large Timescales
References
- Sagan, C. Cosmos; Ballantine Books: New York, NY, USA, 1985. [Google Scholar]
- Koutsoyiannis, D.; Kundzewicz, Z.W. Atmospheric temperature and CO2: Hen-or-egg causality? Sci 2020, 2, 83. [Google Scholar] [CrossRef]
- Πλούταρχος, Συμποσιακά Β’ (Plutarch, Quaestiones Convivales B’)—Βικιθήκη. Available online: https://el.wikisource.org/wiki/Συμποσιακά_Β΄ (accessed on 5 February 2023).
- Chan, K.H.; Hayya, J.C.; Ord, J.K. A note on trend removal methods: The case of polynomial regression versus variate differencing. Econometrica 1977, 45, 737–744. [Google Scholar] [CrossRef]
- Estrella, A. Why does the yield curve predict output and inflation? Econ. J. 2005, 115, 722–744. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Christofides, A.; Kundzewicz, Z.W. Revisiting causality using stochastics: 1. Theory. Proc. R. Soc. A 2022, 478, 20210836. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Christofides, A.; Kundzewicz, Z.W. Revisiting causality using stochastics: 2. Applications. Proc. R. Soc. A 2022, 478, 20210835. [Google Scholar] [CrossRef]
- Young, P.C. Recursive Estimation and Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Young, P.C. Refined instrumental variable estimation: Maximum likelihood optimization of a unified Box-Jenkins model. Automatica 2015, 52, 35–46. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Kestin, T.S.; Karoly, D.J.; Yang, J.I.; Rayner, N.A. Time-frequency variability of ENSO and stochastic simulations. J. Clim. 1998, 11, 2258–2272. [Google Scholar] [CrossRef]
- Wills, R.C.; Schneider, T.; Wallace, J.M.; Battisti, D.S.; Hartmann, D.L. Disentangling global warming, multidecadal variability, and El Niño in Pacific temperatures. Geophys. Res. Lett. 2018, 45, 2487–2496. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Granger, C.W. Testing for causality: A personal viewpoint. J. Econ. Dyn. Control. 1980, 2, 329–352. [Google Scholar] [CrossRef]
- Moraffah, R.; Sheth, P.; Karami, M.; Bhattacharya, A.; Wang, Q.; Tahir, A.; Raglin, A.; Liu, H. Causal inference for time series analysis: Problems, methods and evaluation. Knowl. Inf. Syst. 2021, 63, 3041–3085. [Google Scholar] [CrossRef]
- Pearl, J. Causal inference in statistics: An overview. Stat. Surv. 2009, 3, 96–146. [Google Scholar] [CrossRef]
- Pearl, J.; Glymour, M.; Jewell, N.P. Causal Inference in Statistics: A Primer; Wiley: Chichester, UK, 2016. [Google Scholar]
- Pearl, J. and Mackenzie, D., The Book of Why, The New Science of Cause and Effect, Basic Books: New York, NY, USA, 2018.
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Meinshausen, M.; Nicholls, Z.R.J.; Lewis, J.; Gidden, M.J.; Vogel, E.; Freund, M.; Beyerle, U.; Gessner, C.; Nauels, A.; Bauer, N.; et al. The shared socio-economic pathway (SSP) greenhouse gas concentrations and their extensions to 2500. Geosci. Model Dev. 2020, 13, 3571–3605. [Google Scholar] [CrossRef]
- Sellar, A.A.; Jones, C.G.; Mulcahy, J.P.; Tang, Y.; Yool, A.; Wiltshire, A.; O’Connor, F.M.; Stringer, M.; Hill, R.; Palmieri, J.; et al. UKESM1: Description and evaluation of the UK Earth System Model. J. Adv. Model. Earth Syst. 2019, 11, 4513–4558. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Stochastics of Hydroclimatic Extremes—A Cool Look at Risk, 2nd ed.; Kallipos Open Academic Editions: Athens, Greece, 2022; 346p, ISBN 978-618-85370-0-2. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Time’s arrow in stochastic characterization and simulation of atmospheric and hydrological processes. Hydrol. Sci. J. 2019, 64, 1013–1037. [Google Scholar] [CrossRef]
- Strotz, R.H.; Wold, H.O.A. Recursive vs. nonrecursive systems: An attempt at synthesis (Part I of a triptych on causal chain systems). Econometrica 1960, 28, 417–427. Available online: https://www.jstor.org/stable/1907731 (accessed on 15 March 2023). [CrossRef]
- Hannart, A.; Pearl, J.; Otto, F.E.L.; Naveau, P.; Ghil, M. Causal counterfactual theory for the attribution of weather and climate-related events. Bull. Am. Met. Soc. 2016, 97, 99–110. [Google Scholar] [CrossRef]
- Hannart, A.; Naveau, P. Probabilities of causation of climate changes. J. Clim. 2018, 31, 5507–5524. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Efstratiadis, A.; Mamassis, N.; Christofides, A. On the credibility of climate predictions. Hydrol. Sci. J. 2008, 53, 671–684. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.G.; Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Mamassis, N. A comparison of local and aggregated climate model outputs with observed data. Hydrol. Sci. J. 2010, 55, 1094–1110. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Anagnostopoulos, G.G.; Mamassis, N. Scientific dialogue on climate: Is it giving black eyes or opening closed eyes? Reply to “A black eye for the Hydrological Sciences Journal” by D. Huard. Hydrol. Sci. J. 2011, 56, 1334–1339. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D. On the prediction of persistent processes using the output of deterministic models. Hydrol. Sci. J. 2017, 62, 2083–2102. [Google Scholar] [CrossRef]
- Scafetta, N. CMIP6 GCM validation based on ECS and TCR ranking for 21st century temperature projections and risk assessment. Atmosphere 2023, 14, 345. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. (Eds.) IPCC, Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; 2391p. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Rethinking climate, climate change, and their relationship with water. Water 2021, 13, 849. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nature Climate Change 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.L.; Wu, H.; Zhou, C.; Liu, X.; Leng, P.; Yang, P.; Wu, W.; Tang, R.; Shang, G.F.; et al. Biophysical impacts of earth greening can substantially mitigate regional land surface temperature warming. Nat. Commun. 2023, 14, 121. [Google Scholar] [CrossRef]
- Chen, C.; Park, T.; Wang, X.; Piao, S.; Xu, B.; Chaturvedi, R.K.; Fuchs, R.; Brovkin, V.; Ciais, P.; Fensholt, R.; et al. China and India lead in greening of the world through land-use management. Nat. Sustain. 2019, 2, 122–129. [Google Scholar] [CrossRef]
- Milanković, M. Nebeska Mehanika; Udruženje “Milutin Milanković”: Beograd, Serbia, 1935. [Google Scholar]
- Milanković, M. Kanon der Erdbestrahlung und Seine Anwendung auf das Eiszeitenproblem; Koniglich Serbische Akademice: Beograd, Serbia, 1941. [Google Scholar]
- Milanković, M. Canon of Insolation and the Ice-Age Problem; Agency for Textbooks: Belgrade, Serbia, 1998. [Google Scholar]
- Roe, G. In defense of Milankovitch. Geophys. Res. Lett. 2006, 33, L24703. [Google Scholar] [CrossRef]
- Markonis, Y.; Koutsoyiannis, D. Climatic variability over time scales spanning nine orders of magnitude: Connecting Milankovitch cycles with Hurst–Kolmogorov dynamics. Surv. Geophys. 2013, 34, 181–207. [Google Scholar] [CrossRef]
- Stephens, G.L.; Hakuba, M.Z.; Kato, S.; Gettelman, A.; Dufresne, J.-L.; Andrews, T.; Cole, J.N.S.; Willen, U.; Mauritsen, T. The changing nature of Earth’s reflected sunlight. Proc. R. Soc. A 2022, 478, 1–37. [Google Scholar] [CrossRef]
- Connolly, R.; Soon, W.; Connolly, M.; Baliunas, S.; Berglund, J.; Butler, C.J.; Cionco, R.G.; Elias, A.G.; Fedorov, V.M.; Harde, H.; et al. How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate. Res. Astron. Astrophys. 2021, 21, 131.1–131.68. [Google Scholar] [CrossRef]
- Scafetta, N.; Bianchini, A. The planetary theory of solar activity variability: A review. Front. Astron. Space Sci. 2022, 9, 937930. [Google Scholar] [CrossRef]
- Kamis, J.E. The Plate Climatology Theory: How Geological Forces Influence, Alter, or Control Earth’s Climate and Climate Related Events. Available online: https://books.google.gr/books/?id=7lRqzgEACAAJ (accessed on 10 March 2023).
- Chakrabarty, D. The Climate of History in a Planetary Age; University of Chicago Press: Chicago, IL, USA, 2021; Available online: https://books.google.gr/books?id=ETQXEAAAQBAJ (accessed on 10 March 2023).
- Davis, E.; Becker, K.; Dziak, R.; Cassidy, J.; Wang, K.; Lilley, M. Hydrological response to a seafloor spreading episode on the Juan de Fuca ridge. Nature 2004, 430, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Urakawa, L.S.; Hasumi, H. A remote effect of geothermal heat on the global thermohaline circulation. J. Geophys. Res. Ocean. 2009, 114, C07016. [Google Scholar] [CrossRef]
- Patara, L.; Böning, C.W. Abyssal ocean warming around Antarctica strengthens the Atlantic overturning circulation. Geophys. Res. Lett. 2014, 41, 3972–3978. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A random walk on water. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hydrology and change. Hydrol. Sci. J. 2013, 58, 1177–1197. [Google Scholar] [CrossRef]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Gregor, L.; Hauck, J.; Le Quéré, C.; Luijkx, I.T.; Olsen, A.; Peters, G.P.; et al. Global Carbon Budget 2022. Earth Syst. Sci. Data 2022, 14, 4811–4900. [Google Scholar] [CrossRef]
- Stallinga, P. Residence time vs. adjustment time of carbon dioxide in the atmosphere. Entropy 2023, 25, 384. [Google Scholar] [CrossRef]
- Hansen, J.E.; Sato, M.; Simons, L.; Nazarenko, L.S.; von Schuckmann, K.; Loeb, N.G.; Osman, M.B.; Kharecha, P.; Jin, Q.; Tselioudis, G.; et al. Global warming in the pipeline. arXiv 2022, arXiv:2212.04474. [Google Scholar]
- Bond-Lamberty, B.; Thomson, A. Temperature-associated increases in the global soil respiration record. Nature 2010, 464, 579. [Google Scholar] [CrossRef] [PubMed]
- Arrhenius, S.A. Über die Dissociationswärme und den Einfluß der Temperatur auf den Dissociationsgrad der Elektrolyte. Z. Phys. Chem. 1889, 4, 96–116. [Google Scholar] [CrossRef]
- Patel, K.F.; Bond-Lamberty, B.; Jian, J.L.; Morris, K.A.; McKever, S.A.; Norris, C.G.; Zheng, J.; Bailey, V.L. Carbon flux estimates are sensitive to data source: A comparison of field and lab temperature sensitivity data. Environ. Res. Lett. 2022, 17, 113003. [Google Scholar] [CrossRef]
- Pomeroy, R.; Bowlus, F.D. Progress report on sulfide control research. Sew. Work. J. 1946, 18, 597–640. [Google Scholar]
- Robinson, C. Microbial respiration, the engine of ocean deoxygenation. Front. Mar. Sci. 2019, 5, 533. [Google Scholar] [CrossRef]
- CERES Data Products. SSF1deg—Level 3, Gridded Daily and Monthly Averages of the SSF Product by Instrument. Available online: https://ceres-tool.larc.nasa.gov/ord-tool/jsp/SSF1degEd41Selection.jsp (accessed on 12 March 2023).
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an integrating concept in earth science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Pinskwar, I.; Koutsoyiannis, D. Variability of global mean annual temperature is significantly influenced by the rhythm of ocean-atmosphere oscillations. Sci. Total Environ. 2020, 747, 141256. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Mishonov, A.V.; Reagan, J.R.; Seidov, D.; Yarosh, E.S.; et al. World Ocean heat content and thermosteric sea level change (0–2000 m). Geophys. Res. Lett. 2012, 39, L10603. [Google Scholar] [CrossRef]
- National Oceanographic Data Center, NOAA, Global Ocean Heat and Salt Content. Available online: https://www.ncei.noaa.gov/access/global-ocean-heat-content/index3.html (accessed on 12 March 2023).
- Roemmich, D.; Johnson, G.C.; Riser, S.; Davis, R.; Gilson, J.; Owens, W.B.; Garzoli, S.L.; Schmid, C.; Ignaszewski, M. The Argo Program: Observing the global ocean with profiling floats. Oceanography 2009, 22, 34–43. [Google Scholar] [CrossRef]
- Berner, R.A.; Kothavala, Z. GEOCARB III: A revised model of atmospheric CO2 over Phanerozoic time. Am. J. Sci. 2001, 301, 182–204. [Google Scholar] [CrossRef]
- Veizer, J.; Godderis, Y.; François, L.M. Evidence for decoupling of atmospheric CO2 and global climate during the Phanerozoic eon. Nature 2000, 408, 698–701. [Google Scholar] [CrossRef] [PubMed]
- Jouzel, J.; Lorius, C.; Petit, J.R.; Genthon, C.; Barkov, N.I.; Kotlyakov, V.M.; Petrov, V.M. Vostok ice core: A continuous isotope temperature record over the last climatic cycle (160,000 years). Nature 1987, 329, 403–408. [Google Scholar] [CrossRef]
- Petit, J.R.; Jouzel, J.; Raynaud, D.; Barkov, N.I.; Barnola, J.-M.; Basile, I.; Bender, M.; Chappellaz, J.; Davis, M.; Delayque, G.; et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 1999, 399, 429–436. [Google Scholar] [CrossRef]
- Caillon, N.; Severinghaus, J.P.; Jouzel, J.; Barnola, J.M.; Kang, J.; Lipenkov, V.Y. Timing of atmospheric CO2 and Antarctic temperature changes across Termination III. Science 2003, 299, 1728–1731. [Google Scholar] [CrossRef]
- Soon, W. Implications of the secondary role of carbon dioxide and methane forcing in climate change: Past, present, and future. Phys. Geogr. 2007, 28, 97–125. [Google Scholar] [CrossRef]
- Pedro, J.B.; Rasmussen, S.O.; van Ommen, T.D. Tightened constraints on the time-lag between Antarctic temperature and CO2 during the last deglaciation. Clim. Past 2012, 8, 1213–1221. [Google Scholar] [CrossRef]
- Chowdhry Beeman, J.; Gest, L.; Parrenin, F.; Raynaud, D.; Fudge, T.J.; Buizert, C.; Brook, E.J. Antarctic temperature and CO2: Near-synchrony yet variable phasing during the last deglaciation. Clim. Past 2019, 15, 913–926. [Google Scholar] [CrossRef]
- Parrenin, F.; Masson-Delmotte, V.; Köhler, P.; Raynaud, D.; Paillard, D.; Schwander, J.; Barbante, C.; Landais, A.; Wegner, A.; Jouzel, J. Synchronous change of atmospheric CO2 and Antarctic temperature during the last deglacial warming. Science 2013, 339, 1060–1063. [Google Scholar] [CrossRef]
- Shakun, J.D.; Clark, P.U.; He, F.; Marcott, S.A.; Mix, A.C.; Liu, Z.; Otto-Bliesner, B.; Schmittner, A.; Bard, E. Global warming preceded by increasing carbon dioxide concentrations during the last deglaciation. Nature 2012, 484, 49–54. [Google Scholar] [CrossRef]
- NOAA National Centers for Environmental Information. Temperature Change and Carbon Dioxide Change; 2021. Available online: https://www.ncei.noaa.gov/sites/default/files/2021-11/8%20-%20Temperature%20Change%20and%20Carbon%20Dioxide%20Change%20-%20FINAL%20OCT%202021.pdf (accessed on 12 January 2023).





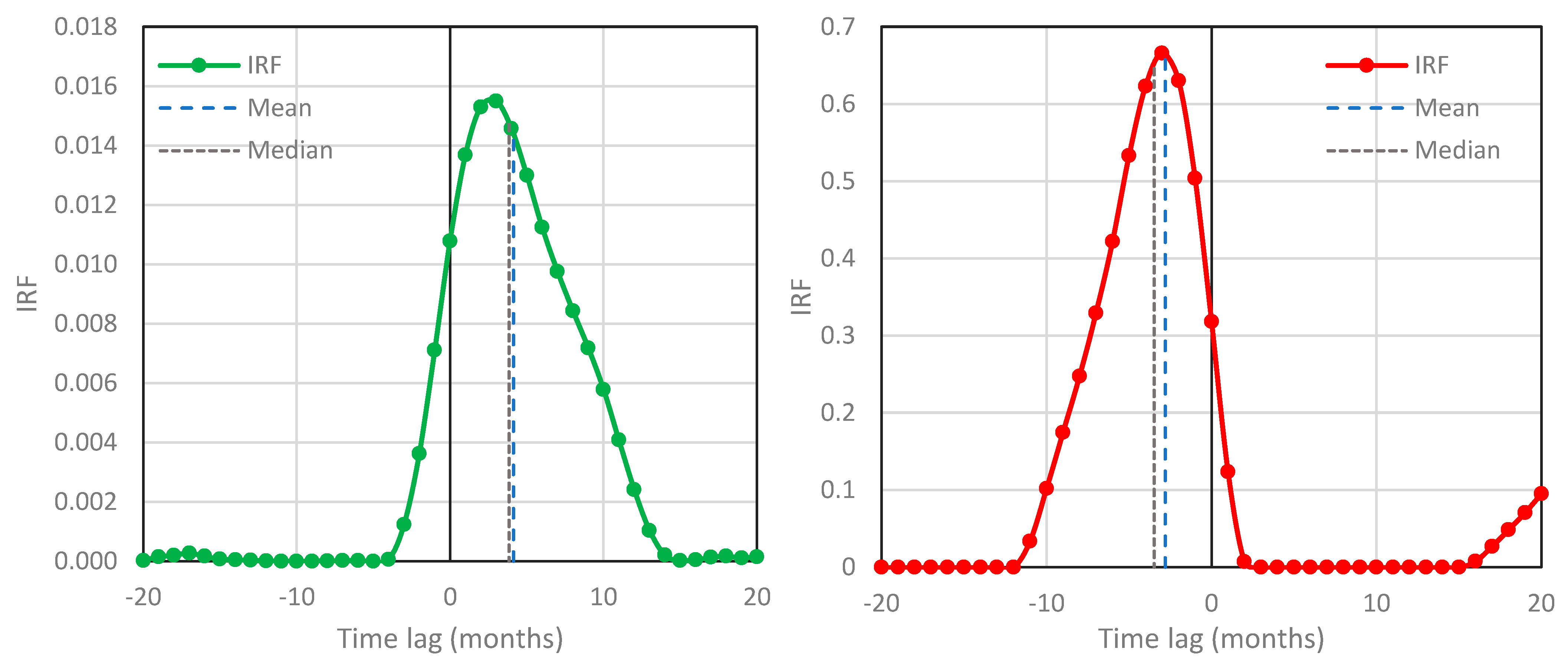
| Case System | # | Direction | ||||||
|---|---|---|---|---|---|---|---|---|
| Monthly timescale, varying Δt | ||||||||
| T year | 1 | 5 | 7.70 | 6.35 | 0.48 | 0.31 | 1.3 × 10–5 * | |
| 2 | –5 | –5.67 | –5.49 | 0.48 | 0.23 | 7.3 × 10–4 * | ||
| T year | 3 | 8 | 7.75 | 6.86 | 0.56 | 0.34 | 3.1 × 10–4 * | |
| 4 | –8 | −6.31 | –6.30 | 0.56 | 0.23 | 4.4 × 10–3 * | ||
| years | 5 | 8 | 8.19 | 7.08 | 0.57 | 0.31 | 3.4 × 10–4 * | |
| 6 | –8 | −6.31 | –6.31 | 0.57 | 0.21 | 4.5 × 10–3 * | ||
| years | 7 | 9 | 10.65 | 10.32 | 0.53 | 0.29 | 1.0 × 10–4 * | |
| 8 | –9 | −6.28 | –6.28 | 0.53 | 0.14 | 3.8 × 10–3 * | ||
| years | 9 | 8 | 11.00 | 11.00 | 0.47 | 0.27 | 5.6 × 10–5 * | |
| 10 | –8 | −6.55 | –6.54 | 0.47 | 0.11 | 3.6 × 10–3 * | ||
| years | 11 | 6 | 11.74 | 12.15 | 0.45 | 0.31 | 3.4 × 10–5 * | |
| 12 | 6 | 9.98 | 11.13 | 0.45 | 0.33 | 7.6 × 10–6 | ||
| 13 | –6 | −6.33 | –6.31 | 0.45 | 0.12 | 7.7 × 10–3 * | ||
| T year | 14 | 10 | 9.76 | 8.91 | 0.40 | 0.35 | 2.0 × 10–4 * | |
| 15 | –10 | –8.51 | –8.35 | 0.40 | 0.18 | 1.1 × 10–3 * | ||
| Annual timescale, year | ||||||||
| T: CMIP6 mean, SSP2-4.5; [CO2]: SSP2-4.5, 1850–2100, w/o roughness constraint | 16 | 0 | –3.75 | –6.20 | 0.36 | 0.90 | 0.095 | |
| 17 | 0 | 9.95 | 15.30 | 0.36 | 0.15 | 0.46 | ||
| As #16 and #17 but for 1850–2021 | 18 | 0 | –6.23 | –8.58 | 0.31 | 0.72 | 0.10 | |
| 19 | 0 | 16.18 | 16.16 | 0.31 | 0.10 | 0.295 | ||
| As #16 and #17 but with roughness constraint | 20 | 0 | –3.65 | –5.55 | 0.36 | 0.84 | 3.5 × 10–5 | |
| 21 | 0 | 6.86 | 1.63 | 0.36 | 0.13 | 7.7 × 10–3 | ||
| As #18 and #19 but with roughness constraint | 22 | 0 | –7.34 | –8.99 | 0.31 | 0.64 | 8.3 × 10–5 | |
| 23 | 0 | 11.26 | 14.77 | 0.31 | 0.13 | 9.4 × 10–3 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koutsoyiannis, D.; Onof, C.; Kundzewicz, Z.W.; Christofides, A. On Hens, Eggs, Temperatures and CO2: Causal Links in Earth’s Atmosphere. Sci 2023, 5, 35. https://doi.org/10.3390/sci5030035
Koutsoyiannis D, Onof C, Kundzewicz ZW, Christofides A. On Hens, Eggs, Temperatures and CO2: Causal Links in Earth’s Atmosphere. Sci. 2023; 5(3):35. https://doi.org/10.3390/sci5030035
Chicago/Turabian StyleKoutsoyiannis, Demetris, Christian Onof, Zbigniew W. Kundzewicz, and Antonis Christofides. 2023. "On Hens, Eggs, Temperatures and CO2: Causal Links in Earth’s Atmosphere" Sci 5, no. 3: 35. https://doi.org/10.3390/sci5030035
APA StyleKoutsoyiannis, D., Onof, C., Kundzewicz, Z. W., & Christofides, A. (2023). On Hens, Eggs, Temperatures and CO2: Causal Links in Earth’s Atmosphere. Sci, 5(3), 35. https://doi.org/10.3390/sci5030035