Abstract
We explore the structural similarities in three different languages, first in the protein language whose primary letters are the amino acids, second in the musical language whose primary letters are the notes, and third in the poetry language whose primary letters are the alphabet. For proteins, the non local (secondary) letters are the types of foldings in space (-helices, -sheets, etc.); for music, one is dealing with clear-cut repetition units called musical forms and for poems the structure consists of grammatical forms (names, verbs, etc.). We show in this paper that the mathematics of such secondary structures relies on finitely presented groups on r letters, where r counts the number of types of such secondary non local segments. The number of conjugacy classes of a given index (also the number of graph coverings over a base graph) of a group is found to be close to the number of conjugacy classes of the same index in the free group on generators. In a concrete way, we explore the group structure of a variant of the SARS-Cov-2 spike protein and the group structure of apolipoprotein-H, passing from the primary code with amino acids to the secondary structure organizing the foldings. Then, we look at the musical forms employed in the classical and contemporary periods. Finally, we investigate in much detail the group structure of a small poem in prose by Charles Baudelaire and that of the Bateau Ivre by Arthur Rimbaud.
1. Introduction
In this paper, we point out for the first time a remarkable analogy between the pattern structure of bonds between amino acids in a protein (the protein secondary structure [1]) and the non local structures observed in tonal music and in poems. We explain the origin of these analogies with finitely generated groups and graph covering theory.
A protein is a long polymeric linear chain encoded with 20 letters (the 20 amino acids). The surjective mapping of the codons to the 20 amino acids is the DNA genetic code. It can be given a mathematical theory with appropriate finite groups [2,3]. In addition, a protein folds in the three dimensional space with structural elements such as coils, -helices and -sheets, or other arrangements that determine its biological function. The number of proteins encoded in genomes depends on the biological organism (typically from 1 to proteins in viruses, from to proteins in bacteria and from to proteins in eukaryotes). The protein database (or PDB) contains about entries [4]. Proteins ensure the language of life, amino acids are the alphabet, proteins are the words and the set of proteins in an organism are the phrases.
Analogously in music, a note is a letter encoding a musical sound. In the 12-tone chromatic scale [5], each of the 12 notes (or letters) has the frequency of the previous note multiplied by . The form refers to the secondary structure of a musical composition in terms of clear-cut units of equal length, for example, A-B-A in the sonata form or A-B-C-B-A in an arch form [6].
Now, we come to human language and the Latin alphabet. There are 26 letters organized into words of various types such as names, adjectives, verbs, and so on. In the following, we will show that a verse in a poem or a phrase in prose have distinctive features, the former being closer to our theory.
Our mathematical theory of the secondary structures in proteins, music and poems relies on the concept of a finitely generated group and the corresponding graph coverings, as explained in Section 2.
We will investigate three applications of the graph covering approach. In Section 3, we look at the secondary structures of two proteins. We take as examples the spike protein of the SARS-Cov-2 virus and a glycoprotein playing a role in the immune system (see [3] for our earlier work). In Section 4, the secondary structures are the musical forms of western music in the classical age and twentieth century music. Then, in Section 5, the secondary structures in the verses of selected poems are obtained from an encoding of the types of words (names, verbs, prepositions, etc.).
A Brief Review of the Literature
After we received an invitation to contribute to the present special issue of Sci “Mathematics and poetry, with a view towards machine learning” we thought that our current group theoretical approach of protein language [3] could be converted into an understanding of the poetic language, as well as an understanding of some musical structures.
Our goal in this subsection is to point out earlier work in the same direction as ours. There are many papers attempting to relate group theory to the genetic code, as reviewed in [2] but we found none of them featuring the secondary structure of proteins along the chain of amino acids, as we did in [3] and as we do below with the graph coverings.
Poetry inspired mathematics has been the common thread of most papers exploring the connection between poems and maths [7,8,9,10]. However, it is more challenging to explain what type of structure and beauty occurs in a poem in the language of mathematics [11]. Perhaps mathematical linguistics is the proper frame for making progress [12] and artificial intelligence (AI) may help in the classification of languages [13].
Although both subjects have been connected for centuries, comparing musical structures to mathematics is a fairly new research domain [14]. For a different perspective, the readers may consult Reference [15].
2. Graph Coverings and Conjugacy Classes of a Finitely Generated Group
Let rel be the relation defining the finitely presented group on r letters (or generators). We are interested in the conjugacy classes (cc) of subgroups of with respect to the nature of the relation rel. In a nutshell, one observes that the cardinality structure of conjugacy classes of subgroups of index d of is all the closer to that of the free group on generators as the choice of rel contains more non local structure. To arrive at this statement, we experiment on protein foldings, musical forms and poems. The former case was first explored in [3].
Let X and be two graphs. A graph epimorphism (an onto or surjective homomorphism) is called a covering projection if, for every vertex of , maps the neighborhood of bijectively onto the neighborhood of . The graph X is referred to as a base graph (or a quotient graph) and is called the covering graph. The conjugacy classes of subgroups of index d in the fundamental group of a base graph X are in one-to-one correspondence with the connected d-fold coverings of X, as it has been known for some time [16,17].
Graph coverings and group actions are closely related.
Let us start from an enumeration of integer partitions of d that satisfy:
a famous problem in analytic number theory [18,19]. The number of such partitions is when .
The number of d-fold coverings of a graph X of the first Betti number r is ([17], p. 41),
Another interpretation of Iso is found in ([20], Euqation (12)). Taking a set of mixed quantum states comprising subsystems, Iso corresponds to the stable dimension of degree d local unitary invariants. For two subsystems, and such a stable dimension is Iso. A table for Iso with small d’s is in ([17], Table 3.1, p. 82) or ([20], Table 1).
Then, one needs a theorem derived by Hall in 1949 [21] about the number of subgroups of index d in
to establish that the number Isoc of connected d-fold coverings of a graph X (alias the number of conjugacy classes of subgroups in the fundamental group of X) is as follows ([17], Theorem 3.2, p. 84):
where denotes the number-theoretic Möbius function.

Table 1.
The number Isoc for small values of first Betti number r (alias the number of generators of the free group ) and index d. Thus, the columns correspond to the number of conjugacy classes of subgroups of index d in the free group of rank r.
The finitely presented groups may be characterized in terms of a first Betti number r. For a group G, r is the rank (the number of generators) of the abelian quotient . To some extent, a group whose first Betti number is r may be said to be close to the free group since both of them have the same minimum number of generators.
3. Graph Coverings for Proteins
As a follow up of our previous paper [3] we first apply the above theory to two proteins of current interest, the spike protein in a variant of SARS-Cov-2 and a protein that plays an important role in the immune system.
3.1. The D614G Variant (Minus RBD) of the SARS-CoV-2 Spike Protein
As a first example of the application of our approach, let us consider the D614G variant (minus RBD: the receptor binding domain) of the SARS-CoV-2 spike protein. In the Protein Data Bank in Europe, the name of the sequence is 6XS6 [22]. D614G is a missense mutation (a nonsynonymous substitution where a single nucleotide results in a codon that codes for a different amino acid). The mutation occurs at position 614 where glycine has replaced aspartic acid worldwide. Glycine increases the transmission rate and correlates with the prevalence of loss of smell as a symptom of COVID-19, possibly related to a higher binding of the RBD to the ACE2 receptor: an enzyme attached to the membrane of heart cells. A picture of the secondary structures can be found in Figure 1.
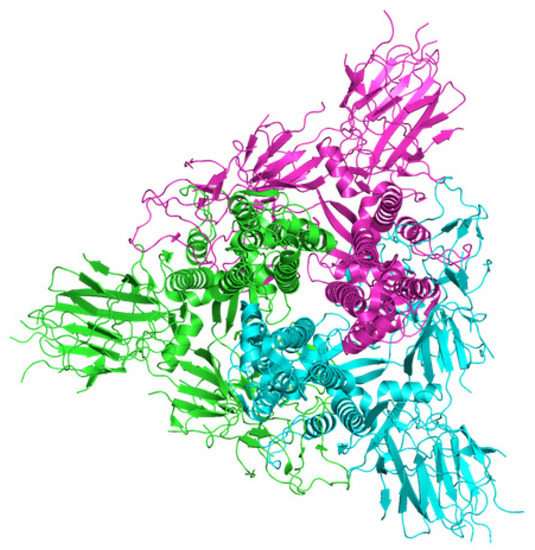
Figure 1.
A picture of the secondary structure of D614G variant (minus RBD) of the SARS-CoV-2 spike protein found in the protein data bank in Europe [22].
The D614G variant (minus RBD) of the SARS-CoV-2 spike protein contains 786 amino acids (aa) forming a (long) word as follows:
AYTNSFTRGVYYPDKVFRSSVLHSTQDLFLPFFSNVTWFHAIHDNPVLPF…
AYRFNGIGVTQNVLYENQKLIANQFNSAIGKIQDSLSSTASALGKLQDVV.
NTQEVFAQVKQIYKTPPIKDFGGFNFSQILPDPSKPSKRSFIEDLLFNKV…
FVTQRNFYEPQIITTDNTFVSGNCDVVIGIVNNTV
Such a protein sequence, comprising 20 amino acids as letters of the primary code, can be encoded in terms of secondary structures. Most of the time, for proteins, one makes use of three types of encoding that are segments of helices (encoded with the symbol H), segments of pleated sheets (encoded by the symbol E) and the segment of random coils (encoded by the segment C) [1,3,23].
A finer structure may be obtained by using methods such as the SST Bayesian method. A summary of the approach can be found in Reference [23].
We used a software prepared in [24] to obtain the following secondary structure
rel(H,E,C,G,I,T,4) =
CCCCCCCCEEEEEECCCCCCCEEEEECCCCCCCCCCEEEEEECCCCCCCC…
HHHHHHHHCC444444CHHHHHHHHHHHHHHHHHHHHCCCGGGGGHHHHH
HHIIIIICCCCCCCCCCCCCCCCCCTTTTTCCCCCCCCCHHHHHHHHHHH…
CCCTTTTTCCCCCTTTTTCCCC44444EEEEEECC,
where G means a helix, 4 means -like turns, I means a right-handed helix and T corresponds to unspecified turns.
For the group analysis, we slightly simplify the problem by taking just one form of turn so that the sequence is encoded with 6 letters only. Then, we further simplify by taking to obtain a 5-letter encoding. We further simplify by taking , then by taking to get 4-letter and 3-letter encodings, respectively. The results are in Table 2.

Table 2.
Group analysis of the D614G variant (minus RBD) of the SARS-CoV-2 spike protein. The bold numbers mean that the cardinality structure of cc of subgroups of G fits that of the free group when the encoding makes use of r letters. In the last column, r is the first Betti number of the generating group .
We observe that the cardinality structure of the cc of subgroups of the finitely presented groups fits the free group when the encoding makes use of letters. This is in line with our results found in [3] on several kinds of proteins.
3.2. The -2-Glycoprotein 1 or Apolipoprotein-H
Our second example deals with a protein playing an important role in the immune system [25]. In the Protein Data Bank, the name of the sequence is 6V06 [26] and it contains 326 aa. All models predict secondary structures mainly comprising -pleated sheets and random coils and sometimes short segments of -helices.
We observe in Table 3 that the cardinality structure of the cc of subgroups of the finitely presented groups approximately fits the free group on two letters for the first three models but not for the RAPTORX model. In one case (with the PORTER model [27]), all first six digits fit those of and higher order digits could not be reached. The reader may refer to our paper [3] where such a good fit could be obtained for the sequences in the arms of the protein complex Hfq (with 74 aa). This complex with the 6-fold symmetry is known to play a role in DNA replication.

Table 3.
Group analysis of apolipoprotein-H (PDB 6V06). The bold numbers means that the cardinality structure of cc of subgroups of fits that of the free group when the encoding makes use of 2 letters. The first model is the one used in the previous Section [24] where we took and . The other models of secondary structures with segments E, H and C are from softwares PORTER, PHYRE2 and RAPTORX. The references to these softwares may be found in our recent paper [3]. The notation r in column 3 means the first Betti number of .
A picture of the secondary structure of the apolipoprotein-H obtained with the software of Ref. [24] is displayed in Figure 2.
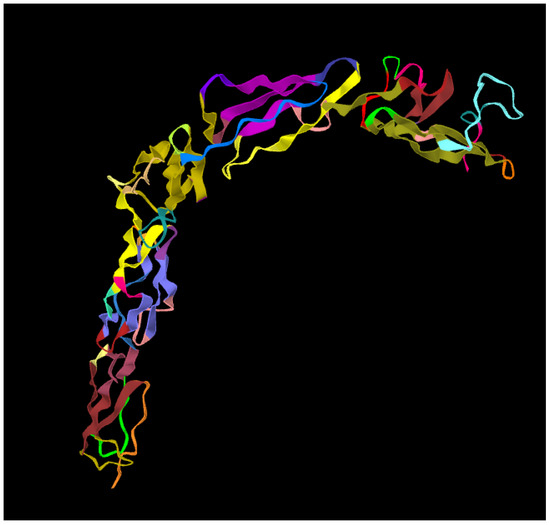
Figure 2.
A picture of the secondary structure of the apolipoprotein-H obtained with the software [24].
4. Graph Coverings for Musical Forms
We accept that this structure determines the beauty in art. We provide two examples of this relationship, first by studying musical forms, then by looking at the structure of verses in poems. Our approach encompasses the orthodox view of periodicity or quasi-periodicity inherent to such structures. Instead of that and the non local character of the structure is investigated thanks to a group with generators given by the allowed generators and a relation rel, determining the position of such successive generators, as we did for the secondary structures of proteins.
4.1. The Sequence Isoc, the Golden Ratio and More
4.1.1. The Fibonacci Sequence
As shown in Table 1, the sequence Isoc only contains 1 in its entries and it is tempting to associate this sequence to the most irrational number, the Golden ratio through the continued fraction expansion .
Let us now take a two-letter alphabet (with letters L and S) and the Fibonacci words defined as , , . The sequence of Fibonacci words is as follows
and its length corresponds to the Fibonacci numbers .
Then, one can check that the finitely-presented group whose relation is a Fibonacci word possesses a cardinality sequence of subgroups equal to Isoc, up to all computable orders, despite the fact that the groups are not the same. It is straightforward to check that the first Betti number r of is 1, as expected.
4.1.2. The Period Doubling Cascade
Other rules lead to a Betti number and the corresponding sequence Isoc(X;1). Let us consider the period-doubling cascade in the logistic map . Period doubling can be generated by repeated use of the substitutions and ., so that the sequence of period doubling is [28]
and the corresponding finitely presented groups also have first Betti numbers equal to 1.
4.1.3. Musical Forms of the Classical Age
Going into musical forms, the ternary structure (most commonly denoted ) corresponding to the Fibonacci word is a Western instrumental genre notably used in sonatas, symphonies and string quartets. The basic elements of sonata forms are the exposition A, the development B and recapitulation A. While the musical form is symmetric, the Fibonacci word corresponding to is asymmetric and used in some songs or ballads from the Renaissance.
In a closely related direction, it was shown that the lengths a and b of sections A and B in all Mozart’s sonata movements are such that the ratio [29].
4.2. The Sequence Isoc in Twentieth Century Music and Jazz
In the 20th century, musical forms escaped the classical channels that were created. With the Hungarian composer Béla Bartók, a musical structure known as the arch form was created. The arch form is a sectional structure for a piece of music based on repetition, in reverse order, so that the overall form is symmetric, most often around a central movement. Formally, it looks like . A well known composition of Bartok with this structure is Music for strings, percussion and celesta [30]. In Table 4, it is shown that the cardinality sequence of cc of subgroups of the group generated with the relation rel= corresponds to Isoc up to the higher index 9 that we could check with our computer. A similar result is obtained with the symmetrical word .

Table 4.
Group analysis of a few musical forms whose structure of subgroups, apart from exceptions, is close to Isoc with (at the upper part of the table) or (at the lower part of the table). Of course, the forms A-B-C and A-B-C-D have the cardinality sequence of cc of subgroups exactly equal to Isoc and Isoc, respectively.
Our second example is a musical form known as twelve-bar blues [31], one of the most prominent chord progressions in popular music and jazz. In this context, the notation A is for the tonic, B is for the subdominant and C is for the dominant, each letter representing one chord. In twelve-bar blues, there are twelve chords arranged as in the first column of Table 4. We observe that the standard twelve-bar blues are different in structure from the sequence of Isoc. However, variations 1 and 2 have a structure close to Isoc. In the former case, the first 9 orders lead to the same digit in the sequence.
Our third example is the musical form A-A-B-C-C. Notably, it is found in the Slow movement from Haydn’s ‘Emperor quartet Opus 76, N°3 [32] (Figure 3), much sooner than the contemporary period. (See also Ref. [33] for the frequent occurrence of the same musical form in djanba songs at Wadeye.) As in the aforementioned examples, the cardinality sequence of the cc of subgroups of the group built with rel=AABCC corresponds to Isoc up to the highest index 9 that we could reach in our calculations.

Figure 3.
Slow movement from Haydn’s ‘Emperor’ quartet Opus 76, N°3.
Further musical forms with 4 letters A, B, C, and D and their relationship to Isoc are provided in the lower part of Table 4.
Not surprisingly, the rank r of the abelian quotient of is found to be 2 when the cardinality structure fits that Isoc in Table 4. Otherwise, the rank is 3. Similarly, the rank r of the abelian quotient of is found to be 3 when the cardinality structure fits that Isoc in Table 4. Otherwise, the rank is 4.
5. Graph Coverings for Prose and Poems
5.1. Graph Coverings for Prose
Let us perform a group analysis of a long sentence in prose. We selected a text by Charles Baudelaire [34]:
- Le gamin du céleste Empire hésita d’abord; puis, se ravisant, il répondit: “Je vais vous le dire ”. Peu d’instants après, il reparut, tenant dans ses bras un fort gros chat, et le regardant, comme on dit, dans le blanc des yeux, il affirma sans hésiter: “Il n’est pas encore tout à fait midi.” Ce qui était vrai.
In Table 5, the group analysis is performed with 3, 4 or 5 letters (in the upper part) and is compared to random sequences with the same number of letters (in the lower part).

Table 5.
Group analysis of an excerpt of a small poem in prose Le vieux saltimbanque by Charles Baudelaire. The text is split into segments encoded by the symbol H (for names and adjectives), E (for verbs), A for prepositions, B for adverbs, or C (for the other types: conjunctions, punctuation marks and so on). The cardinality structure of the cc of subgroups of a small index is compared to the one obtained with 10 runs of a sequence of words of a similar length (i.e., the length 250) with the corresponding number of letters.
The text of the sentence is first encoded with three letters (H for names and adjectives, E for verbs and C otherwise), we observe that the subgroup structure has cardinality close to that of a free group on two letters up to index 3. If one adds one letter A for the prepositions in the sentence (in addition to H, E and C), then the subgroup structure has cardinality close to that of a free group on three letters. If adverbs B are also selected, then the subgroup structure is close to that of the free group . In all three cases, the similarity holds up to index 3 and that the cc of subgroups are the same as in the corresponding free groups. The first Betti numbers of the generating groups are 2, 3 and 4 as expected.
In Table 5, we also computed the cardinality structure of the cc of subgroups of small indexes obtained from a random sequence of 250 letters (like the number of letters in the previously studied sentence of the small poem in prose). One took 10 runs with random sequences having 3, 4 or 5 letters. We see that the cardinality structure of the cc of subgroups for the cases with 4 or 5 letters tends to align to that of the free group (not ). The 3-letter case is the most random one and does not correspond to (or ), in most runs.
5.2. Graph Coverings for Poems
In poems, the verses are generally of a smaller length than that for a sentence in prose. We selected the first strophe of the poem, Le Bateau Ivre, by Arthur Rimbaud. The poem may be found on a wall in Paris, see Figure 4. The verses in the strophe have about 35 letters. We compare the group structure of the four verses in the first strophe to that of random sequences of length 35 in Table 6 (when the encoding is with 3 letters H, E and C) and in Table 7 (when the encoding is with 4 letters H, E, C and A). Adverbs are too rare in verses of such a small length so that we did not considered the 5-letter case.

Figure 4.
Part of the poem Le Bateau Ivre of Arthur Rimbaud on a wall (Rue Férou) in Paris.

Table 6.
Group structure of the poem Le Bateau Ivre’ (The Drunken Boat) by Arthur Rimbaud. Only the first strophe (that has four lines) is analyzed, firstly in its original form, then in an English translation. Each line is split into segments encoded by the symbol H (for names and adjectives), E (for verbs) or C (for the other types: conjunctions, adverbs, prepositions, punctuation marks and so on). The group relation is displayed for the first line only.) The cardinality structure of cc of subgroups of a small index is compared to the one obtained with 10 runs of a sequence of random 3-letter words of similar length (i.e., the length 35).

Table 7.
The same as in Table 6, but each line is split into segments encoded by the symbol H (for names and adjectives), E (for verbs), A for prepositions, or C (for the other types: conjunctions, adverbs, punctuation marks and so on). The cardinality structure of cc of subgroups of a small index is compared to the one obtained with 10 runs of a sequence of random 4-letter words of similar length (i.e., the length 35).
Let us first look at the 3-letter case in Table 6. Apart from the first verse in the strophe, the structure of the poem is very close to that of , up to the index 6 (for the second verse) and up to the index 7 (for verses 3 and 4). Higher order indices could not be reached in our calculations. For the English translation, the closeness to holds as well but is not so perfect. It is not so surprising since the poem was originally composed in French. For a French translation of a poem in English one would have obtained a similar (small) discrepancy to the group structure to . We looked at the cardinality structure of the cc of subgroups by taking random sequences of length 35 in 10 runs and we observe that the closeness to is much less than in the case of the poem.
The group structure with 3 letters can also be obtained for the group structure with 4 letters in Table 7 but the closeness is to (not ), as expected.
6. Conclusions
The graph covering approach has been shown to be useful for understanding how complex structures are encoded in nature and in art. For proteins, there exists a primary encoding with 20 amino acids as letters and the secondary encoding determines the folding of proteins in the 3-dimensional space. This is useful for recognizing the relationship between the structure and function of the protein. We took examples based on a present hot topic: a variant of the SARS-Cov-2 spike protein and the alipoprotein-H. For music, the secondary structures are called musical forms and the choice of them determines the type of music. For poems, we took the French (or English) alphabet with 26 letters, but many other alphabets may be used for the application of our approach. The secondary structures are defined from the encoding of the words (names, verbs and so on).
It is also interesting to speculate about the possible existence of a primary code and a secondary code in other fields, for example, in physics at the elementary level like in particle physics and quantum gravity [35]. According to the experience of the authors of this paper, the structure has much to do with complete quantum information. The reader may consult paper [36] about particle mixings or [3,37] about the genetic code in which finite groups are the players. Here, we are dealing with infinite groups so that the representation theory of finite groups (with characters) has to be defined on finitely-presented groups (most of the time of infinite cardinality). This will be explored further in our next paper [38].
Author Contributions
Conceptualization, M.P., F.F. and K.I.; methodology, M.P. and R.A.; software, M.P.; validation, R.A., F.F. and M.M.A.; formal analysis, M.P. and M.M.A.; investigation, M.P., F.F. and M.M.A.; writing—original draft preparation, M.P.; writing—review and editing, M.P.; visualization, F.F. and R.A.; supervision, M.P. and K.I.; project administration, K.I.; funding acquisition, K.I. All authors have read and agreed to the published version of the manuscript.
Funding
Funding was obtained from Quantum Gravity Research in Los Angeles, CA.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dang, Y.; Gao, J.; Wang, J.; Heffernan, R.; Hanson, J.; Paliwal, K.; Zhou, Y. Sixty-five years of the long march in protein secondary structure prediction: The final strech? Brief. Bioinform. 2018, 19, 482–494. [Google Scholar]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Fang, F.; Irwin, K. Complete quantum information in the DNA genetic code. Symmetry 2020, 12, 1993. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Fang, F.; Irwin, K. Quantum information in the protein codes, 3-manifolds and the Kummer surface. Symmetry 2020, 13, 1146. [Google Scholar] [CrossRef]
- The Protein Data Bank. Available online: Https://pdb101.rcsb.org/ (accessed on 1 January 2021).
- ChromaticScale. Available online: Https://en.wikipedia.org/wiki/Chromatic_scale (accessed on 1 April 2021).
- Musical Form. Available online: Https://en.wikipedia.org/wiki/Musical_form (accessed on 1 April 2021).
- Growney, J. Mathematics in poetry. J. Online Math. Appl. 2006, 6, 1262. [Google Scholar] [CrossRef]
- Glaz, S. Poetry inspired by mathematics: A brief journey through history. J. Math. Arts 2011, 5, 171–183. [Google Scholar] [CrossRef]
- Henderson, C. For the love of poetry and mathematics: January 6, 2012. J. Humanist. Math. 2012, 2, 27–46. [Google Scholar]
- Nichita, F.F. Mathematics and poetry. Unification, unity, union. Sci 2020, 2, 84. [Google Scholar] [CrossRef]
- Aharony, R. Mathematics, poetry and beauty. J. Math. Arts 2014, 8, 5–12. [Google Scholar] [CrossRef]
- Kornai, A. Mathematical Linguistics; Springer: London, UK, 2008. [Google Scholar]
- Monte-Serrat, D.M.; Ruiz, E.E.S.; Cattani, C. Linguistic Theoretical Frameworks for Dealing with AI. Available online: https://www.researchgate.net/project/Linguistic-theoretical-frameworks-for-dealing-with-AI (accessed on 28 September 2021).
- Andreatta, M. From Music to Mathematics and Backwards: Introducing Algebra, Topology and Category Theory into Computational Musicology. In Imagine Math 6; Emmer, M., Abate, M., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Shakhovska, N.; Fedushko, S. Data analysis of music preferences of web users based on social and demographic factors. Procedia Comput. Sci. 2021, in press. [Google Scholar]
- Mednykh, A. Counting conjugacy classes of subgroups in a finitely generated group. J. Algebra 2008, 320, 2209–2217. [Google Scholar] [CrossRef][Green Version]
- Kwak, J.H.; Nedela, R. Graphs and their coverings. Lect. Notes Ser. 2007, 17, 118. [Google Scholar]
- Hardy, G.H.; Wright, E.M. An Introduction to the Theory of Numbers, 6th ed.; Oxford University Press: Oxford, UK, 2008; pp. 361–392. [Google Scholar]
- Planat, M. Quantum 1/f noise in equilibrium: From Planck to Ramanujan. Phys. A 2003, 318, 371. [Google Scholar] [CrossRef]
- Vrna, P. On the algebra of local unitary invariants of pure and mixed quantum states. J. Phys. A Math. Theor. 2011, 44, 225304. [Google Scholar]
- Hall, M., Jr. Subgroups of finite index in free groups. Can. J. Math. 1949, 1, 187–190. [Google Scholar]
- SARS-CoV-2 Spike D614G Variant, Minus RBD, in Protein Data Bank in Europe, Bringing Structure to Biology. Available online: https://www.ebi.ac.uk/pdbe/entry/pdb/6xs6 (accessed on 1 May 2021).
- Protein Secondary Structure. Available online: https://en.wikipedia.org/wiki/Protein_secondary_structure (accessed on 1 May 2021).
- Konagurthu, A.S.; Lesk, A.M.; Allison, L. Minimum message length inference of secondary structure fromprotein coordinate data. Bioinformatics 2012, 28, i97–i105. Available online: https://lcb.infotech.monash.edu/sstweb2/Submission_page.html (accessed on 1 May 2021). [CrossRef]
- McDonnell, T.; Wincup, C.; Bucholz, I.; Pericleous, C.; Giles, I.; Ripoll, V.; Cohen, H.; Delcea, M.; Rahman, A. The role of beta-2-glycoprotein I in health and disease associating structure with function: More than just APS. Blood Rev. 2020, 39, 100610. [Google Scholar] [CrossRef]
- Crystal Structure of Beta-2 Glycoprotein I Purified from Plasma (pB2GPI). Available online: https://www.rcsb.org/structure/6V06 (accessed on 1 May 2021).
- Mirabello, C.; Pollastri, G. Porter, PaleAle 4.0: High-accuracy prediction of protein secondary structure and relative solvent accessibility. Bioinformatics 2013, 29, 2056–2058. [Google Scholar] [CrossRef]
- Flicker, F. Time quasilattices in dissipative dynamical systems. SciPost Phys. 2018, 5, 001. [Google Scholar]
- Putz, J.F. The Golden section and the piano sonatas of Mozart. Math. Mag. 1995, 68, 275–282. [Google Scholar]
- Music for Strings, Percussion and Celesta. Available online: https://en.wikipedia.org/wiki/Music_for_Strings,_Percussion_and_Celesta (accessed on 1 May 2021).
- Twelve-Bar Blues. Available online: https://en.wikipedia.org/wiki/Twelve-bar_blues (accessed on 1 May 2021).
- Haydn-String Quartet, Op. 76, No. 3. Available online: https://www.youtube.com/watch?v=qoWdtGUe5fc (accessed on 1 May 2021).
- Barwick, L. Musical Form and Style in Murriny Patha Djanba Songs at Wadeye (Northern Territory, Australia). Available online: https://core.ac.uk/download/pdf/41240492.pdf (accessed on 1 May 2021).
- Baudelaire, C. Le vieux saltimbanque. In Petits Poèmes en Prose; Michel Lévy fréres: Paris, France, 1869. [Google Scholar]
- Irwin, K.; Amaral, M.; Chester, D. The Self-Simulation hypothesis interpretation of quantum mechanics. Entropy 2020, 22, 247. [Google Scholar]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Informationally complete characters for quark and lepton mixings. Symmetry 2020, 12, 1000. [Google Scholar] [CrossRef]
- Planat, M.; Chester, D.; Aschheim, R.; Amaral, M.M.; Fang, F.; Irwin, K. Finite groups for the Kummer surface: The genetic code and quantum gravity. Quantum Rep. 2021, 3, 68–79. [Google Scholar] [CrossRef]
- Planat, M.; Chester, D.; Aschheim, R.; Amaral, M.M.; Fang, F. Irwin, Character varieties and algebraic surfaces for the topology of quantum computing. in preparation.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).