Transport Properties of Nanostructured Li2TiO3 Anode Material Synthesized by Hydrothermal Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. Characterization
3. Results
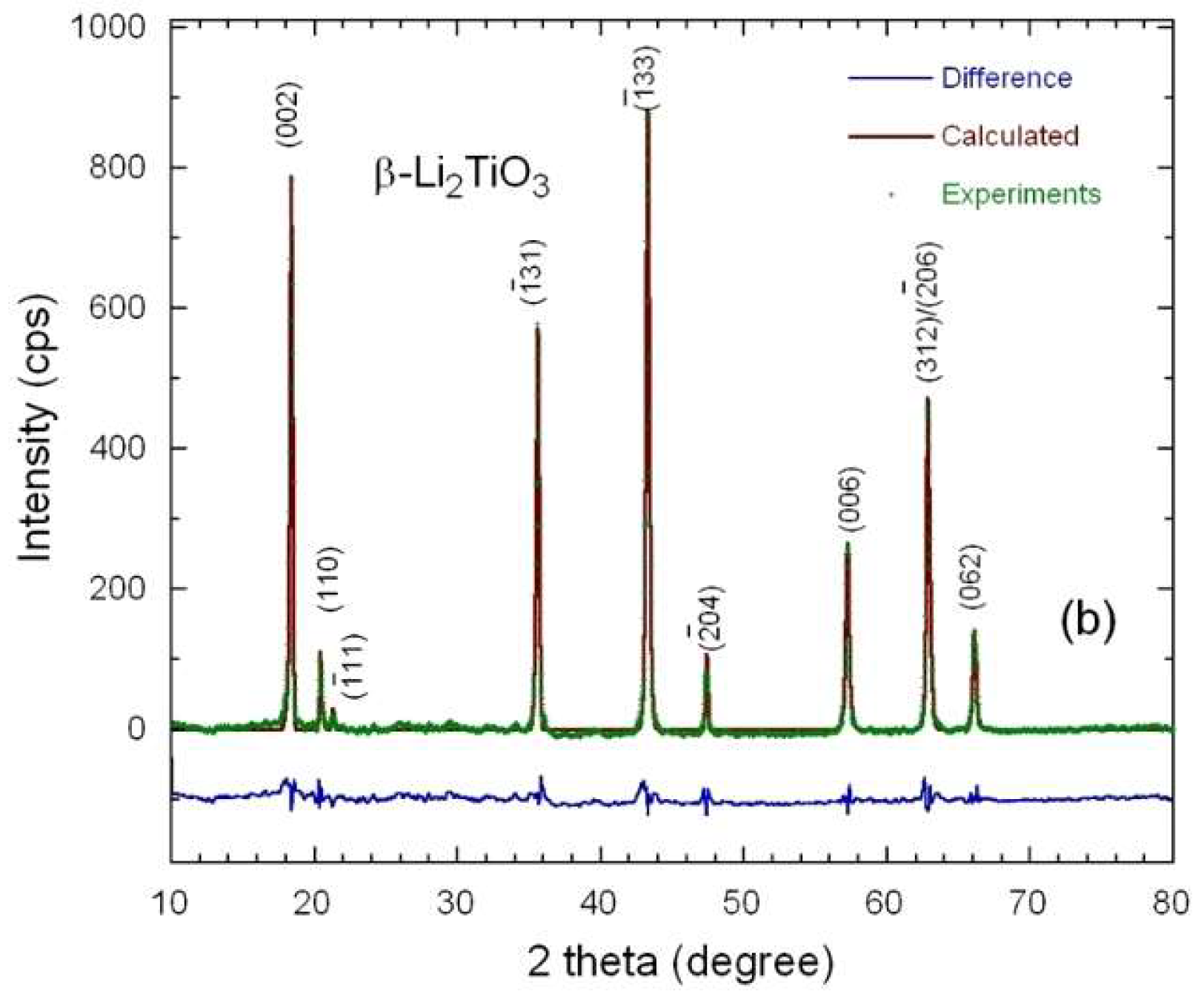
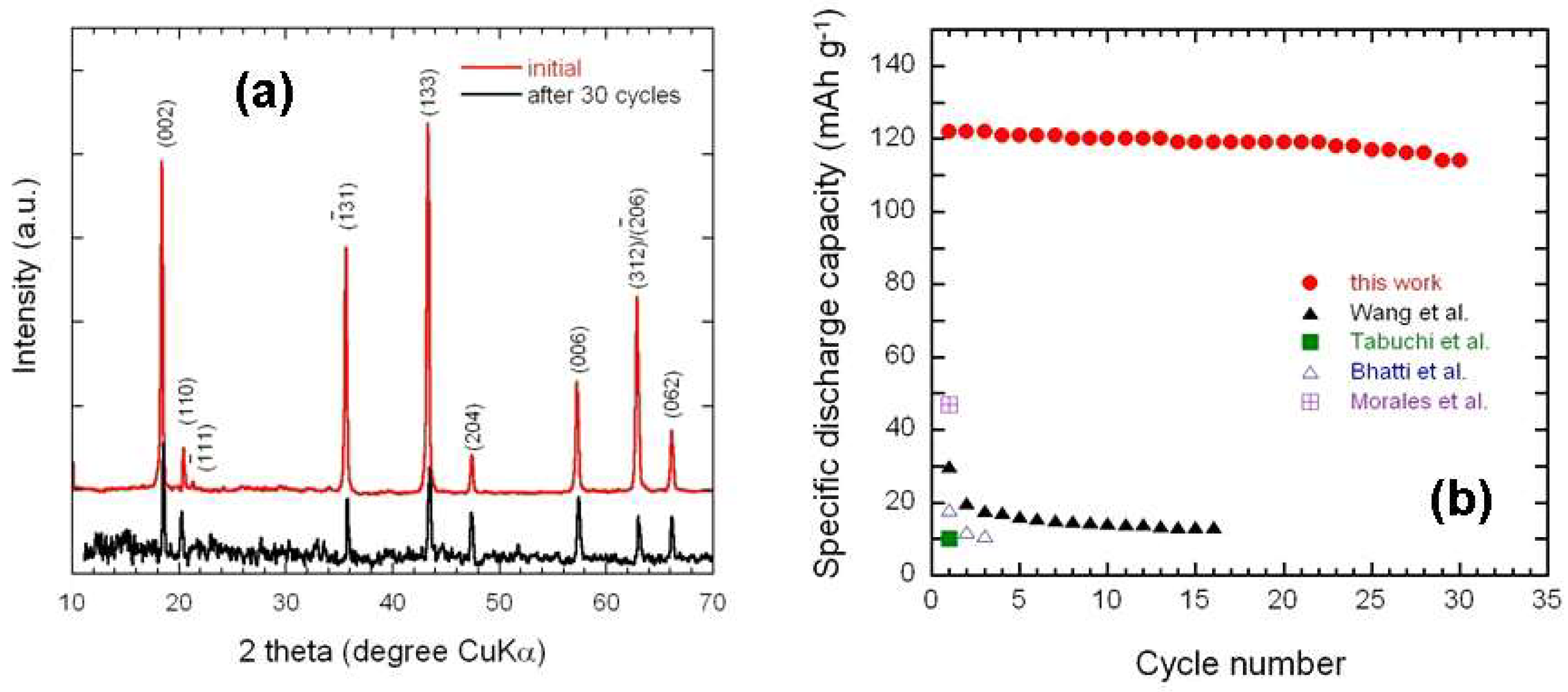
3.1. Elemental and Structural Studies
3.2. Surface Morphology
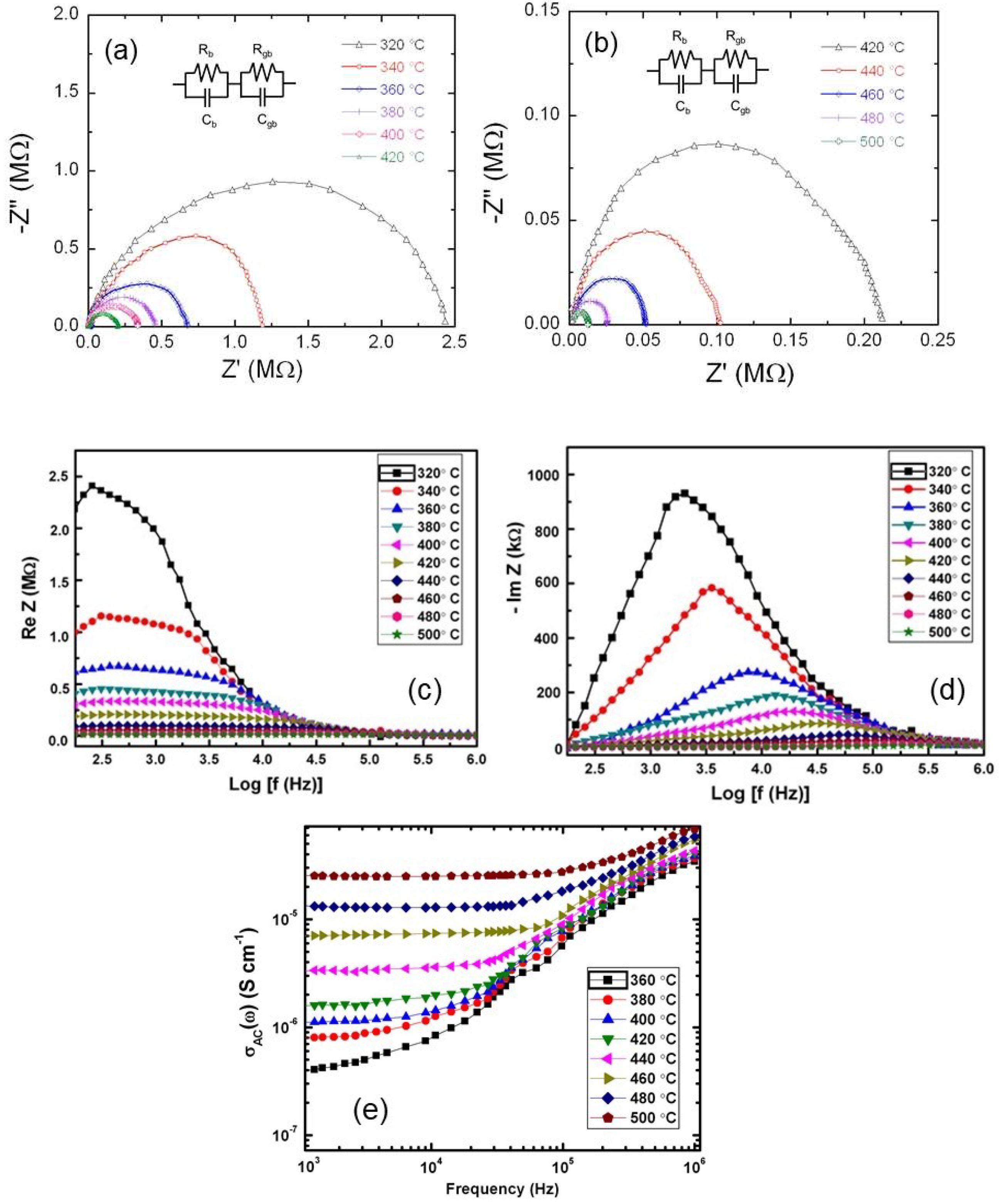
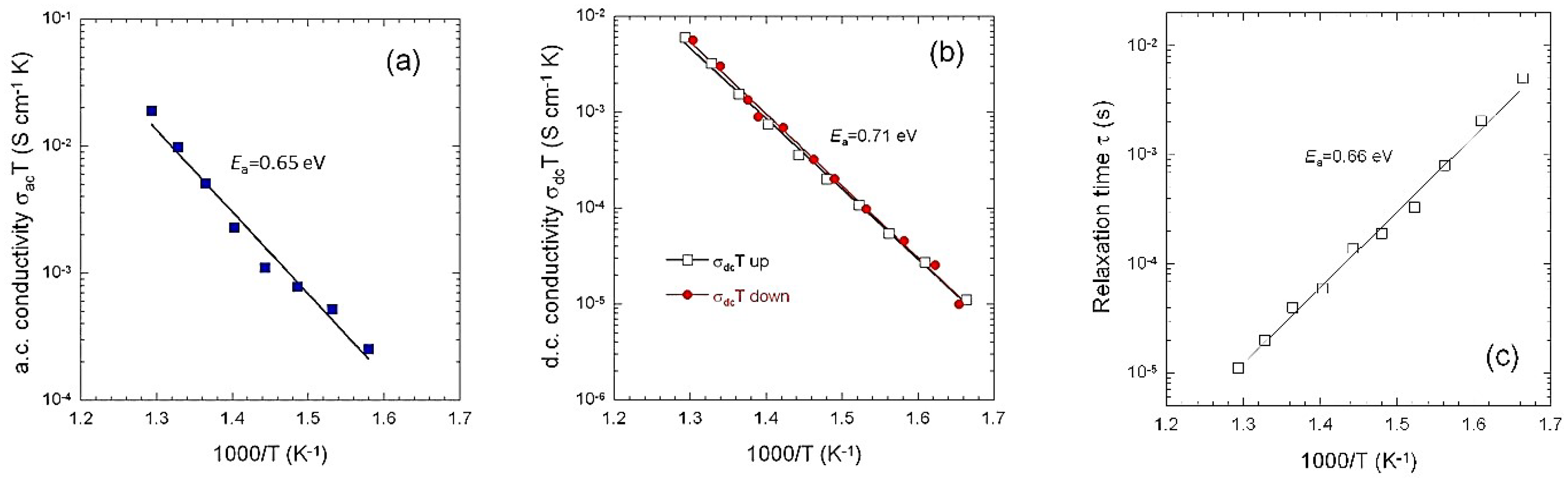
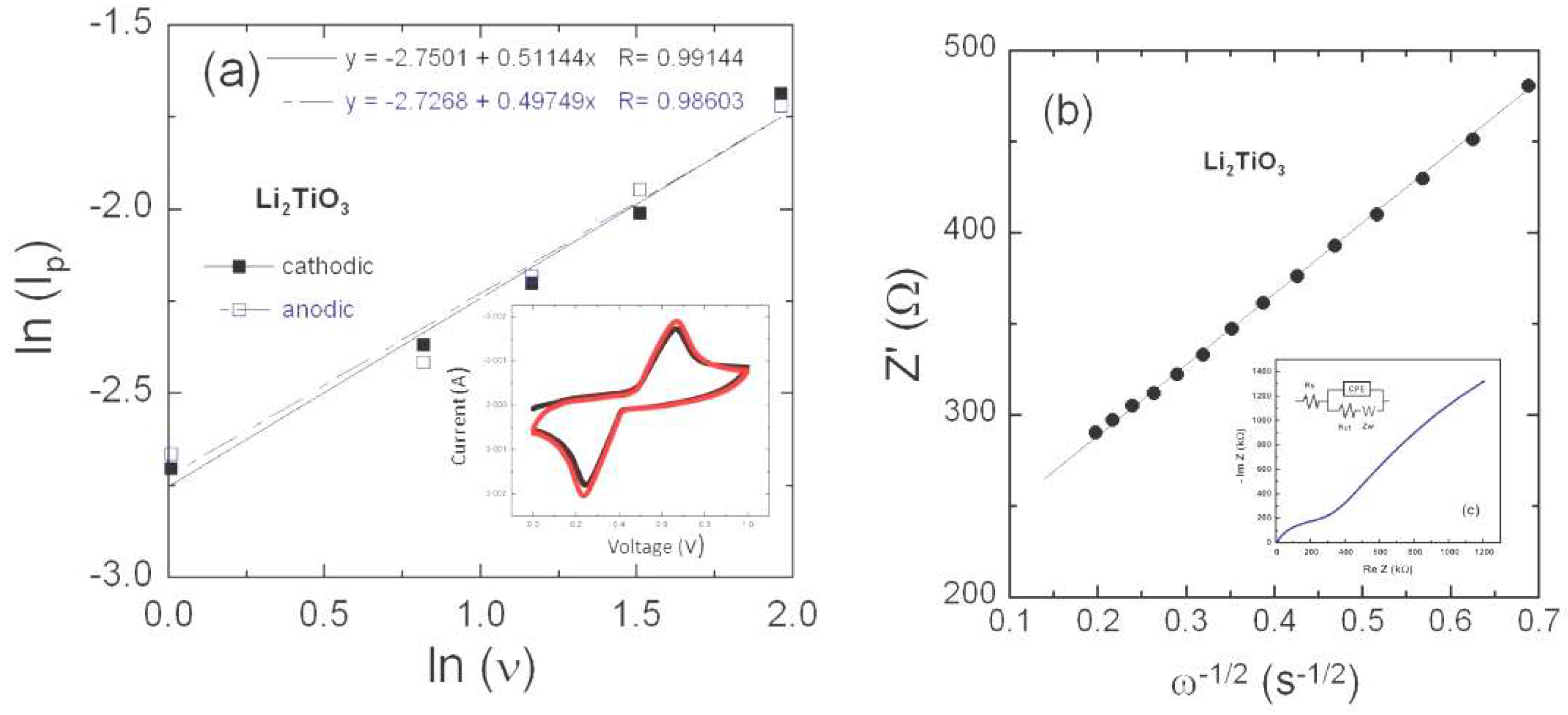
3.3. Electrical Transport
3.4. Li+-ion Diffusivity
4. Discussion
| Method Used | Activation Energy (eV) | Ref. |
|---|---|---|
| 7Li NMR, a.c. conductivity | 0.47–0.80 | [89] |
| a.c. conductivity | 0.81–0.91 | [90] |
| electrical conductivity | 0.60–0.90 | [37] |
| 6,7Li NMR | 0.27 | [74] |
| periodic quantum−chemical DFT | 0.44–0.54 | [75] |
| complex impedance | 0.77/0.88 | [38] |
| d.c. conductivity | 0.86 | [68] |
| 6,7Li NMR | 0.52 | [91] |
| atomistic simulation | 0.51 | [92] |
| DFT calculations | 0.76 | [93] |
| a.c. conductivity | 0.65/0.71 | this work |
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Julien, C.M.; Mauger, A.; Vijh, A.; Zaghib, K. Lithium Batteries: Science and Technology; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Mauger, A.; Xie, H.; Julien, C.M. Composite anodes for lithium-ion batteries: Status and trends. AIMS Mater. Sci. 2016, 3, 1054–1106. [Google Scholar] [CrossRef]
- Aykol, M.; Kim, S.; Hegde, V.I.; Snydacker, D.; Lu, Z.; Hao, S.; Kirklin, S.; Morgan, D.; Wolverton, C. High-throughput computational design of cathode coatings for Li-ion batteries. Nat. Commun. 2016, 7, 13779. [Google Scholar] [CrossRef] [PubMed]
- Krtil, P.; Fattakhova, D. Li insertion into Li-Ti-O spinels: Voltammetric and electrochemical impedance spectroscopy study. J. Electrochem. Soc. 2001, 148, A1045–A1050. [Google Scholar] [CrossRef]
- Pfanzell, M.; Kubiak, P.; Fleischhmmer, M.; Wohlfahrt-Mehrens, M. TiO2 rutile—An alternative anode material for safe lithium-ion batteries. J. Power Sources 2011, 196, 6815–6821. [Google Scholar] [CrossRef]
- Guo, Y.-G.; Hu, Y.-S.; Sigle, W.; Maier, J. Superior electrode performance of nanostructured mesoporous TiO2 (anatase) through efficient hierarchical mixed conducting networks. Adv. Mater. 2007, 19, 2087–2091. [Google Scholar] [CrossRef]
- Armstrong, G.; Armstrong, A.R.; Bruce, P.G.; Reale, P.; Scrosati, B. TiO2(B) nanowires as an improved anode material for lithium-ion batteries containing LiFePO4 or LiNi0.5Mn1.5O4 cathodes and a polymer electrolyte. Adv. Mater. 2006, 18, 2597–2600. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, J.; Chen, Y.; Li, Y. Preparation and characterization of LiTi2O4 anode material synthesized by one-step solid-state reaction. Ionics 2010, 16, 425–429. [Google Scholar] [CrossRef]
- Ogihara, T.; Kodera, T. Synthesis of Li2Ti3O7 anode materials by ultrasonic spray pyrolysis and their electrochemical properties. Materials 2013, 6, 2285–2294. [Google Scholar] [CrossRef]
- Hong, Z.; Wei, M.; Ding, X.; Jiang, L.; Wei, K. Li2ZnTi3O8 nanorods: A new anode material for lithium-ion battery. Electrochem. Commun. 2010, 12, 720–723. [Google Scholar] [CrossRef]
- Zaghib, K.; Simoneau, M.; Armand, M.; Gauthier, M. Electrochemical study of Li4Ti5O12 as negative electrode for Li-ion polymer rechargeable batteries. J. Power Sources 1999, 81–82, 300–305. [Google Scholar] [CrossRef]
- Han, J.-T.; Huang, Y.-H.; Goodenough, J.B. New anode framework for rechargeable lithium batteries. Chem. Mater. 2011, 23, 2027–2029. [Google Scholar] [CrossRef]
- Gicquel, C.; Mayer, M.; Bouaziz, R. Diagramme de phase du système Li2O-TiO2. C. R. Acad. Sci. Ser. C 1972, 275, 1427–1430. [Google Scholar]
- Izquierdo, G.; West, A.R. Phase equilibria in the system Li2O-TiO2. Mater. Res. Bull. 1980, 15, 1655–1660. [Google Scholar] [CrossRef]
- Kleykamp, H. Enthalpy, heat capacity and enthalpy of transformation of Li2TiO3. J. Nucl. Mater. Sci. 2001, 43, 244–248. [Google Scholar] [CrossRef]
- Kleykamp, H. Phase equilibria in the Li-Ti-O system and physical properties of Li2TiO3. Fusion Eng. Des. 2002, 61, 361–366. [Google Scholar] [CrossRef]
- Laumann, A.; Fehr, K.T.; Wachsmann, M.; Holzapfel, M.; Iversen, B.B. Metastable formation of low temperature cubic Li2TiO3 under hydrothermal conditions—Its stability and structural properties. Solid State Ion. 2010, 181, 1525–1529. [Google Scholar] [CrossRef]
- Lang, G. Die kristallstruktur einiger vertreter der verbindungsklasse MeI2MeIVO3 als beitrag zur aufklarung der ordnungsphase von Li2TiO3. Z. Anorg. Allg. Chem. 1954, 276, 77–94. [Google Scholar] [CrossRef]
- Kataoka, K.; Takahashi, Y.; Kijima, N.; Nagai, H.; Akimoto, J.; Idemoto, Y.; Ohshima, K.-I. Crystal growth and structure refinement of monoclinic Li2TiO3. Mater. Res. Bull. 2009, 44, 168–172. [Google Scholar] [CrossRef]
- Laumann, A.; Jensen, K.M.O.; Tyrsted, C.; Bremholm, M.; Fehr, K.T.; Holzapfel, M.; Iversen, B.B. In situ synchrotron X-ray diffraction study of the formation of cubic Li2TiO3 under hydrothermal conditions. Eur. J. Inorg. Chem. 2011, 14, 2221–2226. [Google Scholar] [CrossRef]
- Ramaraghavulu, R.; Buddhudu, S.; Bhaskar-Kumar, G. Analysis of structural and thermal properties of Li2TiO3 ceramic powders. Ceram. Int. 2011, 37, 1245–1249. [Google Scholar] [CrossRef]
- Dorrian, J.F.; Newnham, R.E. Refinement of the structure of Li2TiO3. Mater. Res. Bull. 1969, 4, 179–183. [Google Scholar] [CrossRef]
- Murphy, S.T.; Hine, N.D.M. Point defects and non-stoichiometry in Li2TiO3. Chem. Mater. 2014, 26, 1629–1638. [Google Scholar] [CrossRef]
- Castellanos, M.; West, A.R. Order-disorder phenomena in oxides with rock salt structures: The system Li2TiO3–MgO. J. Mater. Sci. 1979, 14, 450–454. [Google Scholar] [CrossRef]
- Aguas, M.D.; Coombe, G.C.; Parkin, I.P. New solid-state routes to lithium transition metal oxides via reactions with lithium oxide. Polyhedron 1998, 17, 49–53. [Google Scholar] [CrossRef]
- Bhaskar-Kumar, G.; Buddhudu, S. Synthesis and emission analysis of RE3+ (Eu3+ or Dy3+): Li2TiO3 ceramics. Ceram. Int. 2009, 35, 521–525. [Google Scholar] [CrossRef]
- Wu, X.; Wen, Z.; Lin, B.; Xu, X. Sol–gel synthesis and sintering of nano-size Li2TiO3 powder. Mater. Lett. 2008, 62, 837–839. [Google Scholar] [CrossRef]
- Jung, C.H.; Park, J.Y.; Oh, S.J.; Park, H.K.; Kim, Y.S.; Kim, D.K.; Kim, J.H. Synthesis of Li2TiO3 ceramic breeder powders by the combustion process. J. Nucl. Mater. 1998, 253, 203–212. [Google Scholar] [CrossRef]
- Sinha, A.; Nair, S.R.; Sinha, P.K. Single step synthesis of Li2TiO3 powder. J. Nucl. Mater. 2010, 399, 162–166. [Google Scholar] [CrossRef]
- Jung, C.-H.; Lee, S.J.; Kriven, W.M.; Park, J.-Y.; Ryu, W.-S. A polymer solution technique for the synthesis of nano-sized Li2TiO3 ceramic breeder powders. J. Nucl. Mater. 2008, 373, 194–198. [Google Scholar] [CrossRef]
- Zhang, L.; He, G.; Zhaou, D.; Zhou, J.; Yao, Q. Study on transformation mechanism of lithium titanate modified with hydrochloric acid. Ionics 2016, 22, 2007–2014. [Google Scholar] [CrossRef]
- Ma, J.-L.; Fu, Z.-F.; Gao, J.; Zhang, X.-S. A simple method to synthesize nanosized Li2TiO3 powders through high-energy ball-milling. Powder Metall. Met. Ceram. 2015, 54, 410–415. [Google Scholar] [CrossRef]
- Lulewicz, J.D.; Roux, N. Fabrication of Li2TiO3 pebbles by the extrusion–spheronisation–sintering process. J. Nucl. Mater. 2002, 307, 803–806. [Google Scholar] [CrossRef]
- Wang, H.; Yang, M.; Gong, Y.; Feng, L.; Dang, C.; Shia, Y.; Shi, Q.; Wei, J.; Liao, Z.; Lu, T. Fabrication of nanostructured Li2TiO3 ceramic pebbles as tritium breeders using powder particles synthesized via a CTAB-assisted method. Ceram. Int. 2017, 43, 5680–5686. [Google Scholar] [CrossRef]
- Miao, B.; Zeng, W.; Hussain, S.; Mei, Q.; Xu, S.; Zhang, H.; Li, Y. Large scale hydrothermal synthesis of monodisperse hexagonal WO3 nanowire and the growth mechanism. Mater. Lett. 2015, 147, 12–15. [Google Scholar] [CrossRef]
- Wan, Z.; Yu, Y.; Zhang, H.F.; Gao, T.; Chen, X.J.; Xiao, C.J. First-principles study of electronic, dynamical and thermodynamic properties of Li2TiO3. Eur. Phys. J. B 2012, 85, 181–187. [Google Scholar] [CrossRef]
- Fehr, T.; Schmidbauer, E. Electrical conductivity of Li2TiO3 ceramics. Solid State Ion. 2007, 178, 35–41. [Google Scholar] [CrossRef]
- Dash, U.; Sahoo, S.; Chaudhuri, P.; Parashar, S.K.S.; Parashar, K. Electrical properties of bulk and nano Li2TiO3 ceramics: A comparative study. J. Adv. Ceram. 2014, 3, 89–97. [Google Scholar] [CrossRef]
- Kim, J.-S.; Johnson, C.S.; Vaughey, J.T.; Thackeray, M.M.; Hackney, S.A.; Yoon, W.; Grey, C.P. Electrochemical and structural properties of xLi2M’O3 (1-x)LiMn0.5Ni0.5O2 electrodes for lithium batteries (M’ = Ti, Mn, Zr; 0 ≤ x ≤ 0.3). Chem. Mater. 2004, 16, 1996–2006. [Google Scholar] [CrossRef]
- Chauvaut, V.; Cassir, M. Behaviour of titanium species in molten Li2CO3+Na2CO3 and Li2CO3+K2CO3 in the anodic conditions used in molten carbonate fuel cells. II. Electrochemical intercalation of Li+ in Li2TiO3 at 600 °C and 650 °C. J. Electroanal. Chem. 1999, 474, 9–15. [Google Scholar] [CrossRef]
- Tabuchi, M.; Nakashima, A.; Shigemura, H.; Ado, K.; Kobayashi, H.; Sakaebe, H.; Tatsumi, K.; Kageyama, H.; Nakamura, T.; Kanno, R. Fine Li(4-x)/3Ti(2-2x)/3FexO2 (0.18 ≤ x ≤ 0.67) powder with cubic rock-salt structure as a positive electrode material for rechargeable lithium batteries. J. Mater. Chem. 2003, 13, 1747–1757. [Google Scholar] [CrossRef]
- Shigemura, H.; Tabuchi, M.; Sakaebe, H.; Kobayashi, H.; Kageyama, H. Lithium extraction and insertion behavior of nanocrystalline Li2TiO3-LiFeO2 solid solution with cubic rock salt structure. J. Electrochem. Soc. 2003, 150, A638–A644. [Google Scholar] [CrossRef]
- Morales, J.; Santos-Pena, J.; Trocoli, R.; Franger, S. Electrochemical activity of rock-salt-structured LiFeO2-Li4/3Ti2/3O2 nanocomposites in lithium cells. J. Nanopart. Res. 2008, 10, 217–226. [Google Scholar] [CrossRef]
- Shi, J.; Liang, Y.; Li, L.; Peng, Y.; Yang, H. Evaluation of the electrochemical characteristics of silicon/lithium titanate composite as anode material for lithium ion batteries. Electrochim. Acta 2015, 155, 125–131. [Google Scholar] [CrossRef]
- Ko, Y.N.; Choi, S.H.; Kang, Y.C.; Park, S.B. Characteristics of Li2TiO3-LiCrO2 composite cathode powders prepared by ultrasonic spray pyrolysis. J. Power Sources 2013, 244, 336–343. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, A.; Dai, X.; Geng, L.; Li, J.; Li, J. Solid–state synthesis of submicron–sized Li4Ti5O12/Li2TiO3 composites with rich grain boundaries for lithium ion batteries. J. Power Sources 2014, 266, 114–120. [Google Scholar] [CrossRef]
- Bhatti, H.S.; Anjum, D.; Ullah, S.; Ahmed, B.; Habib, A.; Karim, A.; Hasanain, S.K. Electrochemical characteristics and Li+ ion intercalation kinetics of dual-phase Li4Ti5O12/Li2TiO3 composite in the voltage range 0–3 V. J. Phys. Chem. C 2016, 120, 9553–9561. [Google Scholar] [CrossRef]
- Lu, J.; Peng, Q.; Wang, W.; Nan, C.; Li, L.; Li, Y. Nanoscale coating of LiMO2 (M = Ni, Co, Mn) nanobelts with Li+-conductive Li2TiO3: toward better rate capabilities for Li-ion batteries. J. Am. Chem. Soc. 2013, 135, 1649–1652. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Nie, P.; Luo, H.; Zhang, Y.; Wang, J.; Zhang, X. Highly enhanced lithium storage capability of LiNi0.5Mn1.5O4 by coating with Li2TiO3 for Li-ion batteries. J. Mater. Chem. A 2014, 2, 18256–18262. [Google Scholar] [CrossRef]
- Jia, G.; Liu, S.; Yang, G.; Li, F.; Wu, K.; He, Z.; Shangguan, X. Effects of Li2TiO3 coating on the structure and the electrochemical properties of LiNi0.5Mn0.5O2 cathode materials at high voltages. Ionics 2019, 25, 399–410. [Google Scholar] [CrossRef]
- Zhao, E.; Liu, X.; Hu, Z.; Sun, L.; Xiao, X. Facile synthesis and enhanced electrochemical performances of Li2TiO3-coated lithium-rich layered Li1.13Ni0.30Mn0.57O2 cathode materials for lithium-ion batteries. J. Power Sources 2015, 294, 141–149. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Y.; Li, B.; Fu, T.; Xie, D.; Cai, J.; Zhao, J. Improving the electrochemical properties of LiNi0.5Co0.2Mn0.3O2 at 4.6 V cutoff potential by surface coating with Li2TiO3 for lithium-ion batteries. Phys. Chem. Chem. Phys. 2015, 17, 32033–32043. [Google Scholar] [CrossRef] [PubMed]
- Lakshmi-Narayana, A.; Dhananjaya, M.; Guru-Prakash, N.; Hussain, O.M.; Julien, C.M. Nanocrystalline Li2TiO3 electrodes for supercapattery application. Ionics 2017, 23, 3419–3428. [Google Scholar] [CrossRef]
- Lakshmi-Narayana, A.; Dhananjaya, M.; Guru-Prakash, N.; Hussain, O.M.; Mauger, A.; Julien, C.M. Li2TiO3/graphene and Li2TiO3/CNT composites as anodes for high power Li–ion batteries. ChemistrySelect 2018, 3, 9150–9158. [Google Scholar] [CrossRef]
- Hoshino, T.; Kawamura, H.; Dokiya, M.; Takahashi, Y.; Terai, T.; Yamawaki, M. Non-stoichiometry of Li2TiO3 under hydrogen atmosphere conditions. J. Nucl. Mater. 2004, 329, 1300–1304. [Google Scholar] [CrossRef]
- Roisnel, T.; Rodriguez-Carjaval, J. WinPLOTR: A windows tool for powder diffraction pattern analysis. Mater. Sci. Forum 2001, 378, 118–123. [Google Scholar] [CrossRef]
- Langford, J.I.; Wilson, A.J.C. Scherrer after sixty years: A survey and some new results in the determination of crystallite size. J. Appl. Cryst. 1978, 11, 102–113. [Google Scholar] [CrossRef]
- Julien, C. Local cationic environment in lithium nickel-cobalt oxides used as cathode materials for lithium batteries. Solid State Ion. 2000, 136, 887–896. [Google Scholar] [CrossRef]
- Bian, J.J.; Dong, Y.F. Sintering behavior, microstructure and microwave dielectric properties of Li2+xTiO3 (0 ≤ x ≤ 0.2). Mater. Sci. Eng. B 2011, 176, 147–151. [Google Scholar] [CrossRef]
- Zhang, T.; Zuo, R.; Zhang, J. Structure, microwave dielectric properties and low-temperature sintering of acceptor/donor codoped Li2Ti1-x(Al0.5Nb0.5)xO3 ceramics. J. Am. Ceram. Soc. 2016, 99, 825–832. [Google Scholar] [CrossRef]
- Nakazawa, T.; Naito, A.; Aruga, T.; Grismanovs, V.; Chimi, Y. High energy heavy ion induced structural disorder in Li2TiO3. J. Nucl. Mater. 2007, 367, 1398–1403. [Google Scholar] [CrossRef]
- Mukai, K.; Kato, Y.; Nakano, H. Understanding the zero-strain lithium insertion scheme of Li[Li1/3Ti5/3]O4: Structural changes at atomic scale clarified by Raman spectroscopy. J. Phys. Chem. C 2014, 118, 2992–2999. [Google Scholar] [CrossRef]
- Denisova, T.A.; Maksimova, L.G.; Polyalov, E.V.; Zhuravlev, N.A.; Kovyazina, S.A.; Leonidova, O.N.; Khazbibulin, D.F.; Yureva, E.I. Metatitanic acid: Synthesis and properties. Russ. J. Inorg. Chem. 2006, 51, 691–699. [Google Scholar] [CrossRef]
- Amalraj, F.; Markovsky, B.; Sharon, D.; Talianker, M.; Zinigrad, E.; Persky, R.; Haik, O.; Grinblat, J.; Lampert, J.; Schulz-Dobrick, M.; et al. Study of the electrochemical behavior of the “inactive” Li2MnO3. Electrochim. Acta 2012, 78, 32–39. [Google Scholar] [CrossRef]
- Julien, C.M.; Massot, M. Lattice vibrations of materials for lithium rechargeable batteries III Lithium manganese oxides. Mater. Sci. Eng. B 2003, 100, 69–78. [Google Scholar] [CrossRef]
- Li, Z.; Du, F.; Bie, X.; Zhang, D.; Cai, Y.; Cui, X.; Wang, C.; Chen, G.; Wei, Y. Electrochemical kinetics of the Li[Li0.23Co0.3Mn0.47]O2 cathode material by GITT and EIS. J. Phys. Chem. C 2010, 114, 22751–22757. [Google Scholar] [CrossRef]
- Yu, C.-L.; Yanagisawa, K.; Kamiya, S.; Kozawa, T.; Ueda, T. Monoclinic Li2TiO3 nano–particles via hydrothermal reaction: Processing and structure. Ceram. Int. 2014, 40, 1901–1908. [Google Scholar] [CrossRef]
- Dash, U.; Sahoo, S.; Parashar, S.K.S.; Chaudhuri, P. Effect of Li+ ion mobility on the grain boundary conductivity of Li2TiO3 nanoceramics. J. Adv. Ceram. 2014, 3, 98–108. [Google Scholar] [CrossRef]
- Ngai, K.L.; Leon, C. Cage decay, near constant loss, and crossover to cooperative ion motion in ionic conductors: Insight from experimental data. Phys. Rev. B 2002, 66, 064308. [Google Scholar] [CrossRef]
- Eddrief, M.; Dzwonkowski, P.; Julien, C.; Balkanski, M. The ac conductivity in B2O3-xLi2O films. Solid State Ion. 1991, 45, 77–82. [Google Scholar] [CrossRef]
- Dzwonkowski, P.; Eddrief, M.; Julien, C.; Balkanski, M. Electrical a.c. conductivity of B2O3-xLi2O glass thin films and analysis using the electric modulus formalism. Mater. Sci. Eng. B 1991, 8, 193–200. [Google Scholar] [CrossRef]
- Elliott, S.R. Temperature dependence of a.c. conductivity of chalcogenide glasses. Philos. Mag. B 1978, 37, 553–560. [Google Scholar] [CrossRef]
- Jonscher, A.K. The universal dielectric response. Nature 1977, 267, 673–679. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Kerisit, S.; Yang, Z.G.; Graff, G.L.; Liu, J.; Sears, J.A.; Burton, S.D.; Rosso, K.M.; Hu, J.Z. Combined 6,7Li NMR and molecular dynamics study of Li diffusion in Li2TiO3. J. Phys. Chem. C 2009, 113, 20108–20116. [Google Scholar] [CrossRef]
- Islam, M.M.; Bredow, T. Lithium diffusion pathways in β-Li2TiO3: A theoretical study. J. Phys. Chem. C 2016, 120, 7061–7066. [Google Scholar] [CrossRef]
- Sun, X.; Hegde, M.; Zhang, Y.; He, M.; Gu, L.; Wang, Y.; Shu, J.; Radovanovic, P.V.; Cui, B. Structure and electrochemical properties of spinel Li4Ti5O12 nanocomposites as anode for lithium-ion battery. Int. J. Electrochem. Sci. 2014, 9, 1583–1596. [Google Scholar]
- Tang, S.B.; Lai, M.O.; Lu, L. Li-ion diffusion in highly (003) oriented LiCoO2 thin film cathode prepared by pulsed laser deposition. J. Alloys Compd. 2008, 449, 300–303. [Google Scholar] [CrossRef]
- Ho, C.; Raistrick, I.D.; Huggins, R.A. Application of a–c techniques to the study of lithium diffusion in tungsten trioxide thin films. J. Electrochem. Soc. 1980, 127, 343–350. [Google Scholar] [CrossRef]
- Shi, Q.; Hu, R.; Zeng, M.; Zhu, M. A diffusion kinetics study of Li-ion in LiV3O8 thin film electrode. Electrochim. Acta 2010, 55, 6645–6650. [Google Scholar] [CrossRef]
- Xie, J.; Tanaka, T.; Imanishi, N.; Matsumura, T.; Hirano, A.; Takeda, Y.; Yamamoto, O. Li-ion transport kinetics in LiMn2O4 thin films prepared by radio frequency magnetron sputtering. J. Power Sources 2008, 180, 576–581. [Google Scholar] [CrossRef]
- Yang, X.; Yu, R.; Ge, L.; Wang, D.; Zhao, Q.; Wang, X.; Bai, Y.; Yuan, H.; Shu, H. Facile synthesis and performances of nanosized Li2TiO3-based shell encapsulated LiMn1/3Ni1/3Co1/3O2 microspheres. J. Mater. Chem. A 2014, 2, 8362–8368. [Google Scholar] [CrossRef]
- Kim, J.S.; Johnson, C.S.; Thackeray, M.M. Layered xLiMO2∙(1-x)Li2M’O3 electrodes for lithium batteries: A study of 0.95LiMn0.5Ni0.5O2∙0.05Li2TiO3. Electrochem. Commun. 2002, 4, 205–209. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Noguchi, H. Novel layered Li-Cr-Ti-O cathode materials related to the LiCrO2-Li2TiO3 solid solution. J. Electrochem. Soc. 2003, 150, A601–A607. [Google Scholar] [CrossRef]
- Zhang, L.Q.; Wang, X.Q.; Noguchi, H.; Yoshio, M.; Takada, K.; Sasaki, T. Electrochemical and ex situ XRD investigations on (1-x)LiNiO2∙xLi2TiO3 (0.05 ≤ x ≤ 0.5). Electrochim. Acta 2004, 49, 3305–3311. [Google Scholar] [CrossRef]
- Wu, X.W.; Wen, Z.Y.; Xu, X.G.; Han, J.D. Synthesis and ionic conductivity of Mg-doped Li2TiO3. Solid State Ion. 2008, 179, 1779–1782. [Google Scholar] [CrossRef]
- Wu, X.W.; Wen, Z.Y.; Wang, X.Y.; Xu, X.G.; Lin, J.; Song, S.F. Effect of Ta-doping on the ionic conductivity of lithium titanate. Fusion Eng. Des. 2010, 85, 1442–1445. [Google Scholar] [CrossRef]
- Zhu, Y.R.; Yin, L.C.; Yi, T.F.; Liu, H.; Xie, Y.; Zhu, R.S. Electrochemical performance and lithium-ion intercalation kinetics of micron-sized Li4Ti5O12 anode material. J. Alloys Compd. 2013, 547, 107–112. [Google Scholar] [CrossRef]
- Li, S.; Guo, J.; Ma, Q.; Yang, Y.; Dong, X.; Yang, M.; Yu, W.; Wang, J.; Liu, G. Electrospun Li4Ti5O12/Li2TiO3 composite nanofibers for enhanced high-rate lithium ion batteries. J. Solid State Electrochem. 2017, 21, 2779–2790. [Google Scholar] [CrossRef]
- Ruprecht, B.; Wilkening, M.; Ueckerb, R.; Heitjans, P. Extremely slow Li ion dynamics in monoclinic Li2TiO3—probing macroscopic jump diffusion via 7Li NMR stimulated echoes. Phys. Chem. Chem. Phys. 2012, 14, 11974–11980. [Google Scholar] [CrossRef]
- Vitins, G.; Kizane, G.; Lusis, A.; Tiliks, J. Electrical conductivity studies in the system Li2TiO3-Li1.33Ti1.67O4. J. Solid State Electrochem. 2002, 6, 311–319. [Google Scholar] [CrossRef]
- Baklanova, Y.V.; Arapova, I.Y.; Shein, I.R.; Maksimova, L.G.; Mikhalev, K.N.; Denisova, T.A. Charge distribution and mobility of lithium ions in Li2TiO3 from 6,7Li NMR data. J. Struct. Chem. 2013, 54, 111–118. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Fitzpatrick, M.E.; Vovk, R.V.; Chroneos, A. Defect process and lithium diffusion in Li2TiO3. Solid State Ion. 2018, 327, 93–98. [Google Scholar] [CrossRef]
- Ki, K.; Yang, W.; Wang, W.-H.; Li, Y.-T. First principles study of tritium diffusion in Li2TiO3 crystal with lithium vacancy. Materials 2018, 11, 2383. [Google Scholar]

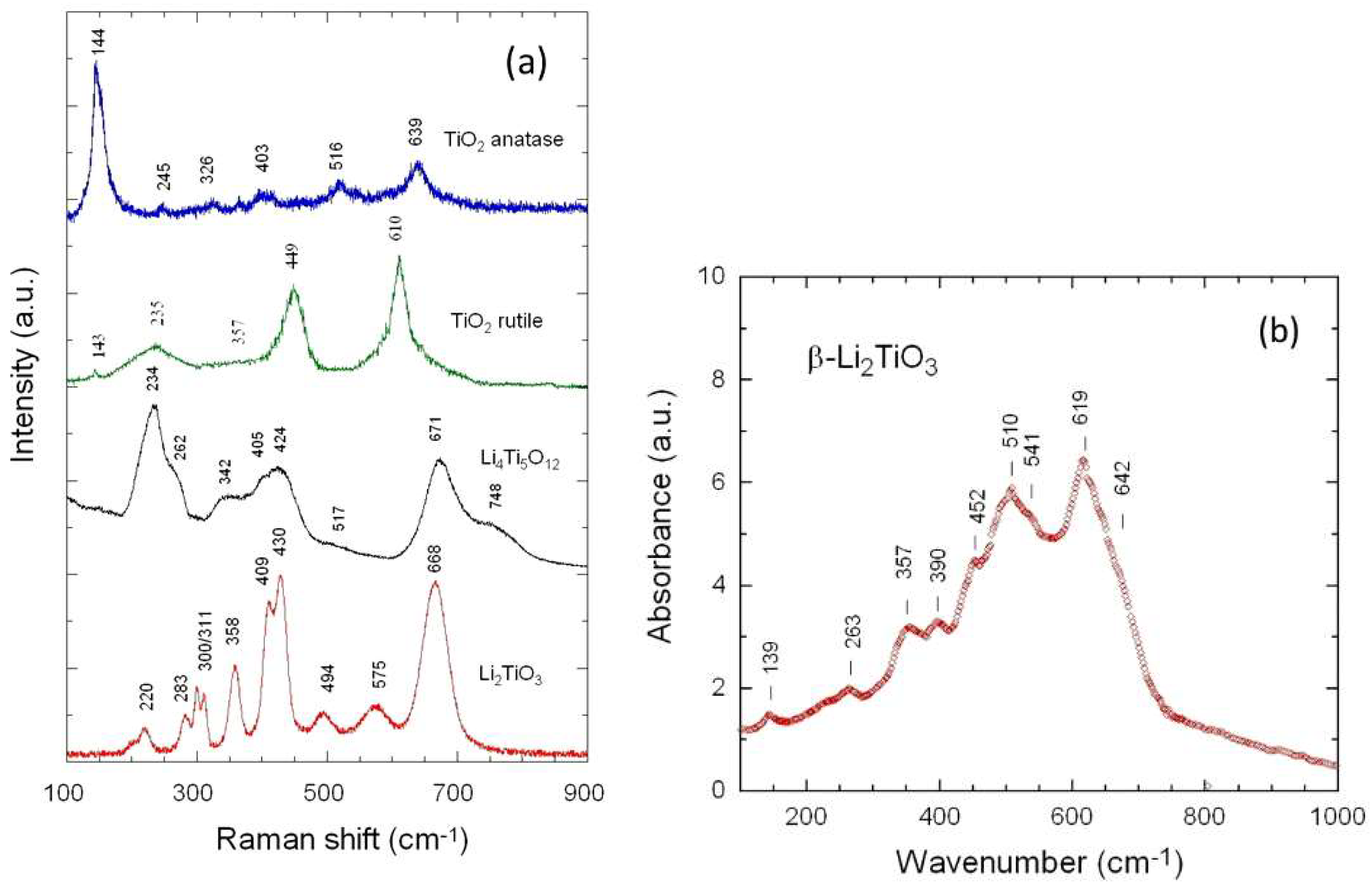

| Raman | Infrared | ||||||
|---|---|---|---|---|---|---|---|
| ωexp. | Intensity * | ωcal. | ωexp. | Intensity * | ωcal. | ||
| 98 | vw | 83 | Ag | ||||
| 211 | w | 214 | Ag | 139 | vw | 143 | BU |
| 277 | m | 278 | Bg | 266 | vw | 263 | Bu |
| 294 | m | 302 | Ag | 357 | m | 355 | Au |
| 303 | m | 314 | Bg | 390 | w | 393 | Au |
| 350 | m | 360 | Ag | 452 | w | 456 | Au |
| 402 | S | 401 | Ag | 510 | S | - | |
| 420 | S | 432 | Bg | 541 | m | 544 | Bu |
| 484 | w | 470 | Bg | 619 | S | 617 | Au |
| 567 | w | 542 | Ag | 642 | s | 634 | Au |
| 658 | S | 617 | Ag | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakshmi-Narayana, A.; Hussain, O.M.; Mauger, A.; Julien, C. Transport Properties of Nanostructured Li2TiO3 Anode Material Synthesized by Hydrothermal Method. Sci 2019, 1, 56. https://doi.org/10.3390/sci1030056
Lakshmi-Narayana A, Hussain OM, Mauger A, Julien C. Transport Properties of Nanostructured Li2TiO3 Anode Material Synthesized by Hydrothermal Method. Sci. 2019; 1(3):56. https://doi.org/10.3390/sci1030056
Chicago/Turabian StyleLakshmi-Narayana, Ambadi, Obili M. Hussain, Alain Mauger, and Christian Julien. 2019. "Transport Properties of Nanostructured Li2TiO3 Anode Material Synthesized by Hydrothermal Method" Sci 1, no. 3: 56. https://doi.org/10.3390/sci1030056
APA StyleLakshmi-Narayana, A., Hussain, O. M., Mauger, A., & Julien, C. (2019). Transport Properties of Nanostructured Li2TiO3 Anode Material Synthesized by Hydrothermal Method. Sci, 1(3), 56. https://doi.org/10.3390/sci1030056






