Abstract
This study developed a neutron-beam-focusing supermirror for grazing-incidence small-angle neutron scattering (GISANS) measurements. We adopted point-to-point beam focusing based on an ellipse whose two foci correspond to a virtual point source and a spot on the detector surface. The focusing supermirror was fabricated by depositing NiC/Ti supermirror film with ion-beam sputtering on a precise elliptic surface of fused quartz figured using the elastic emission machining technique. Neutron measurements at the pulsed neutron reflectometer BL17 of the MLF, J-PARC, successfully demonstrated that the focusing supermirror enhances the beam intensity twentyfold compared with an optimally collimated beam, achieving a signal-to-background ratio of the focal spot as high as 500. The mirror can be readily installed and used at BL17 for time-of-flight GISANS measurements.
1. Introduction
The grazing-incidence small-angle neutron scattering (GISANS) technique [1] is a powerful tool for investigating in-plane nanostructures of surfaces and interfaces. It is measured by changing the glancing angle and/or wavelength of the neutron, which impinges on the sample surface, and the data provides information on depth-dependent structures. At a glancing angle lower than the critical angle of total reflection, structures near the surface are selectively probed, whereas deeply buried structures are revealed at higher glancing angles. This technique has been employed for a significant number of studies on polymer thin films [2] and other layered systems (e.g., [3,4]). GISANS measurements are performed with a wide-band beam at a pulsed neutron beamline, analyzing neutron wavelengths using the time-of-flight method (time-of-flight GISANS) [5]. A single measurement of time-of-flight GISANS offers a broad range of momentum transfer and extensive sensitivity from the sample surface to deeply buried interfaces because a neutron’s scattering depth depends on its wavelength. Since we measure small scattering angles of neutrons in a GISANS experiment, the measurement requires a well-collimated neutron beam that runs from the sample to a neutron detector, forming a small spot at the detector position. If we prepare such a beam by only slit collimations, the slits should restrict the beam very tightly in front of the sample, losing beam intensity severely. Therefore, a device that focuses the beam on the detector position is essential. Furthermore, the focusing device must focus the beam on a small spot at the detector surface, which is far away from it. Therefore, the device should control the beam more precisely than the one used in other neutron scattering experiments, which focuses the beam on the sample position only to enhance the incident beam intensity.
In GISANS measurements, two-dimensional focusing is not necessarily required. In the in-plane direction, we can use a divergent beam focused on a small spot on the detector. The resolution of the momentum transfer in this direction does not deteriorate as long as the divergence is smaller than, for example, 20°. By contrast, we should not use a divergent beam in the depth direction even if the beam is focused on the spot. The divergence of the incident angle mixes different momentum transfers at a single pixel of a detector. It also corresponds to a range of neutron scattering depths. Furthermore, due to the shallow incident angle, we need to restrict the beam size tightly in this direction, not only at the detector position, where it must match the spot size, but also at the sample position. A recent study conducted GISANS measurements with a beam divergent in the depth direction, but the depth resolution had to be abandoned or redeemed by performing an individual neutron reflectivity measurement [6]. For these reasons, the present study pursues one-dimensional focusing along the surface.
In time-of-flight GISANS experiments, focusing devices should function over a broad range of neutron wavelengths. For such a focusing device, a neutron supermirror [7,8] is a promising candidate. It is not easy to focus a neutron beam on a small spot. One reason is that we cannot significantly change the direction of a neutron beam by total reflection or refraction. This is because the neutron’s refractive index is very close to 1 in any material or magnetic field. For instance, a single layer of nickel functions as a neutron’s total reflection mirror, but its critical angle of total reflection is only 0.2° for neutrons of 0.2 nm in wavelength, three or four times smaller than a typical supermirror. Bragg reflection by a crystalline lattice can change the beam direction significantly, but focusing on a small spot would require a very fine-tuned bending of the crystal. On the other hand, a supermirror is a kind of artificial lattice film deposited on a substrate. The film consists of alternative layers of two materials with different refractive indices. One often adopts nickel and titanium because of the high contrast in refractive indices (or scattering length densities). The layered structure of the film follows the surface figure of the substrate, and hence the “bending” of the artificial lattice can be controlled precisely by the substrate figure. Moreover, the thickness of the supermirror layers is gradually increased by adding to the number of layers, and therefore the Bragg angle is distributed according to the layer thickness range, resulting in adjoining Bragg peaks that constitute a reflectivity profile like that of a single-layer film with a large critical angle of total reflection. As a result, a supermirror acts as a total reflection film that reflects neutrons with a wide range of wavelengths. The performance of a supermirror is often characterized by its reflectivity and the critical angle of total reflection (or m, which denotes the ratio of the critical angle of the supermirror to that of nickel). A higher reflectivity results in a higher beam intensity, whereas a larger m gives a broader range of wavelengths of the reflected beam. In addition, it is essential to reduce off-specular scattering at the supermirror and keep it as low as possible in GISANS experiments because the off-specular scattering could become a source of background around the beam spot at the detector position. Nevertheless, we must not install a slit in front of the detector to cut the background neutrons because the slit simultaneously cuts signal neutrons scattered in the sample.
Neutron supermirrors have been widely designed and used for focusing guide tubes (e.g., [9]) in neutron facilities worldwide. However, a guide tube only provides a relatively broad beam, which is unsuitable for GISANS measurements. As regards focusing on a small spot, several fabrications have been reported. For instance, two-dimensional beam focusing has been demonstrated with sequential Kirkpatrick–Baez configurations [10,11] and Montel Kirkpatrick–Baez mirrors [12,13]. One-dimensional focusing by a nested elliptic supermirror [14] and by a segmented elliptic supermirror for neutron reflectivity measurement [15,16,17] has also been reported. Nonetheless, the developments are still halfway to establishment, and the number of applications for measuring scientific samples is limited.
At the Materials and Life Science Experimental Facility (MLF) of the Japan Proton Accelerator Research Complex (J-PARC), NiC/Ti neutron supermirrors have been developed using ion-beam sputtering and applied to focusing supermirrors. NiC has been adopted as a reflector layer instead of Ni because a NiC/Ti supermirror exhibits a lower off-specular scattering intensity than a Ni/Ti supermirror by more than one order of magnitude due to the crystalline size in the NiC layer being significantly smaller than that in the Ni layer [18]. The supermirror development at the MLF has achieved a high reflectivity (>0.82) and a high critical angle of total reflection () [19] with a low ratio of off-specular scattering to specular reflection (<10−4) [18]. A supermirror of has also been fabricated [20]. A large-area ion-beam sputtering machine at the MLF can deposit supermirror films on an area of 500 mm in diameter. Combining the supermirror coating technique with a precise surface-figuring technique by numerically controlled local wet etching [21], we have developed one-dimensional elliptic supermirrors [22,23,24].
This paper describes the design, fabrication, and performance test of a focusing supermirror developed for GISANS measurements at a pulsed neutron beamline. We adopted point-to-point beam focusing based on an ellipse whose two foci correspond to a virtual point source (a beam slit) and a spot on the detector surface. The focusing mirror utilizes the high-performance NiC/Ti supermirror developed at the MLF and deposited on a precisely figured elliptic substrate surface. The mirror targets the pulsed neutron reflectometer BL17 “SHARAKU” at the MLF, J-PARC [25]. SHARAKU is placed at a coupled hydrogen-moderator beam port of the J-PARC spallation neutron source. It has been employed for the structure analysis of thin films in various research fields, such as polymers (e.g., [26,27]) and magnetic materials (e.g., [28]). It can provide information on the chemical composition and magnetic structure in the depth direction of the thin film samples. The implementation of GISANS at a neutron reflectometer would enable the nanometric analysis of not only the depth distribution of materials but also the in-plane structure.
2. Design and Fabrication
Focusing by an elliptic mirror is based on the following features of an ellipse. If a light ray is radiated from one focus of an ellipse and is specularly reflected at the point of intersection with the ellipse, then it reaches the other focus. Additionally, if the light spot at the first focus is of finite size, the reflected light will be focused on a spot of the second focal point at a magnification
where and denote the distance from the first focus to the reflection point and from the reflection point to the second focus, respectively.
In this study, a one-dimensional focusing supermirror was designed according to an ellipse whose parameters are listed in Table 1 to suit the BL17 instrument of MLF, J-PARC. Here, a neutron beam is focused vertically, parallel to the sample surface at BL17. A schematic of the focusing geometry is given in Figure 1, where the ellipse is drawn with a curved dotted line. Slit 1 and an area detector are positioned at the two foci of the ellipse. The surface of the focusing supermirror corresponds to a part of the ellipse characterized by the range of the eccentric angle given in Table 1. A neutron beam is extracted slightly downward from Slit 1 and then reflected upward by the focusing mirror towards the second focus on the detector surface. On the other hand, when the beam is not focused, it is extracted horizontally and collimated with two slits. Note that, in a measurement, a sample is to be placed at the intersection of the focused beamline and the collimated one, just behind Slit 2, to ensure that the two beamlines have the same sample position.

Table 1.
Parameters of the focusing supermirror, based on an ellipse .
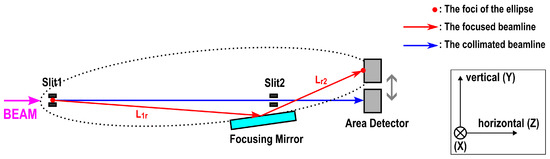
Figure 1.
Geometry of neutron focusing and slit collimation. The red arrows represent the focused beamline, and the blue arrow is the collimated one. The sample stage of BL17 is installed at the intersection of the two beamlines. The area detector can move vertically according to each beamline setting. Along the X direction, the two beamlines are both collimated with the same slit setting. Note that the vertical scale and gradients are significantly exaggerated to facilitate visualization.
Figure 2 shows a photo of the developed focusing supermirror. A substrate of fused quartz was fabricated using the elastic emission machining (EEM) technique [29]. Its surface is a one-dimensional elliptic shape of 400 mm in the longitudinal direction, with parameters in Table 1. The figure error was found to be 188.7 nm PV by measuring with GPI-XP/D and NewView7300 of Zygo, AMETEK, Inc., Middletown, CT, U.S.A. The surface roughness of the elliptic surface was 0.183 nm RMS, measured with NewView7300. Subsequently, NiC/Ti supermirror film () was deposited on the elliptic surface of the substrate using the large-area ion-beam sputtering machine at the MLF. The layer sequence of the film was designed using the algorithm proposed by Hayter and Mook [30]. The total number of layers was 1200, and the thickness of a bilayer ranged from 7.4 nm to 143.6 nm. The rates of sputtering were 0.023 nm s−1 for the NiC layer and 0.012 nm s−1 for the Ti layer. NiC layers were deposited using Ni-C cosputtering [31]. The pressure before and during deposition was Pa and Pa, respectively.

Figure 2.
The focusing supermirror developed for GISANS measurements at BL17.
3. Experimental Section
We performed a test of neutron beam focusing and compared a focused beam spot with an optimally collimated beam spot. The experiment was conducted at the pulsed neutron reflectometer BL17 of the MLF, J-PARC. The proton beam power of the MLF was 730 kW. Figure 3 illustrates the experimental settings. Beam slits other than Slit 2 were placed for the focusing geometry, as shown in the picture. In the collimating geometry, all slits were aligned along the collimated (horizontal) beamline. We noted that the focusing mirror looks at the upper part of the neutron source (the surface of the coupled moderator), while the collimated beamline comes from the central part. This could enhance the intensity gain by the focusing mirror since Harada et al. demonstrated that the upper part of the J-PARC coupled moderator is 1.2∼1.7 times as bright as the central part [32]. The focusing supermirror was placed 7430 mm from Slit 1 at a nominal incident angle of 0.88°, slightly different from the designed position shown in Table 1 due to a technical problem in the experiment. We estimated the geometric error due to this mispositioning. We found that the direction of the reflected beam differs from the designed focusing geometry by ∼+0.005°, resulting in an enlargement of the spot size at the detector by 0.72 mm in the vertical direction. Furthermore, the figure error of the focusing supermirror and the area detector’s spatial resolution of 1.8 mm would contribute to the spot’s blurring. Thus, this paper does not discuss measured spot sizes in detail.
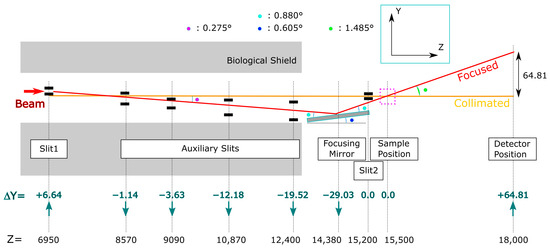
Figure 3.
Configuration of beamline components at BL17. The unit of digits is mm. denotes the vertical position of the focused beamline at each component, measured from the collimated (horizontal) beamline. The blue arrows indicate upward/downward displacements from the horizontal line. The accuracy of is less than 0.1 mm. Z represents the distance from the neutron source with an accuracy of ±1 mm. In this experiment, no sample was placed at the sample position.
Table 2 displays beam sizes at the device positions. They were restricted by slit apertures and the acceptance of the focusing mirror so that they both became 1 × 2 mm2 at the detector position. The vertical aperture of Slit 1 for the focusing beam was determined by the magnification at the mirror center so that the beam was focused on a spot of 1 mm in vertical width at the detector in the designed geometry. In contrast, the acceptance of the mirror is obtained from the mirror length and the incident angle. For the optimum collimation, the vertical slit apertures were calculated using Equations (A5) and (A6) in Appendix A. The difference in the vertical beam restrictions between the two beamlines directly affects the intensity gain due to the focusing. On the other hand, horizontal beam restrictions were 2 mm at Slit 1 and Slit 2 for both beamlines.

Table 2.
Positions of beamline devices installed at BL17. Nominal beam sizes of the focused beam and the collimated one at these positions are also displayed.
The focused beam and the collimated beam were observed at 18,000 mm from the source using a two-dimensional, multiwire-type proportional counter (MWPC) whose pixel size is 0.5 mm × 0.5 mm, spatial resolution 1.8 mm, and sensitive area 128 mm × 128 mm [33,34].
4. Results and Discussion
The total intensity of the focused beam was 2579 cps, while that of the collimated beam was 117 cps, giving a rough estimate of intensity gain of 22.
Figure 4 displays a two-dimensional image of the focused beam and that of the collimated beam observed with the MWPC. Neutrons of 0.22 to 0.88 nm in wavelength were collected from acquired data in which the neutron’s time-of-flight is recorded. The two images have similar spot shapes, but the scale on the color bars suggests that the focusing mirror enhanced the intensity twentyfold. The spot sizes are more extensive than our expectation, that is, a size of 1 mm in height and 2 mm in width. The vertical and horizontal linecuts of the spots are given in Figure 5.
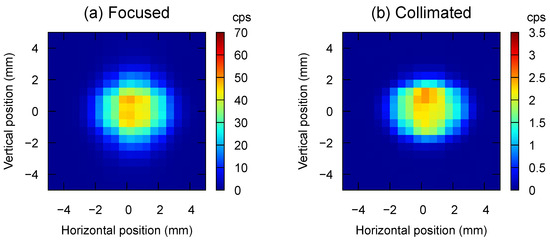
Figure 4.
Two-dimensional intensity profiles of (a) the focused spot and (b) the collimated spot.
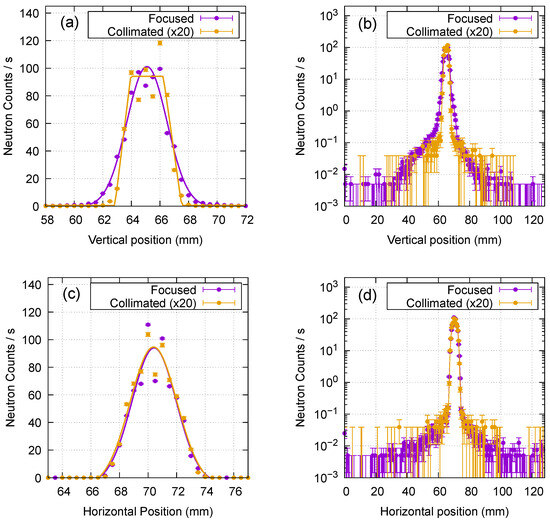
Figure 5.
Intensity profiles cut out at the center of the focused and collimated spots of Figure 4. The collimated beam intensity was multiplied by 20. (a) Vertical profiles on a linear scale with fitted functions. (b) Vertical profiles on a log scale. (c) Horizontal profiles on a linear scale with fitted functions. (d) Horizontal profiles on a log scale. It should be noted that the neutron beam was focused only in the vertical direction.
Vertical intensity profiles at the horizontal center of the spots are compared in Figure 5a,b. Horizontal intensity profiles at the vertical center of the spots are shown in Figure 5c,d. The collimated intensity was multiplied by 20 in these panels. It can be seen that the two peaks look comparable, indicating an intensity gain of ∼20 by the beam focusing.
As we can see in Figure 5a,c, all four profiles have a split peak. The peak splitting cannot be directly ascribed to the figure error of the focusing mirror since the collimated beam also has a split peak. We might attribute it to beamline components such as beam slits or the brightness distribution of the beam source. The profiles of the peaks were fitted to Gaussian functions except for the vertical profile of the collimated peak, which was fitted to a trapezoidal function. The fitting suggested that the vertical peak width of the focused intensity was 3.3 mm in full width at half maximum (FWHM), which is larger than the expected value of 1 mm. This could arise from (1) the finite spatial resolution of the MWPC detector, (2) the mispositioning of the focusing supermirror, and (3) the figure error of the elliptic surface of the supermirror. The effect of (1) can be eliminated if we perform high-resolution knife-edge scans [10,11,13] to measure the FWHM, although the resolution of the knife-edge scan should be taken into account; (2) can be readily corrected by installing the mirror at the predetermined position. However, to reduce the effect of (3), more sophisticated techniques for surface figuring of the substrate and supermirror deposition might be required, which would be challenging. By comparison, the vertical width (FWHM) of the collimated peak was found to be 3.5 mm, which is also larger than the expected width of 1 mm. This should be attributed to the detector resolution. The FWHMs of horizontal profiles were 3.6 mm and 3.8 mm for the focused and collimated beams, respectively. Note that the neutron beam was not focused but collimated in the horizontal direction in both focused and collimated geometries. Again, the horizontal widths are more extensive than the expected value of 2 mm. We ascribe this to the detector’s resolution. It should be noted that the focused spot has slightly wider skirts than the collimated spot in the vertical profiles, as seen in Figure 5a. This indicates a finite range of magnification M due to the mirror length of 400 mm, as the aperture of Slit 1 was determined according to a (nominal) magnification at the mirror center. The narrower profile could enable us to measure a GISANS profile in the smaller momentum transfer region. However, extending the momentum transfer region and the intensity gain would be a trade-off.
We determined the background level of the profile as counts/s, where the profile becomes significantly diffusive, and found the peak’s signal-to-background ratio (S/B ratio) to be 500. The S/B ratio did not significantly improve compared to the collimated spot, as we can see in Figure 5b,d. This result could have arisen from background growth due to off-specular scattering at the supermirror film of the focusing mirror or scattering in the quartz substrate, which must have received the broad and intense neutron beam. We may reduce the latter background and augment the focused spot’s S/B ratio by eliminating neutrons that do not impinge upon the supermirror film but directly hit the substrate with neutron-absorbing materials.
Figure 6 shows the wavelength distributions of neutron intensity in the two spots and their ratio (i.e., intensity gain). We found that neutrons with a wavelength >0.225 nm are efficiently reflected and focused by the supermirror, demonstrating that the mirror functions with an m value of 3.9 at the nominal incident angle of 0.88°. The intensity gain was ≳20 for a wavelength >0.23 nm. The gradual increase in the measured gain as the neutron wavelength increases can be attributed to supermirror reflectivity, which typically increases at longer wavelengths.
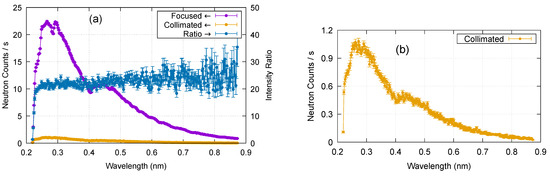
Figure 6.
(a) The intensities at the focused spot and the collimated one and their ratio of dependence on neutron wavelength. Neutrons with a wavelength <0.22 nm were chopped upstream of the mirror position. (b) The intensity profile of the collimated beam with a smaller vertical scale.
The relative intensity of the focused beam to the collimated one can be estimated using Equation (A1) in Appendix A. For the focusing beam, is given by the aperture of Slit 1 and by the acceptance of the focusing mirror (, ). is the distance from Slit 1 to the focusing mirror (). Then, the intensity is estimated as . On the other hand, for the collimated beam, both and are determined with Slit 1 and Slit 2, respectively (, ) and corresponds to the distance between the two slits (). Hence, the collimated intensity results in . Consequently, the intensity gain by the focusing is estimated to be 25.6. Assuming the neutron reflectivity of the supermirror to be 0.8, we reproduce the measured gain ≳20. This result confirms that the focusing optics work as designed. The difference in brightness between the upper and central parts of the J-PARC coupled moderator may also have boosted the intensity gain.
The blurred spot size could stem from the finite spatial resolution of the MWPC detector. Spot sizes and S/B ratios could be measured more precisely using knife-edge scans, which Ice et al. demonstrated for beam spots of less than 0.2 mm [10,11,13]. A neutron imaging plate can take an image with a high resolution of less than 0.2 mm with a high efficiency of 80% [35,36]. However, it cannot exclude high-energy neutrons and gamma rays from its photostimulated luminescence data, resulting in a blurred image of a beam spot and a lowered S/B ratio.
We have just conducted a test measurement of GISANS using the focusing supermirror, the data of which will be published elsewhere.
5. Conclusions
We have developed a one-dimensional focusing supermirror for GISANS measurements. Neutron measurements at the pulsed neutron reflectometer BL17 of the MLF, J-PARC, demonstrated that the focusing supermirror enhances neutron intensity at the spot on the detector twentyfold compared with the optimum beam collimation, keeping the S/B ratio of the spot at 500. Because the focusing supermirror was designed and fabricated to be suitable for BL17, it can be readily installed and used there for time-of-flight GISANS measurements. However, the intensity and the S/B ratio should be improved further to conduct GISANS measurements in a shorter measurement time over a broader range of momentum transfer. For this purpose, it is essential to develop an integrated system of multiple focusing supermirrors and to reduce the background from the illuminated focusing system.
Author Contributions
Conceptualization, D.Y. and K.S.; methodology, D.Y., R.M. and K.S.; software, D.Y., R.M. and H.A.; validation, H.A., T.H., K.A.-S. and N.M.; investigation, D.Y., R.M. and H.A.; resources, K.S. and R.M.; writing—original draft preparation, D.Y.; writing—review and editing, R.M., H.A., K.S., T.H., K.A.-S. and N.M.; supervision, D.Y., R.M., H.A. and K.S.; project administration, H.A.; funding acquisition, H.A. All authors have read and agreed to the published version of the manuscript.
Funding
JSPS KAKENHI Grant Number 22K19074 and JST-Mirai Program Grant Number JPMJMI18A2, Japan.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We thank Kentaro Toh and Tatsuya Nakamura for their helpful comments and discussions on experimental data acquired with MWPC. We thank JTEC Corporation for fabricating the elliptic mirror substrate and measuring the substrate surface. Neutron measurements were performed on BL17 at the Materials and Life Science Experimental Facility of J-PARC under Proposal No. 2022I0017. This work was partly supported by JSPS KAKENHI Grant Number 22K19074 and JST-Mirai Program Grant Number JPMJMI18A2, Japan.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Optimum Slit Colllimation
Slit settings of the optimum beam collimation are obtained as follows. Let us consider a beamline composed of a sufficiently large and homogeneous beam source, a pair of beam slits, and a detector. The intensity of a beam collimated with the slits can be estimated by
where and are the widths of the first and second slit, respectively. is the distance between the two slits. Furthermore, beam width d (spot size) at the detector position is given by
where is the distance from the second slit to the detector. When d is a given constant, is expressed with as
Hence, the beam intensity becomes a quadratic function of ,
which has a maximum (i.e., maximum intensity) at
Then, is calculated with (A3) as
As a result, for a constant d, Equations (A5) and (A6) give the optimum collimation that supplies a maximum beam intensity,
which indicates that for a longer , the intensity of the optimally collimated spot diminishes. Hence, beam focusing is essential in GISANS measurements, which require a long distance between the sample and the detector.
References
- Müller-Buschbaum, P. Grazing incidence small-angle neutron scattering: Challenges and possibilities. Polym. J. 2013, 45, 34–42. [Google Scholar] [CrossRef]
- Hu, M.; Li, X.; William, T.H.; Bras, W.; Rzayev, J.; Russell, T. Using Grazing-incidence Small-Angle Neutron Scattering to Study the Orientation of Block Copolymer Morphologies in Thin Films. Macromolecules 2023, 56, 2418–2428. [Google Scholar] [CrossRef]
- Maruyama, R.; Bigault, T.; Saerbeck, T.; Honecker, D.; Soyama, K.; Courtois, P. Coherent Magnetization Rotation of a Layered System Observed by Polarized Neutron Scattering under Grazing Incidence Geometry. Crystals 2019, 9, 383. [Google Scholar] [CrossRef]
- Liyanage, W.L.N.C.; Tang, N.; Quigley, L.; Borchers, J.A.; Grutter, A.J.; Maranville, B.B.; Sinha, S.K.; Reyren, N.; Montoya, S.A.; Fullerton, E.E.; et al. Three-dimensional structure of hybrid magnetic skyrmions determined by neutron scattering. Phys. Rev. B 2023, 107, 184412. [Google Scholar] [CrossRef]
- Müller-Buschbaum, P.; Metwalli, E.; Moulin, J.-F.; Kudryashov, V.; Haese-Seiller, M.; Kampmann, R. Time of flight grazing incidence small angle neutron scattering. Eur. Phys. J. Spec. Top. 2009, 167, 107–112. [Google Scholar] [CrossRef]
- Vorobiev, A.; Paracini, N.; Cárdenas, M.; Wolff, M. Π-GISANS: Probing lateral structures with a fan shaped beam. Sci. Rep. 2021, 11, 17786. [Google Scholar] [CrossRef] [PubMed]
- Mezei, F. Novel polarized neutron devices: Supermirror and spin component amplifier. Commun. Phys. 1976, 1, 81–85. [Google Scholar]
- Mezei, F.; Dagleish, P.A. Corrigendum and first experimental evidence on neutron supermirrors. Commun. Phys. 1977, 2, 41–43. [Google Scholar]
- Perrichon, A.; Fernandez-Alonso, F.; Wolff, M.; Karlsson, M.; Demmel, F. Neutron Ray-Tracing Simulations of a New Supermirror Guide for the Osiris Spectrometer. J. Surf. Investig. 2020, 14 (Suppl. S1), S169–S174. [Google Scholar] [CrossRef]
- Ice, G.E.; Hubbard, C.R.; Larson, B.C.; Pang, J.W.L.; Budai, J.D.; Spooner, S.; Vogel, S.C. Kirkpatrick-Baez microfocusing optics for thermal neutrons. Nucl. Instrum. Methods Phys. Res. A 2005, 539, 312–320. [Google Scholar] [CrossRef]
- Ice, G.E.; Hubbard, C.R.; Larson, B.C.; Pang, J.W.L.; Budai, J.D.; Spooner, S.; Vogel, S.C.; Rogge, R.D.; Fox, J.H.; Donaberger, R.L. High-performance Kirkpatrick-Baez supermirrors for neutron milli- and micro-beams. Mater. Sci. Eng. A 2006, 437, 120–125. [Google Scholar] [CrossRef]
- Ice, G.E.; Pang, J.W.L.; Tulk, C.; Molaison, J.; Choi, J.-Y.; Vaughn, C.; Lytle, L.; Takacs, P.Z.; Andersen, K.H.; Bigault, T.; et al. Design challenges and performance of nested neutron mirrors for microfocusing on SNAP. J. Appl. Crystallogr. 2009, 42, 1004–1008. [Google Scholar] [CrossRef]
- Ice, G.E.; Choi, J.-Y.; Takacs, P.Z.; Khounsary, A.; Puzyrev, Y.; Molaison, J.J.; Tulk, C.A.; Andersen, K.H.; Bigault, T. Nested neutron microfocusing optics on SNAP. Appl. Phys. A 2010, 99, 635–639. [Google Scholar] [CrossRef]
- Herb, C.; Zimmer, O.; Georgii, R.; Böni, P. Nested mirror optics for neutron extraction, transport, and focusing. Nucl. Instrum. Methods Phys. Res. A 2022, 1040, 167154. [Google Scholar] [CrossRef]
- Hosobata, T.; Yamada, N.L.; Hino, M.; Yoshinaga, H.; Nemoto, F.; Hori, K.; Kawai, T.; Yamagata, Y.; Takeda, M.; Takeda, S. Elliptic neutron-focusing supermirror for illuminating small samples in neutron reflectometry. Opt. Express 2019, 27, 26807. [Google Scholar] [CrossRef]
- Hosobata, T.; Yamada, N.L.; Hino, M.; Yamagata, Y.; Kawai, T.; Yoshinaga, H.; Hori, K.; Takeda, M.; Takeda, S.; Morita, S. Development of precision elliptic neutron-focusing supermirror. Opt. Express 2017, 25, 20012. [Google Scholar] [CrossRef]
- Yamada, N.L.; Hosobata, T.; Nemoto, F.; Hori, K.; Hino, M.; Izumi, J.; Suzuki, K.; Hirayama, M.; Kanno, R.; Yamagata, Y. Application of precise neutron focusing mirrors for neutron reflectometry: Latest results and future prospects. J. Appl. Crystallogr. 2020, 53, 1462–1470. [Google Scholar] [CrossRef]
- Maruyama, R.; Yamazaki, D.; Ebisawa, T.; Soyama, K. Effect of interfacial roughness correlation on diffuse scattering intensity in a neutron supermirror. J. Appl. Phys. 2009, 105, 083527. [Google Scholar] [CrossRef]
- Maruyama, R.; Yamazaki, D.; Ebisawa, T.; Soyama, K. Development of high-reflectivity neutron supermirrors using an ion beam sputtering technique. Nucl. Instrum. Methods Phys. Res. A 2009, 600, 68–70. [Google Scholar] [CrossRef]
- Maruyama, R.; Yamazaki, D.; Ebisawa, T.; Hino, M.; Soyama, K. Development of neutron supermirrors with large critical angle. Thin Solid Films 2007, 515, 5704–5706. [Google Scholar] [CrossRef]
- Yamamura, K. Fabrication of Ultra Precision Optics by Numerically Controlled Local Wet Etching. Ann. CIRP 2007, 56/1, 541–544. [Google Scholar] [CrossRef]
- Yamamura, K.; Nagano, M.; Takai, H.; Zettsu, N.; Yamazaki, D.; Maruyama, R.; Soyama, K.; Shimada, S. Figuring of plano-elliptical neutron focusing mirror by local wet etching. Opt. Express 2009, 17, 6414–6420. [Google Scholar] [CrossRef]
- Yamazaki, D.; Maruyama, R.; Soyama, K.; Takai, H.; Nagano, M.; Yamamura, K. Neutron beam focusing using large-m supermirrors coated on precisely-figured aspheric surfaces. J. Phys. Conf. Ser. 2010, 251, 012076. [Google Scholar] [CrossRef]
- Nagano, M.; Yamaga, F.; Yamazaki, D.; Maruyama, R.; Hayashida, H.; Soyama, K.; Yamamura, K. One-dimensional neutron focusing with large beam divergence by 400mm-long elliptical supermirror. J. Phys. Conf. Ser. 2012, 340, 012034. [Google Scholar] [CrossRef]
- Takeda, M.; Yamazaki, D.; Soyama, K.; Maruyama, R.; Hayashida, H.; Asaoka, H.; Yamazaki, T.; Kubota, M.; Aizawa, K.; Arai, M.; et al. Current Status of a New Polarized Neutron Reflectometer at the Intense Pulsed Neutron Source of the Materials and Life Science Experimental Facility (MLF) of J-PARC. Chin. J. Phys. 2012, 50, 161–170. [Google Scholar]
- Aoki, H. Chain dynamics in spin-coated films of poly(methyl methacrylate) in a solvent annealing process. Polym. J. 2019, 51, 611–616. [Google Scholar] [CrossRef]
- Aoki, H.; Ogawa, H.; Takenaka, M. Neutron Reflectometry Tomography for Imaging and Depth Structure Analysis of Thin Films with In-Plane Inhomogeneity. Langmuir 2021, 37, 196–203. [Google Scholar] [CrossRef]
- Ohtsuka, Y.; Kanazawa, N.; Hirayama, M.; Matsui, A.; Nomoto, T.; Arita, R.; Nakajima, T.; Hanashima, T.; Ukleev, V.; Aoki, H.; et al. Emergence of spin-orbit coupled ferromagnetic surface state derived from Zak phase in a nonmagnetic insulator FeSi. Sci. Adv. 2021, 7, eabj0498. [Google Scholar] [CrossRef] [PubMed]
- Yamauchi, K.; Miura, H.; Inagaki, K.; Mori, Y. Figuring with subnanometer-level accuracy by numerically controlled elastic emission machining. Rev. Sci. Instrum. 2002, 73, 4028–4033. [Google Scholar] [CrossRef]
- Hayter, J.B.; Mook, H.A. Discrete thin-film multilayer design for X-ray and neutron supermirrors. J. Appl. Crystallogr. 1989, 22, 35–41. [Google Scholar] [CrossRef]
- Wood, J.L. Status of supermirror research at OSMC. Proc. SPIE 1992, 1738, 22–29. [Google Scholar]
- Harada, M.; Teshigawara, M.; Ohi, M.; Klinkby, E.; Zanini, L.; Batkov, K.; Oikawa, K.; Toh, Y.; Kimura, A.; Ikeda, Y. Experimental validation of the brightness distribution on the surfaces of coupled and decoupled moderators composed of 99.8% parahydrogen at the J-PARC pulsed spallation neutron source. Nucl. Instrum. Methods Phys. Res. A 2018, 903, 38–45. [Google Scholar] [CrossRef]
- Toh, K.; Nakamura, T.; Sakasai, K.; Soyama, K.; Hino, M.; Kitaguchi, M.; Yamagishi, H. Development of two-dimensional multiwire-type neutron detector system with individual line readout and optical signal transmission. Nucl. Instrum. Methods Phys. Res. A 2013, 726, 169–174. [Google Scholar] [CrossRef]
- Toh, K.; Nakamura, T.; Sakasai, K.; Soyama, K.; Yamagishi, H. Evaluation of two-dimensional multiwire neutron detector with individual line readout under pulsed neutron irradiation. J. Instrum. 2014, 9, C11019. [Google Scholar] [CrossRef]
- Niimura, N.; Karasawa, Y.; Tanaka, I.; Miyahara, J.; Takahashi, K.; Saito, H.; Koizumi, S.; Hidaka, M. An imaging plate neutron detector. Nucl. Instrum. Methods Phys. Res. A 1994, 349, 521–525. [Google Scholar] [CrossRef]
- Niimura, N.; Chatake, T.; Ostermann, A.; Kurihara, K.; Tanaka, I. High resolution neutron protein crystallography. Hydrogen and hydration in proteins. Z. Kristallogr. 2003, 218, 96–107. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).