Does the Maximum Initial Beam Energy for Proton Therapy Have to Be 230 MeV?
Abstract
1. Introduction
2. Materials and Methods
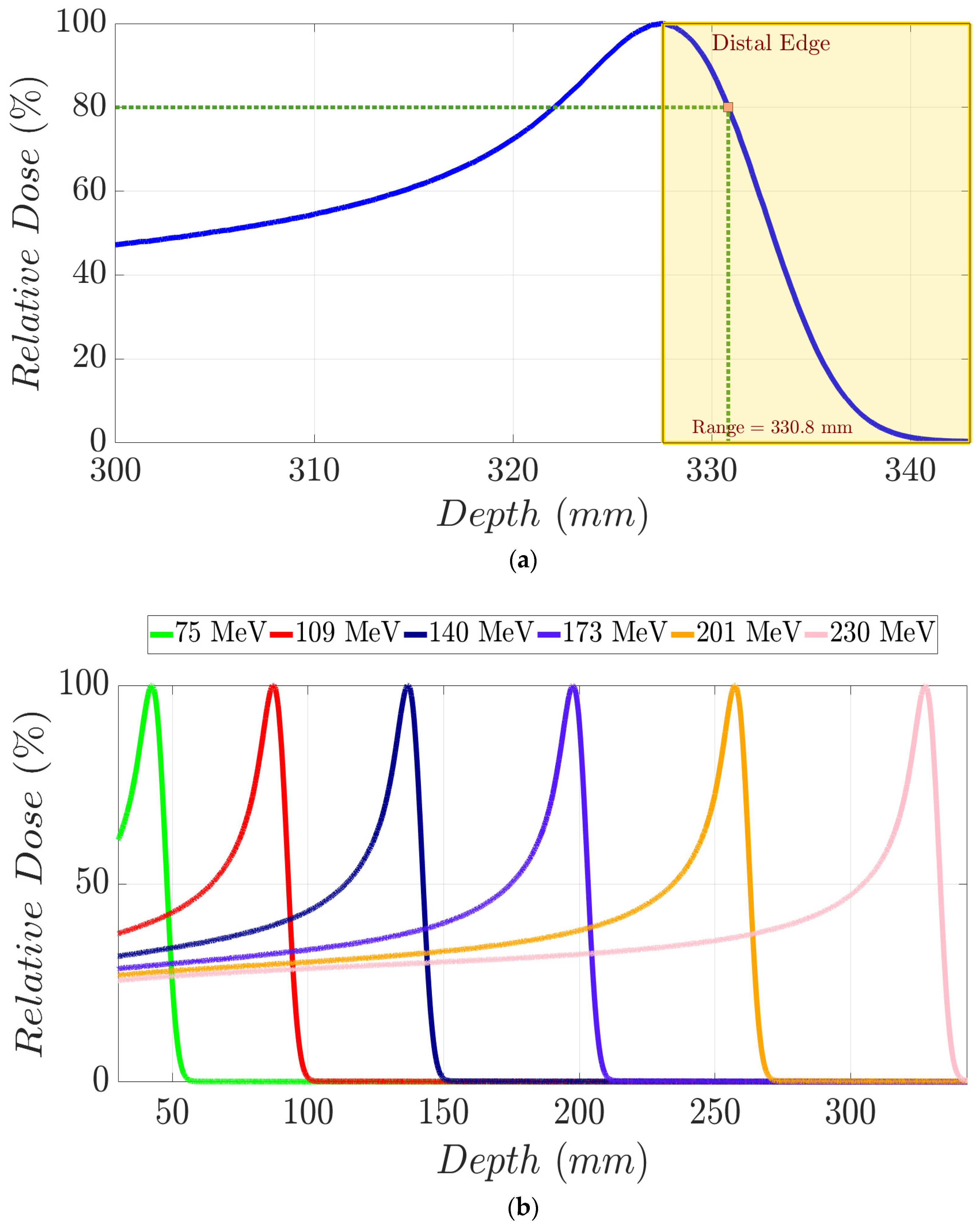
2.1. Monte Carlo Beam Line Simulations
2.2. Treatment Planning System Modelling and Case Preparations
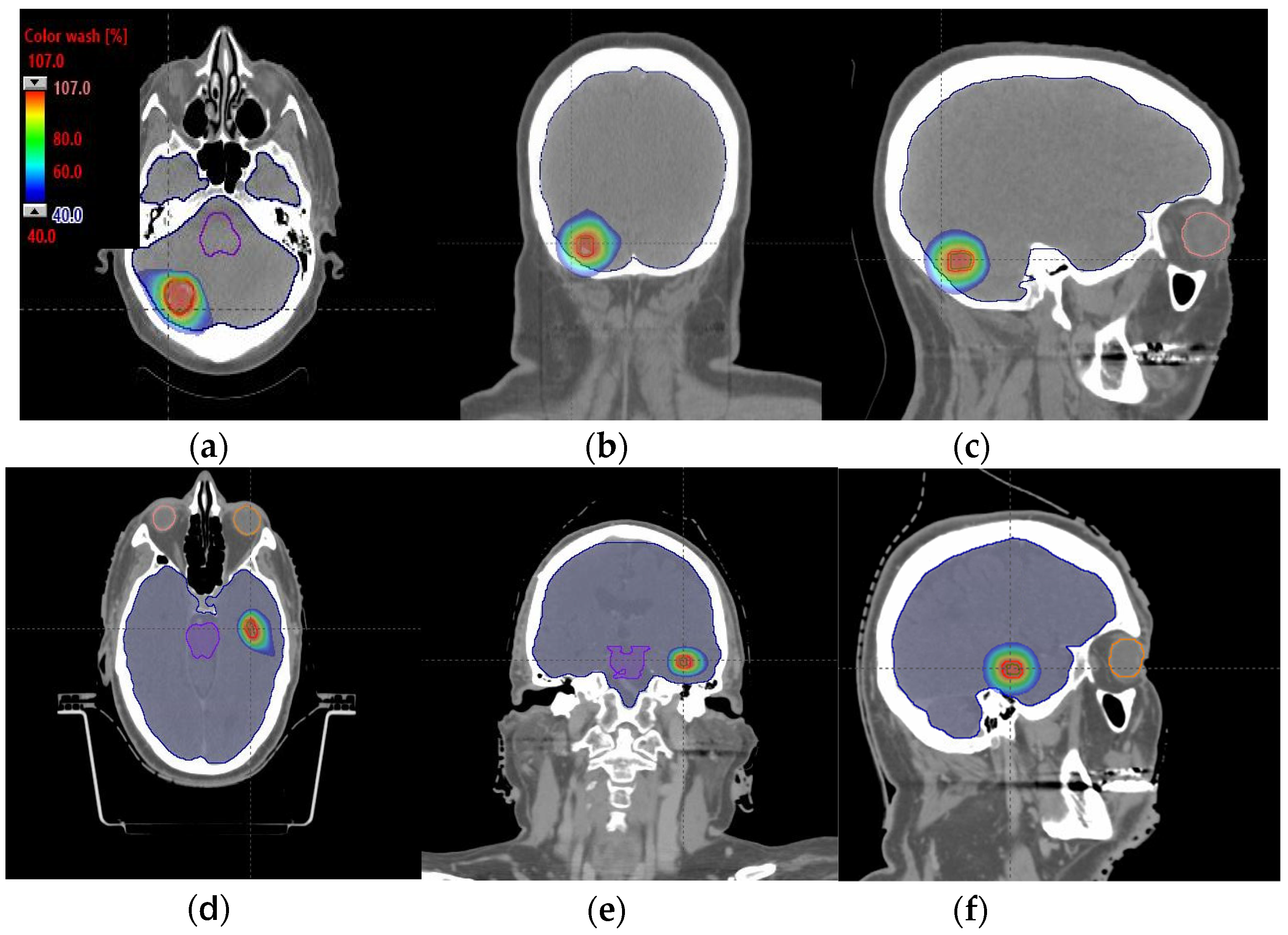
2.3. Brain Patients’ Treatment Plans
2.4. Prostate Patients’ Treatment Plans
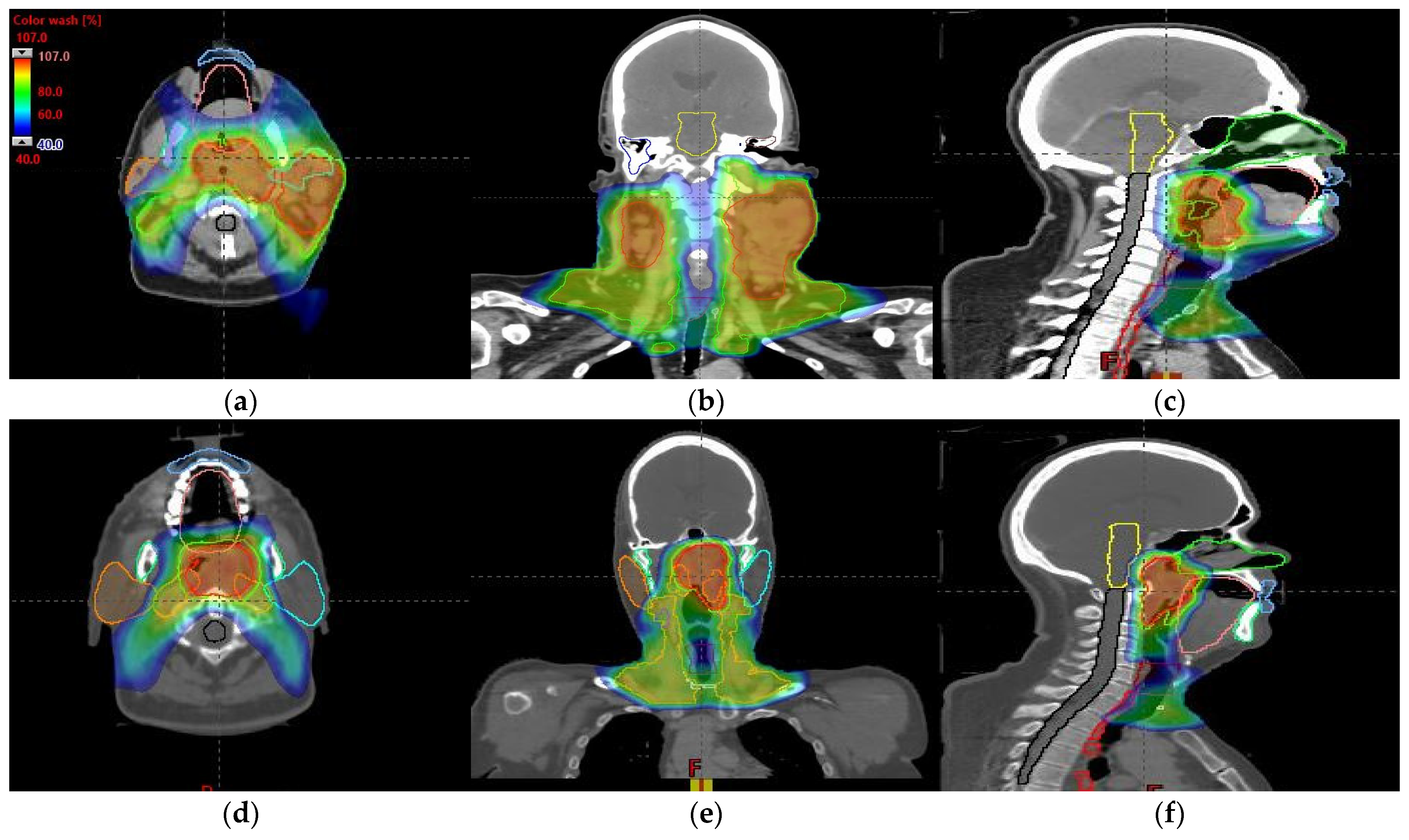
2.5. Head and Neck Patients’ Treatment Plans
3. Results
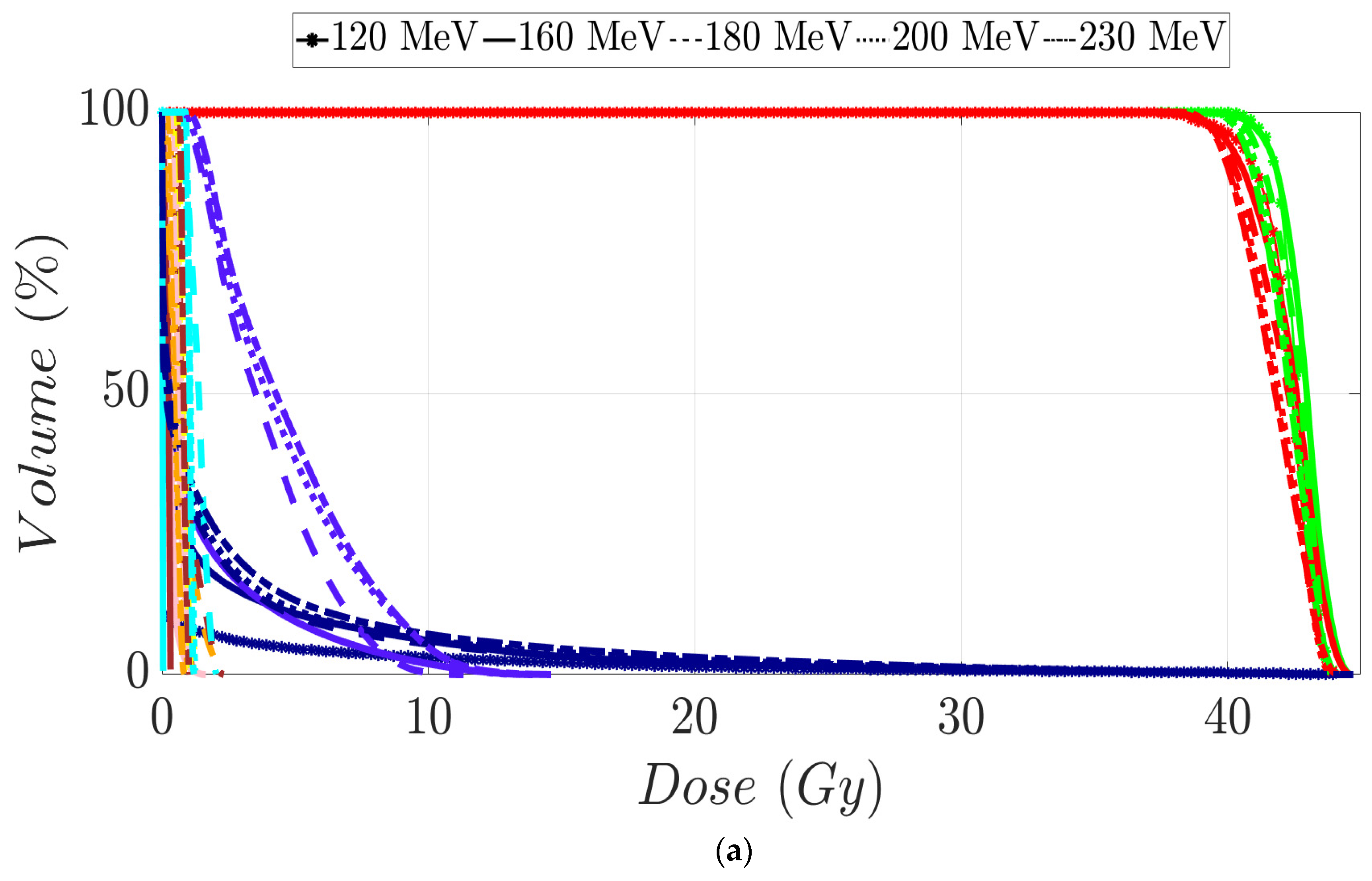
3.1. Brain Patients’ Treatment Plans
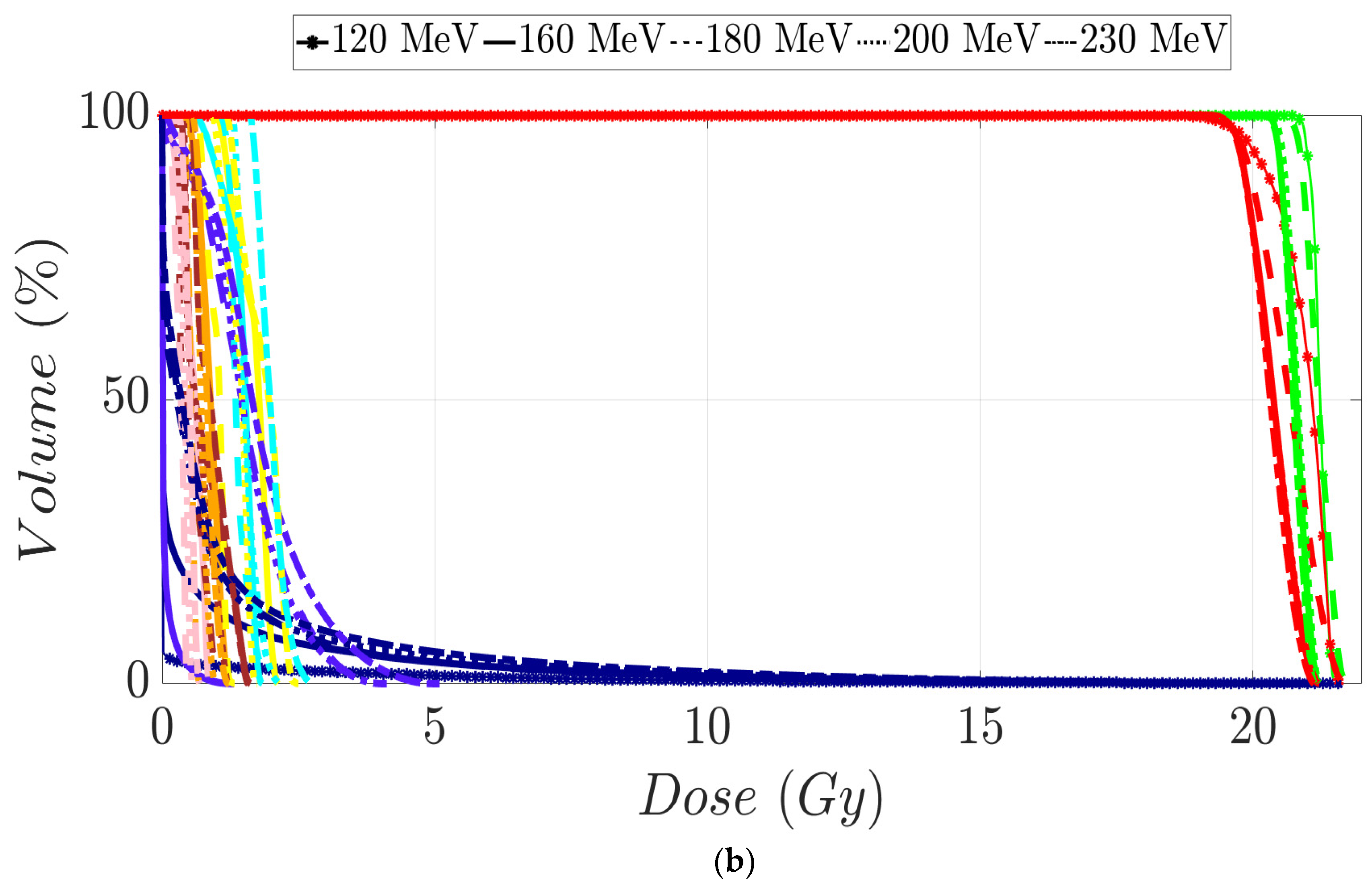
3.2. Prostate Patients Treatment Plans
3.3. Head and Neck Patients’ Treatment Plans
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Newhauser, W.D.; Zhang, R. The physics of proton therapy. Phys. Med. Biol. 2015, 60, R155. [Google Scholar] [CrossRef]
- Berger, M.J.; Coursey, J.S.; Zucker, M.A.; Chang, J. ESTAR, PSTAR, and ASTAR: Computer Programs for Calculating Stopping-Power and Range Tables for Electrons, Protons, and Helium Ions (version 1.2.3). 2005. Available online: http://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html (accessed on 19 August 2024).
- International Commission on Radiation Units and Measurements. Stopping Powers and Ranges for Protons and Alpha Particles; International Commission on Radiation Units and Measurements: Stockholm, Sweden, 1993; 286p. [Google Scholar]
- Paganetti, H.; Beltran, C.; Both, S.; Dong, L.; Flanz, J.; Furutani, K.; Grassberger, C.; Grosshans, D.R.; Knopf, A.-C.; Langendijk, J.A.; et al. Roadmap: Proton therapy physics and biology. Phys. Med. Biol. 2021, 7, 66. [Google Scholar] [CrossRef] [PubMed]
- Mohan, R.; Radhe Mohan, C. A review of proton therapy—Current status and future directions. Precis. Radiat. Oncol. 2022, 6, 164–176. [Google Scholar] [CrossRef] [PubMed]
- Collings, E.W.; Lu, L.; Gupta, N.; Sumption, M.D. Accelerators, Gantries, Magnets and Imaging Systems for Particle Beam Therapy: Recent Status and Prospects for Improvement. Front. Oncol. 2021, 15, 737837. [Google Scholar] [CrossRef] [PubMed]
- Yap, J.; Resta-López, J.; Kacperek, A.; Schnuerer, R.; Jolly, S.; Boogert, S.; Welsch, C. Beam characterisation studies of the 62 MeV proton therapy beamline at the Clatterbridge Cancer Centre. Phys. Medica 2020, 77, 108–120. [Google Scholar] [CrossRef]
- Schippers, M. Proton Accelerators. In Proton Therapy Physics, 2nd ed.; Pagganeti, H., Ed.; CRC Press: Boca Raton, FL, USA, 2018; pp. 69–111. [Google Scholar]
- Graeff, C.; Volz, L.; Durante, M. Emerging technologies for cancer therapy using accelerated particles. Prog. Part. Nucl. Phys. 2023, 131, 104046. [Google Scholar] [CrossRef] [PubMed]
- Lane, S.A.; Slater, J.M.; Yang, G.Y. Image-Guided Proton Therapy: A Comprehensive Review. Cancers. 2023, 15, 2555. [Google Scholar] [CrossRef] [PubMed]
- Johnstone, P.A.S.; Kerstiens, J.; Richard, H. Proton facility economics: The importance of “simple” treatments. J. Am. Coll. Radiol. 2012, 9, 560–563. [Google Scholar] [CrossRef]
- Lodge, M.; Pijls-Johannesma, M.; Stirk, L.; Munro, A.J.; De Ruysscher, D.; Jefferson, T. A systematic literature review of the clinical and cost-effectiveness of hadron therapy in cancer. Radiother. Oncol. 2007, 83, 110–122. [Google Scholar] [CrossRef]
- Peeters, A.; Grutters, J.P.C.; Pijls-Johannesma, M.; Reimoser, S.; De Ruysscher, D.; Severens, J.L.; Joore, M.A.; Lambin, P. How costly is particle therapy? Cost analysis of external beam radiotherapy with carbon-ions, protons and photons. Radiother. Oncol. 2010, 95, 45–53. [Google Scholar] [CrossRef]
- Pijls-Johannesma, M.; Pommier, P.; Lievens, Y. Cost-effectiveness of particle therapy: Current evidence and future needs. Radiother. Oncol. 2008, 89, 127–134. [Google Scholar] [CrossRef] [PubMed]
- Goitein, M.; Gentry, R.; Koehler, A.M. Energy of proton accelerator necessary for treatment of choroidal melanomas. Int. J. Radiat. Oncol. Biol. Phys. 1983, 9, 259–260. [Google Scholar] [CrossRef] [PubMed]
- Moyers, M.F.; Miller, D.W. Range, range modulation, and field radius requirements for proton therapy of prostate cancer. Technol. Cancer Res. Treat. 2003, 2, 445–447. [Google Scholar] [CrossRef]
- Sengbusch, E.; Pérez-Andújar, A.; DeLuca, P.M.; Mackie, T.R. Maximum proton kinetic energy and patient-generated neutron fluence considerations in proton beam arc delivery radiation therapy. Med. Phys. 2009, 36, 364–372. [Google Scholar] [CrossRef] [PubMed]
- Sengbusch, E.R.; Mackie, T.R. Maximum kinetic energy considerations in proton stereotactic radiosurgery. J. Appl. Clin. Med. Phys. 2011, 12, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Dubois, P.A.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Lehrer, E.J.; Prabhu, A.V.; Sindhu, K.K.; Lazarev, S.; Ruiz-Garcia, H.; Peterson, J.L.; Beltran, C.; Furutani, K.; Schlesinger, D.; Sheehan, J.P.; et al. Proton and heavy particle intracranial radiosurgery. Biomedicines 2021, 9, 31. [Google Scholar] [CrossRef]
- Bryant, C.M.; Henderson, R.H.; Nichols, R.C.; Mendenhall, W.M.; Hoppe, B.S.; Vargas, C.E.; Daniels, T.B.; Choo, C.R.; Parikh, R.R.; Giap, H.; et al. Consensus statement on proton therapy for prostate cancer. Int. J. Part. Ther. 2021, 8, 1–16. [Google Scholar] [CrossRef]
- Lin, A.; Chang, J.H.C.; Grover, R.S.; Hoebers, F.J.P.; Parvathaneni, U.; Patel, S.H.; Thariat, J.; Thomson, D.J.; Langendijk, J.A.; Frank, S.J. PTCOG head and neck subcommittee consensus guidelines on particle therapy for the management of head and neck tumors. Int. J. Part. Ther. 2021, 8, 84–94. [Google Scholar] [CrossRef]
- Agosteo, S.; Magistris, M.; Mereghetti, A.; Silari, M.; Zajacova, Z. Shielding data for 100-250 MeV proton accelerators: Double differential neutron distributions and attenuation in concrete. Nucl. Instrum. Methods Phys. Res. B 2007, 265, 581–598. [Google Scholar] [CrossRef]
- Agosteo, S.; Magistris, M.; Silari, M. Shielding of proton accelerators. Radiat. Prot. Dosim. 2011, 146, 414–424. [Google Scholar] [CrossRef] [PubMed]
- Sariyer, D.; Küçer, R.; Küçer, N. Neutron Shielding Properties of Concretes Containing Boron Carbide and Ferro—Boron. Procedia—Soc. Behav. Sci. 2015, 195, 1752–1756. [Google Scholar] [CrossRef]
- Pérez-Andújar, A.; Zhang, R.; Newhauser, W. Monte carlo and analytical model predictions of leakage neutron exposures from passively scattered proton therapy. Med. Phys. 2013, 40, 121714. [Google Scholar] [CrossRef]
- Trinkl, S.; Mares, V.; Englbrecht, F.S.; Wilkens, J.J.; Wielunski, M.; Parodi, K.; Rühm, W.; Hillbrand, M. Systematic out-of-field secondary neutron spectrometry and dosimetry in pencil beam scanning proton therapy. Med. Phys. 2017, 44, 1912–1920. [Google Scholar] [CrossRef] [PubMed]
- Englbrecht, F.S.; Trinkl, S.; Mares, V.; Rühm, W.; Wielunski, M.; Wilkens, J.J.; Hillbrand, M.; Parodi, K. A comprehensive Monte Carlo study of out-of-field secondary neutron spectra in a scanned-beam proton therapy gantry room. Z. Med. Phys. 2021, 31, 215–228. [Google Scholar] [CrossRef]
- Seco, J.; Gu, G.; Marcelos, T.; Kooy, H.; Willers, H. Proton Arc Reduces Range Uncertainty Effects and Improves Conformality Compared With Photon Volumetric Modulated Arc Therapy in Stereotactic Body Radiation Therapy for Non-Small Cell Lung Cancer. Int. J. Radiat. Oncol. Biol. 2013, 87, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Li, X.; Zhang, J.M.; Kabolizadeh, P.; Stevens, C.; Yan, D. Spot-Scanning Proton Arc (SPArc) Therapy: The First Robust and Delivery-Efficient Spot-Scanning Proton Arc Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2016, 96, 1107–1116. [Google Scholar] [CrossRef]
- Gu, W.; Ruan, D.; Lyu, Q.; Zou, W.; Dong, L.; Sheng, K. A novel energy layer optimization framework for spot-scanning proton arc therapy. Med. Phys. 2020, 47, 2072–2084. [Google Scholar] [CrossRef]
- Liu, G.; Li, X.; Zhao, L.; Zheng, W.; Qin, A.; Zhang, S.; Stevens, C.; Yan, D.; Kabolizadeh, P.; Ding, X. A novel energy sequence optimization algorithm for efficient spot-scanning proton arc (SPArc) treatment delivery. Acta Oncol. 2020, 59, 1178–1185. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Liu, G.; Chen, S.; Shen, J.; Zheng, W.; Qin, A.; Yan, D.; Li, X.; Ding, X. Developing an accurate model of spot-scanning treatment delivery time and sequence for a compact superconducting synchrocyclotron proton therapy system. Radiat. Oncol. 2022, 17, 87. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Liu, G.; Li, X.; Ding, X. An evolutionary optimization algorithm for proton arc therapy. Phys. Med. Biol. 2022, 67, 16NT01. [Google Scholar] [CrossRef] [PubMed]

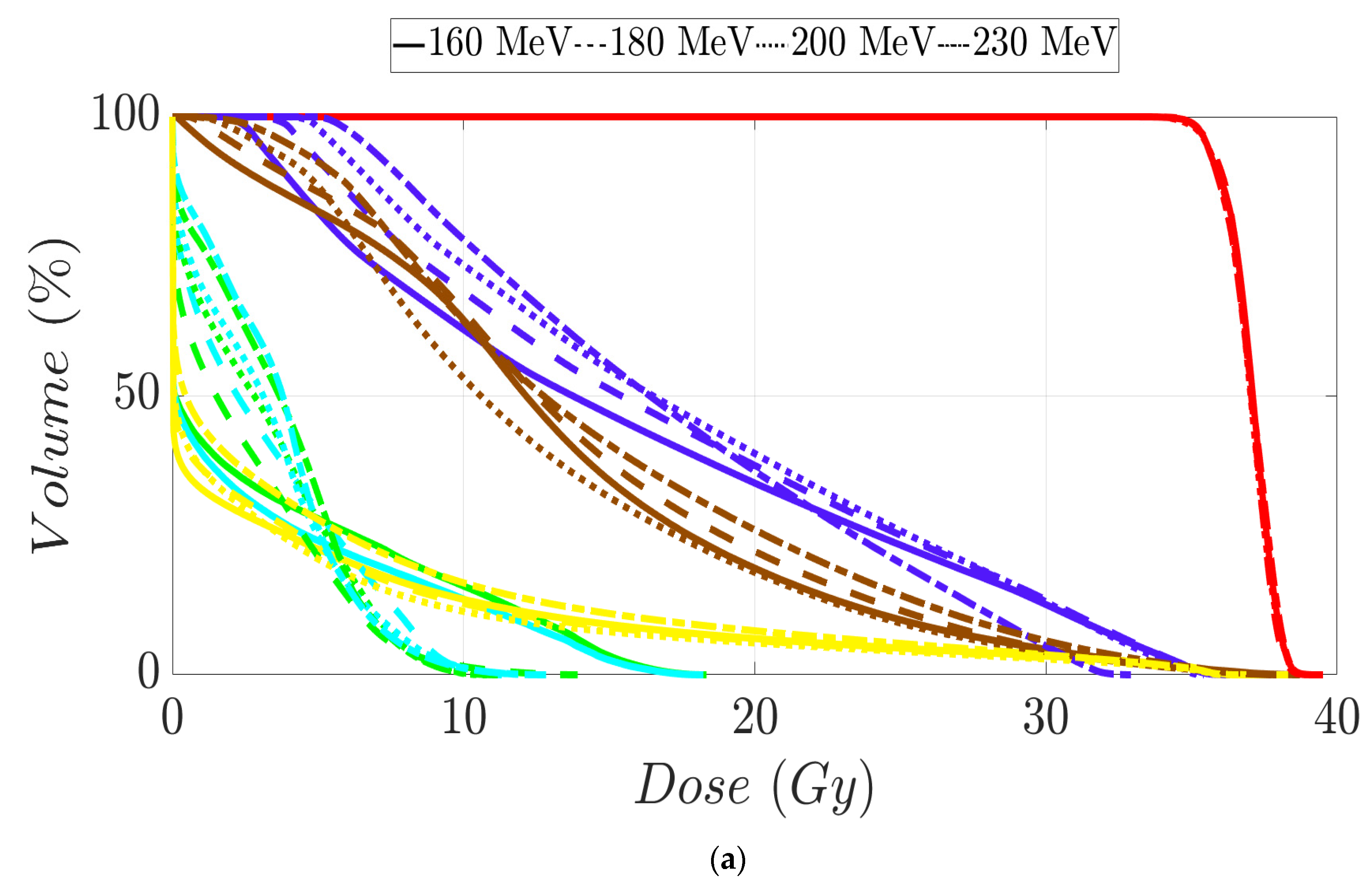
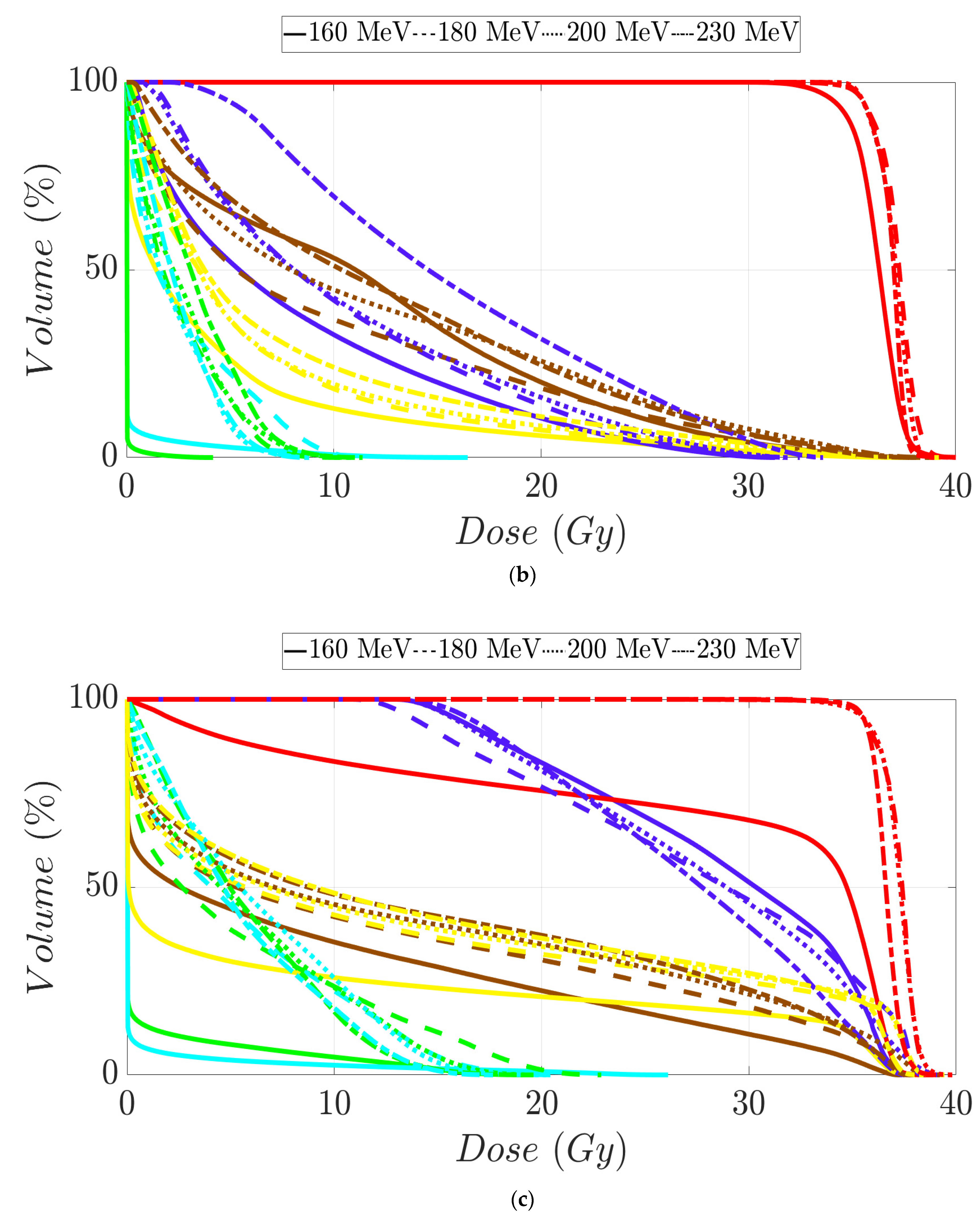
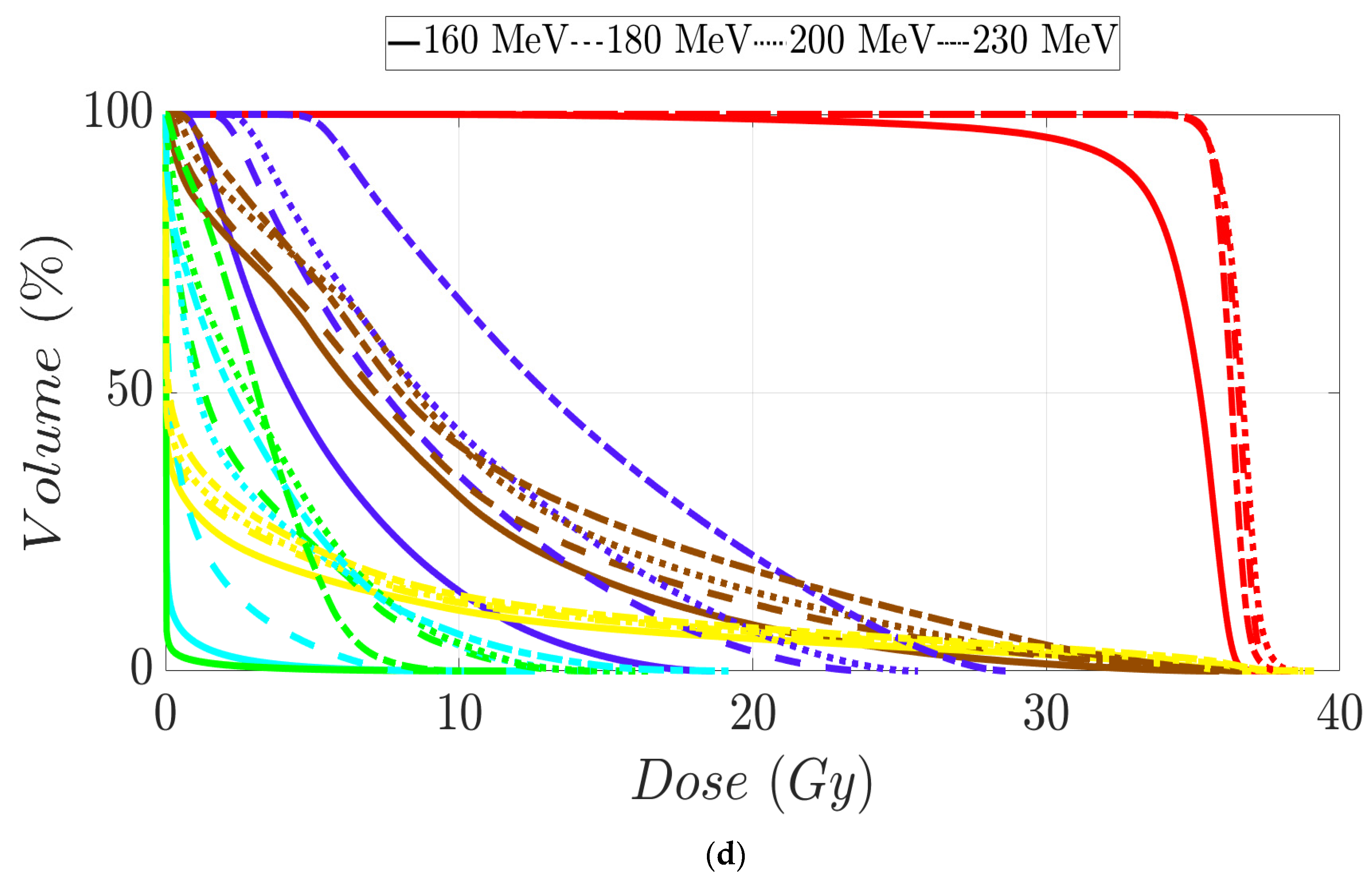

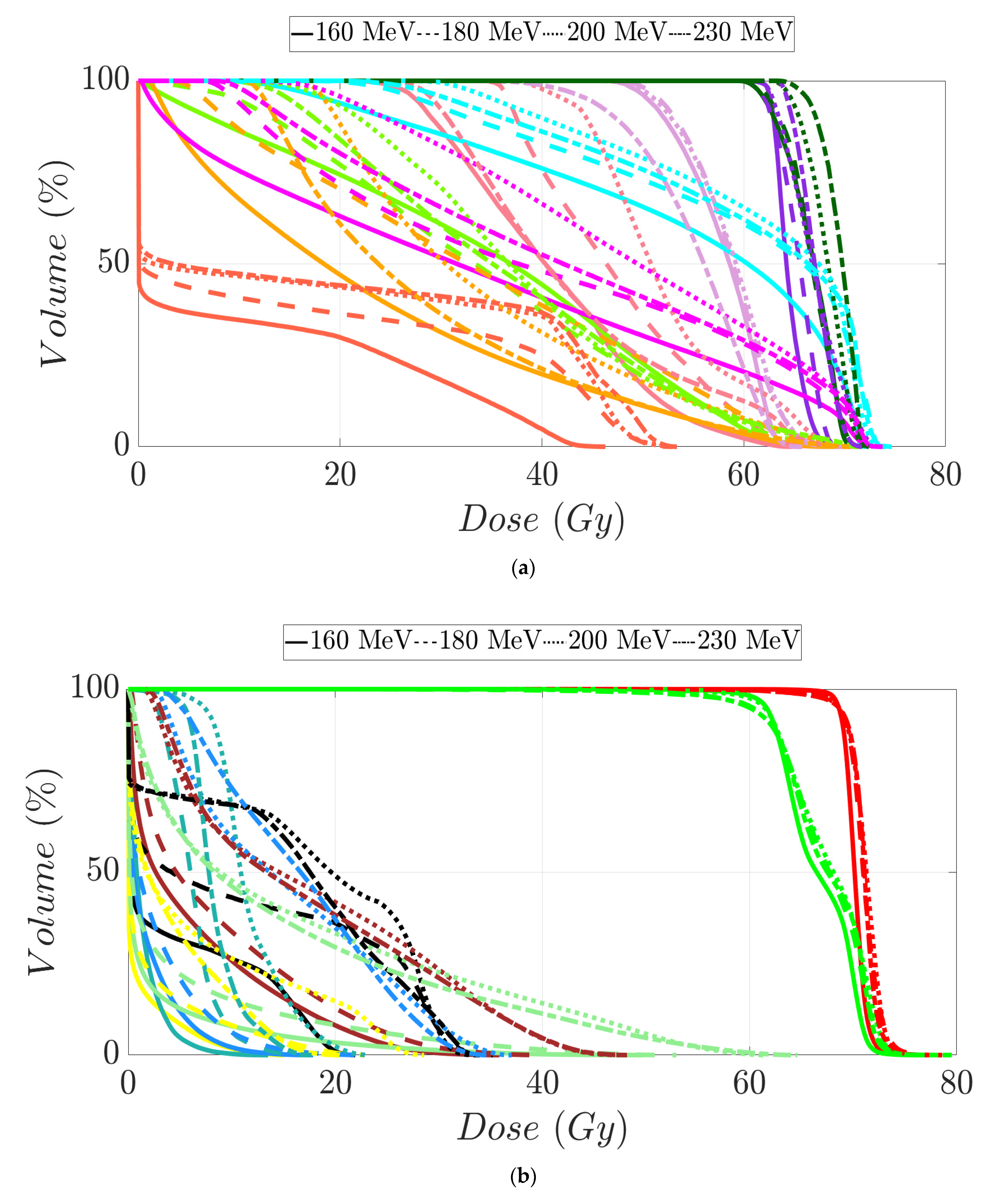

| MIBE (MeV) | |||||
|---|---|---|---|---|---|
| 120 | 160 | 180 | 200 | 230 | |
| PTV V98% (%) | 98 | 98 | 98 | 98 | 98 |
| 98 | 98 | 98 | 98 | 98 | |
| PTV V110% (%) | 0.4 | 0.9 | 0 | 0 | 0.3 |
| 0 | 0 | 0 | 0 | 0 | |
| Left Eye Dmean (Gy) | 0 | 0 | 0.7 | 0.5 | 0.5 |
| 0 | 0.9 | 0.5 | 0.7 | 0.8 | |
| Left Eye Dmax (Gy) | 0 | 0 | 2.6 | 1.1 | 0.9 |
| 0 | 1.3 | 0.7 | 1 | 1.2 | |
| Right Eye Dmean (Gy) | 0 | 0.3 | 0.5 | 0.7 | 0.7 |
| 0 | 0.6 | 0.3 | 0.4 | 0.5 | |
| Right Eye Dmax (Gy) | 0 | 1.6 | 1.1 | 1.3 | 1.1 |
| 0 | 0.9 | 0.5 | 0.6 | 0.7 | |
| Brainstem Dmean (Gy) | 0 | 1.4 | 3.9 | 4.6 | 4.9 |
| 0 | 0.1 | 1.5 | 1.6 | 1.8 | |
| Brainstem Dmax (Gy) | 0 | 13.8 | 11.3 | 14.0 | 14.8 |
| 0 | 1.3 | 4.2 | 4.2 | 5.2 | |
| Left Opt. Nerve Dmean (Gy) | 0 | 0 | 0.8 | 0.7 | 0.8 |
| 0 | 1.7 | 1 | 1.4 | 1.9 | |
| Left Opt. Nerve Dmax (Gy) | 0 | 0 | 1.5 | 1.1 | 1.2 |
| 0 | 2.1 | 1.4 | 1.8 | 2.6 | |
| Right Opt. Nerve Dmean (Gy) | 0 | 0.2 | 0.9 | 0.8 | 0.8 |
| 0 | 0.8 | 0.5 | 0.7 | 1 | |
| Right Opt. Nerve Dmax (Gy) | 0 | 0.3 | 2.4 | 1.2 | 1.1 |
| 0 | 1.6 | 1 | 1.2 | 1.6 | |
| Optic Chiasm Dmean (Gy) | 0 | 0 | 1.4 | 1.1 | 1 |
| 0 | 1.5 | 1.4 | 1.6 | 2 | |
| Optic Chiasm Dmax (Gy) | 0 | 0.1 | 2.1 | 1.3 | 1.1 |
| 0 | 1.9 | 2 | 2.2 | 2.8 | |
| Normal Brain V90% (cc) | 7 | 7.1 | 7.6 | 8.5 | 8.9 |
| 2.3 | 2.7 | 2.3 | 2.9 | 3.4 | |
| Normal Brain Dmax (Gy) | 44.2 | 44.7 | 44.1 | 44.1 | 44.2 |
| 21.7 | 21.2 | 21.6 | 21.1 | 21 | |
| MIBE (MeV) | ||||
|---|---|---|---|---|
| 160 | 180 | 200 | 230 | |
| PTV V98% (%) | 95 | 95 | 95.4 | 95 |
| 78.3 | 95 | 95 | 95 | |
| 35.1 | 95 | 95 | 95 | |
| 37.8 | 95 | 95 | 95 | |
| PTV V107% (%) | 0.7 | 0.8 | 0.2 | 0.5 |
| 0.6 | 1 | 0 | 0.3 | |
| 0 | 0.3 | 1.1 | 0.1 | |
| 0 | 0 | 0 | 0 | |
| Rectum V100% (cc) | 0.4 | 0.2 | 0.2 | 0.3 |
| 0.4 | 0.9 | 0.6 | 0.4 | |
| 0.9 | 3.8 | 5.6 | 3.6 | |
| 0 | 0.1 | 0.1 | 0.1 | |
| Rectum V95% (cc) | 0.9 | 0.7 | 0.7 | 1 |
| 1.1 | 2.5 | 2.7 | 1.6 | |
| 3.3 | 6.9 | 8.7 | 8.1 | |
| 0.1 | 0.7 | 0.7 | 0.9 | |
| Rectum V90% (%) | 2.6 | 2.4 | 2.3 | 3.3 |
| 2 | 3.8 | 4.6 | 3.3 | |
| 7.8 | 14.1 | 17.2 | 17.4 | |
| 0.5 | 1.4 | 1.5 | 2.1 | |
| Rectum V90% (cc) | 1.5 | 1.4 | 1.3 | 1.9 |
| 2.1 | 3.9 | 4.7 | 3.4 | |
| 5 | 9 | 11 | 11.1 | |
| 1 | 2 | 1.5 | 2.2 | |
| Rectum V80% (%) | 5.4 | 5.7 | 4.9 | 7.4 |
| 5.1 | 6.9 | 8.9 | 7.6 | |
| 12 | 19.4 | 23 | 24.5 | |
| 1.6 | 3.4 | 3.9 | 5.9 | |
| Rectum V50% (%) | 23.9 | 27.2 | 22.8 | 31.2 |
| 23.6 | 27.7 | 26.8 | 31.4 | |
| 24.7 | 32.6 | 36.8 | 39.1 | |
| 10.7 | 14.6 | 17.2 | 21.2 | |
| Bladder V100% (cc) | 0.2 | 0.9 | 0.3 | 0.2 |
| 0.2 | 0.9 | 0.3 | 0.2 | |
| 15.8 | 68.4 | 73.8 | 54.4 | |
| 0.5 | 5.6 | 5.9 | 7.4 | |
| Bladder D5.5cc (Gy) | 35.5 | 35.5 | 35.3 | 35.4 |
| 30 | 31.08 | 31.9 | 33.1 | |
| 36.8 | 38.1 | 38.1 | 37.3 | |
| 34.7 | 36.3 | 36.4 | 36.6 | |
| Bladder V90% (%) | 2.5 | 2.2 | 2 | 2.5 |
| 0.8 | 1 | 1.2 | 2 | |
| 15 | 22.4 | 24 | 24.1 | |
| 2 | 2.7 | 2.8 | 3.3 | |
| Bladder V50% (%) | 7.3 | 6.9 | 6.4 | 8.9 |
| 6.8 | 8.6 | 9.8 | 12.6 | |
| 21.6 | 33.7 | 35.8 | 38.2 | |
| 6.4 | 7.7 | 7.8 | 8.5 | |
| Left Femoral Head V40% (%) | 3.4 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | |
| 1.8 | 6.2 | 4.5 | 1.7 | |
| 0 | 0 | 0 | 0 | |
| Right Femoral Head V40% (%) | 4.3 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | |
| 1.9 | 12.3 | 6.2 | 2 | |
| 0 | 0 | 0 | 0 | |
| Penile Bulb V20Gy (cc) | 1 | 1.1 | 1.2 | 1.1 |
| 0.8 | 1 | 1.2 | 2.4 | |
| 3.3 | 3 | 3.2 | 3.2 | |
| 0 | 0.2 | 0.5 | 1.3 | |
| MIBE (MeV) | ||||
|---|---|---|---|---|
| 160 | 180 | 200 | 230 | |
| PTVlow. risk V98% (%) | -- | -- | -- | -- |
| 100 | 100 | 100 | 100 | |
| PTVint. risk V98% (%) | 95.2 | 92.4 | 94 | 91.4 |
| 100 | 100 | 100 | 97 | |
| PTVhigh risk V98% (%) | 95 | 95 | 95 | 95 |
| 95 | 95 | 95 | 95 | |
| PTVhigh risk V107% (%) | 0 | 0.9 | 0.3 | 0.5 |
| 0 | 0 | 0 | 0.1 | |
| Spinal Cord Dmax (Gy) | 22.1 | 35.6 | 33.6 | 34 |
| 19.7 | 30.6 | 30.8 | 36.9 | |
| Brainstem Dmean (Gy) | 1.1 | 2.1 | 6.5 | 4.2 |
| 9.5 | 13.7 | 14.1 | 12.1 | |
| Left Cochlea Dmean (Gy) | 2.8 | 5.5 | 8.3 | 10.6 |
| 12.5 | 14.8 | 14.2 | 33.2 | |
| Left Cochlea Dmax (Gy) | 5.3 | 9.4 | 13 | 15 |
| 19.4 | 19.6 | 18.9 | 40 | |
| Right Cochlea Dmean (Gy) | 3 | 3.2 | 7 | 17 |
| 11 | 16.5 | 15.8 | 29.6 | |
| Right Cochlea Dmax (Gy) | 8 | 5.1 | 9.8 | 20.9 |
| 16.3 | 21.9 | 21.7 | 35.5 | |
| Left Parotid Dmean (Gy) | 53.8 | 58.6 | 61.1 | 59.4 |
| 13.3 | 20.5 | 18.8 | 34.4 | |
| Left Parotid V28Gy (%) | 87.2 | 94.8 | 100 | 97.3 |
| 14.2 | 26.9 | 22.1 | 24.1 | |
| Right Parotid Dmean (Gy) | 22.9 | 33.3 | 34.6 | 28.1 |
| 16.3 | 19.2 | 20.1 | 34.4 | |
| Right Parotid V28Gy (%) | 34.2 | 57.1 | 56.4 | 39.7 |
| 19.9 | 23.5 | 24.5 | 22.7 | |
| Mandible V64Gy (%) | 1.2 | 2.4 | 3.8 | 4 |
| 0.01 | 0.01 | 0.01 | 0.01 | |
| Lips Dmean (Gy) | 1.5 | 6.1 | 11.7 | 8.3 |
| 0.8 | 11 | 13.4 | 10.4 | |
| Left SubMand Dmean (Gy) | 66.8 | 66.6 | 68.2 | 69 |
| 34.2 | 36 | 35.6 | 52 | |
| Right SubMand Dmean (Gy) | 64.7 | 65.3 | 66.9 | 66.6 |
| 34 | 37 | 36.1 | 46 | |
| Oral Cavity V45Gy (%) | 35.5 | 43.7 | 56.9 | 46.2 |
| 15.4 | 21.1 | 21.4 | 26.7 | |
| Esophagus Dmean (Gy) | 10.7 | 15.9 | 19.1 | 19.8 |
| 15.6 | 20.1 | 24.4 | 17.8 | |
| Larynx Dmax (Gy) | 65.1 | 67.1 | 71.1 | 70.2 |
| 55.4 | 53.7 | 54.4 | 54.8 | |
| Thyroid Dmax (Gy) | 68.6 | 69.9 | 71.2 | 65.3 |
| 61.3 | 64 | 60.1 | 60.8 | |
| Nasal Cavity Dmax (Gy) | 50 | 53 | 61.7 | 64.2 |
| 72.9 | 72.5 | 72.1 | 72.6 | |
| Nasal Cavity Dmean (Gy) | 2.4 | 4.6 | 16.3 | 15 |
| 13.1 | 21.8 | 22.9 | 20 | |
| Left Mastoid Dmean (Gy) | 6.4 | 8.4 | 17.6 | 17 |
| 4.8 | 15.4 | 14.1 | 20 | |
| Right Mastoid Dmean (Gy) | 1.8 | 2.8 | 15.6 | 16.6 |
| 6.4 | 18.2 | 21.2 | 16.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beltran, C.J.; Perales, A.; Furutani, K.M. Does the Maximum Initial Beam Energy for Proton Therapy Have to Be 230 MeV? Quantum Beam Sci. 2024, 8, 23. https://doi.org/10.3390/qubs8030023
Beltran CJ, Perales A, Furutani KM. Does the Maximum Initial Beam Energy for Proton Therapy Have to Be 230 MeV? Quantum Beam Science. 2024; 8(3):23. https://doi.org/10.3390/qubs8030023
Chicago/Turabian StyleBeltran, Chris J., Alvaro Perales, and Keith M. Furutani. 2024. "Does the Maximum Initial Beam Energy for Proton Therapy Have to Be 230 MeV?" Quantum Beam Science 8, no. 3: 23. https://doi.org/10.3390/qubs8030023
APA StyleBeltran, C. J., Perales, A., & Furutani, K. M. (2024). Does the Maximum Initial Beam Energy for Proton Therapy Have to Be 230 MeV? Quantum Beam Science, 8(3), 23. https://doi.org/10.3390/qubs8030023








