Modification of Cu Oxide and Cu Nitride Films by Energetic Ion Impact
Abstract
1. Introduction
- (a)
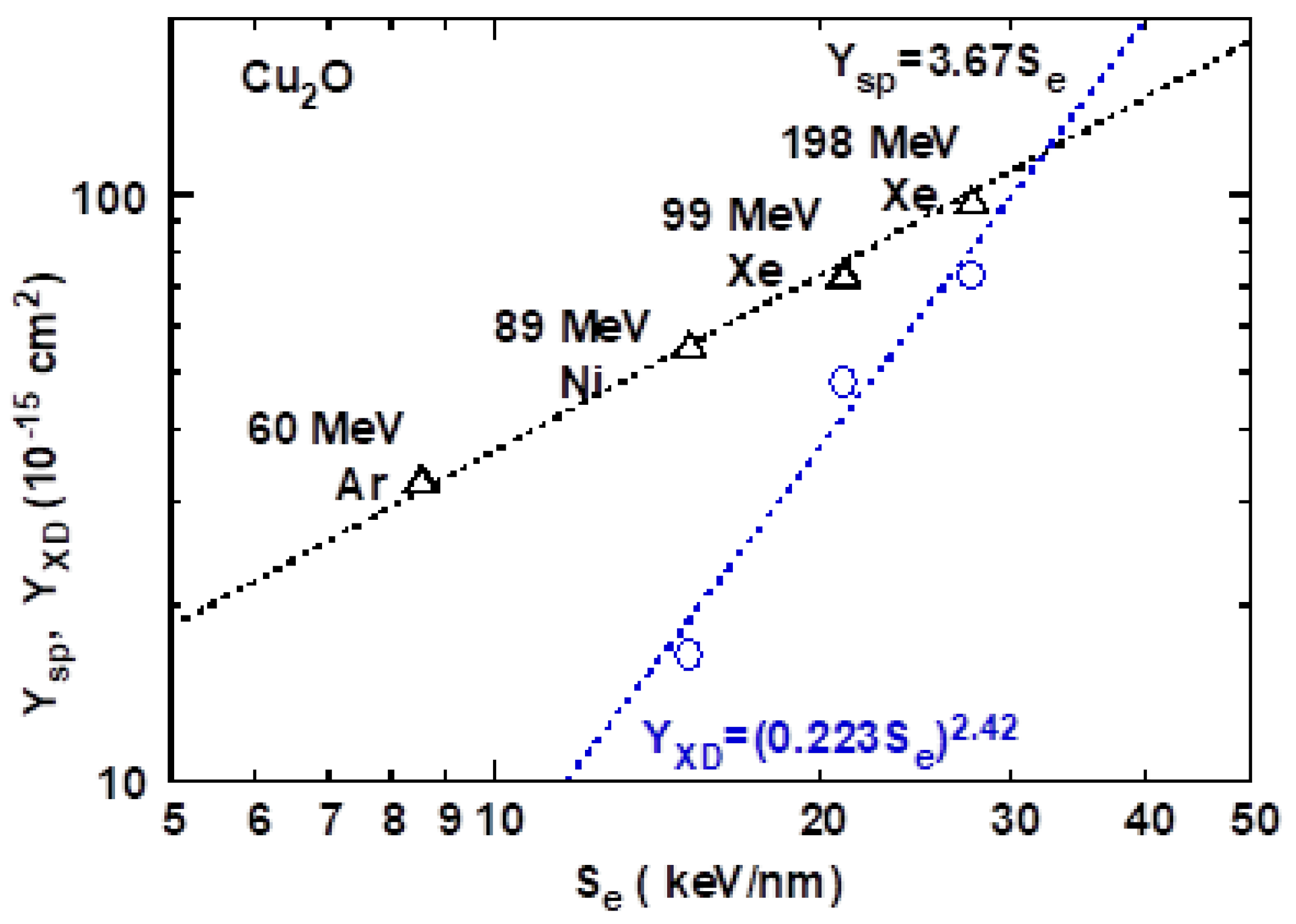
- Electronic sputtering yields per ion (YSP) superlinearly depend on Se and are approximated by the power–law fit: YSP = (BSPSe)Nsp with 1 ≦ NSP ≦ 4 for most cases, BSP being a material-dependent constant.
- (b)
- YSP is larger by 10–103 than nuclear sputtering yields due to elastic collision cascades, which can be estimated assuming a linear dependence on Sn.The representative sputtering yields at Se = 10 keV/nm by monatomic ions at normal incidence vary from 0.42 (MgO) [12] to 844 (WO3) [16], and these yields are plotted as a function of the bandgap (Eg) and elastic constant. It appears that the sputtering yields tend to increase with the bandgap for Eg > 3 eV, and the yields decrease with the elastic constant for oxides. Stoichiometric sputtering has been observed for many materials, although only heavy elements such as U have been detected [7,8,9]. Non-stoichiometric sputtering has been argued for some fluorides (CaF2, LaF3 and UF4) [11]. It should be mentioned that Bragg’s additive rule is applied to obtain stopping powers for compound solids in the present study. The deviation from Bragg’s rule is not serious for oxides and nitrides, being roughly 10% or less; around 1 MeV/u [16]. In most cases, the variation in Se calculated using different versions of TRIM/SRIM is within 10% [16].
2. Materials and Methods
3. Results and Discussion
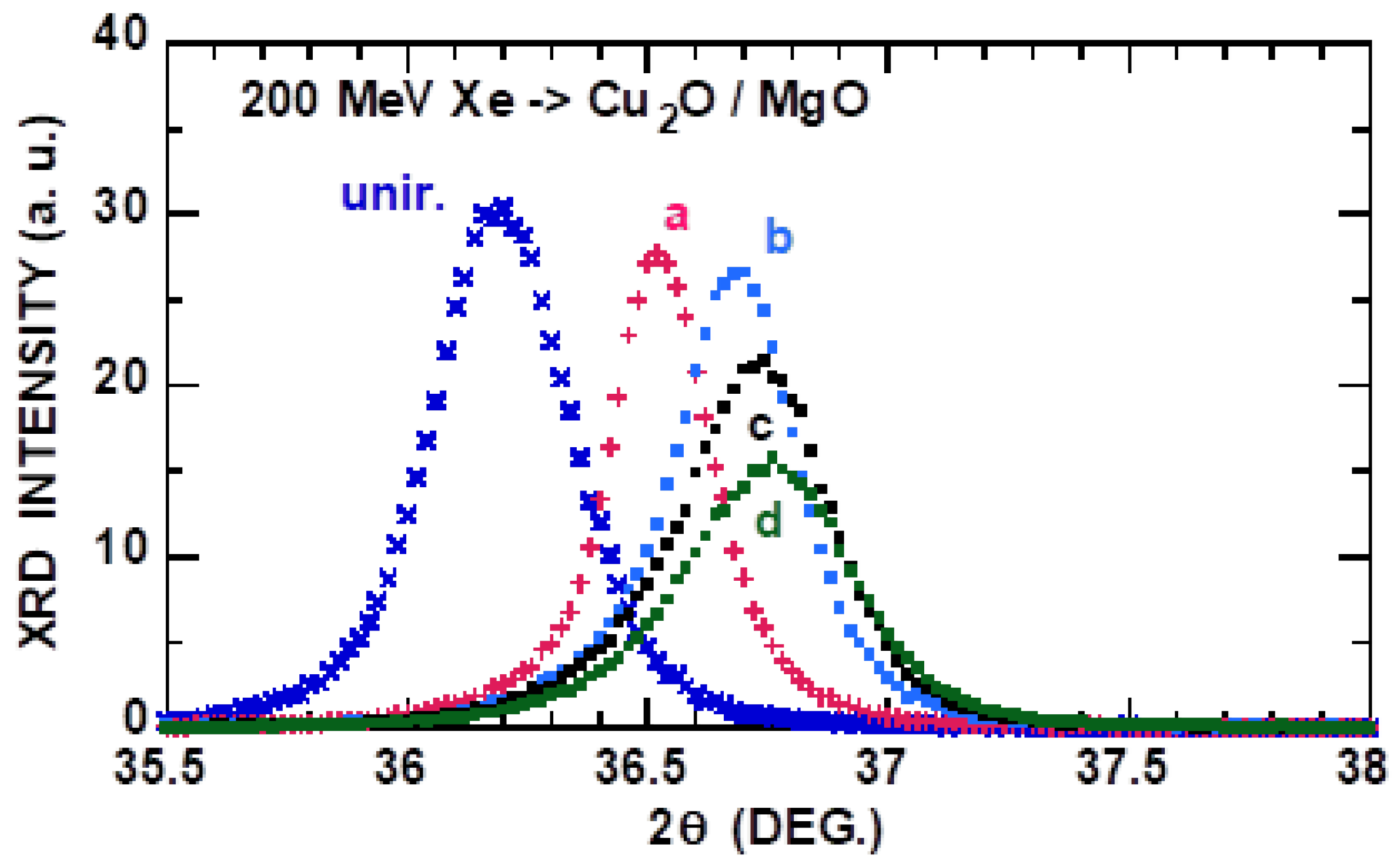
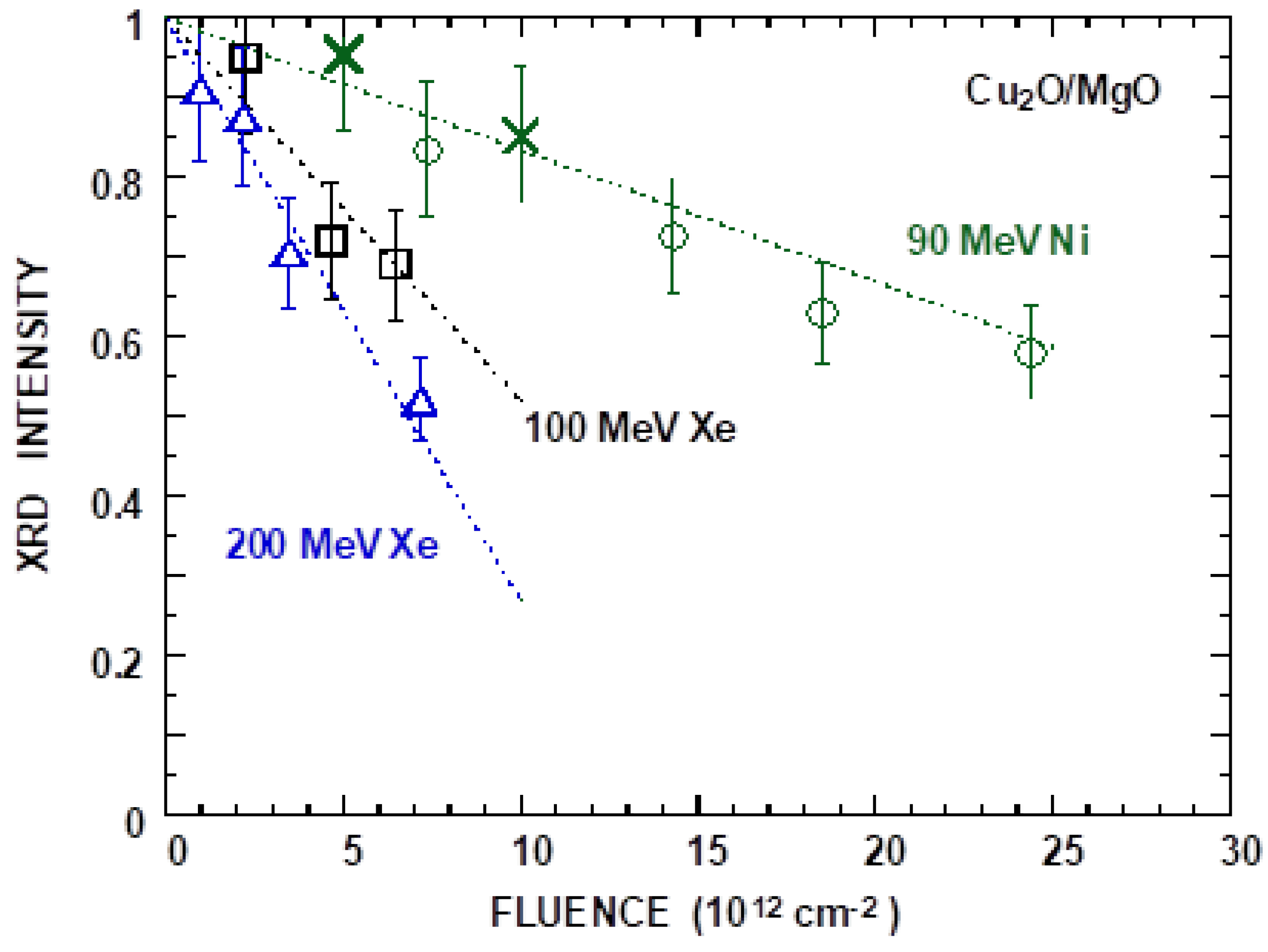
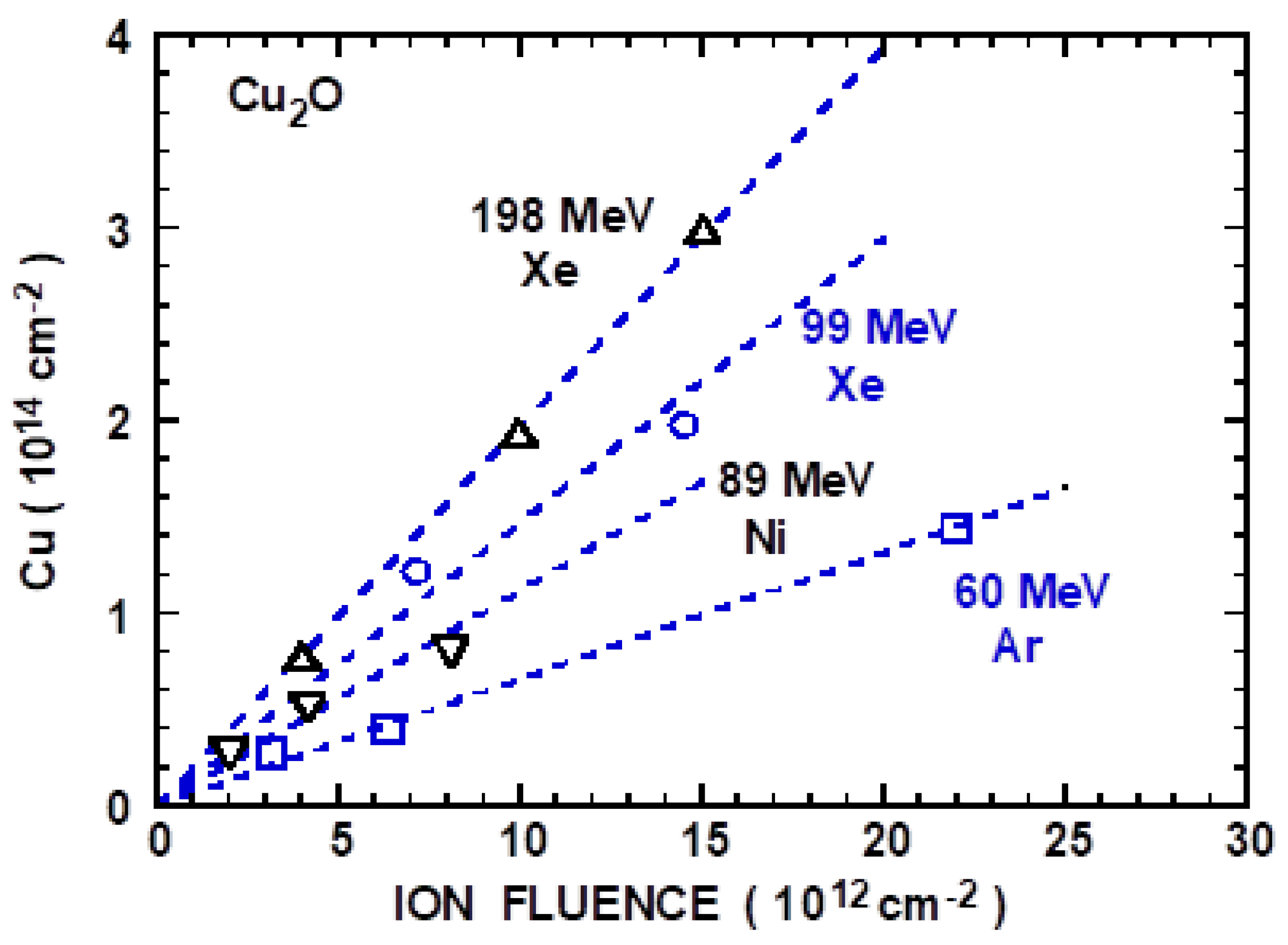
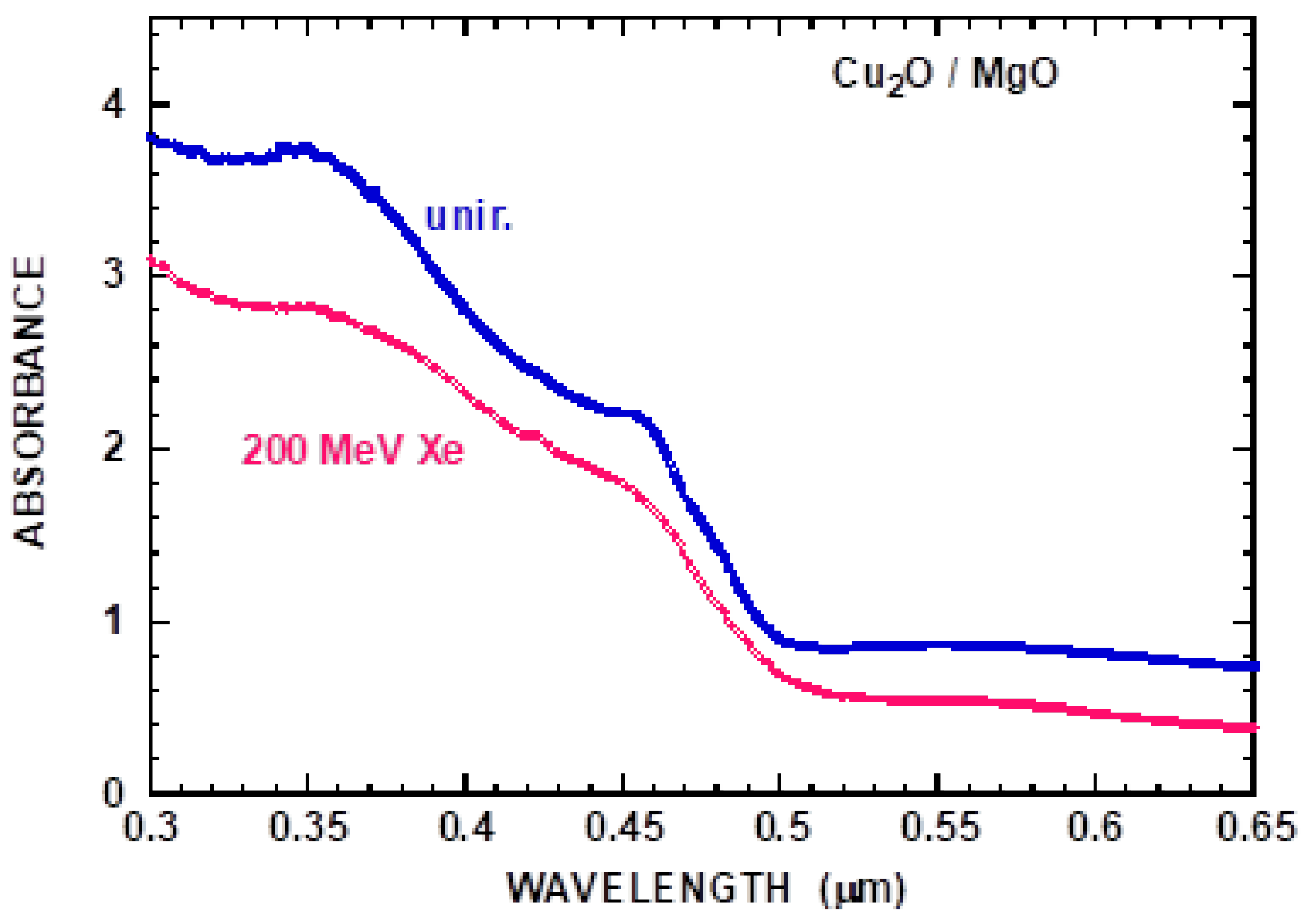
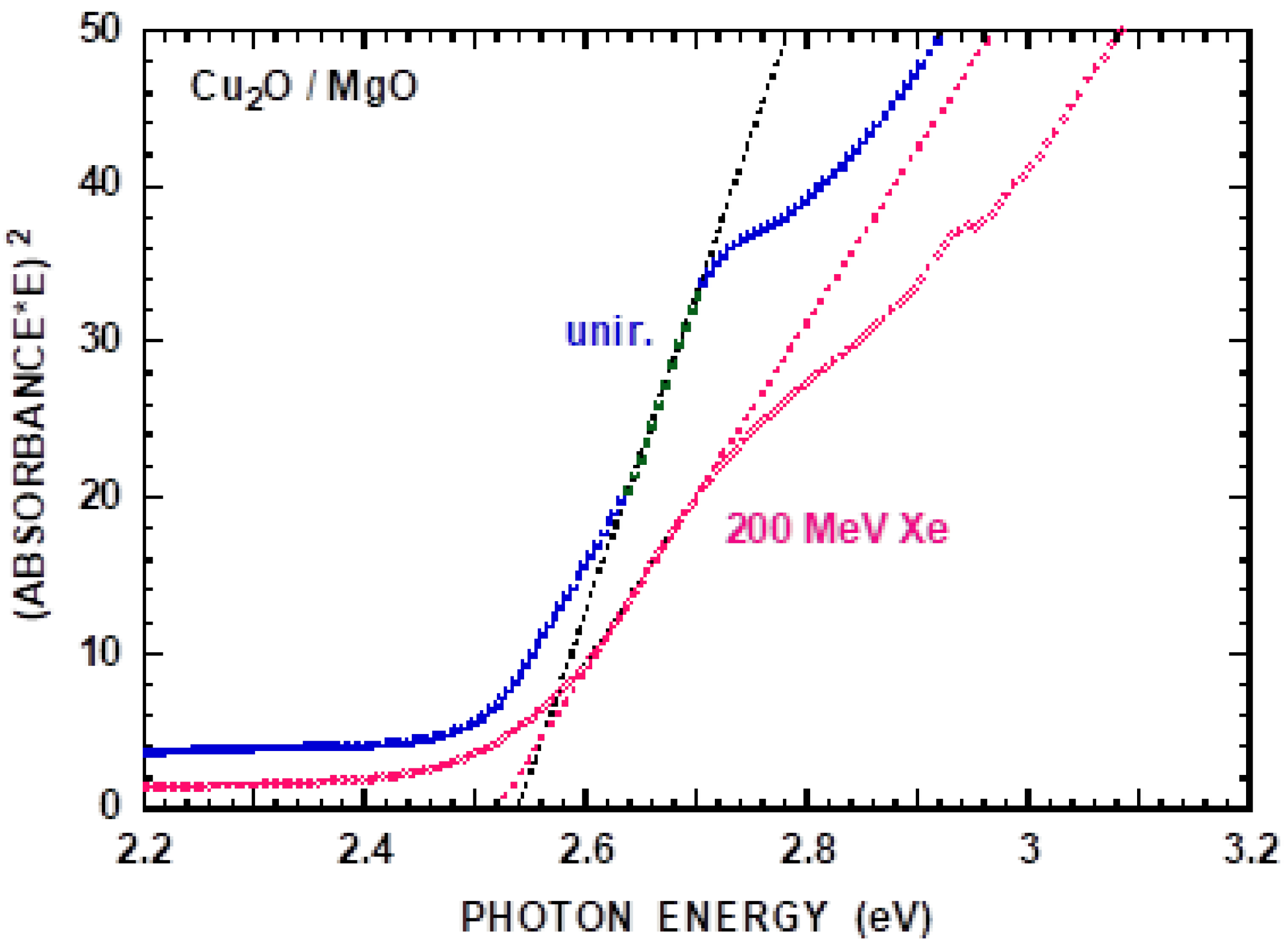
3.1. Cu2O: High-Energy Ion Impact
3.2. Cu2O: Low-Energy Ion Impact
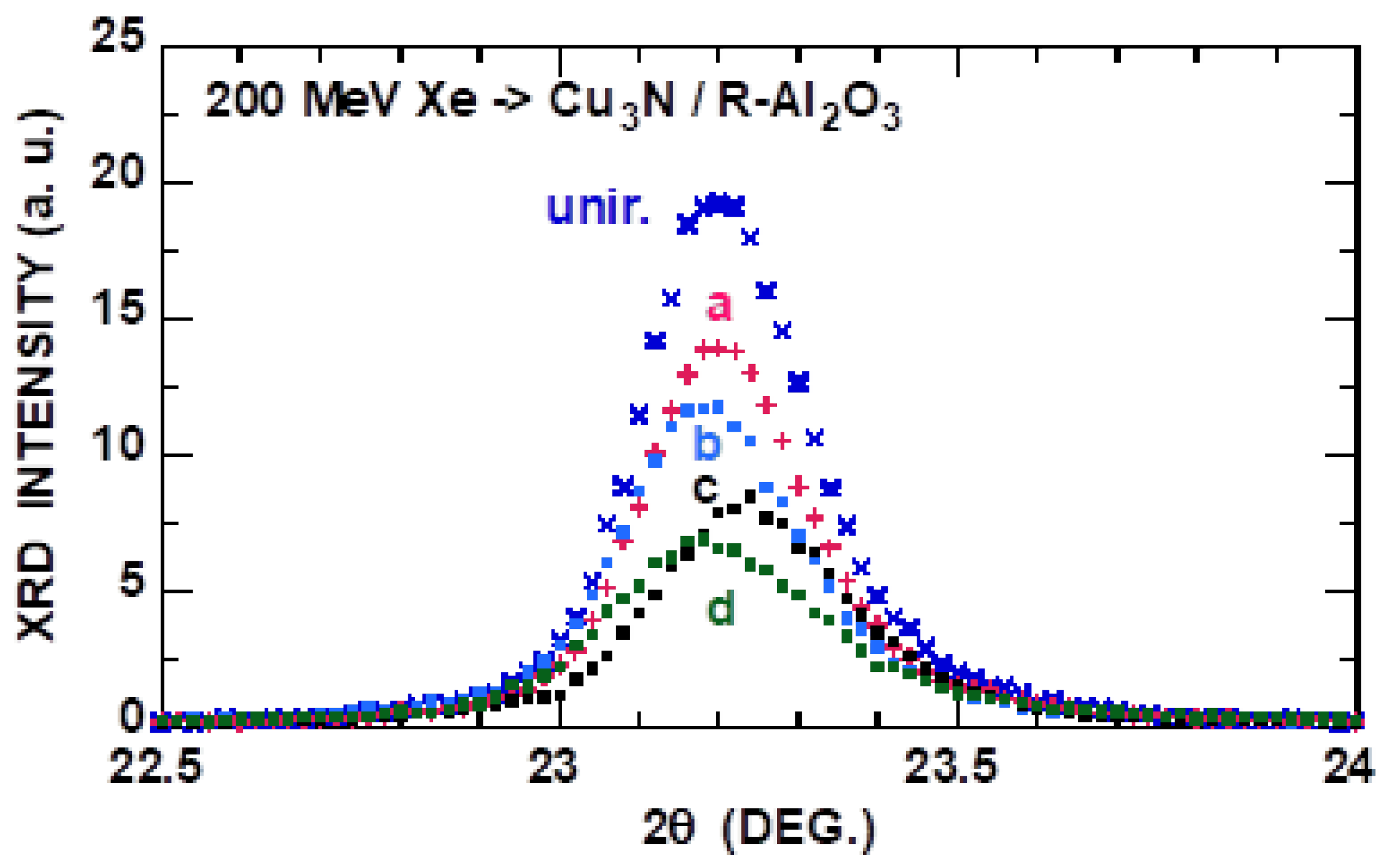
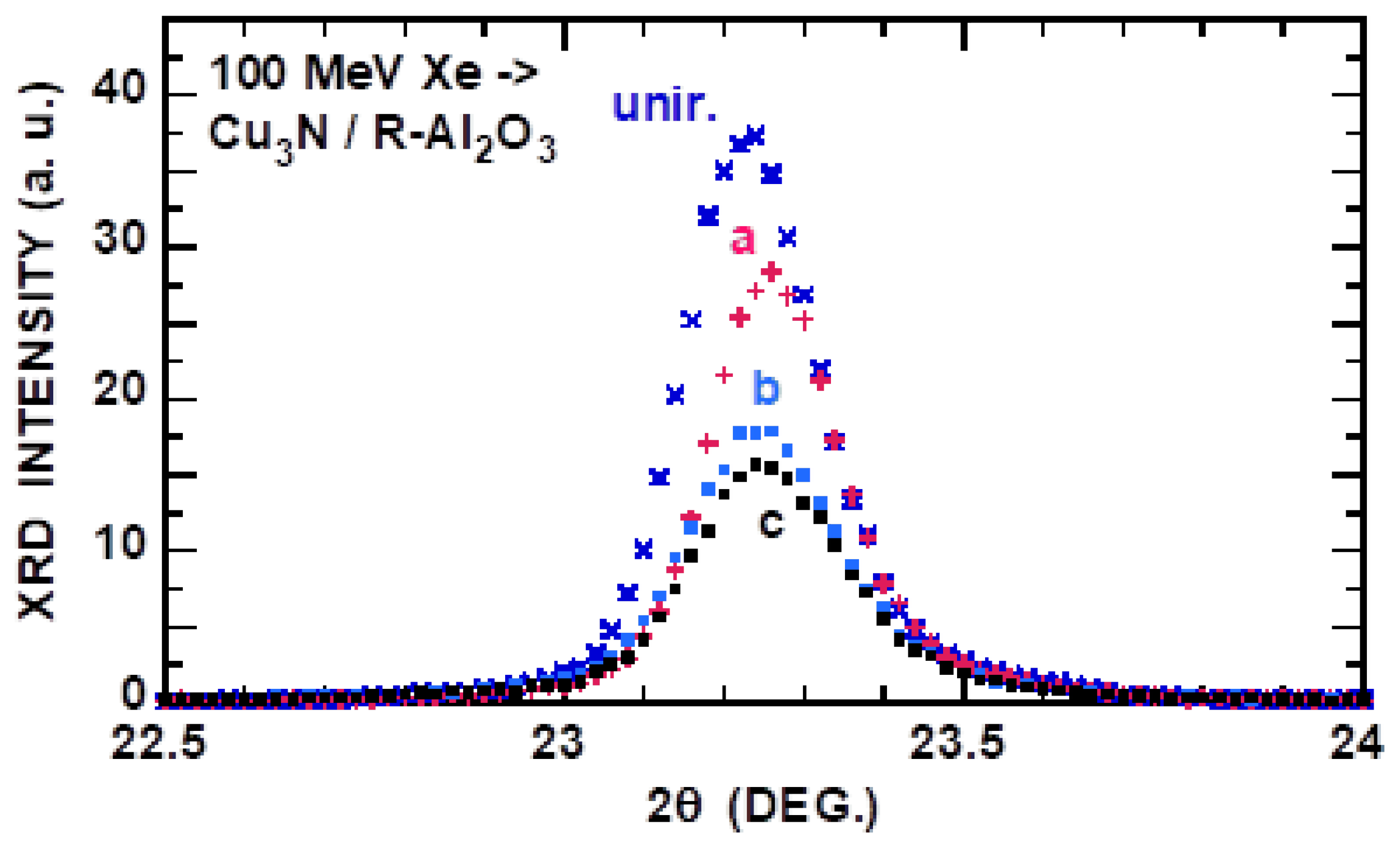
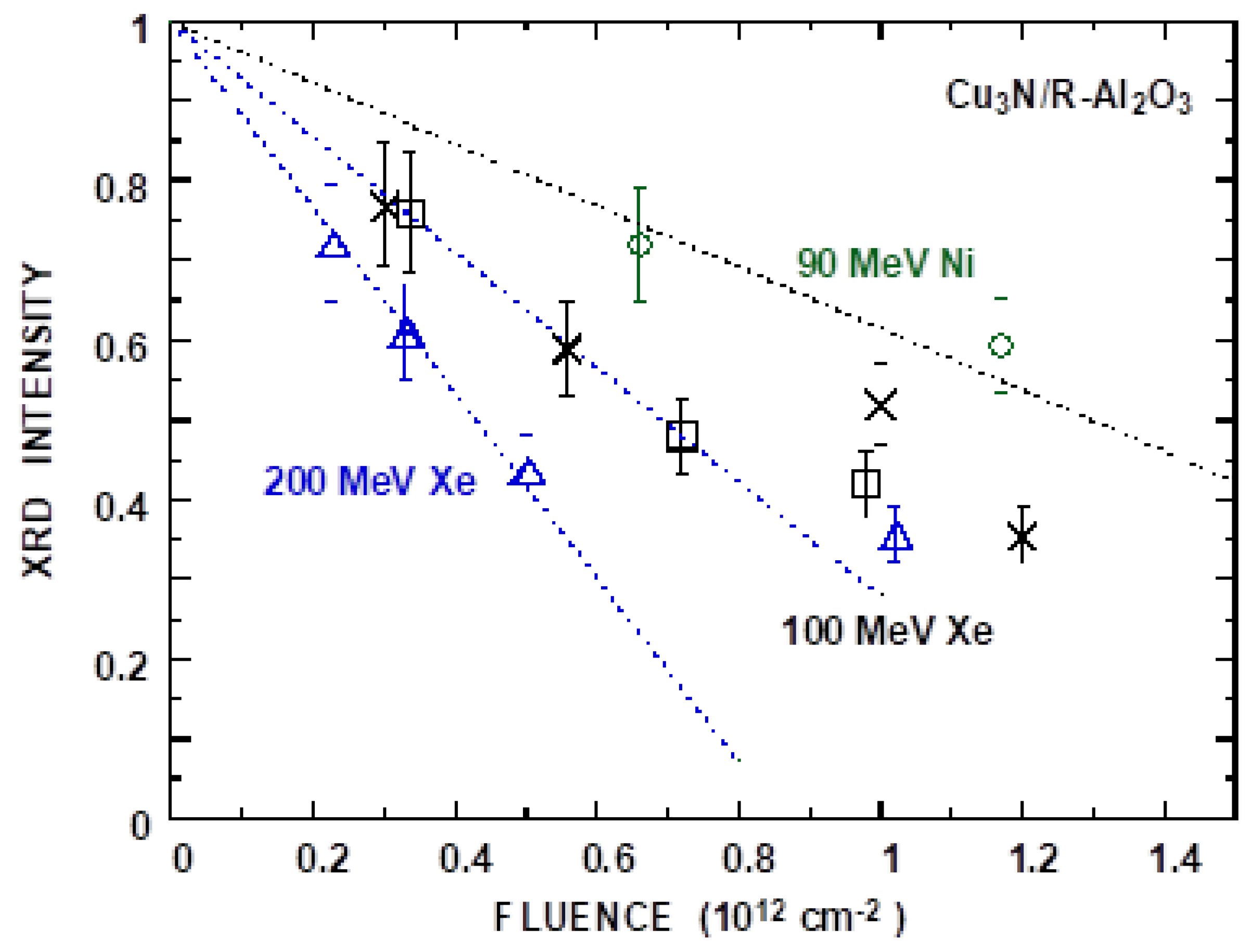
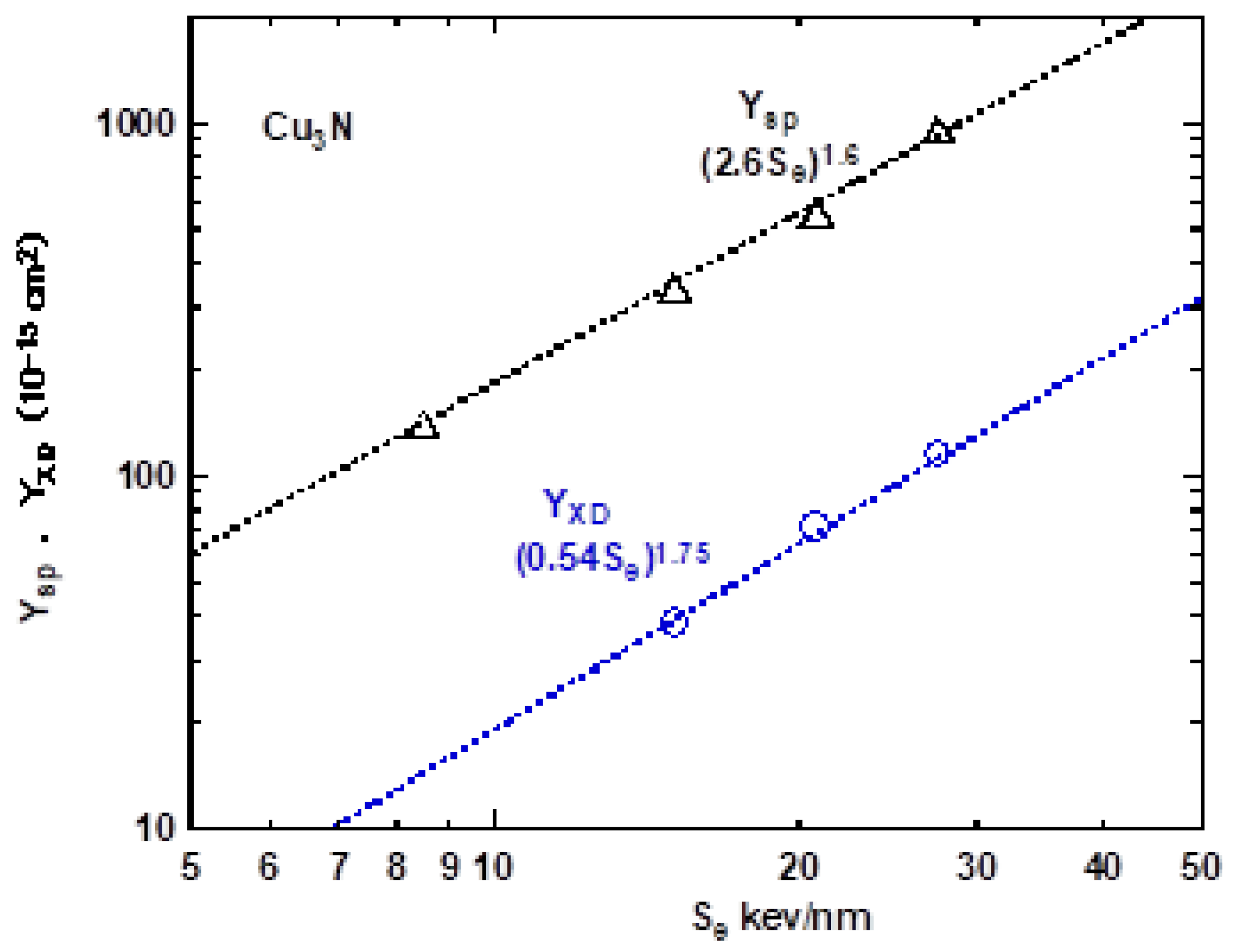
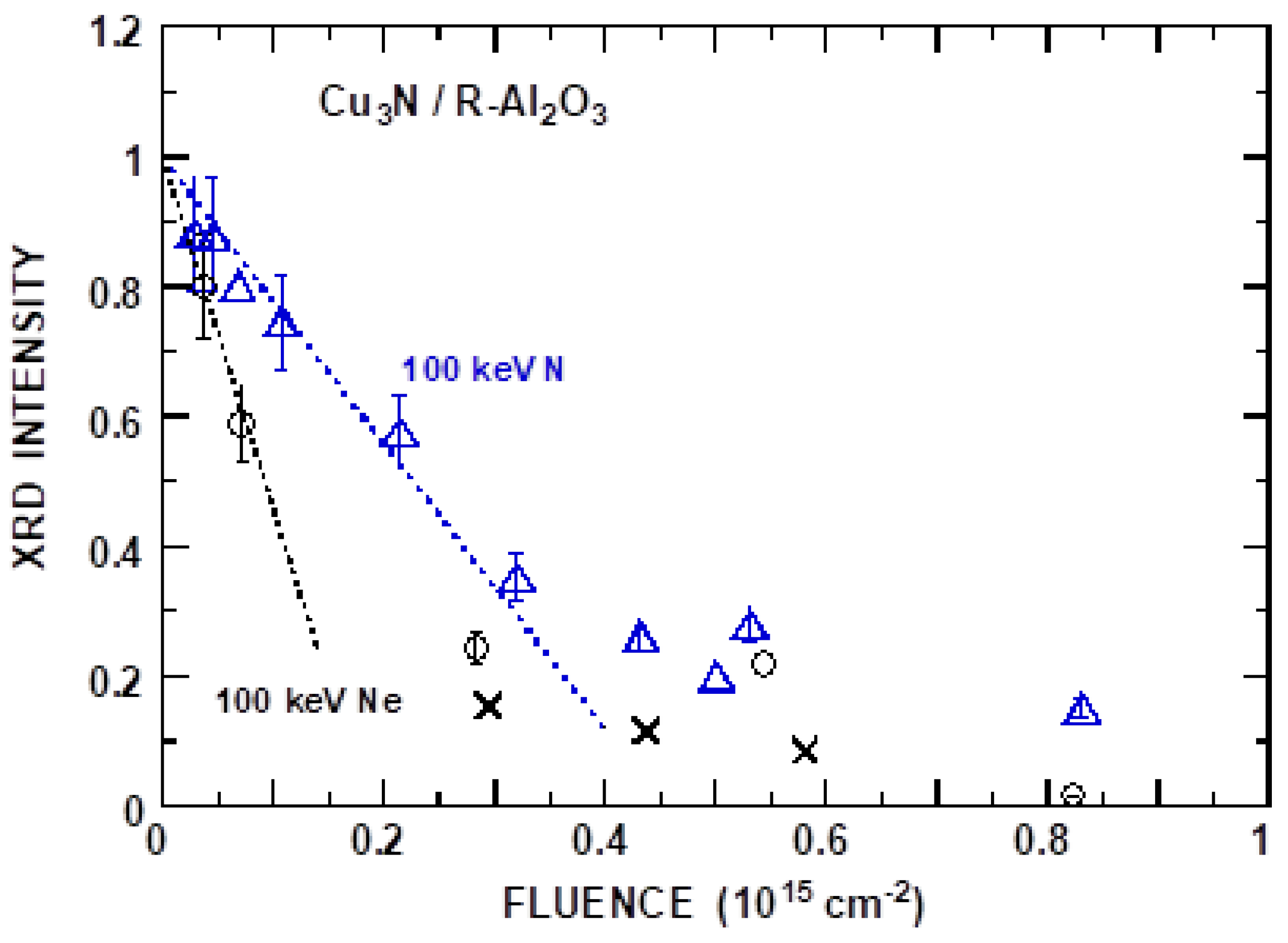
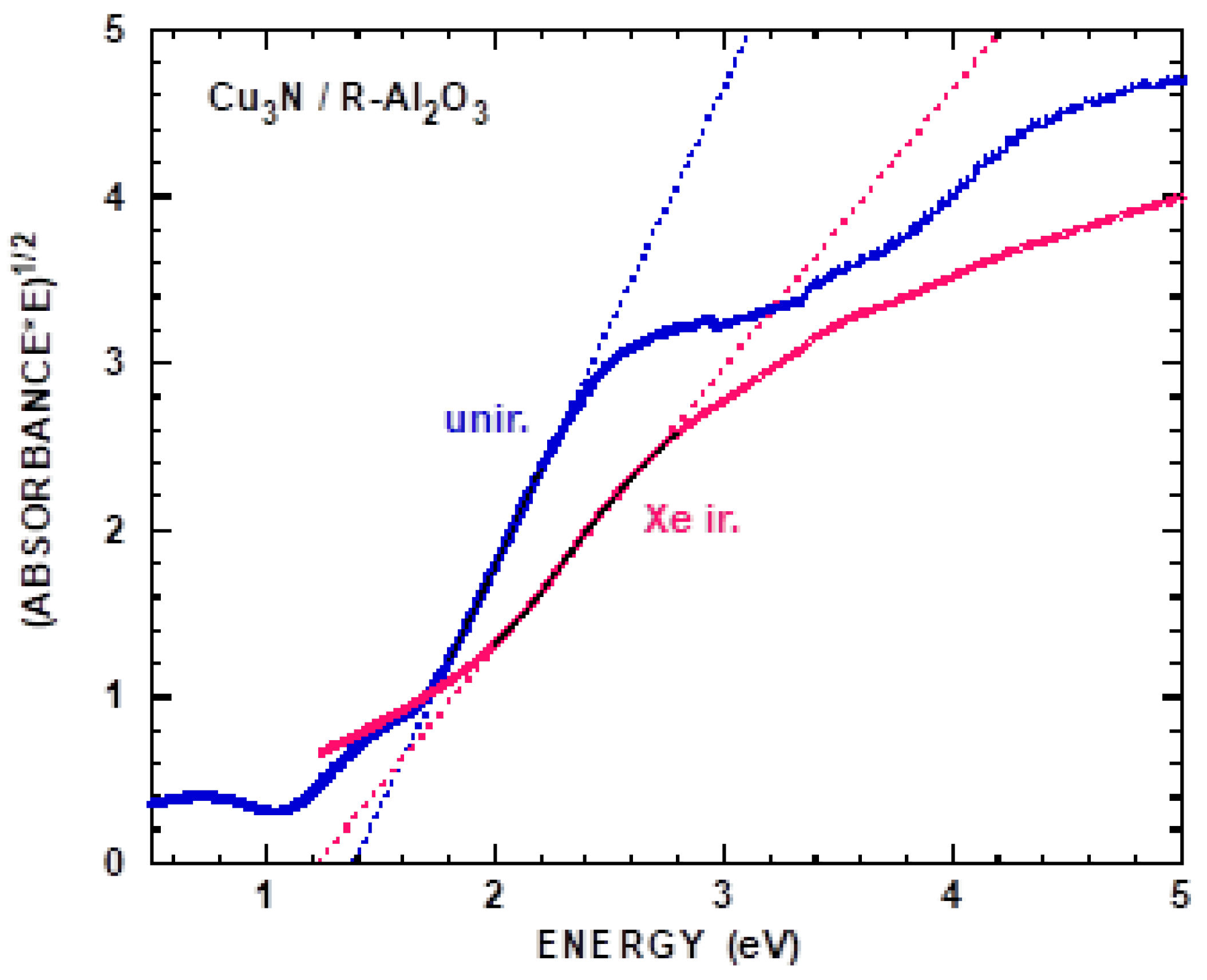
3.3. Cu3N
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, W.L.; Augustyniak, W.M.; Brody, E.; Cooper, B.; Lanzerotti, L.J.; Ramirez, A.; Evatt, R.; Johnson, R.E. Energy Dependence of the Erosion of H2O Ice Films by H and He Ions. Nucl. Instrum. Methods 1980, 170, 321–325. [Google Scholar] [CrossRef]
- Bottiger, J.; Davies, J.A.; L’Ecuyer, J.; Matsunami, N.; Ollerhead, R. Erosion of Frozen-Gas Films by MeV Ions. Radiat. Eff. 1980, 49, 119–124. [Google Scholar] [CrossRef]
- Brown, W.L.; Lanzerotti, L.J.; Marcantonio, K.J.; Johnson, R.E.; Reimann, C.T. Sputtering of Ices by High Energy Particle Impact. Nucl. Instrum. Methods B 1986, 14, 392–402. [Google Scholar] [CrossRef]
- Mejia, C.; Bender, M.; Severin, D.; Trautmann, C.; Boduch, P.; Bordalo, V.; Domaracka, A.; Lv, X.Y.; Martinez, R.; Rothard, H. Radiolysis and sputtering of carbon dioxide ice induced by swift Ti, Ni and Xe ions. Nucl. Instrum. Methods B 2015, 365, 477–481. [Google Scholar] [CrossRef]
- Galli, A.; Vorburger, A.; Wurz, P.; Tulej, M. Sputtering of water ice films: A re-assessment with singly and doubly charged oxygen and argon ions, molecular oxygen, and electrons. Icarus 2017, 291, 36–45. [Google Scholar] [CrossRef]
- Qiu, Y.; Griffith, J.E.; Meng, W.J.; Tombrello, T.A. Sputtering of Silicon and its Compounds in the Electronic Stopping Region. Radiat. Eff. 1983, 70, 231–236. [Google Scholar] [CrossRef]
- Meins, C.K.; Griffith, J.E.; Qiu, Y.; Mendenhall, M.H.; Seiberling, L.E.; Tombrello, T.A. Sputtering of UF4 by High Energy Heavy Ions. Radiat. Eff. 1983, 71, 13–33. [Google Scholar] [CrossRef]
- Bouffard, S.; Duraud, J.P.; Mosbah, M.; Schlutig, S. Angular distribution of the sputtered atoms from UO2 under high electronic stopping power irradiation. Nucl. Instrum. Methods B 1998, 141, 372–377. [Google Scholar] [CrossRef]
- Schlutig, S. Contribution a L’etude de la Pulverisation et de L’endommagement du Dioxyde D’uranuim par les Ions Lourds Rapides. Ph.D. Thesis, University of CAEN, Caen, France, 2001. [Google Scholar]
- Toulemonde, M.; Assmann, W.; Trautmann, C.; Gruner, F. Jetlike Component in Sputtering of LiF Induced by Swift Heavy Ions. Phys. Rev. Lett. 2002, 88, 057602. [Google Scholar] [CrossRef]
- Toulemonde, M.; Assmann, W.; Muller, D.; Trautmann, C. Electronic sputtering of LiF, CaF2, LaF3 and UF4 with 197 MeV Au ions: Is the stoichiometry of atom emission preserved? Nucl. Instrum. Methods B 2017, 406, 501–507. [Google Scholar] [CrossRef]
- Matsunami, N.; Sataka, M.; Iwase, A.; Okayasu, S. Electronic excitation induced sputtering of insulating and semiconducting oxides by high energy heavy ions. Nucl. Instrum. Methods B 2003, 209, 288–293. [Google Scholar] [CrossRef]
- Toulemonde, M.; Assmann, W.; B.-d’Etat, B.; Bender, M.; Bergmaier, A.; Boduch, P.; Negra, S.D.; Duan, J.; E.-Said, A.S.; Gruner, F.; et al. Sputtering of LiF and other halide crystals in the electronic energy loss regime. Eur. Phys. J. D 2020, 74, 144. [Google Scholar] [CrossRef]
- Matsunami, N.; Sataka, M.; Okayasu, S.; Tazawa, M. Electronic sputtering of nitrides by high-energy ions. Nucl. Instrum. Methods B 2007, 256, 333–336. [Google Scholar] [CrossRef]
- Matsunami, N.; Okayasu, S.; Sataka, M.; Tsuchiya, B. Electronic sputtering of SiC and KBr by high energy ions. Nucl. Instrum. Methods B 2020, 478, 80–84. [Google Scholar] [CrossRef]
- Matsunami, N.; Sataka, M.; Okayasu, S.; Tsuchiya, B. Modification of SiO2, ZnO, Fe2O3 and TiN Films by Electronic Excitation under High Energy Ion Impact. Quantum Beam Sci. 2021, 5, 30. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Biersack, J.P.; Littmark, U. The Stopping and Range of Ions in Solids; Pergamon Press: New York, NY, USA, 1985; pp. 1–321. [Google Scholar]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM-The stopping and range of ions in matter (2010). Nucl. Instrum. Methods B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Fleischer, R.L.; Price, P.B.; Walker, R.M. Ion Explosion Spike Mechanism for Formation of Charged-Particle Tracks in Solids. J. Appl. Phys. 1965, 36, 3645–3652. [Google Scholar] [CrossRef]
- Itoh, N.; Duffy, D.M.; Khakshouri, S.; Stoneham, A.M. Making tracks: Electronic excitation roles in forming swift heavy ion tracks. J. Phys. Condens. Matter 2009, 21, 474205. [Google Scholar] [CrossRef]
- Meftah, A.; Brisard, F.; Costantini, J.M.; Dooryhee, E.; H.-Ali, M.; Hervieu, M.; Stoquert, J.P.; Studer, F.; Toulemonde, M. Track formation in SiO2 quartz and the thermal-spike mechanism. Phys. Rev. B 1994, 49, 12457–12463. [Google Scholar] [CrossRef]
- Toulemonde, M.; Bouffard, S.; Studer, F. Swift heavy ions in insulating and conducting oxides: Tracks and physical properties. Nucl. Instrum. Methods B 1994, 91, 108–123. [Google Scholar] [CrossRef]
- Afra, B.; Rodriguez, M.D.; Trautmann, C.; Pakarinen, O.H.; Djurabekova, F.; Nordlund, K.; Bierschenk, T.; Giulian, R.; Ridgway, M.C.; Rizza, G. SAXS investigation of the morphology of swift heavy ion tracks in α–quartz. J. Phys. Condens. Matter. 2013, 25, 045006. [Google Scholar] [CrossRef]
- Kluth, P.; Pakarinen, O.H.; Djurabekova, F.; Giulian, R.; Ridgway, M.C.; Byrne, A.P.; Nordlund, K. Nanoscale density fluctuations in swift heavy ion irradiated amorphous SiO2. J. Appl. Phys. 2011, 110, 123520. [Google Scholar] [CrossRef]
- Benyagoub, A.; Toulemonde, M. Ion tracks in amorphous silica. J. Mater. Res. 2015, 30, 1529–1543. [Google Scholar] [CrossRef]
- Toulemonde, M.; Weber, W.J.; Li, G.; Shutthanandan, V.; Kluth, P.; Yang, T.; Wang, Y.; Zhang, Y. Synergy of nuclear and electronic energy losses in ion-irradiation processes: The case of vitreous silicon dioxide. Phys. Rev. B 2011, 83, 054106. [Google Scholar] [CrossRef]
- Canut, B.; Benyagoub, A.; Marest, G.; Meftah, A.; Moncoffre, N.; Ramos, S.M.M.; Studer, F.; Thevenard, P.; Toulemonde, M. Swift-uranium-ion-induced damage in sapphire. Phys. Rev. B 1995, 51, 12194–12201. [Google Scholar] [CrossRef]
- Khalfaoui, N.; Stoquert, J.P.; Haas, F.; Trautmann, C.; Meftah, A.; Toulemonde, M. Damage creation threshold of Al2O3 under swift heavy ion irradiation. Nucl. Instrum. Methods B 2012, 286, 247–253. [Google Scholar] [CrossRef]
- O’Connell, J.H.; Rymzhanov, R.A.; Skuratov, V.A.; Volkov, A.E.; Kirilkin, N.S. Latent tracks and associated strain in Al2O3 irradiated with swift heavy ions. Nucl. Instrum. Methods B 2016, 374, 97–101. [Google Scholar] [CrossRef]
- Zinkle, S.J.; Skuratov, V.A.; Hoelzer, D.T. On the conflicting roles of ionizing radiation in ceramics. Nucl. Instrum. Methods B 2002, 191, 758–766. [Google Scholar] [CrossRef]
- van Vuuren, A.J.; Ibrayeva, A.D.; Skuratov, V.A.; Zdorovets, M.V. Analysis of the microstructural evolution of silicon nitride irradiated with swift Xe ions. Ceram. Int. 2020, 46, 7155–7160. [Google Scholar] [CrossRef]
- Kitayama, T.; Morita, Y.; Nakajima, K.; Narumi, K.; Saitoh, Y.; Matsuda, M.; Sataka, M.; Tsujimoto, M.; Isoda, S.; Toulemonde, M.; et al. Formation of ion tracks in amorphous silicon nitride films with MeV C60 ions. Nucl. Instrum. Methods B 2015, 356–357, 22–27. [Google Scholar] [CrossRef]
- Mota-Santiago, P.; Vazquez, H.; Bierschenk, T.; Kremer, F.; Nadzri, A.; Schauries, D.; Djurabekova, F.; Nordlund, K.; Trautmann, C.; Mudie, S.; et al. Nanoscale density variations induced by high energy heavy ions in amorphous silicon nitride and silicon dioxide. Nanotechnology 2018, 29, 144004. [Google Scholar] [CrossRef] [PubMed]
- Kucheyev, S.O.; Timmers, H.; Zou, J.; Williams, J.S.; Jagadish, C.; Li, G. Lattice damage produced in GaN by swift heavy ions. J. Appl. Phys. 2004, 95, 5360–5365. [Google Scholar] [CrossRef]
- Mansouri, S.; Marie, P.; Dufour, C.; Nouet, G.; Monnet, I.; Lebius, H.; Benamara, Z.; Al-Douri, Y. Swift heavy ion effects in gallium nitride. Int. J. Nanoelectron. Mater. 2008, 1, 101–106. [Google Scholar]
- Sall, M.; Monnet, I.; Moisy, F.; Grygiel, C.; J.-Leclerc, S.; Della-Negra, S.; Toulemonde, M.; Balanzat, E. Track formation in III-N semiconductors irradiated by swift heavy ions and fullerene and re-evaluation of the inelastic thermal spike model. J. Mater. Sci. 2015, 50, 5214–5227. [Google Scholar] [CrossRef]
- Kamarou, A.; Wesch, W.; Wendler, E.; Undisz, A.; Rettenmayr, M. Swift heavy ion irradiation of InP: Thermal spike modeling of track formation. Phys. Rev. B 2006, 73, 184107. [Google Scholar] [CrossRef]
- Matsunami, N.; Sataka, M.; Okayasu, S.; Ishikawa, N.; Tazawa, M.; Kakiuchida, H. High-energy ion irradiation effects on atomic structures and optical properties of copper oxide and electronic sputtering. Nucl. Instrum. Methods B 2008, 266, 2986–2989. [Google Scholar] [CrossRef]
- Matsunami, N.; Fukuoka, O.; Tazawa, M.; Kakiuchida, H.; Sataka, M. Electronic structure modifications of cuprous-oxide films by ions. Surf. Coat. Technol. 2009, 203, 2642–2645. [Google Scholar] [CrossRef]
- Matsunami, N.; Kakiuchida, H.; Tazawa, M.; Sataka, M.; Sugai, H.; Okayasu, S. Electronic and atomic structure modifications of copper nitride films by ion impact and phase separation. Nucl. Instrum. Methods B 2009, 267, 2653–2656. [Google Scholar] [CrossRef]
- Joint Committee on Powder Diffraction Standards (JCPDS) 50667 (Cu2O) and 21156 (Cu3N).
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Storm, E.; Israel, H.I. Photon Cross Sections from 1 keV to 100 MeV for Elements Z = 1 to Z = 100. Nucl. Data Tables A 1970, 7, 565–681. [Google Scholar] [CrossRef]
- Matsunami, N.; Yajima, T.; Iwahara, H. Permeation of implanted deuterium through SrCeO3 (5% Yb). Nucl. Instrum. Methods B 1992, 65, 278–281. [Google Scholar] [CrossRef]
- Matsunami, N.; Sataka, M.; Okayasu, S.; Tsuchiya, B. Charge State Effect of High Energy Ions on Material Modification in the Electronic Stopping Region. Atoms 2021, 9, 36. [Google Scholar] [CrossRef]
- DuBois, R.D.; Santos, A.C.F.; Olson, R.E. Scaling laws for electron loss from ion beams. Nucl. Instrum. Methods A 2005, 544, 497–501. [Google Scholar] [CrossRef]
- DuBois, R.D.; Santos, A.C.F. Target-Scaling Properties for Electron Loss by Fast Heavy Ions. In Atomic Processes in Basic and Applied Physics; Shevelko, V., Tawara, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Chapter 8; pp. 185–209. [Google Scholar]
- Rodrigues, G.C.; Indelicato, P.; Santos, J.P.; Patte, P.; Parente, F. Systematic calculation of total atomic energies of ground state configurations. At. Data Nucl. Data Tables 2004, 86, 117–233. [Google Scholar] [CrossRef]
- Weber, W.J. Models and mechanisms of irradiation-induced amorphization in ceramics. Nucl. Instrum. Methods B 2000, 166–167, 98–106. [Google Scholar] [CrossRef]
- Chen, A.; Long, H.; Li, X.; Li, Y.; Yang, G.; Lu, P. Controlled growth and characteristics of single-phase Cu2O and CuO films by pulsed laser deposition. Vacuum 2009, 83, 927–930. [Google Scholar] [CrossRef]
- Wang, Y.; Miska, P.; Pilloud, D.; Horwat, D.; Mucklich, F.; Pierson, J.F. Transmittance enhancement and optical band gap widening of Cu2O thin films after air annealing. J. Appl. Phys. 2014, 115, 073505. [Google Scholar] [CrossRef]
- Meyer, B.K.; Polity, A.; Reppin, D.; Becker, M.; Hering, P.; Klar, P.J.; Sander, T.; Reindl, C.; Benz, J.; Eickhoff, M.; et al. Binary copper oxide semiconductors: From materials towards devices. Phys. Status Solidi B 2012, 249, 1487–1509. [Google Scholar] [CrossRef]
- Malerba, C.; Biccari, F.; Ricardo, C.L.A.; D’Incau, M.; Scardi, P.; Mittiga, A. Absorption coefficient of bulk and thin film Cu2O. Sol. Energy Mater. Sol. Cells 2011, 95, 2848–2854. [Google Scholar] [CrossRef]
- Matsunami, N.; Itoh, M.; Kato, M.; Okayasu, S.; Sataka, M.; Kakiuchida, H. Ion induced modifications of Mn-doped ZnO films. Nucl. Instrum. Methods B 2015, 365, 191–195. [Google Scholar] [CrossRef]
- Matsunami, N.; Yamamura, Y.; Itikawa, Y.; Itoh, N.; Kazumata, Y.; Miyagawa, S.; Morita, K.; Shimizu, R.; Tawara, H. Energy Dependence of the Ion-Induced Sputering Yields of Monatomic Solids. Atom. Data Nucl. Data Tables 1984, 31, 1–80. [Google Scholar] [CrossRef]
- Matsunami, N.; Ohno, N.; Tokitani, M.; Tsuchiya, B.; Sataka, M.; Okayasu, S. Modifications of WNOx films by keV D and H ions. Surf. Coat. Technol. 2020, 394, 125798. [Google Scholar] [CrossRef]
- Pierson, J.F. Structure and properties of copper nitride films formed by reactive magnetron sputtering. Vacuum 2002, 66, 59–64. [Google Scholar] [CrossRef]
- Borsa, D.M.; Boerma, D.O. Growth, structural and optical properties of Cu3N films. Surf. Sci. 2004, 548, 95–105. [Google Scholar] [CrossRef]



| Ion | E (MeV) | IP (eV) | Neff | σ1L (10−16 cm2) | LEQ (Cu2O) (nm) | LEQ (Cu3N) (nm) |
|---|---|---|---|---|---|---|
| 58Ni+10 | 90 | 321 | 8 | 0.358(Cu) | 4.6 | 4.6 |
| 0.152(O) | ||||||
| 0.139(N) | ||||||
| 136Xe+14 | 100 | 343 | 12 | 0.376(Cu) | 4.4 | 4.4 |
| 0.159(O) | ||||||
| 0.146(N) | ||||||
| 136Xe+14 | 200 | 343 | 12 | 0.392(Cu) | 4.2 | 4.2 |
| 0.166(O) | ||||||
| 0.152(N) |
| Ion | E (MeV) | YXD (10−15 cm2) | YSP | E* (MeV) | Se* (keV/nm) | Sn* (keV/nm) | ∆Se* (%) |
|---|---|---|---|---|---|---|---|
| 136Xe | 200 | 73 | 98.8 | 198 | 27.55 (27.59) | 0.115 | −0.24 |
| 136Xe | 100 | 48 | 73.8 | 99 | 20.95 (21.61) | 0.202 | −0.62 |
| 58Ni | 90 | 16.5 | 56 | 89 | 15.12 (13.98) | 0.0318 | +0.026 |
| 40Ar | 60 | 33 | 60 | 8.52 (8.45) | 0.014 | 0 |
| Ion | E (keV) | L (nm) | Rp (nm) | <Sn> (keV/nm) | <Se> (keV/nm) | YXD (10−16 cm2) | FR (%) | Sn (keV/nm) | Se (keV/nm) | YSP |
|---|---|---|---|---|---|---|---|---|---|---|
| N | 100 | 76 | 152 | 0.16 | 0.38 | 0.196 | 11 | 0.108 | 0.43 | 0.9 |
| Ne | 100 | 99 | 118 | 0.37 | 0.29 | 0.525 | 34 | 0.251 | 0.408 | 1.87 |
| Ion | E (MeV) | YXD (10−15 cm2) | YSP | E* (MeV) | Se* (keV/nm) | Sn* (keV/nm) | ∆Se* (%) |
|---|---|---|---|---|---|---|---|
| 136Xe | 200 | 116 | 960 | 198 | 27.37 (27.71) | 0.116 | −0.24 |
| 136Xe | 100 | 72 | 556 | 99 | 20.74 (21.64) | 0.204 | −0.62 |
| 58Ni | 90 | 38.5 | 342 | 89 | 15.03 (14.04) | 0.0321 | +0.02 |
| 40Ar | 60 | 142 | 60 | 8.47 (8.49) | 0.0142 | 0 |
| Ion | E (keV) | L (nm) | Rp (nm) | <Sn> (keV/nm) | <Se> (keV/ nm) | YXD (10−15 cm2) | FR (%) | Sn (keV/ nm) | Se (keV/ nm) | YSP |
|---|---|---|---|---|---|---|---|---|---|---|
| N | 100 | 88 | 150 | 0.165 | 0.381 | 2.2 | 17 | 0.106 | 0.363 | 3.2 |
| Ne | 100 | 88 | 116 | 0.363 | 0.303 | 5.4 | 28 | 0.236 | 0.289 | 7.6 |
| Sample | YXD/Se (10−16 cm2) (keV/nm)−1 | YXD/Sn | RXD | Ysp/Se | Ysp/Sn | Rsp |
|---|---|---|---|---|---|---|
| Cu2O | 0.124 (15) | 1.3 | 0.095 | 3.67 | 7.9 | 0.46 |
| 0.256 (25) | 0.20 | |||||
| Cu3N | 26 (15) | 140 | 0.19 | 23 (15) | 31 | 0.7 |
| 38 (25) | 0.27 | 32 (25) | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsunami, N.; Sataka, M.; Okayasu, S.; Tsuchiya, B. Modification of Cu Oxide and Cu Nitride Films by Energetic Ion Impact. Quantum Beam Sci. 2024, 8, 12. https://doi.org/10.3390/qubs8020012
Matsunami N, Sataka M, Okayasu S, Tsuchiya B. Modification of Cu Oxide and Cu Nitride Films by Energetic Ion Impact. Quantum Beam Science. 2024; 8(2):12. https://doi.org/10.3390/qubs8020012
Chicago/Turabian StyleMatsunami, Noriaki, Masao Sataka, Satoru Okayasu, and Bun Tsuchiya. 2024. "Modification of Cu Oxide and Cu Nitride Films by Energetic Ion Impact" Quantum Beam Science 8, no. 2: 12. https://doi.org/10.3390/qubs8020012
APA StyleMatsunami, N., Sataka, M., Okayasu, S., & Tsuchiya, B. (2024). Modification of Cu Oxide and Cu Nitride Films by Energetic Ion Impact. Quantum Beam Science, 8(2), 12. https://doi.org/10.3390/qubs8020012






