High-Transmission Neutron Optical Devices Utilizing Micro-Machined Structures
Abstract
1. Introduction
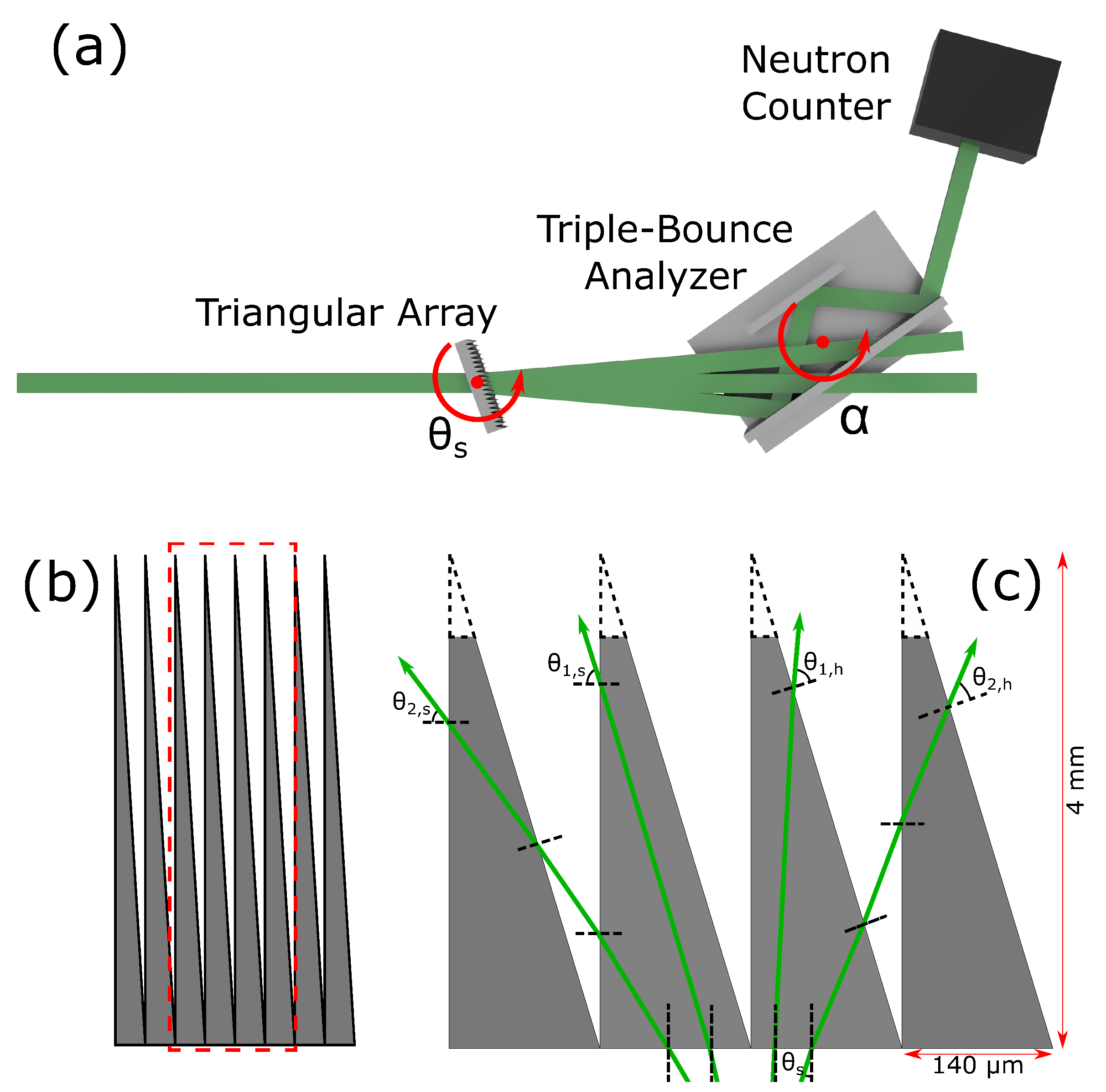
2. Materials and Methods
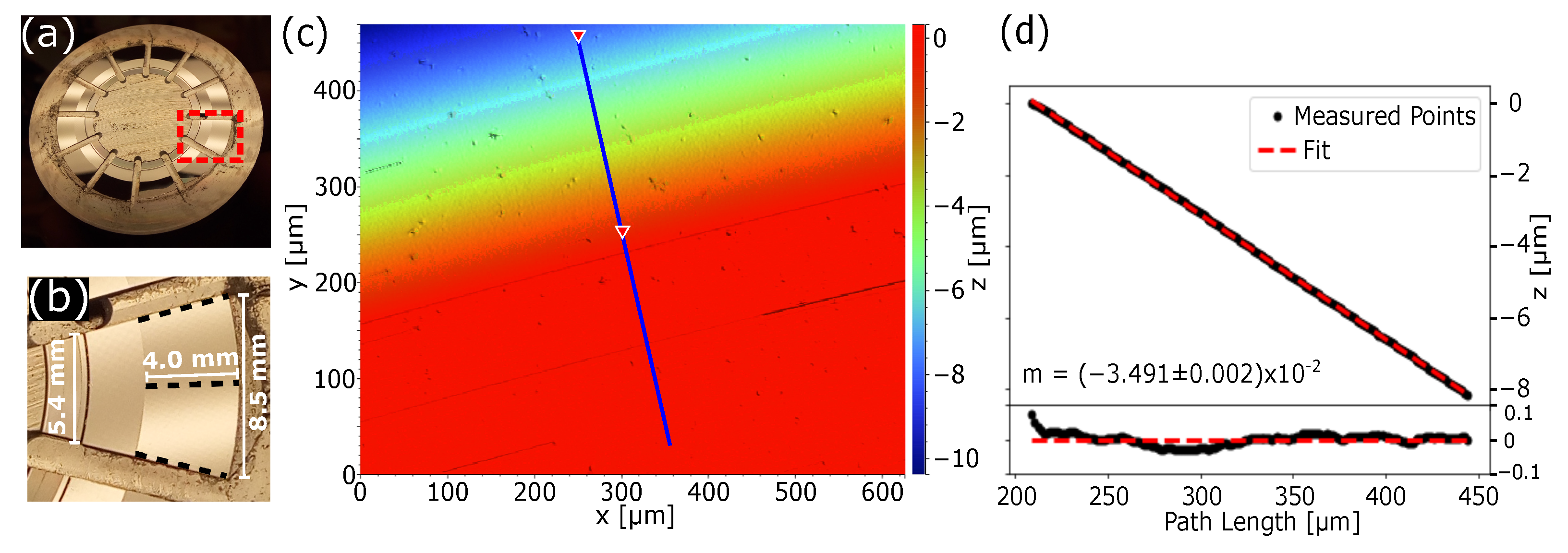
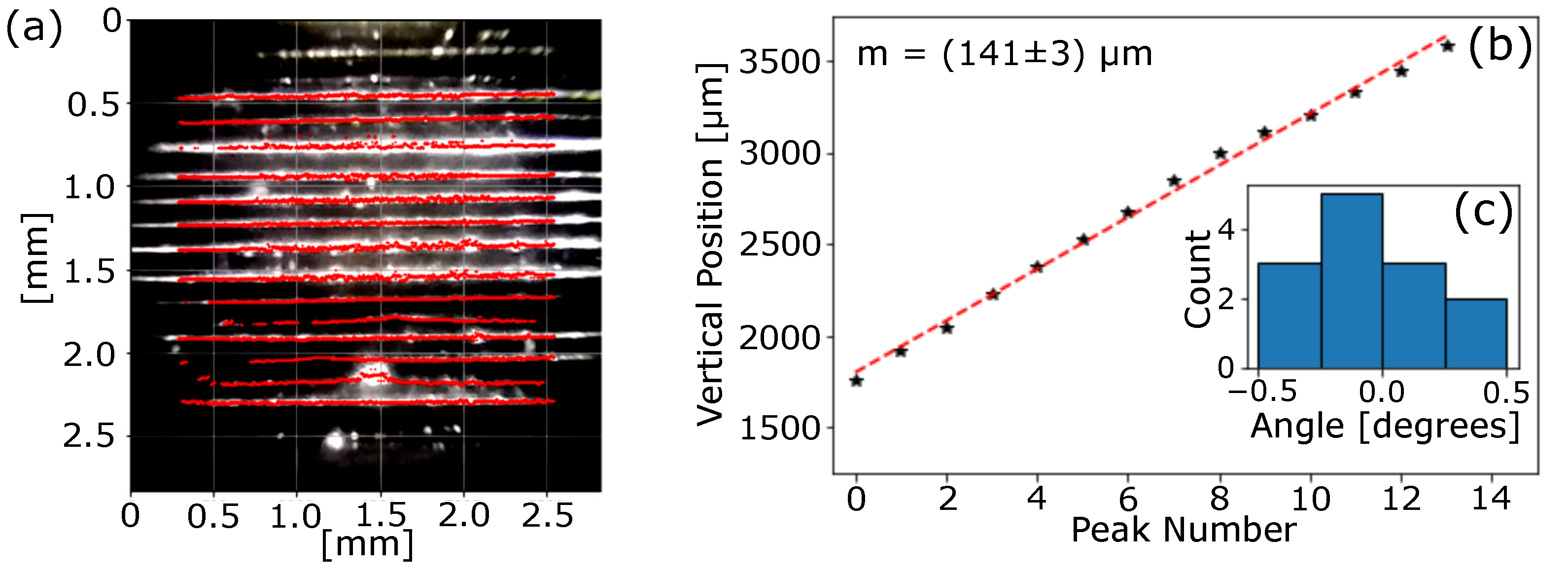
2.1. Micro-Prism Fabrication
2.2. Device Modelling
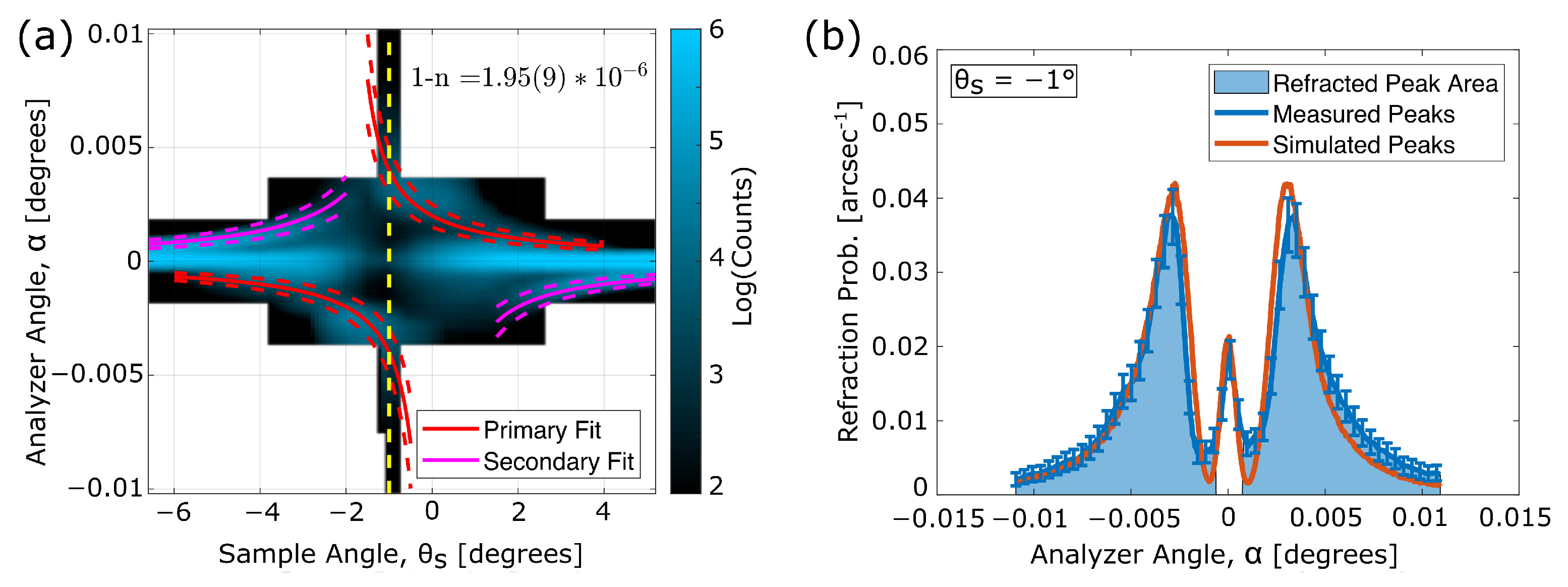
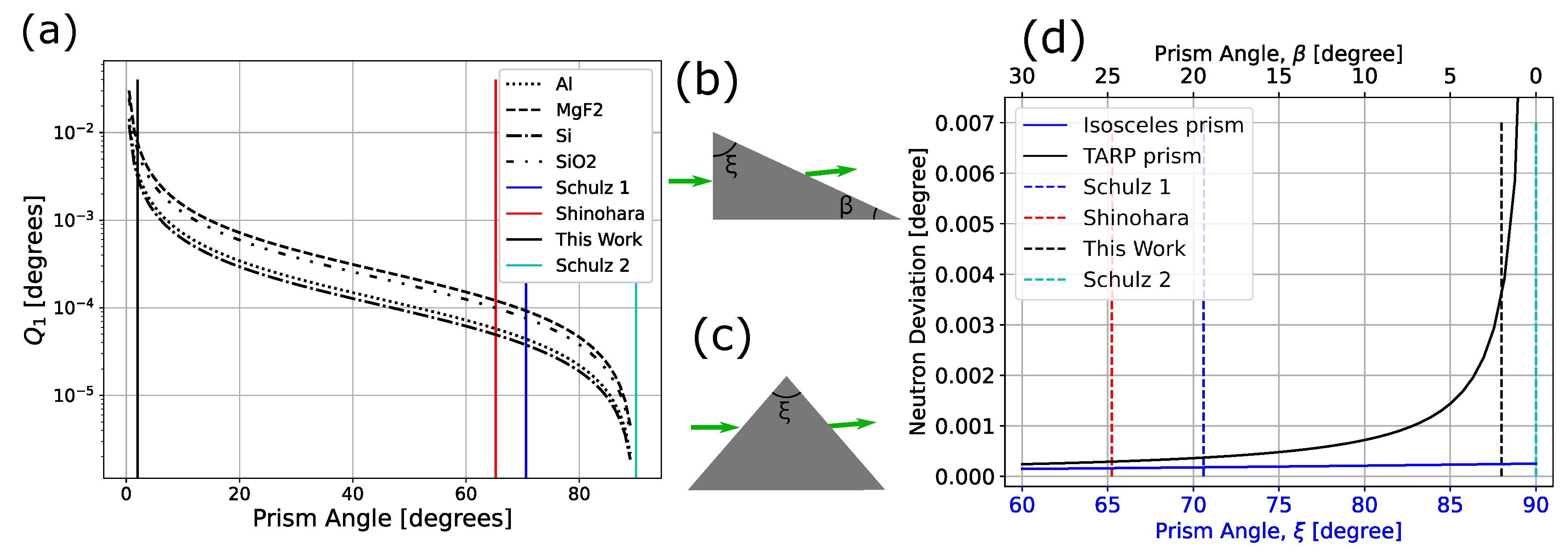
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| SANS | Small angle neutron scattering |
| CRL | Compound refractive lens |
| TARP | Triangular array refractive prism |
| USANS | Ultra-small angle neutron scattering |
| OD | Outer diameter |
| ID | Inner diameter |
| Ra | Roughness average |
References
- Werner, H.R.S. Neutron Interferometry: Lessons in Experimental Quantum Mechanics. Meas. Sci. Technol. 2001, 12, 355. [Google Scholar] [CrossRef]
- Cronin, A.D.; Schmiedmayer, J.; Pritchard, D.E. Optics and interferometry with atoms and molecules. Rev. Mod. Phys. 2009, 81, 1051–1129. [Google Scholar] [CrossRef]
- Eskildsen, M.R.; Gammel, P.L.; Isaacs, E.D.; Detlefs, C.; Mortensen, K.; Bishop, D.J. Compound refractive optics for the imaging and focusing of low-energy neutrons. Nature 1998, 391, 563–566. [Google Scholar] [CrossRef]
- Beguiristain, H.R.; Anderson, I.S.; Dewhurst, C.D.; Piestrup, M.A.; Cremer, J.T.; Pantell, R.H. A simple neutron microscope using a compound refractive lens. Appl. Phys. Lett. 2002, 81, 4290–4292. [Google Scholar] [CrossRef]
- Gary, C.K. Compound Refractive Lenses for Thermal Neutron Applications; Technical Report; Chicago Operations Office: Argonne, IL, USA, 2013. [Google Scholar] [CrossRef]
- Oku, T.; Shimizu, H.M. Neutron lens and prism. Phys. Condens. Matter 2000, 283, 314–317. [Google Scholar] [CrossRef]
- Oku, T.; Iwase, H.; Shinohara, T.; Yamada, S.; Hirota, K.; Koizumi, S.; Suzuki, J.I.; Hashimoto, T.; Shimizu, H.M. A focusing-geometry small-angle neutron scattering instrument with a magnetic neutron lens. Appl. Crystallogr. 2007, 40, s408–s413. [Google Scholar] [CrossRef]
- Shimizu, H.M.; Suda, Y.; Oku, T.; Nakagawa, H.; Kato, H.; Kamiyama, T.; Otani, C.; Sato, H.; Wakabayashi, T.; Kiyanagi, Y. Measurement of cold neutron-beam focusing effect of a permanent sextupole magnet. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 1999, 430, 423–434. [Google Scholar] [CrossRef]
- Shimizu, H.M.; Kato, H.; Oku, T.; Suda, Y.; Ogawa, Y.; Iwasa, H.; Kamiyama, T.; Kiyanagi, Y.; Wakabayashi, T. Cold neutron beam control using magnetic field gradient. Phys. Condens. Matter 1997, 241–243, 172–174. [Google Scholar] [CrossRef]
- Shimizu, H.M.; Oku, T.; Sato, H.; Otani, C.; Kato, H.; Suda, Y.; Nakagawa, H.; Kamiyama, T.; Kiyanagi, Y.; Wakabayashi, T. Magnetic neutron lens. Phys. Condens. Matter 2000, 276–278, 63–64. [Google Scholar] [CrossRef]
- Shimizu, H.M. Development of neutron optical devices. Appl. Phys. Mater. Sci. Process. 2002, 74, 123–129. [Google Scholar] [CrossRef]
- Cremer, J.T., Jr.; Filter, H.; Klepp, J.; Geltenbort, P.; Dewhurst, C.; Oda, T.; Pantell, R.H. Focusing and imaging of cold neutrons with a permanent magnetic lens. Rev. Sci. Instrum. 2020, 91, 013704. [Google Scholar] [CrossRef] [PubMed]
- Littrell, K.C.; Te Velthuis, S.G.; Felcher, G.P.; Park, S.; Kirby, B.J.; Fitzsimmons, M.R. Magnetic compound refractive lens for focusing and polarizing cold neutron beams. Rev. Sci. Instrum. 2007, 78, 035101. [Google Scholar] [CrossRef] [PubMed]
- Arzumanov, S.S.; Govor, L.I.; Morozov, V.I.; Panin, Y.N.; Strepetov, A.N. A convergent neutron lens based on glass capillaries. Instrum. Exp. Tech. 2016, 59, 650–652. [Google Scholar] [CrossRef]
- Kumakhov, M.A.; Sharov, V.A. A neutron lens. Nature 1992, 357, 390–391. [Google Scholar] [CrossRef]
- Wu, H.; Khaykovich, B.; Wang, X.; Hussey, D.S. Wolter Mirrors for Neutron Imaging. In Proceedings of the Physics Procedia, Cochin, India, 22–24 August 2017; Elsevier: Amsterdam, The Netherlands, 2017; Volume 88, pp. 184–189. [Google Scholar] [CrossRef]
- Oku, T.; Morita, S.; Moriyasu, S.; Yamagata, Y.; Ohmori, H.; Takizawa, Y.; Shimizu, H.M.; Hirota, T.; Kiyanagi, Y.; Ino, T.; et al. Development of a Fresnel lens for cold neutrons based on neutron refractive optics. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2001, 462, 435–441. [Google Scholar] [CrossRef]
- Sarenac, D.; Nsofini, J.; Hincks, I.; Arif, M.; Clark, C.W.; Cory, D.; Huber, M.; Pushin, D. Methods for preparation and detection of neutron spin-orbit states. New J. Phys. 2018, 20, 103012. [Google Scholar] [CrossRef] [PubMed]
- Nsofini, J.; Sarenac, D.; Wood, C.J.; Cory, D.G.; Arif, M.; Clark, C.W.; Huber, M.G.; Pushin, D.A. Spin-orbit states of neutron wave packets. Phys. Rev. 2016, 94, 013605. [Google Scholar] [CrossRef]
- Sarenac, D.; Kapahi, C.; Chen, W.; Clark, C.W.; Cory, D.G.; Huber, M.G.; Taminiau, I.; Zhernenkov, K.; Pushin, D.A. Generation and detection of spin-orbit coupled neutron beams. Proc. Natl. Acad. Sci. USA 2019, 116, 20328–20332. [Google Scholar] [CrossRef]
- Sarenac, D.; Henderson, M.E.; Ekinci, H.; Clark, C.W.; Cory, D.G.; DeBeer-Schmitt, L.; Huber, M.G.; Kapahi, C.; Pushin, D.A. Experimental realization of neutron helical waves. Sci. Adv. 2022, 8, eadd2002. [Google Scholar] [CrossRef]
- Kardjilov, N.; Manke, I.; Strobl, M.; Hilger, A.; Treimer, W.; Meissner, M.; Krist, T.; Banhart, J. Three-dimensional imaging of magnetic fields with polarized neutrons. Nat. Phys. 2008, 4, 399–403. [Google Scholar] [CrossRef]
- Jericha, E.; Szeywerth, R.; Leeb, H.; Badurek, G. Reconstruction techniques for tensorial neutron tomography. Phys. Condens. Matter 2007, 397, 159–161. [Google Scholar] [CrossRef]
- Kageyama, M.; Tasaki, S.; Hino, M.; Ebisawa, T.; Yamazaki, D.; Hayashida, H.; Abe, Y. Development of neutron spin phase contrast imaging. Phys. Condens. Matter 2009, 404, 2615–2619. [Google Scholar] [CrossRef]
- Pushin, D.A.; Huber, M.G.; Arif, M.; Shahi, C.B.; Nsofini, J.; Wood, C.J.; Sarenac, D.; Cory, D.G. Neutron Interferometry at the National Institute of Standards and Technology. Adv. High Energy Phys. 2015, 2015, 1–7. [Google Scholar] [CrossRef]
- Sarenac, D.; Huber, M.G.; Heacock, B.; Arif, M.; Clark, C.W.; Cory, D.G.; Shahi, C.B.; Pushin, D.A. Holography with a neutron interferometer. Opt. Express 2016, 24, 22528. [Google Scholar] [CrossRef]
- Lemmel, H.; Brax, P.; Ivanov, A.N.; Jenke, T.; Pignol, G.; Pitschmann, M.; Potocar, T.; Wellenzohn, M.; Zawisky, M.; Abele, H. Neutron interferometry constrains dark energy chameleon fields. Phys. Lett. Sect. Nucl. Elem. Part. High-Energy Phys. 2015, 743, 310–314. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Loidl, R.; Badurek, G.; Baron, M.; Rauch, H. Violation of a Bell-like inequality in single-neutron interferometry. Nature 2003, 425, 45–48. [Google Scholar] [CrossRef]
- Bartosik, H.; Klepp, J.; Schmitzer, C.; Sponar, S.; Cabello, A.; Rauch, H.; Hasegawa, Y. Experimental test of quantum contextuality in neutron interferometry. Phys. Rev. Lett. 2009, 103, 040403. [Google Scholar] [CrossRef] [PubMed]
- Sarenac, D.; Pushin, D.A.; Huber, M.G.; Hussey, D.S.; Miao, H.; Arif, M.; Cory, D.G.; Cronin, A.D.; Heacock, B.; Jacobson, D.L.; et al. Three Phase-Grating Moiré Neutron Interferometer for Large Interferometer Area Applications. Phys. Rev. Lett. 2018, 120, 113201. [Google Scholar] [CrossRef] [PubMed]
- Pushin, D.A.; Sarenac, D.; Hussey, D.S.; Miao, H.; Arif, M.; Cory, D.G.; Huber, M.G.; Jacobson, D.L.; LaManna, J.M.; Parker, J.D.; et al. Far-field interference of a neutron white beam and the applications to noninvasive phase-contrast imaging. Phys. Rev. 2017, 95, 043637. [Google Scholar] [CrossRef]
- Heacock, B.; Sarenac, D.; Cory, D.G.; Huber, M.G.; Hussey, D.S.; Kapahi, C.; Miao, H.; Wen, H.; Pushin, D.A. Angular alignment and fidelity of neutron phase-gratings for improved interferometer fringe visibility. AIP Adv. 2019, 9, 085115. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Grünzweig, C.; Bunk, O.; Frei, G.; Lehmann, E.; David, C. Neutron phase imaging and tomography. Phys. Rev. Lett. 2006, 96, 215505. [Google Scholar] [CrossRef] [PubMed]
- Maier-Leibnitz, H.; Springer, T. Ein interferometer für langsame neutronen. Z. Phys. 1962, 167, 386–402. [Google Scholar] [CrossRef]
- Rauch, H.; Treimer, W.; Bonse, U. Test of a single crystal neutron interferometer. Phys. Lett. 1974, 47, 369–371. [Google Scholar] [CrossRef]
- Rauch, H.; Zeilinger, A.; Badurek, G.; Wilfing, A.; Bauspiess, W.; Bonse, U. Verification of coherent spinor rotation of fermions. Phys. Lett. 1975, 54, 425–427. [Google Scholar] [CrossRef]
- Werner, S.; Kaiser, H.; Arif, M.; Clothier, R. Neutron interference induced by gravity: New results and interpretations. Phys. B C 1988, 151, 22–35. [Google Scholar] [CrossRef]
- Clark, C.W.; Barankov, R.; Huber, M.G.; Arif, M.; Cory, D.G.; Pushin, D.A. Controlling neutron orbital angular momentum. Nature 2015, 525, 504–506. [Google Scholar] [CrossRef]
- Li, K.; Arif, M.; Cory, D.G.; Haun, R.; Heacock, B.; Huber, M.G.; Nsofini, J.; Pushin, D.A.; Saggu, P.; Sarenac, D.; et al. Neutron limit on the strongly-coupled chameleon field. Phys. Rev. 2016, 93, 062001. [Google Scholar] [CrossRef]
- Denkmayr, T.; Geppert, H.; Sponar, S.; Lemmel, H.; Matzkin, A.; Tollaksen, J.; Hasegawa, Y. Observation of a quantum Cheshire Cat in a matter-wave interferometer experiment. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Arif, M.; Brown, D.E.; Greene, G.L.; Clothier, R.; Littrell, K. Multistage position-stabilized vibration isolation system for neutron interferometry. In Proceedings of the Vibration Monitoring and Control. International Society for Optics and Photonics, San Diego, CA, USA, 28–29 July 1994; Volume 2264, pp. 20–26. [Google Scholar]
- Saggu, P.; Mineeva, T.; Arif, M.; Cory, D.G.; Haun, R.; Heacock, B.; Huber, M.G.; Li, K.; Nsofini, J.; Sarenac, D.; et al. Decoupling of a neutron interferometer from temperature gradients. Rev. Sci. Instrum. 2016, 87, 123507. [Google Scholar] [CrossRef]
- Shahi, C.; Arif, M.; Cory, D.; Mineeva, T.; Nsofini, J.; Sarenac, D.; Williams, C.; Huber, M.; Pushin, D. A new polarized neutron interferometry facility at the NCNR. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2016, 813, 111–122. [Google Scholar] [CrossRef]
- Zawisky, M.; Springer, J.; Farthofer, R.; Kuetgens, U. A large-area perfect crystal neutron interferometer optimized for coherent beam-deflection experiments: Preparation and performance. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2010, 612, 338–344. [Google Scholar] [CrossRef]
- Barker, J.G.; Glinka, C.J.; Moyer, J.J.; Kim, M.H.; Drews, A.R.; Agamalian, M. Design and performance of a thermal-neutron double-crystal diffractometer for USANS at NIST. J. Appl. Crystallogr. 2005, 38, 1004–1011. [Google Scholar] [CrossRef]
- Certain trade names and company products are mentioned in the text or identified in an illustration in order to adequately specify the experimental procedure and equipment used. In no case does such identification imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products are necessarily the best available for the purpose.
- Wagh, A.G.; Rakhecha, V.C. Geometric formula for prism deflection. Pramana 2004, 63, 381–385. [Google Scholar] [CrossRef]
- Schulz, J.; Ott, F.; Hülsen, C.; Krist, T. Neutron energy analysis by silicon prisms. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrom. Detect. Assoc. Equip. 2013, 729, 334–337. [Google Scholar] [CrossRef]
- Shinohara, T.; Hirota, K.; Adachi, T.; Ikeda, K.; Shimizu, H.M.; Suzuki, J.I.; Oku, T. Thermal neutron refraction by material prism. Phys. Condens. Matter 2006, 385, 1232–1235. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapahi, C.; Sarenac, D.; Bleuel, M.; Cory, D.G.; Heacock, B.; Henderson, M.E.; Huber, M.G.; Taminiau, I.; Pushin, D. High-Transmission Neutron Optical Devices Utilizing Micro-Machined Structures. Quantum Beam Sci. 2023, 7, 10. https://doi.org/10.3390/qubs7010010
Kapahi C, Sarenac D, Bleuel M, Cory DG, Heacock B, Henderson ME, Huber MG, Taminiau I, Pushin D. High-Transmission Neutron Optical Devices Utilizing Micro-Machined Structures. Quantum Beam Science. 2023; 7(1):10. https://doi.org/10.3390/qubs7010010
Chicago/Turabian StyleKapahi, Connor, Dusan Sarenac, Markus Bleuel, David G. Cory, Benjamin Heacock, Melissa E. Henderson, Michael G. Huber, Ivar Taminiau, and Dmitry Pushin. 2023. "High-Transmission Neutron Optical Devices Utilizing Micro-Machined Structures" Quantum Beam Science 7, no. 1: 10. https://doi.org/10.3390/qubs7010010
APA StyleKapahi, C., Sarenac, D., Bleuel, M., Cory, D. G., Heacock, B., Henderson, M. E., Huber, M. G., Taminiau, I., & Pushin, D. (2023). High-Transmission Neutron Optical Devices Utilizing Micro-Machined Structures. Quantum Beam Science, 7(1), 10. https://doi.org/10.3390/qubs7010010





