Analysis of Ion-Irradiation Induced Lattice Expansion and Ferromagnetic State in CeO2 by Using Poisson Distribution Function
Abstract
1. Introduction
2. Experimental Procedure
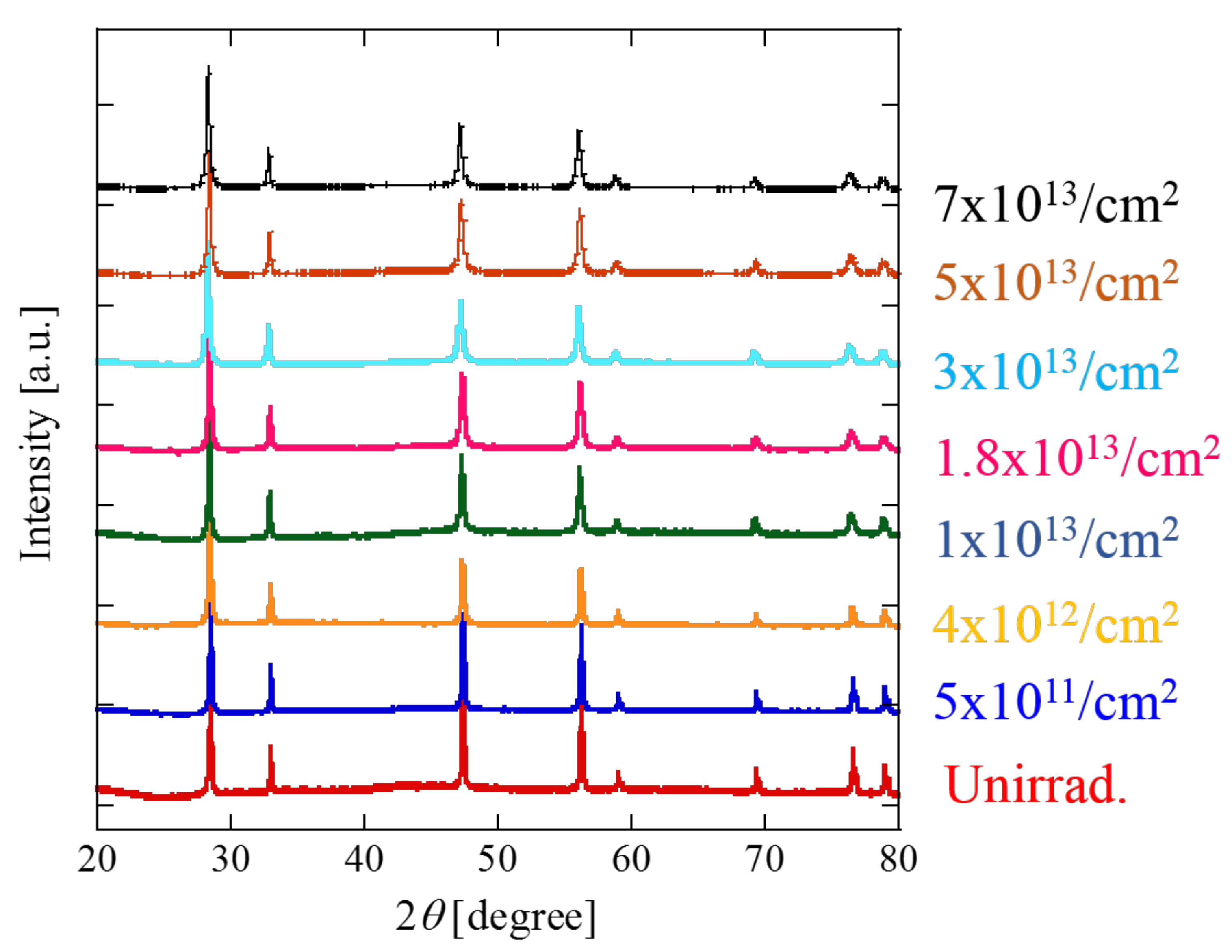
3. Experimental Results
4. Data Analysis
4.1. Binomial Distribution Function and Poisson Distribution Function for the Expression of Track-Overlapping
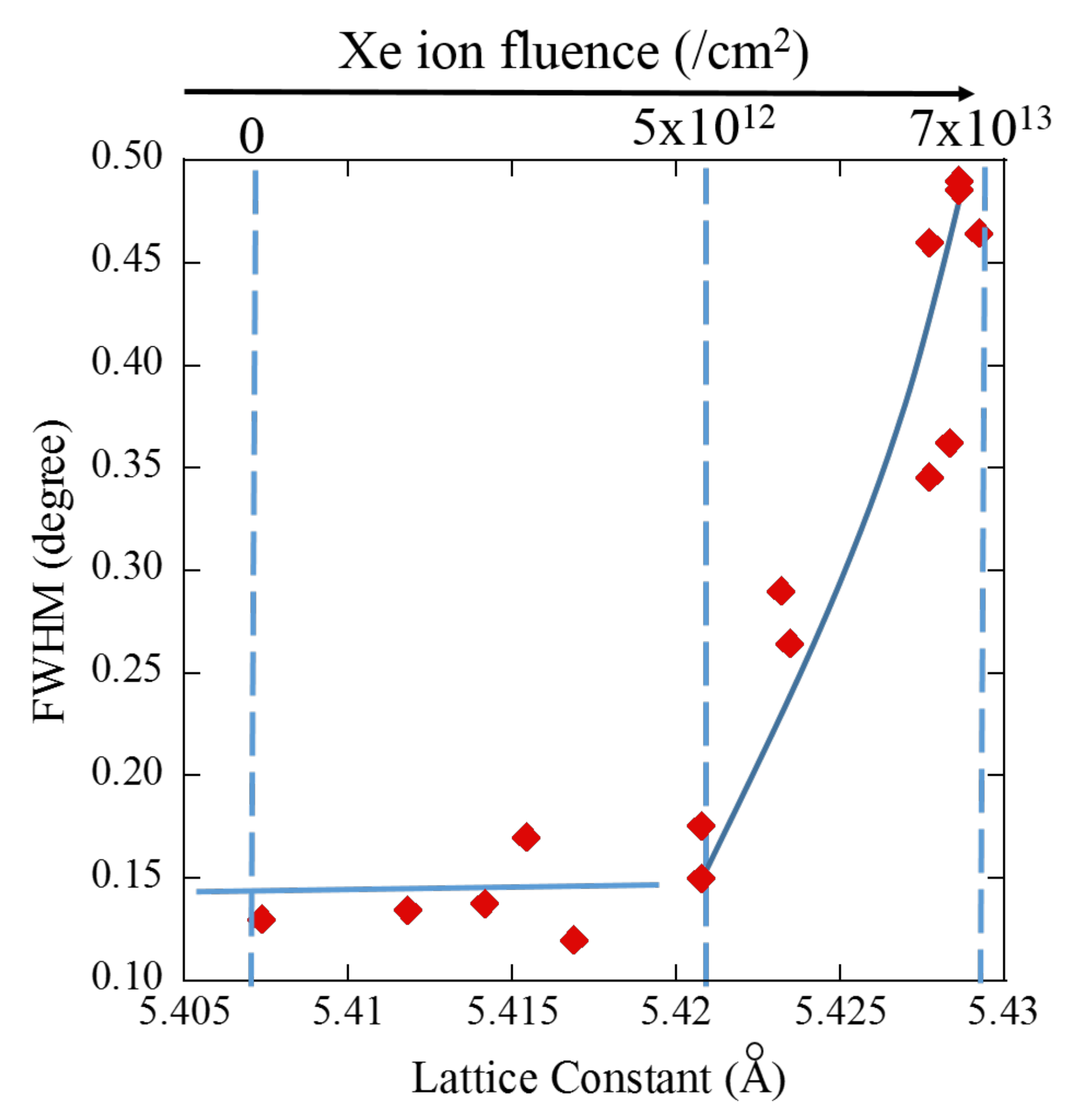
4.2. Analysis of Ion Fluence Dependence of a Lattice Constant for CeO2 by using the Poisson Law
4.3. Analysis of Ion Fluence Dependence of Saturation Magnetization for CeO2 by Using the Poisson Distribution Function
5. Discussion
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shimizu, K.; Kosugi, S.; Tahara, Y.; Yasunaga, K.; Kaneta, Y.; Ishikawa, N.; Hori, F.; Matsui, T.; Iwase, A. Change in magnetic properties induced by swift heavy ion irradiation in CeO2. Nucl. Istrum. Methods 2012, 286, 291–294. [Google Scholar] [CrossRef]
- Zhou, S.; Cizmar, E.; Potzger, K.; Krause, M.; Talut, G.; Helm, M.; Fassbender, J.; Zvyagin, S.A.; Wosnitza, J.; Schmidt, H. Origin of magnetic moments in defective TiO2 single crystals. Phys. Rev. B 2009, 79, 113201. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Venkatesan, M.; Stamenov, P.; Fitzgerald, C.B.; Dorneles, L.S. Magnetism in hafnium dioxide. Phys. Rev. B 2005, 72, 024450. [Google Scholar] [CrossRef]
- Fernandes, V.; Massanek, R.J.O.; Schio, P.; Klein, J.J.; de Oliveira, A.J.A.; Ortiz, W.A.; Mattoso, N.; Varalda, J.; Schreiner, W.H.; Abbate, M.; et al. Dilute-Defect magnetism: Origin of magnetism in nanocrystalline CeO2. Phys. Rev. B 2009, 80, 035202. [Google Scholar] [CrossRef]
- Fernandes, V.; Schio, P.; de Oliveira, A.J.A.; Ortiz, W.A.; Fichtner, P.; Amaral, L.; Graff, I.L.; Varalda, J.; Mattoso, N.; Schreiner, W.H.; et al. Ferromagnetism induced by oxygen and cerium vacancies above the percolation limit in CeO2. J. Phys. Condens. Matter 2010, 22, 216004. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.-Y.; Zhang, H.-W.; Song, Y.-Q.; Yang, Q.-H.; Zhu, H.; Xiao, J.Q. Room-Temperature ferromagnetism in pure and Co doped CeO2 powders. J. Phys. Condens. Matter 2007, 19, 246205. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Lockman, Z.; Aziz, A.; MacManus-Driscoll, J. Size dependent ferromagnetism in cerium oxide (CeO2) nanostructures independent of oxygen vacancies. J. Phys. Condens. Matter 2008, 20, 165201. [Google Scholar] [CrossRef]
- Takaki, S.; Yasuda, K.; Yamamoto, T.; Matsumura, S.; Ishikawa, N. Atomic structure of ion tracks in Ceria. Nucl. Instrum. Methods 2014, 326, 140–144. [Google Scholar] [CrossRef]
- Takaki, S.; Yasuda, K.; Yamamoto, T.; Matsumura, S.; Ishikawa, N. Structure of ion tracks in ceria irradiated with high energy xenon ions. Prog. Nucl. Energy 2016, 92, 306–312. [Google Scholar] [CrossRef]
- Ziegler, J. SRIM—The Stopping and Range of Ions in Matter. Available online: http://www/srim.org/ (accessed on 1 June 2020).
- Benyagoub, A.; Couvreur, F.; Bouffard, S.; Levesque, F.; Dufour, C.; Paumier, E. Phase transformation induced in pure zirconia by high energy heavy ion irradiation. Nucl. Instrum. Methods 2001, 175–177, 417–421. [Google Scholar] [CrossRef]
- Ishikawa, N.; Ohhara, K.; Ohta, Y.; Michikami, O. Binomial distribution function for intuitive understanding of fluence dependence of non-amorphized ion-track area. Nucl. Instrum. Methods 2010, 268, 3273–3276. [Google Scholar] [CrossRef]
- Szenes, G.; Havancsak, K.; Skuratov, V.; Hanak, P.; Zsoldos, L.; Ungar, T. Application of the thermal spike model to latent tracks induced in polymers. Nucl. Instrum. Methods 2000, 166–167, 933–937. [Google Scholar] [CrossRef]
- Chailley, V.; Dooryhee, E.; Bouffard, S.; Balanzat, E.; Levalois, M. Observations by X-ray diffraction of structural changes in mica irradiated by swift heavy ions. Nucl. Instrum. Methods 1994, 91, 162–167. [Google Scholar] [CrossRef]
- Ishikawa, N.; Yamamoto, S.; Chimi, Y. Structural changes in anatase TiO2 thin films irradiated with high-energy heavy ions. Nucl. Instrum. Methods 2006, 250, 250–253. [Google Scholar] [CrossRef]
- Schwab, R.G.; Steiner, R.A.; Mages, G.; Beie, H.-J. Properties of CeO2 and CeO2-x films Part II. High temperature properties. Thin Solid Films 1992, 207, 288–293. [Google Scholar] [CrossRef]
- Sasajima, Y.; Ajima, N.; Osada, T.; Ishikawa, N.; Iwase, A. Molecular dynamics simulation of fast particle irradiation on the single crystal CeO2. Nucl. Instrum. Methods 2013, 314, 202–207. [Google Scholar] [CrossRef]
- Ohno, H.; Iwase, A.; Matsumura, D.; Nishihata, Y.; Mizuki, J.; Ishikawa, N.; Baba, Y.; Hirao, N.; Sonoda, T.; Kinoshita, M. Study on effects of swift heavy ion irradiation in cerium dioxide using synchrotron radiation X-ray absorption spectroscopy. Nucl. Instrum. Methods 2008, 266, 3013–3017. [Google Scholar] [CrossRef]
- Iwase, A.; Ohno, H.; Ishikawa, N.; Baba, Y.; Hirao, N.; Sonoda, T.; Kinoshita, M. Study on the behavior of oxygen atoms in swift heavy ion irradiated CeO2 by means of synchrotron radiation X-ray photoelectron spectroscopy. Nucl. Instrum. Methods 2009, 267, 969–972. [Google Scholar] [CrossRef]
- Iwasawa, M.; Ohmura, T.; Chen, Y.; Kaneta, Y.; Geng, H.Y.; Iwase, A.; Kinoshita, M. First-Principles study on cerium ion behavior in irradiated cerium dioxide. J. Nucl. Mater. 2009, 393, 321–327. [Google Scholar] [CrossRef]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamamoto, Y.; Ishikawa, N.; Hori, F.; Iwase, A. Analysis of Ion-Irradiation Induced Lattice Expansion and Ferromagnetic State in CeO2 by Using Poisson Distribution Function. Quantum Beam Sci. 2020, 4, 26. https://doi.org/10.3390/qubs4030026
Yamamoto Y, Ishikawa N, Hori F, Iwase A. Analysis of Ion-Irradiation Induced Lattice Expansion and Ferromagnetic State in CeO2 by Using Poisson Distribution Function. Quantum Beam Science. 2020; 4(3):26. https://doi.org/10.3390/qubs4030026
Chicago/Turabian StyleYamamoto, Yuki, Norito Ishikawa, Fuminobu Hori, and Akihiro Iwase. 2020. "Analysis of Ion-Irradiation Induced Lattice Expansion and Ferromagnetic State in CeO2 by Using Poisson Distribution Function" Quantum Beam Science 4, no. 3: 26. https://doi.org/10.3390/qubs4030026
APA StyleYamamoto, Y., Ishikawa, N., Hori, F., & Iwase, A. (2020). Analysis of Ion-Irradiation Induced Lattice Expansion and Ferromagnetic State in CeO2 by Using Poisson Distribution Function. Quantum Beam Science, 4(3), 26. https://doi.org/10.3390/qubs4030026




