Ab Initio Molecular Dynamics Simulations to Interpret the Molecular Fragmentation Induced in Deoxyribose by Synchrotron Soft X-Rays

Abstract

It has been suggested that core ionization in DNA atoms could induce complex, irreparable damage. Synchrotron soft X-rays have been used to probe the damage induced by such events in thin films of DNA components. In a complementary approach, we investigate the fragmentation dynamics following a carbon or oxygen K-shell ionization in 2-deoxy-D-ribose (DR), a major component in the DNA chain. Core ionization of the sugars hydration layer is also studied. To that aim, we use state-of-the-art ab initio Density Functional Theory-based Molecular Dynamics (MD) simulations. The ultrafast dissociation dynamics of the core ionized molecule, prior Auger decay, is modeled for about 10 fs. We show that the core-ionization of oxygen atoms within DR or its hydration layer may induce proton transfers towards nearby molecules, before Auger decay. In a second step, we model an Auger effect occurring either at the beginning or at the end of the core–hole dynamics. Two electrons are removed from the deepest valence molecular orbitals localized on the initially core-ionized oxygen atom (O*), and this electronic state is propagated by means of Ehrenfest MD. We show an ultrafast dissociation of the DR²⁺ molecule C-O* bonds, which, in most cases, seems independent of the time at which Auger decay occurs.

1. Introduction

Ionizing radiations, such as hard X-rays, high-energy electrons, or swift ions, are used in cancer therapies to kill malignant cells. It has been suggested that inner-shell ionization in DNA constituent atoms could be partly responsible for cell death upon irradiation with heavy ions [1] or γ-rays [2]. Inner-shell ionizations are indeed particularly violent events. After a predissociation phase of a few femtoseconds, core holes in light atoms, such as carbon and oxygen, deexcite by ejecting an Auger electron with nearly 100% probability. Core ionization thus leads to the double ionization of the molecule and to the emission of two few hundred electronvolts electrons. In the sub-keV energy range, electrons have inelastic mean free paths of a few nanometers [3], and may thus induce clusters of ionizations in the vicinity of the core-ionized molecule. If taking place in DNA, or its hydration layer, inner-shell ionizations are thus expected to induce complex, irreparable, DNA damage [4]. DNA complex damage is critical for the cell because it can lead to important biological consequences such as chromosome aberrations, cell death, and cell conversion to malignancy [5,6,7,8].

Soft X-rays (0.1–5 keV) are particularly well adapted to investigate such events as they mainly interact through the removal of K-shell electrons as long as the photons energy is above the atoms K-shell binding energy (284 and 543 eV, for carbon and oxygen, respectively [9]). Soft X-rays are however poorly penetrating radiations, so that condensed phase experiments remain a challenge. Different setups have been designed to irradiate biological samples either with X-ray tubes [10] or at synchroton facilities (for a review see [11]). The latter offer the advantage that any photon energy may be selected, thus allowing to compare biological effects upon irradiation with photons below and above a particular K-edge. Various biological endpoints have been investigated, such as cellular inactivation, chromosome aberration, and damage to plasmid or cellular DNA (for a review see [11]).

Such studies provide an integrated response of the biological system to the initial core ionization event. Investigating specifically the molecular damage originating from a core ionization is however complicated in the condensed phase, because the photo- and Auger electrons induce many additional ionizations in the medium. Gas phase studies thus appear as a very elegant solution, as they allow selecting the primary ionization event thanks to coincidence measurements [12,13]. However, it has been shown that the environment of the target molecule might have a strong influence on its fragmentation pattern [14].

Ab Initio Molecular Dynamics (MD) simulations may help interpreting how a specific primary physical event affects a biomolecule, such as a DNA or RNA building block, embedded in liquid water. Such methods have been applied to model the ultrafast fragmentation induced by a core vacancy, before Auger decay [15,16,17]. The method allows to target different atomic sites in the biomolecule (direct effect) or the atoms of neighboring water molecules (indirect effect). In parallel, tools were developed in order to model the fragmentation of doubly ionized molecules [14,18,19]. Note that this method enables removal of the two electrons from any outer shell molecular orbital (MO) of the sample. In the present paper, we will show how these two different methods may be combined to help the interpretation of synchrotron irradiation experiments. We will focus on a deoxyribose (DR) molecule embedded in liquid water. The sugar is in its furanose conformation, which is the form it adopts in DNA.

2. Results

2.1. Ultrafast Dissociation of Core Ionized Deoxyribose

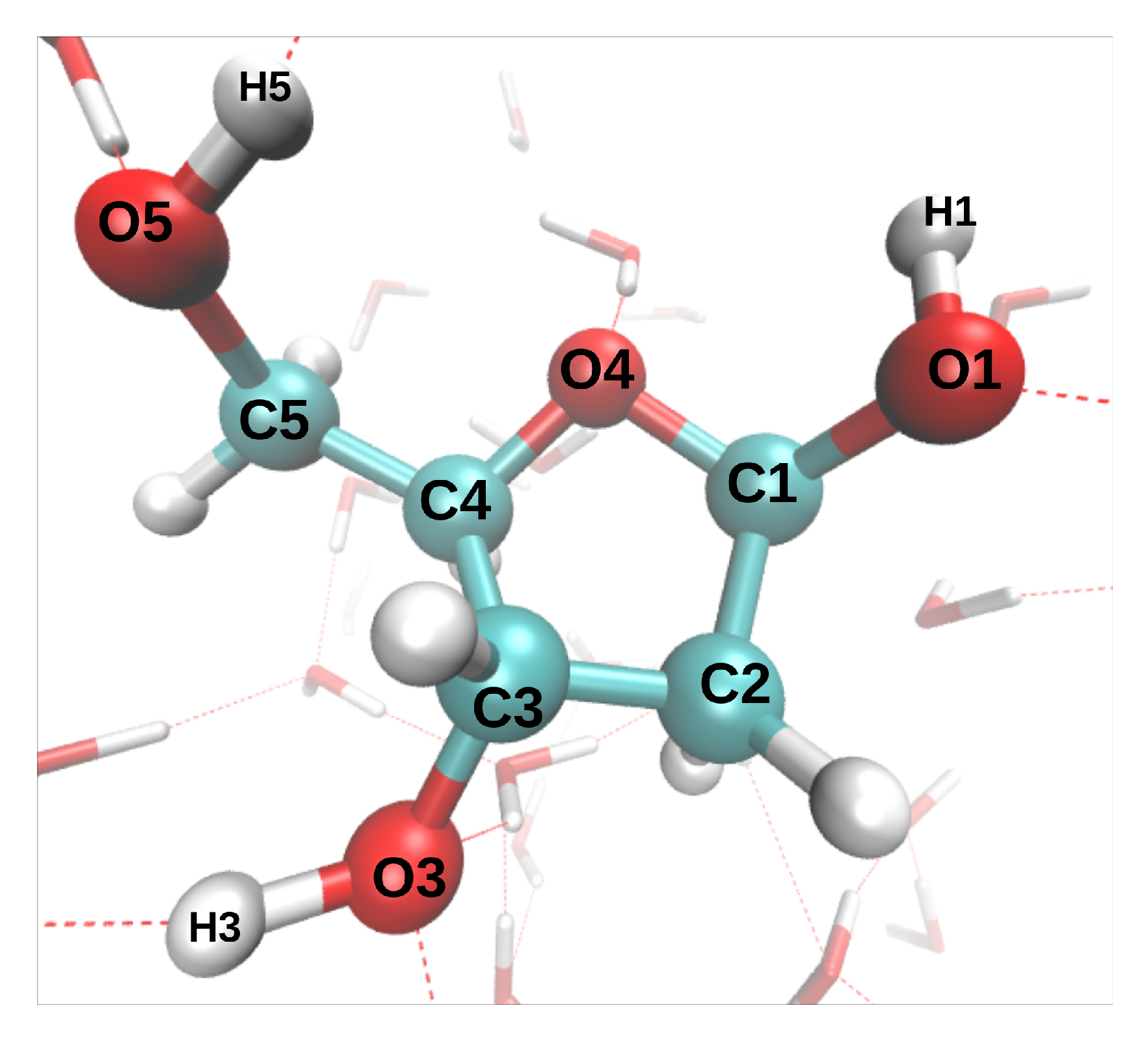
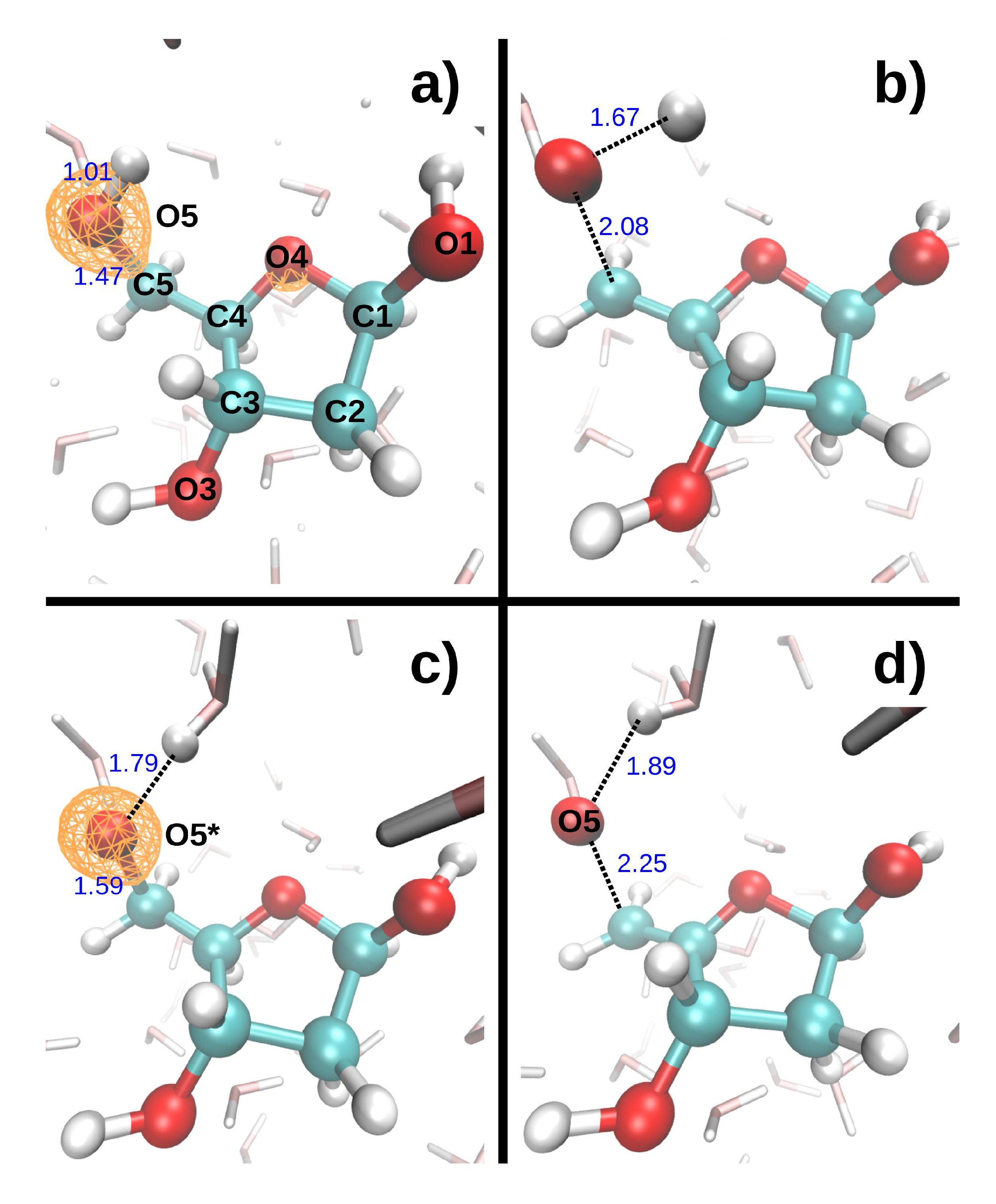
In a previous paper [17], we have modeled the dynamics induced by the removal of oxygen K-shell electrons from a deoxyribose molecule embedded in liquid water (direct effect). The only investigated initial configuration (atomic positions and velocities) is shown in Figure 1. The C-O* bonds length increased by 0.1–0.2 Å during the 9.7 fs dynamics (the asterisk will always indicate the core-ionized atom). The hydroxyl groups, however, displayed very different bond elongations, from 0.05 Å for O3*-H3 to 0.78 Å for O5*-H5. To study indirect effects, two additional MD were performed, in which the core hole was localized on a water molecule donating an hydrogen bond (HB) either to O1 or O4. In both cases, one of the O*-H bonds broke during the 9.7 fs dynamics, and the proton was transferred either to another water molecule or to O4, respectively.

In the present paper, we have completed this study by investigating five additional initial configurations, thus allowing a statistical analysis of the results. Core holes were localized on the different carbon and oxygen atoms of the sugar (direct effect). The results will be compared to simulations of the isolated molecule [20] to infer the role of the environment on the dissociation patterns. Core holes were also localized on the water molecules forming an HB with the sugar (indirect effect).

2.1.1. Hydration of the Sugar

We present first the DR hydration during the 1.2 ps dynamics of the neutral system, along which the six initial configurations were selected. Such simulation time is short for a full analysis of the hydration but our purpose here is to describe the starting point for the ensuing nonequilibrium dynamics. The radial distribution functions (RDF) between the different DR oxygen atoms and the water hydrogen atoms exhibited a first minimum around 2.4 Å, as did the RDF between the different hydrogen atoms belonging to the DR hydroxyl groups and the water oxygen atoms (see Supplementary Materials, Figure S1). The number of water molecules in the first coordination sphere of the different DR atoms are shown in

Table 1. First hydration layer of the DR ring oxygen and hydroxyl groups. Statistics was performed along a 1.2 ps MD of the neutral system.

DR Group	Number of Water Hydrogen Within 2.4 Å of the DR Oxygen	Number of Water Oxygen Within 2.4 Å of the DR Hydrogen
Ring oxygen (O4)	0.93	-
O1H1	1.74	1.0
O3H3	1.95	1.0
O5H5	2.0	1.0

.

2.1.2. Direct Effect

We have studied the consequence of carbon or oxygen K-shell ionizations in a deoxyribose molecule embedded in liquid water. Carbon K-shell vacancies did not induce any significant bond elongation during the 9.7 fs MD. On the contrary, when the core hole is localized on the oxygen atoms, the length of the CO* and O*H bonds systematically increases, as shown in

Table 2. Average bond elongation due to the presence of a K-shell vacancy during 9.7 fs on the oxygen atom O* of a DR molecule embedded in water. Statistics performed on 6 different initial configurations.

O*	Bond	Elongation (Å)	Bond	Elongation (Å)
O1	C1 - O1	0.22 ± 0.10 Å	O1 - H1	0.57 ± 0.29 Å
O3	C3 - O3	0.17 ± 0.05 Å	O3 - H3	0.34 ± 0.29 Å
O4	C1 - O4	0.17 ± 0.02 Å	C4 - O4	0.13 ± 0.03 Å
O5	C5 - O5	0.15 ± 0.03 Å	O5 - H5	0.53 ± 0.34 Å

. The elongation of the CO* bonds was always below 0.34 Å at the end of all the 9.7 fs core hole MD. These results are similar to those obtained in the gas phase [20]. Thus, the CO* bonds elongation does not seem to be influenced much by the DR environment. In particular, the largest average bond elongation is induced by core vacancies on O1 in both phases.

On the contrary, although O*H bonds are not much affected by the presence of the K-shell vacancy on O* in the gas phase [20], these bonds may undergo very large elongations in liquid water, as shown in Table 2. In fact, the elongation of the O*H bonds could reach 0.93 Å at the end of the 9.7 fs core hole dynamics. Considering OH bonds to be dissociated when the OH distance is larger than 1.5 Å, we find that the O3-H3 bond breaks in two configurations out of six, and the O1-H1 and O5-H5 bonds in four configurations out of six. The released proton is always transferred to a neighboring water molecule to form an hydronium ion (H₃O⁺).

The dissociation of O*H bonds appears to depend strongly on the local environment of the hydroxyl groups, and, more specifically, on the presence of a water molecule (labeled H₂Ow) accepting an hydrogen bond from the sugar (O*H…O_w). When the initial distance between the DR hydrogen atom and O_w is less than ~1.8 Å, respectively, greater than ~1.9 Å, the DR hydroxyl group (O*H) always, respectively, never, dissociates to form H₃${\mathrm{O}}_w^{+}$. A similar influence of hydration on NH bond dissociation was found in a uracil molecule embedded in water, when the core hole was localized on the nitrogen atoms [16].

2.1.3. Indirect Effect

We have investigated the ultrafast dissociation of the water molecules which belong to the deoxyribose primary hydration shell, after a core ionization was placed on the oxygen atom (O*), but before Auger decay. One of the O*H bonds always exhibits a longer elongation than the other. It reaches on average 1.66 ± 0.23 Å at t = 9.7 fs, compared to 1.12 ± 0.19 Å for the second bond. These values do not seem to depend on whether the water molecule accepts or donates an HB to the sugar. The species formed at the end of the 9.7 fs dynamics are listed in

Table 3. Species formed after a core ionization was placed during 9.7 fs on a water molecule hydrogen bonded to a DR molecule embedded in water. Statistics performed on 6 different initial configurations.

The Core-Ionized Water Molecule	Number of MD	A Proton is Emitted Towards	Species Formed	Occurrence
donates an HB to the DR ring oxygen	6	DR	DR−H+ + O*H	2
		H2O	H3O+ + O*H	2
			(H2O−H−O*H)+	1
donates an HB to the DR hydroxyl groups	31	DR	DR−H+ + O*H	5
			(DR−H−O*H)+	1
		H2O	H3O+ + O*H	15
			(H2O−H−O*H)+	2
		DR, H2O	DR−H+ + O*−H−OH2	2
			DR−H−O* + H3O+	4
			(DR−H−O*−H−OH2)+	1
accepts an HB from the DR hydroxyl groups	18	H2O	H3O+ + O*H	8
			(H2O−H−O*H)+	3
		H2O, H2O	2 H3O+ + O*−	1
			H3O+ + O*−H−OH2	3
			(H2O−H−O*−H−OH2)+	1

.

Let us consider the water molecules which donate an HB to the sugar. In most cases (24/37), the core-ionized water molecule emits only one proton, either towards the sugar (DR−H⁺ + O*H) or towards another water molecule (H₃O⁺ + O*H). In a few additional cases (4/37), the emitted hydrogen is less than 1.5 Å away from both the core-ionized and HB acceptor molecules ((DR−H−O*H)⁺ or (H₂O−H−O*H)⁺). More rarely, both O*H bonds undergo significant elongation (in seven cases out of 37).

Let us now consider the water molecules which accept an HB from the sugar hydroxyl groups. In 11 cases, the water molecule has one broken bond leading to the formation of an H₃O⁺, the second O*H bond is significantly elongated in 3 out of these 11 MD. One dynamics results in the complete fragmentation of the core-ionized molecule.

As a conclusion, two species are formed (O*H and H₃O⁺) in the vicinity of the sugar, and/or protons may be transferred towards the sugar during the lifetime of the core vacancy. The species thus formed could in turn damage the sugar by an indirect effect. It should however be mentioned that, in most cases, Auger decay will take place well before the molecules dissociation since the lifetime of a K-shell vacancy is ≃4.1 fs in water [21]. We have in fact estimated that, in liquid water, only ~16% of the core-ionized water molecules will have one or both ${\mathrm{O}}_w^{*}$H bonds broken before Auger decay [16].

2.2. Dissociation of Doubly Ionized DR after Auger Effect

How to localize the double hole after Auger effect? In Born Oppenheimer MD (BOMD), one cannot localize the initial charges on a single molecule in the condensed phase. The Ehrenfest time-dependent density functional theory (TDDFT) method must thus be applied to propagate a dicationic electronic state prepared by emptying one of the localized valence molecular orbitals of the sample [18]. It has to be noticed that Auger effect can lead to many different channels since the Auger electron can be ejected from different orbitals. The calculation of the branching ratios of the Auger deexcitation channels would be prohibitive in view of the number of MO of the system. Here, we chose to remove the two electrons from the deepest valence MO localized on the oxygen atom which had the K-shell vacancy before Auger decay (O*). Although the selected deexcitation process might not be the most probable, it is the most energetic leading to the fastest fragmentation process, and it may thus be modeled in a reasonable computational time.

As this method is very computationally consuming, we restrict our study to a single initial configuration, and to the dissociation induced by the removal of a K-shell electron from the DR oxygen atoms (direct effects). The initial configuration (t = 0) is the one shown in Figure 1, and the four core–hole dynamics, one for each oxygen atom, are those described in details in [17]. The geometry of the sugar evolves while the oxygen atom has a K-shell vacancy. In fact, the O*H bond is broken at the end of two out of the four core–hole dynamics. It should however be stressed that the lifetime of the oxygen K vacancy is only 4.7 fs [22]. As a consequence, approximately 87% of the core-ionized molecules undergo Auger decay before 9.7 fs. Furthermore, Auger decay will most probably happen almost immediately after core ionization, so that the DR²⁺ geometry will be very similar to that of the initial configuration (shown in Figure 1). We have therefore modeled two extreme scenarios. In the first scenario, the DR undergoes Auger decay at t = 0, when no structural change has been induced by the K-shell vacancy. We have thus performed four DR²⁺ Ehrenfest TDDFT MD, all starting with the same geometry, that is the initial configuration shown in Figure 1, but removing the two electrons from each of the four deepest valence MO localized on the DR oxygen atoms. In the second scenario, the DR undergoes Auger decay at the end of the 9.7 fs core hole dynamics, when the structural change induced by the K vacancy is maximal. We have thus performed four DR²⁺ Ehrenfest TDDFT MD, starting from four different geometries, those generated at the end of the four core hole dynamics, and removing the two electrons from the deepest valence MO localized on the core-ionized atom (O*).

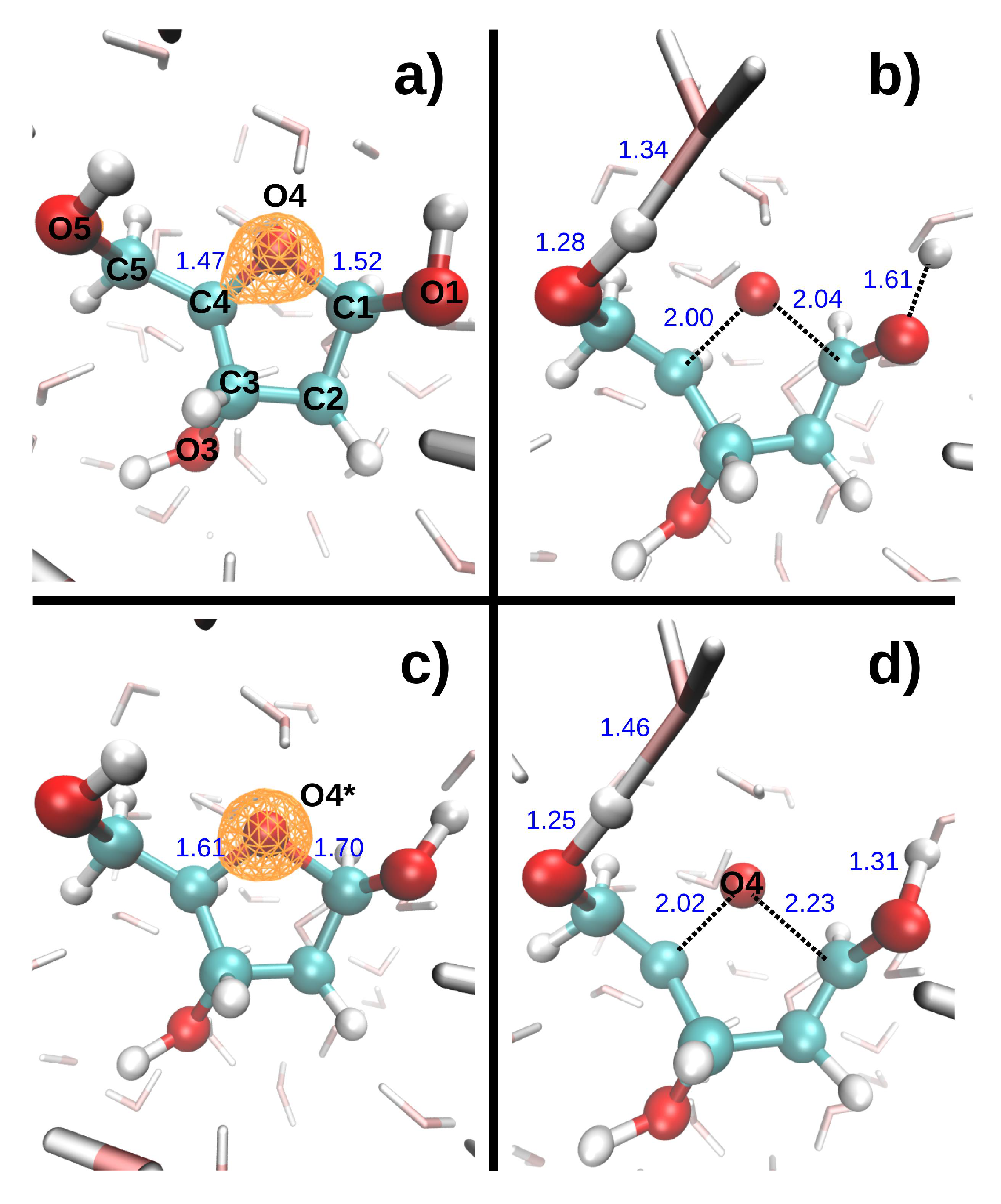
Figure 2 shows the dissociation dynamics induced by a double hole localized on the DR ring oxygen (O4) after Auger decay. In the first scenario (Figure 2, top), the O4 core hole decays at t = 0. The C1-O4 and C4-O4 bonds then break very rapidly, at 8.7 and 9.0 fs, respectively. It should be noted that these bonds only elongated by 0.14 and 0.18 Å, respectively, when a core hole was localized on O4 during 9.7 fs. In the second scenario (Figure 2, bottom), the O4 core hole decays at 9.7 fs. The C1-O4 and C4-O4 bonds then break at 15.4 and 18.9 fs, respectively. The presence of a core vacancy on O4 thus seems only to delay the dissociation of the C-O4 bonds. In both scenarios, the O5-H5 bond length increases slightly during the 9.6 fs DR²⁺ dynamics, whereas the O1-H1 elongates more in the first scenario than in the second.

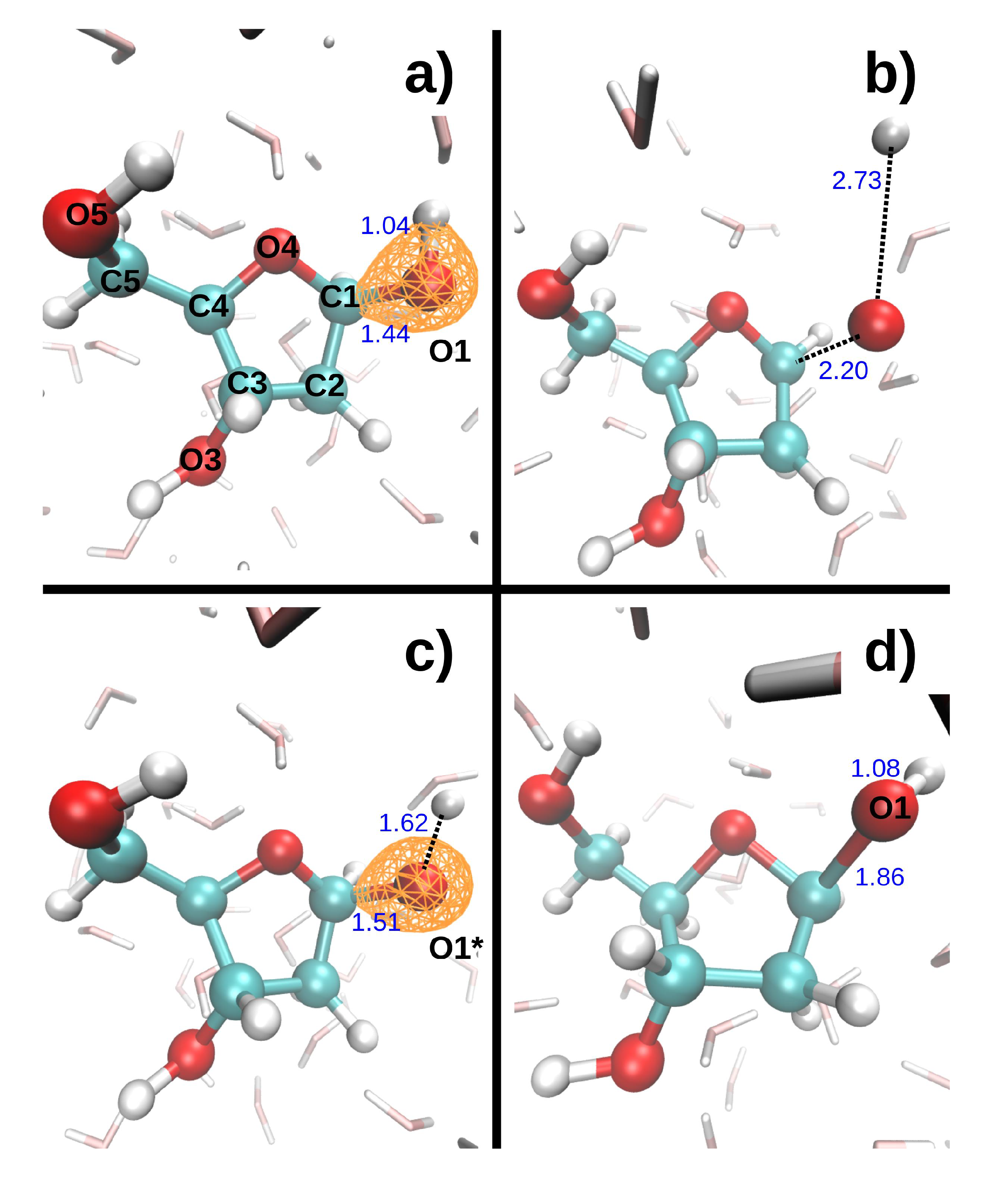
Figure 3 shows the dissociation dynamics induced by a double hole localized on O1 after Auger decay. In the first scenario (Figure 3, top), the O1 core hole decays at t = 0. The O1-H1 and C1-O1 bonds then break within a few femtoseconds (see

Table 4. Dissociation dynamics after a core hole was placed on O1 at t = 0.

Auger Decay Time (fs)	Dissociation O1-H1	Time (fs) C1-O1	Maximum Kinetic H1	Energy (eV) O1
0	2.7	7.5	5.3	0.10
9.7	8.7	-	0.98	0.05

). H1 first collides on a neighboring water oxygen (O_w1) at ~5 fs, after which it moves further away from O1. The kinetic energy of H1 exhibits large variations. It first increases up to a maximum value of 5.3 eV as H1 departs from the DR. It then decreases to a minimum value of 2.6 eV when H1 is closest to the water molecule. After the collision, it reaches a second maximum of 4.3 eV, and then gradually decreases again. Meanwhile, the kinetic energy of O1 increases up to 0.1 eV during about 5 fs, and then remains fairly constant. In the second scenario (Figure 3, bottom), the O1 core hole decays at 9.7 fs. It should be noted that the O1-H1 bond breaks during the O1 core–hole dynamics, at t = 8.7 fs (see Table 4). During the subsequent DR²⁺ dynamics, H1 also collides with O_w1, but it is retrodiffused back towards O1 so that the O1-H1 bond forms again at t = 15.0 fs. In the meantime, the C1-O1 bond elongates up to 1.86 Å at t = 19.3 fs. The maximum kinetic energy reached by both H1 and O1 is lower in the second than in the first scenario (see Table 4).

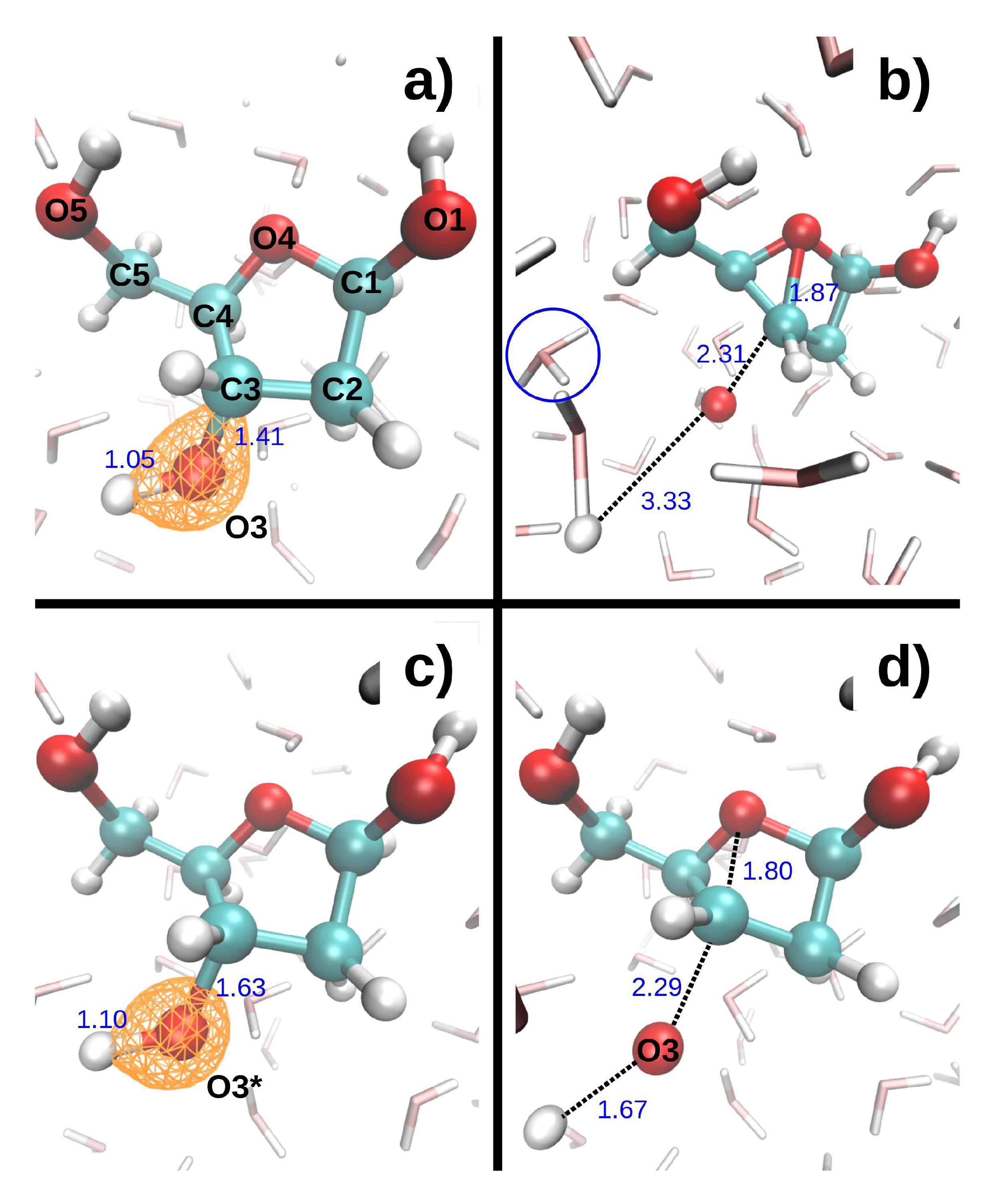
Figure 4 shows the dissociation dynamics induced by a double hole localized on O3 after Auger decay. In the first scenario (Figure 4, top), the O3 core hole decays at t = 0. The O3-H3 and C3-O3 bonds then break within a few femtoseconds (see

Table 5. Dissociation dynamics after a core hole was placed on O3 at t = 0.

Auger Decay Time (fs)	Dissociation O3-H3 Time (fs)	Time (fs) C3-O3	Maximum H3	Kinetic Energy (eV) O3
0	3.0	7.0	5.7	0.15
9.7	12.3	15.6	4.9	0.08

). H3 first collides with a neighboring water oxygen (O_w3) at ~6.3 fs, but the deviation angle is small and it moves further away from O3. In the second scenario (Figure 4, bottom), the O3 core hole decays at 9.7 fs. The O3-H3 and C3-O3 bonds only elongate slightly during the O3 core hole dynamics, but then break very rapidly during the subsequent DR²⁺ dynamics (see Table 5). H3 collides with O_w3 at ~14.8 fs. The deviation angle is larger than in the first scenario, but H3 also moves away from O3 after the collision. The maximum kinetic energy reached by both H3 and O3 is lower in the second than in the first scenario (see Table 5). Interestingly, a bond forms between C3 and O4 in both scenarios.

Figure 5 shows the dissociation dynamics induced by a double hole localized on O5 after Auger decay. In the first scenario (Figure 5, top), the O5 core hole decays at t = 0. The O5-H5 and C5-O5 bonds then break within a few femtoseconds (see

Table 6. Dissociation dynamics after a core hole was placed on O5 at t = 0.

Auger Decay Time (fs)	Dissociation O5-H5	Time (fs) C5-O5	Maximum H5	Kinetic Energy (eV) O5
0	2.8	8.6	4.6	0.06
9.7	6.1	16.6	1.3	0.08

). H5 first collides on a neighboring water oxygen (O_w5). It is then scattered back towards O5 so that the O5-H5 distance diminishes towards the end of the dynamics. In the second scenario (Figure 5, bottom), the O5 core hole decays at 9.7 fs. It should be noted that the O5-H5 bond breaks during the O5 core–hole dynamics, at t = 6.1 fs. H5 then binds to O_w5. This bond undergoes large vibrations, between 0.81 and 1.26 Å, but H5 remains bound to O_w5 during the subsequent DR²⁺. The C5-O5 bond breaks at 16.6 fs. The maximum kinetic energy reached by both H5 and O5 is lower in the second than in the first scenario (see Table 5).

To summarize, when a double hole is localized on the DR oxygen atoms, the bonds involving this oxygen atom are very rapidly broken, typically after 3 fs for the OH bonds, and 7 to 9 fs for the CO bonds. The elongation of these bonds is much faster than that induced by a core vacancy on the same oxygen atom. Moreover, in most cases, the CO bond breakage during the DR²⁺ dynamics does not seem to depend much on the time at which Auger decay occurs. This is not the case for the protons dynamics. For one part, their kinetic energy is lower when the OH bond breaks during the core hole dynamics, than when it breaks during the DR²⁺ dynamics. However, the protons trajectories also differ when the OH bond breaks after Auger decay in the two scenarios. In fact, we have recently shown that the trajectories of the protons ejected from an H₂O²⁺ molecule are very sensitive to slight perturbations of the system [19].

3. Discussion

Different theoretical methods have been used to understand the fragmentation of molecules after K-shell ionization and Auger effect. In many cases, the fragmentation of molecules upon inner-shell ionization is not specific with respect to the initially localized ionization site, in contrast with the case of ClCH₂Br where a strong site-specific fragmentation was observed [23]. In a recent publication [24], the lack of site specificity was attributed to the character of the dicationic electronic states after Auger decay in the case of ethyl trifluoroacetate molecule. This could be proved by a calculation of the Auger rates for the many involved final dicationic electronic states after Auger effect. In the gas phase and for small molecules, this kind of calculations is feasible. In many cases, statistical methods are used [25], where fast conversion processes quickly transfer electronic excitation energy of the dication into vibrational degrees of freedom. In these models, the identities of the electronic states populated via Auger decay are not taken into account, and the only important parameter determining the fragmentation remains the internal energy.

All these modeling methods are used for K holes induced in gas phase molecules. When a molecule is embedded in water, calculating Auger rates seems hardly computationally practicable in view of the number of atoms. The effect of the solvent has to be taken into account since even transfer of charges can take place during the K hole dynamics (10 fs), so we performed core hole molecular dynamics with K holes on the different atoms of the DR and on different configurations of the DR embedded in water and on different water molecules of the solvent. This allowed us to exhibit cases where transfer of charge from the molecule to the solvent is produced before Auger effect. As the localization of the charge after Auger decay may have a key role in the fragmentation of the dication we prolongated the K hole dynamics by a TDDFT Ehrenfest MD where the initial state is dicationic by emptying the most energetic valence orbital. TDDFT Ehrenfest MD propagate the wavefunction calculating the mean forces at each step, ensuring the propagation of distribution of charges. As a first trial we only emptied the most energetic valence orbital around the oxygen atoms where the K hole was located at the end of the K hole dynamics. In the major part of our simulation we noticed no specificity of the localization of the K hole. However, a study of less energetic emptied orbital has to be achieved in a forthcoming publication in comparison with initial configuration without a K hole and the same emptied orbital.

Indeed this study is not exhaustive but it allowed to exhibit some particular trends on the effect of K hole versus Auger effect. We have studied the dynamics of a core-ionized deoxyribose molecule embedded in liquid water and as a first conclusion we can notice that carbon K-shell vacancies did not induce any systematic change in the molecules geometry during the 10 fs MD. On the contrary, oxygen K-holes always induced an elongation of the CO* and O*H bonds. The CO* bond length increased by $0.17\pm 0.06$ on average during the 10 fs MD, a behavior very similar to that of the isolated molecule [20]. O*H bond lengths exhibited much larger variations, increasing between 0.04 and 0.93 Å during the 10 fs MD. These variation may be related to the initial hydration state of the core-ionized hydroxyl groups. In fact, O*H bonds did not elongate in the isolated molecule [20]. In water molecules, the oxygen core vacancy often leads to the dissociation of at least one of the two ${\mathrm{O}}_w^{*}$H bonds during the lifetime of the core vacancy (≃4.1 fs in water [21]). In such cases, the proton is ejected either towards the sugar to form DR−H⁺ or towards another water molecule to form H₃O⁺.

The removal of two electrons from the deepest valence orbital localized on the DR oxygen atoms leads to a very fast dissociation of the CO bonds involving the core-ionized atom. In most cases, this effect does not seem to depend on the time at which Auger decay occurs. Within 10 fs after Auger decay, the sugar thus loses the ring oxygen when the double hole is localized on O4, and the hydroxyl groups when the double hole is localized on O1, O3 or O5.

4. Materials and Methods

All simulations were performed in the microcanonical ensemble with the plane-wave Kohn–Sham-based DFT Car–Parrinello molecular dynamics code CPMD [26]. Core electrons were replaced by pseudopotentials of the Trouiller-Martins form [27]. The Kleinman-Bylander integration scheme was used for all atom type. The exchange and correlation energy was calculated using the generalized gradient approximation (GGA) functional Becke–Lee–Yang–Parr (BLYP) [28,29]. The long-range electrostatic potential was computed using the standard Ewald summation scheme and a compensating background was thus used for the charged simulations.

The system consists of one deoxyribose molecule and 58 water molecules enclosed in a periodically repeated cubic box of size 12.43 Å. The initial configurations for the dynamics of the ionized system were extracted from a 1.2 ps Car-Parrinello MD of the neutral system [26] that followed a 5 ps long equilibration [17]. Both equilibration and initial CPMD dynamics were performed with 0.024 fs timesteps and 100 au fictitious electronic mass. Except when otherwise stated, the plane-wave basis set was truncated at an energy cutoff of 70 Ry (Ry: 1 Ry = 2.17989 × 10¹⁸ J). The average temperature of the systems was 324 ± 13 K. We have selected five different configurations (atomic positions and velocities) separated by 240 fs time intervals, which were used as initial configurations for the core hole dynamics in order to take into account different degrees of hydration of the deoxyribose.

Briefly, the removal of K-shell electrons from the deoxyribose molecules was described by substituting the 1s² pseudopotential of one of the carbon or oxygen atoms of the molecule by a pseudopotential corresponding to a 1s¹ state at $t=0$. The atomic positions and velocities are assumed to be the same as those of the neutral molecule before ionization (vertical transition). The lifetime of a carbon K-shell vacancy is 8.24 fs, whereas that of oxygen is 4.71 fs [22]. Born Oppenheimer MD were thus performed for 9.7 fs, with a 0.024 fs timestep, and an energy cutoff of 110 Ry. For each initial configuration investigated, we have placed a core hole on each of the five carbon and four oxygen atoms of the sugar, and also on the oxygen atoms of the water molecules forming an hydrogen bond with the sugar. One-hundred-and-three BOMD were thus generated in addition to the six dynamics presented in paper [17].

We have studied the fragmentation induced not only by the presence of a core hole on the sugar oxygen atoms, but also by the double vacancy following Auger decay. To do so, the effective Wannier orbitals [30,31] of all the molecules in the sample were determined for the configuration at the end of the core hole dynamics, that is at t = 9.7 fs. After this, the pseudopotential corresponding to the 1 s¹ state of the core-ionized atom was replaced by a 1s² pseudopotential. The initial nonstationary electronic state of the doubly charged sample is prepared by removing two electrons from the deepest valence MO localized on O* [18]. We have selected that MO among all the possible channels of deexcitation because it is the most violent event and by consequence the quickest of all possible events. The deoxyribose molecule is doubly ionized, while all the other molecules of the sample remain strictly neutral. The electronic structure is then propagated for 9.6 fs by Ehrenfest dynamics [32,33]. In our calculations, the numerical integration of the time-dependent Kohn-Sham equations was performed using an iterative Crank–Nicholson algorithm with a time step of Δt ≤ 0.00024 fs combined with a two-step Runge–Kutta scheme to maintain Δt² order accuracy [34]. The ions are propagated alongside the electrons in the Ehrenfest scheme, which is expected to be valid at these very short time scales. Because of the very small time step used in the real time propagation of electrons, the total simulation time was limited to 9.6 fs. When modeling an Auger decay occurring at t = 0, we do not take into account the presence of a K-hole vacancy in the calculation of the valence MO (displayed in Figure 2a, Figure 3a, Figure 4a and Figure 5a).

The analysis of the fragments charges were performed in the Bader scheme [35]. CO and OH bonds are considered broken, when the bond length is greater than 2.0 and 1.5 Å, respectively.