The Helical Magnet MnSi: Skyrmions and Magnons
Abstract
:1. What Makes MnSi So Interesting?
2. How Everything Began
3. From the Neutron Small-Angle Scattering Results to the Skyrmion Interpretation
4. Magnons in MnSi
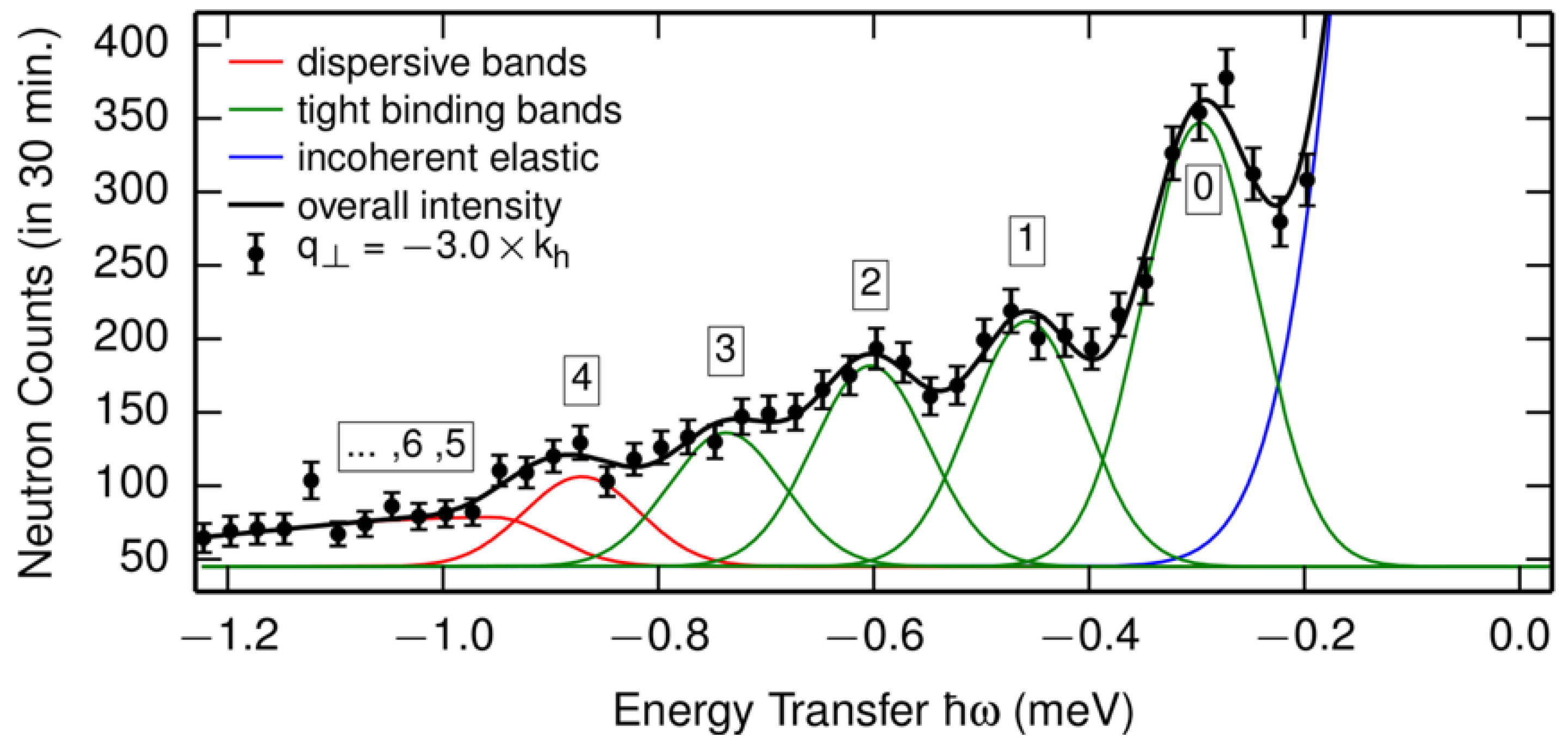
4.1. Helimagnons
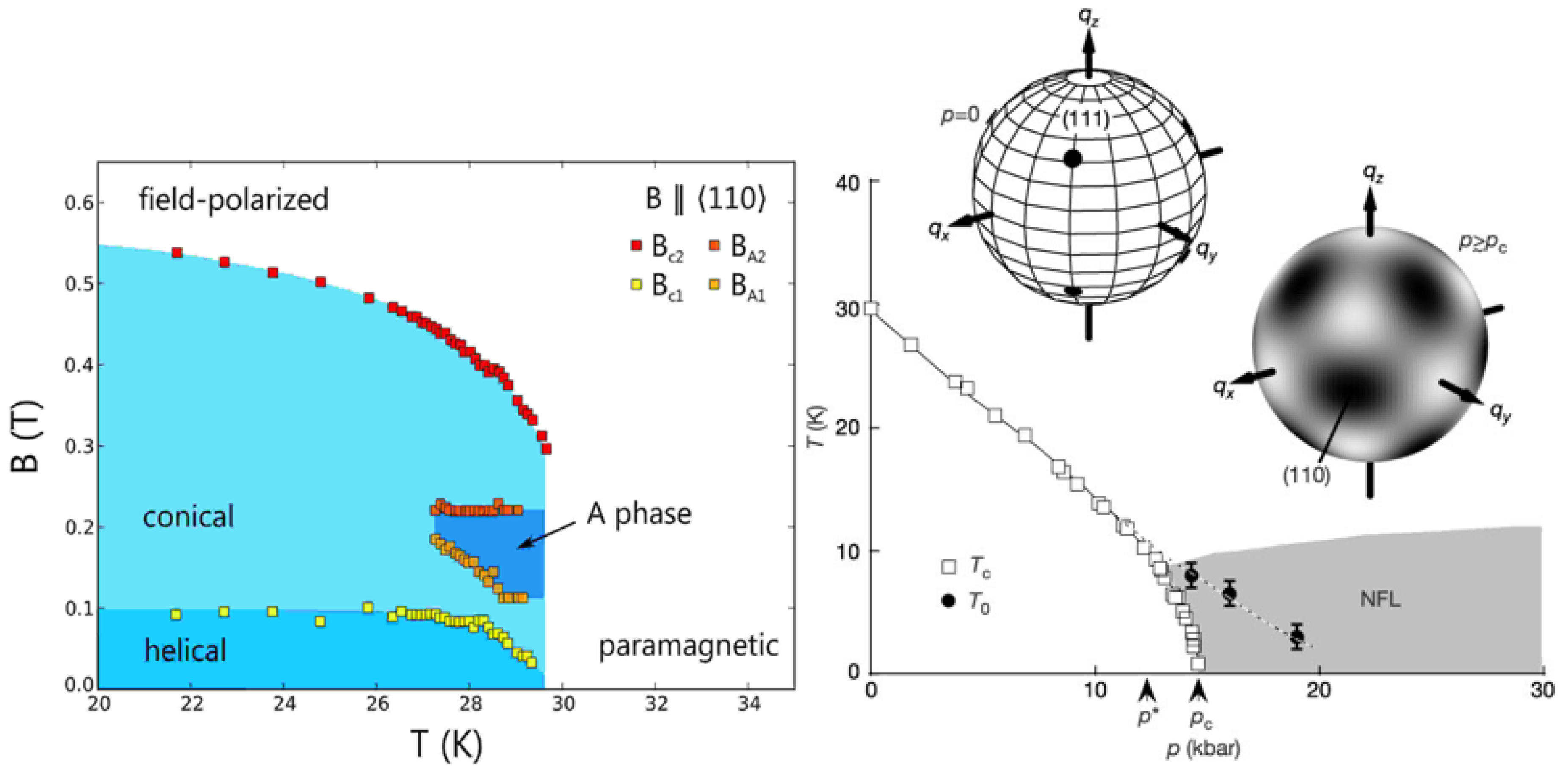
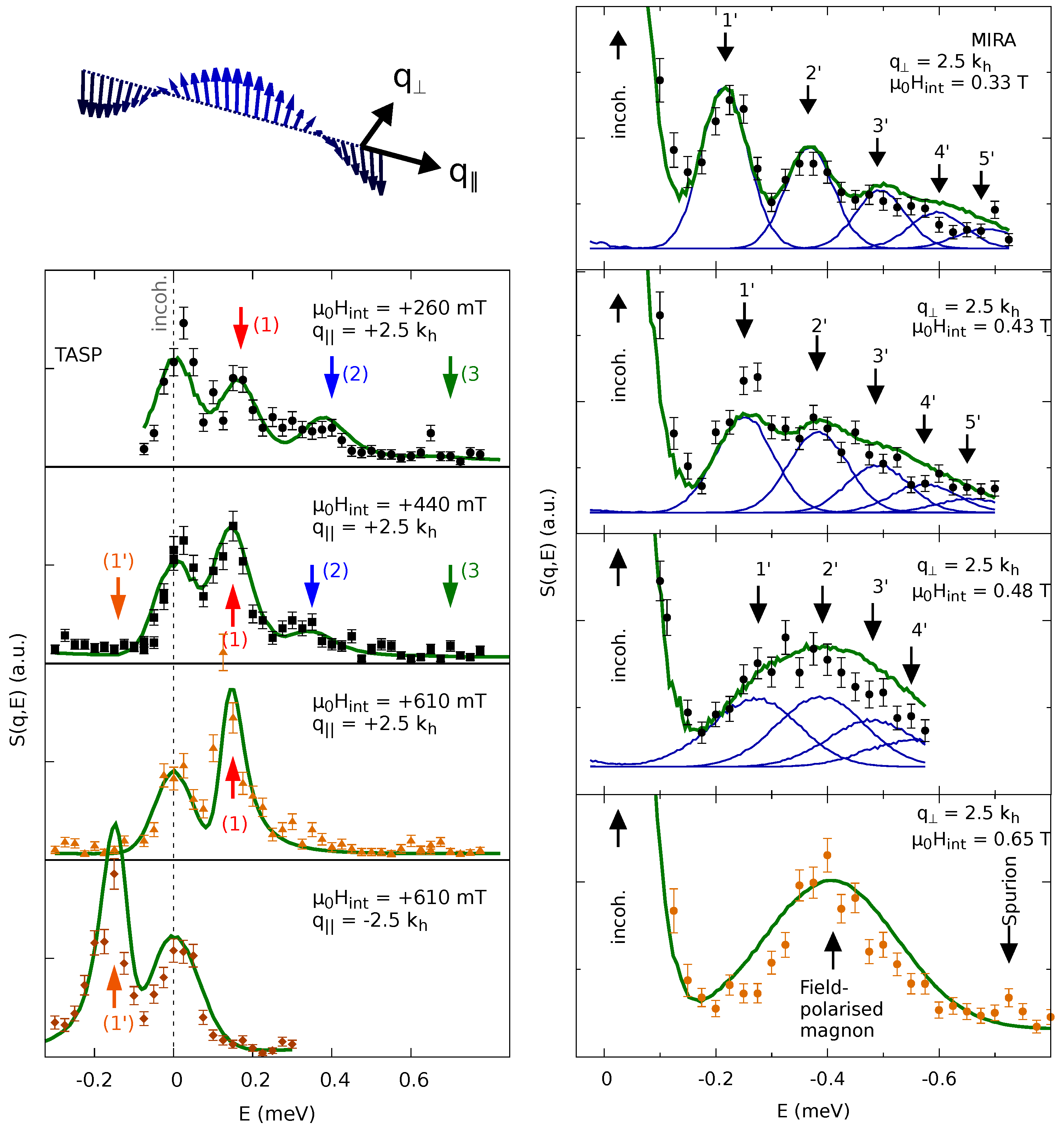
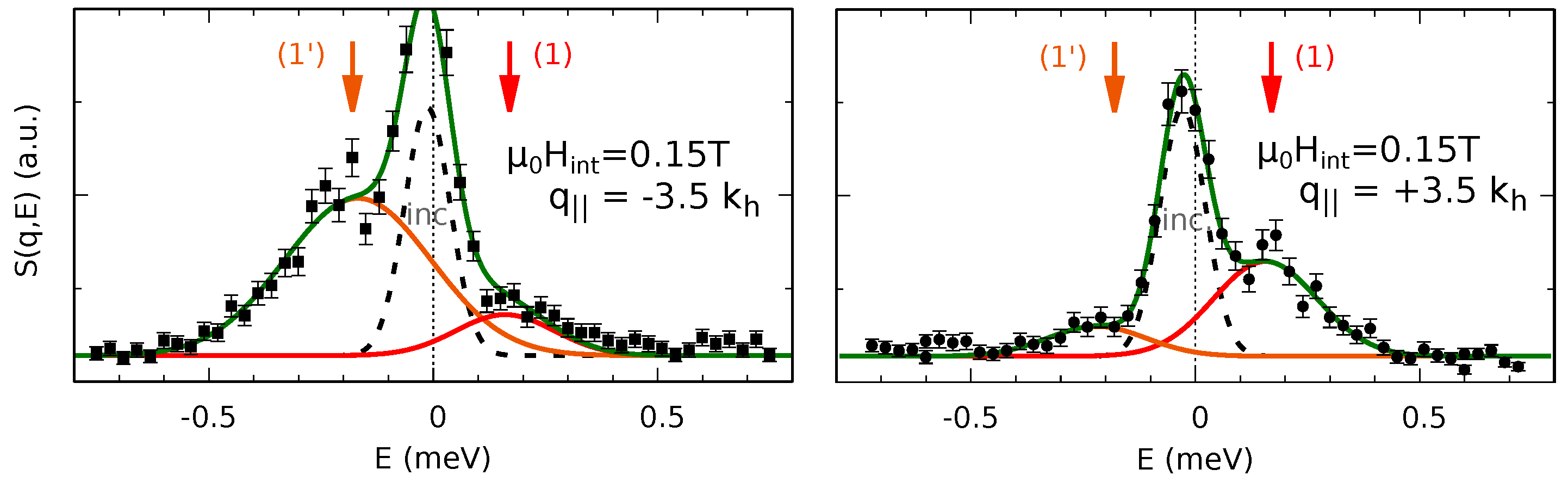
4.2. Conical and in the Field-Polarized Phase
4.3. Skyrmion Phase
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| DMI | Dzyaloshinsky-Moriya interaction |
| SOC | Spin-orbit coupling |
References
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral Magnet. Science 2009, 323, 5916. [Google Scholar] [CrossRef] [PubMed]
- Pleiderer, C.; Reznik, D.; Pintschovius, L.; Löhneysen, H.; M, M.G.; Rosch, A. Partial order in the non-Fermi-liquid phase of MnSi. Nature 2004, 427, 227. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, Y.; Shirane, G.; Tarvin, J.A.; Koghi, M. Magnetic excitations in the weak intinerant ferromagnet MnSi. Phys. Rev. B 1977, 16, 4956. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Noda, Y.; Fincher, C.; Shirane, G. Low-energy paramagnetic spin fluctuations in the weak itinerant ferromagnet MnSi. Phys. Rev. B 1982, 25, 254. [Google Scholar] [CrossRef]
- Kadowaki, K.O.; Date, M. Magnetization and Magnetoresistance of MnSi. I. J. Phys. Sot. Jpn. 1982, 51, 2433. [Google Scholar] [CrossRef]
- Bak, P.; Jensen, M.H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980, 12, L881–L885. [Google Scholar] [CrossRef]
- Shirane, G.; Cowley, R.; Majkrazk, C.; Sokoloff, J.; Pagonis, B.; Perry, C.; Ishikawa, Y. Spiral magnetic correlation in cubic MnSi. Phys. Rev. B 1983, 28, 6251. [Google Scholar] [CrossRef]
- Sorensen, S.A. Neutron Scattering Studies of Modulated Magnetic Structures. Ph.D. Thesis, Riso National Laboratory, Roskilde, Denmark, 1999. [Google Scholar]
- Roessli, B.; Böni, P.; Fischer, W.; Endoh, Y. Chiral Fluctuations in MnSi above the Curie Temperature. Phys. Rev. Lett. 2002, 88, 237204. [Google Scholar] [CrossRef] [PubMed]
- Komatsubara, T.; Kusaka, S.; Ishikawa, Y. Proceedings of the 6th International Conference on Internal Friction and Ultrasonic Attenuation in Solids; University of Tokyo Press: Tokyo, Japan, 1977; Volume 1, p. 237. [Google Scholar]
- Lebech, B.; Harris, P.; Mortensen, K.; Greorgy, C.; Boenhof, N.; Jermey, M.; Brown, S. Magentic phase diagram of MnSi. J. Magn. Magn. Mater. 1995, 140, 119–120. [Google Scholar] [CrossRef]
- Grigoriev, S.V.; Maleyev, S.V.; Okorokov, A.I.; Chetverikov, Y.O.; Eckerlebe, H. Field-induced reorientation of the spin helix in MnSi near Tc. Phys. Rev. B 2006, 73, 224440. [Google Scholar] [CrossRef]
- Pfleiderer, C.; Neubauer, A.; Muehlbauer, S.; Jonietz, F.; Janoschek, M.; Legl, S.; Ritz, R.; Muenzer, W.; Franz, C.; Niklowitz, P.; et al. Quantum order in the chiral magnet MnSi. J. Phys. Condensed Matter 2009, 21, 164215–164221. [Google Scholar] [CrossRef] [PubMed]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101–103. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Bogdanov, A.; Hubert, A. The stability of vortex-like structures in uniaxial ferromagnets. J. Magn. Magn. Mater. 1999, 195, 182–192. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Rößler, U.K.; Wolf, M.; Müller, K.H. Magnetic structures and reorientation transitions in noncentrosymmetric uniaxial antiferromagnets. Phys. Rev. B 2002, 66, 214410. [Google Scholar] [CrossRef]
- Schulz, T.; Ritz, R.; Bauer, A.; Halder, M.; Wagner, M.; Franz, C.; Pfleiderer, C.; Everschor, K.; Garst, M.; Rosch, A. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 2012, 8, 301–304. [Google Scholar] [CrossRef]
- Volovik, G. Linear momentum in ferromagnets. J. Phys. C Solid State Phys. 1987, 20, L83. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.S.L. Generalization of the Landau-Lifshitz-Gilbert Equation for Conducting Ferromagnets. Phys. Rev. Lett. 2009, 102, 086601. [Google Scholar] [CrossRef] [PubMed]
- Zang, J.; Mostovoy, M.; Han, J.H.; Nagaosa, N. Dynamics of Skyrmion Crystals in Metallic Thin Films. Phys. Rev. Lett. 2011, 107, 136804. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef] [PubMed]
- Ritz, R.; Halder, M.; M, M.W.; C, C.F.; Bauer, A.; Pfleiderer, C. Formation of a topological non-Fermi liquid in MnSi. Nature 2013, 497, 231. [Google Scholar] [CrossRef] [PubMed]
- Janoschek, M.; Jonietz, F.; Link, P.; Pfleiderer, C.; Böni, P. Helimagnons in the skyrmion lattice of MnSi. J. Phys. Conf. Ser. 2010, 200, 032026. [Google Scholar] [CrossRef]
- Schwarze, T.; Waizner, J.; Garst, M.; Bauer, A.; Stasinopoulos, I.; Berger, H.; Pfleiderer, C.; Grundler, D. Universal helimagnon and skyrmion excitations in metallic, semiconducting and insulating chiral magnets. Nat. Mater. 2015, 14, 478. [Google Scholar] [CrossRef] [PubMed]
- Kugler, M.; Brandl, G.; Waizner, J.; Janoschek, M.; Georgii, R.; Bauer, A.; Seemann, K.; Rosch, A.; Pfleiderer, C.; Böni, P.; et al. Band Structure of Helimagnons in MnSi Resolved by Inelastic Neutron Scattering. Phys. Rev. Lett. 2015, 115, 097203. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, Y.; Noda, Y.; Uemura, Y.J.; Majkrzak, C.F.; Shirane, G. Paramagnetic spin fluctuations in the weak itinerant-electron ferromagnet MnSi. Phys. Rev. B 1985, 31, 5884. [Google Scholar] [CrossRef]
- Garst, M.; Waizner, J.; Grundler, D. Collective spin excitations of helices and magnetic skyrmions: Review and perspectives of magnonics in non-centrosymmetric magnets. J. Phys. D Appl. Phys. 2017, 50, 293002. [Google Scholar] [CrossRef]
- Weber, T.; Waizner, J.; Tucker, G.S.; Georgii, R.; Kugler, M.; Bauer, A.; Pfleiderer, C.; Garst, M.; Böni, P. Field dependence of nonreciprocal magnons in chiral MnSi. Phys. Rev. B 2018, 97, 224403. [Google Scholar] [CrossRef]
- Sato, T.J.; Okuyama, D.; Hong, T.; Kikkawa, A.; Taguchi, Y.; Arima, T.h.; Tokura, Y. Magnon dispersion shift in the induced ferromagnetic phase of noncentrosymmetric MnSi. Phys. Rev. B 2016, 94, 144420. [Google Scholar] [CrossRef]
- Fobes, D.; Weber, T.; Waizner, J.; Kugler, M.; Bauer, A.; Georgii, R.; Link, P.; Ehlers, G.; Bewley, R.; Pfleiderer, C.; et al. Spin Excitations of the Skyrmion Lattice in MnSi. In Proceedings of the Bulletin of the American Physical Society, Los Angeles, CA, USA, 5–9 March 2018. [Google Scholar]
- Weber, T.; Waizner, J.; Tucker, G.S.; Beddrich, L.; Skoulatos, M.; Georgii, R.; Bauer, A.; Pfleiderer, C.; Garst, M.; Böni, P. Non-reciprocal magnons in non-centrosymmetric MnSi. AIP Adv. 2018, 8, 101328. [Google Scholar] [CrossRef]
- Weber, T.; Steffens, P.; Bauer, A.; Böni, P.; Garst, M. Polarisation-Dependence of the Spin Excitations of the Skyrmion Lattice in MnSi. ILL Reports 79803 and 80215. 2018; Unpublished work. [Google Scholar]
- Georgii, R.; Weber, T.; Brandl, G.; Skoulatos, M.; Janoschek, M.; Mühlbauer, S.; Pfleiderer, C.; Böni, P. The multi-purpose three-axis spectrometer (TAS) MIRA at FRM II. Nuclear Instrum. Methods Phys. Res. Sect. A 2017. [Google Scholar] [CrossRef]
- Semadeni, F.; Roessli, B.; Böni, P. Three-axis spectroscopy with remanent benders. Phys. B Condensed Matter 2001, 297, 152–154. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgii, R.; Weber, T. The Helical Magnet MnSi: Skyrmions and Magnons. Quantum Beam Sci. 2019, 3, 4. https://doi.org/10.3390/qubs3010004
Georgii R, Weber T. The Helical Magnet MnSi: Skyrmions and Magnons. Quantum Beam Science. 2019; 3(1):4. https://doi.org/10.3390/qubs3010004
Chicago/Turabian StyleGeorgii, Robert, and Tobias Weber. 2019. "The Helical Magnet MnSi: Skyrmions and Magnons" Quantum Beam Science 3, no. 1: 4. https://doi.org/10.3390/qubs3010004
APA StyleGeorgii, R., & Weber, T. (2019). The Helical Magnet MnSi: Skyrmions and Magnons. Quantum Beam Science, 3(1), 4. https://doi.org/10.3390/qubs3010004





