Distinct Recrystallization Pathways in a Cold-Rolled Al-2%Mg Alloy Evidenced by In-Situ Neutron Diffraction
Abstract
1. Introduction
2. Material and Methods
2.1. Samples Preparation
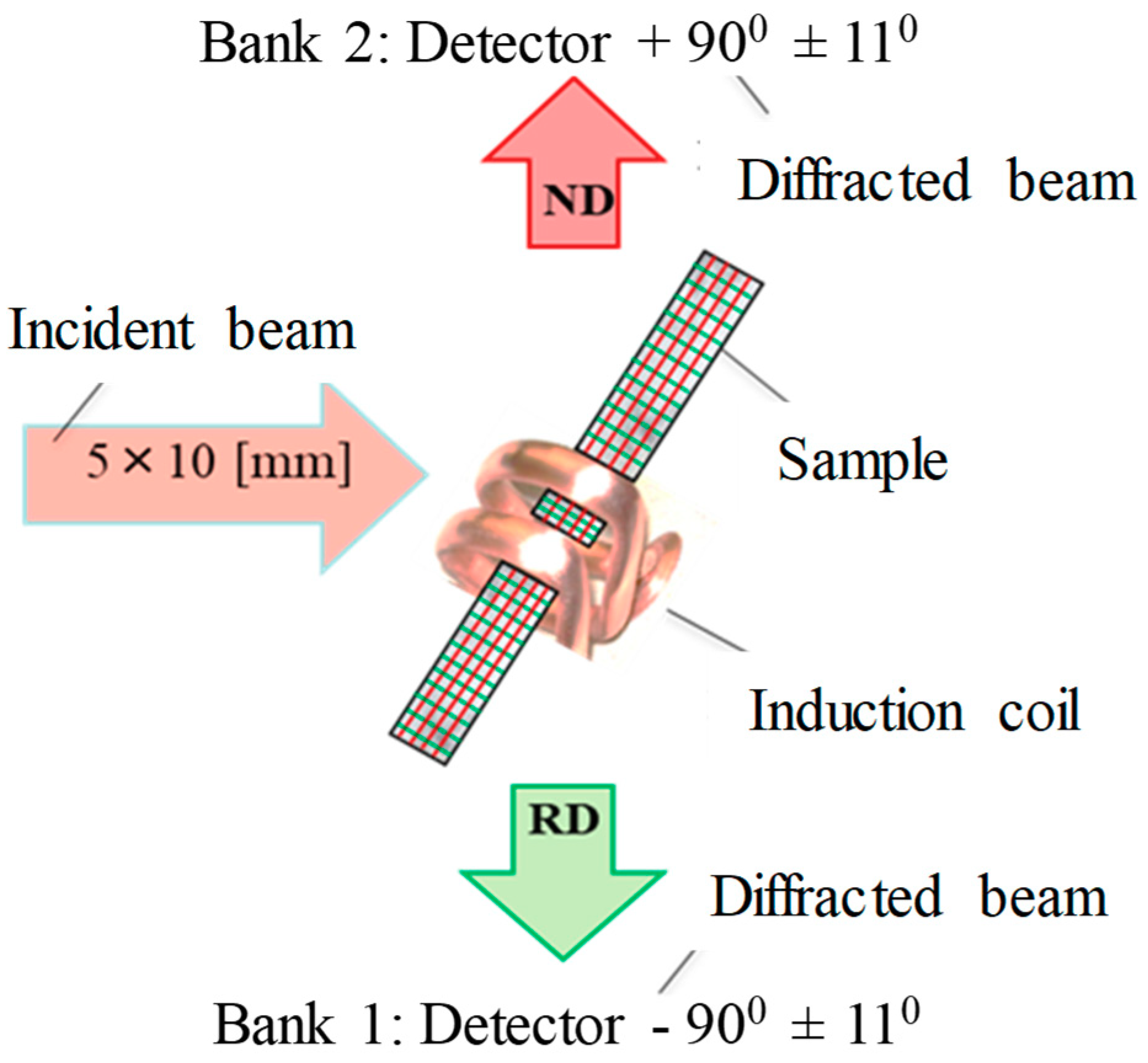
2.2. Neutron Diffraction Texture Characterizations
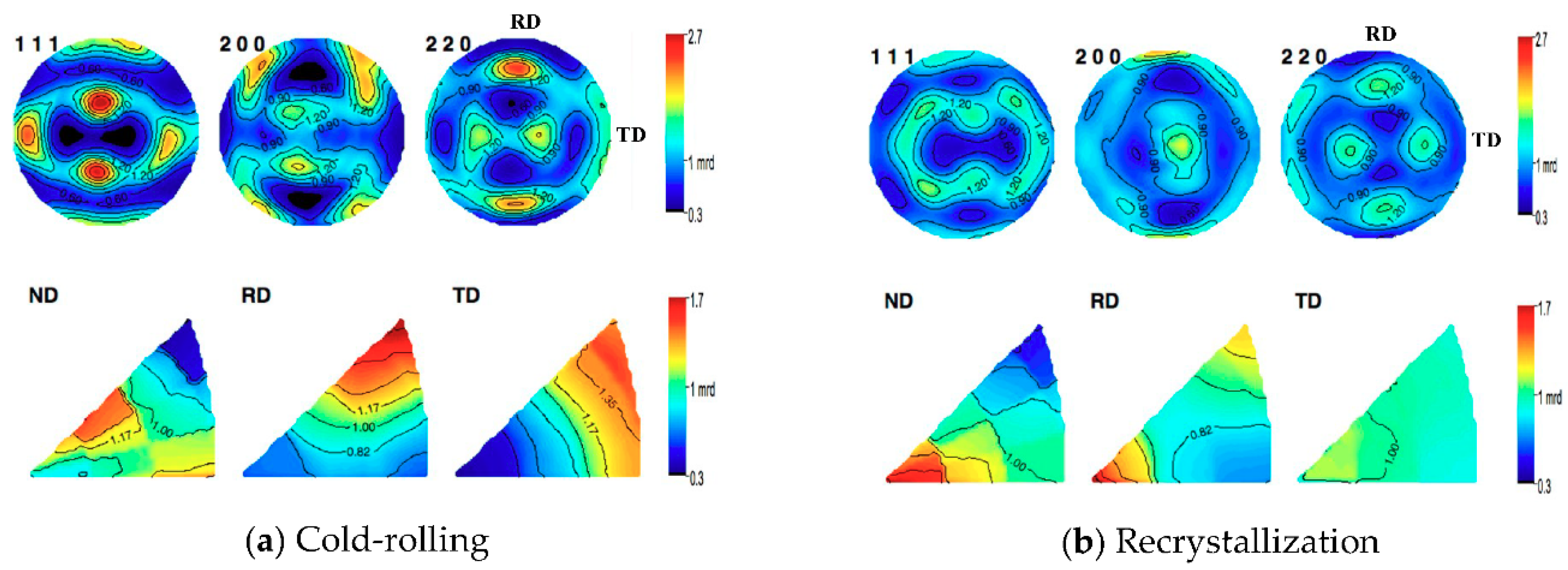
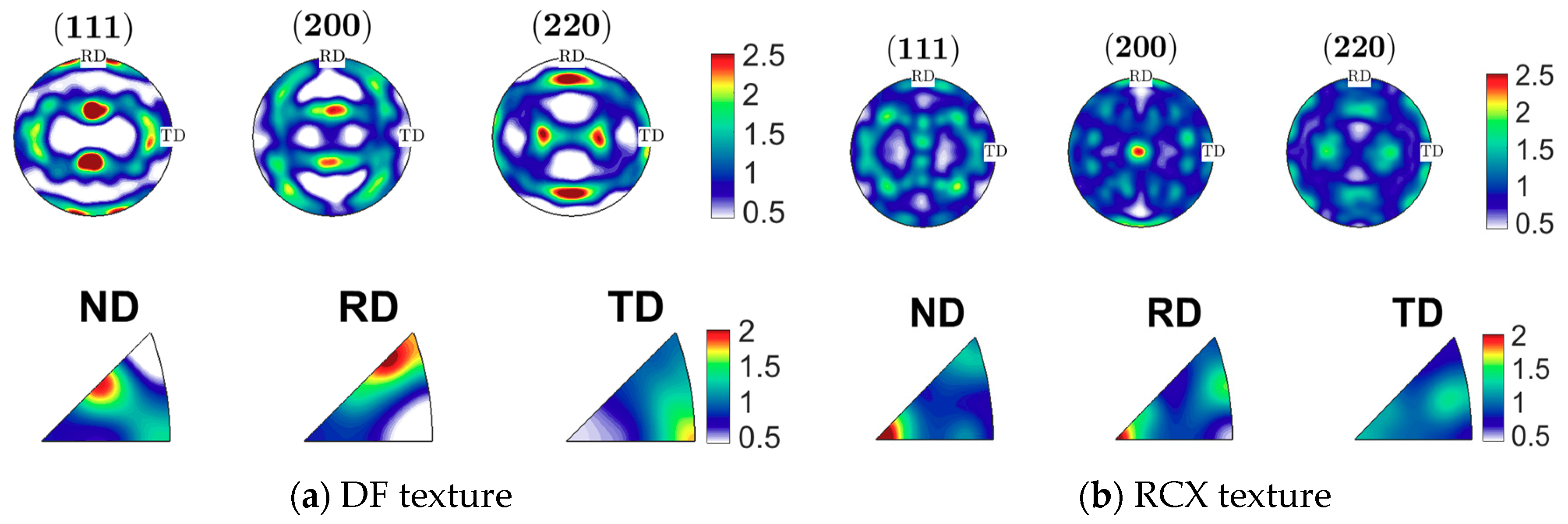
3. Results
3.1. Texture Decomposition Method
3.2. The Recrystallization Kinetics
4. Discussion
5. Conclusions
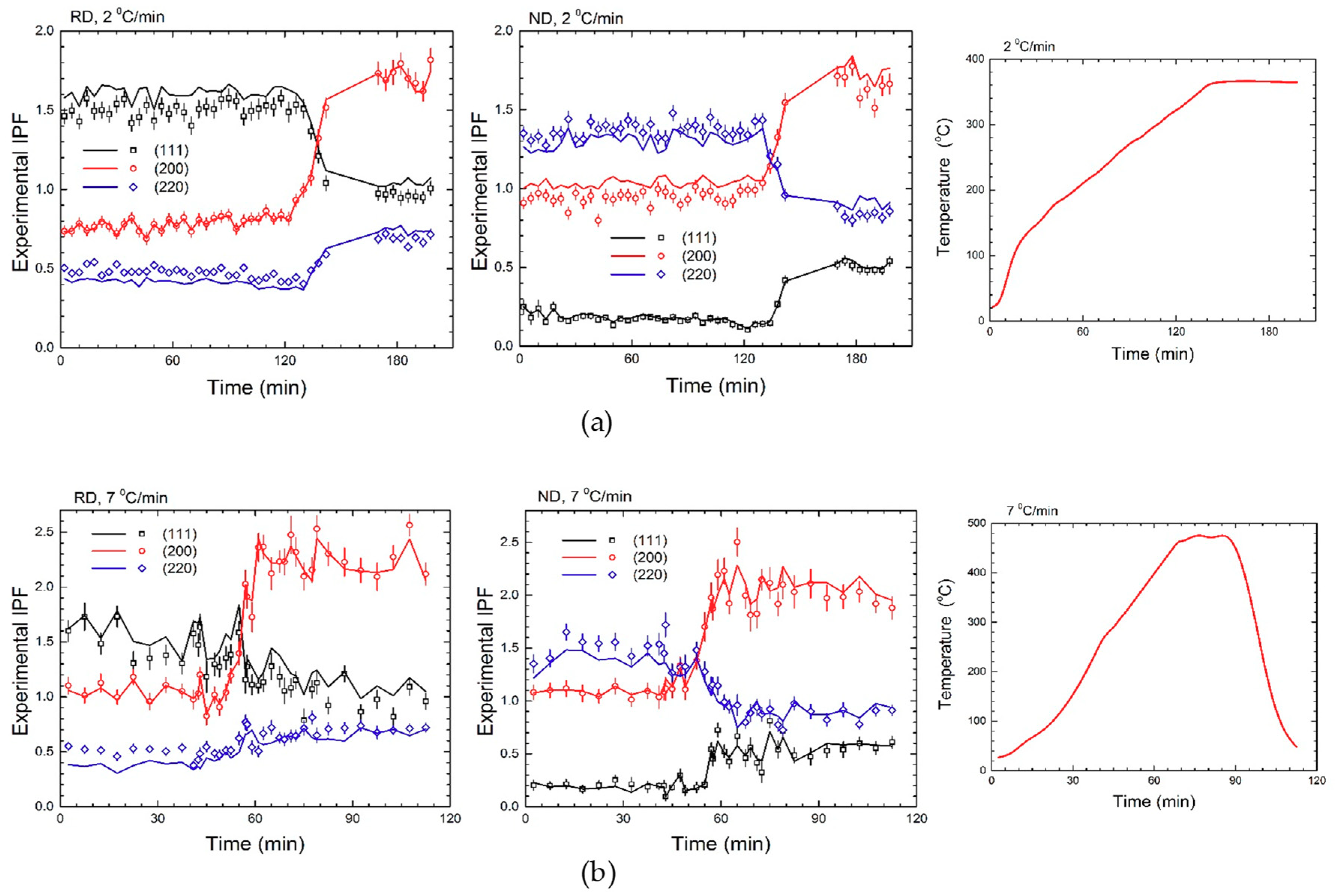
- (a)
- The ex situ and in-situ neutron diffraction measurements performed at HIPPO and VULCAN on an Al(2%Mg) alloy allowed for identification of the main texture components characterizing the deformation and recrystallization textures.
- (b)
- A new QMC method of analyzing the diffraction data recorded along ND and RD allowed the texture decomposition in standard components and provided their volume fractions evolution during isochronal heating.
- (c)
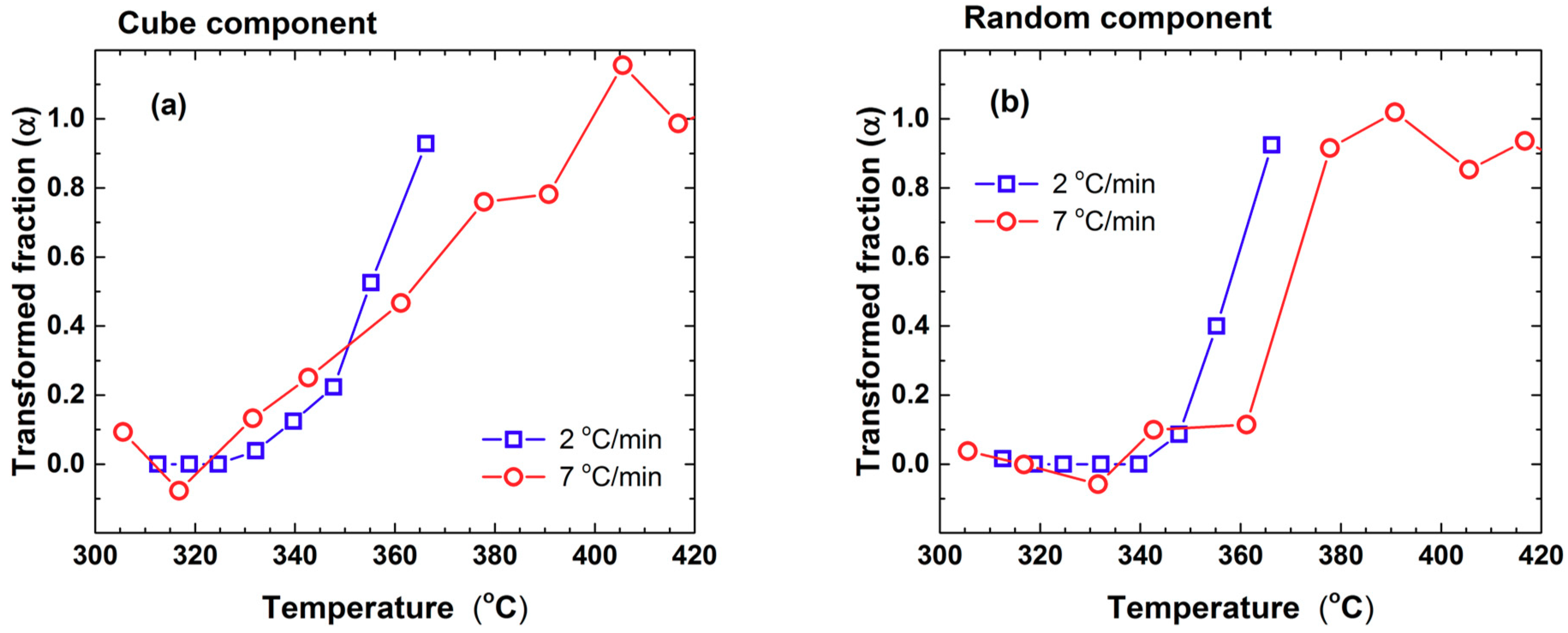
- The kinetics of recrystallization for random texture component can be analyzed using an analytic method to estimate the apparent activation energy.
- (d)
- Due to the presence of an initial content of cube texture, the sample annealed under 7 °C/min displayed an early start and more RCX at the end of the process.
- (e)
- The new QMC method of neutron diffraction data analysis may be extended to other instruments with more complex detector arrangements and may include texture component-dependent peak profile contributions as well.
Authors Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hjelen, J.; Orsund, R.; Nes, E. On the origin of recrystallization textures in aluminium. Acta Metall. Mater. 1991, 39, 1377–1404. [Google Scholar] [CrossRef]
- Lucke, K.; Engler, O. Effects of particles on development of microstructure and texture during rolling and recrystallisation in fcc alloys. Mater. Sci. Technol. 1990, 6, 1113–1130. [Google Scholar] [CrossRef]
- Radhakrishnan, B.; Sarma, G.; Weiland, H.; Baggethun, P. Simulations of deformation and recrystallization of single crystals of aluminium containing hard particles. Model. Simul. Mater. Sci. Eng. 2000, 8, 737–750. [Google Scholar] [CrossRef]
- Engler, O.; Lucke, K. Mechanisms of recystallization texture formation in aluminium alloys. Scr. Metall. Mater. 1992, 27, 1527–1532. [Google Scholar] [CrossRef]
- Engler, O.; Vatne, H.E.; Nes, E. The roles of oriented nucleation and oriented growth on recrystallization textures in commercial purity aluminium. Mater. Sci. Eng. 1996, 205, 187–198. [Google Scholar] [CrossRef]
- Nes, E.; Vatne, H.E. The 400<111> orientation relationship in recrystallization. Z. Metallkd. 1996, 87, 448–453. [Google Scholar]
- Engler, O. On the origin of the R orientation in the recrystallization textures of aluminum alloys. Metall. Mater. Trans. A 1999, 30, 1517–1527. [Google Scholar] [CrossRef]
- Duckham, A.; Engler, O.; Knutsen, R.D. Moderation of the recrystallization texture by nucleation at copper-type shear bands in Al-1Mg. Acta Mater. 2002, 50, 2881–2893. [Google Scholar] [CrossRef]
- Liu, W.C.; Li, Z.; Man, C.-S. Effect of heating rate on the microstructure and texture of continuous cast AA 3105 aluminum alloy. Mater. Sci. Eng. A 2008, 478, 173–180. [Google Scholar] [CrossRef]
- Wang, W.X.; Zhang, J.X.; Wang, Z.J.; Liu, W.C. A comparative study of the transformation kinetics of recrystallization texture of CC and DC 3003 aluminum alloys. Mater. Charact. 2018, 141, 412–422. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, A.; Kumar, A.; Chouhan, R.N.; Khatirkar, R.K. Microstructure and texture development during deformation and recrystallisation in strip cast AA8011 aluminum alloy. J. Alloys Compd. 2018, 742, 369–382. [Google Scholar] [CrossRef]
- Hirsch, J.; Lücke, K. Mechanism of deformation and development of rolling textures in polycrystalline F.C.C. metals—I. Description of rolling texture development in homogeneous CuZn alloys. Acta Metall. 1988, 36, 2863–2882. [Google Scholar] [CrossRef]
- Liu, W.C.; Li, J.; Yuan, H.; Yang, Q.X. Effect of recovery on the recrystallization texture of an Al–Mg alloy. Scr. Mater. 2007, 57, 833–836. [Google Scholar] [CrossRef]
- Smallman, R.E.; Lee, C.S. Advances in the theory of deformation and recrystallization texture formation. Mater. Sci. Eng. 1994, 184A, 97–112. [Google Scholar] [CrossRef]
- Hutchinson, W.B. Nucleation of recrystallization. Scr. Metall. 1992, 27, 1471–1475. [Google Scholar] [CrossRef]
- Liebmann, B.; Lucke, K.; Masing, G. Orientation dependency of the rate of growth during primary recrystallization of A1 single crystals. Z. Metallkd. 1956, 47, 57–63. [Google Scholar]
- Humphreys, F.J. Characterisation of fine-scale microstructures by electron backscatter diffraction (EBSD). Scr. Mater. 2004, 51, 771–776. [Google Scholar] [CrossRef]
- Schafer, C.; Mohles, V.; Gottstein, G. Modeling the effect of heating rate on recrystallization texture evolution in AA3103. Adv. Eng. Mater. 2010, 12, 981–988. [Google Scholar] [CrossRef]
- Attallah, M.M.; Strangwood, M.; Davis, C.L. Influence of the heating rate on the initiation of primary recrystallization in a deformed Al–Mg alloy. Scr. Mater. 2010, 63, 371–374. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Q.; Li, F. A review of texture evolution mechanisms during deformation by rolling in aluminum alloys. J. Mater. Eng. Perform. 2018, 27, 3350–3373. [Google Scholar] [CrossRef]
- Nes, E.; Solberg, J.K. Growth of cube grains during recrystallization of aluminium. Meter. Sci. Technol. 1986, 2, 19–21. [Google Scholar] [CrossRef]
- Bailey, J.E.; Hirsch, P.B. The recrystallization process in some polycrystalline metals. Proc. R. Soc. Lond. 1962, 267, 11–30. [Google Scholar] [CrossRef]
- Dillamore, I.L.; Katoh, H. The Mechanisms of Recrystallization in Cubic Metals with Particular Reference to Their Orientation-Dependence. Met. Sci. 1974, 8, 73–83. [Google Scholar] [CrossRef]
- Umezawa, A.; Inagaki, H. Formation of cube recrystallized grains in high purity aluminum. Z. Metallkd. 2006, 97, 49–58. [Google Scholar] [CrossRef]
- Miszczyk, M.M.; Paul, H.; Driver, J.H.; Poplewska, J. The influence of deformation texture on nucleation and growth of cube grains during primary recrystallization of AA1050 alloy. Acta Mater. 2017, 129, 378–387. [Google Scholar] [CrossRef]
- Radhakrishnan, B.; Sarma, G. Coupled simulations of texture evolution during deformation and recrystallization of fcc and bcc metals. Mater. Sci. Eng. 2008, 494, 73–79. [Google Scholar] [CrossRef]
- Radhakrishnan, B.; Sarma, G. The effect of coarse non-deformable particles on the deformation and static recrystallization of aluminium alloys. Philos. Mag. E 2004, 84, 2341–2366. [Google Scholar] [CrossRef]
- Sarma, G.B.; Radhakrishnan, B. Modeling microstructural effects on the evolution of cube texture during hot deformation of aluminum. Mater. Sci. Eng. A 2004, 385, 91–104. [Google Scholar] [CrossRef]
- Sidor, J.J.; Petrov, R.H.; Kestens, L.A.I. Modeling the crystallographic texture changes in aluminum alloys during recrystallization. Acta Mater. 2011, 59, 5735–5748. [Google Scholar] [CrossRef]
- Wang, Y.D.; Wang, X.-L.; Stoica, A.D.; Almer, J.D.; Lienert, U.; Haeffner, D.R. Separating the recrystallization and deformation texture components by high-energy X-rays. J. Appl. Cryst. 2002, 35, 684–688. [Google Scholar] [CrossRef]
- Liss, K.D.; Clemens, H.; Bystrzanowski, S.; Stark, A.; Buslaps, T.; Schimansky, F.P.; Gerling, R.; Scheu, C.; Schreyer, A. Recrystallization and phase transitions in a γ-TiAl-based alloy as observed by ex situ and in-situ high-energy X-ray diffraction. Acta Mater. 2006, 54, 3721–3735. [Google Scholar] [CrossRef]
- Liss, K.D.; Schmoelzer, T.; Yan, K.; Reid, M.; Peel, M.; Dippenaar, R.; Clemens, H. In-situ study of dynamic recrystallization and hot deformation behavior of a multiphase titanium aluminide alloy. J. Appl. Phys. 2009, 106, 113526. [Google Scholar] [CrossRef]
- Lauridsen, E.M.; Poulsen, H.F.; Nielsen, S.F.; Jensen, D.J. Recrystallization kinetics of individual bulk grains in 90% cold-rolled aluminium. Acta Mater. 2003, 51, 4423–4435. [Google Scholar] [CrossRef]
- Poulsen, S.O.; Lauridsen, E.M.; Lyckegaard, A.; Oddershede, J.; Gunlach, C.; Curfs, C.; Jensen, D.J. In-situ measurements of growth rates and grain-averaged activation energies of individual grain during recrystallization of 50% cold-rolled aluminium. Scr. Mater. 2011, 64, 1003–1006. [Google Scholar] [CrossRef]
- Branger, V.; Mathon, M.H.; Baudin, T.; Penelle, R. “In-situ” neutron diffraction study of the cube crystallographic texture development in Fe53%-Ni alloy during recrystallization. Scr. Mater. 2000, 43, 325–330. [Google Scholar] [CrossRef]
- Lonardelli, I.; Gey, N.; Wenk, H.R.; Humbert, M.; Vogel, S.C.; Lutterotti, L. In-situ observation of texture evolution during α → β and β → α phase transformation in titanium alloys investigated by neutron diffraction. Acta Mater. 2007, 55, 5718–5727. [Google Scholar] [CrossRef]
- Aydogan, E.; El-Atwani, O.; Takajo, S.; Vogel, S.C.; Maloy, S.A. High temperature microstructural stability and recrystallization mechanisms in 14WT alloys. Acta Mater. 2018, 148, 467–481. [Google Scholar] [CrossRef]
- Christien, F.; Telling, M.T.F.; Knight, K.S.; Le gall, R. A method for the monitoring of metal recrystallization based on the in-situ measurement of the elastic energy release using neutron diffraction. Rev. Sci. Instrum. 2015, 86, 053901. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L.; Holden, T.M.; Rennich, G.Q.; Stoica, A.D.; Liaw, P.K.; Choo, H.; Hubbard, C.R. VULCAN—The engineering diffractometer at the SNS. Phys. B Condens. Matter 2006, 385, 673–675. [Google Scholar] [CrossRef]
- Vogel, S.C.; Hartig, C.; Lutterotti, L.; Von Dreeele, R.B.; Wenk, H.R.; Williams, D.J. Texture measurements using the new neutron diffractometer HIPPO and their analysis using the Rietveld method. Powder Diffr. 2004, 19, 65–68. [Google Scholar] [CrossRef]
- Reiche, H.M.; Vogel, S.C. A versatile automated sample changer for texture measurements on the high-pressure preferred orientation neutron diffractometer. Rev. Sci. Instrum. 2010, 81, 093302. [Google Scholar] [CrossRef] [PubMed]
- Reiche, H.M.; Vogel, S.C.; Mosbrucker, P.; Larson, E.J.; Daymond, M.R. A furnace with rotating load frame for in-situ high temperature deformation and creep experiments in a neutron diffraction beam line. Rev. Sci. Instrum. 2012, 83, 053901. [Google Scholar] [CrossRef] [PubMed]
- Lutterotti, L.; Matthies, S.; Wenk, H.R.; Schultz, A.J.; Richardson, J. Combined texture and structure analysis of deformed limestone from time-of-flight neutron diffraction spectra. J. Appl. Phys. 1997, 81, 594–600. [Google Scholar] [CrossRef]
- Wenk, H.R.; Lutterotti, L.; Vogel, S. Texture analysis with the new HIPPO TOF diffractometer. Nucl. Instrum. Methods Phys. Res. A 2003, 515, 575–588. [Google Scholar] [CrossRef]
- Wenk, H.R.; Lutterotti, L.; Vogel, S.C. Rietveld texture analysis from TOF neutron diffraction data. Powder Diffr. 2010, 25, 283–296. [Google Scholar] [CrossRef]
- Xu, P.G.; Harjo, S.; Ojima, M.; Suzuki, H.; Ito, T.; Gong, W.; Vogel, S.C.; Inoue, J.; Tomota, Y.; Aizawa, K.; et al. High stereographic resolution texture and residual stress evaluation using time-of-flight neutron diffraction. J. Appl. Phys. 2018, 51, 746–760. [Google Scholar] [CrossRef] [PubMed]
- Stoica, G.M.; Stoica, A.D.; An, K.; Ma, D.; Wang, X.L. Extracting grain-orientation-dependent data from in-situ time-of-flight neutron diffraction. I. Inverse pole figures. J. Appl. Cryst. 2014, 47, 2019–2029. [Google Scholar] [CrossRef]
- Ma, D.; Stoica, A.D.; Wang, Z.; Beese, A.M. Crystallographic texture in an additively manufactured nickel-base superalloy. Mater. Sci. Eng. A 2017, 684, 47–53. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX–Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef]
- An, K. VDRIVE—Data Reduction and Interactive Visualization Software for Event Mode Neutron Diffraction; ORNL Report No. ORNL-TM-2012-621; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2012. [Google Scholar]
- Clausen, B. SMARTSWare Los Alamos National Laboratory Report; LAUR-04-6581; Los Alamos National Laboratory: Los Alamos, NM, USA, 2003. [Google Scholar]
- Matthies, S.; Vinel, G.W.; Helmig, K. Standard Distributions in Texture Analysis; Akademie-Verlag: Berlin, Germany, 1987; Volumes I–III, pp. 1987–1990. [Google Scholar]
- Tarasiuk, J.; Wierzbanowski, K.; Bacroix, B. Texture decomposition into Gauss-shaped functions: Classical and genetic algorithm methods. Comput. Mater. Sci. 2004, 29, 179–186. [Google Scholar] [CrossRef]
- Bohlke, T.; Haus, U.; Schulze, V. Crystallographic texture approximation by quadratic programming. Acta Mater. 2006, 54, 1359–1368. [Google Scholar] [CrossRef]
- Dessieux, L.L.; Stoica, A.D.; Bingham, P.R. Single crystal to polycrystal neutron transmission simulation. Rev. Sci. Instrum. 2018, 89, 025103. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnan, B.; Sarma, G.B.; Zacharia, T. Modeling the kinetics and microstructural evolution during static recrystallization—Monte Carlo simulation of recrystallization. Acta Mater. 1998, 46, 4415–4433. [Google Scholar] [CrossRef]
- Benchabane, G.; Boumerzoug, Z.; Gloriant, T.; Thibon, I. Microstructural characterization and recrystallization kinetics of cold-rolled copper. Phys. B Condens. Matter 2011, 406, 1973–1976. [Google Scholar] [CrossRef]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef]
- Friedman, H.I. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. J. Polym. Sci. Part C 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Liu, F.; Sommer, F.; Bos, C.; Mittemeijer, E.J. Analysis of solid state phase transformation kinetics: Models and recipes. Int. Mater. Rev. 2007, 52, 192–212. [Google Scholar] [CrossRef]
- Sidor, J.; Miroux, A.; Petrov, R.; Kestens, L. Microstructural and crystallographic aspects of conventional and asymmetric rolling processes. Acta Mater. 2008, 56, 2495–2507. [Google Scholar] [CrossRef]
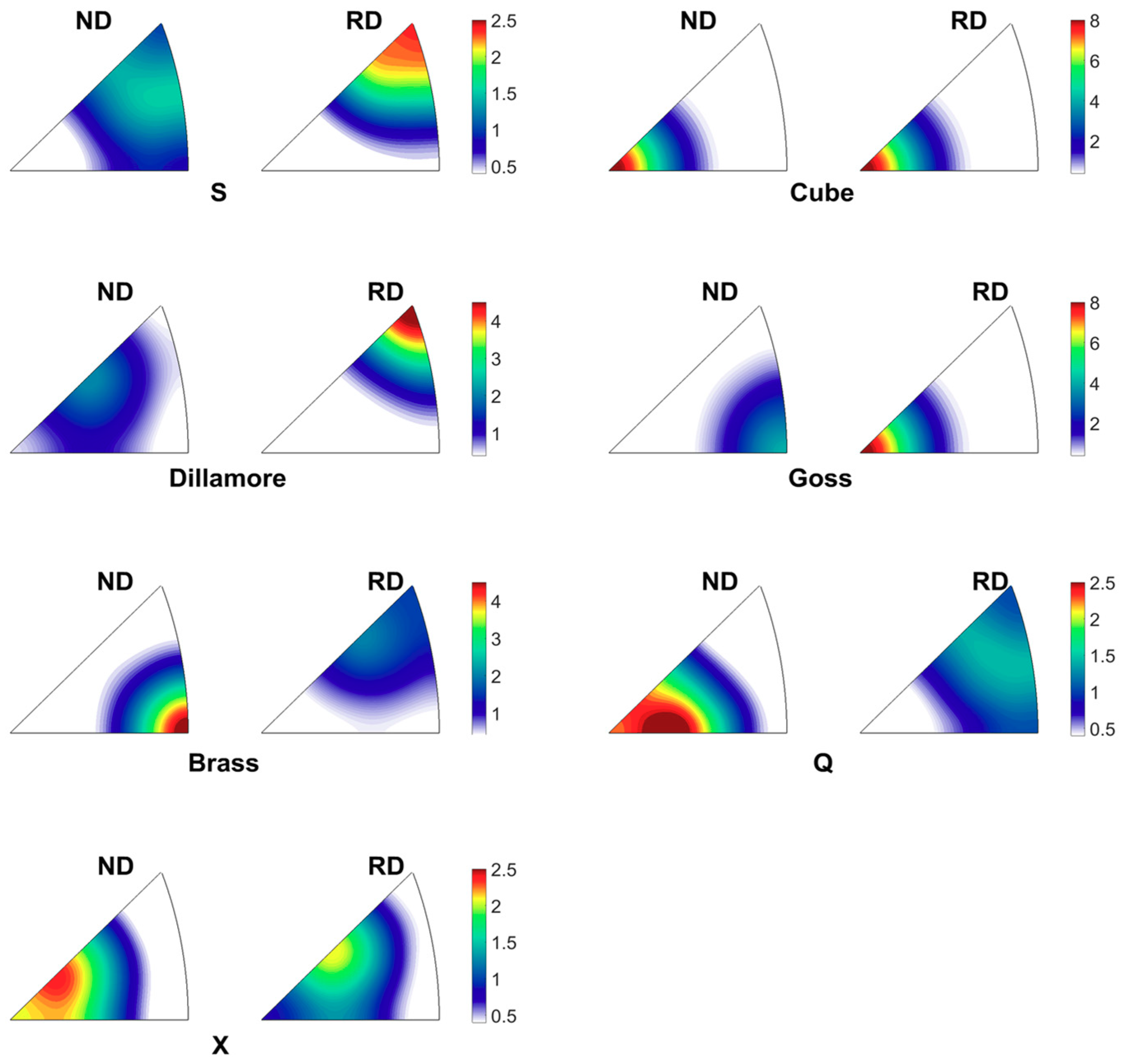

| RD | Random mrd | S {123}<634> | Dillamore {4411}<11118> | Brass {110}<112> | X {114}<311> | Cube {001}<100> | Goss {011}<100> | Q {310}<123> |
|---|---|---|---|---|---|---|---|---|
| <111> | 1 | 2.73 | 4.70 | 1.84 | 0.31 | 0.00 | 0.00 | 0.94 |
| <001> | 1 | 0.03 | 0.00 | 0.16 | 0.77 | 7.22 | 7.23 | 0.18 |
| <011> | 1 | 0.43 | 0.23 | 0.25 | 0.18 | 0.01 | 0.02 | 1.09 |
| <113> | 1 | 0.88 | 0.45 | 1.44 | 2.10 | 0.89 | 0.85 | 1.08 |
| <133> | 1 | 1.22 | 1.22 | 0.85 | 0.39 | 0.01 | 0.01 | 1.42 |
| <012> | 1 | 0.38 | 0.10 | 0.47 | 1.01 | 0.63 | 0.64 | 0.66 |
| <112> | 1 | 1.91 | 1.84 | 2.23 | 1.56 | 0.10 | 0.11 | 1.46 |
| <135> | 1 | 0.80 | 0.47 | 0.90 | 1.00 | 0.20 | 0.20 | 1.17 |
| ND | Random mrd | S {123}<634> | Dillamore {4411}<11118> | Brass {110}<112> | X {114}<311> | Cube {001}<100> | Goss {011}<100> | Q {310}<123> |
|---|---|---|---|---|---|---|---|---|
| <111> | 1 | 0.84 | 0.25 | 0.05 | 0.05 | 0.00 | 0.11 | 0.01 |
| <001> | 1 | 0.05 | 0.39 | 0.01 | 1.77 | 7.17 | 0.02 | 2.10 |
| <011> | 1 | 1.07 | 0.37 | 4.65 | 0.16 | 0.01 | 4.14 | 0.34 |
| <113> | 1 | 0.97 | 2.03 | 0.21 | 1.92 | 0.84 | 0.26 | 1.38 |
| <133> | 1 | 1.53 | 0.51 | 1.98 | 0.17 | 0.01 | 2.04 | 0.17 |
| <012> | 1 | 0.69 | 1.07 | 1.41 | 1.28 | 0.63 | 1.34 | 1.65 |
| <112> | 1 | 1.44 | 1.47 | 0.20 | 0.74 | 0.10 | 0.27 | 0.41 |
| <135> | 1 | 1.18 | 1.15 | 1.46 | 0.83 | 0.19 | 1.43 | 0.85 |
| Random | S | Dillamore | Brass | X | Cube | Goss | Q | |
|---|---|---|---|---|---|---|---|---|
| DF at 2 °C/min | 0.00 | 0.11 | 0.15 | 0.15 | 0.31 | 0.00 | 0.07 | 0.21 |
| DF at 7 °C/min | 0.02 | 0.15 | 0.12 | 0.15 | 0.31 | 0.03 | 0.07 | 0.16 |
| RCX at 2 °C/min | 0.43 | 0.11 | 0.02 | 0.00 | 0.06 | 0.10 | 0.07 | 0.21 |
| RCX at 7 °C/min | 0.38 | 0.15 | 0.05 | 0.00 | 0.00 | 0.19 | 0.07 | 0.16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stoica, G.M.; Dessieux, L.L.; Stoica, A.D.; Vogel, S.C.; Muralidharan, G.; Radhakrishnan, B.; Gorti, S.B.; An, K.; Ma, D.; Wang, X.-L. Distinct Recrystallization Pathways in a Cold-Rolled Al-2%Mg Alloy Evidenced by In-Situ Neutron Diffraction. Quantum Beam Sci. 2018, 2, 17. https://doi.org/10.3390/qubs2030017
Stoica GM, Dessieux LL, Stoica AD, Vogel SC, Muralidharan G, Radhakrishnan B, Gorti SB, An K, Ma D, Wang X-L. Distinct Recrystallization Pathways in a Cold-Rolled Al-2%Mg Alloy Evidenced by In-Situ Neutron Diffraction. Quantum Beam Science. 2018; 2(3):17. https://doi.org/10.3390/qubs2030017
Chicago/Turabian StyleStoica, Grigoreta M., Luc L. Dessieux, Alexandru D. Stoica, Sven C. Vogel, Govindarajan Muralidharan, Balasubramaniam Radhakrishnan, Sarma B. Gorti, Ke An, Dong Ma, and Xun-Li Wang. 2018. "Distinct Recrystallization Pathways in a Cold-Rolled Al-2%Mg Alloy Evidenced by In-Situ Neutron Diffraction" Quantum Beam Science 2, no. 3: 17. https://doi.org/10.3390/qubs2030017
APA StyleStoica, G. M., Dessieux, L. L., Stoica, A. D., Vogel, S. C., Muralidharan, G., Radhakrishnan, B., Gorti, S. B., An, K., Ma, D., & Wang, X.-L. (2018). Distinct Recrystallization Pathways in a Cold-Rolled Al-2%Mg Alloy Evidenced by In-Situ Neutron Diffraction. Quantum Beam Science, 2(3), 17. https://doi.org/10.3390/qubs2030017







