Application of Enhanced K-Means and Cloud Model for Structural Health Monitoring on Double-Layer Truss Arch Bridges

Abstract

Bridges, as vital infrastructure, require ongoing monitoring to maintain safety and functionality. This study introduces an innovative algorithm that refines bridge component performance assessment through the integration of modified K-means clustering, silhouette coefficient optimization, and cloud model theory. The purpose is to provide a reliable method for monitoring the safety and serviceability of critical infrastructure, particularly double-layer truss arch bridges. The algorithm processes large datasets to identify patterns and manage uncertainties in structural health monitoring (SHM). It includes field monitoring techniques and a model-driven approach for establishing assessment thresholds. The main findings, validated by case studies, show the algorithm’s effectiveness in enhancing clustering quality and accurately evaluating bridge performance using multiple indicators, such as statistical significance, cluster centroids, average silhouette coefficient, Davies–Bouldin index, average deviation, and Sign-Rank test p-values. The conclusions highlight the algorithm’s utility in assessing structural integrity and aiding data-driven maintenance decisions, offering scientific support for bridge preservation efforts.

1. Introduction

1.1. Background and Significance

Bridges serve as pivotal nodes in transportation networks, with their safety being paramount to the stability of socio-economic systems. The double-layer truss arch bridge, a large-span structure often tasked with carrying significant transportation burdens, is subject to environmental erosion, traffic loads, and material aging. Therefore, regular structural performance assessments are crucial to ensure the safe operation of bridges, encompassing real-time monitoring data analysis, load-bearing capacity evaluation, and other critical aspects. Utilizing modern sensors and data processing technologies for health monitoring can enhance the overall performance and safety of bridges.

The introduction of an improved clustering-silhouette coefficient (SC) algorithm for the performance evaluation of double-layer truss arch bridges addresses this gap. By integrating advanced computational techniques, such as the modified K-means clustering algorithm, SC evaluation, and cloud model theory, this comprehensive algorithm offers a dynamic performance assessment tool for bridge health monitoring. It allows for the precise detection of stress anomalies and the assessment of the overall performance of bridge components, which is crucial for timely maintenance and the preservation of structural integrity.

The significance of this study lies in its potential to revolutionize bridge health monitoring practices. By providing a more accurate, data-driven approach to performance evaluation, it supports informed decision-making in bridge maintenance and management. The proposed method not only enhances the predictive capabilities of bridge health assessments but also contributes to the body of knowledge in structural engineering and computational intelligence, paving the way for smarter and safer infrastructure management.

In essence, the integration of an improved clustering-silhouette coefficient within the cloud model framework for bridge health monitoring is a monumental step towards proactive, intelligent systems that ensure the enduring safety and reliability of our bridge networks.

1.2. Literature Review

1.2.1. Current Study’s Bridge Performance Assessment in Structural Health Monitoring

Current research methods of bridge performance assessment in structural health monitoring (SHM) have been evolving to incorporate advanced technologies and techniques, covering various aspects from visual evaluations to complex dynamic analyses. Researchers have proposed multiple methods to enhance the accuracy and efficiency of bridge assessments. For instance, in the field of Sustainable Building Design (SBD), Gharehbaghi et al. [1] proposed a holistic sustainable framework for rating the sustainable performance of buildings. This framework includes a multi-dimensional assessment method and compares case studies from Australia, the United Kingdom, and the USA. The study highlights the importance of incorporating sustainable practices in building design and assessment. Nondestructive Evaluation (NDE) tools and SHM techniques [2,3] play a crucial role in assessing the condition of bridges. The Federal Highway Administration (FHWA) also provides resources such as the Robotic Assisted Bridge Inspection Tool (RABIT™) and NDE protocols for bridge assessment [2]. Additionally, vibration-based SHM methods are being explored for accurate damage quantification in steel bridges [4]. The development of deep learning-based approaches for bridge condition assessment is gaining traction as an alternative to traditional inspection methods [5]. These approaches leverage SHM systems to improve the accuracy and efficiency of bridge performance assessment. Overall, the current research landscape in bridge performance assessment in SHM is focused on integrating advanced technologies, such as NDE tools, and deep learning methods to enhance the accuracy and reliability of bridge condition assessment [6]. The diversification and refinement of bridge assessment technologies have significantly improved the safety and durability of bridge structures. These studies provide a rich theoretical and practical foundation for bridge assessments. Future research in this field, such as the integration of clustering methods and cloud models, aims to further improve the performance assessment of bridges and ensure their structural safety and resilience, offering more reliable data support for bridge maintenance and management.

1.2.2. The State of the Art of Clustering, Quality Assessment, and Cloud Algorithms

Predictive maintenance is a common goal for bridge performance assessment in bridge health monitoring. By using clustering and quality assessment algorithms, bridge health monitoring systems can predict when maintenance is needed, thus preventing failures and extending the lifespan of the bridge. In bridge health monitoring, sensors collect data on structural integrity, while clustering and quality assessment algorithms process these data to identify patterns and anomalies, which largely rely on the machine learning technologies.

Machine learning techniques [7] can be categorized into three types: supervised learning, unsupervised learning, and semi-supervised learning. In supervised learning, algorithms generate functions that map inputs to outputs, with applications in classification and regression. Unsupervised learning deals with unlabeled input data and unknown outcomes, finding applications in clustering, dimensionality reduction, and association rule learning. Semi-supervised learning involves a mix of labeled and unlabeled instances.

As a machine learning method, clustering analysis algorithms are numerous and widely applied. K-means clustering [8] is an algorithm that requires a preset number of clusters. Although efficient, it is sensitive to noise and outliers. Gaussian Mixture Models (GMM) [9,10] are based on probabilistic models and can handle complex data distributions. Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [11] can identify noise and outliers. Hierarchical Clustering (HC) [12] constructs a hierarchical tree structure and is suitable for small dataset analysis. Density Peak Clustering (DPC) [13,14] forms clusters by identifying density peaks. Kohonen clustering [15] obtained classification patterns in normal operating conditions and is straightforward for outlier detection. Spectral Clustering (SC) [16,17] uses graph theory and matrix operations, making it suitable for data with complex shapes. Self-Organizing Maps (SOM) [18] are a neural network-based clustering algorithm. By constructing a low-dimensional grid and adjusting weight vectors, it clusters input data samples into different grid units, suitable for clustering analysis, feature extraction, and anomaly detection. Affinity Propagation (AP) [19] achieves clustering through message passing without needing a preset number of clusters. Mean Shift Clustering (MSC) [20] is based on density gradients and is suitable for clustering non-convex shapes.

These clustering algorithms demonstrate their advantages in handling different types of data and meeting specific application needs, but they also have certain limitations. These limitations include sensitivity to parameters and noise, an inability to automatically determine the optimal number of clusters, poor performance with high-dimensional data, dependence on measurement scales, subjectivity in result interpretation, the impact of algorithm choice on results, efficiency issues in handling large-scale data, assumptions about data distribution, and the stability of clustering results. These drawbacks limit the performance and universality of clustering algorithms in different application scenarios. Researchers often use a combination of these machine learning methods or integrate other methods for targeted analysis. Specifically, for the application of machine learning methods in the performance evaluation of cables/suspenders, Shunlong Li et al. [21] proposed a state evaluation method based on machine learning. They used the GMM and Bayesian Information Criterion (BIC) to analyze the tension ratio of stay cables, thereby assessing their safety status, and ensured the evaluation was independent of external factors through preprocessing.

To evaluate the quality of these clustering methods, several approaches of Cluster Quality Evaluation Methods can be used as follows. The Elbow Method (EM) [22] seeks for the optimal number of clusters by calculating the sum of squared errors (SSE) for different numbers of clusters. The silhouette coefficient method [23,24] evaluates the cohesion within clusters and the separation between clusters. The higher the value is, the better the clustering quality is. The Davies–Bouldin index (DBI) [25] measures the separation between clusters and the compactness within clusters. Lower values indicate better clustering. The Rand Index (RI) [26] and Adjusted Rand Index (ARI) [27,28] evaluate the quality by comparing the clustering results with the true labels. A Principal Component Analysis (PCA) [29] can be used for the dimensionality reduction of multiple parameters. Cross-Validation [30,31] assesses the stability and generalization ability of clustering by splitting the dataset.

The cloud model (CM) theory was originally introduced by Prof. Deyi Li in 1995 [32], grounded in the principles of probability and fuzzy set theory. Since its inception, the theory has been continuously refined and expanded through subsequent studies. In the context of the normal cloud model, a decision-making method has been applied in the evaluation of distribution network planning, showcasing the versatility of cloud models in different domains [33]. Furthermore, the cloud model method has also been introduced in the evaluation of rock slope stability, addressing the issue of fixed weights in traditional fuzzy analysis methods [34]. Additionally, the cloud model is introduced to construct an assessment model to account for the randomness and fuzziness [35]. Also, the cloud model can be combined with the variable weight theory to determine the indicator’s weight [36].

1.3. Research Gaps and Objectives

Despite the extensive application of clustering analysis, silhouette coefficients, and structural performance assessment techniques within their individual domains, their comprehensive integration into performance evaluations of bridge component systems via SHM, particularly within truss arch composite frameworks, remains rare in the current applications. Cluster analysis may suffer from dependency on initial conditions, leading to local rather than global optima, while the silhouette coefficient has limited interpretability for high-dimensional data, primarily being applicable to two-dimensional contexts. Additionally, its application of the silhouette coefficient may not always provide clear boundaries for cluster evaluation. To simplify calculations and enhance the clarity of the cluster quality assessment, an improved silhouette coefficient is proposed. This modification is necessary to provide a more intuitive and quantitative indicator for evaluating the relative position of each data point within its assigned cluster and the overall quality of the clustering.

From the above, this paper will propose an innovative method for assessing the performance of various components in double-layer truss arch bridges, including arch ribs, trusses, and hangers. The approach integrates an improved K-means clustering algorithm, a silhouette coefficient assessment, and the cloud model theory. It analyzes field health monitoring data, applies nonlinear structural analysis, and utilizes the enhanced K-means for data clustering. The silhouette coefficient and cloud model theory assess the clustering quality, ensuring the accurate detection of stress anomalies across components and a holistic evaluation of their operational performance. A case study validates the method’s effectiveness for comprehensive bridge health assessment and its utility in bridge maintenance strategy formulation.

2. Methodology

2.1. Framework Construction for Performance Assessment of Suspender Cable System

The research framework in Figure 1 comprehensively addresses the assessment and monitoring of bridge performance. In this study, we defined the research scope, collected monitoring data, set evaluation thresholds, analyzed data preliminarily, identified key features with PCA, grouped data through clustering analysis, conducted assessment with silhouette analysis, and predicted structural safety using the cloud model considering data uncertainty.

The methodology section meticulously constructs a framework for evaluating the performance of the suspender cable system of double-layer truss arch bridge (see Figure 1a), introduces a refined K-means clustering approach (see Figure 1e), and details the enhancement techniques that bolster the silhouette coefficient (SC) indicator (see Figure 1f). It further elaborates on the development of a cloud model-based framework for assessing clustering quality and the strategies for setting assessment levels and executing multi-parameter indicator cloud clustering.

Transitioning into the application phase, the case study (see Figure 1a) of a double-layer truss arch bridge is presented, offering a detailed account of the bridge’s characteristics, the finite element method-driven stress threshold determination (see Figure 1b), and the intricacies of data acquisition (see Figure 1c) for field monitoring. This practical application is pivotal in validating the theoretical constructs developed earlier in the paper.

The results and discussion section delves into the analysis of key components identified through characteristic analysis and the PCA method (see Figure 1d), followed by an eigenvalue analysis corresponding to each cluster level post-modification. It scrutinizes the impact of the improved clustering algorithm on the case bridge components and assesses the effects on cluster quality and performance metrics (see Figure 1e). The section culminates in a cloud model-based cluster quality assessment (see Figure 1f) of the suspender cables, evaluating the impact of various single-parameter cloud model (see Figure 1g) parameters on clustering quality.

2.2. Revised K-Means Clustering Method

2.2.1. Description

The K-means clustering method is a process that begins with K initial cluster centers and refines them by reassigning data points based on Euclidean distance to the nearest center and then updating the center as the mean of its assigned points. This cycle repeats until the centers no longer change significantly, resulting in an optimized clustering where the sum of distances within each cluster is minimized, and an indicator function R efficiently classifies each data point into its respective cluster.

2.2.2. Enhancement Techniques

The enhanced K-means clustering algorithm is an iterative process designed to partition data into K distinct clusters. It begins by randomly selecting K clusters as initial centroids, K = 3 and μ_k= [μ₁, μ₂, …, μ_K]. After that, the raw data matrix σ_p(t) = [σ_p1(t), σ_p2(t), …, σ_pn(t)] was input and sorted into an ascending order matrix x_p = [x_p1, x_p2, …, x_pn]. The algorithm then enters a loop, where each time-serial data point is assigned to the nearest centroid by using the Squared Euclidean Distance method [37] and determined by the expression $R_p\left(t\right)=\arg \min dist\left({\sigma }_{p,i}(t),{\mu }_K\right)$, and the original centroids are recalculated as the mean of their assigned data points. This process repeats until the centroids’ positions change insignificantly, indicating convergence, or the algorithm reaches a predefined maximum number of iterations. The end result is a set of assigned labels and centroids that minimize the variance within each cluster, effectively organizing the data into distinct groups. Details can be seen in Appendix A.

2.3. Enhanced Silhouette Coefficient Indicator

2.3.1. Modifications to the Silhouette Coefficient

Assessing the goodness of clustering results was usually performed using some commonly used clustering metrics such as silhouette coefficient (SC) [23,38], Davies–Bouldin index (DBI) [39], and other indicators. The SC metric can be used to measure the similarity of each sample to other samples within its cluster and the degree of difference from other clusters. The application of these metrics provided an objective evaluation framework for clustering results, ensuring the rigor of the research and the reliability of the conclusions.

For the performance parameter stress state σ_pi(t) of the i-th component at time t and the corresponding target threshold σ_pi,Obj(t), the average SC ${\overline{s}}_i$ can be defined as follows:

$${\overline{s}}_i={\displaystyle \sum _{t=t_0}^{t_{Total}}\left({\sigma }_{pi,Obj}(t)-{\sigma }_{pi}(t)\right)/\max \left\{{\sigma }_{pi}(t), {\sigma }_{pi,Obj}(t) \right\}}$$

(1)

where the value range from time point t₀ to t_Total is between [−1, 1]. The closer this metric is to 1, the better the clustering effect; the closer it is to −1, the worse the clustering effect; and a value close to 0 indicates overlapping samples. The SC provides a method for measuring clustering quality by considering the similarity and dissimilarity between samples.

To overcome these limitations, this paper proposed an improved strategy: by sorting the original data, the impact of randomness during system initialization and iteration can be effectively reduced, ensuring the consistency and accuracy of clustering results. This method improved the robustness of the K-means algorithm by optimizing the initialization process of cluster centers, making it more stable and effective when handling real data.

2.3.2. Construction of a Cloud Model-Based Clustering Quality Assessment Framework

To appraise the efficacy of the K-means clustering, the SC is a measure used to assess the quality of clustering, reflecting the cohesion and separation of clusters, which is also a standard metric for gauging clustering algorithm performance [23,38]. This indicator quantifies the affinity of each data point to its cluster peers and the divergence from points in alternate clusters. It is well suited for monitoring the variability in the mechanical behavior of structural elements—like arch ribs, trusses, and hangers—throughout the testing time serial t within the interval [t₁, t_n]. The SC effectively evaluates the clustering quality by measuring the alignment of component states with predefined thresholds.

The improved silhouette coefficient is calculated by considering both the cohesion within a cluster and the separation from neighboring clusters. The cohesion is measured by the average distance between data points within the same cluster, represented by ${\lambda }_i\left(t,k\right)={\displaystyle \sum _{t=t_0}^{t_n}dist({\mu }_i(t_j,k),{\mu }_i(t_p,k))/(n-1)}$, while separation is measured by the average distance to the nearest neighboring cluster center, denoted by ${\beta }_i\left(t,k\right)=\underset{j\ne k}{\min }({\displaystyle \sum _{l=1,l\ne k}^{K}dist(C_i(t,k),C_i(t,l))/(K-1))}$. The SC indicator $S_i(t,k)=\left({\mu }_{i,Obj}\left(k\right)-{\lambda }_i\left(t,k\right)\right)/\max \left({\mu }_{i,Obj}\left(k\right),{\lambda }_i\left(t,k\right)\right)$ is then computed using these values with a range of [−1, 1], where values close to 1 indicate good clustering quality.

To simplify and make the silhouette coefficient more accessible, the separation component is set to a fixed value, ensuring clear cluster boundaries and good clustering effects. The modified SC S′_i(t, k) is then adjusted to account for this fixed separation threshold, providing a clear assessment of the suitability of the stress dataset of the i-th hanger in cluster k at time t.

$${S^{\prime }}_i(t,k)=\left(S_i(t,k)-\min (S_i(t,k))\right)/\left(\max (S_i(t,k)-\min (S_i(t,k)\right)$$

(2)

Finally, to align with standard cloud model parameter intervals and reflect clustering effects more intuitively, the SC is normalized to a range of [0, 1] through a normalization process. The modified SC, S′_i(t, k), provides a quantitative measure where values closer to 1 indicate better clustering effects, and values closer to 0 indicate poorer clustering effects. This normalized coefficient offers a clear and direct assessment of the clustering quality for the stress dataset of each hanger over the time period from t₁ to t_n.

2.4. Methods for Setting Assessment Levels and Multi-Parameter Indicator Cloud Clustering

2.4.1. Setting Assessment Grading Standards

In accordance with the activation mechanism of the positive cloud generator [40,41], the SC cluster quality assessment intervals and their respective standard cloud model parameters were established. Leveraging current experience, the cluster quality is categorized into four evaluation grades: Grade I, Grade II, Grade III, and Grade IV, corresponding to four distinct percentile ranges of the adjusted silhouette coefficient S′_i(t, k), namely (75, 100], (50, 75], (25, 50], and (0, 25] (see in Figure 2).

For the SC S_i′(t, k) across these four percentile ranges, the standard cloud model’s characteristic parameters are determined using a normal distribution, including the expected value EX_k, entropy EN_k, and hyper-entropy HE_k. The expression can be determined by EX_k= ($\overline{\gamma }$_k,max + $\overline{\gamma }$_k,min)/2, EN_k= ($\overline{\gamma }$_k._max − $\overline{\gamma }$_k,min)/6, and HE_k = 1/250, with k ranging from 1 to 4. Here, $\overline{\gamma }$_k,max and $\overline{\gamma }$_k,min denote the maximum and minimum scores within each level’s range. The EX value indicates the midpoint of the SC for each range, signifying the central tendency of the coefficient. Accordingly, the EX value for the standard cloud model characteristic parameters corresponding to the four SC intervals are 0.875, 0.625, 0.375, and 0.125. The entropy value EN, which mirrors the fluctuation within the range, is uniformly set at 1/24. The hyper-entropy value HE, reflecting the uncertainty of the entropy, is uniformly set at 0.004.

2.4.2. Cloud Clustering Quality Assessment of Single-Parameter Indicator

Based on the trigger mechanism of the reverse cloud generator [41], the cloud clustering quality assessment corresponding to the single-parameter indicator monitoring data silhouette coefficient Si′(t,k) can be calculated as follows:

$$E{X}_i={\displaystyle \frac{1}{n}}{\displaystyle \sum _{j=1}^n{\overline{\gamma }}_{ij}}$$

(3a)

$$E{N}_i=\sqrt{{\displaystyle \frac{\pi }{2}}}\cdot {\displaystyle \frac{1}{n}}\left|{\overline{\gamma }}_{ij}-E{X}_i\right|$$

(3b)

$$H{E}_i=\sqrt{{\Lambda }_i^2-E{N}_i^2}$$

(3c)

where $\overline{\gamma }$_ij represents the silhouette coefficient, EX_i is the expectation of the parameter indicator cloud, EN_i is the entropy of the indicator cloud, HE_ij is the hyper-entropy of the indicator cloud, and Λ_i is the standard deviation of the score for the ith indicator and Λ_i≥ EN_i.

To assess the overall cloud clustering quality, the average silhouette coefficient provided a comprehensive measurement of the clustering quality for the entire system at a given time. In cases where the reverse cloud generator operates, triggering based on the clustering quality, the mechanism would adjust the parameters to optimize the silhouette coefficient, thereby enhancing the clarity and separation of the clusters.

2.4.3. Comprehensive Cloud Clustering Quality Assessment of Multi-Parameter Indicator System

Based on the calculated parameters of the indicator clouds and combined with the corresponding indicator weights, the comprehensive cloud was obtained, with the specific formula being

$$E{X}_C={\displaystyle \sum _{i=1}^m(E{X}_{C,i}\cdot {\omega }_i)/{\displaystyle \sum _{i=1}^m{\omega }_i}}$$

(4)

$$E{N}_C={\displaystyle \sum _{i=1}^m(E{N}_{C,i}\cdot {\omega }_i^2)}/{\displaystyle \sum _{i=1}^m{\omega }_i^2}$$

(5)

$$H{E}_C={\displaystyle \sum _{i=1}^m(H{E}_{C,i}\cdot {\omega }_i^2)/{\displaystyle \sum _{i=1}^m{\omega }_i^2}}$$

(6)

where ω_i is the weight assigned to the single-parameter indicators. Once the comprehensive assessment cloud was calculated, it was compared with the standard assessment cloud maps to identify the standard cloud map that bore the closest resemblance to the comprehensive assessment cloud. This comparison was then used to determine the clustering quality assessment level of the existing bridge.

3. Determination Method of Component Stress State and Structural Load-Bearing Threshold

3.1. Determining Method of Stress State Based on Field Monitoring

The field monitoring methodology for arch ribs and truss girders can be ascertained through the use of strain gauges. The readings from these gauges, when multiplied by the elastic modulus of the steel materials, provide a direct measurement of stress within the structures. This approach eliminates the need for complex calculations, offering a straightforward and reliable method to assess the structural integrity and performance under various load conditions. By continuously monitoring the strain data, engineers can identify potential issues early, ensuring timely maintenance and a high level of safety for the bridge.

For the cable system of the ith cable with unit length mass ρ_i, cable length l_i, material modulus of elasticity E_i, and section moment of inertia I_i, the time-domain signal measured by sensors is x_i(t). By applying the fast Fourier transform (FFT), this signal is converted into the frequency-domain signal F_i(ω) at any time t. The fundamental frequency of the ith cable, representing the cable tension vibration frequency, can be denoted as f_i1(t).

Assuming the cable is simply supported at both ends and has a small vertical span ratio, the cable vibrates only in the vertical plane. Using classical beam theory and neglecting bending or shear effects on the cross-section, the tension force T_C,i of the ith cable can be expressed as $T_{C,i}(t)=4{\rho }_i{l}_i^2{f}_{1,i}^2(t)-{\pi }^2{E}_i{I}_i/l_i^2$, referred to from Gui et al. [42] and Lei et al. [43], and can be calculated with its boundary conditions requiring both ends of the cable to have zero displacement and curvature. Since the tension force and frequency change inconsistently under the same temperature conditions due to the initial horizontal tension, the effect of temperature is disregarded [44], and the elongation rate change of the cable before and after loading is minimal.

When the cable’s bending stiffness EI is low, the term π²EI/l² can be omitted from the formula. Accordingly, the stress σ_pi(t) of the ith cable can be simplified to σ_pi(t) = T_C,i/A_C,i, where A_C,i(t) is the cross-sectional area of the cable, assumed to be constant regardless of changes due to external forces or corrosion. The cable stress σ_C,i(t) should not exceed the cable material’s ultimate tensile strength f_u,C. The stress state matrix σ_C(t) for n cables is thus σ_C(t) = [σ_C,1(t_m), …, σ_C,n(t_m)]. For newly constructed bridges, the degradation of cable material properties need not be considered.

3.2. Model-Driven Target Threshold Determination

3.2.1. Explanation of the Model-Driven Method

The model-driven method is a sophisticated approach used in the performance assessment of truss arch composite systems, where the complexity of the structural ultimate state arises from the different degrees of redundancy in the forces experienced by each component. This method aims to ensure the safety and reliability of the entire structure by considering the simultaneous attainment of the ultimate state by all critical components, such as arch ribs, main trusses, and hangers.

In an ideal scenario, the model-driven method envisions that all key structural elements will reach their ultimate state concurrently. This simultaneous occurrence is crucial for maintaining the structural integrity and for preventing the failure of any single element that could compromise the entire system.

However, in practical situations, certain components, particularly hangers, may reach their ultimate state earlier than others due to material yield or the limitations of ultimate strength. This premature reaching of the ultimate state by some elements can lead to the entire bridge structure attaining its limit load-bearing capacity, while other components might still be operating well below their own ultimate states.

The model-driven method addresses this complexity by employing advanced modeling techniques and nonlinear analysis to predict and evaluate the behavior of each component under extreme conditions. It uses models such as the Von Mises bilinear model to simulate material nonlinearity and to determine the ultimate load-bearing capacity (R_u,max) of the bridge. This capacity is then used to ascertain the individual capacities of the main truss, arch ribs, and hangers, ensuring that the design accounts for the potential variability in the performance of different components.

By iteratively refining the model and adjusting parameters, the model-driven method converges towards a solution that closely represents the actual structural behavior. This approach is essential for the accurate assessment of the bridge’s load-bearing capacity and for ensuring that the structure can safely accommodate the design loads without surpassing the critical thresholds of any of its components.

3.2.2. Determining the Target Threshold for the Suspender Cable System

To determine the bridge’s capacity under extreme conditions, it was imperative to integrate considerations of geometric and material nonlinearities. Establishing the target threshold for the hanger system was a vital approach guided by model-driven methods. By employing material nonlinear models such as the Von Mises bilinear model [45], the bridge’s ultimate load-bearing capacity, denoted as R_u,max, was derived from structural nonlinear analysis, as illustrated in Equation (7a), which is placed in

Table 1. Calculation process of threshold determination of ultimate bearing capacity of components.

NO.	Step	Details Description
1	Determine structural model	Construct an appropriate stability calculation model based on the actual conditions of the bridge.
2	Define loading conditions	Identify the load conditions that the bridge must withstand, including dead weight, live load, and temperature effects.
3	Define nonlinear models	Consider both material nonlinearity and geometric nonlinearity of the structure to predict potential states of nonlinear failure or collapse.
4	Conduct nonlinear stability analysis	Utilize numerical analysis methods, such as the finite element method, to account for material nonlinearity and geometric nonlinearity. Gradually increase the load to analyze the structural response and assess stability.
5	Assess limit states	Determine if the bridge is at a limit state based on the analysis results. Evaluate the limit state of the structural system by analyzing parameters such as displacement, stress, and strain.
		$R_{u,\max }({\sigma }_j,d_j)=\arg \min R({\sigma }_{\max ,j},d_{\max ,j})$	(7a)
		$R_{u,\max }({\sigma }_j,d_j)\to {\sigma }_{u,j},d_{u,j}$	(7b)
6	Establish target limit thresholds for components	Establish the limit thresholds for each component’s performance parameters based on the identified limit states of the structural system.

. This capacity was then leveraged to ascertain the individual load-bearing capacities of the main truss, arch ribs, and hanger system, as shown in Equation (7b). These steps constituted an iterative refinement process, where adjustments and corrections to the model were made to closely simulate the actual structural behavior.

In the equations, σ_j = (σ_T, σ_A, σ_C) represent the stresses in the main truss, arch ribs, and hangers, respectively, while d_j = (d_T, d_A, d_C) denote the corresponding displacements. The term “max” signifies the maximum value of stress or displacement, and “u” indicates the ultimate state. Equation (7a) selects the minimum of the maximum strains among the main truss, arch ribs, and hangers to define the ultimate state of the bridge structure system, ensuring equilibrium and stability when each key component reaches its ultimate capacity. Equation (7b) calculates and determines the theoretical ultimate load-bearing capacities for each main truss, arch rib, and hanger when the bridge structure system is deemed to have reached its theoretical ultimate state. This process encompassed structural analysis and simulation, utilizing sophisticated numerical methods to predict the actual behavior and load-bearing capacity of each component under extreme loading conditions.

4. Case Study: Application in Double-Layer Truss Arch Bridges

4.1. Description of the Selected Bridge

To implement the algorithmic model introduced in this manuscript and to scrutinize the viability and efficacy of the proposed safety monitoring approaches, performance assessment metrics, and maintenance strategies, a fully constructed double-layer steel truss arch bridge (see Figure 3a,b) in Zhongshan City, Guangdong Province, has been selected for study. The bridge’s primary truss features an all-welded integral node plate truss configuration, with a span of 153 m. Two primary trusses are positioned transversely, separated by 37.3 m, and the central lines of the upper and lower trusses exhibit a height difference of approximately 10 m (see Figure 3b), with a standard inter-segment distance of 10.6 m. The arch ribs are designed with a box-shaped cross-section reinforced by ribs, fully welded, and shaped in a parabolic form, with a central span of 150 m and a rise of 37.5 m, achieving a rise-to-span ratio of 1/4. The bridge deck is composed of an orthotropic steel deck, ultra-high-performance concrete (UHPC), and a SMA13 asphalt concrete surfacing layer. The bridge is equipped with 22 suspender cables, specified as 2 × PES7-91, with an ultimate tensile strength of 1770 MPa and an elastic modulus exceeding 1.9 × 10⁵ MPa. The suspender cables are pin-jointed at both ends, encapsulated with PE protection and fitted with magnetic flux sensors that feed data into a data acquisition system. During the bridge’s completion phase, all suspender cable vibration frequencies were tested. In the operational phase, magnetic flux sensors, data acquisition systems, and solar power systems were installed at the mid-span and quarter points to monitor and record the magnetic flux variations of the suspender cables in real time, which are then translated into suspender cable sectional strains using theoretical formulas.

In Figure 3c–e, strain sensors and magnetic flux sensors are strategically placed on the bridge’s main truss, arch ribs, and suspender cables, with four strain sensors on the main truss cross-section, ten on the arch rib cross-section, and two magnetic flux sensors on the suspender cable cross-section. The specific arrangement in

Table 2. Sensor placement, quantity, and code installed on the test bridge.

Member	Sensor Types	Test Point Code	Locations
Arch rib	Strain sensors	A1, A2, A3, A4, A5, A6, A7, A8, A9, A10	See Figure 3c
Truss girder	Strain sensors	T1, T2, T3, T4	See Figure 3c
Suspender cable	Magnetic Flux sensors	C3-1, C6-1	See Figure 3d

is as follows: strain sensors are positioned at L/4 and L/2 along the main truss, with two at the bottom of the upper and lower cross-sections at the mid-span and one at the quarter point; strain sensors are also placed at the arch foot and L/4 and L/2 on the arch ribs, with two at each of the quarter points and the apex of the arch ribs. This sensor arrangement is designed for the real-time monitoring and documentation of the bridge’s data, providing a foundation for the assessment and maintenance of the bridge’s structural integrity.

4.2. FEM-Driven Stress Objected Thresholds for Bridge Components

4.2.1. Description of Finite Element Model

In this case study, the main truss and steel bridge deck are constructed using Q345qD material, while the arch ribs are fabricated predominantly from Q420qD and Q345qD. The hangers are characterized by a nominal yield strength of 1670 MPa and an ultimate tensile strength of 1770 MPa (see

Table 3. Material properties.

Material	fy/MPa	fu/MPa	Location	Reference
Q420qD	420	540	From arch foot to 1/4L and 3/4L	[46]
Q345qD	345	490	From top to 1/4L and 3/4L, Truss girder	[46,47,48]
C1670	1670	1770	Suspender cables	Design files

). To capture the nonlinear behavior of these materials, a Von Mises bilinear model is applied across all three. For the modeling of the arch ribs and the main truss, beam elements are utilized to represent their cross-sections, whereas the hangers are represented by tension-only truss elements, which more accurately reflect their load-bearing characteristics and nonlinear responses.

This study delves into the ultimate load-bearing capacity of bridges in the elastoplastic phase and evaluates the mechanical performance of the cable/stay system under extreme conditions through the application of a structural nonlinear analysis. The methodology includes steps such as an elastic buckling analysis, nonlinear data integration, parameter refinement, detailed computational simulations, and the derivation of load–displacement curves. By imposing a unit load on the bridge surface, the study determines the elastic buckling eigenvalues and eigenvectors and subsequently accounts for material and geometric nonlinearities to ascertain the critical load of a double-layer truss arch bridge. The bridge is deemed to have reached its ultimate load-bearing capacity when the load–displacement or load–strain curves exhibit a stable plateau.

Employing MIDAS CIVIL software for elastoplastic buckling analysis, the study comprehensively addresses the geometrric nonlinearity due to significant deformations and factors such as the material’s yield strength. An incremental arc-length method is applied to ensure the precision of the computational outcomes. This approach offers a meticulous framework for comprehending the behavior of bridges under diverse loading conditions and corroborates the structural response via finite element computations, as depicted in Figure 4.

4.2.2. Verification of the Proposed Method’s Effectiveness and Practicality

Figure 4 presents the finite element analysis results, highlighting that the transverse rib section of the upper main truss in the bridge is the first to exhibit local instability as it reaches the material’s yield strength and, subsequently, its ultimate tensile and compressive strengths. These conditions are critical for assessing the nonlinear ultimate bearing capacity of the bridge’s materials. Stress and displacement levels of the upper structural components of the double-layer truss arch bridge are derived from these states.

Figure 5 details the displacement and stress conditions for the arch ribs, chords, web members, and suspender cables of the bridge in three states: as built (OS), material yield (YS), and ultimate bearing (US). The ultimate state calculations indicate that while the transverse rib section of the upper main truss reaches yield and ultimate strength first, the arch rib section experiences the maximum compressive stress of −425 MPa at the bridge’s ultimate bearing capacity. The web member section shows tensile and compressive strengths of 340 MPa and −397 MPa, respectively, exceeding the material’s yield strength.

The maximum displacements for the arch ribs, upper chords, and lower chords are recorded as −222.29 mm, −366.78 mm, and −365.52 mm, respectively. In the ultimate state, the maximum deflection-to-span ratios for these components are 1/410, nearing the specification limit of 1/500 for steel truss bridges, validating the reasonableness of the bridge’s ultimate state determination.

Comparing displacement states across OS, YS, and US reveals the greatest vertical displacements in truss members, with the upper and lower chords showing similar magnitudes. The stress analysis across these states shows the highest tensile stress and largest variation in the suspender cables. The arch ribs exhibit the highest absolute stress values, increasing from 151 MPa in OS to 281 MPa in YS and peaking at 425 MPa in US. A consistent stress increase is observed in the chords and web members, reflecting the growing internal forces as the bridge approaches material limits.

For the suspender cables C3-1 and C6-1, the maximum stress values are 351.2 MPa, 717.4 MPa, and 1087 MPa in the OS, YS, and US stage, respectively. These values are crucial for establishing threshold ranges for each cable under different states. Exceeding these thresholds may indicate cable failure or the bridge reaching its ultimate capacity, which is vital for structural health and safety assessments, guiding maintenance and reinforcement measures.

4.3. Data Acquisition to Bridge Field Monitoring

4.3.1. Data Acquisition and Spectral Analysis of Suspender Cables

During the time interval from 00:14:19 to 23:12:43 on 23 July 2023, actual vibration time-domain data were collected for two suspension cables, designated as C3-1 and C6-1, situated at the mid-span and quarter points of the arch ribs. A Fourier transform approach was applied to perform a spectral analysis, identifying the maximum peak value of the vibration frequency at each time point as the representative frequency for the respective suspension cables.

Figure 6a–d display the measured vibration frequency time-domain data and corresponding spectrograms for the suspension cables C3-1 and C6-1 at four specific time points. Figure 6e illustrates the outcomes of the spectral analysis, indicating that the vibration frequencies for both suspension cables fluctuate within the range of 5.344 to 10.562 Hz.

Through a spectral analysis, the actual cable tensions and the associated stress variations of the suspension cables were ascertained. Figure 6f demonstrates how the measured vibration frequencies of the C3-1 and C6-1 suspension cables were converted into stress variations. The mid-span suspension cable C6-1 of the arch rib has a corrected length of 22.515 m, accounting for a 2.5 m deduction for the anchor head, while the quarter-point suspension cable C3-1 has a corrected length of 15.875 m with the same deduction. During the testing interval, the recorded maximum stress values for C3-1 and C6-1 suspension cables were 1049.94 MPa and 992.26 MPa, respectively, and the minimum values were 247.57 MPa and 123.07 MPa, respectively, indicating a notable disparity between the extremes.

Upon comparing the maximum measured cable tensions of C3-1 and C6-1 with their theoretical load-bearing capacities of 1085 MPa and 1083 MPa, respectively, it is observed that the measured tensions approach the theoretical limits. Conversely, the minimum measured tensions significantly deviate from the theoretical capacities and are substantially below the material’s ultimate tensile strength of 1770 MPa.

4.3.2. Monitored Data of Bridge Components

The data selected for the research time period in this paper spans from 00:00:00 on 23 July 2023, to 23:59:59 on the same day. The sensors on the bridge primarily consist of strain sensors and fluxgate sensors, with specific installation locations and quantities detailed in Figure 3 and Table 2. The sensors are powered and transmitted through a data acquisition system and solar power supply system installed on the outer side of the bridge deck at the mid-span.

The strain data collected from the arch ribs and main trusses are all obtained with vibrating wire strain gauges. Sensors are installed at different positions on the arch ribs, main trusses, and cables, with 10, 4, and 2 sensor measurement points, respectively. The monitored strain data are plotted in Figure 7.

5. Results and Discussion

5.1. Selection of Key Components Based on Characteristic Analysis and PCA Method

5.1.1. Characteristic of Monitoring Parameters Based on Cloud Rain Diagram

For the 10 arch rib strain measurement points (A1 to A10), 4 main truss section strain measurement points (T1 to T4), and 2 cable force measurement points (C3-1 and C6-1) on the double-layer truss arch bridge, the cloud rain diagram in Figure 8 offers a comprehensive view of the monitoring data variations in Figure 7 across the double-layer truss arch bridge, identifying several key observations:

The strain measurements at points A1 through A9 are notably consistent with minimal outliers, yet point A10 stands out with a higher frequency of extreme values within its dense data region, hinting at potential irregularities.

While T1 and T4 show some outliers within their dense data regions, possibly pointing to specific issues or variability, the other two measurement points on the truss section maintain a stress variation within a narrow 10 MPa range, indicating a general stability.

The monitoring data for C3-1 and C6-1 are centered in two separate dense regions, revealing a bimodal distribution. This pattern suggests the influence of different factors, such as loading conditions, material properties, or structural configurations, on these cables.

The cable stress demonstrates greater sensitivity to changes under identical loads compared to the arch rib and truss section stresses, indicating a more dynamic response to external forces.

Despite the presence of outliers and the bimodal distribution in the suspender cables, the overall structural performance is stable, as indicated by the majority of the monitoring data. However, these exceptions necessitate a more in-depth examination to uphold the bridge’s safety and reliability.

In essence, the monitoring data from the majority of points signals a reliable structural performance, yet the identified outliers and the distinct bimodal distribution in the suspender cables demand closer scrutiny to ensure the structural integrity of the bridge. The heightened sensitivity of the cable stress to load variations emphasizes the need for vigilant monitoring and analysis, which should be considered in the selection of key bridge components.

5.1.2. Selection of Key Components

The PCA method was applied to identify key measurement points on the arch ribs and main trusses as well as between the arch ribs and the cables. The results are illustrated in Figure 8.

Notably, the strain measurement point on the upstream side of the left arch foot section (A1), the strain measurement point on the upstream side of the left arch rib at the 3/4 span (A7), the strain measurement point on the upstream side of the main beam at mid-span (T4), and the position of cable C6-1 are all identified as critical measurement points.

The arch foot and mid-span areas are critical regions where stress concentrations are likely to occur due to the bending moments and shear forces. The 3/4L span location on the arch rib is a zone where the load distribution changes, affecting the overall stress pattern in the bridge. The cable force measurement points, such as C6-1, are crucial for understanding the tension forces in the cables, which are essential for the stability and safety of the bridge. Therefore, the application of a PCA to these measurement points ensures that the most representative and informative data are strategically rational for analysis, which is essential for the accurate assessment of the structural integrity and performance of the double-layer truss arch bridge.

5.2. Eigenvalue Analysis of Key Components after Modified Cluster

In this part, the K-means clustering analysis was applied to the stress data of key components during a specific testing period. The number of clusters was set to 3, with a maximum of 100 iterations, and the algorithm was terminated when the centroid movement was less than 1 × 10⁻⁴. The algorithm ultimately returned the cluster labels for each data point and the coordinates of the cluster centers.

Table 4. Eigenvalue analysis results of key components corresponding to each cluster level/MPa.

Eigenvalue	Cluster Level	Arch Ribs		Truss Girder	Suspender Cable
		A1	A7	T4	C6
Mean (Std)	1	209.089 (1.051)	218.641 (1.008)	209.184 (0.000)	222.671 (49.631)
	2	209.826 (1.014)	219.367 (1.079)	216.255 (2.130)	947.944 (9.063)
	3	210.538 (0.900)	222.764 (0.000)	217.965 (1.092)	984.763 (7.755)
Min/Max	1	208.612/209.374	218.194/219.000	209.184/209.184	123.070/251.560
	2	209.471/210.123	219.035/219.847	215.465/217.041	935.160/961.710
	3	210.207/210.837	222.764/222.764	217.153/218.199	966.850/992.260

provides statistical eigenvalue analysis results for the truss girder, arch ribs, and suspender cables, segmented by cluster level after a modified cluster. The mean, standard deviation (Std), maximum (Max), and minimum (Min) values are reported for each level, reflecting the distribution and variability of eigenvalues. The eigenvalues for the suspender cables show a substantial range, particularly at cluster level 2, where the standard deviation is markedly higher than in other components. The maximum eigenvalue for the suspender cables peaks at 992.26, while the minimum is notably lower at 123.07, suggesting a wide spectrum of dynamic responses within the structural system.

Additionally, an enhanced cluster analysis of on-site measured data has identified that the stress conditions of the main truss, arch ribs, and suspender cable cross-sections in the first cluster are quite consistent, with values predominantly around 210 MPa. Similar stress conditions are observed for the main truss and arch ribs in the second and third clusters, also around 210 MPa. However, there is a notable disparity in stress conditions when comparing these to the suspender cable sections, which can be largely attributed to the significant cable stretching during the construction phase. The variance analysis has shown that while the maximum variance for the main truss and arch ribs across the three clusters is 2.13 MPa, the variance for the suspender cables is considerably higher, peaking at 49.631 MPa in the first cluster, as opposed to 9.063 MPa for the second and 7.755 MPa for the third.

5.3. Assessment of Cluster Quality Using a Cloud Model for Suspender Cables

Using the improved clustering algorithm, cloud model formulas, and various clustering target thresholds, the single-parameter cloud model for the hangers was determined. A Principal Component Analysis (PCA) was employed to ascertain the weight coefficients of each parameter, ultimately assessing the quality of the clustering effect of the hanger system, as shown in

Table 5. Single parameter and system parameter of suspender cable cloud model.

Suspender Cable	Single Parameter			System Parameter
	EX	EN	HE	EXC	ENC	HEC
C3-1	0.936	0.118	0.108	0.938	0.11	0.098
C6-1	0.942	0.095	0.08

.

From the perspective of the expectation (EX) parameter, the value for the hanger C6-1 is higher than that for C3-1, indicating that C6-1 outperforms C3-1 in this parameter. In terms of entropy (EN), C6-1 has a lower value (0.0945) compared to C3-1 (0.1183), suggesting that C6-1 has less uncertainty or energy consumption in this parameter. Regarding hyper-entropy (HE), C6-1 also exhibits a lower value than C3-1, indicating less uncertainty in this parameter for C6-1. Consequently, when considering the single-parameter cloud model, C6-1 demonstrates superior performance across the expectation (EX), entropy (EN), and hyper-entropy (HE) parameters compared to C3-1, signifying that C6-1 has better overall performance.

The clustering quality effect assessment of the hanger system, calculated using the single-parameter and system cloud model parameters in Table 5 for different clustering target values, is presented in Figure 9. When the clustering target threshold is set to 1, the sample cloud center point obtained by normal sampling is 0.938, with a 96% confidence interval ranging from 0.701 to 1.175. The vast majority of the hanger system sample points fall within the I-Grade—excellent category. Therefore, the clustering quality achieved by the improved K-means clustering–silhouette coefficient–cloud model is effective.

6. Discussion

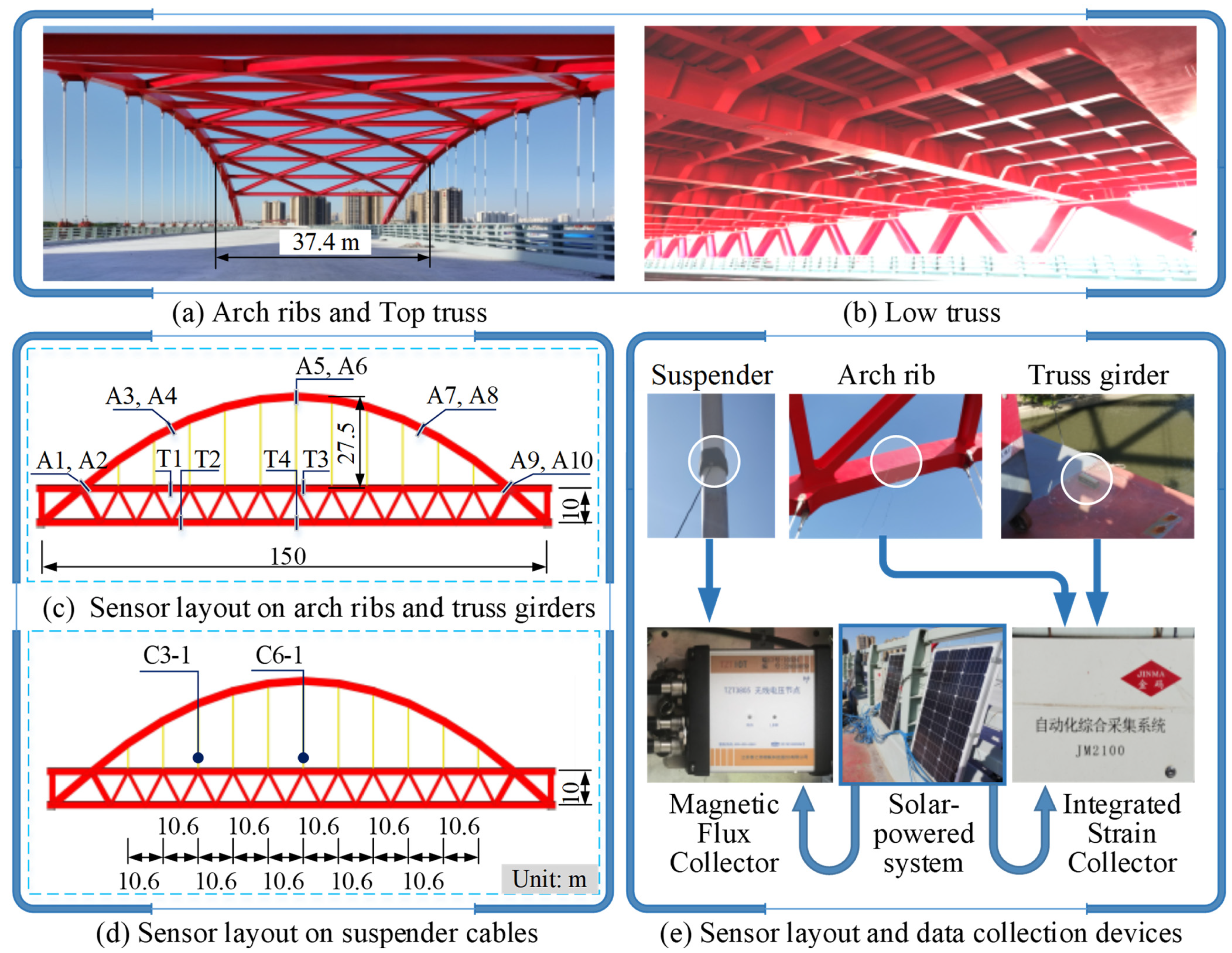
6.1. Effects of Clustering Algorithm Improvement on Case Bridge Components

6.1.1. Comparison of Clustering Distributions of All Components among UM, MC, and 3*DP Method

Figure 10 presents a comparative analysis of clustering distribution results obtained using the UM and MC methods as well as the dimensionless data derived from tripling the original monitoring data, referred to as three times the original dimensional data (3*DP).

The clustering results from both the UM and MC methods are categorized into three groups, numbered 1 to 3. In contrast, the 3*DP data, which represent the original monitoring data scaled by a factor of three, exhibit a broader range of categories, specifically from 0 to 3.

Among the ten measurement points on the arch rib section, points A1, A2, A4, A5, A6, A7, A8, and A9 show similar distribution patterns across the three clustering groups in their bar charts.

For the four measurement points on the truss girder section, the distribution patterns of the MC and 3*DP methods in the bar charts of the clustering results are consistently similar across all categories.

Regarding the two measurement points on the cable section, for the C3-1 cable, the distribution patterns of the MC and 3DP methods in the bar charts of the clustering results are alike, while there is a noticeable difference when compared to the UM method. For the C6-1 cable, the clustering results from the UM, MC, and 3DP methods all exhibit certain differences, indicating a more complex response to the clustering analysis.

After the cluster analysis, the cluster centers for the stress of suspender cable C3-1 are identified as 247.57 MPa, 957.73 MPa, and 1011.68 MPa. Correspondingly, the cluster centers for the stress of suspender cable C6-1 are 949.20 MPa, 222.67 MPa, and 986.04 MPa. The largest cluster center is located in the third category for both, indicating that this category corresponds to the most unfavorable stress on the cable structural system. Therefore, it is necessary to analyze separately the stress of the suspender cables with the largest cluster in the third category to assess the performance changes of the cable structural system. Of course, analyzing the cluster analysis results of the three types of cable stresses on the one hand can reflect the relative distances between the three cluster centers and on the other hand reflect the average change in the performance of the cables during the test period. Thus, it is essential to combine both situations to evaluate the performance of the cables.

6.1.2. Comparison of Key Components’ Cluster between UM and MC Method

The cloud rain diagram in Figure 11 offers critical insights into the clustering outcomes of measurement points, delineating the differences between the UM and MC approaches.

An analysis of the semi-violin plot reveals a key distinction. While measurement point A7 maintains similar clustering patterns in both UM and MC states, the other points show notable variability. This suggests that the MC adjustments have influenced different measurement points in unique ways, indicating a need for a tailored strategy for each point.

Examining the box plots for the four key parameter measurement points, we observe a consistent alignment of the interquartile range and lower quartile with clustering points 2 and 1, irrespective of the clustering state. The uniformity of the whisker ranges, with minimums at 1 and maximums at 3, underscores a stable distribution pattern, indicative of reliable clustering across the board.

The jitter scatter plot provides further detail. Points A1 and C6-1 exhibit a balanced distribution across all three clustering points, suggesting a strong clustering characteristic. In contrast, A7 and T4 display an uneven distribution, hinting at sensitivity to fluctuations or a deviation from the overall trend, particularly in light of the MC adjustments.

Looking at the distribution of mean points, we see that for A1, T4, and C6-1, the MC state has shifted to higher values compared to the UM state. This shift indicates a more pronounced allocation of results to the three clusters following the improvements. However, for A7, the mean point in the MC state is lower than in the UM state, suggesting a potential decrease in its representativeness post-enhancement.

These observations highlight the varying effectiveness of the MC measures against the UM state and underscore the need for a nuanced strategy to ensure consistent clustering efficacy. It also points to a dual requirement: reinforcing robust points to maintain stability in the MC state and calibrating more sensitive points to ensure ongoing precision and reliability in the monitoring system.

6.2. Impact of Algorithm on Cluster Quality and Performance Metrics

Table 6. Comparison of performance evaluation results of suspender cable by using different evaluation indicators.

Parameter		C3-1			C6-1
		UM	MC	RMC-UM (%)	UM	MC	RMC-UM (%)
Cluster centroids	Cluster 1	247.566	247.566	0	222.671	222.671	0
	Cluster 2	974.479	957.732	−1.719	947.944	949.205	0.133
	Cluster 3	1047.374	1011.682	−3.408	984.764	986.044	−0.165
ASC of single-parameter clustering		0.816	0.734	−10.049	0.905	0.905	0
DBI of single-parameter clustering		0.221	0.498	125.339	0.273	0.266	−2.564
AD (%) from target threshold for Cluster 3		40.826	42.843	4.940	44.364	44.291	0.130
p-value (×10−5) of Sign-Rank test for Cluster 3		6250	28.678	−99.541	6.1035	12.207	100

presents a comparative analysis of the clustering evaluation metrics for C3-1 and C6-1 hangers corresponding to the targeted stress thresholds, with the relative error R_MC-UM = (MC-UM)/UM×100%, including the average silhouette coefficient (ASC), Davies–Bouldin index (DBI), average deviation (AD), and p-value by the Sign-Rank test from target values. A lower DBI indicates a better clustering performance, with higher separation between clusters and tighter cohesion within clusters [39].

(1) Comparison of Cluster Centroids

For Cluster 1, both C3-1 and C6-1 showed no difference in centroids calculated by the UM and MC methods. In Cluster 2, MC resulted in a slightly lower centroid for C3-1 by 1.719% and a slightly higher centroid for C6-1 by 0.133% compared to UM. In Cluster 3, MC lowered the centroid for C3-1 by 3.408% and for C6-1 by 0.165%. Overall, the difference in centroids calculated by UM and MC for C3-1 and C6-1 ranged from 0% to 3.5%.

(2) Average Silhouette Coefficient

For C3-1, MC showed a lower silhouette coefficient than UM, with a difference of −10.049%, suggesting better separation with UM. For C6-1, the silhouette coefficient remained stable at 0.905 with both methods.

Across all conditions, C6-1 had a higher ASC with MC (0.905) than C3-1 (0.816 and 0.734), indicating better clustering quality with higher coefficients. However, for C3-1, the silhouette coefficient was lower with MC (0.734) than UM (0.816), suggesting slightly better separation with MC.

(3) Davies–Bouldin Index

C3-1′s DBI was 125.339% higher with MC than UM, indicating a potential decrease in clustering separation. C6-1′s index was only 2.564% higher with MC, showing minimal change. Generally, a lower index indicates better clustering. C3-1 had a lower index with UM (0.221) than MC (0.498), while C6-1′s index was slightly lower with UM (0.273) than MC (0.266), suggesting better separation with UM for C3-1.

(4) Average Deviation from Target Threshold

Using the same material limit stress target threshold of 1770 MPa for Cluster 3, the average deviation for C3-1 and C6-1 with UM was 40.826% and 42.843%, respectively, compared to 44.364% and 44.291% with MC. The difference in deviation for C3-1 between MC and UM was two percentage points, with a difference rate of 4.94%. For C6-1, the deviation was almost identical between the two methods, with a difference rate of 0.13%, indicating stable clustering results.

(5) Sign-Rank Test p-value Analysis

In Cluster 3, the p-values for C3-1 and C6-1 showed significant differences between UM and MC. For C3-1, MC’s p-value was significantly lower than UM’s, with a difference rate of −99.541%, indicating superior statistical significance with MC. For C6-1, MC’s p-value was double that of UM, suggesting a potential decrease in statistical significance with MC.

The Sign-Rank test results indicate that MC provided enhanced statistical significance for C3-1 in Cluster 3, while for C6-1, the significance was reduced. Since a lower p-value typically indicates higher statistical significance, MC may be more advantageous for C3-1.

In summary, the distribution, characteristics, and noise level of the data significantly impact the choice of algorithm and clustering results. The modified K-means (MC) algorithm showed different clustering effects compared to the unmodified K-means (UM) when processing data for C3-1 and C6-1. Statistical significance was higher for MC in Cluster 3 for C3-1, as evidenced by a lower p-value. In terms of centroid values, MC significantly affected the centroids for C3-1 in Cluster 2 and 3, usually yielding lower values than UM. In terms of clustering quality metrics, UM generally performed better in deviation and the Davies–Bouldin index, suggesting higher separation. For silhouette coefficient stability, C6-1 showed stable clustering effects with both methods, with a high silhouette coefficient. The choice of algorithm should be based on specific clustering objectives and data characteristics, considering multiple indicators, including statistical significance, centroid values, deviation, Davies–Bouldin index, and silhouette coefficient.

6.3. Influence of Single-Parameter Cloud Model Parameters on Clustering Quality

Figure 12 illustrates the predictive reliability and clustering quality of the clustering results for the hanger components C3-1 and C6-1 based on their single-parameter EX, EN, and HE values.

(a) When analyzing the 96% confidence interval [CI_lower, EX, CI_upper, EX] corresponding to the structural system’s expectation value, the width of the confidence interval, CI_HE = CI_upper, EN − CI_lower, EN, exhibits a trend of decreasing initially and then increasing with the increase in the single-parameter EX value. At an optimal EX value, the predictive reliability of the structural system is at its peak. However, as the EX value continues to rise or fall, the confidence interval widens, indicating increased uncertainty and decreased predictive reliability, reflecting a decline in the model’s predictive capability under extreme conditions.

(b) As the single-parameter EN value increases, both the single-parameter cloud model and the system cloud model’s entropy values also increase, while the HE value remains constant. Under the 96% confidence interval, the width of the confidence interval, CI_HE, gradually widens, signifying that the uncertainty in clustering quality rises with an increase in EN. Specifically, as the EN value doubles from 0.5 to 1.3 times, the CI_HE value increases from 0.224 to 0.59, indicating that predictions are more certain at lower entropy values, and uncertainty grows as the entropy value increases.

(c) The clustering quality of the single-parameter indicator cloud shows an increasing trend with the increase in HE. The hyper-entropy of the system cloud model increases with the hyper-entropy of the single-parameter cloud model, indicating an increase in system complexity or uncertainty. Nonetheless, the system’s EX_C and EN_C values remain stable, suggesting that the system’s predictive ability and uncertainty are maintained at a relatively constant state during changes in hyper-entropy. The evaluation of the confidence interval shows that CI_{lower, HE} and CI_upper,EN are relatively stable across the entire range of hyper-entropy values, indicating consistency and reliability in the measurement results. The width of the confidence interval, CI_HE, varies within a narrow range, emphasizing the precision of the clustering results. The analysis of the confidence interval width, CI_HE, reveals that it remains essentially unchanged with the increase in the single-parameter hyper-entropy value, indicating that the uncertainty of the predictive results is maintained at a relatively stable level across the entire range of hyper-entropy values.

In summary, the research findings underscore the significant impact of expectation, entropy, and hyper-entropy values on the accuracy and uncertainty of predictions within structural system forecasting and the clustering analysis. By meticulously adjusting these parameters, it is possible to enhance predictive reliability while gaining a better understanding and management of the uncertainties inherent in the forecasting process.

7. Conclusions and Future Work

7.1. Summary of Findings

The research employs an enhanced clustering-silhouette coefficient–cloud model algorithm for the performance assessment of bridge components, specifically applied to operational maintenance of double-layer truss arch bridges, to guide maintenance decisions and ensure structural safety. The findings conclude that this method effectively supports the evaluation and preservation of critical bridge infrastructure.

(1) The study introduces an advanced clustering-silhouette coefficient–cloud model algorithm for assessing performance changes in bridge health monitoring. This integrated approach, capable of processing large datasets for pattern recognition and addressing uncertainty and fuzziness through expectation, entropy, and hyper-entropy parameters, offers a comprehensive data analysis tool for evaluating bridge component performance.

(2) The research concludes that the enhanced algorithm effectively assesses bridge health, emphasizing the need for the detailed scrutiny of suspender cable stress to safeguard structural integrity.

(3) PCA application ensures the strategic selection of data for precise structural evaluation, and the eigenvalue analysis points to notable stress variance, particularly within cluster levels, revealing the dynamic behavior of bridge components.

(4) The superior clustering quality, indicated by a high sample cloud center point and a 96% confidence interval in the excellent category, attests to the method’s efficacy. The study underscores the pivotal role of parameter tuning in enhancing predictive accuracy and managing uncertainties, advocating for algorithm selection tailored to specific clustering goals and data attributes for effective bridge maintenance and safety.

7.2. Contributions and Innovations

This study introduces an innovative approach to bridge health monitoring through the development and application of an enhanced clustering-silhouette coefficient–cloud model algorithm. The key contributions and innovations of this study are as follows:

(1) The creation of a novel algorithm that integrates a clustering analysis with silhouette coefficient optimization and cloud model theory, providing a sophisticated tool for handling large datasets and identifying patterns within bridge performance data.

(2) A comprehensive method for evaluating the performance of bridge components, particularly focusing on the dynamic responses of suspender cables, which are critical to the structural integrity of the bridge.

(3) The incorporation of expectation, entropy, and hyper-entropy parameters to address uncertainty and fuzziness in the monitoring data, leading to more reliable predictions and assessments, which demonstrates of the effectiveness of the improved K-means clustering method through high-quality clustering metrics, including a 96% confidence interval in the excellent category.

(4) Offering insights into the selection of algorithms based on specific clustering objectives and data characteristics, taking into account multiple indicators for optimal structural health monitoring, taken a double-layer truss arch bridge as the example.

These contributions and innovations represent a significant advancement in the field of structural health monitoring, providing a robust, reliable, and practical methodology for assessing and ensuring the safety and performance of critical bridge infrastructures.

7.3. Limitations and Recommendations for Future Research

It is important to note that the specific analysis approach depends on the selection of appropriate cloud model parameters and their sensitivity to the clustering quality assessment. This study focused on the development of an enhanced clustering algorithm and its application to bridge health monitoring, identifying the significant impact of cloud model parameters on the assessment process. Hence, future research shall focus on the following:

(1) Conducting a thorough sensitivity analysis of the cloud model parameters to determine their individual and collective influence on the clustering quality assessment, ensuring that the algorithm’s response to parameter variations is well understood.

(2) Extending the research to different types of bridge structures and materials to evaluate the adaptability and effectiveness of the cloud model-based clustering assessment across a broader range of engineering applications.

(3) Investigating the potential of integrating the cloud model-based clustering method with other SHM techniques, such as machine learning and artificial intelligence, to enhance the predictive capabilities and diagnostic accuracy of the system.