Improved Blob-Based Feature Detection and Refined Matching Algorithms for Seismic Structural Health Monitoring of Bridges Using a Vision-Based Sensor System

Abstract

The condition and hazard monitoring of bridges play important roles in ensuring their service continuity not only throughout their entire lifespan but also under extreme conditions such as those of earthquakes. Advanced structural health monitoring (SHM) systems using vision-based technology, such as surveillance, traffic, or drone cameras, may assist in preventing future impacts due to structural deficiency and are critical to the emergence of sustainable and smart transportation infrastructure. This study evaluates several feature detection and tracking algorithms and implements them in the vision-based SHM of bridges along with their systematic procedures. The proposed procedures are implemented via a two-span accelerated bridge construction (ABC) system undergoing a large-scale shake-table test. The research objectives are to explore the effect of refined matching algorithms on blob-based features in improving their accuracies and to implement the proposed algorithms on large-scale bridges tested under seismic loads using vision-based SHM. The procedure begins by adopting blob-based feature detectors, i.e., the scale-invariant feature transform (SIFT), speeded-up robust features (SURF), and KAZE algorithms, and their stability is compared. The least medium square (LMEDS), least trimmed square (LTS), random sample consensus (RANSAC), and its generalization maximum sample consensus (MSAC) algorithms are applied for model fitting, and their sensitivity for removing outliers is analyzed. The raw data are corrected using mathematical models and scaled to generate displacement data. Finally, seismic vibrations of the bridge are generated, and the seismic responses are compared. The data are validated using target-tracking methods and mechanical sensors, i.e., string potentiometers. The results show a good agreement between the proposed blob feature detection and matching algorithms and target-tracking data and reference data obtained using mechanical sensors.

1. Introduction

Structural health monitoring (SHM) has emerged as a beneficial system for assessing structural performance under ambient and forced vibrations either in laboratory or field environments, especially in monitoring civil infrastructure. Key civil infrastructure systems like bridges are mostly equipped with SHM systems to allow monitoring of traffic, wind, and other environmental loading as well as natural hazard incidents such as earthquakes. In bridge monitoring, most SHM systems use wireless network systems or even mechanical sensors with wires that may interfere with traffic and practically provide data at limited locations. Their installment and implementation are also challenging, especially for some locations such as under bridges, bridges over water, or highly elevated bridges. High sampling rates that are mostly used by these types of sensors also require more data processing to capture the low-vibration frequency of flexible-type bridges or long-span bridges. Moreover, when considering SHM for reconnaissance efforts, rapid bridge evaluation that will reveal whether to open or close it after the earthquake; this decision strongly depends on the bridge’s condition in the aftermath. These quick assessments are challenging using current monitoring inspection procedures since they are unable to capture the global behavior of the bridge during earthquakes, and they are further incapable of monitoring the progress of more permanent forms of damage such as plastic deformation, rotation, and drifts.

Advanced SHM technologies using cameras, i.e., vision-based technology, offer advantages over their SHM counterparts [1,2,3,4,5]. A larger field of view that depends on the camera type and setting enables the monitoring of a broader bridge area and provides options for assessing the deck and bent of the bridge all in one setting. Lower camera video sampling rates also allow for the dynamic characterization of a bridge under a very low to high excitation, from low ambient vibration to the high amplitude of earthquakes. The global response of bridges recorded at the bent, deck, base, and abutment levels generate valuable data for estimating permanent damage to bridges. Moreover, an intelligent robotic system provided by an unmanned aerial vehicle (UAV) or drone, which is also integrated with camera technology, is capable of recording bridges and other infrastructure during earthquakes or any vibration events; it does so without disturbances from ground movement due to its airborne operation [6,7,8,9,10].

The vast development of computer vision (CV) algorithms greatly supports either laboratory or field implementations of vision-based SHM. Tracking algorithms using well-known template matching techniques such as digital image correlation (DIC) have been proven one of the most effective procedures in generating structural displacement, strain mapping, and other structural dynamic characteristics [3,4,11,12]. As this technique requires stamping on the surface area of the specimen in the form of spray-painting or artificial targets, it is challenging to implement in real-life structures, especially for long-term monitoring. Therefore, advancement in CV feature detection, extraction, and tracking algorithms offers advantages in object recognition using the natural features of these structures. Multiscale feature detection and description algorithms such as the scale-invariant feature transform (SIFT) [13], speeded-up robust features (SURF) [14], and KAZE [15] algorithms are among the most popular algorithms that demonstrate high repeatability and distinctiveness with various forms of image transformation such as noise and blurring. Matching algorithms, such as the greedy nearest neighbor, optimal fair or full, or exact algorithm, are selected to match features between images depending on the matching goal. The returned matching features may not be exact; therefore, it is necessary to filter the outliers using an optimization algorithm such as random sample consensus (RANSAC) or its variants, namely, the M-estimator SAC (MSAC) [16], progressive SAC (PROSAC) [17], or maximum likelihood estimator SAC (MLESAC) [18] algorithm, of which selection is based on its accuracy, speed, robustness, or optimality [19].

Performing feature detection and description on digital images is primarily to extract specific features based on which descriptor is used. Among the available detectors like edge or corner detectors, the blob-based detector is the simplest method that aims to analyze the shape features of an object in the image that contrast their backgrounds in color, brightness, or other properties. The SURF and SIFT algorithms are among the frequently used operators that can extract blob-based features in the image and have been implemented in bridge SHM [20,21]. Meanwhile, the KAZE algorithm is not commonly selected in bridge monitoring; however, previous work has reported its implementation in wind turbine monitoring [22]. Their matching accuracies, i.e., the number of tracked and matched features after the detection and extraction steps, have barely been reported in previous works. Therefore, the objectives of this study are to explore the effect of refined matching algorithms on blob-based features in improving their accuracies and to implement the proposed algorithms on large-scale bridges tested under seismic loads using vision-based SHM. The major contributions of this study are a detailed procedure that exploits the impact of selecting detection and matching operators to improve blob-based feature performance and a CV-oriented procedure for seismic SHM using vision-based sensors. The remainder of this paper is organized as follows. In Section 2, selected blob-based feature detectors and matching and refined matching algorithms are explained. The testing setup of two-span accelerated bridge construction (ABC) bridge for implementing the proposed algorithms is given in Section 3. Their results and important constraints are presented and their accuracies verified in Section 4, and conclusions are drawn in Section 5.

2. Methodology

Computer vision algorithms cover a wide range of operators that can detect, extract, and match features within image sequences recorded from tests. Their general procedures are adopted in this study, as shown in Figure 1, together with the selected operators. They start by detecting blob-based features and continue with the matching procedure. Then, the proposed refined matching algorithm is applied to improve the number of correctly matched pairs. In Figure 1, three blob-based feature detectors, i.e., SURF, SIFT, and KAZE, are used to detect blob features in test images. These features are then matched with the nearest neighbour (NN) algorithm. Four operators are proposed to return more exact matching, i.e., the least median of squares (LMEDS), least trimmed square (LTS), random sample consensus (RANSAC), and M-estimator sample consensus (MSAC) algorithms. These algorithms have commonly been used in distance or matching problems in previous works [23,24,25,26,27,28]. The details of the proposed procedure are provided in the next subsections.

2.1. Blob-Based Feature Detection Algorithm

In CV image registration, there are five general stages of relating image sequence characteristics so the image datasets can be transformed into a single unified coordinate system. They are feature detection and description, matching, refined matching to filter outliers, image transformation, and reconstruction. Feature detector operators are algorithms that detect features in the image that can be in the form of edges, corners, lines, blobs, etc. The three blob feature descriptors selected in this study are SURF, SIFT, and KAZE. SURF [14] detectors are based on the determinant of the Hessian matrix $\mathcal{H},$ as shown in Equation (1) in point $\mathrm{x}=(\mathrm{x},\mathrm{y})$ at scale $\mathsf{\sigma }$. They use integral images to improve the algorithm speed, relying on Gaussian space analysis where ${\mathrm{L}}_{\mathrm{x}\mathrm{x}}(\mathrm{x},\mathsf{\sigma })$ is the convolution of the Gaussian second-order derivative of image $\mathrm{I}$ in point $\mathrm{x}$ and for ${\mathrm{L}}_{\mathrm{x}\mathrm{y}}(\mathrm{x},\mathsf{\sigma })$ and ${\mathrm{L}}_{\mathrm{y}\mathrm{y}}(\mathrm{x},\mathsf{\sigma })$. Specific bin dimensions are used to describe the detected blob features with Haar wavelet distribution within certain regions. The dimensions can be extended to 64-D or even 128-D depending on the change of image perspective.

$$\mathcal{H}\left(x,\sigma \right)=\left[\begin{array}{cc}{L}_{xx}(x,\sigma )& L_{xy}(x,\sigma )\\ L_{xy}(x,\sigma )& L_{yy}(x,\sigma )\end{array}\right]$$

(1)

The most well-known feature descriptor is SIFT [13], which is based on the difference of Gaussian (DoG) operator, i.e., an approximation of Laplacian of Gaussian. Local maxima on an image are searched using DoG to detect feature points at various scales. It is strongly invariant to image scale and rotations with affine variations; however, it has a high computational cost. SURF, on the other hand, has a low computational cost compared to SIFT. Equation (2) describes the convolution of difference $D$ between two Gaussians at different scales within image $I\left(x,y\right),$ in which $G$ corresponds to the Gaussian function.

$$D\left(x,y,\sigma \right)=\left(G\left(x,y,k\sigma \right)-G\left(x,y,\sigma \right)\right)\ast I(x,y)$$

(2)

The KAZE detector is also computed at multiple scale levels based on the normalized determinant of the Hessian matrix. It uses non-linear diffusion filtering that benefits blurred image processing as it reduces noise and maintains the boundaries of regions in subject images simultaneously. A moving window is used to select the maxima of the detector. Feature points are detected by discovering major orientations in circular regions around each detected feature. Similar to SIFT and SURF, KAZE features are also invariant to rotation, scale, and limited affine. This detector has more uniqueness at varying scales; therefore, it also increases the computational time. Equation (3) shows the typical nonlinear diffusion formula with divergence $div,$ conductivity function $c,$ gradient operator $\nabla ,$ and image luminance $L.$

$$\frac{\partial L}{\partial t}=div\left(c(x,y,t\right)·\nabla L$$

(3)

2.2. Matching Algorithm

Following the blob-based feature detection, the next step is to search for the most similar matches of blob-based features within image sequences. This is the most computationally expensive segment of y computer vision algorithms as it involves searching and tracking for the most similar matches to high-dimensional vectors. Therefore, a robust yet efficient algorithm is required to perform fast searching and tracking in such large datasets. Nearest neighbor (NN) is selected in this study as it provides speedy computation in several orders of magnitude. The NN problem consists of pre-processing a set of points $X$ such that the operation in Equation (4) can be performed efficiently. Equation (4) describes the NN search in a metric space. It is defined as follows: for a set of feature points $X=\left\{x_1,x_2,x_3,\dots ,x_n\right\}$ in a metric space $M$ with a query point $q\in M$, the element NN $(q,X)\in X$ is searched such that the match is the closest to $q$ with respect to a metric distance $d:M\times M\to \mathbb{R}.$

$$NN\left(q,X\right)={argmin}_{x\in X }d(q,x)$$

(4)

2.3. Proposed Refined Matching Algorithm

It is known that working with high-dimensional features will mostly produce incorrect searches and matches. Many practical applications of the NN algorithm return approximate matches with some outliers, meaning that some results are estimated yet still close to the exact matches. Therefore, in image registration, it is common that NN is just a part of complete procedures combined with applications of other CV algorithms that contain other approximations. The refined matching procedures used to filter the outliers selected in this study are the least median of squares (LMEDS) [29], least trimmed square (LTS) [30], random sample consensus (RANSAC) [31], and M-estimator sample consensus (MSAC) [18] algorithms. Both the LMEDS and LTS estimators are common regression estimators. Considering a sample with $n$ observations consisting of inliers and outliers, the sample with the least maximal squared residual is called LMEDS, while the sample with the highest residual sum of squares is defined as LTS. LMEDS estimator estimates the parameters by solving the nonlinear minimization problem and reduces the median of squared standardized residuals for the entire dataset. Meanwhile, LTS consists of finding a subset of cases whose deletion from the dataset would lead to the regression with the smallest residual sum of squares. It is regression-, scale-, and affine-equivariant and is used as a general-purpose high-breakdown method.

The RANSAC algorithm is widely used to detect unique transformation by random sampling. The corresponding transformation is estimated, and the adequacy of the transformation to the rest of the data is then tested. The transformation that yields the most effective consensus is then kept. RANSAC is a robust and fast algorithm, yet several important parameters need to be set in the analysis. The RANSAC step relates to the theory of a minimal sample set, which the initial set is randomly selected from the input. It is followed by computing the model parameters, after which RANSAC requires the setting of a certain threshold that iteratively checks which observations of the entire dataset are consistent with the hypothetical model. It specifies the maximum distance from a point of interest to a hypothetical model. When it fits the criterion, the point is treated as a hypothetical inlier; otherwise, it is treated as an outlier. The estimated model is exact when an adequate amount of points which are classified as exact observations (inliers) are reached. MSAC is a generalization of the RANSAC estimator that is principally used to robustly estimate multiple new relations from point correspondences. MSAC implements the same sampling approach as RANSAC to generate exact solutions. However, it selects the solution that maximizes the likelihood rather than just the number of inliers.

3. Testing Setup

The proposed methods in Section 2 are experimentally evaluated on a two-span accelerated bridge construction (ABC) through a shake-table test. ABC is a bridge construction that uses state-of-the-art design, materials, and construction methods safely and cost-effectively. ABC not only improves site constructability and projects’ construction schedule but also reduces impacts on traffic and project delays due to weather conditions. The tested ABC bridge shown in Figure 2 is a one-third-scale two-span reinforced concrete bridge with seismic connections. The length of each span (in the longitudinal direction) is 10.4 m with a 3.4 m width in the transverse direction. It has a two-column pier in the middle, which is spaced at 1.8 m with a height of 2.1 m. The bridge sits on a seat-type abutment at both ends. The bidirectional ground motion that was recorded during the 1994 Northridge earthquake was scaled according to a design-level (DE) seismic demand. Three tests with increasing seismic intensity from 20% and up to 75% of the DE level are selected to investigate the effect of each applied algorithm on the feature matching as well as the seismic response of the ABC bridge system. More details about the design, construction, and studies of the tested ABC bridge can be found in [32,33]. The bridge is placed on three biaxial shake tables manufactured by MTS. Each table measures 4.3 × 4.5 m with a stroke of ±300 mm. It can reach a peak velocity of 1000 mm/s) and an acceleration of 1 g with a 50-ton payload (about 445 kN). All three tables are constrained to act together as a single large table, with the option to be operated individually with independent motions depending on the loading requirements. The specification of the SHM system is given in

Table 1. SHM system specifications.

Sensor	CMOS	Shutter	$3$–$41.654 \mathsf{\mu }\mathrm{s}$	Format	.tiff
Lens	35 mm	Image resolution (pix.)	$2560\times 2048$	Image type	Monochrome

. The camera lens is 35 mm with a CMOS sensor. The image is set to monochrome to accelerate the later image processing using the proposed algorithms. The camera’s full ROI is used, with 2560 × 2048 image pixels and a record duration of 30 s with 30 Hz sampling rates or 30 frames-per-second rates. The reference sensor $R,$ as shown in Figure 2c, is a string potentiometer recorded at 256 Hz; therefore, adjustment of displacement is required later to enable the comparison.

Vision-based SHM of the ABC bridge has been previously reported in [3]. The difference between this study and previous works lies in its methods, i.e., the CV algorithms applied to image sequences that later affect the seismic data. Prior work needed a stereophotogrammetry technique to generate the three-dimensional coordinates of the features shown in Figure 2d. Then, these features were tracked using tracking algorithms to detect the change in each feature coordinate within the image sequences. Therefore, previous work required a set of photogrammetry images and test images, also involving two steps in processing the vision-based data. Meanwhile, this work simply uses test data without the prerequisite of taking photogrammetric images. The proposed algorithms are directly applied to the test images, and the displacement data are generated using the scale factor method [34].

4. Results and Discussions

4.1. Blob-Based Feature Detection and Matching Results

Following the method described in Section 2, this section explores the results of the selected feature detection and matching algorithms using the images of the tested ABC bridge in Figure 2. The selected algorithms for blob-based feature detections are SURF, SIFT, and KAZE. Their thresholding is given in

Table 2. Selected algorithm for blob-based feature detections.

Parameters	Algorithm
	SURF	SIFT	KAZE
Threshold	6000	0.05	0.005
Matching	Nearest neighbour (NN)	Nearest neighbour (NN)	Nearest neighbour (NN)

, i.e., with the matching NN algorithm. Two figures of each test are taken to visualize the results of each algorithm and the bridge’s condition before and after testing, i.e., an image taken at the beginning of the test at $\mathrm{t}=0, {\mathrm{I}}_{1,\mathrm{t}=0}$ and at the end of the test at $\mathrm{t}=\mathrm{T},$ ${\mathrm{I}}_{\mathrm{N},\mathrm{t}=\mathrm{T}}.$ Figure 3 shows the results of blob-based features and NN matching using each algorithm. The red and blue circles indicate detected blob features on ${\mathrm{I}}_{1,\mathrm{t}=0}$ and ${\mathrm{I}}_{\mathrm{N},\mathrm{t}=\mathrm{T}}$, respectively. Magenta lines show the matching results for both correct and incorrect matchings. Straight lines connecting red and blue blob features show correct matching, while crossing lines demonstrate an incorrect match between images. Algorithm selections and matching feature results are given in

Table 3. Results of algorithm selection and matching features.

Algorithm	SURF	SIFT	KAZE
$I_{1, t=0}$	387	448	909
$I_{N, t=T}$	632	499	1610
Matching feat.	229	254	533
NN Accuracy (%)	59.17	56.69	58.63

. Table 3 shows that the number of detected blob features on each image varies along with the selection of the algorithm. More blobs are detected using KAZE; however, less than 60% of matching accuracies are computed. It is clear that NN matching does not return 100% exact matches; rather, some features are paired incorrectly and identified as outliers, as shown in Figure 3.

The next step is to remove the outliers and refine the matching using the LMEDS, LTS, RANSAC, and MSAC algorithms, which is proposed to improve the matching accuracy of the NN algorithm. The selected thresholds ($TH)$ as parameters are 0.001, 0.01, 0.1, and 1. The results are given in

Table 4. Exact feature matching methods with their respective accuracies using the LMEDS, LTS, RANSAC, and MSAC refined matching algorithms.

SURF Detection
Ref. Alg.	LMEDS		LTS		RANSAC		MSAC
TH	Exact Match	Acc. (%)	Exact Match	Acc. (%)	Exact Match	Acc. (%)	Exact Match	Acc. (%)
0.001	193	49.87	194	50.13	364	94.06	363	93.80
0.01	193	49.87	194	50.13	328	84.75	329	85.01
0.1	193	49.87	194	50.13	254	65.63	252	65.12
1	193	49.87	194	50.13	172	44.44	167	43.15
SIFT Detection
Ref. Alg.	LMEDS		LTS		RANSAC		MSAC
TH	Exact Match	Acc. (%)	Exact Match	Acc. (%)	Exact Match	Acc. (%)	Exact Match	Acc. (%)
0.001	224	50	224	50	421	93.97	409	91.29
0.01	224	50	224	50	372	83.04	388	86.61
0.1	224	50	224	50	310	69.20	289	64.51
1	224	50	224	50	229	51.12	241	53.79
KAZE Detection
Ref. Alg.	LMEDS		LTS		RANSAC		MSAC
TH	Exact Match	Acc. (%)	Exact Match	Acc. (%)	Exact Match	Acc. (%)	Exact Match	Acc. (%)
0.001	454	49.94	455	50	877	96.48	881	96.92
0.01	454	49.94	455	50	828	91.09	831	91.42
0.1	454	49.94	455	50	651	71.62	702	77.23
1	454	49.94	455	50	440	48.40	446	49.06

with the example of matching using threshold = 0.1 given in Figure 4. Similar to Figure 3, Figure 4 also shows an example of images taken at the beginning of the test at $t=0, I_{1, t=0},$ and at the end of the test at $t=T,$ $I_{N, t=T}.$ Figure 4a, f, and k show SURF, SIFT and KAZE detections, respectively, in which blob features are matched using only the NN algorithm. Incorrect pairs are shown as crossed lines between images, which are improved further using the selected refined matching algorithms. Correct pairs are shown for all blob features after applying refined matching algorithms in Figure 4b–e for the SURF detector, Figure 4g–j for the SIFT detector, and Figure 4l–o for the KAZE detector. LMEDS and LTS return similar matching results at each increment in the threshold (193 features and 194 features associated with 49.87% and 50.15% matching accuracies for LMEDS and LTS, respectively). Meanwhile, both RANSAC and MSAC results show their effectiveness throughout each selected threshold. The highest improvement is obtained from the smallest threshold of 0.001 using the KAZE detection algorithm: 96.48% and 96.92% accuracies for RANSAC and MSAC, respectively. As the threshold increases, the number of returned exact matches decreases and drops to 44.44% and 43.15% using RANSAC and MSAC detected by SURF.

Table 5. Changes in matching accuracies $\left({∆}_{\mathit{a}\mathit{c}\mathit{c}.}\right(\mathrm{\%}\left)\right)$ with their respective algorithms.

Alg.	SURF Detection				SIFT Detection				KAZE Detection
Ref. Alg.	(1)	(2)	(3)	(4)	(1)	(2)	(3)	(4)	(1)	(2)	(3)	(4)
TH	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$	${∆}_{acc.}$ $(\%)$
0.001	−9.30	−9.04	34.88	34.63	−6.70	−6.70	37.28	34.60	−8.69	−8.64	37.84	38.28
0.01	−9.30	−9.04	25.58	25.84	−6.70	−6.70	26.34	29.91	−8.69	−8.64	32.45	32.78
0.1	−9.30	−9.04	6.46	5.94	−6.70	−6.70	12.50	7.81	−8.69	−8.64	12.98	18.59
1	−9.30	−9.04	−14.73	−16.02	−6.70	−6.70	−5.58	−2.90	−8.69	−8.64	−10.23	−9.57
(1) LMEDS (2) LTS (3) RANSAC (4) MSAC

shows the change in matching accuracies of each blob-based feature detection algorithm with their respective refined matching algorithm and threshold. LMEDS and LTS have no effect in improving the matching accuracies of blob features detected by SURF, SIFT, and KAZE. The applied algorithms even impair some features, resulting in a decrease of 9.30% and 9.04% in matching accuracies for LMEDS and LTS, respectively. RANSAC and MSAC, on the other hand, are proven to improve the matching accuracies by 37.28% and 34.60% using the SIFT detector and by 37.84% and 38.28% using the KAZE detector at the lowest threshold of 0.001. However, increasing threshold intensifies the incorrect matching as at threshold = 1, RANSAC and MSAC return false matching rates of 5.58% and 2.9% using the SIFT detector and 10.23% and 9.57% using the KAZE detector.

4.2. Seismic Response of the ABC Bridge

The blob-based feature detection and matching results in the previous section suggest that RANSAC and MSAC returned more exact matches as compared to their counterparts, i.e., LMEDS and LTS. Careful selection should be considered, however, when choosing the threshold parameters, since higher thresholds may decrease the accuracy of NN matching. The next procedure is to generate the seismic response of the tested bridge and to compare the results from prior work using target-tracking and reference sensors to the results of the proposed blob-based feature refined matching. Based on Figure 2, two comparisons are made: the first at the bent cap level and the second at the west and east sides of the bridge girder. At the bent cap level, the results of target-tracking method $S$ and reference string potentiometer $R$ are compared to the blob-based feature KAZE and RANSAC refined matching $BK$ results. At the girder level, only the target-tracking method of the feature at the east $\left(E\right)$ and west $\left(W\right)$ sides is compared to blob-based feature matching using KAZE combined with RANSAC, $BK,$ since the reference sensors are not available at the girder level. KAZE combined with RANSAC is selected as an example of refined matching in this section because it generates the highest accuracies as compared to LMEDS, LTS, and MSAC.

The seismic response of the ABC bridge at the bent cap level is given in Figure 5 and at the girder level is shown in Figure 6. The displacement time histories are given for each level of design earthquake, from 20% to 75% design earthquake, DE. Since the recordings of vision-based measurement and reference sensor types have different time reference and sampling rates, the displacement responses from the reference sensor $R$ are adjusted to have a similar starting time as the target-tracking $S$ and KAZE combined with RANSAC, i.e., the $BK$ measurements in Figure 5. As the sampling rates are also different between both systems, the vision-based system uses a practical 30Hz or 30 image-per-second rate, while the reference sensor $R$ uses 256 Hz; resampling is conducted on vision-based results. Therefore, to accurately compare the sensor data, the results in Figure 5 are after resampling of vision-based results, i.e., the resampling of the $S$ and $BK$ displacement results. The tolerance is 0.0001 in the signal processing. Meanwhile, the results at girder level do not require any further signal processing since the results in Figure 6 are taken from vision-based data. Only the result of features $E$ and $W$ is generated using the target-tracking method, while the $BK$ result uses the proposed blob-based feature detector KAZE and refined matching RANSAC algorithms.

To measure the accuracy of the proposed blob-based feature KAZE detector and RANSAC matching the target-tracking and reference sensor results, an error analysis is performed using the root mean square error (RMSE). A summary of the RMSE computed in millimeter (mm) units is given in

Table 6. Measurement differences from the shake-table tests between the target-tracking method $S,E,W$ and reference string potentiometer $R$ and blob feature KAZE combined with RANSAC matching $BK$.

EQ Test	RMSE (mm)
	S to BK	R to BK	E to BK	W to BK
RUN#1-25%DE	0.02	0.17	0.08	0.06
RUN#2-50%DE	1.09	0.96	0.16	0.22
RUN#3-75%DE	1.02	1.15	0.50	0.38

. As shown in the table, the normalized RMSE is very low, with a lowest result of 0.02 mm and a highest result of 1.15 mm. This confirms the accuracy of blob-based feature KAZE and RANSAC matching and also justifies the technique and the camera’s practical 30 fps sampling rates. A slight difference is shown between the proposed algorithm and string potentiometer measurements, from R to BK at 75% DE. This is reasonable because as the seismic load increases, the error also becomes larger. Furthermore, this is because no triangulation is considered for the reference sensor R data, even though the impact of seismic shake on the bridge should observe the possibility that the string potentiometer is no longer aligned after the shakes. Therefore, based on the equivalent response shown in Figure 5 and Figure 6 together with the RMSE discussion above and the results in Table 6, the validity of the proposed algorithms is proven.

5. Conclusions

This study explores the effect of blob-based feature detectors combined with refined matching algorithms in improving their matching accuracies and then implements them on a two-span ABC bridge tested under seismic loads. The SHM is conducted using vision-based systems. The major contributions of this study are a detailed procedure that explores the impact of selecting detection and matching operators with their parameters to improve blob-based feature performance and a CV-oriented procedure implemented on seismic SHM using vision-based sensors. The study uses three design earthquake tests to quantify the effect of each selected algorithm on the matching accuracy. The main conclusions and key findings of this study are as follows:

• Using only the NN algorithm to return the exact match is not efficient, as only less than 60% of correct matches are returned for SURF, SIFT, and KAZE detectors. This confirms the results of previous works stating that using only the NN algorithm to find exact matches is challenging; combining it with a refined matching algorithm is necessary to improve the results.
• The LMEDS and LTS algorithms have no effect on refining the false matching; rather, they decrease the number of correct matches as well as the accuracies from NN matching. The change in their thresholds also has no impact; they show a constant number of matching features either at low- or high-threshold selection.
• RANSAC and MSAC, however, are proven to increase the number of correct matches as well as the matching accuracies of blob-based features using SURF, SIFT, and KAZE. Careful selection of threshold is mandatory because the matching accuracies decrease following the increase in the threshold. There is a chance that with selection of a higher threshold, the number of correct feature matches will even decrease from NN matching numbers, similar to when using LMEDS or LTS.
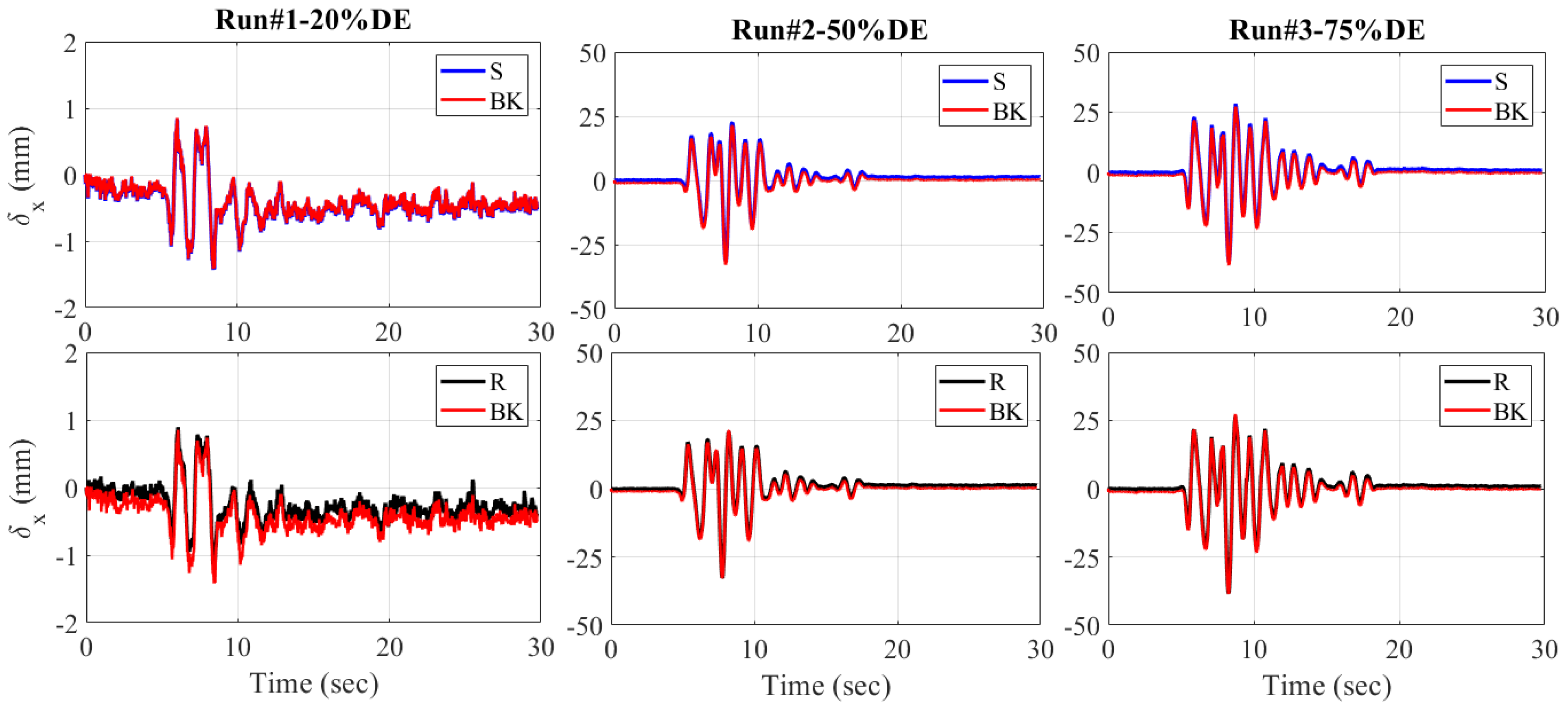
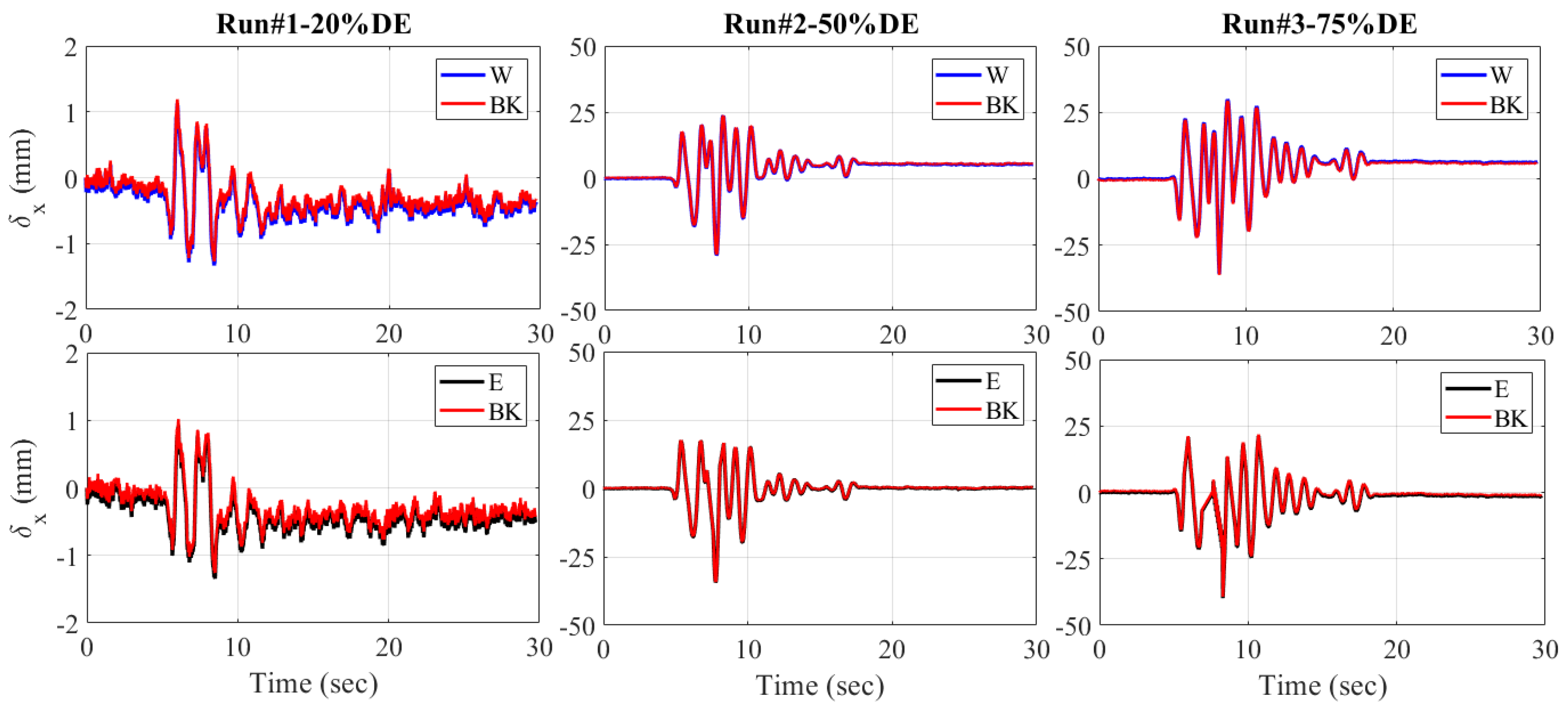
• The ABC bridge seismic test verifies the potential and accuracy of the proposed blob-based feature and refined matching algorithms, especially for bridge displacement responses. The displacement responses of the proposed algorithms show a similar trend to previous studies using target-tracking and string potentiometers. A minimum error of 0.02 mm is computed, while a slightly higher RMSE of 1.15 mm is calculated for the response to the higher-magnitude design earthquake.
• Overall, it is concluded that the proposed blob-based feature detection and refined matching algorithms have the potential for implementation in vision-based SHM of bridges. The combination of the blob-based feature detector SURF, SIFT, or KAZE with NN matching then refined with RANSAC and MSAC is proven to generate more accurate matching results. Therefore, they are recommended for implementation in detecting, extracting, and matching blob-based features of interest on bridge structures. Additionally, further study about detecting natural features on bridges or other civil infrastructures using the proposed algorithms is recommended.