Abstract
Model correlation techniques are methods used to compare two different models, usually a numerical model and an experimental model. According to the structural dynamic modification theory, the experimental mode shapes estimated by modal analysis can be expressed as a linear combination of the numerical mode shapes through a transformation matrix . In this paper, matrix is proposed as a novel model correlation technique to detect discrepancies between the numerical and the experimental models in terms of mass. The discrepancies in stiffness can be identified by combining the numerical natural frequencies and the matrix . This methodology can be applied to correlate the numerical and experimental results of civil (bridges, dams, towers, buildings, etc.), aerospace and mechanical structures and to detect damage when using structural health monitoring techniques. The technique was validated by numerical simulations on a lab-scaled two-span bridge considering different degradation scenarios and experimentally on a lab-scaled structure, which was correlated with two numerical models.
1. Introduction
In structural dynamics, model correlation techniques [,] are methods used to compare two different models, which may consist of two experimental models, two numerical models and, most frequently, a numerical model with an experimental model [,]. Two experimental models are compared in damage detection and structural health monitoring applications or in modal analysis [,] where it is common to compare the experimental modal parameters estimated using different modal identification techniques [,,,]. Two numerical models can be compared for mesh convergence investigations or for comparing a full model with a reduced model [,], among other applications. The normalized relative frequency difference (NRFD) [], which compares natural frequencies, and the modal assurance criterion (MAC) [], which compares mode shapes, are the most commonly used correlation techniques due to their extensive adoption in real applications and ease of implementation. Hereafter, subscript ‘B’ is used to denote the numerical model, while subscript ‘A’ is used to refer to the experimental model.
A good correlation between a numerical and an experimental model demands a good correlation in mass and stiffness, as well as in the internal (joints) and external (supports) boundary conditions []. The significance of correlation techniques is highlighted by their diverse applications in various fields, such as in civil (bridges, dams, towers [,], buildings, etc.), aerospace and mechanical structures. It is important to note that correlation techniques can be used either as the main goal, i.e., to know the correlation between two models, or as a preliminary step to achieve other goals, like in damage detection, model updating, etc. The success of these applications largely depends on the proper use of correlation techniques. In the following paragraphs, the main applications of correlation techniques are described.
Model updating is a technique used to improve the correlation between numerical and experimental models by updating finite element models [,,]. Model updating techniques can be classified into direct methods and iterative methods [,,,]. Direct methods (also known as matrix methods) update the elements of the stiffness and mass matrices in a one-step procedure, so they do not require iteration, and a good correlation is usually achieved []. Many authors have applied direct methods in the past [,,]; however, the updated mass and stiffness matrices have little physical meaning and cannot be directly related to physical changes in the finite element models []. On the other hand, iterative methods (also known as parameter updating methods) modify iteratively some parameters. Iterative methods can be subdivided into sensitivity methods and optimization methods. Iterative methods allow a wide choice of parameters to be updated [], which requires a sensitivity analysis to assess the impact of modifications in the model parameters. However, the user must preselect the physical parameters to be included in the sensitivity analysis. Additionally, due to uncertainties in the sensitivity analysis, the selection of final parameters requires some engineering judgment and expertise. For all these reasons, it is important to identify in advance if the discrepancies between the models are in terms of mass, stiffness or both. Another possible classification is to divide iterative methods into deterministic and stochastic methods []. The iterative deterministic maximum likelihood method transforms the model updating problem into an optimization problem, and the objective function is defined in terms of residuals between different types of numerically and experimentally obtained data sets; most often, natural frequencies and mode shapes are used [,,,,,].
Correlation techniques also play an important role in modal identification techniques. In the case of frequency domain decomposition (FDD), the modal assurance criterion (MAC) is used to define the single degree of freedom (SDOF) spectral density function [], comparing the reference vector (singular vector at the picked frequency) with the singular vectors estimated on both sides of the picked frequency from the FDD.
Moreover, correlation techniques are also used in automated operational modal analysis (AOMA). In the case of time-domain parametric techniques such as the Covariance-Driven Stochastic Subspace Iteration method (SSI-COV), once the modal parameters are estimated for each modal order, the spurious modes and the physical modes are separated using different stabilization criteria, most of them being based on the variation of modal parameters corresponding to two consecutive increasing orders, i.e., relative distance in frequency (NRFD), relative distance in damping coefficient and/or similarity of mode shapes through MAC [,,,]. Then, correlation techniques are crucial in the clustering process, where the estimated modes that represent the same physical mode are grouped. In the past, the most common procedure was to calculate the Euclidean distance between the objects to be clustered, considering natural frequencies and damping ratios. However, the modal damping ratios are not very suitable for distinguishing modes, and a new methodology was proposed based on the estimates of the natural frequencies and mode shapes []. This methodology for calculating distances between clusters has been applied up to the present [,,,,].
Structural health monitoring (SHM) is another field where correlation techniques play a significant role. Dynamic SHM methods, those that use vibration responses to gather information about changes in a structure’s dynamic properties, can be classified as model-based SHM or data-based SHM []. Model-based techniques use a finite element model of the structure to predict the dynamic response of the structure and allow damage to be detected and located. This numerical model must be well correlated with the real structure, so model updating techniques must be applied. Modal-based techniques observe changes in modal parameters with respect to a predefined reference condition to detect structural damage; that is, the correlation between two models is studied. Several methods have been proposed to detect damage in the past decades, the most common techniques being those based on natural frequencies and those based on mode shapes and their derivatives [,].
Structural health monitoring techniques seek to determine damage in the structure based on monitoring the deviations of the modal properties with respect to a normal condition of the structure (undamaged condition). However, one of the main difficulties faced by modal monitoring is the sensitivity of the modal properties due to environmental variations. The varying weather conditions (temperature, humidity, wind speed and direction, water content of the soil, etc.) can modify the experimental modal parameters of a structure [,]. These effects must be removed when using correlation and model updating techniques, as well as with damage detection and localization methods. Among these environmental factors, it has been identified that, in most cases, temperature is one of the environmental factors that generate the greatest variation in modal parameters for concrete and steel structures [].
Damage can be detected and localized from modal parameter (natural frequencies, mode shapes, modal curvature) variations estimated from acceleration responses []. However, damage assessment from experimental data is also highly susceptible to uncertainty, due to the difficulty in distinguishing between variations of modal parameters due to environmental conditions or the presence of damage [].
It is worth noting that when applying correlation techniques to experimental models [,], it is important to consider that the modal parameters are only known in a reduced frequency band (truncated model) and the mode shapes are only known in a few degrees of freedom (DOFs) [,,,]. The common procedure is to work with a reduced numerical model, although expansion techniques can be utilized to obtain a full modal matrix (in terms of DOFs) [,].
Although NRFD and MAC are the most used correlation techniques, numerous correlation methods can be found in the current literature, which will be explained in detail in the following section. However, each correlation method compares a certain characteristic [], i.e., a single technique capable of comparing two models with respect to different dynamic characteristics does not exist, and multiple methods are commonly used. Moreover, if the correlation between two models with closely spaced modes is studied, a good correlation can exist in terms of mass and stiffness between the models, but low values of modal assurance criteria (MAC) can be obtained because the mode shapes can rotate in the local subspace spanned by the closely spaced modes [,].
Structural dynamic modification (SDM) is a technique to study the effects of structural modifications (material, geometry, etc.) on the dynamic behavior of a structural system. According to the structural dynamic modification theory [,,], when a model A (experimental) can be considered a dynamic modification of a model B (numerical), the experimental modal matrix can be expressed as a linear combination of the numerical mode shapes, through a transformation matrix [], denoted in this paper as matrix .
In this paper, it is proposed to use the transformation matrix as a new model correlation technique, using the orthogonality properties of the mode shapes with respect to the mass and stiffness matrices. The inner product can be utilized to determine whether there are discrepancies between models in terms of mass (T-Mass), whereas the inner product of the matrix over the natural frequencies of the numerical model allows the identification of discrepancies in terms of stiffness (T-Stiffness). The proposed technique can also be applied successfully to systems with repeated or closely spaced modes []. When applying these techniques, the natural frequencies and mass-normalized mode shapes of both the numerical and the experimental models are needed. In the case of unscaled experimental mode shapes, the technique can still be applied, but less information is obtained because the information provided by the diagonal terms of T-Mass and T-Stiffness cannot be used. In this latter case, the experimental natural frequencies are not needed (they cannot be used).
The new technique was applied successfully in two examples. The first example involved a numerical model of a two-span lab-scaled bridge, assembled in ABAQUS, where different degradation scenarios (mass changes and stiffness changes) were considered in the simulations. In the second example, the experimental modal parameters of a steel cantilever beam were used to analyze the correlation with a numerical model, where the support was modeled with different boundary conditions. This novel approach was able to identify the source of discrepancy between models in terms of mass, stiffness or both.
The paper is organized as follows. Firstly, a review of the most commonly used correlation techniques is carried out in the following section. In Section 3, the concepts of T-Mass and T-Stiffness for correlating two models are presented, along with some indexes for measuring the level of discrepancies. Section 4 compares the proposed techniques with some of the correlation methods existing in the literature based on the orthogonality of the mode shapes with respect to the mass matrix. In Section 5, the tools proposed in this paper are validated through numerical simulations of a two-span lab-scaled bridge subject to different degradation scenarios. Finally, in Section 6, the experimental modal parameters of a steel cantilever beam were used to correlate the experimental structure with two numerical models assembled in ABAQUS.
2. Introduction to Modal Correlation Techniques
The model correlation techniques can be classified into four categories: eigenvalue-based criteria, eigenvector-based criteria, frequency-response-based criteria and orthogonality methods. A brief review of these methods is provided in the following sections.
2.1. Eigenvalue-Based Criteria
The criteria based on eigenvalues compare a set of natural frequencies of two models [,,,]. The normalized relative frequency difference (NRFD) is the most used method. The NRFD corresponding to the j-th mode is calculated with the following expression:
where and indicate the j-th natural frequency of the two models. When using this technique, mode pairing is mandatory.
Similar indexes are the NFD, which compares the relative difference between all natural frequencies, and the NFCC, which gives the standard deviation of corresponding natural frequencies [].
The acceptable limits for the most commonly used correlation techniques in the aerospace industry are often dictated by large agencies such as NASA [] and ESA (European Space Agency) []. According to (ESA) [], the eigenfrequency deviation in test-analysis correlation must be less than 3%.
2.2. Eigenvector-Based Criteria
The criteria based on eigenvectors compare a set of mode shapes, and mode pairing is also mandatory. The modal scale factor (MSF) was initially proposed, but it was not widely used because it depends on the normalization technique used to scale the mode shapes. The best-known method is the modal assurance criterion (MAC) [,,,,,,,,,,] which compares the shapes of two eigenvectors based on the inner product. If two vectors (model B) and (model A) are compared, the MAC is given by
where the superscript ‘T’ indicates transpose. The MAC is always a real value, so that if the vectors are complex, the MAC is calculated with the expression
where the superscript ‘H’ indicates a complex conjugate.
The MAC takes on values from zero (representing no consistent correspondence) to one (representing consistent correspondence). To have a good correlation between a numerical and an experimental mode, ESA [] requires a MAC of at least 0.9 for the fundamental bending modes of a spacecraft.
If the vectors are normalized to the unit length (vectors and , where subscript ‘L’ indicates mode shape normalized to the unit length), Equation (2) simplifies to
The uncertainty quantification of the modal assurance criterion (MAC) was investigated in [].
Several modifications or variants of the MAC have also been proposed in the literature. The AUTOMAC (MAC of a model with itself) is commonly used to detect spatial aliasing [,]. COMAC (Co-Ordinate MAC) correlates two models for each individual DOF [,]. MAC is not a true orthogonality check since the mass or stiffness matrices are not included in the calculation. To overcome this limitation, mass-weighed MAC (NCO) and stiffness-weighed MAC (WMAC) have also been proposed as correlation techniques of eigenvectors [,].
A similar index to MAC is the normalized modal difference (NMD) [], which is given by the equation
However, the disadvantage of NMD is that it is not a bounded function.
MAC can also be defined as , where is the angle between vectors and . A linear MAC (LMAC) can be defined as []
Energy-based variants of the modal assurance criteria have also been proposed in the literature [,,,], where MAC is enhanced with physical information about the stiffness of the structure using modal strain energies. In [], a correlation technique (RMAC) was proposed for rotors, and in [], the authors proposed two indexes for systems with fluid–structure interaction based on potential energy (POTMAC) and kinetic energy (KINMAC).
When an experimental mode shape is compared with one of two closely spaced modes in the FE model, the correlation with the individual mode shape is often low. D’ambrogio and Fregolent [,] proposed to correlate the experimental mode shape with a linear combination of the two numerical mode shapes and , which, for two closely spaced modes, is calculated with the equation:
2.3. Frequency-Response-Based Criteria
Frequency-response-based criteria are used to compare frequency response functions (FRFs). One such criterion is the frequency response assurance criterion (FRAC), which compares the FRFs at a particular DOF, i.e., it is similar to MAC. The FRAC at the i-th DOF between the numerical model (subscript ‘B’) and the experimental model (subscript ‘A’) is calculated using the following equation [,,]:
Another criterion is the Response Vector Assurance Criterion (RVAC), which compares FRFs for all DOFs at a single frequency. The Frequency Domain Assurance Criterion (FDAC) [], the Frequency Response Scale Factor (FRSF) [] or the Modal FRF Assurance Criterion (MFAC) also use mode shapes and FRFs for modal correlation []. Marinone [] compared some of the most common FRF correlation techniques and found that the Nyquist Error, RMS Error and R2 Error provide the best assessment. Recently, the FRFSM [] and variations of it [] were also proposed.
2.4. Orthogonality Criteria
It is well known that the mode shapes are orthogonal with respect to the mass and the stiffness matrices. If is the mass matrix and the modal matrix of a numerical model, the inner product
is a diagonal matrix containing the modal masses .
On the other hand, the inner product of the mode shapes over the numerical stiffness matrix is also a diagonal matrix containing the modal stiffnesses:
where is a diagonal matrix containing the squared numerical natural frequencies.
Based on these properties, several techniques have been proposed to compare numerical and experimental models. The cross-orthogonality check (COC) [,] is obtained as the inner product of the experimental mode shapes over the numerical mass matrix:
The COC can also be defined as the inner product of the numerical mode shapes over the experimental mass matrix ():
However, this expression is rarely used in practice because the experimental mass matrix is rarely known.
Another way of assessing correlation is with the pseudo-orthogonality check (POC) []. The inner product of the numerical and experimental mode shapes over the numerical mass matrix is defined as
is an identity matrix in an ideal case (, i.e., when the two sets of modes are perfectly correlated, whereas any off-diagonal element can be seen as a coupling of modes.
Coppolino [,] applied the pseudo-orthogonality check () for the correlation of test and finite element models in the aerospace field. He proposed to augment the set of experimental mode shapes using quasi-static residual vectors, which are appropriate for structures subject to distributed and localized perturbations [,].
The POC can also be defined as the inner product of the numerical and experimental mode shapes over the stiffness matrix as
3. New Approach to Model Correlation Using Transformation Matrix
In order to present the proposed methodology, a brief introduction to the basis of structural dynamic modification is necessary. Here, a discrete numerical model is considered, described by the stiffness matrix and the mass matrix , and a discrete experimental model that represents reality, defined by the stiffness matrix and the mass matrix , is also considered.
According to the structural dynamic modification theory [,,], the experimental model can be considered a dynamic modification of the numerical one. The mass matrix of the experimental model can be expressed as
where is the mass change matrix.
Similarly, the stiffness matrix of the experimental model can be expressed as
where is the stiffness change matrix.
The experimental mass-normalized modal matrix A can be expressed as a linear combination of the mass-normalized numerical modal matrix B by means of the expression [,,,]
where is a transformation matrix.
If the experimental mode shapes are not mass-normalized (unscaled) [,,,], they still can be expressed as a linear combination of the numerical mass-normalized mode shapes using the equation
where the subscript ‘’ indicates unscaled.
The matrices and are related by the equation
where is a diagonal matrix containing the experimental scaling factors [,,] that relate the scaled and the unscaled mode shape matrices:
3.1. The T-Mass
If Equation (15) is pre-multiplied and post-multiplied by the mass-normalized experimental mode shapes, it becomes
The inner product can also be expressed as
Substituting Equation (22) in Equation (21) and considering that the modal masses corresponding to mass-normalized mode shapes are dimensionless unity, Equation (21) becomes
From Equation (23), it is inferred that, if there are no discrepancies in terms of mass between the numerical and the experimental mode shapes, then 0, and Equation (23) results in []
This means that the product is an identity matrix, which indicates that the experimental mode shapes are orthogonal with respect to the mass matrix (see Equation (22)), or alternatively, the column vectors of matrix are orthogonal to each other.
In the case of unscaled experimental mode shapes, Equation (21) is expressed as
and Equation (23) as
where is a diagonal matrix containing the modal masses.
If there are no mass discrepancies between the two models, Equation (26) leads to
From Equation (27), it is inferred that the matrix is a diagonal matrix in the case of no mass discrepancies, and the column vectors in matrix are also orthogonal to each other.
From previous equations, it is derived that the product (or ) contains information about differences in mass between the numerical and the experimental models (Figure 1).
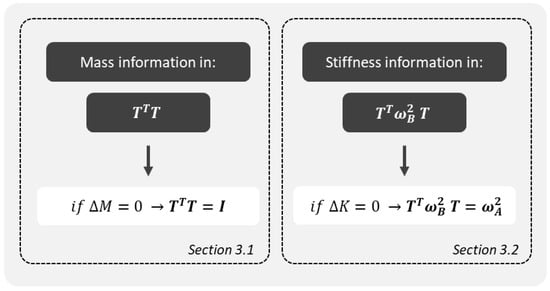
Figure 1.
Source of information about changes in mass or stiffness.
In order to have an indicator of mass discrepancies between both models, the angles between the vectors of matrix T are proposed, denoted hereafter as T-Mass. Angles equal to 90° indicate perfect orthogonality, i.e., no discrepancies in mass, and the order of discrepancies increases with decreasing angles. T-Mass is not affected by the normalization used in the experimental mode shapes, meaning the same angles are obtained using matrix or matrix .
Alternatively, an indicator between 0 and 1 (1 for no discrepancies in mass) can be obtained by dividing all terms of the T-Mass matrix by 90° (T-Mass-norm). Additionally, The AUTOMAC of vectors in matrix (or matrix could also be used as an indicator of discrepancies in terms of mass (see Table 1).

Table 1.
Proposed indicators for identifying mass discrepancies.
3.2. The T-Stiffness
If Equation (16) is pre-multiplied and post-multiplied by the mass-normalized experimental mode shapes, it becomes
Substituting Equation (17) in Equation (28) and considering that the modal masses corresponding to mass-normalized mode shapes are dimensionless unity, Equation (28) becomes
Here, and are diagonal matrices containing the natural frequencies of the experimental and numerical models, respectively.
From Equation (29), it is inferred that, if there are no discrepancies in terms of stiffness between the numerical and the experimental models, then 0, and Equation (29) results in []
This means that the inner product is a diagonal matrix containing the natural frequencies in the diagonal.
In the case of unscaled experimental mode shapes, Equation (29) is expressed as
which leads to the following equation if 0:
Here, the inner product is also a diagonal matrix containing the modal stiffnesses in the diagonal.
From the previous equations, it is derived that the column vectors of the matrices and are orthogonal with respect to the eigenvalue matrix when there are no discrepancies, in terms of stiffness between the numerical and the experimental models. That is, (or ) contains information about stiffness changes (Figure 1).
In order to have an indicator of stiffness discrepancies between two models, the angles between the vectors of matrix T and matrix are proposed, denoted hereafter as T-Stiffness. Angles equal to 90° indicate perfect orthogonality, i.e., no discrepancies in stiffness, and the order of discrepancies increases with decreasing angles. T-Stiffness is not affected by the normalization used in the experimental mode shapes, meaning the same angles are obtained using matrix or matrix .
Alternatively, an indicator between 0 and 1 (1 for no discrepancies in stiffness) can be obtained by dividing all the T-Stiffness elements by 90° (T-Stiffness-norm). Additionally, the MAC between vectors in matrix (or matrix ) and vectors in matrix (or ) could also be used as an indicator of discrepancies in terms of stiffness (see Table 2).

Table 2.
Proposed indicators for identifying stiffness discrepancies.
4. Relationships between T-Mass and Cross-Orthogonality
In this section, the methodology proposed in Section 3 is compared with previous works existing in the literature about cross-orthogonality and pseudo-orthogonality checks. To accomplish this, the equations proposed by different authors are rewritten based on the matrix .
When comparing numerical and experimental models, it is necessary to reduce the numerical mass and stiffness matrices, and the results of the cross-orthogonality and the pseudo-cross orthogonality depend on the reduction technique utilized. Hereafter, it is assumed that the matrix estimated with the full set of DOFs is the same as the matrix estimated with the active DOFs (measured DOFs) []. With this assumption, the reduction of matrices is not necessary, as demonstrated below.
Regarding the cross-orthogonality , Heylen et al. [] proposed the same expression as Equation (11), but the authors use the notation-mixed orthogonality :
However, the columns of matrix must be normalized in such a way that the diagonal elements are set equal to 1. After rescaling, the (r,s) term of matrix is given by
where and are the r-th and s-th column vectors of matrix , respectively.
A similar index is proposed by the European Cooperation for Space Standardization (ECSS) [], which defines the auto-orthogonality check as
where and are column vectors (mode shapes) of the experimental modal matrix . Equation (35) can also be expressed as
Regarding the pseudo-orthogonality check , Heylen et al. [] proposed the same expression as Equation (13), but the authors used the notation cross-orthogonality :
Again, the columns of the matrix must be normalized in such a way that the diagonal elements are set equal to 1:
A similar index to is proposed by the European Cooperation for Space Standardization (ECSS) [], but they use the notation cross-orthogonality check , which is calculated with the expression
where is the r-th column vector (mode shape) of the numerical modal matrix . Equation (39) can also be expressed as
A similar expression was proposed in [], denoted Normalized Cross-Orthogonality , which is defined as
where the weighing matrix can be the mass matrix .
All the diagonal elements obtained with , and are equal to unity, but this is not the case with . All these indexes consider a good correlation if the off-diagonal elements do not exceed 0.1 [,]. However, Heylen et al. [] state that the interpretation of these orthogonality indexes is not very clear.
In this section, mass-normalized mode shapes were considered in all the equations. , and are not sensitive to the normalization used in the mode shapes (the same results are obtained with any scaling technique). However, the results obtained with depend on the normalization used in the mode shapes, which must be taken into account for the interpretation of the results.
5. Numerical Simulations: A Lab-Scaled Two-Span Bridge
The accuracy and effectiveness of the technique proposed in this paper are first investigated with a numerical model of a lab-scaled bridge. A two-span steel bridge (see Figure 2), with a rectangular section of cm and a full integral abutment at the left border (modeled as fixed support) and simply supported at the mid-point (pier) and the right border (abutment), was assembled in ABAQUS. The model was meshed with 200 quadratic beam elements (B22). The following mechanical properties were considered for the steel: mass-density , Poisson ratio and Young Modulus . This case (CASE 0) was considered as the numerical model (model B according to previous sections).

Figure 2.
Two-span beam. CASE 0.
CASE 0 was perturbed with mass and stiffness modifications, which are considered as the experimental cases (models A). In CASE 1 (Figure 3a), a mass loss of 25% is considered in a part of the right span, which corresponds to a total mass loss of 6.25%. In CASE 2 (Figure 3b), a loss of stiffness was simulated by substituting the fixed support with a pinned support and a rotational spring with stiffness . Regarding CASE 3 (Figure 3c), a stiffness loss was also simulated by introducing a hinge and a rotational spring with the same stiffness at the mid-point of the first span.
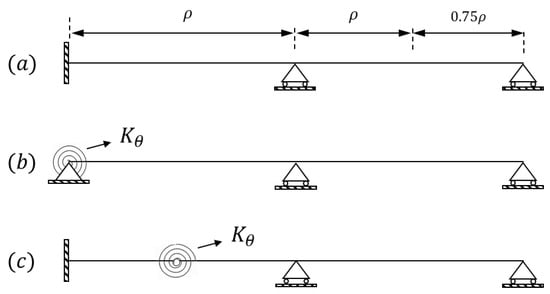
Figure 3.
Perturbations of CASE 0: (a) CASE 1. (b) CASE 2. (c) CASE 3.
The natural frequencies corresponding to the first eight modes are presented in Table 3.

Table 3.
Natural frequencies of the two-span beam.
Matrix was estimated for all the cases (CASES 0–1, CASES 0–2 and CASES 0–3), considering 10 DOFs (indicated with arrows in Figure 2) and 8 modes in both the numerical and the experimental models using Equation (17). No errors were taken into consideration for the modal parameters.
The T-Mass and T-Stiffness matrices corresponding to CASES 0–1 (mass change only) are presented in Table 4 and Table 5, respectively. As expected, the vectors of matrices and (see Table 5) are perfectly orthogonal (with T-Stiffness values equal to or very close to 90°) because there are no discrepancies in terms of stiffness. Regarding the angles between the vectors of matrix , T-Mass (see Table 4) shows that all the angles are less than 90°, with the minimum being 84.5849°, thus corroborating discrepancies in terms of mass between the models of CASE 0 and CASE 1.

Table 4.
T-Mass for CASES 0–1.

Table 5.
T-Stiffness for CASES 0–1.
With respect to CASES 0–2 and CASES 0–3, T-Mass is presented in Table 6 for CASES 0–2 and in Table 7 for CASES 0–3. As can be observed, the vectors are perfectly orthogonal (with T-Mass angles equal to or very close to 90°), confirming that there are no discrepancies in terms of mass. Regarding T-Stiffness, the results are presented in Table 8 for CASES 0–2 and in Table 9 for CASES 0–3. In both cases, T-Stiffness values have decreased significantly, confirming discrepancies in terms of stiffness between CASE 0 and CASES 2 and 3.

Table 6.
T-Mass for CASES 0–2.

Table 7.
T-Mass for CASES 0–3.

Table 8.
T-Stiffness for CASES 0–2.

Table 9.
T-Stiffness for CASES 0–3.
In order to prove that this technique is sensitive to the magnitude of stiffness loss, five simulations of CASE 2 were performed by changing the stiffness of the rotational spring in the range . T-Stiffness elements, located at the lower triangular part of the matrix and corresponding to these simulations, are shown with circles in Figure 4. It can be observed that this technique is sensitive to stiffness loss, as all the angles decrease with increasing discrepancies in terms of stiffness.
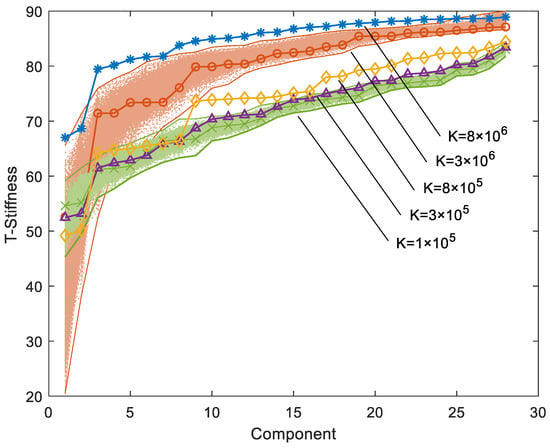
Figure 4.
T-Stiffness (in ascending order) for different stiffness losses in CASES 0–2.
The elements of matrix can be affected by noise in the components of the mode shapes. In order to study this effect, one thousand simulations of CASE 2 with spring stiffnesses and were performed considering random errors of in the components of the experimental mode shapes. The angles obtained are shown in Figure 4 in green and red color, respectively. It can be observed that the minimum angles of the T-Stiffness are very sensitive to errors in the mode shapes, but only a slight variation can be observed in the rest of the angles.
Similarly, five simulations were also performed on CASE 1 decreasing the mass density of the right part of the second span in the range (where is the mass density corresponding to CASE 0). The T-Mass elements, located at the lower triangular part of the matrix, are shown with circles in Figure 5. It can be observed that this technique is also sensitive to mass changes since all the angles decrease with decreasing mass density. Furthermore, the effect of a random error of in the components of the experimental mode shapes was also studied by performing one thousand simulations of cases and . The results are shown in Figure 5 in green and red color, respectively.
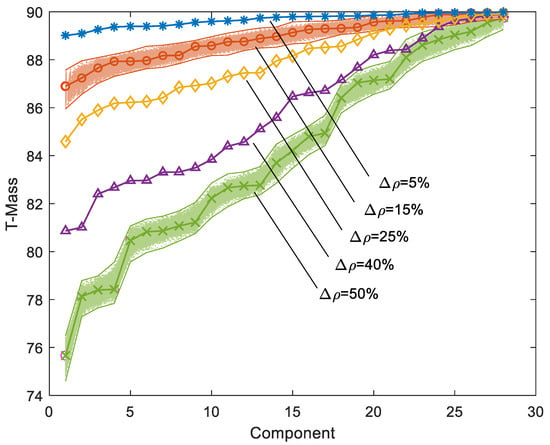
Figure 5.
T-Mass (in ascending order) for different mass losses in CASES 0–1.
It is also worth noting that the angles between the vectors of matrix do not depend on the normalization used in the mode shapes. However, if the mode shapes are mass-normalized, the diagonal elements of the inner product provide additional information. Table 10 shows the diagonal elements of for all cases when the mode shapes are mass-normalized, together with the modal masses (unity for all the cases and all the modes) of the experimental systems. The mass distribution of CASES 0, 2 and 3 is the same, and according to Equation (24), the inner product (CASES 0–2 and 0–3) must be an identity matrix. As shown in Table 10, the diagonal elements of are very close to unity, indicating no discrepancies in terms of mass, the small discrepancies being due to modal truncation (the components of the matrix corresponding to the last higher modes are estimated with less accuracy). With respect to CASES 0–1, there are discrepancies in terms of mass, and values different from one were obtained (see Table 10). Diagonal elements higher than unity indicate a mass loss in the structure, i.e., . However, this is not the case for mode 8, which can again be explained by the effect of truncation (this effect can be minimized by using the local correspondence principle []).

Table 10.
Diagonal elements of matrix.
Regarding the inner product , according to Equation (30), the diagonal elements must be equal to the natural frequencies when there are no discrepancies in terms of stiffness and the mode shapes of both systems are mass-normalized. Table 11 shows the diagonal elements of for all cases, together with the natural frequencies . The diagonal elements are very close to for CASES 0–1 (with ratios very close to one), indicating no discrepancies in terms of stiffness. Given that CASES 2 and 3 were modified with changes in stiffness, the ratios differ from unity, with ratios higher than one indicating a stiffness loss in the structure, i.e., (except for the value corresponding to mode 8 due to modal truncation).

Table 11.
Diagonal elements of matrix.
6. An Experimental Cantilever Beam
In this section, an experimental-numerical correlation study was conducted on a 1.875 m long steel cantilever beam with a rectangular hollow section of 100 × 40 × 4 mm. The experimental modal parameters were estimated using operational modal analysis (OMA), so the experimental mode shapes are unscaled. Responses were recorded in 8 DOFs using eight accelerometers with a sensitivity of 100 mV/g, located as shown in Figure 6. The structure was artificially excited by applying repetitive hits randomly in time and space [], and the responses were recorded for 3 min at a sampling frequency of 2000 Hz.
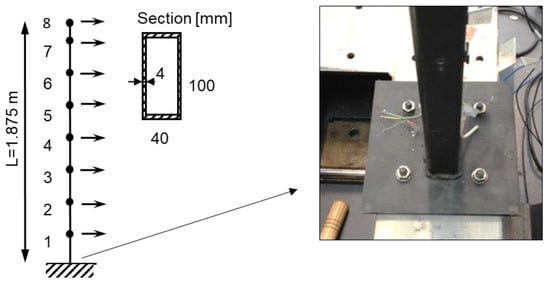
Figure 6.
Test setup for the cantilever beam and detail of support.
The experimental modal parameters were identified with the Subspace Stochastic Identification method (SSI) [] using ARTeMIS Modal. The experimental natural frequencies corresponding to the first five modes are presented in Table 12.

Table 12.
Natural frequencies for the cantilever beam.
Additionally, two numerical models were assembled in ABAQUS using 30 beam linear elements B21 (see Figure 7). Fixed support was considered in the first numerical model (denoted as FE Fixed). In the second model (denoted as FE Spring), the fixed support was substituted by pinned support and a rotational spring in order to better simulate the real support conditions at the bottom of the beam structure (see Figure 7). All other geometrical and mechanical properties remained unchanged. The spring stiffness was tuned using data from static experimental tests, in which different force values were applied to DOF 8, and the corresponding displacements were measured. Then, a MATLAB iterative process was employed to obtain the optimal value of the rotational spring which resulted in .

Figure 7.
Numerical models of the cantilever beam.
The natural frequencies of the first seven modes, which were obtained by solving the eigenvalue problem [,,], are presented in Table 12.
The modal assurance criterion (MAC) between the different models is presented in Table 13, Table 14 and Table 15.

Table 13.
MAC between the numerical fixed model and the experimental model.

Table 14.
MAC between the experimental model and the numerical model with rotational spring.

Table 15.
MAC between the numerical fixed model and the numerical model with rotational spring.
It is inferred from Table 12 and Table 13 that there are discrepancies in the natural frequencies (maximum error 25.95%) and mode shapes (MAC in the range 0.921–0.999) between the experimental model (denoted as EXP) and the FE Fixed model. However, the frequency difference and the MAC do not provide information about the source of the discrepancies.
Table 14 shows a very good correlation for the mode shapes between the experimental model and the FE Spring model. The correlation in terms of natural frequencies improved compared to the FE Fixed model, with a maximum error of 16.63% (Table 12). This means that the FE Spring model represents with better accuracy the dynamic behavior of this structure, as expected.
Comparing both numerical models, Table 12 and Table 15 indicate discrepancies in natural frequencies (maximum of 16.23%) and mode shapes (MAC in the range 0.958–0.998).
The discrepancies in terms of mass between the different models were studied with the T-Mass correlation technique (Table A16 and Table A20). The components located in the lower triangular part of the T-Mass matrix, which contains the angles between the vectors of matrix , are presented in Figure 8.
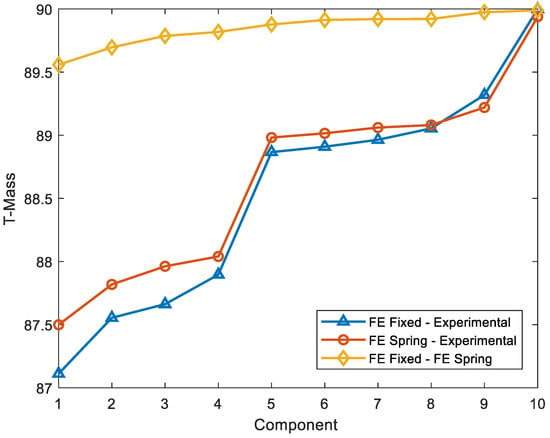
Figure 8.
T-Mass (in ascending order) for different cases.
No discrepancies in terms of mass are observed between the two numerical models (FE Fixed—FE Spring) (see Figure 8), with T-Mass angle values higher than 89.56°. This was expected because the only difference between the two models is the substitution of the fixed support for a pinned support with a rotational spring. From Figure 8, it is also inferred that a larger discrepancy in terms of mass exists between the experimental and both numerical models, with all the T-Mass values less than those corresponding to the FE Fixed—FE Spring models. Moreover, T-Mass values corresponding to cases FE Spring—EXP and FE Fixed—EXP are very similar. This was also expected because there were no differences in terms of mass between the numerical models.
The discrepancies in terms of stiffness were analyzed using the proposed T-Stiffness correlation technique (Table A18 and Table A22). It can be observed in Figure 9 that a better correlation in terms of stiffness is obtained with the FE Spring—EXP models, with the minimum angle in T-Stiffness being 78.55°. Larger discrepancies exist in the cases FE Spring—EXP models, as well as between both numerical models (FE Fixed—FE Spring). It can be seen in Figure 9 that the curves corresponding to the FE Fixed—EXP and FE Fixed—FE Spring models are close, indicating similar levels of discrepancies in terms of stiffness. This is consistent with the errors of similar order obtained in natural frequencies between these models (Table 12).
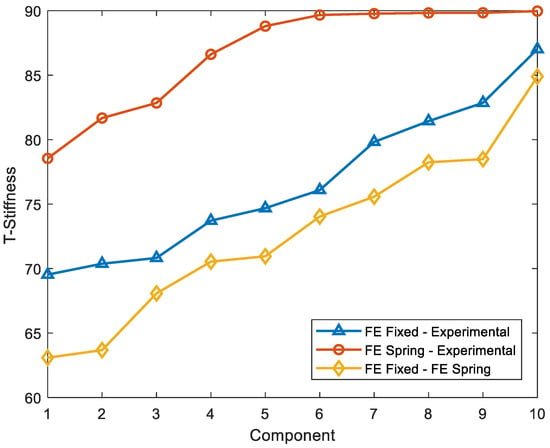
Figure 9.
T-Stiffness (in ascending order) for different cases.
However, the experimental modal parameters could be affected by noise in the measurements or other processing and identification errors, which are not present in the numerical simulations. In order to study this effect, an error of 2% in the components of mode shapes of the FE Spring model was considered in 500 simulations (Figure 10). Figure 10 shows that the minimum T-Stiffness angle values are very sensitive to errors in the mode shapes, whereas there is a slight variation in the rest of the angles.
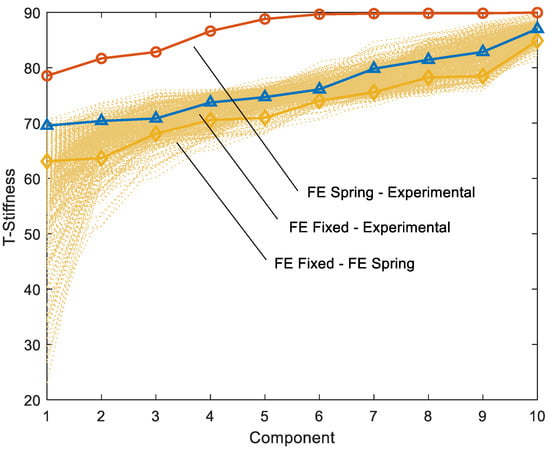
Figure 10.
T-Stiffness results of 500 simulations considering an error of 2% in the components of mode shapes of the FE Spring model.
From the analysis presented in this section, it is inferred that the FE Spring model presents a better correlation with the experimental model (FE Spring—EXP) than the FE Fixed model (FE Fixed—EXP). Therefore, there are fewer discrepancies in natural frequencies, and the values of MAC are very close to unity for all the modes. However, the T-Mass indicates that the differences in mass between both numerical models and the experimental model (FE Fixed—EXP and FE Spring—EXP) are of the same order. Moreover, the T-Stiffness shows that a better correlation in stiffness is achieved with the FE Spring model (FE Spring—EXP).
In order to enhance the information obtained by the T-Mass and T-Stiffness correlation techniques, the full matrices for the cantilever beam are presented in Appendix B. Additionally, the alternative indicators for T-Mass and T-Stiffness in the range 0–1 (T-Mass-norm and T-Stiffness-norm) are also presented in Appendix B (Table A17, Table A19, Table A21 and Table A23).
7. Discussion
In Section 5, the new correlation approaches based on the transformation matrix (T-Mass and T-Stiffness) were validated by numerical simulations on a two-span beam assembled in ABAQUS, considering different mass and stiffness degradation scenarios.
T-Mass and T-Stiffness were compared with techniques existing in the literature (already discussed in Section 4), and matrices defined by Heylen et al. [], and and matrices according to ECSS [], which are included in Appendix A. Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6 show that depends on the normalization method, and different results are obtained using mass or length normalization.
For CASES 0–1, mass discrepancies are not detected (off-diagonal elements < 0.1), neither by the (Table A1 and Table A2) nor the (Table A10). However, discrepancies have been observed with the (Table A7), with the largest off-diagonal value being 0.259, and (Table A13), with the largest off-diagonal value being 0.249. This indicates that the thresholds used in and should be different from those considered in the and
For CASES 0–2 (no mass discrepancies), the off-diagonal elements of (Table A3 and Table A4) and (Table A11) are less than 0.1, indicating a good correlation. However, off-diagonal elements higher than 0.1 are obtained with (Table A8) and (Table A14), which do not meet the quality criterion established in []. A good correlation in mass (Table A5, Table A6, Table A9, Table A12 and Table A15) is obtained for CASES 0–3 with all the indexes.
From the simulations, it is inferred that , , and provide insight into the magnitude of discrepancies between models, but they are not sufficiently reliable. On the other hand, T-Mass is more robust than , , and since the angles between the vectors of the matrix consistently decrease as the mass discrepancies increase (Table 4, Table 6 and Table 8).
In Section 6, the experimental modal parameters of an experimental steel cantilever beam were used to correlate the experimental structure with a numerical model modeled with fixed support. Significant discrepancies in natural frequencies (maximum error of 25.95%) and mode shapes (MAC in the range 0.921–0.999) were found between the experimental model and the FE model with fixed support. With respect to T-Mass, slight discrepancies in mass were identified, whereas T-Stiffness identified larger discrepancies in terms of stiffness.
Then, the numerical model with fixed support was updated, substituting the fixed support with a pin support with a rotational spring. A very good correlation was obtained for the mode shapes between the experimental model and the FE Spring model, whereas the discrepancies in the natural frequencies were reduced significantly. Since the mass was not modified, the T-Mass (Figure 8) provides similar results for the FE Spring—EXP and FE Fixed-EXP cases. With respect to the discrepancies in stiffness, the T-Stiffness (Figure 9) confirms a better correlation (in terms of stiffness) between the experimental model and the numerical model with pin-spring support.
8. Conclusions
In this paper, the concepts of T-Mass and T-Stiffness were proposed as new tools to correlate numerical and experimental models. These techniques can be used complementary to other correlation techniques and allow us to know if the discrepancies can be attributed to mass, stiffness or both. T-Mass and T-Stiffness are not dependent on the closeness of the modes, and they can be applied successfully to systems with separated modes and also to systems with repeated or closely spaced modes.
In the T-Mass technique, the inner product must be an identity matrix if there are no discrepancies in mass, and the angles between the vectors of matrix have been used to detect discrepancies in mass. Alternatively, the AUTOMAC of vectors in matrix can also be used as an indicator of discrepancies in terms of mass.
In the T-Stiffness technique, the inner product must be a diagonal matrix containing the natural frequencies , if there are no discrepancies in stiffness. In this case, the angles between the vectors of matrices and were used as a stiffness correlation technique. Alternatively, the MAC between vectors in matrix and vectors in matrix can be used to detect discrepancies in stiffness.
In Section 4, the proposed techniques (T-Mass and T-Stiffness) were thoroughly compared with existing correlation methods widely used in the literature, addressing their differences and similarities, as well as advantages and limitations. AOCECSS, COCECSS and COM are not sensitive to the normalization used in the mode shapes (the same results are obtained with any scaling technique). However, the results obtained with depend on the mode shape normalization technique.
The new correlation approaches based on the transformation matrix (T-Mass and T-Stiffness) were first validated by numerical simulations. A two-span beam was assembled in ABAQUS, and different mass and stiffness degradation scenarios were considered in the simulations. It was demonstrated that the T-Mass and T-Stiffness matrices can be utilized successfully to know if the discrepancies between the two models are due to differences in mass or stiffness. ‘False positives’ were obtained with COM and COCECSS in cases with no discrepancies in mass, which indicates that these indexes can be sensitive to measurement errors, overfitting or other sources of error. On the other hand, T-Mass is more robust, with all the values (angles between vectors) consistently decreasing with increasing differences in mass. The robustness of T-Mass and T-Stiffness indicators was validated considering errors in the components of the mode shapes in the simulations.
Then, experimental modal parameters of an experimental steel cantilever beam were used to correlate the experimental structure with two numerical models. The first numerical model was modeled with fixed support, whereas the second model was supported by a pin with a rotational spring. Slight discrepancies in mass were identified (T-Mass). However, larger discrepancies were obtained in terms of stiffness (T-Stiffness), being higher for the FE Fixed—Experimental than for the FE Spring—Experimental cases. These results indicate that, in this practical case, the use of a rotational spring improved the correlation between models. Again, the technique was validated considering also the effect of the noise present in the experimental responses, which might affect the accuracy of the experimental modal parameters.
The effectiveness of the proposed techniques depends on the precision achieved in the estimation of the experimental modal parameters, the number of available experimental modes (modal truncation), and the number of degrees of freedom (DOFs) measured in the experiments. On the other hand, the effectiveness of the techniques improves if the experimental modal masses are known. However, the modal mass is the least reliable parameter when classical modal analysis is used.
Future work concerns relating changes in the terms of matrix T with the magnitude and location of discrepancies between models and studying the sensitivity of the techniques to errors in the experimental modal masses (when they are estimated with classical modal analysis).
Author Contributions
Conceptualization, M.A.L. and R.B.; methodology, M.A.L., P.F.F. and N.G.F.; software, N.G.F.; validation, M.A.L., R.B., P.F.F. and N.G.F.; formal analysis, M.A.L., R.B., P.F.F. and N.G.F.; investigation, M.A.L., R.B., P.F.F. and N.G.F.; resources, M.A.L. and P.F.F.; data curation, P.F.F. and N.G.F.; writing—original draft preparation M.A.L. and N.G.F. writing—review and editing, M.A.L., P.F.F. and N.G.F.; visualization, N.G.F.; supervision, M.A.L. and P.F.F.; project administration, M.A.L. and P.F.F.; funding acquisition, M.A.L. and P.F.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministry of Science and Innovation through the projects MCI-20-PID2019-105593GB-I00/AEI/10.13039/501100011033 and MCI-21-PRE2020-094923.
Data Availability Statement
The data used in this paper are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Additional Results of the Two-Span Beam

Table A1.
MOM defined by Heylen et al. for CASES 0–1 (mass normalization).
Table A1.
MOM defined by Heylen et al. for CASES 0–1 (mass normalization).
| 1.000 | 0.074 | 0.094 | 0.046 | −0.007 | 0.009 | −0.036 | 0.029 |
| 0.069 | 1.000 | 0.064 | 0.032 | −0.010 | 0.002 | −0.020 | 0.016 |
| 0.095 | 0.068 | 1.000 | 0.065 | −0.056 | −0.027 | 0.001 | 0.005 |
| 0.043 | 0.032 | 0.060 | 1.000 | −0.043 | −0.025 | 0.012 | −0.003 |
| −0.007 | −0.010 | −0.054 | −0.046 | 1.000 | 0.067 | −0.078 | 0.057 |
| 0.008 | 0.002 | −0.025 | −0.025 | 0.064 | 1.000 | −0.065 | 0.049 |
| −0.036 | −0.021 | 0.001 | 0.013 | −0.079 | −0.069 | 1.000 | −0.056 |
| 0.025 | 0.015 | 0.004 | −0.003 | 0.050 | 0.045 | −0.048 | 1.000 |

Table A2.
MOM defined by Heylen et al. for CASES 0–1 (length normalization).
Table A2.
MOM defined by Heylen et al. for CASES 0–1 (length normalization).
| 1.000 | 0.072 | 0.094 | 0.044 | −0.007 | 0.008 | −0.035 | 0.023 |
| 0.072 | 1.000 | 0.066 | 0.032 | −0.010 | 0.002 | −0.020 | 0.013 |
| 0.094 | 0.066 | 1.000 | 0.062 | −0.055 | −0.025 | 0.001 | 0.004 |
| 0.045 | 0.032 | 0.063 | 1.000 | −0.045 | −0.025 | 0.012 | −0.002 |
| −0.007 | −0.010 | −0.055 | −0.045 | 1.000 | 0.064 | −0.077 | 0.046 |
| 0.009 | 0.002 | −0.027 | −0.026 | 0.067 | 1.000 | −0.067 | 0.041 |
| −0.037 | −0.021 | 0.001 | 0.013 | −0.080 | −0.066 | 1.000 | −0.046 |
| 0.031 | 0.018 | 0.005 | −0.003 | 0.062 | 0.053 | −0.059 | 1.000 |

Table A3.
MOM defined by Heylen et al. for CASES 0–2 (mass normalization).
Table A3.
MOM defined by Heylen et al. for CASES 0–2 (mass normalization).
| 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.002 |
| 0.000 | 0.000 | 0.000 | 1.000 | 0.002 | −0.002 | 0.002 | −0.007 |
| 0.000 | 0.000 | 0.000 | 0.002 | 1.000 | −0.002 | 0.002 | −0.007 |
| 0.000 | 0.000 | 0.000 | −0.002 | −0.002 | 1.000 | 0.000 | 0.007 |
| 0.000 | 0.000 | 0.000 | 0.002 | 0.002 | 0.000 | 1.000 | −0.007 |
| 0.001 | 0.001 | −0.002 | −0.007 | −0.007 | 0.008 | −0.008 | 1.000 |

Table A4.
MOM defined by Heylen et al. for CASES 0–2 (length normalization).
Table A4.
MOM defined by Heylen et al. for CASES 0–2 (length normalization).
| 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.002 |
| 0.000 | 0.000 | 0.000 | 1.000 | 0.002 | −0.002 | 0.002 | −0.006 |
| 0.000 | 0.000 | 0.000 | 0.002 | 1.000 | −0.002 | 0.002 | −0.006 |
| 0.000 | 0.000 | 0.000 | −0.002 | −0.002 | 1.000 | 0.000 | 0.007 |
| 0.000 | 0.000 | 0.000 | 0.002 | 0.002 | 0.000 | 1.000 | −0.007 |
| 0.001 | 0.002 | −0.002 | −0.008 | −0.008 | 0.009 | −0.009 | 1.000 |

Table A5.
MOM defined by Heylen et al. for CASES 0–3 (mass normalization).
Table A5.
MOM defined by Heylen et al. for CASES 0–3 (mass normalization).
| 1.000 | 0.002 | 0.001 | 0.001 | −0.003 | −0.008 | −0.004 | 0.002 |
| 0.002 | 1.000 | 0.003 | 0.002 | −0.009 | −0.021 | −0.010 | 0.005 |
| 0.001 | 0.003 | 1.000 | 0.001 | −0.003 | −0.008 | −0.004 | 0.002 |
| 0.001 | 0.002 | 0.001 | 1.000 | −0.001 | −0.003 | −0.001 | 0.001 |
| −0.003 | −0.009 | −0.003 | −0.001 | 1.000 | 0.018 | 0.009 | −0.005 |
| −0.008 | −0.022 | −0.008 | −0.004 | 0.019 | 1.000 | 0.022 | −0.014 |
| −0.004 | −0.010 | −0.004 | −0.001 | 0.009 | 0.021 | 1.000 | −0.008 |
| 0.002 | 0.005 | 0.002 | 0.001 | −0.005 | −0.013 | −0.008 | 1.000 |

Table A6.
MOM defined by Heylen et al. for CASES 0–3 (length normalization).
Table A6.
MOM defined by Heylen et al. for CASES 0–3 (length normalization).
| 1.000 | 0.002 | 0.001 | 0.001 | −0.003 | −0.008 | −0.004 | 0.002 |
| 0.002 | 1.000 | 0.003 | 0.002 | −0.009 | −0.021 | −0.010 | 0.004 |
| 0.001 | 0.003 | 1.000 | 0.001 | −0.003 | −0.008 | −0.003 | 0.002 |
| 0.001 | 0.002 | 0.001 | 1.000 | −0.001 | −0.003 | −0.001 | 0.001 |
| −0.003 | −0.009 | −0.003 | −0.001 | 1.000 | 0.018 | 0.009 | −0.004 |
| −0.008 | −0.022 | −0.008 | −0.004 | 0.019 | 1.000 | 0.022 | −0.012 |
| −0.004 | −0.010 | −0.004 | −0.001 | 0.009 | 0.022 | 1.000 | −0.006 |
| 0.002 | 0.006 | 0.002 | 0.001 | −0.006 | −0.016 | −0.009 | 1.000 |

Table A7.
COM defined by Heylen et al. for CASES 0–1.
Table A7.
COM defined by Heylen et al. for CASES 0–1.
| 1.000 | −0.109 | 0.105 | −0.048 | −0.008 | 0.009 | −0.038 | −0.028 |
| 0.037 | 1.000 | −0.072 | 0.033 | 0.011 | −0.001 | 0.017 | 0.013 |
| −0.007 | 0.017 | 1.000 | −0.129 | −0.073 | −0.035 | 0.010 | 0.000 |
| 0.001 | −0.003 | 0.073 | 1.000 | 0.061 | 0.033 | −0.019 | −0.007 |
| 0.000 | 0.000 | 0.014 | −0.027 | 1.000 | 0.197 | −0.125 | −0.079 |
| 0.000 | 0.000 | 0.003 | −0.006 | −0.135 | 1.000 | −0.096 | −0.059 |
| 0.000 | 0.000 | 0.000 | 0.001 | 0.033 | 0.054 | 1.000 | 0.259 |
| 0.000 | 0.000 | 0.001 | 0.000 | 0.006 | 0.011 | −0.219 | 1.000 |

Table A8.
COM defined by Heylen et al. for CASES 0–2.
Table A8.
COM defined by Heylen et al. for CASES 0–2.
| 1.000 | −0.039 | −0.006 | −0.008 | 0.003 | −0.004 | −0.001 | 0.002 |
| 0.038 | 1.000 | −0.027 | −0.031 | 0.010 | −0.013 | −0.006 | 0.008 |
| 0.007 | 0.024 | 1.000 | −0.073 | 0.013 | −0.016 | −0.006 | 0.009 |
| 0.009 | 0.031 | 0.071 | 1.000 | 0.041 | −0.047 | −0.016 | 0.021 |
| −0.003 | −0.009 | −0.013 | −0.036 | 1.000 | 0.100 | 0.017 | −0.021 |
| 0.005 | 0.014 | 0.019 | 0.047 | −0.096 | 1.000 | −0.057 | 0.067 |
| 0.002 | 0.005 | 0.007 | 0.016 | −0.019 | 0.045 | 1.000 | 0.129 |
| −0.004 | −0.012 | −0.015 | −0.033 | 0.035 | −0.077 | −0.132 | 1.000 |

Table A9.
COM defined by Heylen et al. for CASES 0–3.
Table A9.
COM defined by Heylen et al. for CASES 0–3.
| 1.000 | −0.013 | −0.001 | 0.000 | 0.002 | −0.005 | −0.003 | 0.001 |
| 0.015 | 1.000 | −0.005 | −0.001 | 0.003 | −0.011 | −0.007 | 0.004 |
| 0.002 | 0.007 | 1.000 | −0.002 | −0.001 | 0.000 | −0.001 | 0.001 |
| 0.001 | 0.002 | 0.003 | 1.000 | −0.002 | 0.002 | 0.000 | 0.000 |
| 0.001 | 0.005 | 0.004 | 0.003 | 1.000 | 0.038 | 0.000 | 0.001 |
| −0.003 | −0.010 | −0.008 | −0.005 | −0.057 | 1.000 | −0.006 | −0.001 |
| −0.001 | −0.003 | −0.002 | −0.001 | −0.009 | 0.028 | 1.000 | 0.002 |
| 0.000 | 0.002 | 0.001 | 0.001 | 0.005 | −0.013 | −0.010 | 1.000 |

Table A10.
AOC defined by the ECSS for CASES 0–1.
Table A10.
AOC defined by the ECSS for CASES 0–1.
| 1.000 | 0.072 | 0.094 | 0.044 | −0.007 | 0.009 | −0.036 | 0.027 |
| 0.072 | 1.000 | 0.066 | 0.032 | −0.010 | 0.002 | −0.020 | 0.016 |
| 0.094 | 0.066 | 1.000 | 0.063 | −0.055 | −0.026 | 0.001 | 0.004 |
| 0.044 | 0.032 | 0.063 | 1.000 | −0.045 | −0.025 | 0.012 | −0.003 |
| −0.007 | −0.010 | −0.055 | −0.045 | 1.000 | 0.065 | −0.078 | 0.054 |
| 0.009 | 0.002 | −0.026 | −0.025 | 0.065 | 1.000 | −0.067 | 0.047 |
| −0.036 | −0.020 | 0.001 | 0.012 | −0.078 | −0.067 | 1.000 | −0.052 |
| 0.027 | 0.016 | 0.004 | −0.003 | 0.054 | 0.047 | −0.052 | 1.000 |

Table A11.
AOCECSS defined by the ECSS for CASES 0–2.
Table A11.
AOCECSS defined by the ECSS for CASES 0–2.
| 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.002 |
| 0.000 | 0.000 | 0.000 | 1.000 | 0.002 | −0.002 | 0.002 | −0.007 |
| 0.000 | 0.000 | 0.000 | 0.002 | 1.000 | −0.002 | 0.002 | −0.007 |
| 0.000 | 0.000 | 0.000 | −0.002 | −0.002 | 1.000 | 0.000 | 0.008 |
| 0.000 | 0.000 | 0.000 | 0.002 | 0.002 | 0.000 | 1.000 | −0.008 |
| 0.001 | 0.001 | −0.002 | −0.007 | −0.007 | 0.008 | −0.008 | 1.000 |

Table A12.
AOCECSS defined by the ECSS for CASES 0–3.
Table A12.
AOCECSS defined by the ECSS for CASES 0–3.
| 1.000 | 0.002 | 0.001 | 0.001 | −0.003 | −0.008 | −0.004 | 0.002 |
| 0.002 | 1.000 | 0.003 | 0.002 | −0.009 | −0.022 | −0.010 | 0.005 |
| 0.001 | 0.003 | 1.000 | 0.001 | −0.003 | −0.008 | −0.004 | 0.002 |
| 0.001 | 0.002 | 0.001 | 1.000 | −0.001 | −0.003 | −0.001 | 0.001 |
| −0.003 | −0.009 | −0.003 | −0.001 | 1.000 | 0.019 | 0.009 | −0.005 |
| −0.008 | −0.022 | −0.008 | −0.003 | 0.019 | 1.000 | 0.022 | −0.014 |
| −0.004 | −0.010 | −0.004 | −0.001 | 0.009 | 0.022 | 1.000 | −0.008 |
| 0.002 | 0.005 | 0.002 | 0.001 | −0.005 | −0.014 | −0.008 | 1.000 |

Table A13.
COCECSS defined by the ECSS for CASES 0–1.
Table A13.
COCECSS defined by the ECSS for CASES 0–1.
| 0.999 | 0.108 | 0.104 | 0.048 | −0.008 | 0.009 | −0.036 | 0.027 |
| 0.037 | −0.994 | −0.071 | −0.032 | 0.011 | −0.001 | 0.016 | −0.013 |
| −0.007 | −0.017 | 0.989 | 0.128 | −0.072 | −0.035 | 0.010 | 0.000 |
| 0.001 | 0.003 | 0.072 | −0.990 | 0.060 | 0.032 | −0.019 | 0.007 |
| 0.000 | 0.000 | 0.014 | 0.026 | 0.986 | 0.193 | −0.121 | 0.076 |
| 0.000 | 0.000 | 0.003 | 0.006 | −0.134 | 0.979 | −0.092 | 0.057 |
| 0.000 | 0.000 | 0.000 | −0.001 | 0.032 | 0.053 | 0.964 | −0.249 |
| 0.000 | 0.000 | 0.001 | 0.000 | 0.006 | 0.011 | −0.212 | −0.963 |

Table A14.
COCECSS defined by the ECSS for CASES 0–2.
Table A14.
COCECSS defined by the ECSS for CASES 0–2.
| 0.999 | −0.039 | 0.006 | 0.008 | 0.003 | −0.004 | 0.001 | −0.002 |
| 0.038 | 0.998 | 0.027 | 0.031 | 0.009 | −0.013 | 0.005 | −0.008 |
| 0.007 | 0.024 | −0.997 | 0.073 | 0.013 | −0.016 | 0.006 | −0.009 |
| 0.009 | 0.031 | −0.071 | −0.994 | 0.041 | −0.046 | 0.016 | −0.021 |
| −0.003 | −0.009 | 0.013 | 0.036 | 0.994 | 0.099 | −0.017 | 0.021 |
| 0.005 | 0.014 | −0.019 | −0.047 | −0.096 | 0.990 | 0.057 | −0.066 |
| 0.002 | 0.005 | −0.007 | −0.016 | −0.019 | 0.045 | −0.990 | −0.127 |
| −0.004 | −0.012 | 0.015 | 0.033 | 0.035 | −0.076 | 0.131 | −0.989 |

Table A15.
COCECSS defined by the ECSS for CASES 0–3.
Table A15.
COCECSS defined by the ECSS for CASES 0–3.
| −1.000 | 0.013 | 0.001 | 0.000 | 0.002 | 0.005 | 0.003 | −0.001 |
| −0.015 | −1.000 | 0.005 | 0.001 | 0.003 | 0.011 | 0.007 | −0.004 |
| −0.002 | −0.007 | −1.000 | 0.002 | −0.001 | 0.000 | 0.001 | −0.001 |
| −0.001 | −0.002 | −0.003 | −1.000 | −0.002 | −0.002 | 0.000 | 0.000 |
| −0.001 | −0.005 | −0.004 | −0.003 | 0.998 | −0.038 | 0.000 | −0.001 |
| 0.003 | 0.010 | 0.008 | 0.005 | −0.057 | −0.999 | 0.006 | 0.001 |
| 0.001 | 0.003 | 0.002 | 0.001 | −0.009 | −0.028 | −1.000 | −0.002 |
| 0.000 | −0.002 | −0.001 | −0.001 | 0.005 | 0.012 | 0.010 | −1.000 |
Appendix B. Additional Results of the Experimental Cantilever Beam

Table A16.
T-Mass between the experimental model and the numerical model with fixed support.
Table A16.
T-Mass between the experimental model and the numerical model with fixed support.
| ----- | 89.05 | 88.91 | 89.32 | 87.66 |
| 89.05 | ----- | 88.96 | 87.90 | 90.00 |
| 88.91 | 88.96 | ----- | 88.87 | 87.55 |
| 89.32 | 87.90 | 88.87 | ----- | 87.11 |
| 87.66 | 90.00 | 87.55 | 87.11 | ----- |

Table A17.
T-Mass-norm between the experimental model and the numerical model with fixed support.
Table A17.
T-Mass-norm between the experimental model and the numerical model with fixed support.
| ----- | 0.989 | 0.988 | 0.992 | 0.974 |
| 0.989 | ----- | 0.988 | 0.977 | 1.000 |
| 0.988 | 0.988 | ----- | 0.987 | 0.973 |
| 0.992 | 0.977 | 0.987 | ----- | 0.968 |
| 0.974 | 1.000 | 0.973 | 0.968 | ----- |

Table A18.
T-Stiffness between the experimental model and the numerical model with fixed support.
Table A18.
T-Stiffness between the experimental model and the numerical model with fixed support.
| ----- | 89.13 | 89.18 | 89.59 | 89.59 |
| 87.02 | ----- | 86.02 | 87.38 | 88.64 |
| 82.86 | 79.82 | ----- | 83.70 | 86.30 |
| 81.43 | 73.72 | 74.69 | ----- | 83.88 |
| 70.38 | 70.82 | 69.53 | 76.09 | ----- |

Table A19.
T-Stiffness-norm between the experimental model and the numerical model with fixed support.
Table A19.
T-Stiffness-norm between the experimental model and the numerical model with fixed support.
| ----- | 0.990 | 0.991 | 0.995 | 0.995 |
| 0.967 | ----- | 0.956 | 0.971 | 0.985 |
| 0.921 | 0.887 | ----- | 0.930 | 0.959 |
| 0.905 | 0.819 | 0.830 | ----- | 0.932 |
| 0.782 | 0.787 | 0.773 | 0.845 | ----- |

Table A20.
T-Mass between the experimental model and the numerical model with rotational spring.
Table A20.
T-Mass between the experimental model and the numerical model with rotational spring.
| ----- | 89.06 | 89.02 | 89.22 | 87.96 |
| 89.06 | ----- | 89.98 | 87.82 | 89.94 |
| 89.02 | 88.98 | ----- | 89.08 | 88.04 |
| 89.22 | 87.82 | 89.08 | ----- | 87.50 |
| 87.96 | 89.94 | 88.04 | 87.50 | ----- |

Table A21.
T-Mass-norm between the experimental model and the numerical model with rotational spring.
Table A21.
T-Mass-norm between the experimental model and the numerical model with rotational spring.
| ----- | 0.990 | 0.989 | 0.991 | 0.977 |
| 0.990 | ----- | 0.989 | 0.976 | 0.999 |
| 0.989 | 0.989 | ----- | 0.990 | 0.9780 |
| 0.991 | 0.976 | 0.990 | ----- | 0.972 |
| 0.977 | 0.999 | 0.978 | 0.972 | ----- |

Table A22.
T-Stiffness between the experimental model and the numerical model with rotational spring.
Table A22.
T-Stiffness between the experimental model and the numerical model with rotational spring.
| ----- | 89.90 | 89.98 | 89.73 | 89.89 |
| 89.83 | ----- | 89.92 | 89.79 | 89.74 |
| 89.84 | 89.67 | ----- | 89.69 | 89.98 |
| 82.85 | 86.62 | 88.80 | ----- | 89.99 |
| 81.68 | 78.55 | 89.77 | 89.97 | ----- |

Table A23.
T-Stiffness-norm between the experimental model and the numerical model with rotational spring.
Table A23.
T-Stiffness-norm between the experimental model and the numerical model with rotational spring.
| ----- | 0.999 | 1.000 | 0.997 | 0.999 |
| 0.998 | ----- | 0.999 | 0.998 | 0.997 |
| 0.998 | 0.996 | ----- | 0.997 | 1.000 |
| 0.921 | 0.962 | 0.987 | ----- | 1.000 |
| 0.908 | 0.873 | 0.997 | 1.000 | ----- |
References
- Friswell, M.I.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Springer: Dordrecht, The Netherlands, 1995; Volume 38, ISBN 978-90-481-4535-5. [Google Scholar]
- Rigner, L. Modal assurance criteria value for two orthogonal modal vectors. In Proceedings of the International Modal Analysis Conference, Santa Barabara, CA, USA, 2–5 February 1998. [Google Scholar]
- Pascual, R.; Golinval, J.; Razeto, M. Frequency Domain Correlation Technique for Model Correlation and Updating. In Proceedings of the International Modal Analysis Conference, Orlando, FL, USA, 3–6 February 1997. [Google Scholar]
- Allemang, R.J.; Brown, D. Correlation Coefficient for Modal Vector Analysis. In Proceedings of the 1st International Modal Analysis Conference, Orlando, FL, USA, 8–10 November 1982; International Society for Optical Engineering and Society for Experimental Mechanics: Orlando, FL, USA, 1982; pp. 110–116. [Google Scholar]
- Mendes Maia, N.; Montalvão Silva, J. Theoretical and Experimental Modal Analysis; Research Studies Press: New York, USA, 1997. [Google Scholar]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Brincker, R.; Ventura, C.E. Introduction to Operational Modal Analysis; John Wiley & Sons, Ltd.: Chichester, UK, 2015; ISBN 9781118535141. [Google Scholar]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing; Katholieke Universiteit Leuven: Leuven, Belgium, 2007; ISBN 907380261X 9789073802612. [Google Scholar]
- Ewins, D.J. Model validation: Correlation for updating. Sadhana 2000, 25, 221–234. [Google Scholar] [CrossRef]
- Allemang, R.J. The modal assurance criterion—Twenty years of use and abuse. Sound Vib. 2003, 37, 14–21. [Google Scholar]
- Ponzo, F.C.; Auletta, G.; Ielpo, P.; Ditommaso, R. DInSAR–SBAS satellite monitoring of infrastructures: How temperature affects the “Ponte della Musica” case study. J. Civ. Struct. Health Monit. 2024, 14, 745–761. [Google Scholar] [CrossRef]
- Venanzi, I.; Kita, A.; Cavalagli, N.; Ierimonti, L.; Ubertini, F. Earthquake-induced damage localization in an historic masonry tower through long-term dynamic monitoring and FE model calibration. Bull. Earthq. Eng. 2020, 18, 2247–2274. [Google Scholar] [CrossRef]
- Borlenghi, P.; Gentile, C.; Saisi, A. Detecting and localizing anomalies on masonry towers from low-cost vibration monitoring. Smart Struct. Syst. 2021, 27, 319–333. [Google Scholar] [CrossRef]
- Avitabile, P.; Mains, M. Finite Element Model Correlation. In Handbook of Experimental Structural Dynamics; Springer: New York, NY, USA, 2020; pp. 1–39. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The sensitivity method in finite element model updating: A tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite element model updating of a bowstring-arch railway bridge based on experimental modal parameters. Eng. Struct. 2012, 40, 413–435. [Google Scholar] [CrossRef]
- Abasi, K.; Asayesh, M.; Nikravesh, M. Comparing of Direct and Sensitivity-Base Model Updating Methods in Structural Dynamics and Its Application for Updating of Cantilever Model. In Proceedings of the Volume 14: New Developments in Simulation Methods and Software for Engineering Applications, Boston, MA, USA, 31 October–6 November 2008; pp. 157–164. [Google Scholar] [CrossRef]
- Yang, Y.B.; Chen, Y.J. A new direct method for updating structural models based on measured modal data. Eng. Struct. 2009, 31, 32–42. [Google Scholar] [CrossRef]
- Kammer, D.C. Optimum approximation for residual stiffness in linear system identification. AIAA J. 1988, 26, 104–112. [Google Scholar] [CrossRef]
- Berman, A.; Nagy, E.J. Improvement of a Large Analytical Model Using Test Data. AIAA J. 1983, 21, 1168–1173. [Google Scholar] [CrossRef]
- Ereiz, S.; Duvnjak, I.; Fernando Jiménez-Alonso, J. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]
- Barros, B.; Conde, B.; Cabaleiro, M.; Riveiro, B. Deterministic and probabilistic-based model updating of aging steel bridges. Structures 2023, 54, 89–105. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Naranjo-Perez, J.; Pavic, A.; Sáez, A. Maximum Likelihood Finite-Element Model Updating of Civil Engineering Structures Using Nature-Inspired Computational Algorithms. Struct. Eng. Int. 2021, 31, 326–338. [Google Scholar] [CrossRef]
- Hofmeister, B.; Bruns, M.; Rolfes, R. Finite element model updating using deterministic optimisation: A global pattern search approach. Eng. Struct. 2019, 195, 373–381. [Google Scholar] [CrossRef]
- Li, D.; Zhang, J. Finite element model updating through derivative-free optimization algorithm. Mech. Syst. Signal Process. 2023, 185, 109726. [Google Scholar] [CrossRef]
- Altunel, F.; Çelik, M.; Çalişkan, M. A Correlation Improvement Technique for Model Updating of Structures. Int. J. Struct. Stab. Dyn. 2016, 16, 1550049. [Google Scholar] [CrossRef]
- Cuadrado, M.; Pernas-Sánchez, J.; Artero-Guerrero, J.A.; Varas, D. Model updating of uncertain parameters of carbon/epoxy composite plates using digital image correlation for full-field vibration measurement. Measurement 2020, 159, 107783. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Fan, G.; Li, J.; Hao, H. Improved automated operational modal identification of structures based on clustering. Struct. Control Health Monit. 2019, 26, 1545–2255. [Google Scholar] [CrossRef]
- Romanazzi, A.; Scocciolini, D.; Savoia, M.; Buratti, N. Iterative hierarchical clustering algorithm for automated operational modal analysis. Autom. Constr. 2023, 156, 105137. [Google Scholar] [CrossRef]
- Zini, G.; Betti, M.; Bartoli, G. A quality-based automated procedure for operational modal analysis. Mech. Syst. Signal Process. 2022, 164, 108173. [Google Scholar] [CrossRef]
- Sun, M.; Li, Q. Reliable modal estimation of high-rise structures via synergistic usage of multiple stabilization diagram-based operational modal analysis techniques. Structures 2023, 56, 105051. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E. Online automatic identification of the modal parameters of a long span arch bridge. Mech. Syst. Signal Process. 2009, 23, 316–329. [Google Scholar] [CrossRef]
- Dong, X. Finite Element Model Updating through Smooth Nonconvex Optimization; Georgia Institute of Technology: Atlanta, GA, USA, 2019. [Google Scholar]
- García-Fernández, N.; Aenlle, M.; Álvarez-Vázquez, A.; Muniz-Calvente, M.; Fernández, P. A review on fatigue monitoring of structures. Int. J. Struct. Integr. 2023, 14, 133–165. [Google Scholar] [CrossRef]
- Sun, X.; Ilanko, S.; Mochida, Y.; Tighe, R.C. A Review on Vibration-Based Damage Detection Methods for Civil Structures. Vibration 2023, 6, 843–875. [Google Scholar] [CrossRef]
- Frigui, F.; Faye, J.P.; Martin, C.; Dalverny, O.; Peres, F.; Judenherc, S. Global methodology for damage detection and localization in civil engineering structures. Eng. Struct. 2018, 171, 686–695. [Google Scholar] [CrossRef]
- Ditommaso, R.; Ponzo, F.C. Identifying Damage in Structures: Definition of Thresholds to Minimize False Alarms in SHM Systems. Buildings 2024, 14, 821. [Google Scholar] [CrossRef]
- Ditommaso, R.; Iacovino, C.; Auletta, G.; Parolai, S.; Ponzo, F.C. Damage Detection and Localization on Real Structures Subjected to Strong Motion Earthquakes Using the Curvature Evolution Method: The Navelli (Italy) Case Study. Appl. Sci. 2021, 11, 6496. [Google Scholar] [CrossRef]
- De Roeck, G.; Peeters, B.; Maeck, J. Dynamic Monitoring of Civil Engineering Structures. In Proceedings of the Computational Methods for Shell and Spatial Structures, Chania-Crete, Greece, 4–7 June 2000. [Google Scholar]
- Lein, C.; Beitelschmidt, M. Comparative study of model correlation methods with application to model order reduction. In Proceedings of the 26th ISMA (International Conference on Noise and Vibration Engineering), Leuven, Belgium, 15–17 September 2014. [Google Scholar]
- Mercer, J.F.; Aglietti, G.S.; Kiley, A.M. Model Reduction and Sensor Placement Methods for Finite Element Model Correlation. AIAA J. 2016, 54, 3941–3955. [Google Scholar] [CrossRef]
- Brincker, R.; Lopez-Aenlle, M. Mode shape sensitivity of two closely spaced eigenvalues. J. Sound Vib. 2015, 334, 377–387. [Google Scholar] [CrossRef]
- Aenlle, M.; Pacheco-Chérrez, J.; Brincker, R. Sensitivity analysis of a system with two closely spaced modes using structural dynamic modification. Mech. Syst. Signal Process. 2024, 206, 110894. [Google Scholar] [CrossRef]
- Sestieri, A.; D’Ambrogio, W. A modification method for vibration control of structures. Mech. Syst. Signal Process. 1989, 3, 229–253. [Google Scholar] [CrossRef]
- Sestieri, A. Structural dynamic modification. Sadhana 2000, 25, 247–259. [Google Scholar] [CrossRef]
- Avitabile P Twenty years of structural dynamic modification—A review. Sound Vib. 2003, 37, 14–27.
- Brincker, R.; Skafte, A.; López-Aenlle, M.; Sestieri, A.; D’Ambrogio, W.; Canteli, A. A local correspondence principle for mode shapes in structural dynamics. Mech. Syst. Signal Process. 2014, 45, 91–104. [Google Scholar] [CrossRef]
- NASA-STD-5002a|; NASA TECHNICAL STANDARD: Load Analyses of Spacecraft and Payloads. NASA: Washington, DC, USA, 2019.
- ECSS-E-ST-32-11C; Modal Survey Assessment. European Cooperation for Space Standardization: Noordwijk, The Netherlands, 2008.
- Vacher, P.; Jacquier, B.; Bucharles, A. Extensions of the MAC criterion to complex modes. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 20–22 September 2010; pp. 2713–2725. [Google Scholar]
- Fotsch, D.; Ewins, D.J. Application of MAC in the frequency domain. In Proceedings of the International Modal Analysis Conference, San Antonio, TX, USA, 7–10 February 2000. [Google Scholar]
- Greś, S.; Döhler, M.; Mevel, L. Uncertainty quantification of the Modal Assurance Criterion in operational modal analysis. Mech. Syst. Signal Process. 2021, 152, 107457. [Google Scholar] [CrossRef]
- Lieven, N.; Ewins, D.J. Spatial correlation of mode shapes: The coordinate modal assurance criterion (COMAC). In Proceedings of the 6th International Modal Analysis Conference (IMAC), Kissimmee, FL, USA, 1–4 February 1988. [Google Scholar]
- Morales, C.A. Comments on the MAC and the NCO, and a linear modal correlation coefficient. J. Sound Vib. 2005, 282, 529–537. [Google Scholar] [CrossRef]
- Brehm, M.; Zabel, V.; Bucher, C. An automatic mode pairing strategy using an enhanced modal assurance criterion based on modal strain energies. J. Sound Vib. 2010, 329, 5375–5392. [Google Scholar] [CrossRef]
- Yan, W.-J.; Huang, T.-L.; Ren, W.-X. Damage Detection Method Based on Element Modal Strain Energy Sensitivity. Adv. Struct. Eng. 2010, 13, 1075–1088. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Lei, Y.; Gu, J. Structural damage identification based on modal frequency strain energy assurance criterion and flexibility using enhanced Moth-Flame optimization. Structures 2020, 28, 1119–1136. [Google Scholar] [CrossRef]
- Mikota, G. A model correlation criterion for rotors. J. Sound Vib. 2019, 441, 106–110. [Google Scholar] [CrossRef]
- Mikota, G.; Mikota, J. Energy related model correlation criteria for modal analysis of fluid-structure interaction systems. J. Sound Vib. 2020, 483, 115480. [Google Scholar] [CrossRef]
- D’Ambrogio, W.; Fregolent, A. Higher-order MAC factor for the correlation of close and multiple modes. Mech. Syst. Signal Process. 2003, 17, 599–610. [Google Scholar] [CrossRef]
- D’Ambrogio, W.; Fregolent, A. Correlation of close modes using S2MAC. In Proceedings of the 2002 International Conference on Noise and Vibration Engineering, Leuven, Belgium, 15–17 September 2002. [Google Scholar]
- Zang, C.; Grafe, H.; Imregun, M. Frequency-Domain Criteria For Correlating And Updating Dynamic Finite Element Models. Mech. Syst. Signal Process. 2001, 15, 139–155. [Google Scholar] [CrossRef]
- Marinone, T.; Moya, A. Comparison of FRF correlation techniques. In Model Validation and Uncertainty Quantification, Volume 3: Proceedings of the 33rd IMAC, A Conference and Exposition on Structural Dynamics; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; Volume 3, pp. 299–309. [Google Scholar] [CrossRef]
- Lee, D.; Ahn, T.-S.; Kim, H.-S. A metric on the similarity between two frequency response functions. J. Sound Vib. 2018, 436, 32–45. [Google Scholar] [CrossRef]
- Manring, L.H.; Schultze, J.F.; Zimmerman, S.J.; Mann, B.P. Improving magnitude and phase comparison metrics for frequency response functions using cross-correlation and log-frequency shifting. J. Sound Vib. 2022, 539, 117255. [Google Scholar] [CrossRef]
- Coppolino, R.N. Modal Test-Analysis Correlation Using Left-Hand Eigenvectors. In Topics in Modal Analysis & Testing; Proceedings of the 37th IMAC; Springer: Cham, Switzerland, 2020; Volume 8, pp. 301–310. [Google Scholar] [CrossRef]
- Coppolino, R.N. The Integrated Test Analysis Process for Structural Dynamic Systems, Synthesis SEM Lectures on Experimental Mechanics; Morgan & Claypool Publishers: San Rafael, CA, USA, 2020. [Google Scholar]
- López-Aenlle, M.; Brincker, R.; Pelayo, F.; Canteli, A.F. On exact and approximated formulations for scaling-mode shapes in operational modal analysis by mass and stiffness change. J. Sound Vib. 2012, 331, 622–637. [Google Scholar] [CrossRef]
- López-Aenlle, M.; Fernández, P.; Brincker, R.; Fernández-Canteli, A. Scaling-factor estimation using an optimized mass-change strategy. Mech. Syst. Signal Process. 2010, 24, 1260–1273. [Google Scholar] [CrossRef]
- Bernal, D. Modal Scaling from Known Mass Perturbations. J. Eng. Mech. 2004, 130, 1083–1088. [Google Scholar] [CrossRef]
- Aenlle, M.; García-Fernández, N.; Pelayo, F. Rotation of mode shapes in structural dynamics due to mass and stiffness perturbations. Mech. Syst. Signal Process. 2024, 212, 111269. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).