Numerical Analysis of Rubberized Steel Fiber Reinforced Concrete Beams Subjected to Static and Blast Loadings
Abstract
1. Introduction
2. Finite Element Analysis
2.1. Static Numerical Simulation
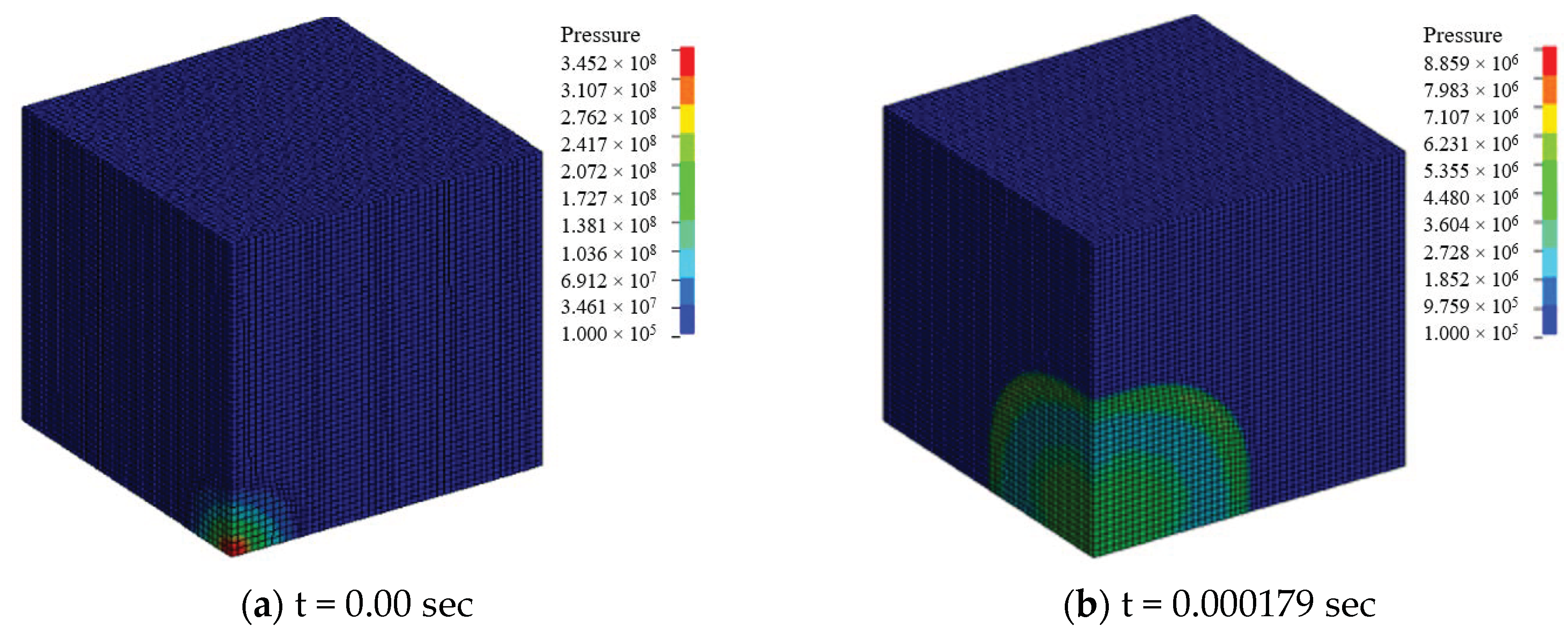
2.2. Blast Numerical Simulation
3. Static FE Results
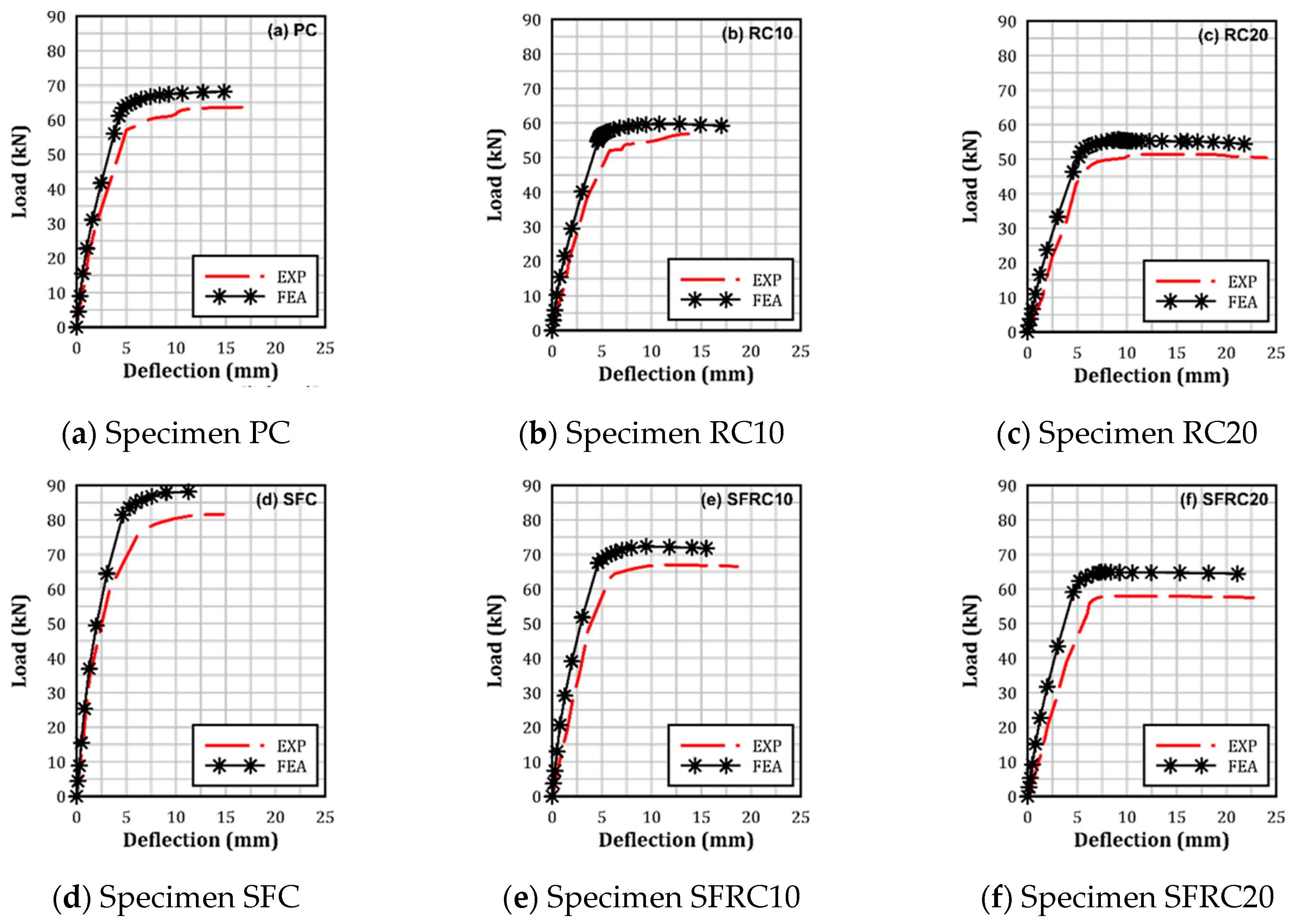
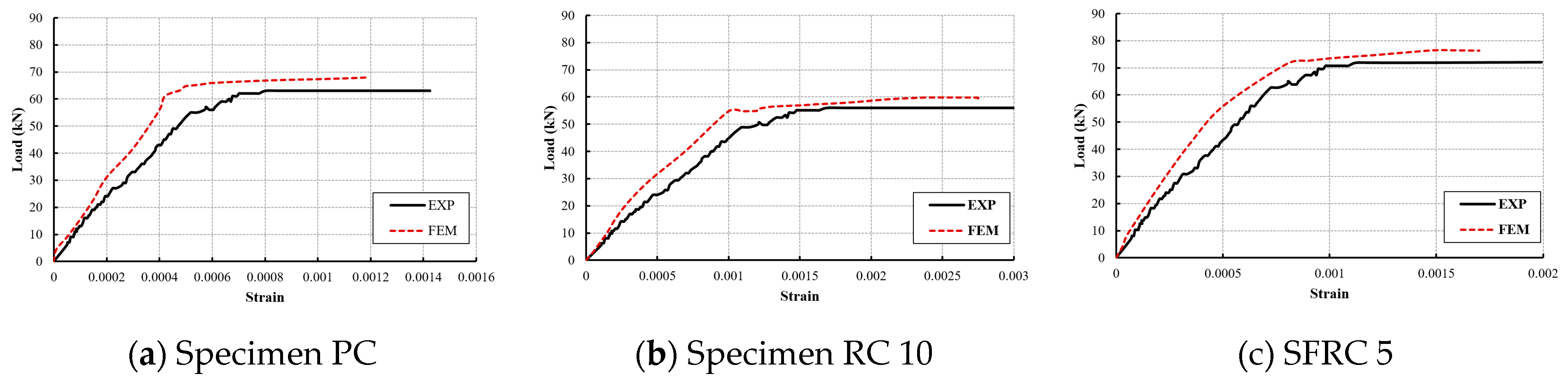
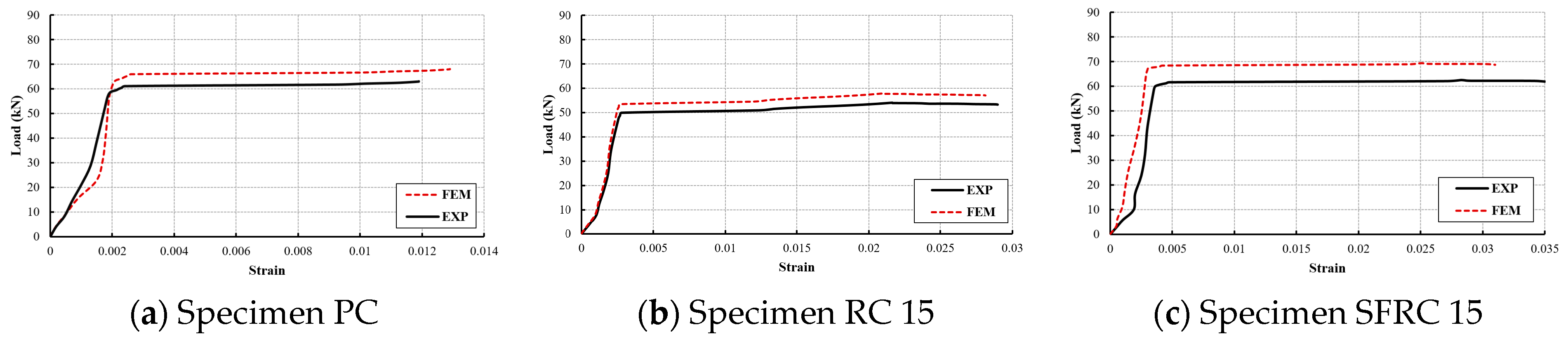
3.1. Validation
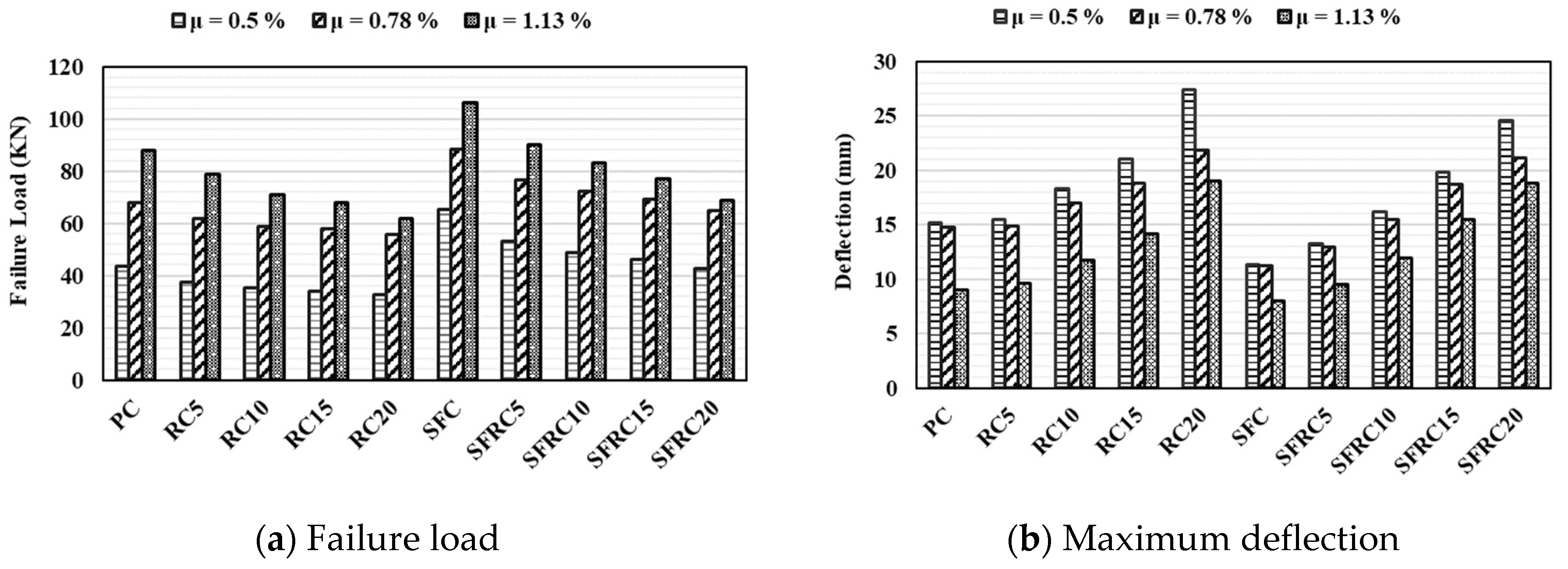
3.2. Effect of Reinforcement Ratio
4. Dynamic FE Results
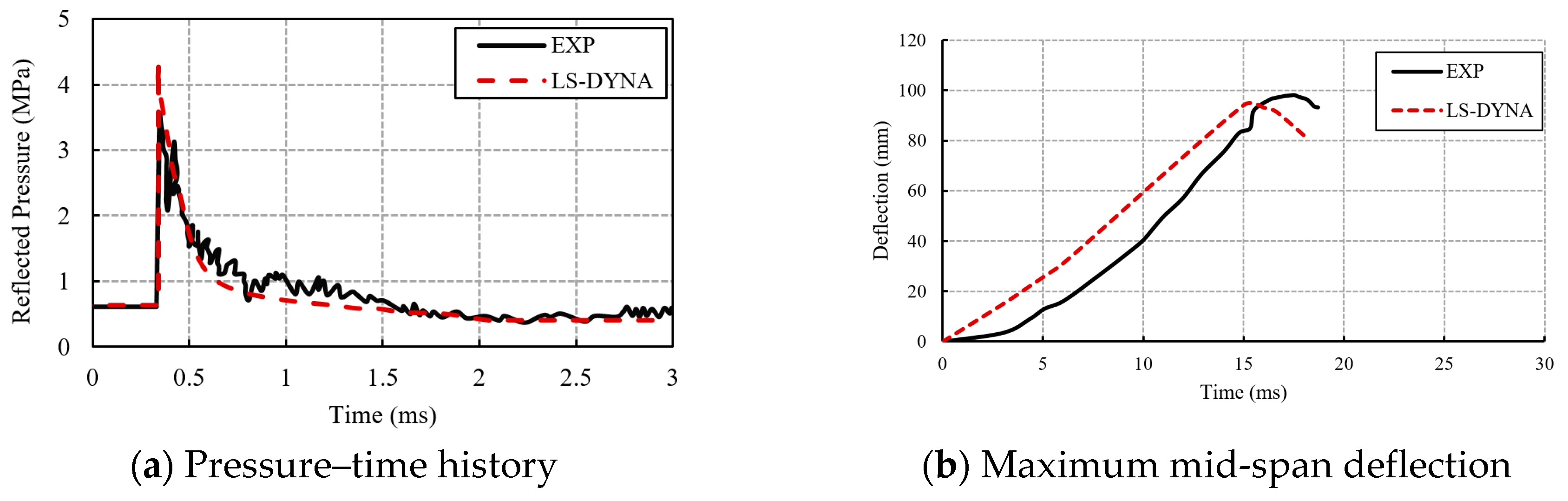
4.1. FE Model Validation
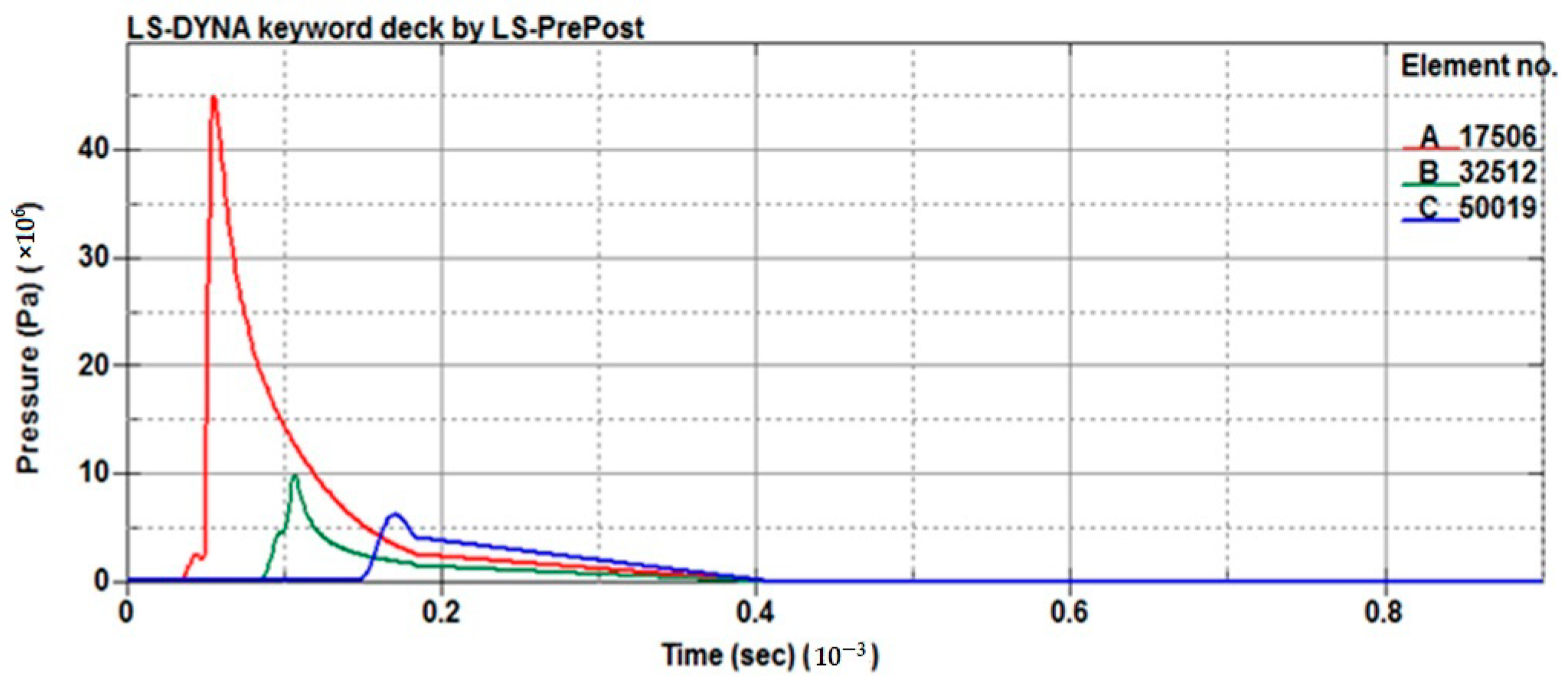
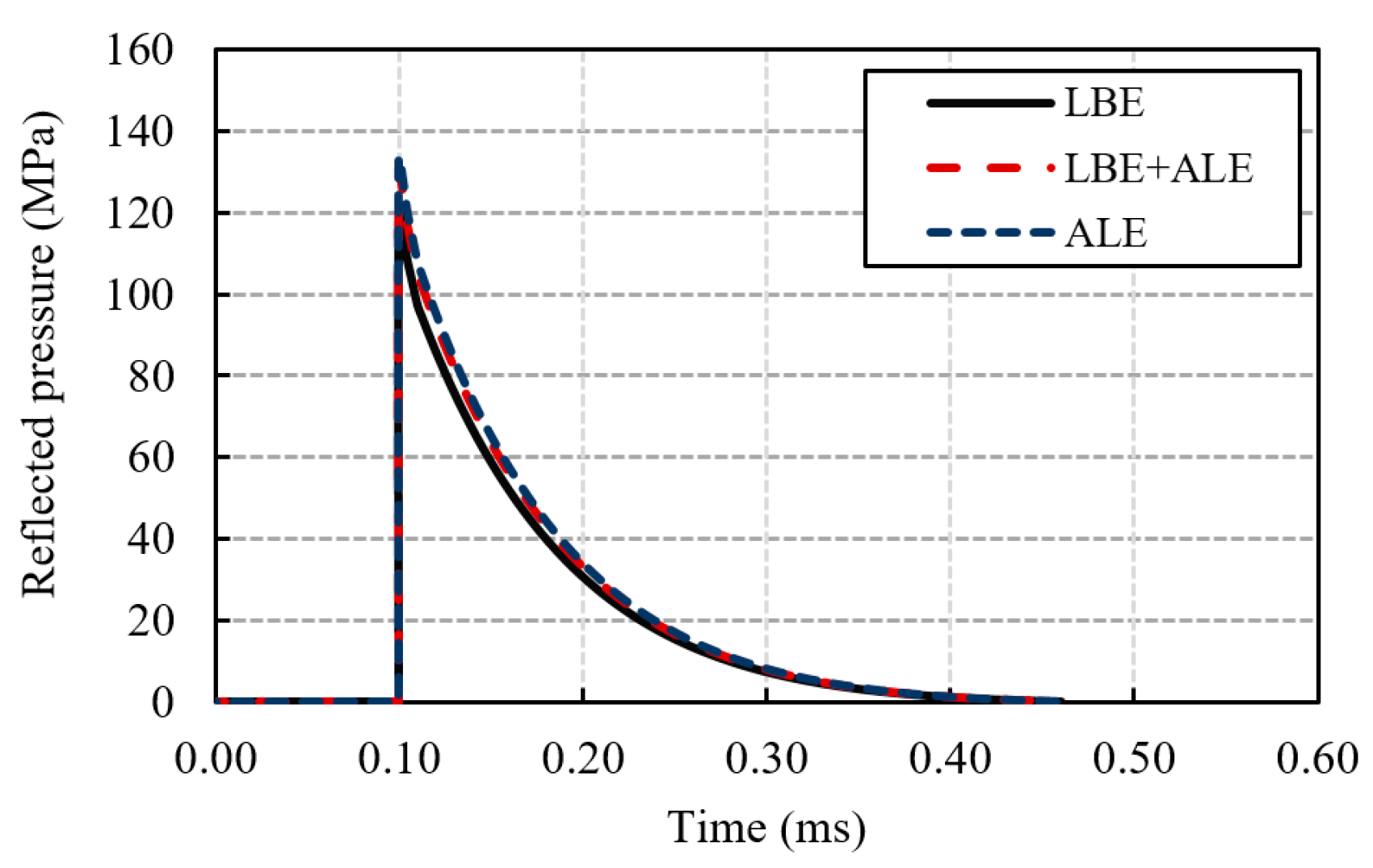
4.2. Comparison between the Different Blast Load Modeling Approaches
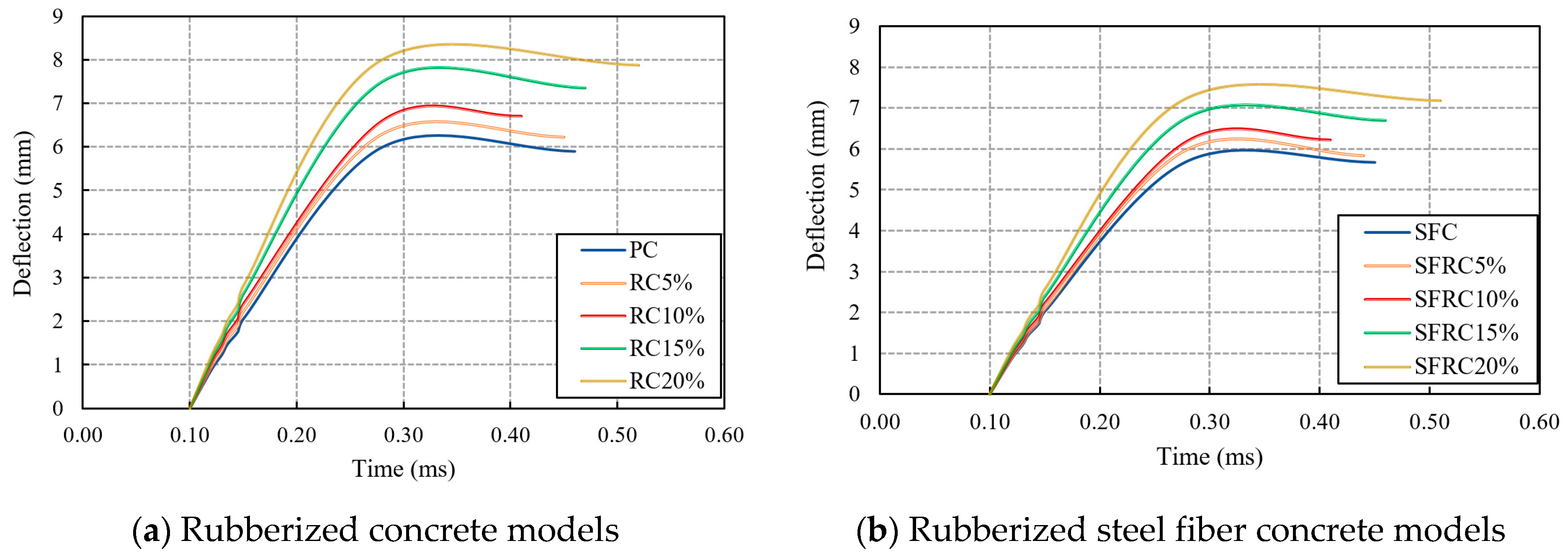
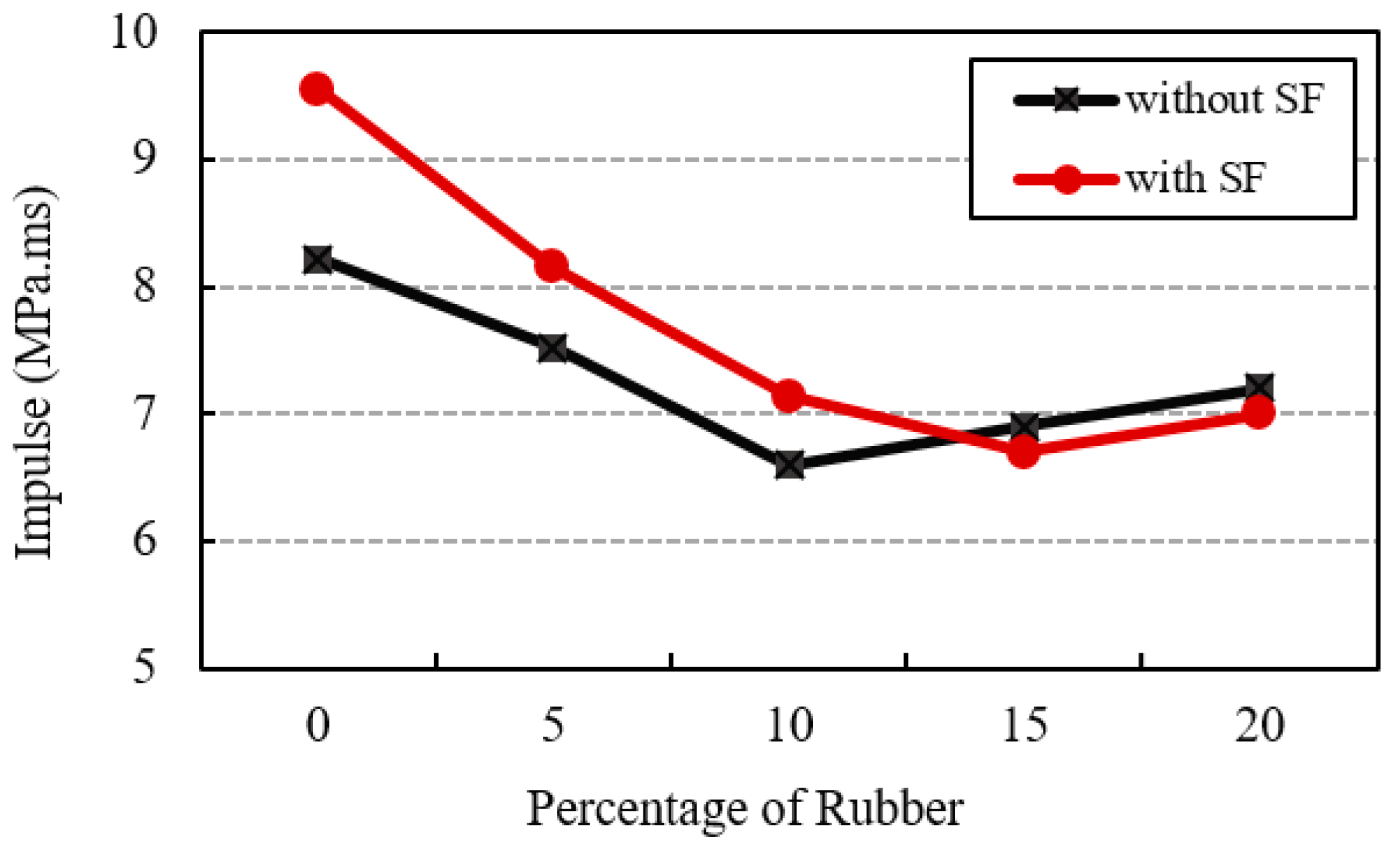
4.3. Rubberized and Rubberized Steel Fiber Concrete Material Response
5. Conclusions
- Static response of concrete is important to ensure the applicability of the concrete for structural engineering design practice and safety margins. The changes in maximum deflection caused by different reinforcement ratios demonstrate the importance of reinforcement design in improving structural integrity. Engineers can improve the stiffness, load-bearing capacity, and overall structural resilience by applying appropriate reinforcement.
- While rubberized concrete with high rubber content, greater than 10%, showed brittle failure at the compression side, reducing the reinforcement ratio to meet minimum code requirements revealed a notable shift in failure behavior. Specifically, under static loading, the rubberized RC beams tended to exhibit ductile behavior on the tension side.
- The LBE method showed a lower peak pressure and impulse compared to both ALE and the coupled methods, with differences of less than 15%. Notably, the computational time for the LBE approach was approximately 1/5 to 1/15 times less than that of the other methods. However, in more complex scenarios, such as simulating entire structure or when dealing with structural openings, it is recommended to investigate and evaluate the suitability of different approaches.
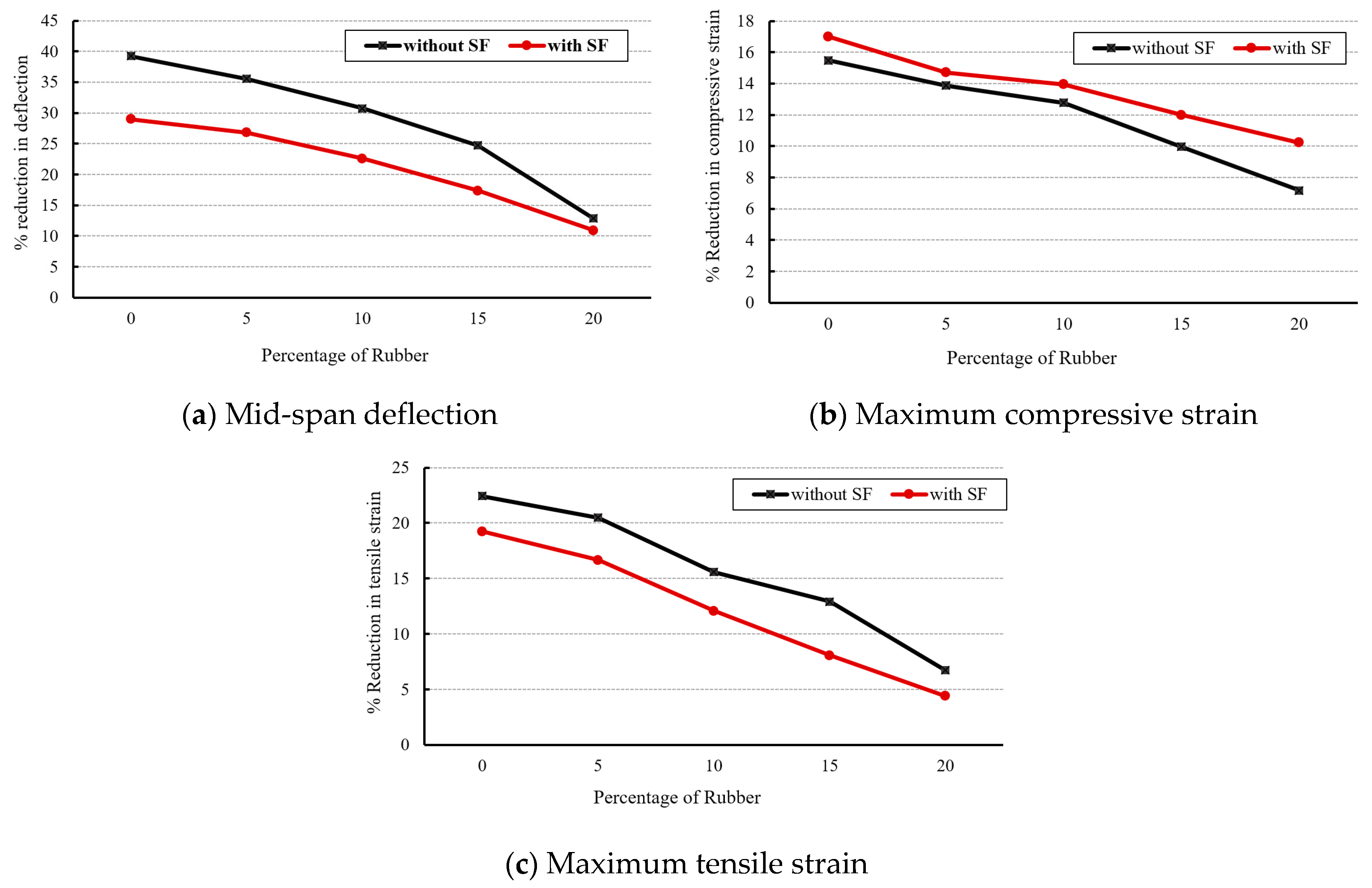
- Increasing the rubber percentage improves ductility and energy absorption, but reduces blast load capacity. However, the incorporation of steel fibers maintains high ductility and enhances blast load capacity, leading to a blast load capacity similar to that of normal concrete with 10% rubber.
- An optimal concrete mixture characterized by improved ductility, energy absorption, and blast load capacity, achieved by combining 5–10% rubber with steel fibers.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, B.; Liu, F.; Song, D.; Jiang, Z. Numerical study on damage mechanism of RC beams under close-in blast loading. Eng. Fail. Anal. 2015, 51, 9–19. [Google Scholar] [CrossRef]
- Ellingwood, B.R. Mitigating risk from abnormal loads and progressive collapse. J. Perform. Constr. Facil. 2006, 20, 315–323. [Google Scholar] [CrossRef]
- Goel, M.D.; Matsagar, V.A. Blast-resistant design of structures. Pract. Period. Struct. Des. Constr. 2014, 19, 04014007. [Google Scholar] [CrossRef]
- Rajkumar, D.; Senthil, R.; Kumar, B.B.M.; AkshayaGomathi, K.; Velan, S.M. Numerical study on parametric analysis of reinforced concrete column under blast loading. J. Perform. Constr. Facil. 2020, 34, 04019102. [Google Scholar] [CrossRef]
- Cui, J.; Shi, Y.; Li, Z.-X.; Chen, L. Failure analysis and damage assessment of RC columns under close-in explosions. J. Perform. Constr. Facil. 2015, 29, B4015003. [Google Scholar] [CrossRef]
- Turgut, P.; Gurel, M.A.; Pekgokgoz, R.K. LPG explosion damage of a reinforced concrete building: A case study in Sanliurfa, Turkey. Eng. Fail. Anal. 2013, 32, 220–235. [Google Scholar] [CrossRef]
- Elbelbisi, A.; Elsisi, A.; Saffarini, M.H.; Salim, H.; Chen, Z. Enhanced Blast Response Simulation of LG Panels Using an Elasto-Damage Model with the Finite Element Method. Buildings 2023, 13, 3025. [Google Scholar] [CrossRef]
- Li, S.; Rong, X.; Hu, J.; Wang, M.; Qu, Q.; Huang, J.; Guo, X. Risk assessment method of gas explosion based on quantification of margins and uncertainties (QMU): A case study on beam structures in buildings. Structures 2023, 50, 52–62. [Google Scholar] [CrossRef]
- Tai, Y.; Chu, T.; Hu, H.; Wu, J. Dynamic response of a reinforced concrete slab subjected to air blast load. Theor. Appl. Fract. Mech. 2011, 56, 140–147. [Google Scholar] [CrossRef]
- Leppänen, J. Concrete subjected to projectile and fragment impacts: Modelling of crack softening and strain rate dependency in tension. Int. J. Impact Eng. 2006, 32, 1828–1841. [Google Scholar] [CrossRef]
- Rabczuk, T.; Eibl, J. Modelling dynamic failure of concrete with meshfree methods. Int. J. Impact Eng. 2006, 32, 1878–1897. [Google Scholar] [CrossRef]
- Lu, Y. Modelling of concrete structures subjected to shock and blast loading: An overview and some recent studies. Struct. Eng. Mech. Int. J. 2009, 32, 235–249. [Google Scholar] [CrossRef]
- Elbelbisi, A.; El-Sisi, A.; Mahmoud, M.E.; Newberry, M.; Salim, H. Influence of interlayer types and thicknesses on the blast performance of laminated glass panels. Structures 2023, 57, 105231. [Google Scholar] [CrossRef]
- Elbelbisi, A.; El-Sisi, A.; Knight, J.; Philipps, J.C.; Newberry, M.; Salim, H. Influence of panels size on the static and dynamic performance of laminated glass panels. Constr. Build. Mater. 2023, 399, 132562. [Google Scholar] [CrossRef]
- Gong, S.; Lu, Y.; Tu, Z.; Jin, W. Validation study on numerical simulation of RC response to close-in blast with a fully coupled model. Struct. Eng. Mech. Int. J. 2009, 32, 283–300. [Google Scholar] [CrossRef]
- Brandt, A.M. Fibre reinforced cement-based (FRC) composites after over 40 years of development in building and civil engineering. Compos. Struct. 2008, 86, 3–9. [Google Scholar] [CrossRef]
- Barnett, S.J.; Lataste, J.-F.; Parry, T.; Millard, S.G.; Soutsos, M.N. Assessment of fibre orientation in ultra high performance fibre reinforced concrete and its effect on flexural strength. Mater. Struct. 2010, 43, 1009–1023. [Google Scholar] [CrossRef]
- Fehling, E.; Bunje, K.; Schmidt, M. Gärtnerplatz–Bridge over River Fulda in Kassel: Multispan Hybrid UHPC-Steel Bridge. In Designing and Building with UHPFRC; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Chin, W.J.; Kim, Y.J.; Cho, J.-R.; Park, J.S. Dynamic characteristics evaluation of innovative UHPC pedestrian cable stayed bridge. Engineering 2012, 4, 869–876. [Google Scholar] [CrossRef]
- Rebentrost, M.; Wight, G. Perspective on UHPCs from a specialist construction company. In Designing and Building with UHPFRC; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; pp. 189–208. [Google Scholar] [CrossRef]
- Ngo, T.; Mendis, P.; Krauthammer, T. Behavior of ultrahigh-strength prestressed concrete panels subjected to blast loading. J. Struct. Eng. 2007, 133, 1582–1590. [Google Scholar] [CrossRef]
- Barnett, S.J. Development of advanced concrete materials for anti-terrorism applications. Struct. Eng. 2008, 86, 28–29. [Google Scholar]
- Li, J.; Wu, C.; Hao, H. An experimental and numerical study of reinforced ultra-high performance concrete slabs under blast loads. Mater. Des. 2015, 82, 64–76. [Google Scholar] [CrossRef]
- Vedernikov, A.; Gemi, L.; Madenci, E.; Özkılıç, Y.O.; Yazman, Ş.; Gusev, S.; Sulimov, A.; Bondareva, J.; Evlashin, S.; Konev, S.; et al. Effects of high pulling speeds on mechanical properties and morphology of pultruded GFRP composite flat laminates. Compos. Struct. 2022, 301, 116216. [Google Scholar] [CrossRef]
- Vedernikov, A.; Tucci, F.; Carlone, P.; Gusev, S.; Konev, S.; Firsov, D.; Akhatov, I.; Safonov, A. Effects of pulling speed on structural performance of L-shaped pultruded profiles. Compos. Struct. 2021, 255, 112967. [Google Scholar] [CrossRef]
- Elshazli, M.T.; Saras, N.; Ibrahim, A. Structural response of high strength concrete beams using fiber reinforced polymers under reversed cyclic loading. Sustain. Struct. 2022, 2, 000018. [Google Scholar] [CrossRef]
- Elshazli, M.T.; Ramirez, K.; Ibrahim, A.; Badran, M. Mechanical, durability and corrosion properties of basalt fiber concrete. Fibers 2022, 10, 10. [Google Scholar] [CrossRef]
- Eisa, A.S.; Elshazli, M.T.; Nawar, M.T. Experimental investigation on the effect of using crumb rubber and steel fibers on the structural behavior of reinforced concrete beams. Constr. Build. Mater. 2020, 252, 119078. [Google Scholar] [CrossRef]
- Alam, I.; Mahmood, U.A.; Khattak, N. Use of rubber as aggregate in concrete: A review. Int. J. Adv. Struct. Geotech. Eng. 2015, 4, 92–96. [Google Scholar]
- Gupta, T.; Sharma, R.K.; Chaudhary, S. Impact resistance of concrete containing waste rubber fiber and silica fume. Int. J. Impact Eng. 2015, 83, 76–87. [Google Scholar] [CrossRef]
- Bu, C.; Zhu, D.; Liu, L.; Lu, X.; Sun, Y.; Yu, L.; OuYang, Y.; Cao, X.; Wang, F. Research progress on rubber concrete properties: A review. J. Rubber Res. 2022, 25, 105–125. [Google Scholar] [CrossRef]
- Prasad, M.G.; Golla, S.Y.; Prabhanjan, N.; Krishna, A.S.; Alok, G. Mechanical properties of rubberized concrete using truck scrap rubber. Mater. Today Proc. 2021, 39, 849–854. [Google Scholar] [CrossRef]
- He, L.; Cai, H.; Huang, Y.; Ma, Y.; Van Den Bergh, W.; Gaspar, L.; Valentin, J.; Vasiliev, Y.E.; Kowalski, K.J.; Zhang, J. Research on the properties of rubber concrete containing surface-modified rubber powders. J. Build. Eng. 2021, 35, 101991. [Google Scholar] [CrossRef]
- Huang, W.; Huang, X.; Xing, Q.; Zhou, Z. Strength reduction factor of crumb rubber as fine aggregate replacement in concrete. J. Build. Eng. 2020, 32, 101346. [Google Scholar] [CrossRef]
- Yu, Z.; Tang, R.; Li, F.; Hu, Y.; Liu, G.; Qin, Y.; Huang, Q. Experimental study and failure criterion analysis on combined compression-shear performance of rubber concrete (RC) with different rubber replacement ratio. Constr. Build. Mater. 2021, 288, 123105. [Google Scholar] [CrossRef]
- Elshazli, M.T.; Ibrahim, A.; Eidelpes, E.; Ilevbare, G.O. Degradation mechanisms in overpack concrete of spent nuclear fuel dry storage systems: A review. Nucl. Eng. Des. 2023, 414, 112632. [Google Scholar] [CrossRef]
- Ganjian, E.; Khorami, M.; Maghsoudi, A.A. Scrap-tyre-rubber replacement for aggregate and filler in concrete. Constr. Build. Mater. 2009, 23, 1828–1836. [Google Scholar] [CrossRef]
- Najim, K.; Hall, M. A review of the fresh/hardened properties and applications for plain-(PRC) and self-compacting rubberised concrete (SCRC). Constr. Build. Mater. 2010, 24, 2043–2051. [Google Scholar] [CrossRef]
- Onuaguluchi, O.; Panesar, D.K. Hardened properties of concrete mixtures containing pre-coated crumb rubber and silica fume. J. Clean. Prod. 2014, 82, 125–131. [Google Scholar] [CrossRef]
- Phale, A.R. Environmental Impact and Waste Management of Used Tyres in the RSA; University of Johannesburg: Johannesburg, South Africa, 2012. [Google Scholar]
- Rashad, A.M. A comprehensive overview about recycling rubber as fine aggregate replacement in traditional cementitious materials. Int. J. Sustain. Built Environ. 2016, 5, 46–82. [Google Scholar] [CrossRef]
- Shu, X.; Huang, B. Recycling of waste tire rubber in asphalt and portland cement concrete: An overview. Constr. Build. Mater. 2014, 67, 217–224. [Google Scholar] [CrossRef]
- Kordoghli, S.; Paraschiv, M.; Kuncser, R.; Tazerout, M.; Prisecaru, M.; Zagrouba, F.; Georgescu, I. Managing the environmental hazards of waste tires. J. Eng. Stud. Res. 2014, 20, 1–11. [Google Scholar] [CrossRef]
- Wang, T.; Xiao, F.; Zhu, X.; Huang, B.; Wang, J.; Amirkhanian, S. Energy consumption and environmental impact of rubberized asphalt pavement. J. Clean. Prod. 2018, 180, 139–158. [Google Scholar] [CrossRef]
- Jawjit, W.; Kroeze, C.; Rattanapan, S. Greenhouse gas emissions from rubber industry in Thailand. J. Clean. Prod. 2010, 18, 403–411. [Google Scholar] [CrossRef]
- Yang, X.; You, Z.; Perram, D.; Hand, D.; Ahmed, Z.; Wei, W.; Luo, S. Emission analysis of recycled tire rubber modified asphalt in hot and warm mix conditions. J. Hazard. Mater. 2019, 365, 942–951. [Google Scholar] [CrossRef]
- Wiśniewska, P.; Haponiuk, J.T.; Colom, X.; Saeb, M.R. Green Approaches in Rubber Recycling Technologies: Present Status and Future Perspective. ACS Sustain. Chem. Eng. 2023, 11, 8706–8726. [Google Scholar] [CrossRef]
- Li, W.; Wang, Q.; Jin, J.; Li, S. A life cycle assessment case study of ground rubber production from scrap tires. Int. J. Life Cycle Assess. 2014, 19, 1833–1842. [Google Scholar] [CrossRef]
- Topçu, İ.B.; Demir, A. Durability of rubberized mortar and concrete. J. Mater. Civ. Eng. 2007, 19, 173–178. [Google Scholar] [CrossRef]
- Grinys, A.; Augonis, A.; Daukšys, M.; Pupeikis, D. Mechanical properties and durability of rubberized and SBR latex modified rubberized concrete. Constr. Build. Mater. 2020, 248, 118584. [Google Scholar] [CrossRef]
- Thiagarajan, G.; Vasudevan, A.K.; Robert, S. Numerical modeling of concrete slabs reinforced with high strength low alloy vanadium steel bars subjected to blast loads. Spec. Publ. 2011, 281, 1–16. [Google Scholar]
- Schleyer, G.K.; Barnett, S.J.; Millard, S.G.; Wight, G.; Rebentrost, M. UHPFRC Panel Testing; The Institution of Structural Engineers: London, UK, 2011. [Google Scholar]
- Wang, Z.; Wu, J.; Wang, J.-G. Experimental and numerical analysis on effect of fibre aspect ratio on mechanical properties of SRFC. Constr. Build. Mater. 2010, 24, 559–565. [Google Scholar] [CrossRef]
- Teng, T.-L.; Chu, Y.-A.; Chang, F.-A.; Shen, B.-C.; Cheng, D.-S. Development and validation of numerical model of steel fiber reinforced concrete for high-velocity impact. Comput. Mater. Sci. 2008, 42, 90–99. [Google Scholar] [CrossRef]
- Mao, L.; Barnett, S.; Begg, D.; Schleyer, G.; Wight, G. Numerical simulation of ultra high performance fibre reinforced concrete panel subjected to blast loading. Int. J. Impact Eng. 2014, 64, 91–100. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, J.-B.; Huang, F.-L. Behavior of reinforced concrete beams and columns subjected to blast loading. Def. Technol. 2018, 14, 550–559. [Google Scholar] [CrossRef]
- Ottosen, N.S. A failure criterion for concrete. J. Eng. Mech. Div. 1977, 103, 527–535. [Google Scholar] [CrossRef]
- Marais, S.; Tait, R.; Cloete, T.; Nurick, G. Material testing at high strain rate using the split Hopkinson pressure bar. Lat. Am. J. Solids Struct. 2004, 1, 219–339. [Google Scholar]
- Schwer, L.; Teng, H.; Souli, M. LS-DYNA Air Blast Techniques: Comparisons with Experiments for Close-in Charges. In Proceedings of the 10th European LS-DYNA Conference 2015, Würzburg, Germany, 15–17 June 2015. [Google Scholar]
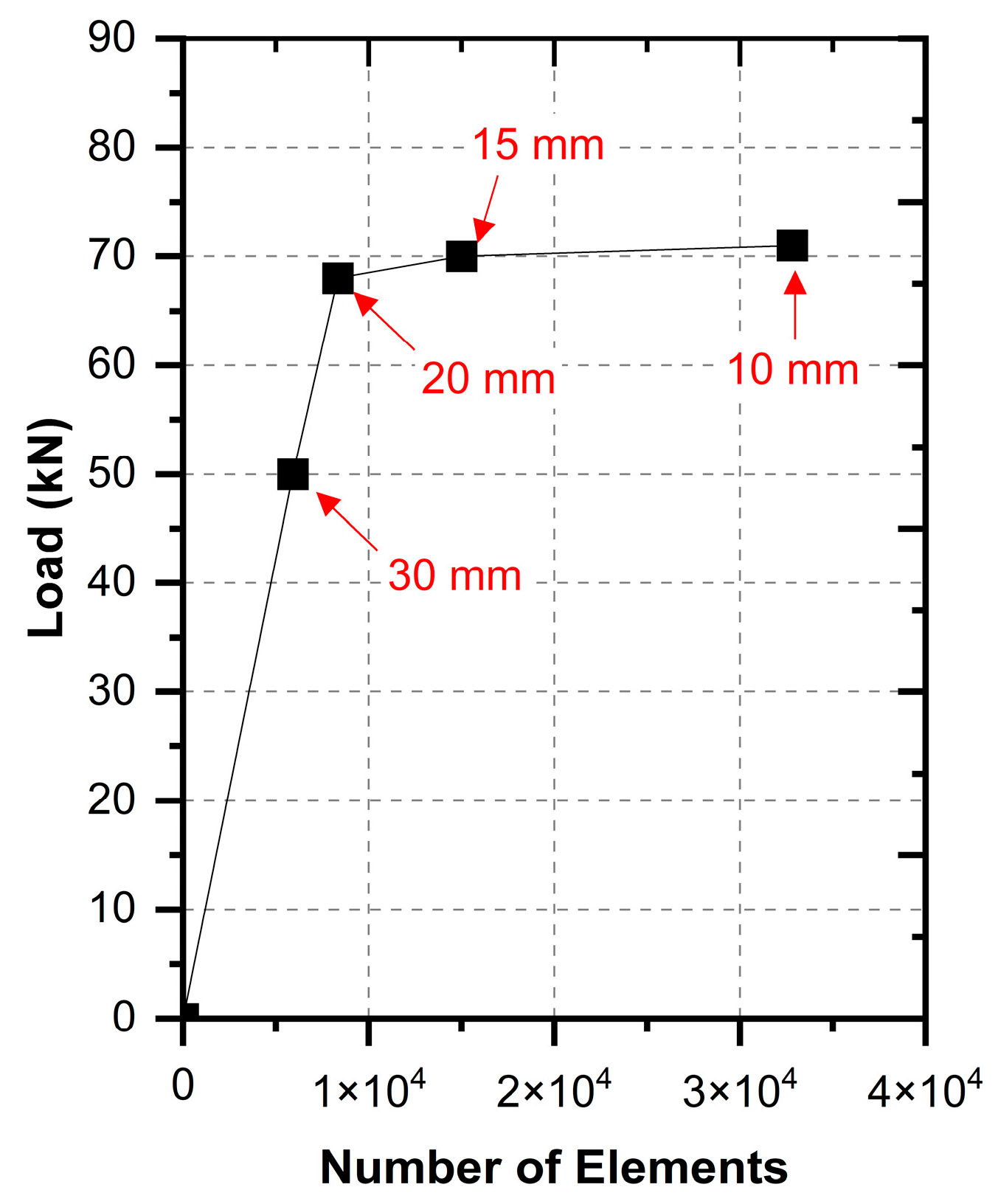
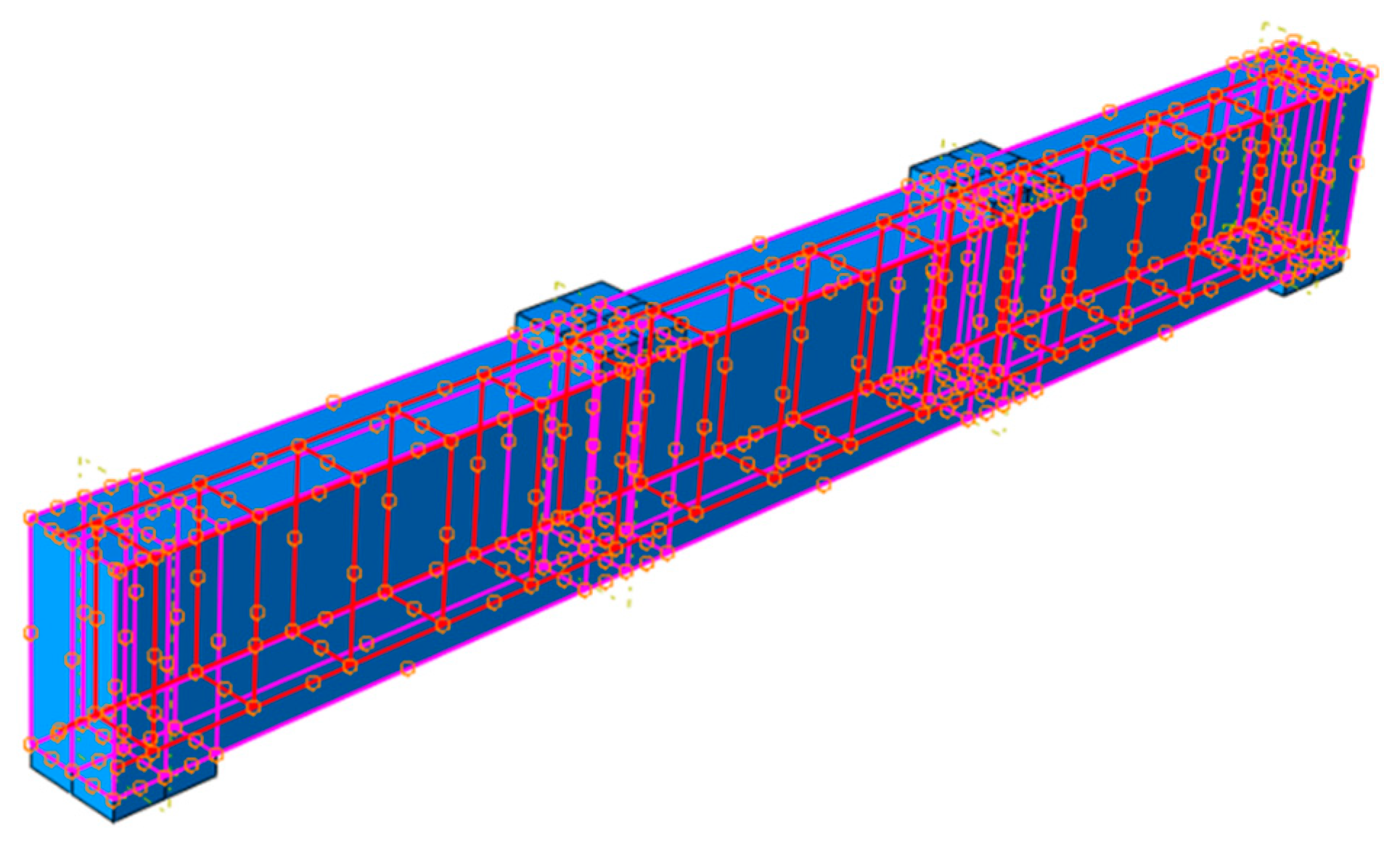
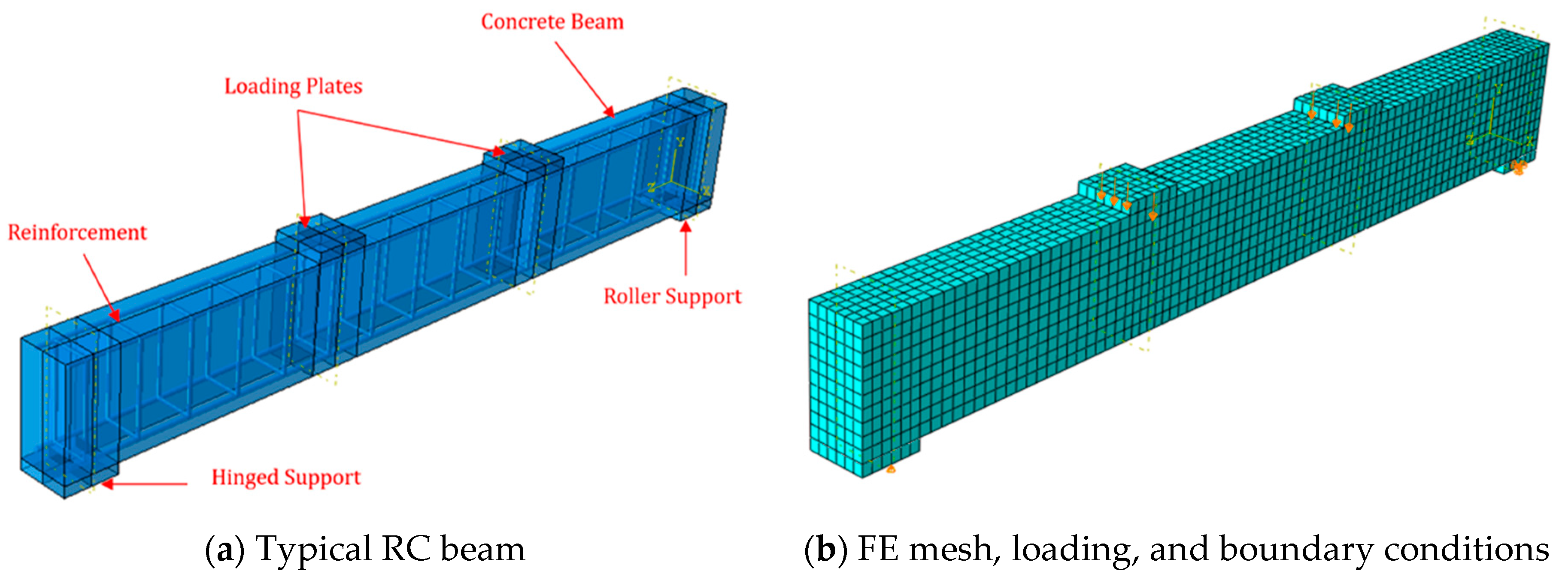

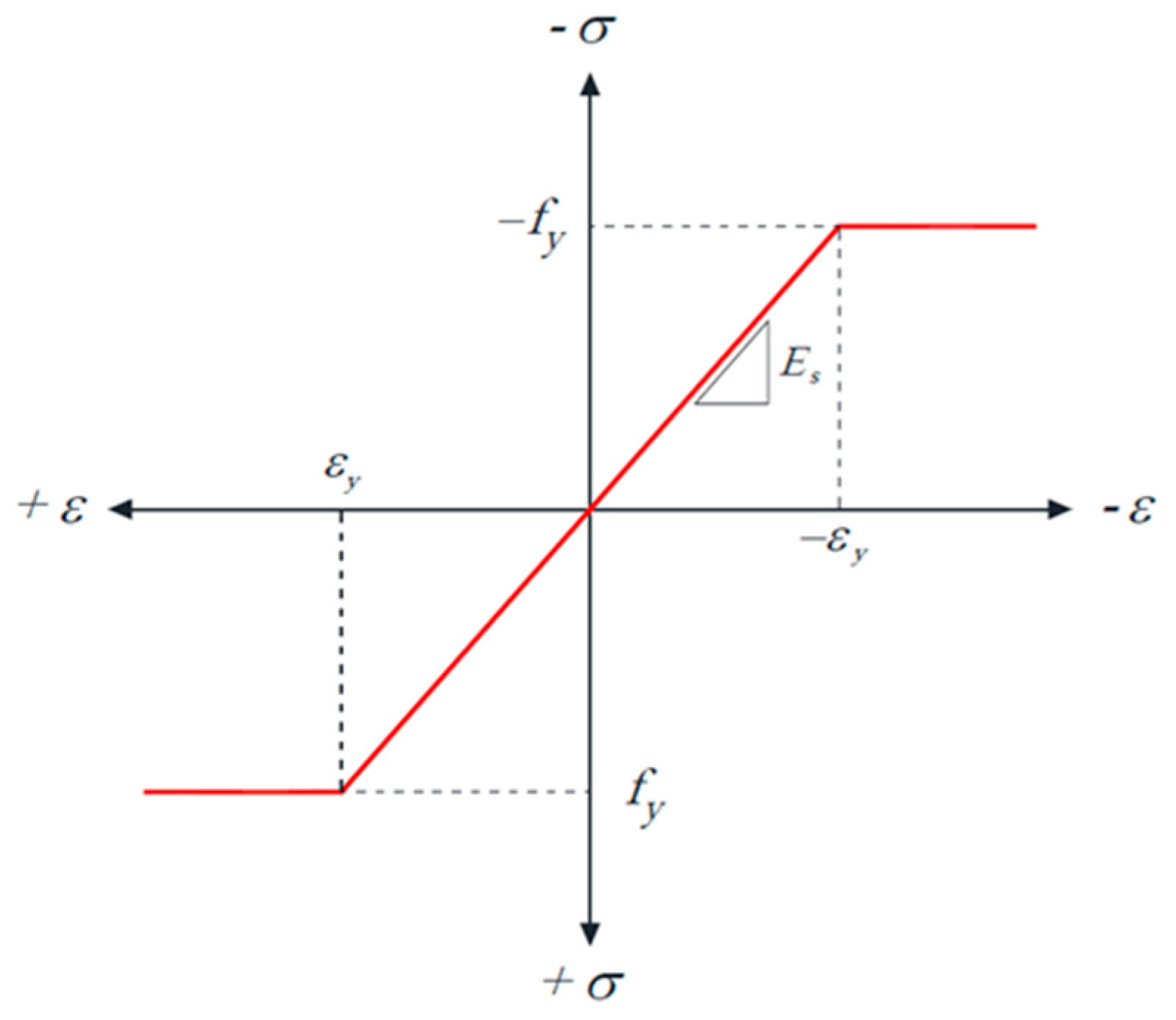








| No. | Mix | Compressive Strength (MPa) | Modulus of Elasticity (MPa) | Splitting Tensile Strength (MPa) | Modulus of Rupture (MPa) |
|---|---|---|---|---|---|
| 1 | PC | 44.20 | 17,612 | 3.40 | 6.89 |
| 2 | RC5 | 39.80 | 15,258 | 2.55 | 6.72 |
| 3 | RC10 | 33.70 | 13,348 | 2.26 | 6.33 |
| 4 | RC15 | 25.70 | 10,072 | 2.12 | 5.78 |
| 5 | RC20 | 18.00 | 6970 | 1.98 | 5.44 |
| 6 | SFC | 47.20 | 22,845 | 6.65 | 8.67 |
| 7 | SFRC5 | 44.30 | 20,704 | 4.81 | 8.05 |
| 8 | SFRC10 | 39.50 | 18,200 | 4.22 | 7.11 |
| 9 | SFRC15 | 32.20 | 15,043 | 3.92 | 6.57 |
| 10 | SFRC20 | 24.17 | 11,505 | 3.47 | 6.22 |
| Parameter | Value | |
|---|---|---|
| C0 | Mass Density | 1.29 Kg/m3 |
| C1 | Null Constant | 0 |
| C2 | Null Constant | 0 |
| C3 | Null Constant | 0 |
| C4 | Null Constant | 0.4 |
| C5 | Null Constant | 0.4 |
| C6 | Null Constant | 0 |
| E0 | Initial internal energy. | 2.50 × 105 Pa |
| V0 | Initial relative volume. | 1 |
| Parameter | Value | |
|---|---|---|
| A | EOS Coefficient | 3.712 × 1011 |
| B | EOS Coefficient | 3.231 × 109 |
| R1 | EOS Coefficient | 4.15 |
| R2 | EOS Coefficient | 0.95 |
| OMEG | Null Constant | 0.30 |
| E0 | Null Constant | 7.0 × 109 Pa |
| V0 | Null Constant | 1 |
| E0 | Initial internal energy. | 2.50 × 105 Pa |
| V0 | Initial relative volume. | 1 |
| No. | Model Label | Failure Load (kN) | Difference % | Maximum Deflection (mm) | Difference % | ||
|---|---|---|---|---|---|---|---|
| EXP. | FE | EXP. | FE | ||||
| 1 | PC | 64 | 68 | 6.25 | 15.7 | 14.8 | 6 |
| 2 | RC5% | 60 | 62 | 3.33 | 15.9 | 14.9 | 6.7 |
| 3 | RC10% | 56 | 59 | 5.36 | 18.9 | 17.2 | 9.88 |
| 4 | RC15% | 53 | 57 | 7.55 | 20 | 18.8 | 6.38 |
| 5 | RC20% | 51 | 54 | 5.88 | 22.8 | 21.8 | 4.58 |
| 6 | SFC | 81 | 88 | 8.64 | 12.9 | 11.8 | 9.32 |
| 7 | SFRC5% | 72 | 76 | 5.55 | 13.8 | 12.9 | 6.97 |
| 8 | SFRC10% | 67 | 72 | 7.46 | 17 | 15.5 | 9.67 |
| 9 | SFRC15% | 62 | 69 | 11.29 | 19 | 17.76 | 6.98 |
| 10 | SFRC20% | 58 | 64 | 10.34 | 21.9 | 21.11 | 3.74 |
| No. | Model | μ (%) | Failure Load | Maximum Deflection | εcmax | εtmax | Failure Mode |
|---|---|---|---|---|---|---|---|
| 1 | PC | 0.5 | 43.5 | 15.2 | 0.0013 | 0.0135 | Tension Side |
| 0.78 | 68.0 | 14.81 | 0.0012 | 0.0129 | Tension Side | ||
| 1.13 | 88.0 | 9.00 | 0.0010 | 0.0100 | Tension Side | ||
| 2 | RC5 | 0.5 | 37.4 | 15.50 | 0.0020 | 0.0206 | Tension Side |
| 0.78 | 62.0 | 14.89 | 0.0019 | 0.0191 | Tension Side | ||
| 1.13 | 79.0 | 9.60 | 0.0016 | 0.0152 | Tension Side | ||
| 3 | RC10 | 0.5 | 35.2 | 18.28 | 0.0031 | 0.0290 | Tension Side |
| 0.78 | 59.0 | 17.04 | 0.0028 | 0.0261 | Tension Side | ||
| 1.13 | 71.0 | 11.80 | 0.0024 | 0.0220 | Tension Side | ||
| 4 | RC15 | 0.5 | 34.0 | 21.00 | 0.0069 | 0.0320 | Tension Side |
| 0.78 | 57.8 | 18.87 | 0.0059 | 0.0281 | Compression | ||
| 1.13 | 68.0 | 14.20 | 0.0053 | 0.0245 | Compression | ||
| 5 | RC20 | 0.5 | 32.7 | 27.37 | 0.0210 | 0.0400 | Tension Side |
| 0.78 | 55.6 | 21.81 | 0.0172 | 0.0322 | Compression | ||
| 1.13 | 62.0 | 19.00 | 0.0160 | 0.0300 | Compression | ||
| 6 | SFC | 0.5 | 65.2 | 11.35 | 0.0010 | 0.0138 | Tension Side |
| 0.78 | 88.2 | 11.27 | 0.0009 | 0.0130 | Tension Side | ||
| 1.13 | 106.0 | 8.00 | 0.0008 | 0.0105 | Tension Side | ||
| 7 | SFRC5 | 0.5 | 53.0 | 13.30 | 0.0018 | 0.0260 | Tension Side |
| 0.78 | 76.6 | 12.98 | 0.0017 | 0.0240 | Tension Side | ||
| 1.13 | 90.0 | 9.50 | 0.0015 | 0.0200 | Tension Side | ||
| 8 | SFRC10 | 0.5 | 48.7 | 16.20 | 0.0024 | 0.0330 | Tension Side |
| 0.78 | 72.3 | 15.50 | 0.0022 | 0.0290 | Tension Side | ||
| 1.13 | 83.0 | 12.00 | 0.0019 | 0.0255 | Tension Side | ||
| 9 | SFRC15 | 0.5 | 46.1 | 19.80 | 0.0056 | 0.0370 | Tension Side |
| 0.78 | 69.3 | 18.76 | 0.0050 | 0.0310 | Tension Side | ||
| 1.13 | 77.0 | 15.50 | 0.0044 | 0.0285 | Tension Side | ||
| 10 | SFRC20 | 0.5 | 42.7 | 24.61 | 0.0160 | 0.0430 | Tension Side |
| 0.78 | 64.9 | 21.11 | 0.0137 | 0.0340 | Balanced | ||
| 1.13 | 69.0 | 18.80 | 0.0123 | 0.0325 | Compression |
| No | Model Label | Reflected Pressure (MPa) | Impulse (MPa·ms) | No | Model Label | Reflected Pressure (MPa) | Impulse (MPa·ms) |
|---|---|---|---|---|---|---|---|
| 1 | PC | 120.00 | 8.22 | 6 | SFC | 128.04 | 9.55 |
| 2 | RC5% | 115.05 | 7.52 | 7 | SFRC5% | 124.80 | 8.15 |
| 3 | RC10% | 109.09 | 6.60 | 8 | SFRC10% | 118.11 | 7.14 |
| 4 | RC15% | 95.24 | 6.90 | 9 | SFRC15% | 104.35 | 6.70 |
| 5 | RC20% | 87.59 | 7.20 | 10 | SFRC20% | 98.36 | 7.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawar, M.T.; Eisa, A.S.; Elshazli, M.T.; Ibrahim, Y.E.; El-Zohairy, A. Numerical Analysis of Rubberized Steel Fiber Reinforced Concrete Beams Subjected to Static and Blast Loadings. Infrastructures 2024, 9, 52. https://doi.org/10.3390/infrastructures9030052
Nawar MT, Eisa AS, Elshazli MT, Ibrahim YE, El-Zohairy A. Numerical Analysis of Rubberized Steel Fiber Reinforced Concrete Beams Subjected to Static and Blast Loadings. Infrastructures. 2024; 9(3):52. https://doi.org/10.3390/infrastructures9030052
Chicago/Turabian StyleNawar, Mahmoud T., Ahmed S. Eisa, Mohamed T. Elshazli, Yasser E. Ibrahim, and Ayman El-Zohairy. 2024. "Numerical Analysis of Rubberized Steel Fiber Reinforced Concrete Beams Subjected to Static and Blast Loadings" Infrastructures 9, no. 3: 52. https://doi.org/10.3390/infrastructures9030052
APA StyleNawar, M. T., Eisa, A. S., Elshazli, M. T., Ibrahim, Y. E., & El-Zohairy, A. (2024). Numerical Analysis of Rubberized Steel Fiber Reinforced Concrete Beams Subjected to Static and Blast Loadings. Infrastructures, 9(3), 52. https://doi.org/10.3390/infrastructures9030052









