Numerical Modeling of Cracked Arch Dams. Effect of Open Joints during the Construction Phase
Abstract
1. Introduction
2. Methods
2.1. General Approach
2.2. Numerical Approach
- Models involving nonlinear materials;
- Transient models;
- Thermal effect;
- Analysis of the separation between the dam and the ground.
2.3. Calibration
- A range of values of the studied properties is set, with some exploration values for each one. Initially, the design values are used, with the addition of several higher values. The exploration points are the pairs that result from the combination of these values.
- The error is calculated in each case by comparing simulations with the auscultation records of the devices that record the greatest movements (the three upper three of the central cantilevers). The following is used as an error calculation formula: . With i the points where the auscultation devices have been installed, ui the radial movements of the simulation at point i, and ui.obj the real radial movements recorded at point i.
- A maximum allowable error is set that will serve to delimit the solution domain. Using linear interpolation of the obtained errors, the coordinates of points on the solution domain contour are calculated.
- The centroid of the solution domain is found from these contour points and the error is verified by solving a numerical simulation based on such values.
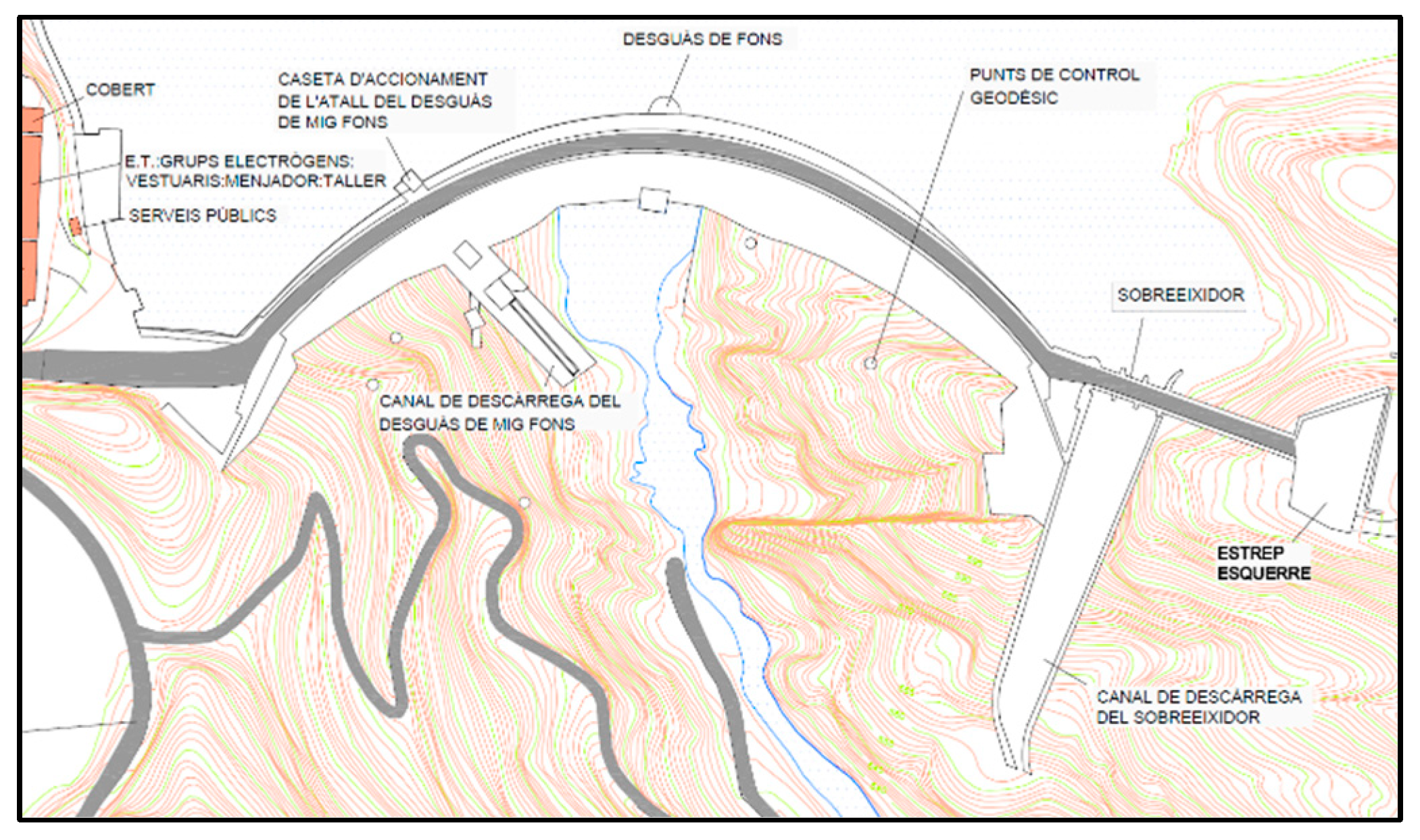
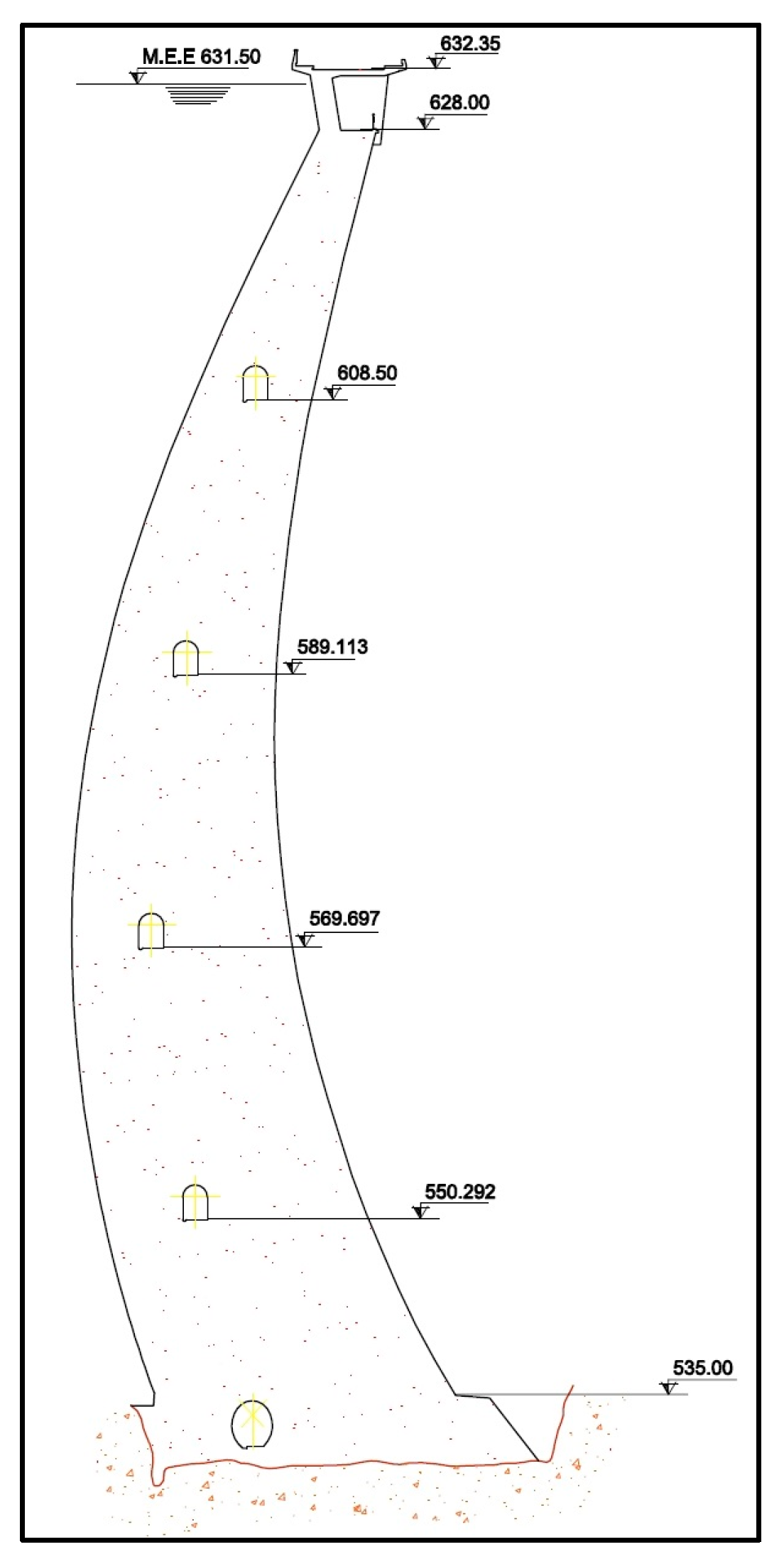
2.4. Study Case
Geometry
- -
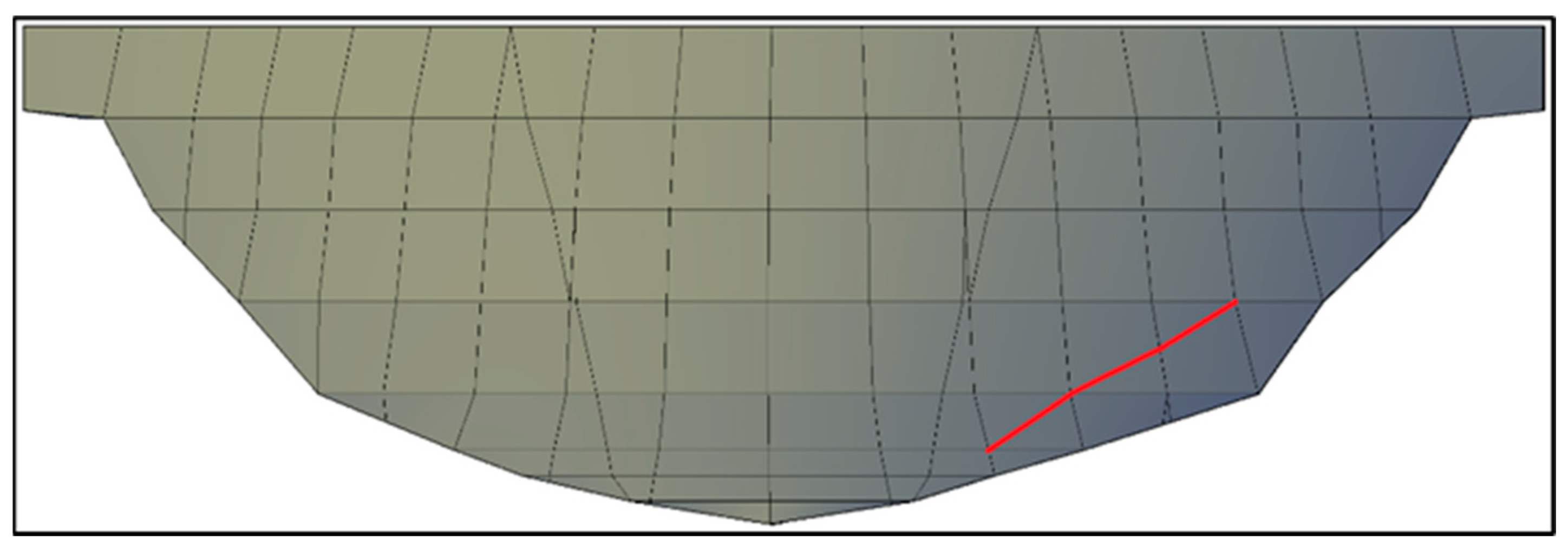
- Horizontal, near the base (Figure 5). This crack has a length of 91.5 m, a depth of 50% of the dam thickness, and is located 9.5 m above the base of the dam.
- -
- On one side, parallel to bedrock contact (Figure 6). This crack has a length of 60.7 m, a depth of 50% of the thickness of the dam, and begins at 9.5 m above the base elevation of the dam, ending at 38.5 m.
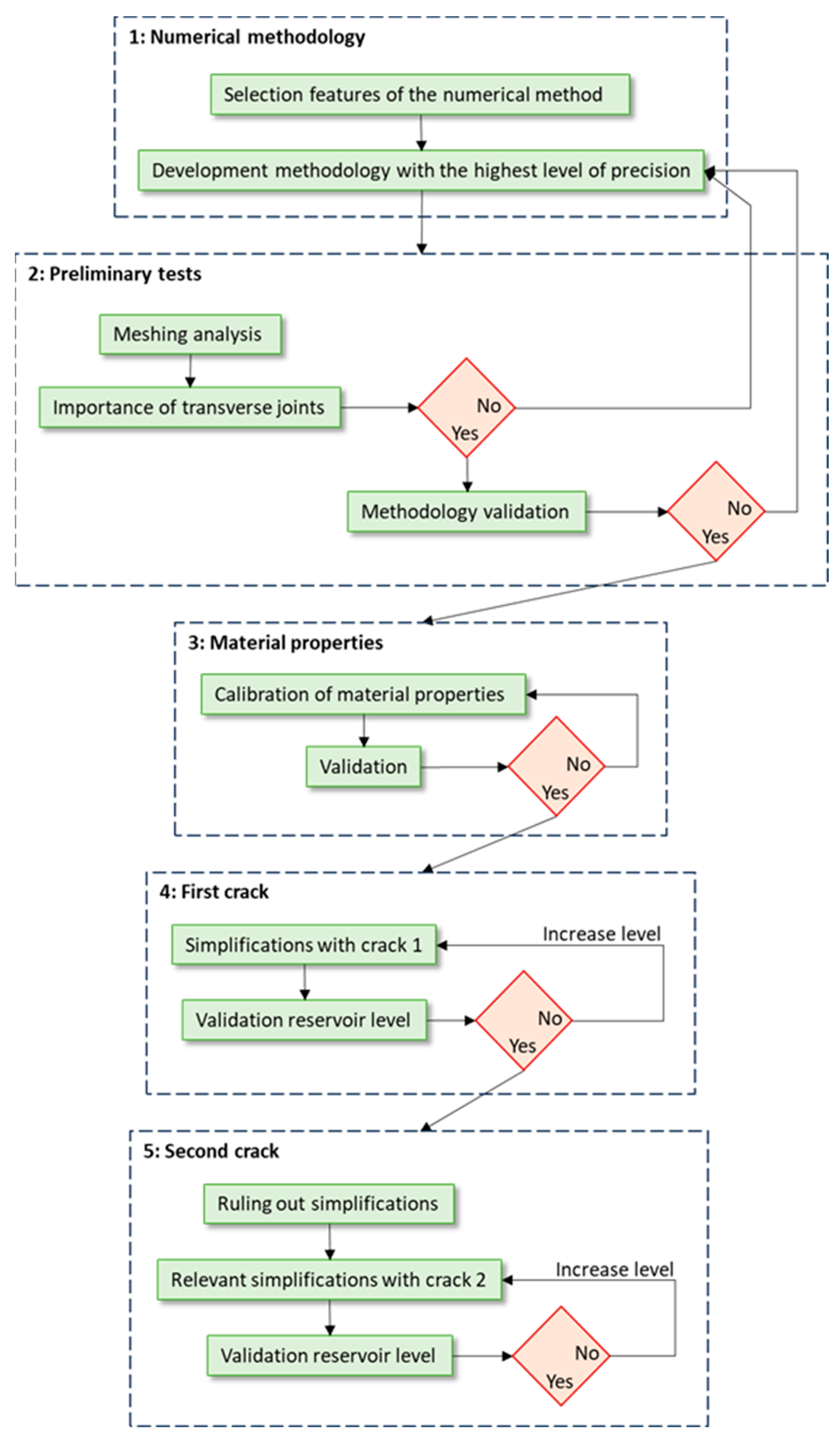
3. Proposed Methodology for Numerical Modeling
3.1. Base Methodology
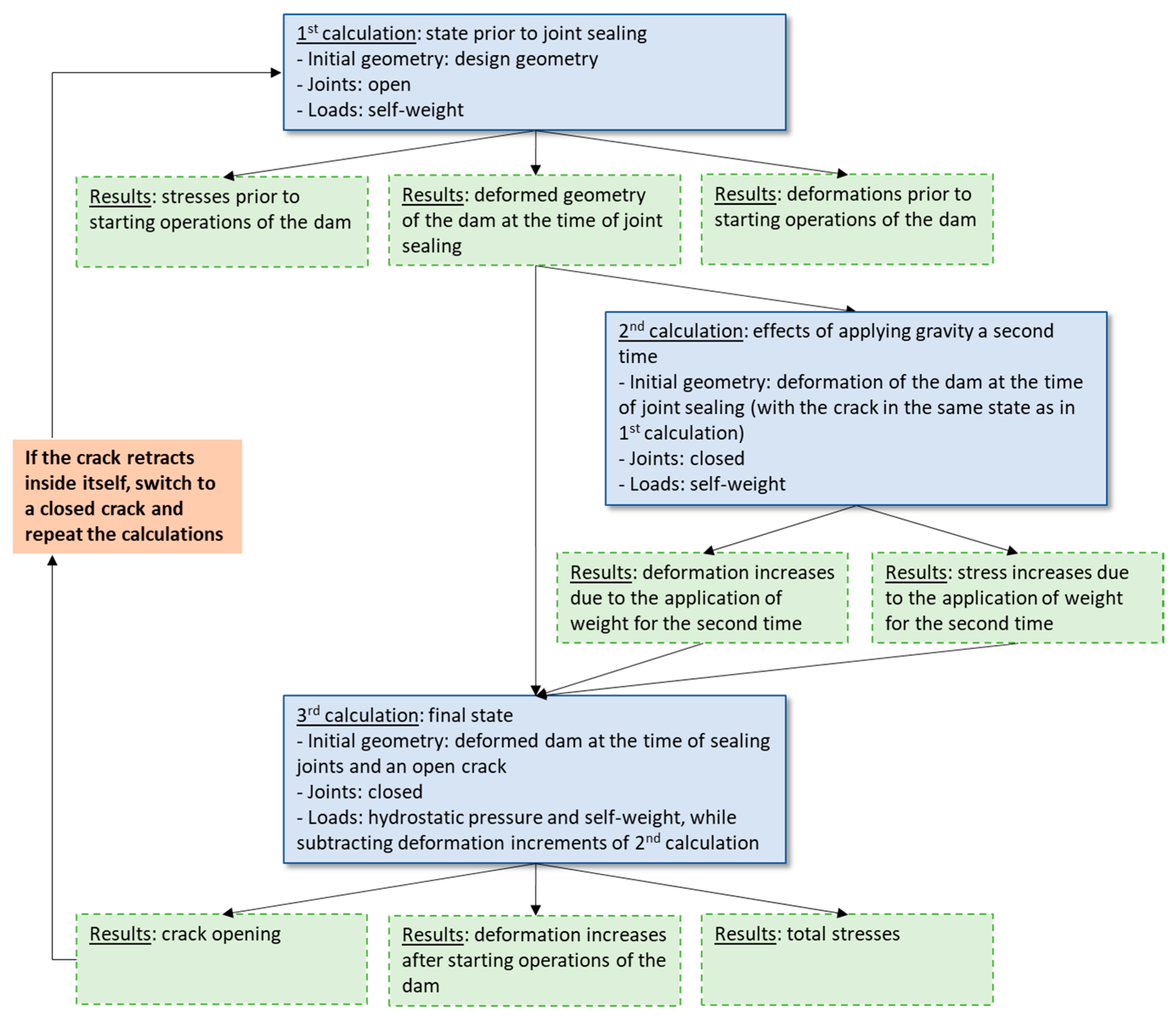
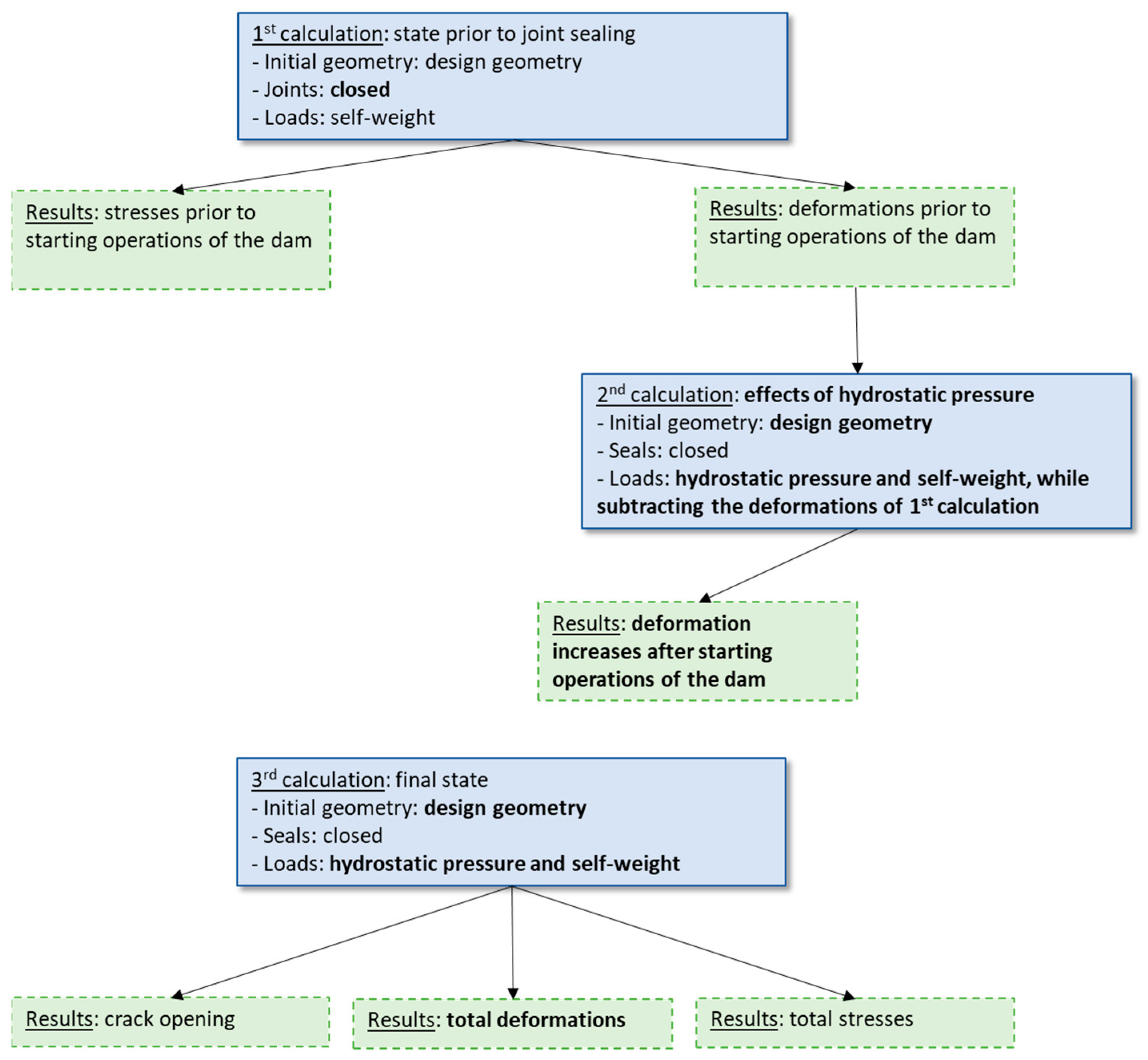
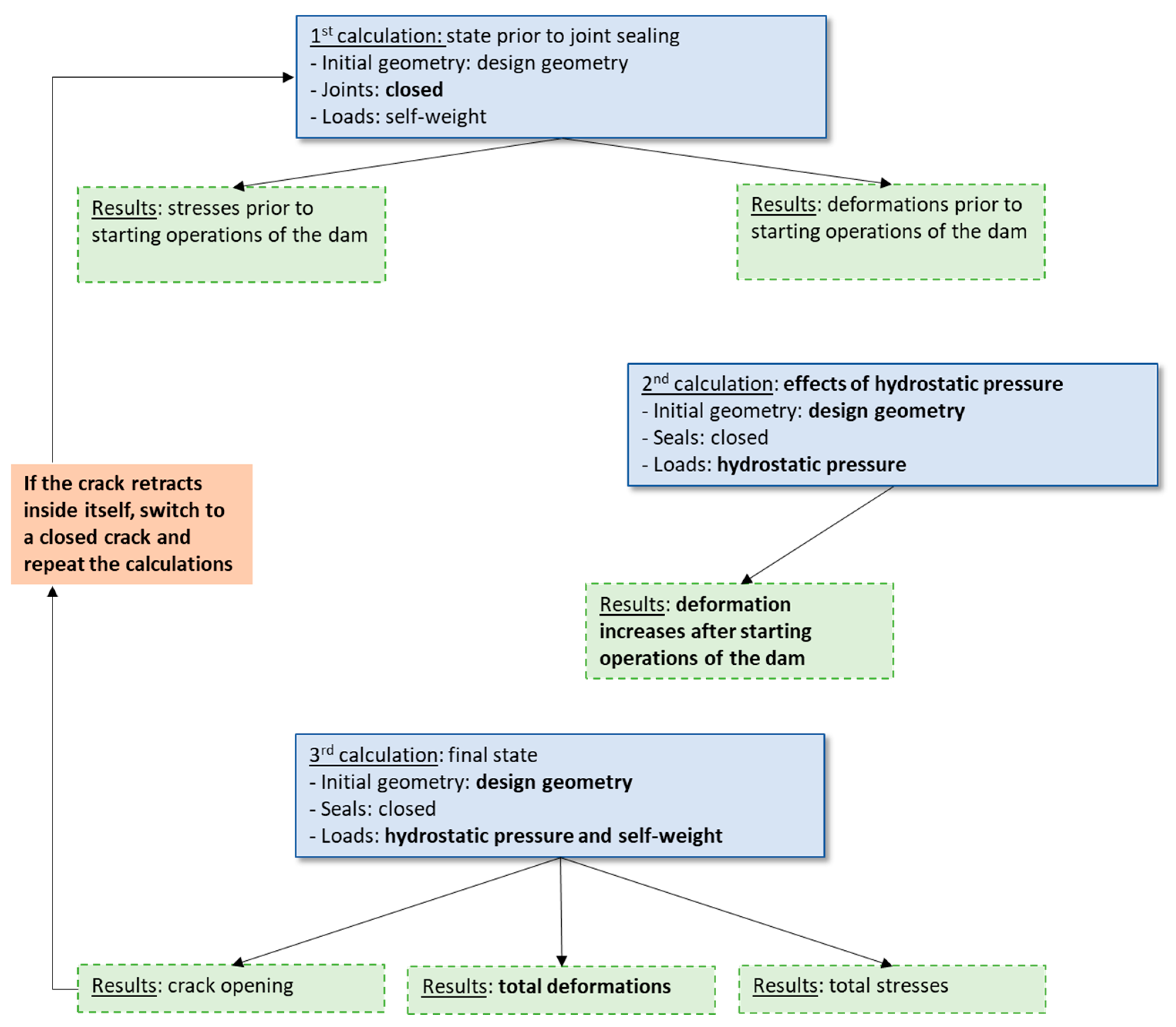
- Initial calculation with open joints, without any crack and with self-weight being the only load;
- Final calculation on the monolithic dam and with a crack and subjected to hydrostatic pressure.
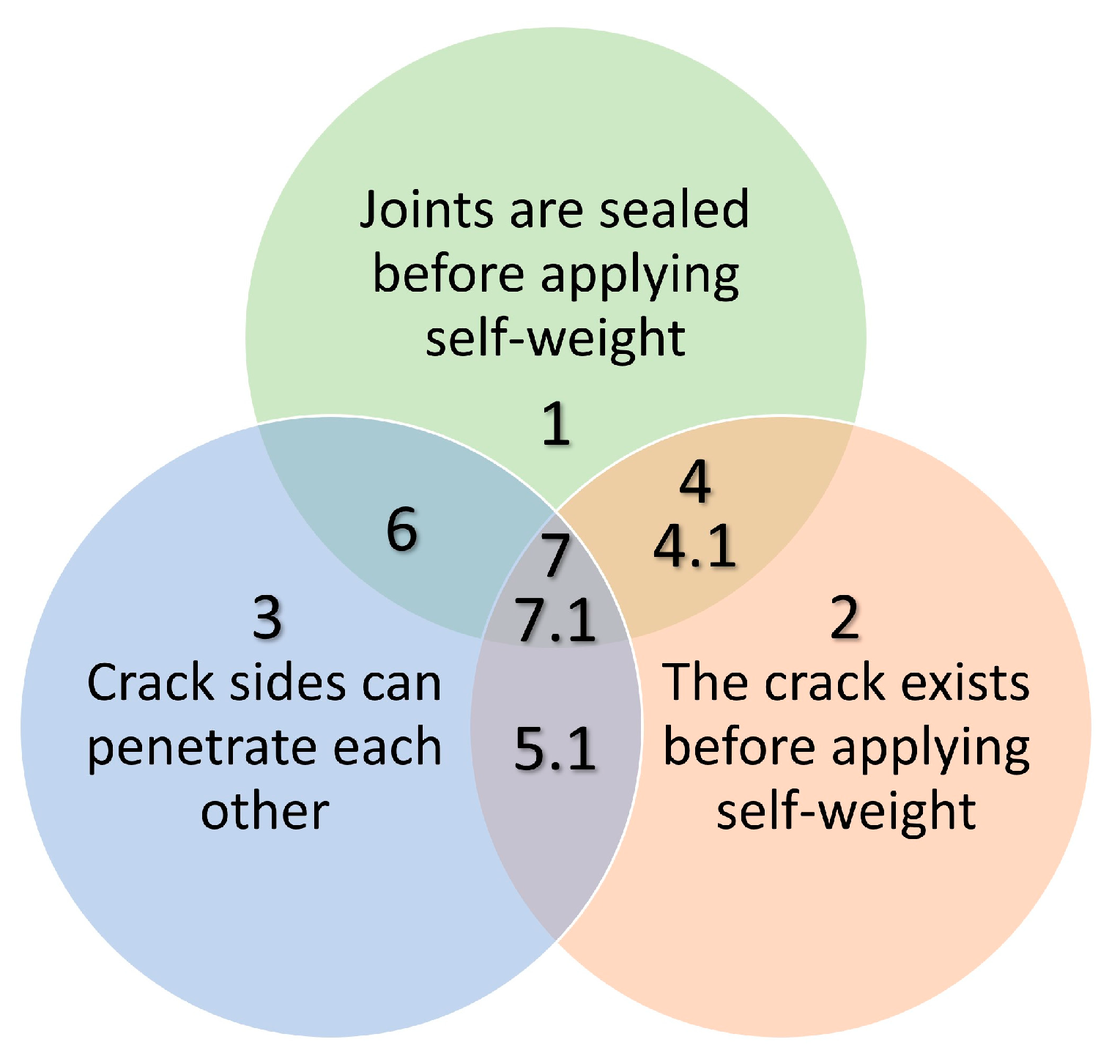
3.2. Methodology Simplifications
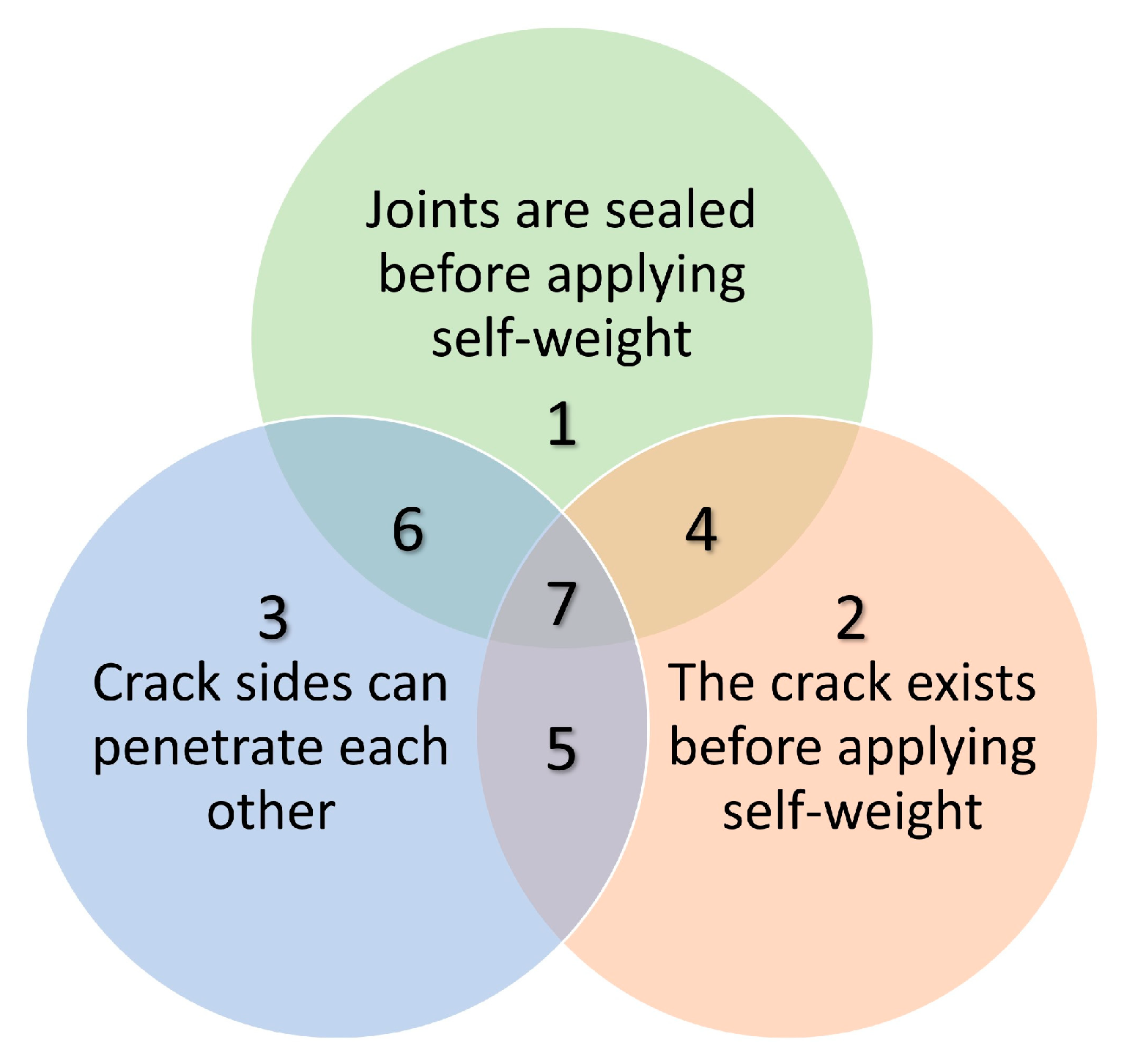
- Simplification A: the transverse joints are closed before self-weight is applied. In this way the cantilevers can never deform independently of each other. The methodology still consists of a first phase before starting operations where only self-weight is applied and a second phase beginning with the deformed geometry of the previous phase where hydrostatic pressure and a crack are applied.
- Simplification B: the crack already exists at the beginning of the simulation. In this case the self-weight is applied on an already-cracked dam.
- Simplification C: the crack faces are disconnected, allowing the upper side of the crack to pass through the lower side in its movement. Therefore, the crack faces can either separate (open crack) or ride over each other (with a non-existent penetration, which in reality corresponds to a closed crack). In these simplifications, if the final result indicates that the sides of the crack cross each other, it is necessary to repeat the simulation, establishing that the joint cannot open, as shown in the scheme of Figure 8. As already discussed in Section 3.1, the deformations that are subtracted in the 3rd calculation are not equal to those caused by gravity in the 3rd calculation. There is an exception when the crack can close on itself in the first calculation and another exception when the crack is not free to open in any of the calculations (this happens in simplification C where the calculation is repeated, i.e., when the hydrostatic pressure is not sufficient to open the crack).
4. Results and Discussion
4.1. Preliminary Tests
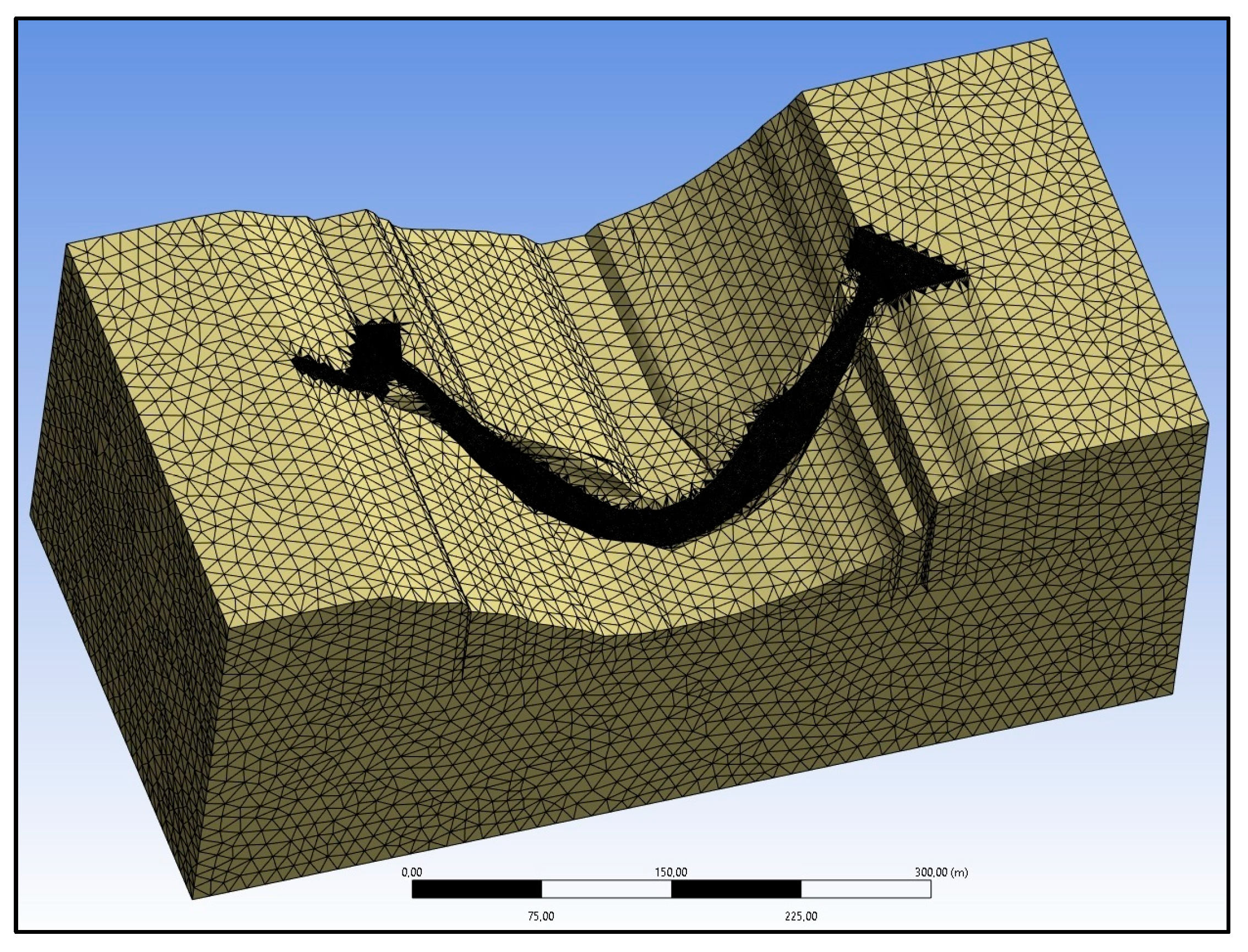
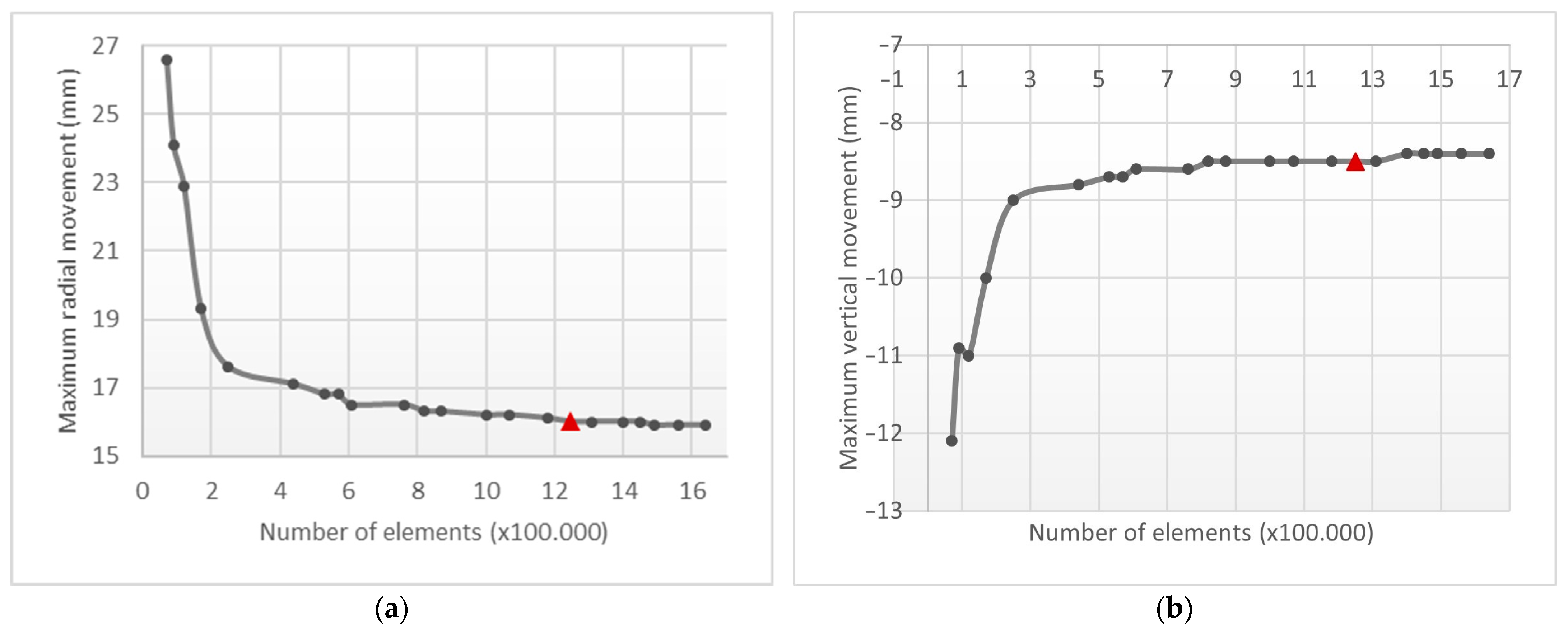
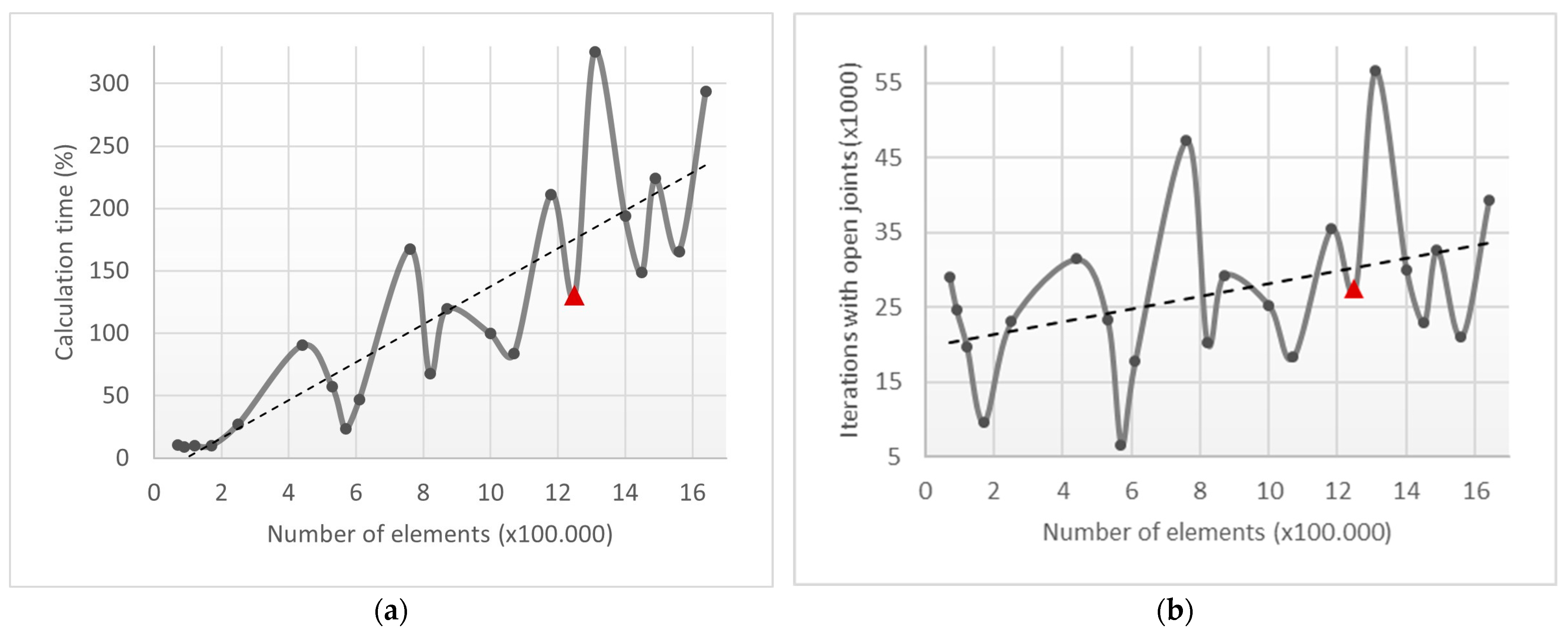
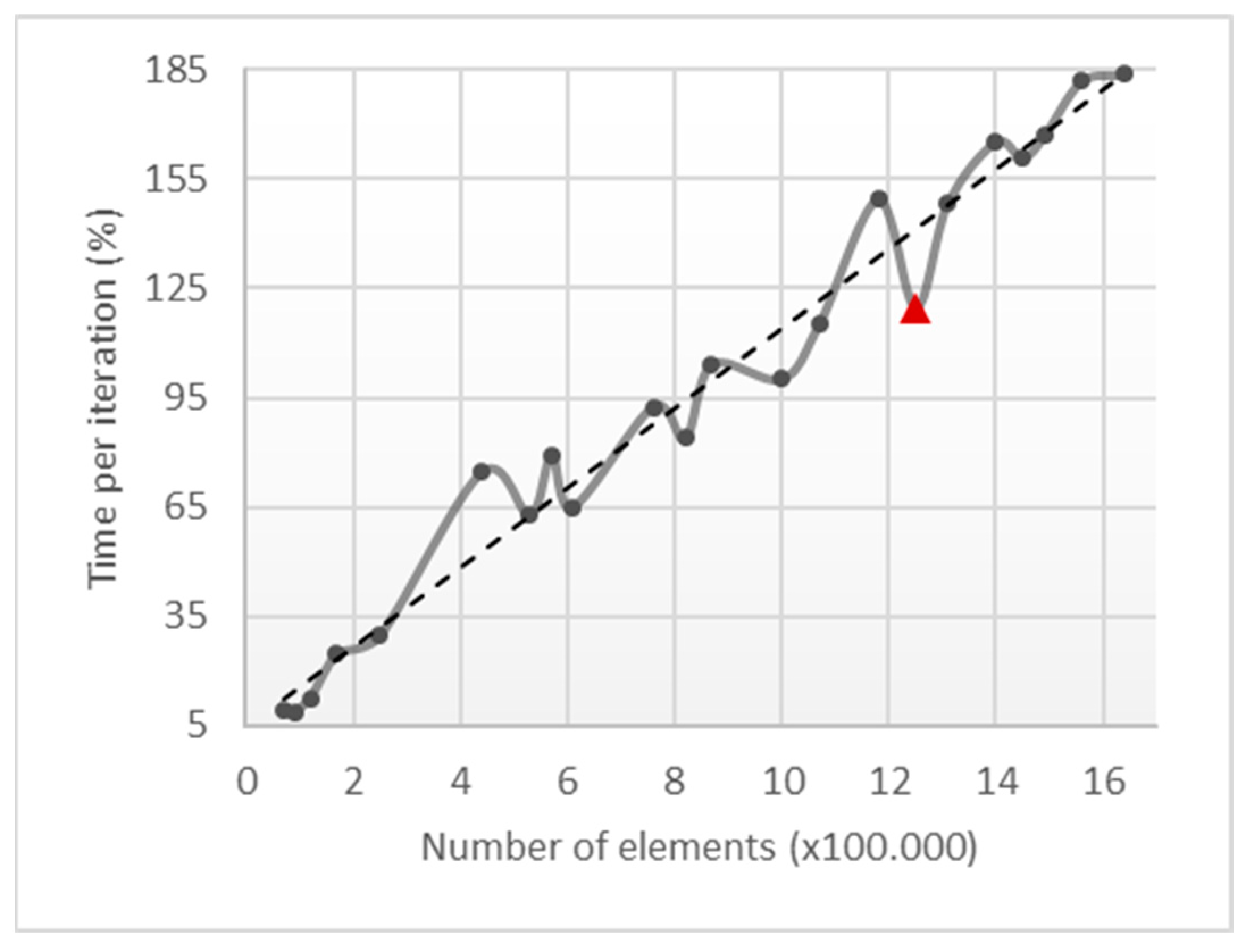
4.1.1. Mesh Analysis
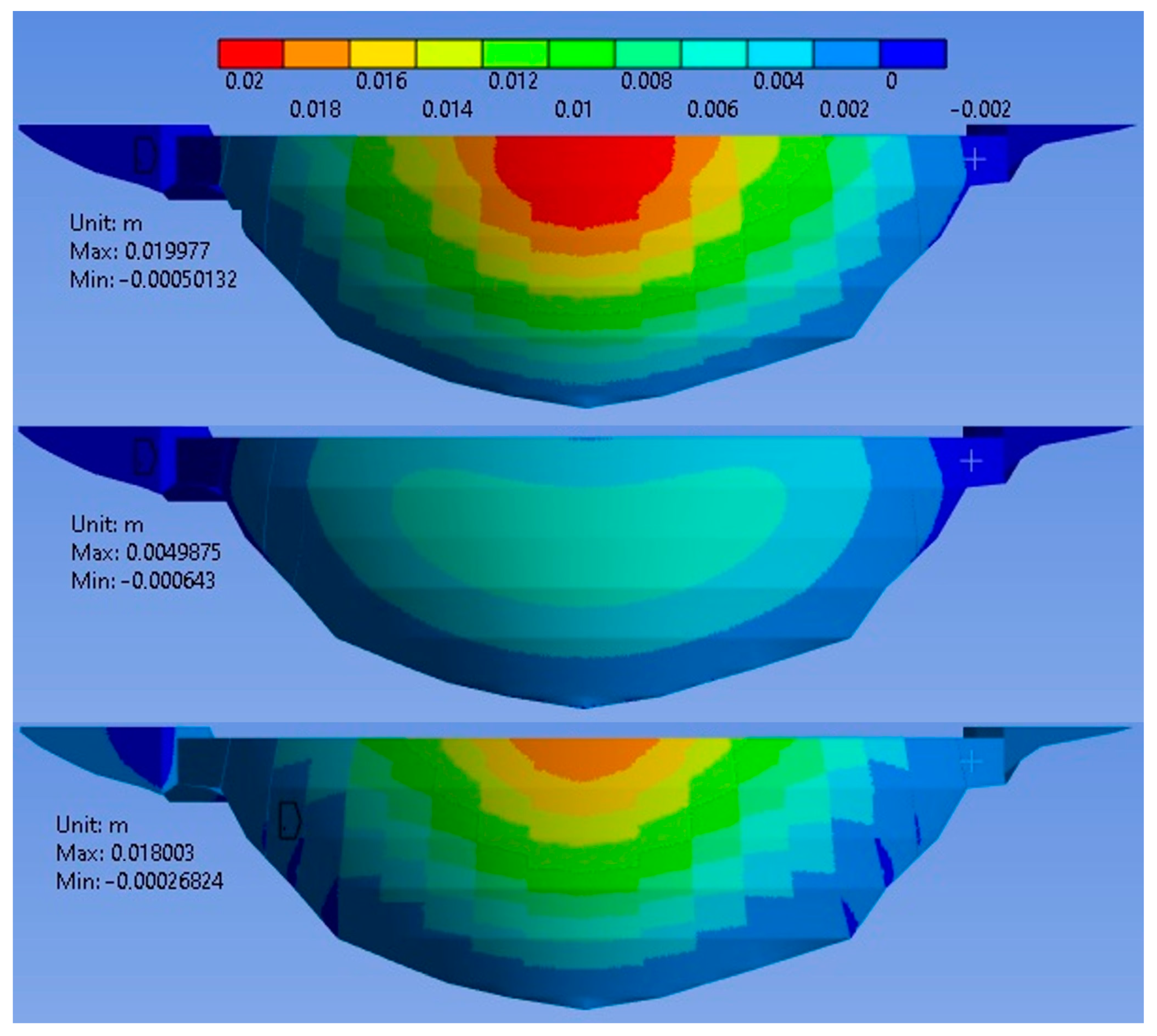
4.1.2. Importance of Considering Open Joints
4.1.3. Validation of the Proposed Methodology
- In the remaining areas of the dam, it was found that, assuming an empty reservoir level, the resulting total stresses are equivalent to those obtained in the first calculation. Again, the variation is not zero due to the inherent inaccuracy of the numerical calculation.
- In the area around the upstream dam–bedrock contact, the discrepancies between the results of the methodology and one-step numerical calculation are not negligible. This zone corresponds to an area of high stresses and a geometry with a large number of corners. As a result, this leads to fictitious stress increases due to the resolution of numerical models (which applies to any FEM technique), even though in reality there would be a smoother stress distribution in this area. In the absence of reference values, it becomes unclear whether the error made by the proposed methodology would be significantly greater than the error made by the direct numerical computation. It should be noted that this particularity of the results applies to stresses and not to movements (due to the mathematical formulation of the FEM).
4.2. Calibration Tests
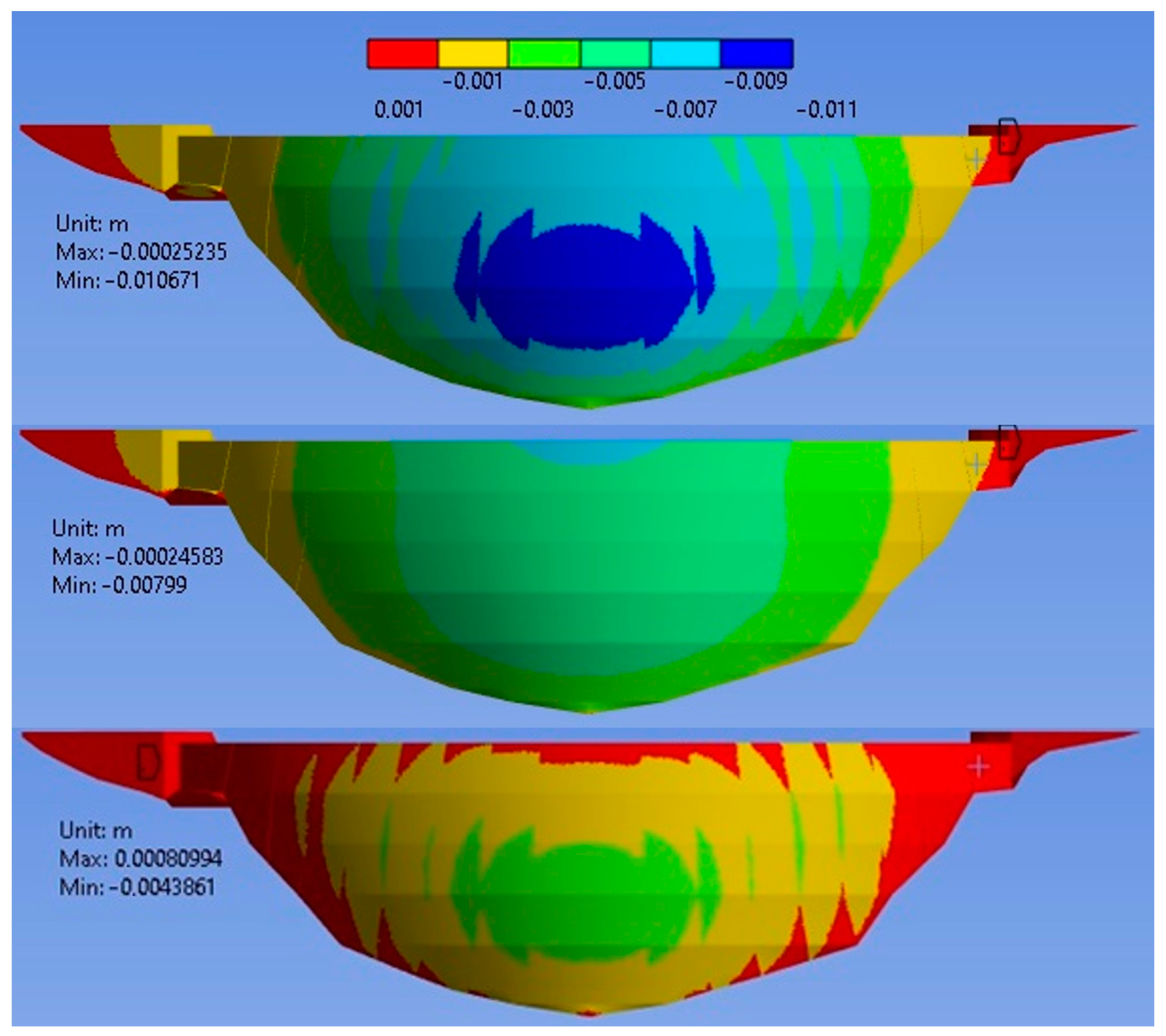
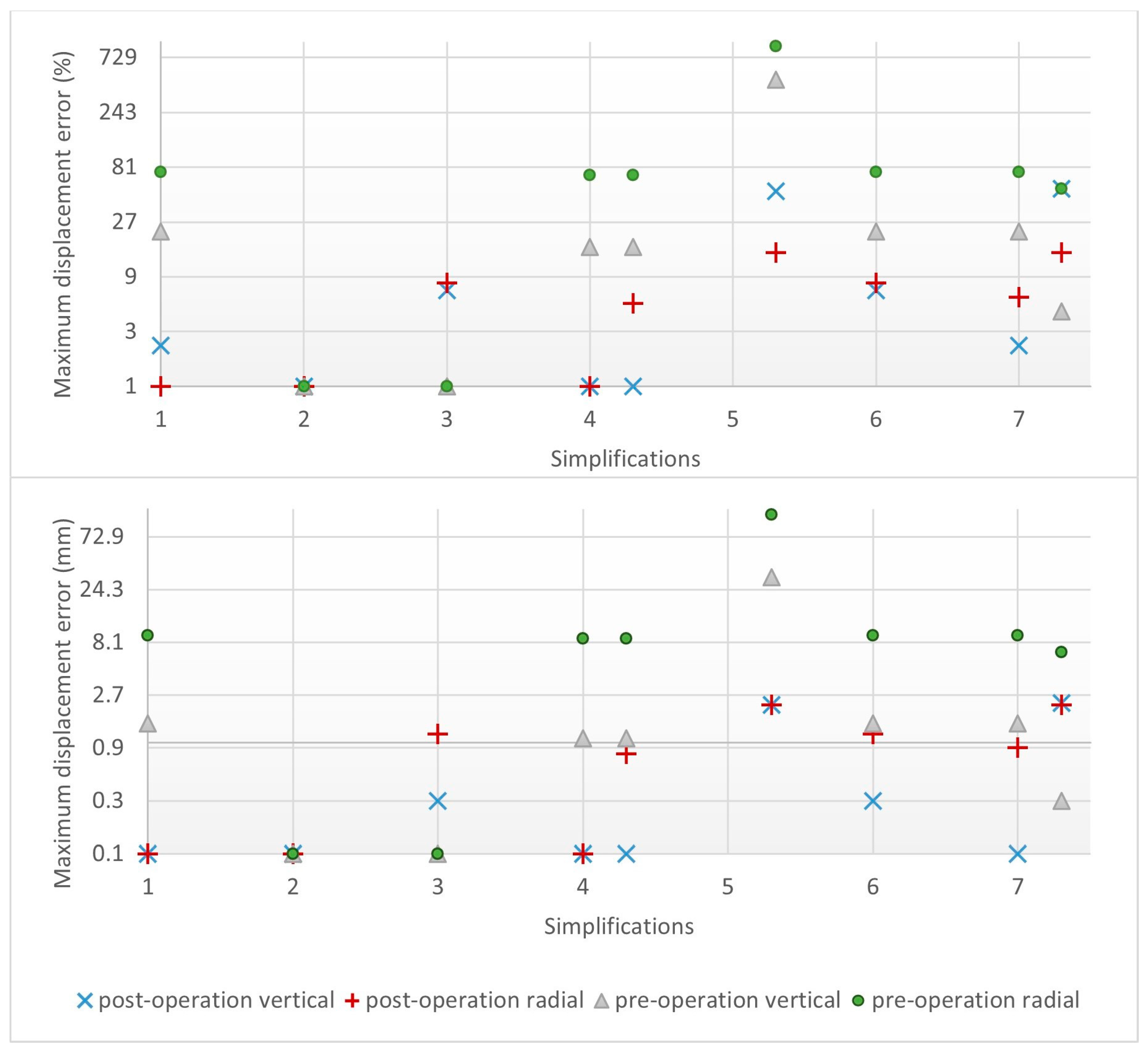
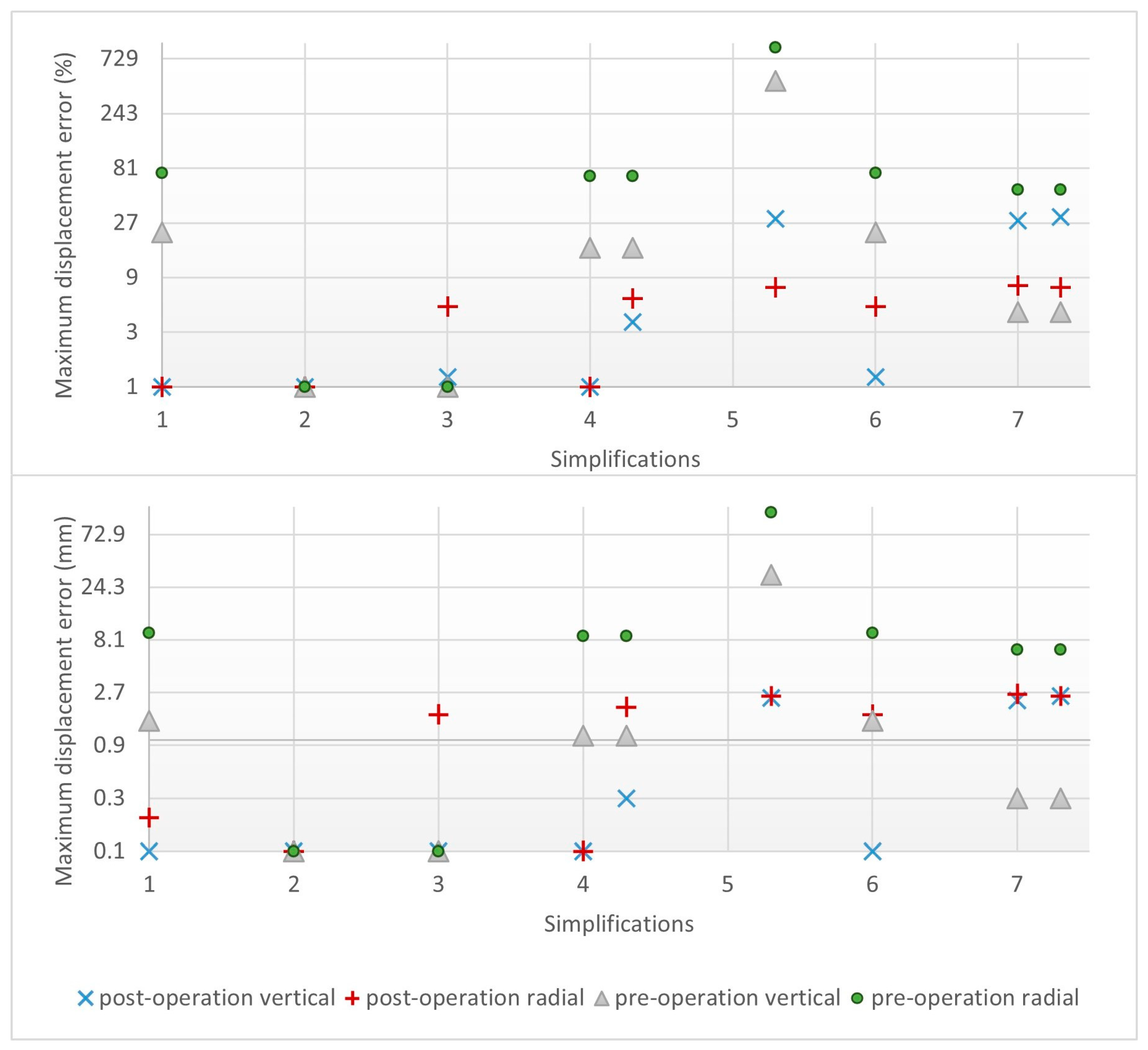
4.3. Accuracy for Different Simplifications: Crack 1
4.3.1. Absolute and Relative Displacement Errors
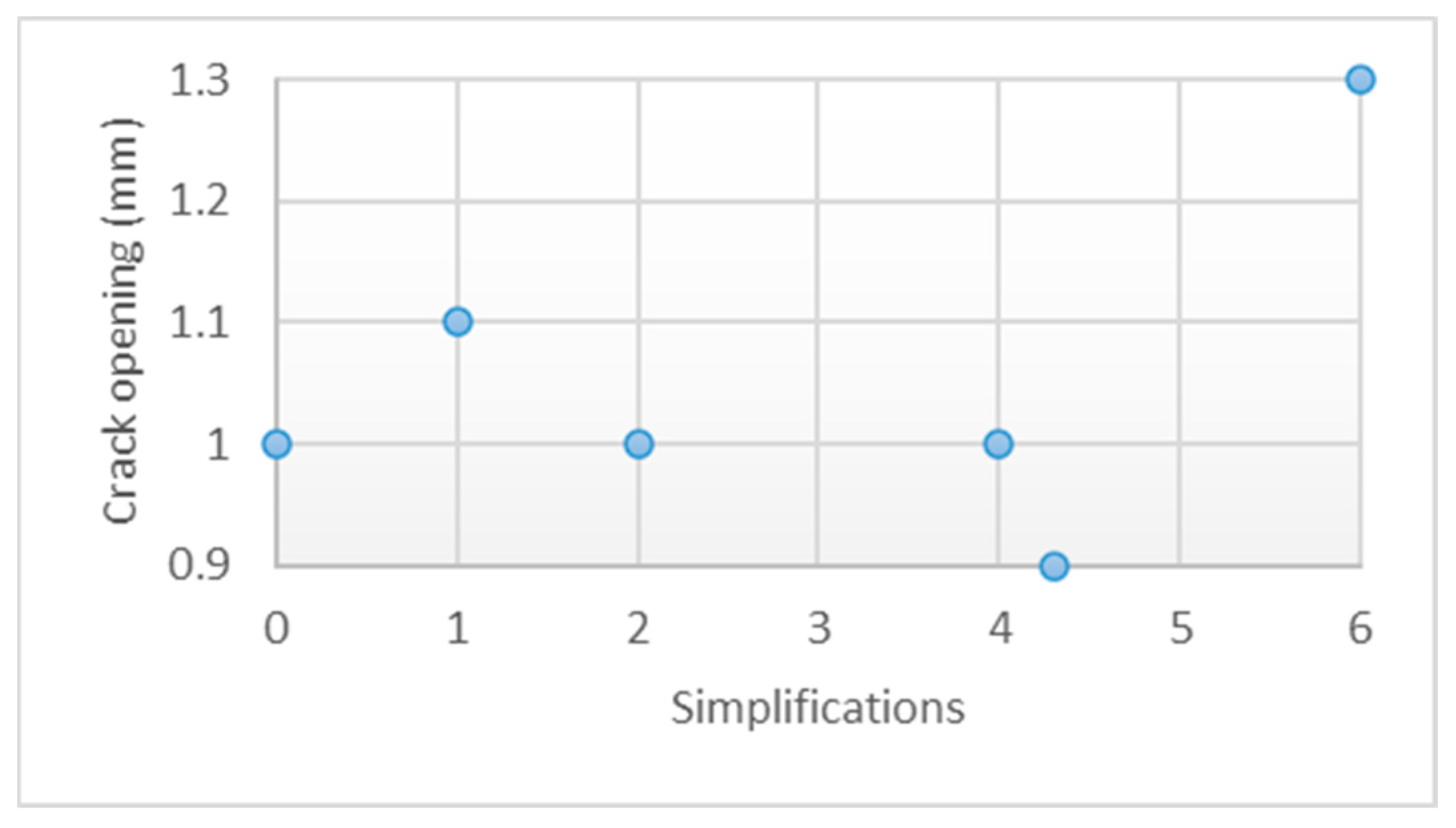
4.3.2. Crack Opening
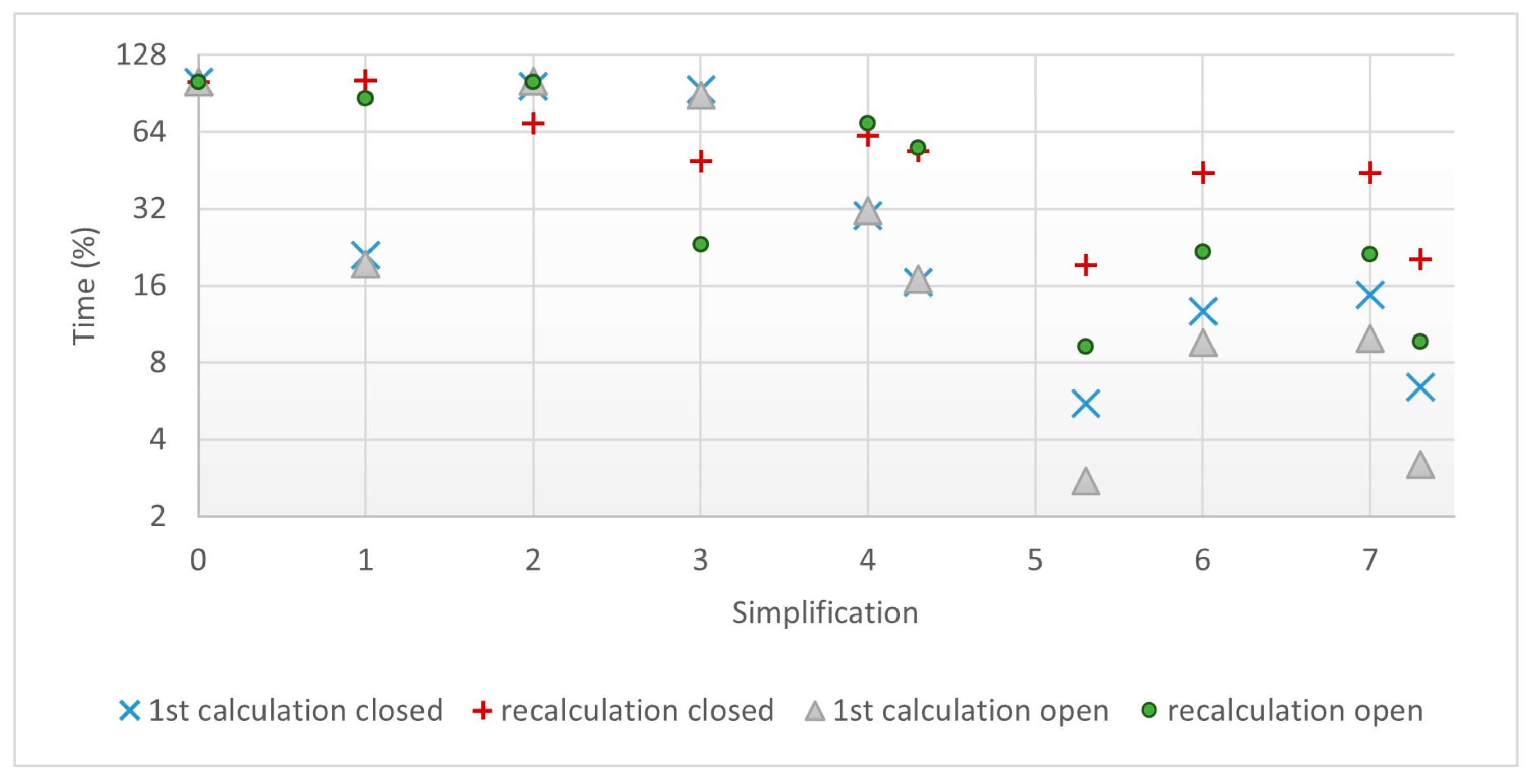
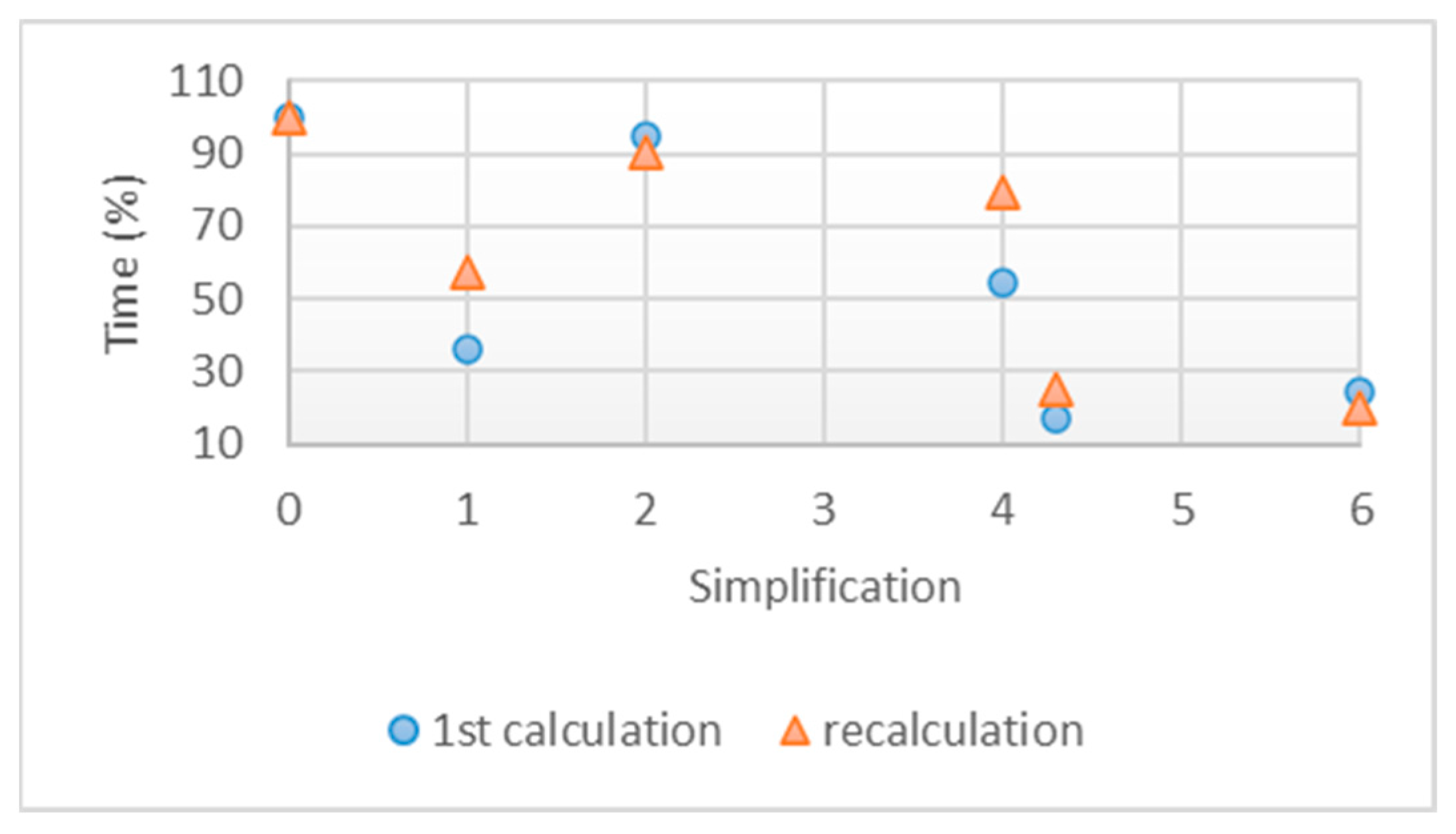
4.3.3. Calculation Time
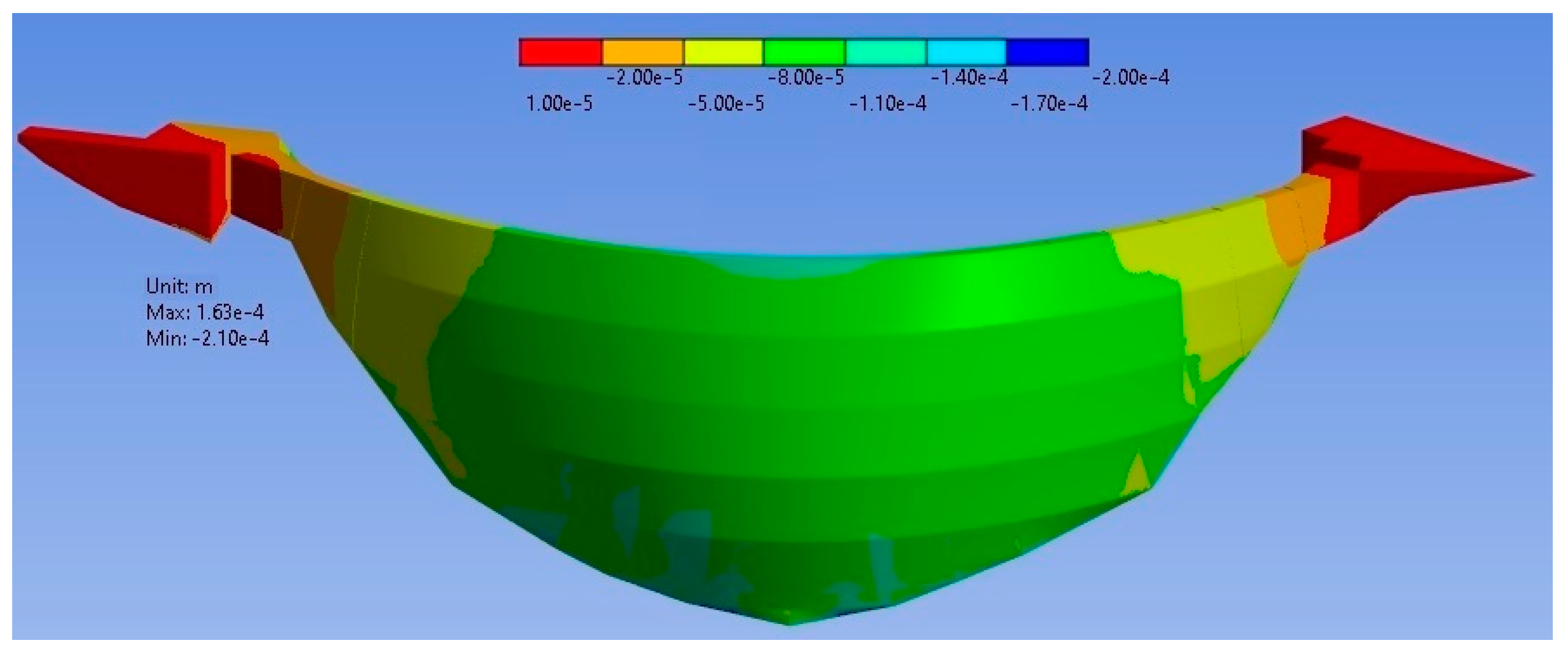
4.4. Accuracy for Different Simplifications: Crack 2
5. Conclusions
5.1. Before Hydraulic Pressure
5.2. After Hydraulic Pressure
- If a single calculation is to be performed, the recommendation is to use the complete (accurate) approach. Since the difference in calculation time between the fastest and slowest simulation is an acceptable time for a single simulation.
- If several calculations are to be performed by varying only the loads after the application of the hydraulic pressure, it is also recommended to use the complete (accurate) approach. The difference in calculation time between the fastest and the slowest simulation remains an acceptable time for a study.
- If many calculations are to be made by changing the loads prior to starting operations or the geometry (including cracks), it may be convenient to use simplification 1 or 2, depending on the availability of calculation time and the required accuracy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Li, Z. Global Sensitivity Analysis of the Static Performance of Concrete Gravity Dam from the Viewpoint of Structural Health Monitoring. Arch. Comput. Methods Eng. 2021, 28, 1611–1646. [Google Scholar] [CrossRef]
- ICOLD World Register of Dams. General Synthesis. Number of Dams by Country Members. Available online: https://www.icold-cigb.org/article/GB/world_register/general_synthesis/number-of-dams-by-country (accessed on 29 February 2024).
- ICOLD/CIGB. Constitution Statuts; ICOLD/CIGB: Paris, France, 2011. [Google Scholar]
- Hariri-Ardebili, M.A.; Saouma, V.E. Seismic Fragility Analysis of Concrete Dams: A State-of-the-Art Review. Eng. Struct. 2016, 128, 374–399. [Google Scholar] [CrossRef]
- Gharibdoust, A.; Aldemir, A.; Binici, B. Seismic Behaviour of Roller Compacted Concrete Dams under Different Base Treatments. Struct. Infrastruct. Eng. 2020, 16, 355–366. [Google Scholar] [CrossRef]
- ASCE. Report Card for America’s Infrastructure; ASCE: Reston, VA, USA, 2021. [Google Scholar]
- Hariri-Ardebili, M.A. MCS-Based Response Surface Metamodels and Optimal Design of Experiments for Gravity Dams. Struct. Infrastruct. Eng. 2018, 14, 1641–1663. [Google Scholar] [CrossRef]
- Oliveira, S.; Faria, R. Numerical Simulation of Collapse Scenarios in Reduced Scale Tests of Arch Dams. Eng. Struct. 2006, 28, 1430–1439. [Google Scholar] [CrossRef]
- Zheng, D.; Huo, Z.; Li, B. Arch-Dam Crack Deformation Monitoring Hybrid Model Based on XFEM. Sci. China Technol. Sci. 2011, 54, 2611–2617. [Google Scholar] [CrossRef]
- Wang, W.; Ding, J.; Wang, G.; Zou, L.; Chen, S. Stability Analysis of the Temperature Cracks in Xiaowan Arch Dam. Sci. China Technol. Sci. 2011, 54, 547–555. [Google Scholar] [CrossRef]
- Zhuang, D.; Ma, K.; Tang, C.; Cui, X.; Yang, G. Study on Crack Formation and Propagation in the Galleries of the Dagangshan High Arch Dam in Southwest China Based on Microseismic Monitoring and Numerical Simulation. Int. J. Rock Mech. Min. Sci. 2019, 115, 157–172. [Google Scholar] [CrossRef]
- Leitão, N.S.; Castilho, E. Chemo-Thermo-Mechanical FEA as a Support Tool for Damage Diagnostic of a Cracked Concrete Arch Dam: A Case Study. Eng 2023, 4, 1265–1289. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Wang, G.; Jin, F. Non-Linear Seismic Response of Arch Dams with Contraction Joint Opening and Joint Reinforcements. Earthq. Eng. Struct. Dyn. 2000, 29, 1547–1566. [Google Scholar] [CrossRef]
- Luo, D.; Lin, P.; Li, Q.; Zheng, D.; Liu, H. Effect of the Impounding Process on the Overall Stability of a High Arch Dam: A Case Study of the Xiluodu Dam, China. Arab. J. Geosci. 2015, 8, 9023–9041. [Google Scholar] [CrossRef]
- Khaneghahi, M.H.; Alembagheri, M.; Soltani, N. Reliability and Variance-Based Sensitivity Analysis of Arch Dams during Construction and Reservoir Impoundment. Front. Struct. Civ. Eng. 2019, 13, 526–541. [Google Scholar] [CrossRef]
- Xue, B.; Du, X.; Wang, J.; Yu, X. A Scaled Boundary Finite-Element Method with B-Differentiable Equations for 3D Frictional Contact Problems. Fractal Fract. 2022, 6, 133. [Google Scholar] [CrossRef]
- Salazar, F.; Vicente, D.J.; Irazábal, J.; de-Pouplana, I.; San Mauro, J. A Review on Thermo-Mechanical Modelling of Arch Dams During Construction and Operation: Effect of the Reference Temperature on the Stress Field. Arch. Comput. Methods Eng. 2020, 27, 1681–1707. [Google Scholar] [CrossRef]
- Ansys Inc. The Ansys Mechanical Finite Element Analysis Software, Version R2; Academic Research Mechanical: Canonsburg, PA, USA, 2022. [Google Scholar]
- Santillán, D. Mejora de Los Modelos Térmicos de Las Presas Bóveda En Explotación. Aplicación al Análisis Del Efecto Del Cambio Climático; Universidad Politécnica de Madrid: Madrid, Spain, 2014. [Google Scholar]
- Conde López, E.R.; Toledo, M.Á.; Salete Casino, E. The Centroid Method for the Calibration of a Sectorized Digital Twin of an Arch Dam. Water 2022, 14, 3051. [Google Scholar] [CrossRef]
- Santillán, D.; Salete, E.; Toledo, M.Á. A Methodology for the Assessment of the Effect of Climate Change on the Thermal-Strain–Stress Behaviour of Structures. Eng. Struct. 2015, 92, 123–141. [Google Scholar] [CrossRef]
- Concrete Masonry Handbook; Portland Cement Association: Chicago, IL, USA, 1951.
- PCI Design Handbook; Helmuth Wilden, P.E., Ed.; Precast/Prestressed Concrete Institute: Chicago, IL, USA, 1971. [Google Scholar]
- Lin, P.; Zhou, W.; Liu, H. Experimental Study on Cracking, Reinforcement, and Overall Stability of the Xiaowan Super-High Arch Dam. Rock Mech. Rock Eng. 2015, 48, 819–841. [Google Scholar] [CrossRef]
- Conde, A.; Toledo, M.Á.; Salete, E. Analyzing Cracking in Arch Dams. A Literature-Review Based Approach. Eng. Fail. Anal. 2024; in press. [Google Scholar]
- Hariri-Ardebili, M.A.; Saouma, V.E. Sensitivity and Uncertainty Quantification of the Cohesive Crack Model. Eng. Fract. Mech. 2016, 155, 18–35. [Google Scholar] [CrossRef]
- Conde López, E. Método Del Centroide Para Calibración de Modelos Númericos Tenso-Deformacionales de Presas Bóveda; Universidad Politécnica de Madrid: Madrid, Spain, 2022. [Google Scholar]










| 1990 | 1991 | 2006 | 2007 | |
|---|---|---|---|---|
| March | 8.97 | 8.90 | 7.99 | 7.88 |
| April | 8.94 | 8.68 | 11.70 | 12.08 |
| Material | Foundation | Concrete |
|---|---|---|
| Density (kg/m3) | 3000 | 2400 |
| Modulus of elasticity (N/m2) | 1.962 × 1010 | 2.452 × 1010 |
| Poisson’s ratio | 0.25 | 0.22 |
| Element Size * (m) | 1.00 | 1.02 | 1.04 | 1.05 | 1.07 | 1.10 | 1.12 | 1.15 | 1.20 | 1.235 | 1.319 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of nodes × 10−5 | 25.0 | 23.7 | 22.7 | 22.2 | 21.3 | 20.0 | 19.2 | 18.0 | 16.5 | 15.4 | 13.3 |
| Number of elements × 10−5 | 16.4 | 15.6 | 14.9 | 14.5 | 14.0 | 13.1 | 12.5 | 11.8 | 10.7 | 10.0 | 8.7 |
| Element Size * (m) | 1.35 | 1.40 | 1.55 | 1.60 | 1.65 | 1.80 | 2.40 | 3.00 | 3.60 | 4.20 | 4.80 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of nodes × 10−5 | 12.6 | 11.7 | 9.4 | 8.8 | 8.2 | 6.9 | 3.8 | 2.6 | 1.9 | 1.4 | 1.1 |
| Number of elements × 10−5 | 8.2 | 7.6 | 6.1 | 5.7 | 5.3 | 4.4 | 2.5 | 1.7 | 1.2 | 0.9 | 0.7 |
| Parameter | Low | Design | High | Units |
|---|---|---|---|---|
| Density (Concrete) | 2100 | 2400 | 2600 | kg/m3 |
| Poisson’s Ratio (Concrete) | 0.154 | 0.22 | 0.286 | - |
| Poisson’s Ratio (Soil) | 0.175 | 0.25 | 0.325 | - |
| Young’s Modulus (Concrete) | 17,164 | 24,520 | 31,876 | MPa |
| Young’s Modulus (Soil) | 13,734 | 19,620 | 25,506 | MPa |
| Max. Radial Displacement | Max. Vertical Displacement | |||
|---|---|---|---|---|
| Parameter | Low | High | Low | High |
| Density (Concrete) | −0.2% | 0.2% | −0.1% | 0.3% |
| Poisson’s Ratio (Concrete) | 0.8% | −0.9% | 1.4% | −2.1% |
| Poisson’s Ratio (Soil) | 0.3% | −0.2% | −0.5% | 0.8% |
| Young’s Modulus (Concrete) | −34.6% | 18.6% | −32.3% | 17.7% |
| Young’s Modulus (Soil) | −8.4% | 4.4% | −9.9% | 5.7% |
| Concrete (MPa) | ||||
|---|---|---|---|---|
| 24,520 | 31,876 | 39,232 | ||
| Soil (MPa) | 19,620 | 0.96454459 | 0.09823328 | 0.02290233 |
| 25,506 | 0.75630712 | 0.04730953 | 0.06258044 | |
| 31,392 | 0.63728901 | 0.02915880 | 0.10764353 | |
| 37,278 | 0.56073436 | 0.02344675 | 0.14367899 | |
| 43,164 | 0.50762649 | 0.02283556 | 0.17308593 | |
| 49,050 | 0.46889552 | 0.02448376 | 0.19845217 |
| Concrete (MPa) | ||||
|---|---|---|---|---|
| 31,873.5 | 31,876.0 | 31,884.1 | ||
| Soil (MPa) | 41,580.4 | 0.0230 | ||
| 43,164.0 | 0.0230 | 0.02283556 | 0.0230 | |
| 43,751.2 | 0.0230 |
| Cantilever 2-I | Cantilever 1-D | |||
|---|---|---|---|---|
| P0 measurement | −0.60 mm | 4.93% | −0.94 mm | 8.0% |
| P1 measurement | 0.04 mm | −0.4% | −0.52 mm | 5.6% |
| P2 measurement | 0.69 mm | −10.5% | 0.08 mm | −1.3% |
| Cantilever 2-I | Cantilever 1-D | |||
|---|---|---|---|---|
| P0 measurement | 0.04 mm | 0.4% | 1.00 mm | 13.9% |
| P1 measurement | −0.66 mm | −10.1% | 0.12 mm | 2.1% |
| P2 measurement | −1.21 mm | −27.5% | −0.80 mm | −20.1% |
| Description | Average Reduction in Calculation Time | Error in Maximum Vertical Movements | Error in Maximum Radial Movements | Recommendation for Use | |
|---|---|---|---|---|---|
| Complete approach | The most accurate approach | - | - | - | Single or low number of calculations |
| Simplification 6 | Transverse joints are closed before self-weight is applied and crack sides can pass through themselves | −83% | 4.0% 1/1.0% 2 | 6.5% 1/6.3% 2 | Large number of calculations with changes in the geometry or crack locations |
| Simplification 1 | Transverse joints are closed before self-weight is applied | −72% | 1.1% 1/8.3% 2 | 0.6% 1/2.3% 2 | Low number of calculations with changes in the geometry or crack locations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conde, A.; Salete, E.; Toledo, M.Á. Numerical Modeling of Cracked Arch Dams. Effect of Open Joints during the Construction Phase. Infrastructures 2024, 9, 48. https://doi.org/10.3390/infrastructures9030048
Conde A, Salete E, Toledo MÁ. Numerical Modeling of Cracked Arch Dams. Effect of Open Joints during the Construction Phase. Infrastructures. 2024; 9(3):48. https://doi.org/10.3390/infrastructures9030048
Chicago/Turabian StyleConde, André, Eduardo Salete, and Miguel Á. Toledo. 2024. "Numerical Modeling of Cracked Arch Dams. Effect of Open Joints during the Construction Phase" Infrastructures 9, no. 3: 48. https://doi.org/10.3390/infrastructures9030048
APA StyleConde, A., Salete, E., & Toledo, M. Á. (2024). Numerical Modeling of Cracked Arch Dams. Effect of Open Joints during the Construction Phase. Infrastructures, 9(3), 48. https://doi.org/10.3390/infrastructures9030048











