System Reliability Analysis of Concrete Arch Dams Considering Foundation Rock Wedges Movement: A Discussion on the Limit Equilibrium Method

Abstract

In this paper, a discussion on the applicability and limitations of the limit equilibrium method is presented. In this manner, the reliability of a concrete arch dam-foundation system under static loading is evaluated by considering a set of potentially moveable rock wedges in the foundation. The safety of the system is assessed utilizing a quasi-analytical method, which employs the limit equilibrium method and numerical analysis to calculate the sliding safety factors and the dam trust forces, respectively. The reliability is evaluated using the Latin Hypercube Sampling method. Random variables in the system are the friction angle, cohesion, and the Grout Curtain Efficiency Coefficient. In the end, the influence of two parametric variables of discontinuities, elastic slip and rock mass deformability modulus, on the rock wedges’ sliding safety factor is evaluated by comparing the results of the quasi-analytical method with the purely numerical method. The results show that in the case of complicated geotechnical conditions, the limit equilibrium method may not reflect real-world failure scenarios.

1. Introduction

Abutment stability analysis is one of the most critical and challenging parts of an arch dam design due to complex geotechnical conditions and high uncertainties in geometry and material properties. Therefore, a reliability analysis of the abutment’s stability is usually unavoidable [1].

Safety evaluation of the abutments’ rock wedges usually requires a lot of effort due to the 3-dimensional phenomenon and, in most cases, the irregular geometry of the critical wedge. This importance can be more complicated when, instead of a single rock wedge, a system of wedges is under study. The wedge systems naturally are created with the intersection of joint sets or bedding stratifications with other discontinuities of the abutment, e.g., significant joints, faults, and structural joints.

The main approaches for evaluation of the rock wedges’ stability can be categorized into three groups [2]: the Limit Equilibrium Method (LEM) [3], block theory [4], and numerical methods such as the Discrete Element Method (DEM), the Finite Volume Method (FVM), and the Finite Element Method (FEM) [5,6].

The LEM, or a combination of the LEM and numerical methods, is the most commonly used method among the others and has been widely discussed in the literature [7,8,9,10,11]. Londe employed the LEM for rock wedges’ stability analysis of several concrete dams like the Malpasset and Vouglans dams [3]. Jiang et al. improved the LEM equilibrium equations and used them for rock wedges’ stability evaluation of the Jinping dam [12]. However, their studies focused only on some of the shortcomings of the LEM, such as failure mode assessment and critical surface identification. Aydan and Kumsar validated the LEM using experimental results [13]. They accepted similar assumptions for the wedges evaluated with the LEM and the experimental test. Mirzabozorg et al. used the LEM–FEM for stability analysis of the Luzzone concrete arch dam [9]. In their research, the FEM has been utilized to calculate the dam thrust forces acting on the critical wedge. Some other researchers developed a probabilistic approach for stability analysis of the wedges using the LEM [10,14,15,16]. They considered the direction and friction angle of the wedge’s planes as random variables and compared the results with the deterministic one.

The LEM’s fundamental assumptions are almost standard in all the research mentioned above. These assumptions include

(1)

The model geometry consists of a simple predefined wedge constructed by two or three plane discontinuities and a plane slope face.

(2)

The wedge and the surrounding medium are rigid and impermeable.

(3)

The wedge does not rotate during the movement, a natural consequence of the former assumption.

(4)

The direction of the applied loads does not change during the wedge movement.

(5)

All external forces pass through the wedge’s center of gravity.

(6)

Shear and normal stresses are uniform on the sliding planes.

(7)

The shear forces acting on the sliding planes are parallel to the intersection of the planes.

(8)

Partial separation does not occur on the sliding planes (i.e., the plane is either in compression or tension).

(9)

The planes behave perfectly plastic under the applied loads, i.e., no elastic sliding is allowed.

(10)

There is no clear relationship between the instability of the wedge and the connected dam.

The geometry limitation is one of the most significant disadvantages of the LEM, as a natural critical wedge may have more faces coming from intersections of different discontinuities, and its geometry is usually unknown at the beginning of the analysis. Identifying the critical wedges is the subject of some published studies [17,18]. However, these studies just assess wedges’ kinematic stability, which means the effect of externally applied forces is neglected. Chan and Einstein replaced the surrounding medium with artificial supports to estimate the stress distribution on the sliding planes and the rotational movement more realistically [19]. Furthermore, Wang et al. included the shear forces’ directions in the LEM’s equations [20].

Despite the efforts in the literature to advance the LEM, the basic simple algorithm is usually applied in practice because (1) the effectiveness of the improvements in the final safety evaluation of the wedges is not well highlighted; (2) each study just has focused on a specific aspect of the traditional version of the LEM. Hence, the need for a comprehensive model that addresses multiple aspects, such as complex geometries, deformable blocks, and non-uniform external forces, remains unmet; and (3) most commercial software is still based on the traditional algorithm.

The widespread application of the traditional LEM in the safety and stability analysis of geotechnical structures, such as dam-foundation systems, highlights the need to evaluate the LEM simplifying assumptions’ impact in capturing real-world failure scenarios.

This research, first in Section 2, shows the applicability of the LEM in the reliability analysis of concrete arch dam-foundation systems subjected to rock wedge instability. For this reason, in Section 3 and Section 4, the reliability of a set of rock wedges incorporated in the left abutment of a concrete arch dam foundation is evaluated by a quasi-analytical approach that employs the finite volume numerical model of the dam-foundation system and the LEM to calculate the dam static thrust forces and the wedges sliding safety factors, respectively. The reliability analysis uses the Latin Hypercube Sampling (LHS) method, a powerful and efficient sampling method in complex systems such as dam-foundation systems. Random variables are the friction angle, cohesion, and the Grout Curtain Efficiency Coefficient (GEC).

The second part of this study, which is presented in Section 5, will prepare a comparison between the results of the quasi-analytical method and the purely numerical method, focusing on explaining the effect of the LEM fundamental assumptions on the sliding safety factor. To achieve this goal, in some of the previously generated sample points, the wedges’ safety factor will be extracted from the numerical model with the help of the Strength Reduction Factor method and for different values of discontinuities’ elastic slip and rock mass deformability modulus. Then, these results will be compared and discussed with the corresponding ones once they are calculated using the quasi-analytical method.

2. Reliability Analysis of a Dam-Wedge System Using the LEM–FVM

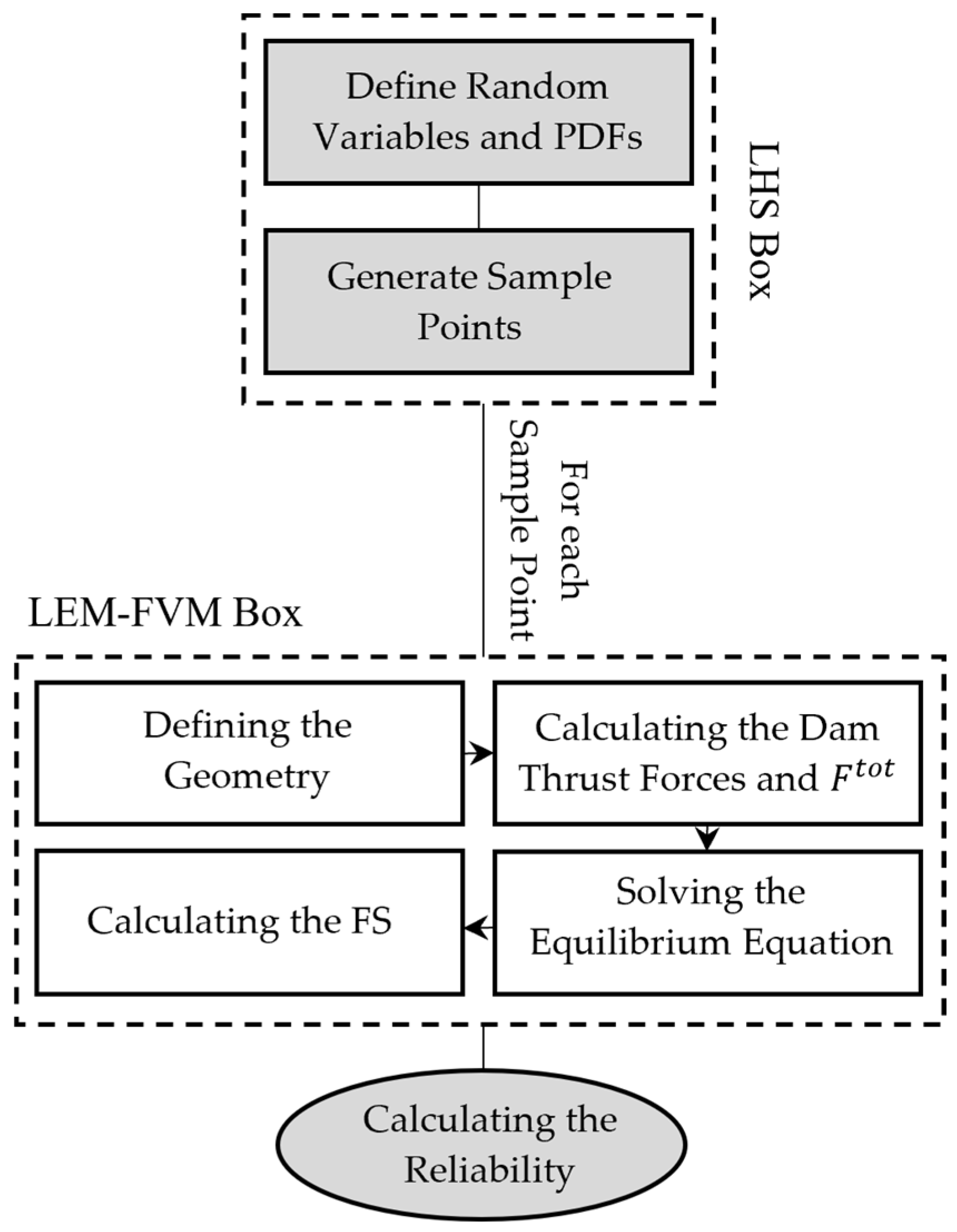
Dam-foundation structures are complex systems, especially under heterogeneous geological conditions. To be able to consider the uncertainties in a foundation with several discontinuities constructing critical wedges, a reliability analysis using a quasi-analytical method of the LEM–FVM may be used. The procedure is illustrated in Figure 1 and is explained in the following.

2.1. The LHS Box

According to Figure 1, the first stage in the reliability analysis of a dam-foundation system is the LHS Box, where, firstly, the proper random variables, as well as their Probability Density Functions (PDF), are chosen, and secondly, the random sample points are generated.

Based on the LEM necessary input parameters, three different random variables have been defined in this study: the friction angle and cohesion of the foundation’s wedges discontinuities and the Grout Curtain Efficiency Coefficient (GEC). GEC in concrete dam projects may significantly vary by time and location. Moreover, the intersection of the grout curtain with the foundation discontinuities can affect the GEC. This variable for the planes located downstream of the grout curtain is defined as:

$$GEC=1-{\displaystyle \frac{U_{real}}{U_{max}}}$$

(1)

where U_real and U_max are the uplift pressure of the plane with and without considering the grout curtain, respectively. In this definition, GEC varies between 0 and 1, where 0 implies full uplift pressure acting on the plane while 1 indicates a dry plane.

Some researchers have shown that the normal distribution is the most appropriate PDF for geotechnical parameters resulting from various random effects [21,22,23,24,25]. In the case when there is a lack of a specific probabilistic study for the dam site, normal distributions with the mean values extracted from the dam site reports can be used for the random variables.

Furthermore, some investigations revealed that the coefficients of variation (COV) for the friction angle and cohesion usually change in a narrow band of [10%,15%] and [20%,25%], respectively [10,14,26,27,28,29]. Therefore, in this article, COVs of 15% and 25% are considered for the friction angle and cohesion of the discontinuity, respectively. In the case of GEC, which usually has more uncertainties than the other variables, a slightly high value of the COV is chosen so that the sample points capture a wide range of dry to saturated planes (i.e., COV = 50%).

For complex dam-foundation systems, the Latin Hypercube Sampling (LHS) method has been proven to be a powerful and efficient sampling method used widely in many projects [22,23,24]. Soltani et al. (2019) studied the effect of thermal loading on the probabilistic risk of arch dams’ failure. They employed three different probabilistic methods for their work, which include (1) the first-order second-moment method (FOSM), (2) the first-order reliability method (FORM), and (3) Monte-Carlo simulation with Latin Hypercube Sampling (MC-LHS). They concluded that in the reliability analysis of concrete arch dams, the MC-LHS method is the more reliable and precise method and that more straightforward methods may underestimate the failure probability [30].

LHS uses a stratified sampling technique for generating near-random samples of input variables, which ensures that the sample points cover the entire range of the input variable [26,27]. Unfortunately, there is no straight formulation to calculate the optimum sample size in the LHS method [31]. Soltani et al. (2019) used a trial-and-error technique to determine an efficient sample size for the reliability analysis of a dam-foundation system with 30 different random variables [30]. They concluded that 1000 realizations of the variables are fair enough to achieve a certain confidence level. Khaneghahi et al. (2019) used the same value for reliability analysis of the Dez concrete arch dam [32]. The random variables in their research included material strength parameters of the foundation, dam body concrete, and structural joints. Therefore, in this article, 1000 realizations of the variables are considered relatively high and reach a reasonable degree of accuracy.

It is worth mentioning that the sample points generated by LHS are primarily based on uncorrelated variables. However, the strong correlation between the friction angle and the cohesion cannot be neglected. In this case, Rank Correlation Sampling (RCS) can be implemented to transform uncorrelated samples into correlated ones. In this method, the samples’ sorting changes to achieve the desired correlation (value of −0.5 between the friction angle of cohesion. Refer to Iman and Conover (1982) for more information on this method [33].

2.2. The LEM–FVM Box

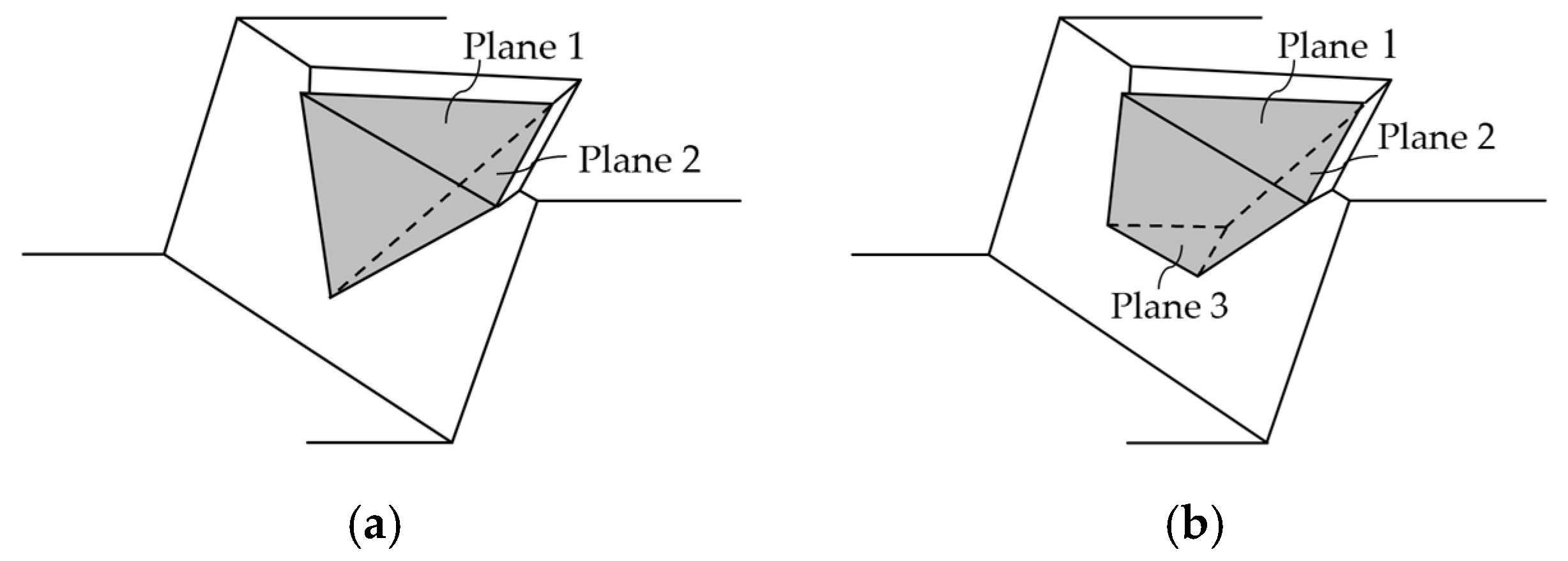
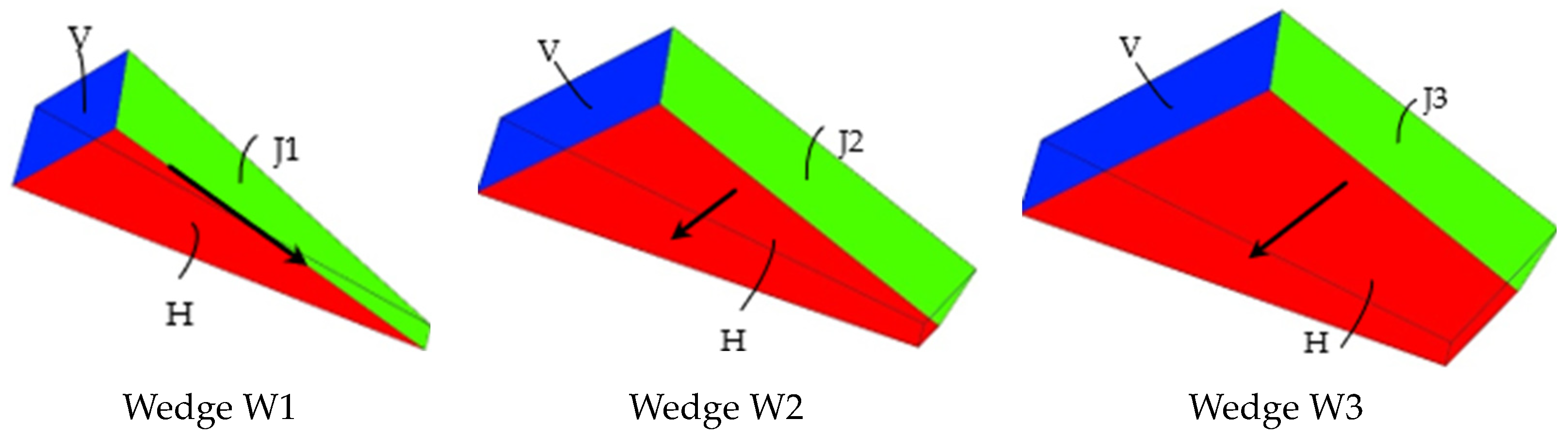
The second stage in the system’s reliability analysis is the rock wedges’ stability analysis. In this study, the quasi-analytical method of the LEM–FVM is used. The term quasi refers to using the FVM to calculate the dam thrust forces acting on the analyzed wedge. The rest of the formulas are the pure analytical formulations of the LEM. According to the LEM–FVM box in Figure 1, firstly, the critical wedges are recognized and equated to one of the simple wedges shown in Figure 2 by defining the equivalent direction and area for planes 1, 2, and, if needed, plane 3. Critical wedge identification can be achieved through engineering judgment or, for more complex geometries, by employing advanced methods, such as those in references [4,17,18], based on a kinematic approach. In the second step, the applied loads and load cases are defined. In this article, the loading includes the wedge self-weight, the dam body thrust forces, and uplift pressure on the wedge’s planes:

$$F_i^{tot}=W_i^R+F_i^{Tr}+F_i^U,\hspace{1em}\hspace{1em}i=x,y,\mathrm{and}z$$

(2)

where $F_i^{tot},W_i^R,F_i^{Tr}$, and $F_i^U$ are the total forces acting on the wedge, the weight of the rock wedge, the dam thrust force, and the uplift pressure of the planes in i direction, respectively. The wedge self-weight is calculated simply by multiplying the rock mass density by the wedge volume. The dam thrust forces are obtained from the dam’s numerical (FV) model. In this way, the numerical model of the dam and foundation is analyzed under the self-weight of the dam and hydrostatic pressure acting on the dam body, and then, the nodal forces at the dam’s base in the location of the corresponding wedge are extracted. Details regarding the model geometry, material properties, loading, and boundary conditions are provided in Section 3.

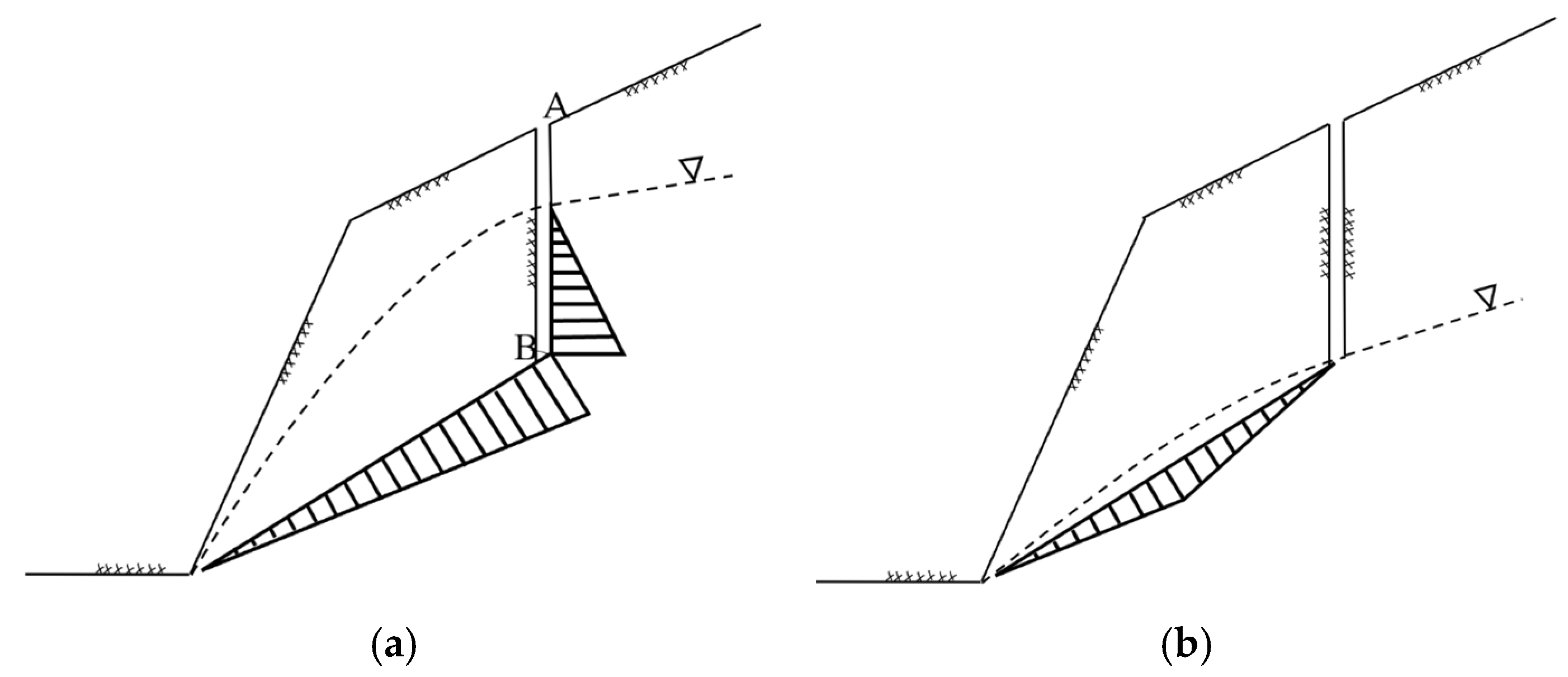
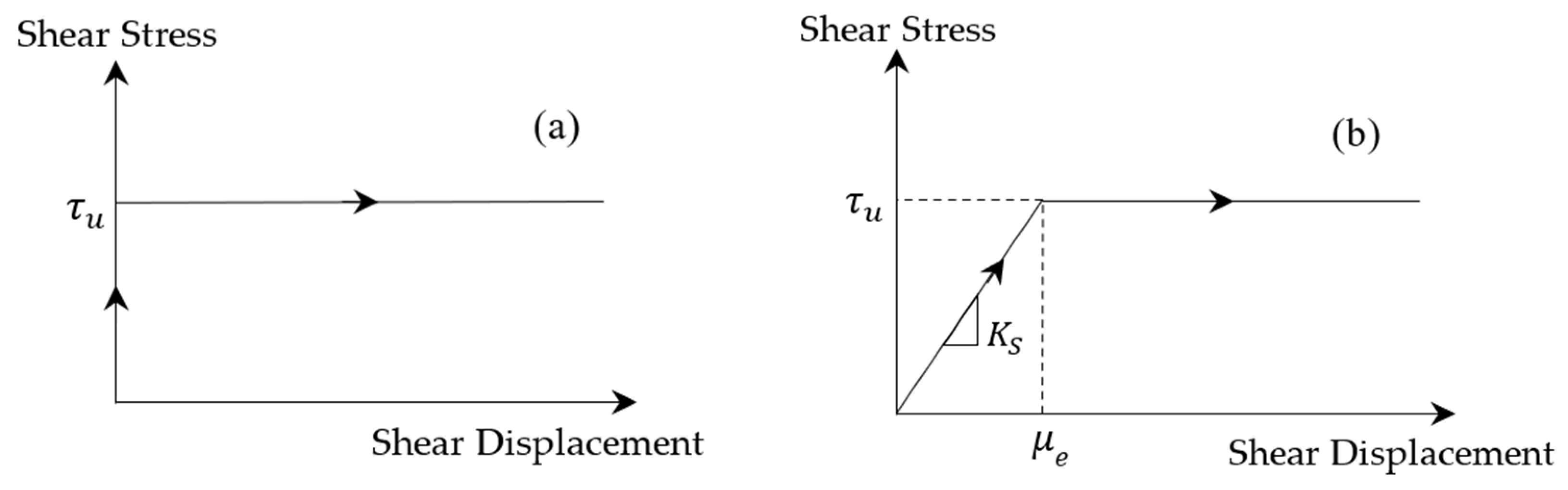
In the LEM, uplift pressure distribution on the wedge’s planes may be considered as either type 1 (Figure 3a) or type 2 (Figure 3b) [34]. Figure 3a shows the condition where all planes are wet while Figure 3b assumes one of them is completely drained. In the condition type 1 (Figure 3a), the water surface elevation moves between points A and B according to the GEC at each sample point.

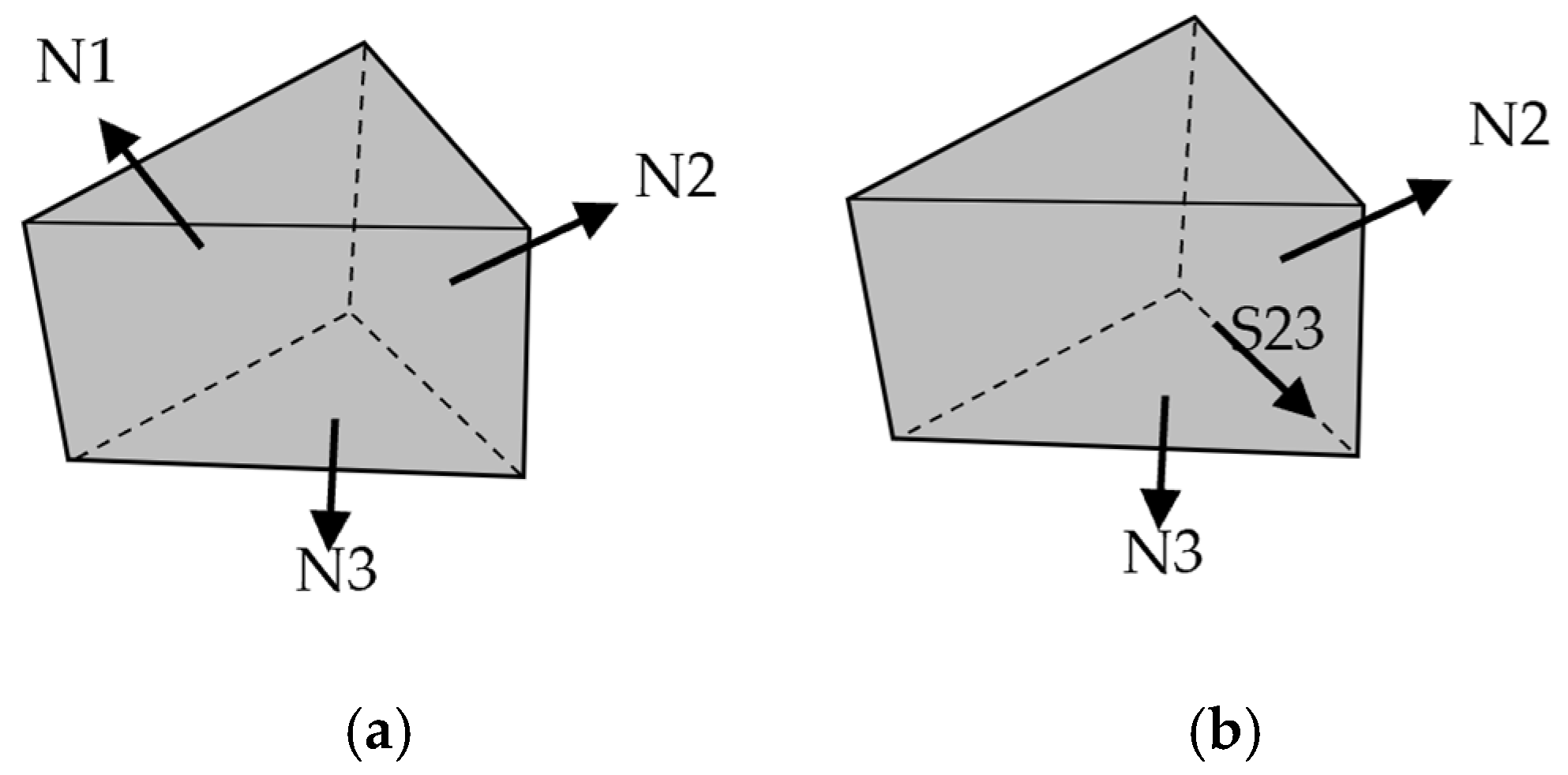
The next step is calculating the wedge’s sliding safety factor by solving the equilibrium equations. For the rock wedge of Figure 2b, the normal reaction forces of planes 1, 2, and 3 ($N_1, N_2$, and $N_3$ in Figure 4a) can be calculated according to static equilibrium. Positive normal reaction force implies tensile force, i.e., the plane is open, and sliding cannot occur. Depending on which plane is open, different sliding modes may happen [3]:

Mode 1: No plane is open ($N_1\le 0, N_2\le 0, and N_3\le 0$), which means the wedge is perfectly stable.

Mode 2: Just plane 1 is open ($N_1\ge 0 , N_2\le 0, and N_3\le 0$), so the wedge may slide along the intersection of planes 2 and 3. In this step, shear force along this intersection ($S_{23}$) is calculated while plane 1 is ignored (Figure 4b). The wedge sliding factor of safety is:

$$FS={\displaystyle \frac{S_{23}}{{(N}_2\tan \left({\phi }_2\right)+c_2{A}_2)+{(N}_3\tan \left({\phi }_3\right)+c_3{A}_3)}}$$

(3)

where ${\phi }_j$, $c_j,$ and $A_j$ are the friction angle, cohesion, and area of the plane j, j = 2 and 3.

Mode 3: Just plane 2 is open ($N_2\ge 0 , N_1\le 0, and N_3\le 0$). Like the former mode, the wedge may slide along the intersection of planes 1 and 3, and the wedge sliding factor of safety can be computed similarly to the Equation (3).

Mode 4: Just plane 3 is open ($N_3\ge 0 , N_1\le 0, and N_2\le 0$), which is similar to modes 2 and 3.

Mode 5: Planes 1 and 2 are open ($N_1\ge 0 , N_2\ge 0, and N_3\le 0$), so the wedge may slide along plane 3. In this state, the shear force on plane 3 ($S_3$) is calculated while planes 1 and 2 are ignored. In this case, the wedge sliding factor of safety can be driven by:

$$FS={\displaystyle \frac{S_3}{N_3\tan \left({\phi }_3\right)+c_3{A}_3}}$$

(4)

Mode 6: Planes 1 and 3 are open ($N_1\ge 0,N_3\ge 0, and N_2\le 0$) and sliding mode is like mode 5.

Mode 7: Planes 2 and 3 are open ($N_2\ge 0,N_3\ge 0, and N_3\le 0$). This is equivalent to modes 5 and 6.

Mode 8: All of the planes are open ($N_2\ge 0,N_3\ge 0, and N_3\ge 0$). In this case, the wedge is unstable.

In the studies concerning the stability evaluation of a set of critical rock wedges, such as in the case of repeated rock wedges created by the joint sets, failure of the wedge system may occur when at least one of the sub-wedges fails:

$${FS}_{sys}=\min \left\{{FS}_1,{FS}_2,\dots , {FS}_n\right\}$$

(5)

where ${FS}_{sys}$ $and {FS}_{i}i=\mathrm{1,2},\dots ,n,$ are sliding safety factors of the wedge system and wedge i, respectively.

2.3. The Reliability Calculation

To calculate the reliability in the methods relying on the sample points, s like the case of this article, firstly, for each sample point, the failure is checked based on the limit-state function given by:

g(X) = f(X) − ϵ ≥ 0

(6)

where f(X) is the response parameter for random variable vector X, and ϵ is the acceptable threshold value. In this paper, we are using the sliding safety factors as the response parameter, and the results are presented for different values of the threshold ϵ $=[1,\infty )$. The exceedance probability of failure is defined as:

$$P_f={\displaystyle \frac{Number of failed samples}{Total number of the samples}}$$

(7)

Finally, the reliability of the system can be expressed as:

$$R=1-P_f$$

(8)

3. Case Study

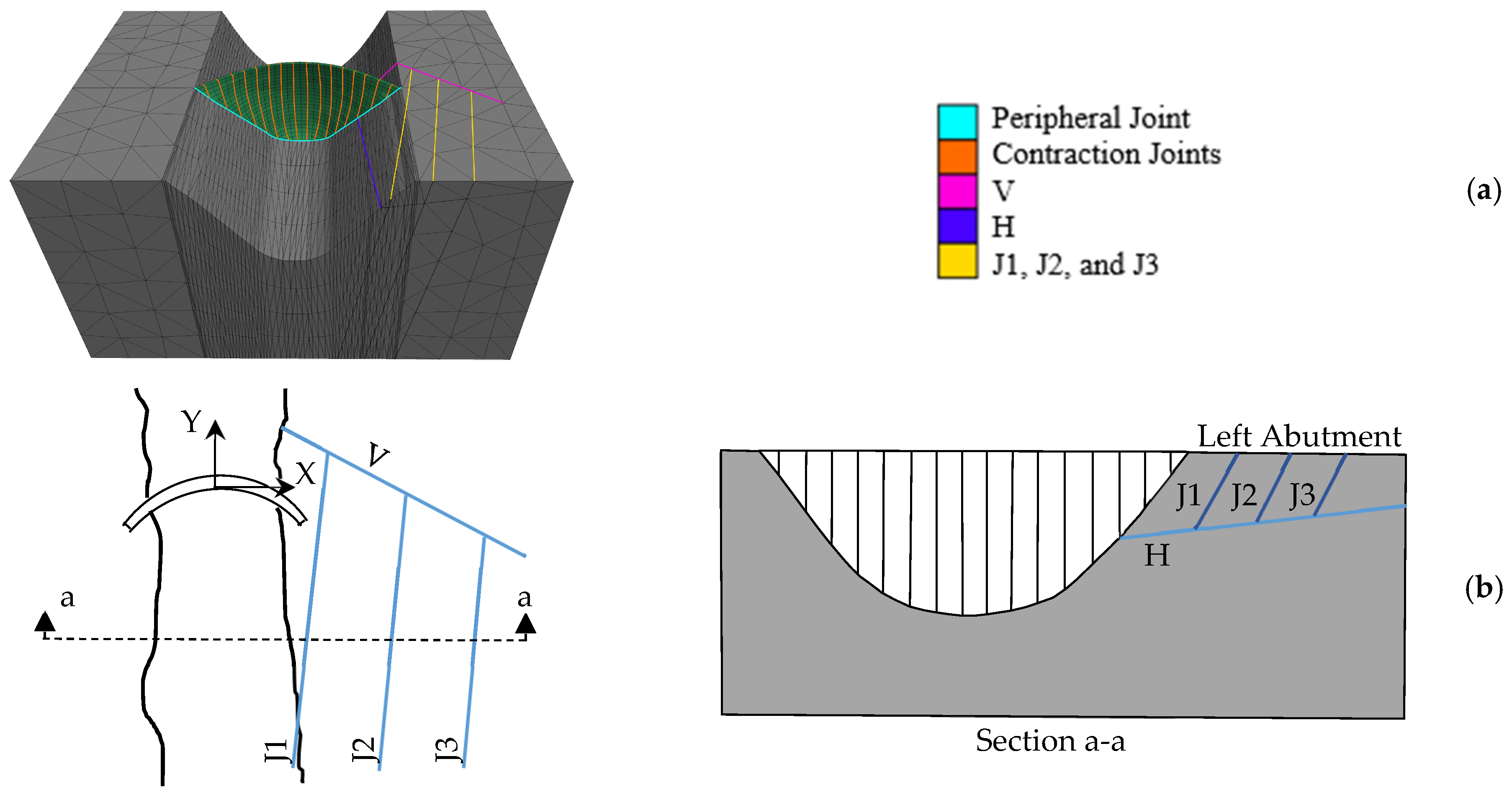
The case study is considered a typical double-curvature concrete arch dam with a height of 150 m and a crest length of 350 m (Figure 5a). The numerical model was created in FLAC3D v6.00, a software based on explicit finite volume formulation [35]. The model contains a set of potentially movable rock wedges, each constructed by three discontinuities (Figure 5b). Characteristics of the foundation discontinuities and the wedges are tabulated in

Table 1. Characteristics of the foundation discontinuities.

Discontinuity	Dip (°)	Dip Direction (°)	Friction Angle (°)	Cohesion (MPa)
V	90	40	35	0.2
H	10	300	20	0.05
J1	80	280	35	0.2
J2	80	280	35	0.2
J3	80	280	35	0.2

and

Table 2. Characteristics of the critical rock wedges in the foundation.

Wedge	Plane 1	Plane 2	Plane 3	Wedge Volume (m3)
W1	V	H	J1	290,421
W2	V	H	J2	574,389
W3	V	H	J3	1,161,900

, respectively. As mentioned before, the random variables in this study are the friction angle and cohesion of the wedge’s planes and GEC to account for the most uncertain parameters in the methodology. The statistical parameters for the chosen case study are listed in

Table 3. Statistical characteristics of the random variables.

Parameter	Description	Probability Function	Statistical Parameter
C_V	Cohesion of plane V	Normal	$mean=0.2 \mathrm{M}\mathrm{p}\mathrm{a}$ $COV=25\mathrm{\%}$
C_J1,2,3	Cohesion of planes J1, J2, and J3	Normal	$mean=0.2 \mathrm{M}\mathrm{p}\mathrm{a}$ $COV=25\mathrm{\%}$
C_H	Cohesion of plane H	Normal	$mean=0.05 \mathrm{M}\mathrm{p}\mathrm{a}$ $COV=25\mathrm{\%}$
$\mathsf{\phi }\_\mathrm{V}$	Friction angle of plane V	Normal	$mean=35°$ $COV=20\mathrm{\%}$
$\mathsf{\phi }\_\mathrm{J}\mathrm{1,2},3$	Friction angle of planes J1, J2, and J3	Normal	$mean=35°$ $COV=20\mathrm{\%}$
$\mathsf{\phi }\_\mathrm{H}$	Friction angle of plane H	Normal	$mean=20°$ $COV=20\mathrm{\%}$
Ω	Grout Curtain Efficiency Coefficient	Normal	$mean=0.7$ $COV=50\mathrm{\%}$

.

The material parameters used for the numerical model are according to

Table 4. Material properties of the rock mass, dam body concrete, and model discontinuities.

Parameter	Rock Mass	Mass Concrete	Dam Discontinuities		Foundation Discontinuities
			Contraction	Peripheral	V	H	J1	J2	J3
Unit Weight (Kg/m3)	2570	2420	-	-	-	-	-	-	-
Elastic Modulus (GPa)	10	27.8	-	-	-	-	-	-	-
Poison Ratio	0.2	0.22	-	-	-	-	-	-	-
Normal Stiffness (GPa/m)	-	-	40	40	324	346.4	324	324	324
Shear Stiffness (GPa/m)	-	-	8	8	135	144.3	135	144.3	144.3
Friction Angle (°)	-	-	40	56	35	20	35	35	35
Cohesion (MPa)	-	-	0	0	0.2	0.05	0.2	0.2	0.2
Tensile Strength (MPa)	-	-	0	0.5	0	0	0	0	0

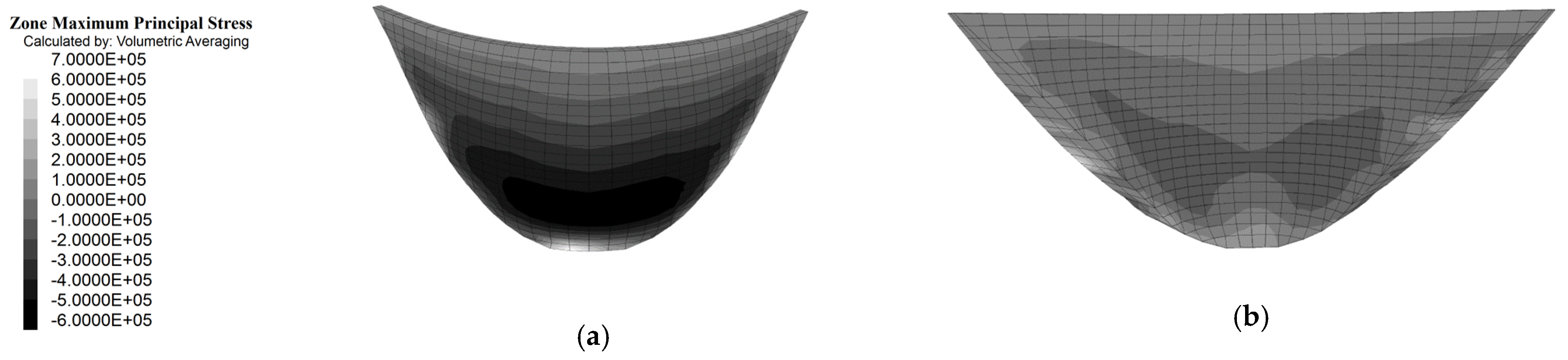
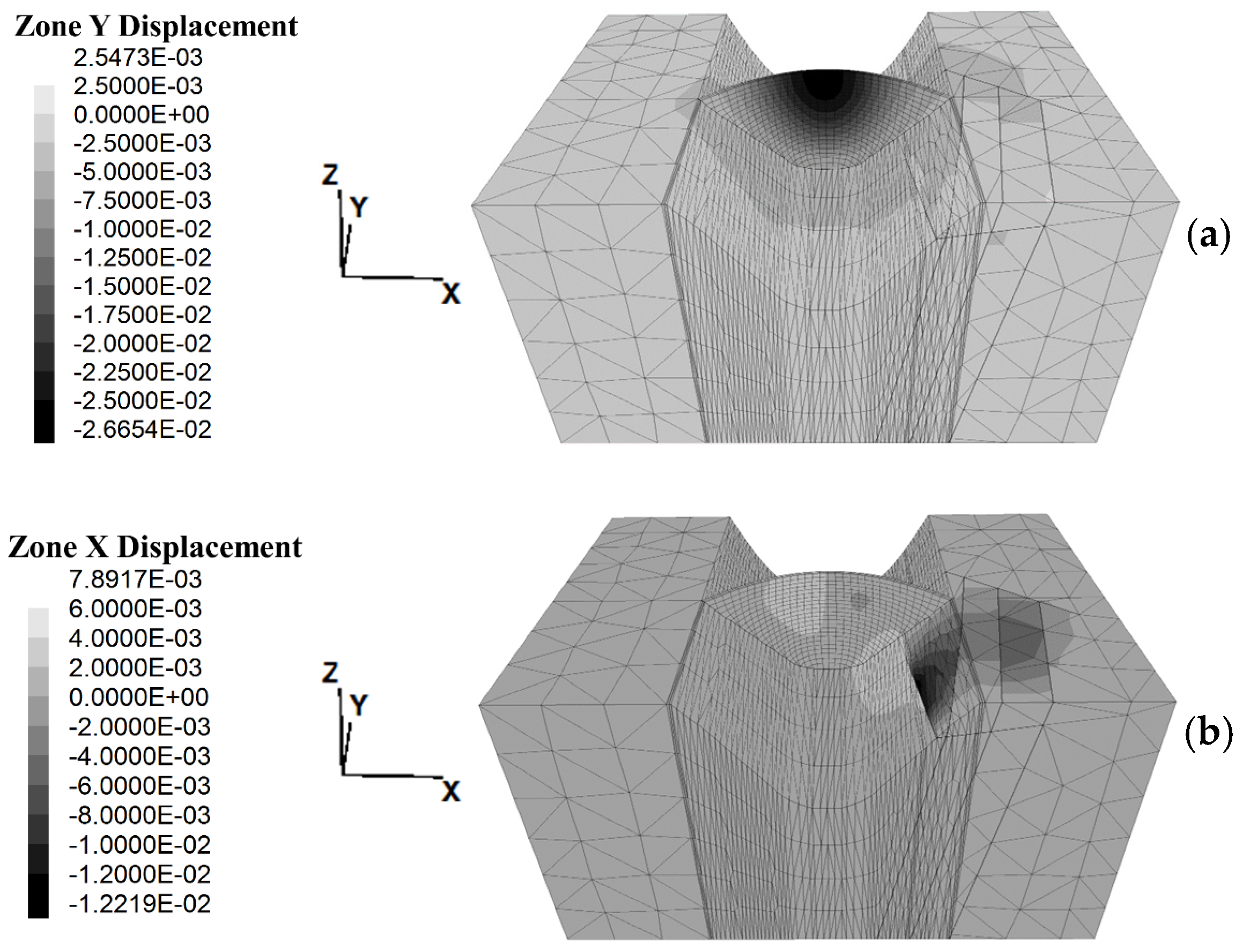
. The loading in the numerical model includes the dam and foundation self-weight and hydrostatic pressure at the maximum water level. Figure 6, Figure 7 and Figure 8 illustrate the contours of dam maximum principal stresses, the dam-foundation displacements, and the wedges displacements for section a-a (refer to Figure 5), respectively. As shown in Figure 6, the maximum principal tensile stress is located in the upstream face with the value of 0.7 Mpa. 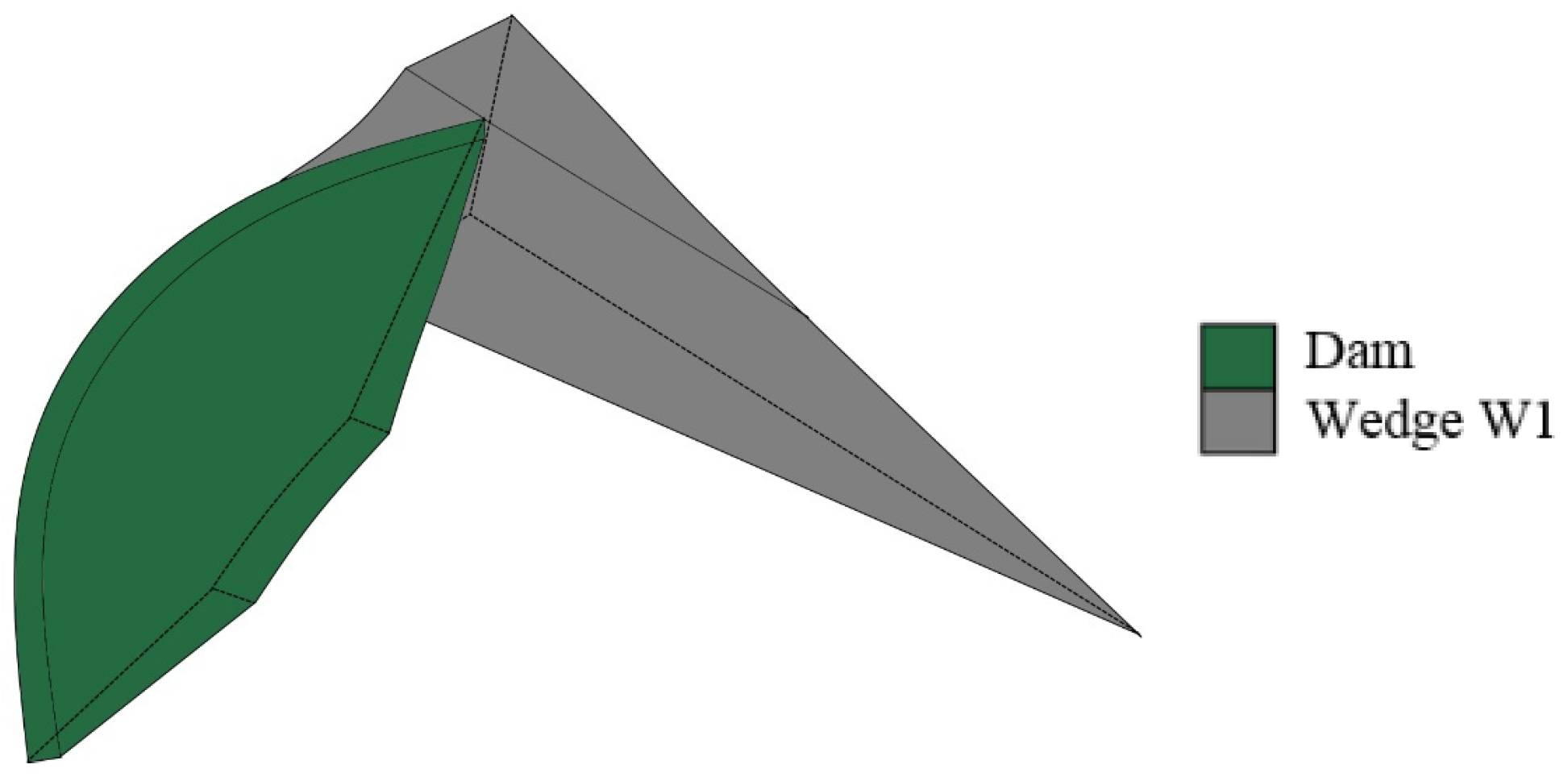According to Figure 7, the maximum displacement of the dam body in the river direction is 27 mm. Furthermore, the maximum rock mass displacement occurs in the location of the wedge W1 and is −8 mm and −12 mm in the Y and X direction, respectively. The 3-dimensional view of this wedge is depicted in Figure 9.

The focus of this study is on wedge W1, as the primary numerical analysis has shown a notable sliding feature in its location (Figure 8). For this wedge, the reliability will be calculated using three different assumptions of the uplift pressure on this wedge planes: model (1) dry planes, model (2) uplift pressure type 1 (refer to Figure 3), and model (3) uplift pressure type 2. Then, in model 4, the stability of a system of wedges with the sub-wedges of W1, W2, and W3 is regarded to show the importance of wedges W2 and W3 in the overall safety of the system. As described before, in this situation, system failure occurs when at least one of the sub-wedges fails. The four models are listed in

Table 5. Models defined for the reliability analysis of the rock wedges.

Model Name	Wedge	Applied Loads
		${\mathit{W}}^{\mathit{R}}$	${\mathit{F}}^{\mathit{T}\mathit{r}}$	${\mathit{F}}^{\mathit{U}}$
Model 1	W1	√	√	-
Model 2	W1	√	√	Type 1
Model 3	W1	√	√	Type 2
Model 4	W1, W2 and W3	√	√	-

.

4. Reliability Analysis Results

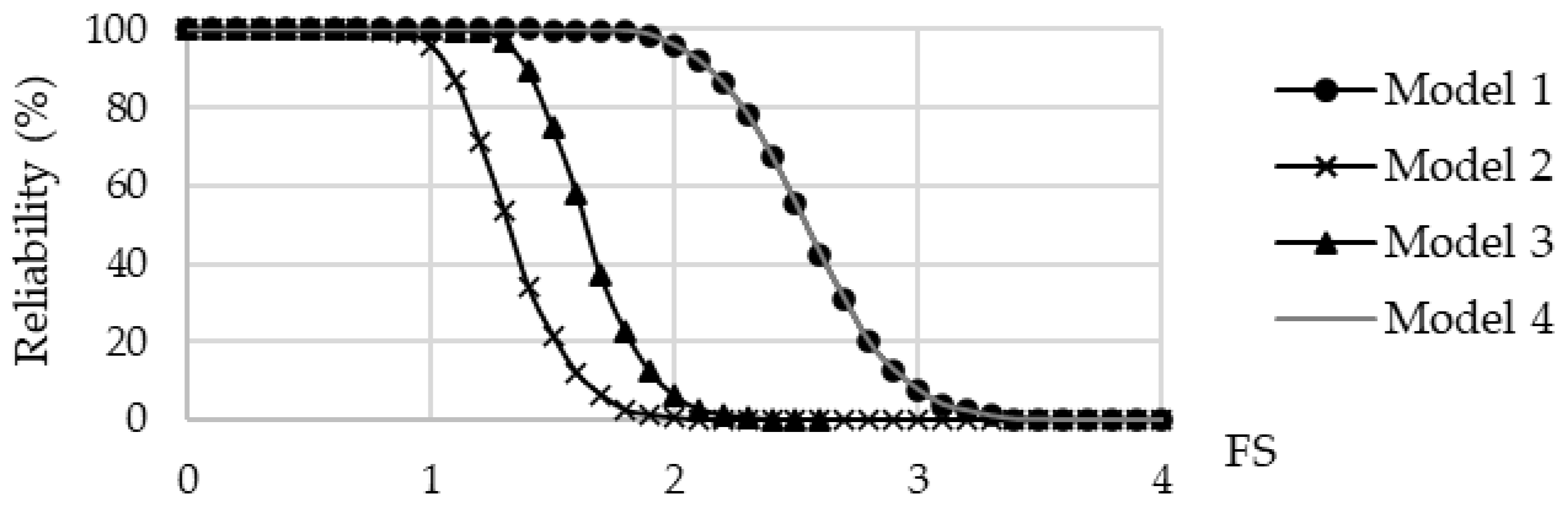
Figure 10 illustrates the reliability curves versus sliding safety factors for models 1 to 4. According to this figure, the reliability decreases with including uplift pressure to the analysis (models 2 and 3). The reliability to FS = 1.5 for the models with dry foundation (models 1 and 4) is 100%, while this value for models 2 and 3 is 22% and 75%, respectively. It can be seen that even with changing the assumption of uplift pressure distribution, the reliability can change significantly (models 2 and 3). This shows the importance of groundwater site investigations in reducing the uncertainties surrounding the foundation pore pressure.

According to the figure, the reliability curves for models 1 and 4 are identical. This implies that the critical wedge in the system of wedges (model 4) is the same as that analyzed in model 1, i.e., wedge W1. This answer is rational as the wedge W1 is the lowest of the wedges in the series-connected wedges in the dam’s abutment, and any instability in the abutment probably starts with the instability of this wedge. Figure 11 shows the critical sliding modes for wedges W1, W2, and W3 in model 4. The critical sliding mode for wedge W1 is sliding across the intersection of planes H and J1, while that for wedges W2 and W3 is sliding on plane H.

5. Comparison between the Results of the Quasi-Analytical and the Purely Numerical Method

In this section, a comparison between the results of the quasi-analytical method and the purely numerical method is prepared. This comparison aims to determine the effect of the two fundamental assumptions of the LEM, the rigidity of the wedge and the perfectly plastic behavior of the wedge’s planes, on the sliding safety factor. In this manner, the subsequent procedure will be followed:

• In some of the sample points previously generated and for models 1 to 4, the wedge’s safety factors will be extracted from the FVM and compared with the ones calculated using the quasi-analytical method (the subject of Section 4).

The safety factor in the FVM will be calculated using the Strength Reduction Factor method (SRF). In this method, the shear strength parameters of the rock wedges’ discontinuities progressively reduce to bring the wedges’ discontinuities to a state of plastic (irreversible) sliding [36]:

$${\phi }_{cr}={tan}^{-1}\left({\displaystyle \frac{tan\phi }{SF}}\right)$$

(9)

$$C_{cr}=\left({\displaystyle \frac{C}{SF}}\right)$$

(10)

where ${\phi }_{cr}$ and $C_{cr}$ are the critical friction angle and cohesion of the discontinuities, respectively.

For a fair comparison, the foundation will be regarded as rigid rock mass, and its discontinuities elastic slips will be considered a small value of 3 mm to simulate the perfectly plastic behavior of the planes. In a numerical model followed by the Mohr-Coulomb shear strength criterion for the discontinuities, the elastic slip controls the shear stiffness of the wedge’s planes by:

$$K_s={\displaystyle \frac{{\tau }_u}{{\mu }_e}}={\displaystyle \frac{{\sigma }_{n }tan\phi +C}{{\mu }_e}}$$

(11)

where ${\mu }_s$, ${\tau }_u$, and ${\sigma }_n$ are the discontinuity’s elastic slip, shear strength, and normal stress, respectively.

As mentioned above, the comparison is performed on some of the sample points to reduce the number of numerical model runs. The selected sample points are those with the minimum sliding safety factor in Section 4, i.e., by the quasi-analytical method. The minimum safety factor for models 1 to 4 occurred in sample 535 with values of 1.41, 0.73, 0.9, and 1.41, respectively.

II.

The FVM will be run for the same sample point (sample point 535) and the models 1 to 4; however, this time for various discontinuities’ elastic slip and rock mass deformability modulus values. This aims to show how the assumptions of the rigid wedge and perfectly plastic sliding planes affect the results.

Elastic slip is a characteristic parameter of discontinuities, and in natural sites, it may vary from several millimeters to several centimeters according to the discontinuity’s flexibility. Therefore, this study considers this parameter in the [3–15] mm interval. It is worth mentioning that, in numerical solutions, the smaller elastic slip is usually avoided to achieve better convergence. For the deformability modulus of the rock mass (Er), two values of 5 GPa and 15 Gpa, frequently encountered in concrete dam sites, will be chosen.

5.1. Comparison of the Results

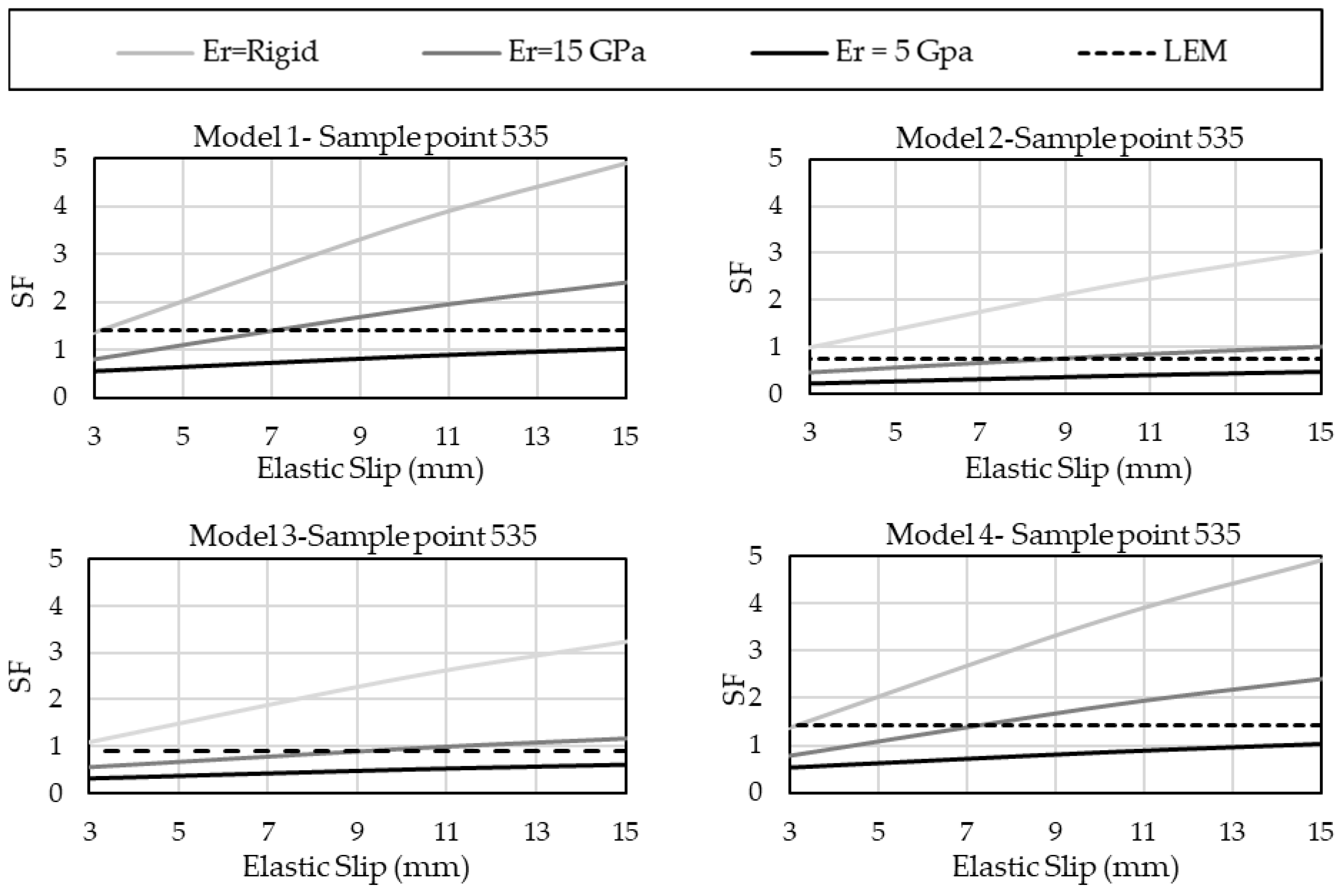
Figure 12 shows the safety factors obtained from the FVM for different values of elastic slip and foundation deformability modulus. In this figure, the dashed lines are the corresponding safety factor calculated by the quasi-analytical method, which we simply call the LEM. As seen from this figure, in all the models (models 1 to 4), the foundation safety factor increases with increased rock mass deformability modulus and elastic slip.

According to the figure, for the rigid foundation and elastic slip of 3 mm, the sliding safety factors of the two methods are remarkably similar. This indicates that accepting two assumptions of the rigid wedge and the rigid-perfectly plastic behavior of the sliding planes leads to an equal safety factor in both the LEM and numerical methods. However, the results for the rest of the cases are significantly different.

Compared to the FVM, although the LEM leads to more conservative results for the strong rock mass, it overestimates the SFs when a soft rock is under study. The reason is that in the LEM, the shear and normal stresses on the sliding planes are assumed uniform, and as a result, partial separation does not occur. The partial separation that mostly happens in soft rock masses may trigger sliding and cause fewer safety factors. Regarding the medium-strength rock masses (in this study, Er = 15 Gpa), the comparison remarkably depends on the elastic slip or, in other words, the shear stiffness of the discontinuities; the SFs calculated by the LEM for flexible discontinuities (high elastic slip) are less than the corresponding values derived from the FVM, while for the brittle discontinuities (elastic slip < 7 mm) is just the opposite.

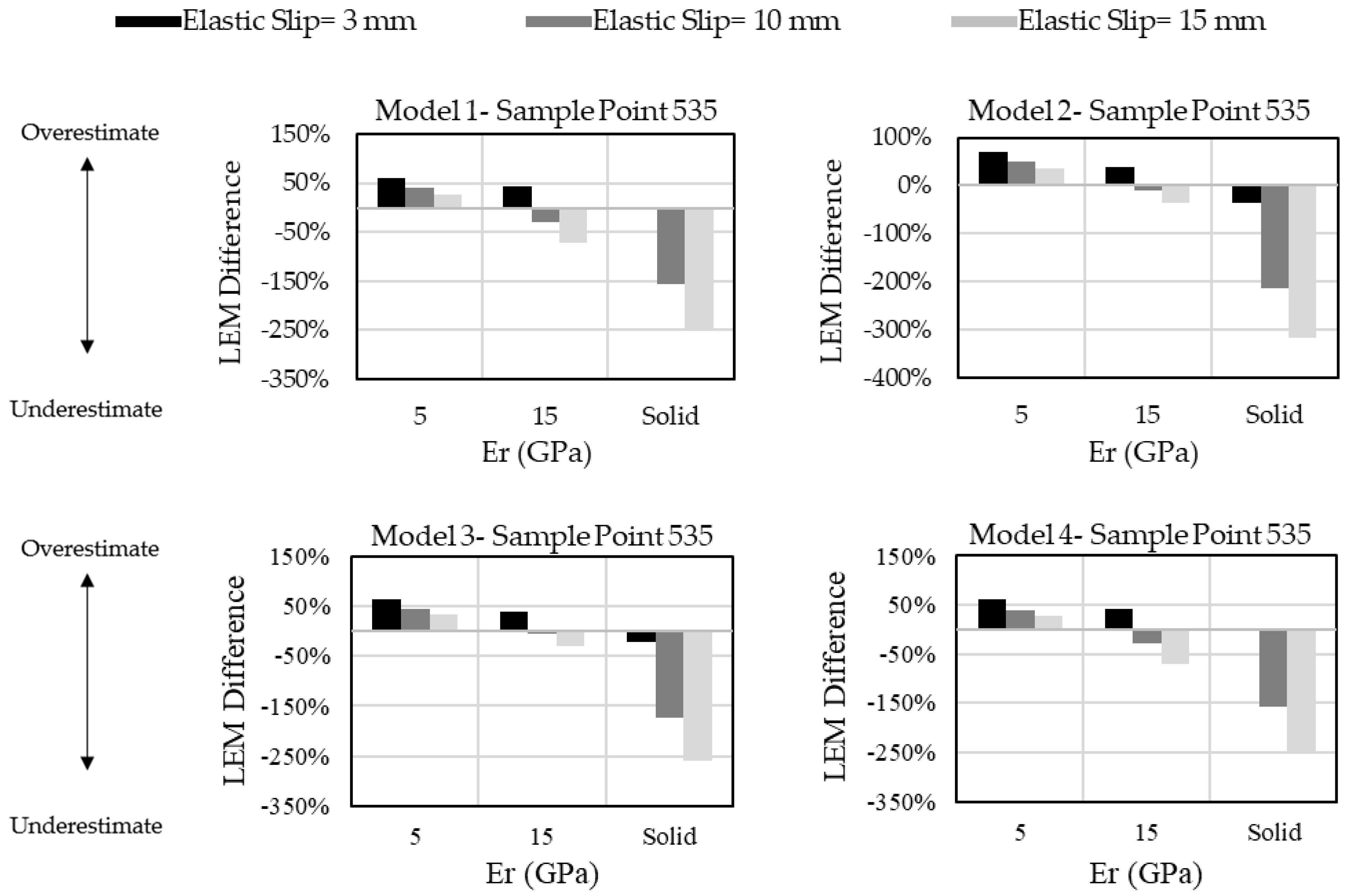
In Figure 13, the differences between the LEM’s safety factors and the FVM results in sample point 535 are shown. According to this figure, the minimum difference happens in model 1 for rigid rock and brittle discontinuities (elastic slip 3 mm), with a value of 2.7%. The maximum difference belongs to model 2 with the value of 317%, where a rigid wedge but a highly flexible discontinuity (elastic slip 15 mm) is under study. Figure 14 shows a comparison of the shear behavior of the discontinuities in the LEM and the numerical model.

5.2. Some Other Insights into the LEM

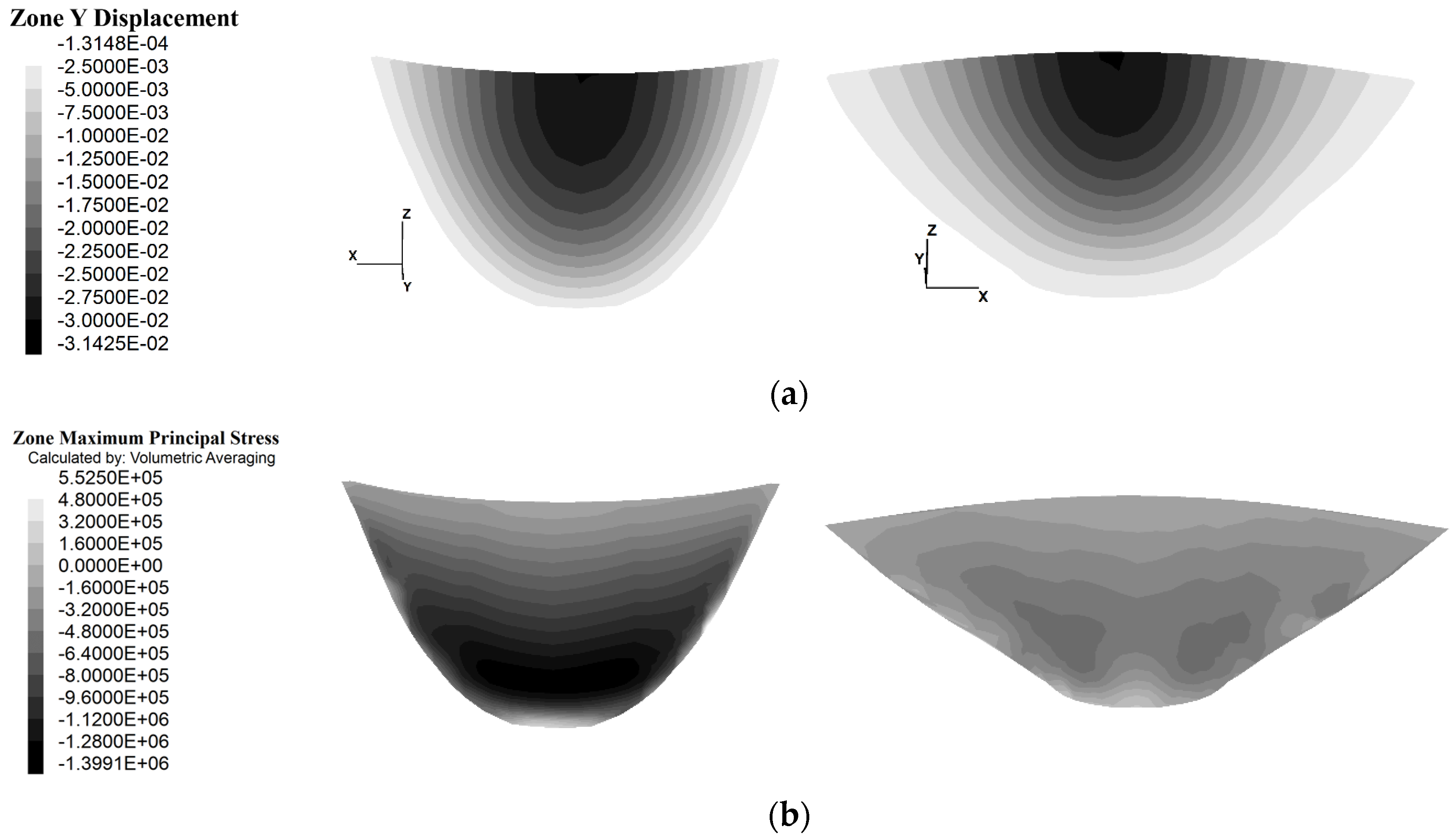
Figure 15 depicts the dam body displacement and maximum principal tensile stress for model 2-sample point 535, where the foundation safety factor calculated by the LEM is approximately 0.73. As can be seen from this figure, there is no abnormal behavior in the dam body. The dam body’s maximum displacement and principal tensile stress are 31 mm and 0.55 MPa, respectively. This indicates that a wedge with a safety factor of less than one in the abutment of a concrete arch dam, even when it is in touch with the dam body, does not necessarily result in the instability of the dam body. Caution must be taken in decision making based only on safety factors derived from the LEM.

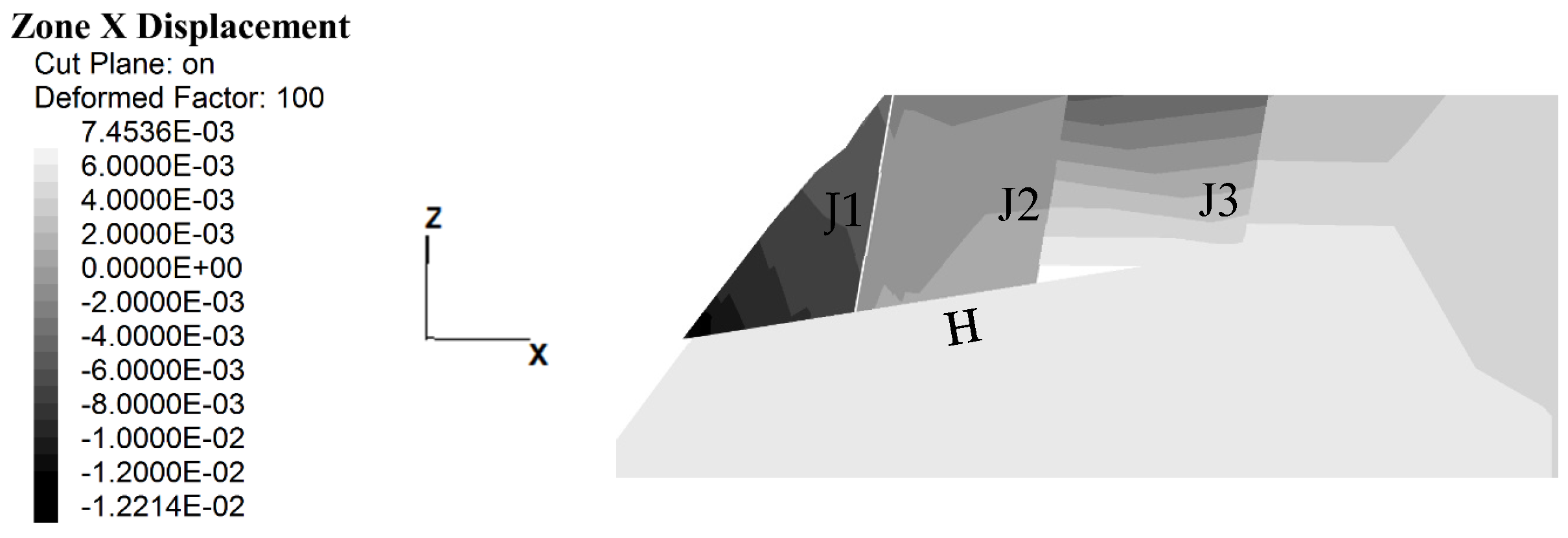
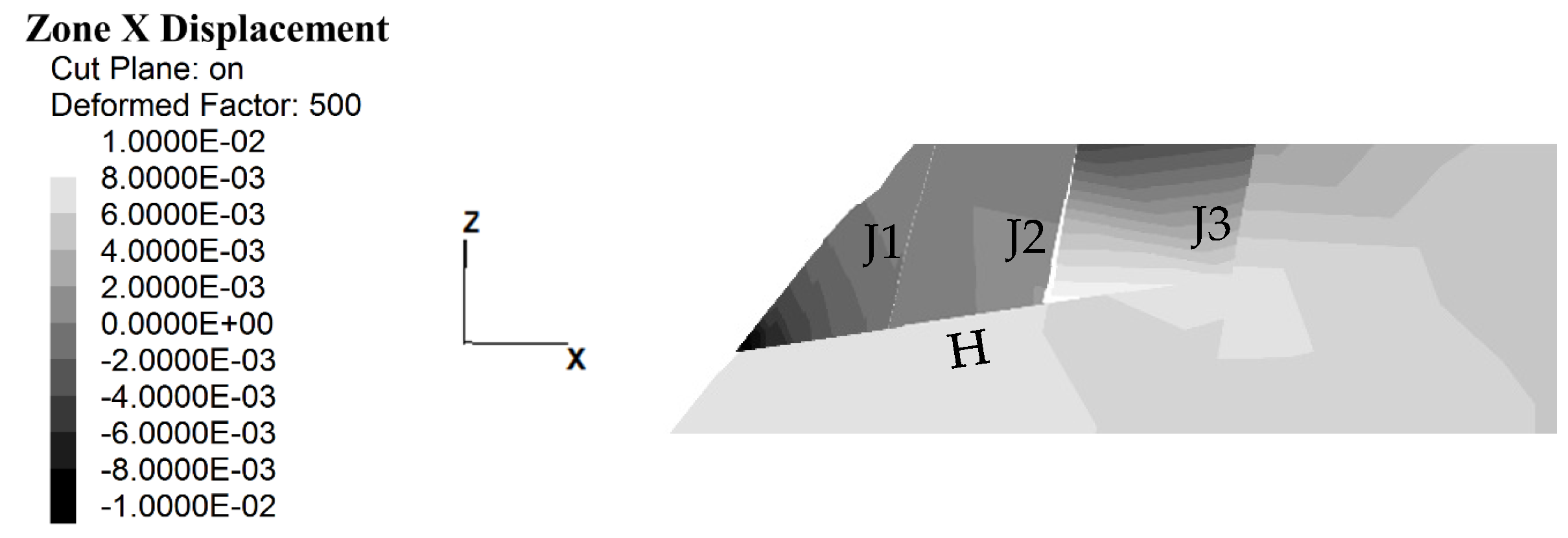
Ultimately, a comparison between the LEM and the numerical model is made on the recognized critical wedge in model 4 (the model with a system of wedges). As explained in Section 4, in model 4, the LEM has recognized wedge W1 as the critical wedge for all the analyzed sample points. Figure 16 shows a cut of the wedges analyzed by the numerical model and for the input parameters corresponding to model 4, sample point 85. In this figure, the maximum displacement for wedges W1, W2, and W3 in the X direction are −10 mm, −4 mm, and −1 mm, respectively. Therefore, in the numerical model also, wedge W1 can be named as the critical wedge among the other two. As a result, it can be concluded that the LEM can be efficiently utilized as a tool for recognizing the critical wedges in dam-foundation systems.

6. Conclusions

This study provides insight into the widely used method of limit equilibrium in the stability analysis of rock wedges. This article is divided into two parts:

The first section demonstrates how the LEM can be applied to the reliability assessment of the potentially movable rock wedges located in the foundation of concrete arch dams. A quasi-analytical method has been recommended that hires the numerical model of the dam-foundation system and the LEM to calculate the dam static thrust forces and the wedges sliding safety factors, respectively. The procedure has been used to assess the reliability of a set of rock wedges integrated into the left abutment of a concrete arch dam foundation. The reliability is evaluated by the Latin Hypercube Sampling (LHS) method, and the random variables are the friction angle, cohesion, and the Grout Curtain Efficiency Coefficient (GEC).

The loading involves the wedge self-weight, the dam body thrust forces, and uplift pressure on the wedge’s discontinuities. The dam thrust forces have been extracted from the dam’s numerical model analyzed under the dam’s self-weight and hydrostatic pressure at full water level.

In this study, four distinct models have been created based on the wedge geometry and applied loads: model 1 involves wedge W1 under self-weight and dam thrust forces; model 2 includes the same wedge and loading in addition to the uplift pressure type 1 (i.e., plane J1 is assumed to be drained while other planes are still wet); model 3 refers to model 2 but with the uplift pressure type 2 (i.e., plane J1 is assumed to be drained while other planes are still wet); and model 4 involves a series system with wedge W1, W2, and W3 under self-weight and dam thrust force loading. After calculating the sliding safety factor for every model and each set of parameters corresponding to each sample point, the reliability curves have been determined.

The reliability curves for models 1 to 3 have shown that uplift pressure in the discontinuities can significantly decrease the model’s reliability. It has been shown that the reliability can change significantly even when the uplift pressure distribution assumption is changed (models 2 and 3). This demonstrates how valuable the groundwater site studies are in minimizing the level of uncertainty regarding foundation pore pressure. Moreover, it has been observed that the reliability curves for models 1 and 4 are the same, meaning that the critical wedge in model 4’s wedge system is the same wedge that model 1 examined, i.e., wedge W1.

The second part of this study has prepared a comparison between the results of the quasi-analytical and purely numerical methods, focusing on the effect of LEM fundamental assumptions on the sliding safety factor. To achieve this goal, in sample point 535 (the sample point with minimum safety factor calculated in the previous part), the wedge’s safety factors have been extracted from the numerical model with the help of the Strength Reduction Factor method and for different values of discontinuities’ elastic slip and rock mass deformability modulus. Then, these results were compared and discussed with the corresponding ones once they were calculated using the quasi-analytical method.

The findings demonstrate that in all the models (models 1 to 4), the foundation safety factor increases with increased rock mass deformability modulus and elastic slip. According to the results, for the rigid foundation and highly brittle joints (elastic slip of 3 mm), the sliding safety factors of the LEM and the numerical method are remarkably similar. This indicates that regardless of the other LEM assumptions, accepting two assumptions of the rigid wedge and the rigid, perfectly plastic behavior of the sliding planes leads to an equal safety factor in both the LEM and numerical methods. Nevertheless, the results for the rest of the cases are significantly different. Compared to the FVM, while the LEM yields more conservative results for the strong rock mass, it overestimates the SFs when a soft rock is under study. This can be because partial separation is impossible in the LEM since it assumes uniform shear and normal loads on the sliding planes. The partial separation that mostly happens in soft rock masses may trigger sliding and cause lower safety factors. In the case of medium-strength rock masses (in this study, Er = 15 GPa), the comparison mainly depends on the elastic slip or, in other words, the shear stiffness of the discontinuities; the SFs calculated by the LEM for flexible discontinuities (high elastic slip) are less than the corresponding values derived from the FVM, while the opposite is true for the brittle discontinuities (elastic slip < 7 mm).

In conclusion, the LEM is a practical and straightforward method that can be used widely in the reliability analysis of rock wedges. However, in the case of complicated geotechnical, geological, and operational conditions such as soft geotechnical layers, highly elastic discontinuities, significantly fractured zones, and fast operational phases, which may change the uplift pressure assumptions, it is recommended to make informed decisions by comparing the LEM results with other accessible methods, like numerical methods. Furthermore, understanding the sources of the LEM’s limitations can present engineers with new challenges and guide them in identifying specific areas for enhancement. Future research could explore the development of a more comprehensive algorithm that incorporates the deformability of the sliding wedge and surrounding media, accounts for the elastoplastic behavior of discontinuities, and considers non-uniform stress distributions within the wedge.