Abstract
This paper presents a generic component for Analytic Hierarchy Process (AHP)-based decision support in risk management. The component was originally dedicated to railway transportation issues; however, its generality enabled it to extend its functionality for other domains too. To show the generality of the module and possibility of its application in other domains, an environmental case was run. Its goal was to select methods for planning the post-mining heap revitalization process, especially decision-making focusing on the selection of the most advantageous revitalization option on the basis of the Analytic Hierarchy Process and different, non-financial factors, e.g., social, environmental, technological, political, etc. Taking into account expert responses, the suggested solution was related to energy production.
Keywords:
railway; safety; environment; revitalization; multi-criteria; decision-making; risk management 1. Introduction
Risk management [1] plays an important role in many branches of industry [2,3,4]. For that reason, the Central Threat Register (CTR) [5,6]—a tool for supporting decision-making in railway transportation—was developed. The tool was designed and developed as a domain dictionary that was possible to apply in branches other than railway transportation. This thought came directly from well-defined analyses of two cases [5], where the Analytic Hierarchy Process (AHP) methodology was used to select proper safety measures for threats identified during the risk analysis.
In addition to the use of the AHP embedded in the CTR, there are known attempts to use the AHP in railroad management, which are also listed in the article [7], with examples using MCDA methods (the already mentioned AHP, or ANP—Analytic Network Process) to plan transport routes for passengers or cargo trains [8], to assess alternatives for a transport network’s development [9] and how to apply AHP to railway safety [10]. The AHP method, in combination with other methods, is increasingly a part of quantitative evaluation systems, including environmental aspects, related to railroads. An example is the combination of AHP with the Delphi method and the GIS system [11]. The case presented there is an attempt to discuss the relationship between railroads and landscape and the use of AHP to develop a system for quantitative evaluation of the railroad landscape, taking into account historical, tourist, ecological, visual quality, etc., aspects. Another example is the use of AHP to assess environmental risk in the area of railway construction: Ref. [12] describes the impacts of spoil disposal areas (SDAs) in high-speed railway engineering, and [13] addresses the study of the water–soil environmental risk assessment during railway construction.
The degradation of areas and objects caused by industrial activities, especially mining, remains a serious ecological problem. It brings risks to human health, the natural environment and the economy. Sustainable and environmentally friendly development of post-industrial degraded areas can be achieved through their revitalization.
The revitalization of such areas is difficult and costly; it requires coordinated and multi-directional activities. The planning process of these activities is very complex; it requires the identification, management, analysis and a huge amount of diversified information, which is used as the decision-maker’s input to work out the target revitalization plan. The specialized software tools may be very helpful to support the planning of the revitalization, especially to take control of the decision input data and to help users in more difficult and troublesome analytical activities.
The Analytic Hierarchy Process (AHP) is one of the approaches for decision-making support, and the above mentioned system—CTR—provides this technique. The overall generality of the CTR system made us try to apply the method just to the environmental case of post-industrial area revitalization.
The case described in this paper is related to the SUMAD project (Sustainable Use of Mining Waste Dumps) [14]. The foundation of the SUMAD methodology is included in the paper [15]. This paper discusses MCDM, especially AHP applications in the revitalization of different degraded areas [16,17]. Some analogies to the SUMAD methodology are observed, but none of these papers present the holistic approach embracing the identification of the AHP criteria and options based on detailed analyses of domain data—there are only general risk issues in some of these papers. The SUMAD methodology works out iteratively a certain number of revitalization alternatives (here: options) free of unacceptable risks, with acceptable financial parameters and non-financial parameters (social, political, legal, etc.) provided to the decision-makers, who make their decisions manually.
The novelty of this paper concerns the preparation of the AHP criteria and options through exhaustive, independent, iterative analyses and calculations based on detailed domain data with respect to three pillars of the SUMAD methodology: risk reduction assessment, cost–benefit assessment and SUMAD qualitative criteria (here: social, environmental, political, legal, etc.) assessment performed by the domain experts.
As a result:
- A set of reasonable, clearly defined revitalization alternatives is worked out (i.e., that are free of unacceptable risks, having acceptable financial and non-financial parameters), which can be used directly as options in the AHP. Such options are based on evidence included in the SUMAD Revitalization plan document;
- For AHP criteria, elaborated as aggregated data from the risk, cost–benefit and SUMAD qualitative criteria assessments, all data are documented and justified.
All data are based on expert knowledge and analyses. The SUMAD analytic process is well documented and the SUMAD Revitalization plan can be used as the evidence and input to the decision process. No ad hoc or subjective information is included in the decision process, which now is more immune to manipulation and the decision quality is improved. Stakeholders representing different interests can participate in the tool-supported AHP. The data from the SUMAD process are the reference point and input for the AHP decision process.
This paper brings a novelty element to the SUMAD decision process. AHP enhances the SUMAD decision process by replacing manual and informal decisions by the AHP-based ones.
This paper is organized as follows: It starts with brief description of the context of decision-making, which is followed by an overview of AHP. Afterwards, the CTR system and its AHP module are briefly described. Then, the context of environmental data is provided, while the most important part refers to the environmental case analysis—a hypothetical heap revitalization.
2. Making Decisions
Decision-making in the above-mentioned areas (railroad and environment, revitalization), like any other decision-making problem in real life, always requires some compromise when choosing the right option, taking into account various criteria. Hence the need for a method from the field of multi-criteria decision-making methods (MCDMs). Many such methods are known and used, and attempts are made to classify and divide them [18,19]. One of the state-of-the-art MCDM approaches is the Analytic Hierarchy Process [20]. The AHP is a descriptive approach willingly utilized when one needs to quantify intangibles that can be performed by making comparisons to determine how important or preferable they are for the assessor to then make trade-offs to select the best option. It was developed by Thomas L. Saaty in the 1970s [20], and it is one of the most popular multi-criteria methods [21,22]. The goal is to solve the decision problem, i.e., to indicate the best of the several options available to choose from. This goal is presented in the diagrams as the top in the hierarchical structure, in which the decision criteria (and sub-criteria, if considered) are listed on subsequent levels, and below, a list of available options (Figure 1).
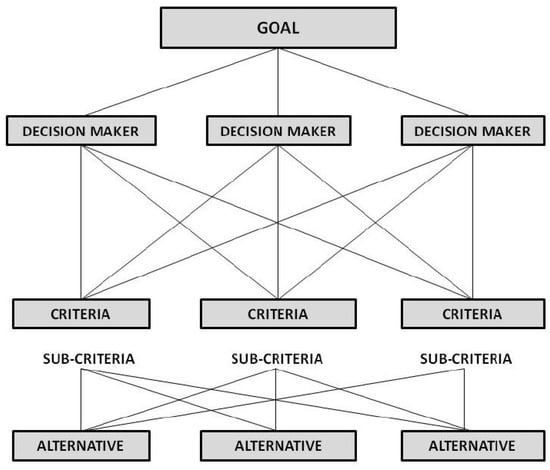
Figure 1.
AHP decision problem diagram [23].
The Analytic Network Process—quite similar to the AHP—was also proposed by Sa-aty [24,25]. The decision problem, presented in AHP as a hierarchical structure, in fact often has a more complicated structure and includes various types of dependencies between criteria or available options. By using ANP, it is possible to model dependencies and feedback as a kind of a network structure. Still, the priorities are determined using pairwise comparisons, just like in AHP. However, the description of the problem is not a simple top–bottom hierarchical structure, but rather a network with connections between elements on different levels as well as loops within a single element (Figure 2).
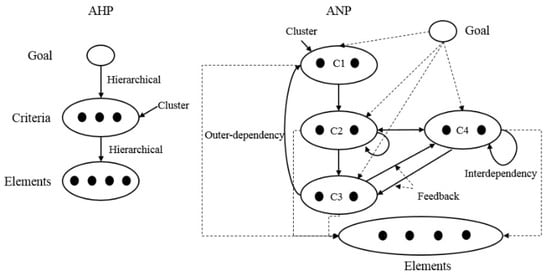
Figure 2.
Difference between linear, hierarchical (left) and nonlinear network (right) [26].
When calculating priorities, apart from the matrix of comparisons of elements, the so-called supermatrix must be prepared to include in calculations interrelationships between the elements. The ANP is a more complex method than the AHP, which is why the AHP is more used in practice. The ANP requires more pairwise comparisons, and the number of comparisons raises with the number of dependencies. It causes calculations, and the inconsistency analysis is difficult without the supporting software (while for the AHP it can be performed “on paper” or using just a spreadsheet).
The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), according to [27], is a method belonging to a “compromising model”, and it selects an alternative that is the closest to the ideal solution and the farthest from the negative-ideal solution. In the case of the TOPSIS method, the decision matrix contains distinguishable alternatives (rows) and criteria (columns). The element is the value of the i-th alternative with respect to the j-th criterion. For this matrix, a normalized decision matrix Z is then constructed. Based on the Z matrix, ideal and non–ideal solutions are determined. Then, the distances of each alternative value from the ideal and negative-ideal pattern are computed. They can be computed as Euclidean distances, so the relative closeness of alternatives with respect to can be defined and the alternatives can be ranked.
Extensions to the TOPSIS method are also known, such as the fuzzy TOPSIS method (based on positive triangular fuzzy numbers) presented in [28]. The use of fuzzy numbers in the TOPSIS method has been proposed to address situations where it is difficult to express evaluations with real numbers, due to the lack of knowledge and data, or due to imprecise subjective evaluations.
The Preference Ranking Optimization METHod for Enrichment Evaluation (PROMETHEE) method is also based on pairwise comparisons of selected alternatives with respect to the set of criteria [29]. There are several variants of the method. PROMETHEE I allows one to set up a partial preorder of alternatives, while PROMETHEE II helps to establish a complete preorder. For each alternative, the so-called outranking flows are calculated, which tell how the considered alternative a is outranking all others. There are positive and negative outrankings being calculated. The higher value of , and the lower , the better the alternative.
Data Envelopment Analysis (DEA) [30] is used to measure the productive efficiency of the so-called decision-making units (DMUs). DMUs are in our case understood as possible alternatives being evaluated. An example of such an evaluation using DEA based on the Malmquist Productivity Index (MPI)model, on the Epsilon-Based Measure(EBM), or a combination of these methods, can be found in studies conducted in various fields, including [31,32,33].
In order to achieve better results from the decision-making process, combinations of different methods are also proposed. An example is the TOPSIS method combined sometimes with the AHP method, and in such a case AHP is used to determine vector w (weights of criteria) [34].
Additionally, studies can be found regarding the combination of the AHP and TOPSIS methods in the area of environmental applications. One can mention the decision-making problem regarding the implementation of photovoltaic panels [35]. The paper [36] presents an example of using both the AHP and DEA methods combined. This combination was also used to support the selection of the best location for the construction of photovoltaic farms. Here, the DEA method was used for pre-selection, conducted on the basis of measuring the efficiency indicators of a given location, and then the AHP method was used to rank the locations that achieved good results regarding efficiency.
Among the multi-criteria decision support methods, the literature offers various examples of other methods (to mention, for example, VIKOR [37], EDAS [38]), which deal with decision support in the areas of transportation and environmental decision efficiency [39,40,41,42,43].
In this paper, the shift from the railway domain-based system (Central Threat Register—CTR) into an environmental application will be presented. A brief description of this DSS is presented in Section 4; however, the more detailed presentation was already published in [5].
In the end, the AHP was chosen, which is the most common choice in the literature and is also widely used, as a review of citations (between 2012 and 2022) on MCDMs shows ([18], Table 3. therein).
3. Analytic Hierarhy Process
During the assessment process, a pairwise comparison is carried out, using a 9-level numerical scale, where value “1” indicates equal importance, and the higher value, the stronger the importance of the compared element. Value “9” indicates an extreme importance of one element over the other (Table 1).

Table 1.
The fundamental scale of absolute numbers [20].
The assessors express their preferences (for the criteria and for the options) using the scale and making pairwise comparisons. The results of these comparisons are formed into a square matrix with a dimension equal to the number of compared elements (Equation (1)).
where is the value that tells how much more important element i is than element j with respect to k criterion, and is a reciprocal matrix, whose elements fulfill Equation (2).
Such comparisons are made first to assess the importance of the individual criteria and then to compare individual options against each of the criterion. For example, if we use three criteria (e.g., price, execution time, impact on environment) to evaluate the available options, then the options are compared three times (three matrices are created), each time taking into account a different evaluation criterion.
The next step in the AHP method is derivation of priority vectors, which can be achieved using different methods (e.g., mean of normalized values, right/left eigenvalue method, geometric mean), as described in [44]. As the final result, priorities give the ranking of the assessed elements.
Comparisons, or verdicts within AHP assessments, are given using a fixed scale (without intermediate values), and these verdicts are subjective preferences of the assessors whose involvement and accuracy may vary. Therefore, the scores in comparison matrices are burdened with a certain level of inconsistency. This can be determined and referenced to an acceptable level.
The Consistency Ratio () can be determined using Equation (3):
where the Consistency Index () of the matrix is calculated as
where:
- n—dimension of the matrix;
- —the largest eigenvalue of the matrix;
- —a consistency index determined on the basis of random values of a matrix of the same dimension.
There are tables of typical values for matrices of different dimensions [20,45,46], determined on the basis of many (100, 500, 1000, 100,000) simulations using matrices, where the values of which are completely random. The AHP method also makes it possible to combine different assessments, e.g., those carried out independently by different experts, or representatives of groups interested in the results of decisions [47,48].
4. System and Component Overview
The Central Threat Register (CTR) [5] is a complete tool for risk analysis and decision support in general rail transport. It was developed several years ago as a result of cooperation with domain experts and security experts. A wide study confirmed that the solution is in compliance with European and Polish requirements for railway transport.
The most important components of the system are as follows:
- knowledge base module;
- data exchange and anonymization module;
- threat and risk assessment module;
- decision support module.
In this paper, we will show the application of the last-mentioned module in a completely different domain. However, to have a better overview of the whole system, all above-mentioned modules and the CTR application will be also briefly described.
The knowledge base is a module that binds four aspects of risk management:
- threats;
- vulnerabilities (causes);
- consequences (effects);
- safety measures (security measures).
The knowledge base items are kept in a relation to risk analysis results (provided by specialized organizations) as well as to more detailed information about potentially hazardous incidents, possible threats or previously occurred events. When a new event is assigned to one of the existing threats, the statistics of its occurrence are modified and later used during the threat assessment for the purposes of estimating probability and potential effects of the threat materialization. If a new-type threat occurs, which cannot be associated with any existing threat, it is possible to update the KB with this new threat.
Another component—the data exchange and anonymization module—is responsible for each event classification by means of two possible catalogs: a basic catalog based on numbers and letters, which functions in the Polish railway system (required in reports sent to the Office of Rail Transport) and the additional one which is the CSI classification (required by global reports). Such an approach helps to generate reports required by the railway transport supervising authorities and to generate basic reports about railway safety.
The threat and risk assessment module takes into consideration two risk assessment methodologies: the Probability and Consequence Matrix (PCM) and FMEA. Each of them tries to analyze and to calculate the risk on the basis of the event occurrence frequency and the level of losses. To be more precise, the FMEA analysis makes it possible to estimate the detectability of a given threat. The occurrence frequency of the event is determined based on the number of events in relation to the executed train-kilometers in a given period of time. The losses are estimated based on human victims as well as financial losses and ensuing delays.
The final component—the decision support module, strictly related to the railway domain—makes it possible to provide the contact between domain experts and system users during the process of the railway risk management as well as the interaction during the application of the Analytical Hierarchy Process (AHP) method.
The presented system made it possible to run two cases strictly related with the railway transportation safety. The first of them took into consideration possible railway traction break due to icing, and tried to provide the most possibly successful preventative actions to avoid the traction break. All actions are presented in Figure 3.
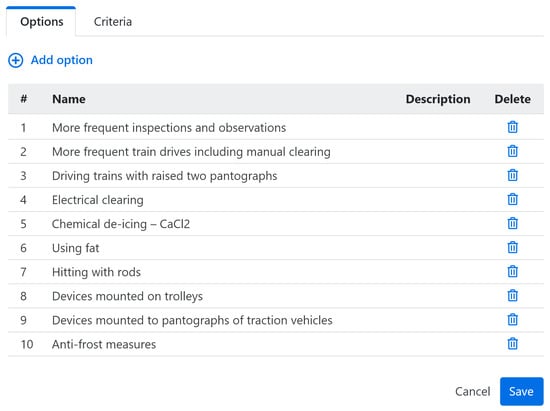
Figure 3.
Sample configuration for AHP: list of security measures.
An analogous list of comparison criteria contained the following: impact on security, time of execution, cost, feasibility, ease of implementation, efficiency and impact on the environment.
Experts had the opportunity to make the direct comparison of security measures (according to the above-mentioned criteria) with intuitive sliders (Figure 4).
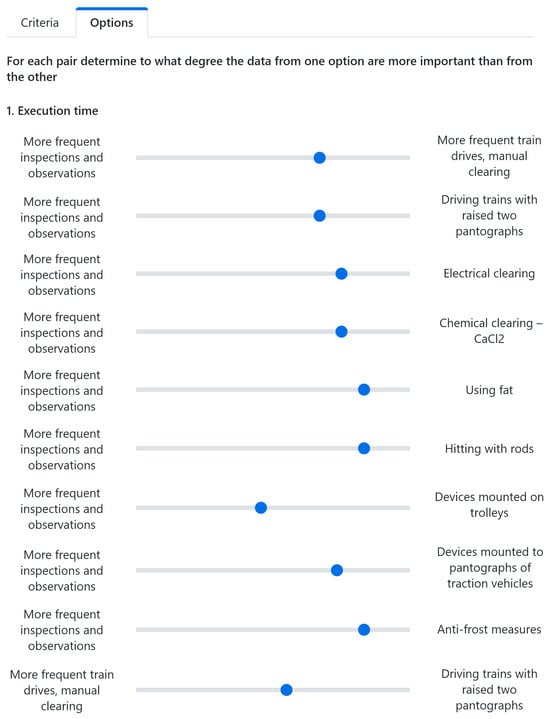
Figure 4.
Direct comparisons in the AHP (only several of 45 direct comparison sliders are presented due to the high total length of the corresponding system window).
In the paper [5], another case of the AHP analysis was presented. It involved an expert to rank the train collision prevention procedures. It concluded that the presented system—CTR—and to be more precise, one of its core modules—AHP implementation—could become a separate and autonomous tool for decision support in many other domains. The next sections will prove the usability of the tool in the environmental context.
After taking into consideration a few expert responses, it was possible to build the final ranking of options (Figure 5).
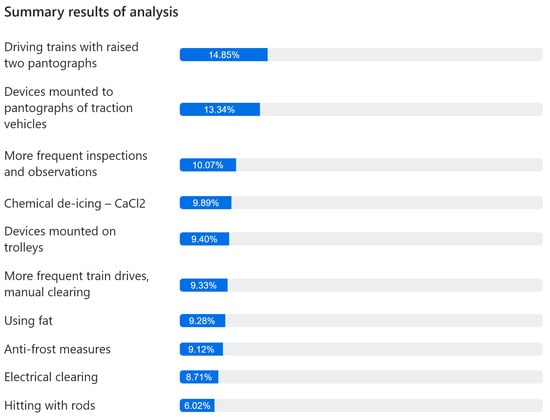
Figure 5.
Summary results of the AHP.
5. The AHP for the Environmental Case
The case study is based on the methodology worked out in the EU RFCS SUMAD (Sustainable Use of Mining Waste Dumps) project [14]. The SUMAD decision process concerns the selection of the target revitalization alternative (RVA) for implementation from several possible alternatives for a given post-mining heap. The decision is based on the aggregated information from detailed analyses embraced by the SUMAD methodology [15]. Each of the considered alternatives is the subject of the following:
- Exhaustive risk reduction assessment (RRA);
- Cost–benefit assessment (CBA);
- Qualitative criteria assessment (QCA) of different non-financial factors, e.g., social, environmental, technological, political, etc.
The decision-maker selects manually the target revitalization alternative considering results of theses analyses. It is possible to modify alternatives when their parameters obtained from analyses are unsatisfied. The modified alternatives are analyzed again. Revitalization alternatives are worked out iteratively, until the set of alternatives is reasonable for the decision-maker. The case concerns the idea to enhance the manual SUMAD decision process by supplementing it using the AHP. Revitalization alternatives from the SUMAD process play the roles of the AHP options. The AHP criteria should be elaborated using the analyses results, especially aggregated information from analyses. The case presents how to elaborate the decision criteria for the AHP and to assess/modify options (here: alternatives) before using them in the AHP. Decisions are focused on the concrete object—a heap. The deeper the knowledge related to the decision object is acquired, the more adequate a decision could be obtained.
The AHP exemplification concerns a hypothetical heap (HH), the same as was presented in the paper [15]. The description of the HH is complete but simplified for the paper purposes. The hypothetical heap description can be expressed as follows:
The mining HH waste landfill, relatively young, was established in the period 1986–2010.
The waste consistency is characterized as a mixture of roof rocks, floor rocks and coal overgrowth, and the vast majority are represented by claystones, stigmaria soils, clay siderites, occasionally mudstones and—rarely—sandstones. The main heap materials are gravel, loam and shales and have rather poor geological parameters (possible unstable heap surface, subsidence basins around the heap, increased soil moisture, landfill leachate containing dangerous substances, groundwater pollution).
On the east slope, a certain amount of coal waste is included (possible detrimental smells and a nuisance to nearby residents, uncontrolled destruction of slopes or surface, spontaneous combustion from coal).
The waste has the following shape parameters: 90 [ha] of area, average angle of slope from 1:3 to 1:6, ca. 30 [m] of height and volume: 30 million [m].
HH is located in the zone, where the concentrations of SO, NO, CO and benzene do not exceed the lower assessment threshold, while the concentration of PM10 dust is between the upper and lower assessment threshold.
The main pollutants are water reactive materials, like CaO, MgO, K and Na, inorganic toxins, like As, Ba and Pb and organic toxins such as carbon tetrachloride and chloroform (landfill leachate containing dangerous substances, possible groundwater pollution).
Rare vegetation includes natural succession of shrubs and rushes. Wildlife mostly includes amphibians, land fowl, waterfowl and small herbivorous mammals.
Surrounding water embraces an artificial watercourse reservoir flawing along the southern foot of HH, a drainage ditch running from SW to NE, a small natural lake and a catchment of three small rivers.
The annual meteorological average data are as follows:
The agricultural landscape exists around HH with a small share of forest communities. On the eastern side of the heap, 600 m from its edge, there are residential buildings of farms, magazines, railway, local roads, and further, a shopping center. There are no cultural heritage objects within the environmental impact.
Limited past revitalization actions embrace leveling of degraded areas, concrete production, ad hoc partial afforestation and soil cleaning.
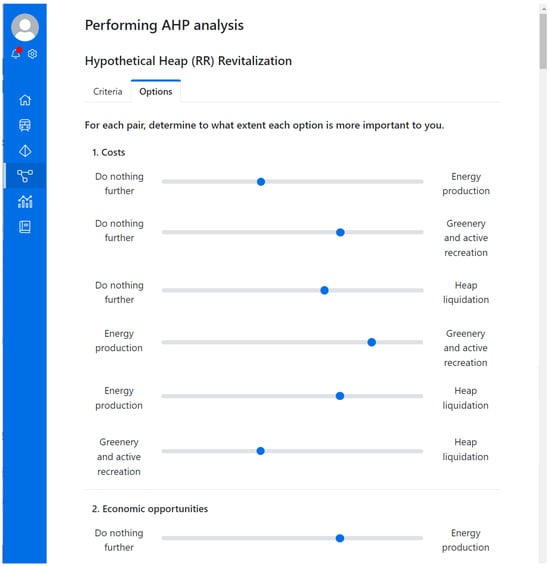
5.1. Defining Options
The case started from the identification of the decision subject’s (revitalization area—heap) properties and its current status, which is called the Revitalization Alternative “zero” RVA[0]. It embraces the revitalization activities performed ad hoc in the past. It is the reference point for other revitalization activities and analyses, and it represents the strategy “Do nothing further”. In this state, a heap implies certain, usually unaccepted risk, generates cost, brings almost no benefits and is burdensome to people living around it and to the natural environment. The rest of the Revitalization Alternatives RVA[i], where i = [1…N−1] include the following (Figure 6):
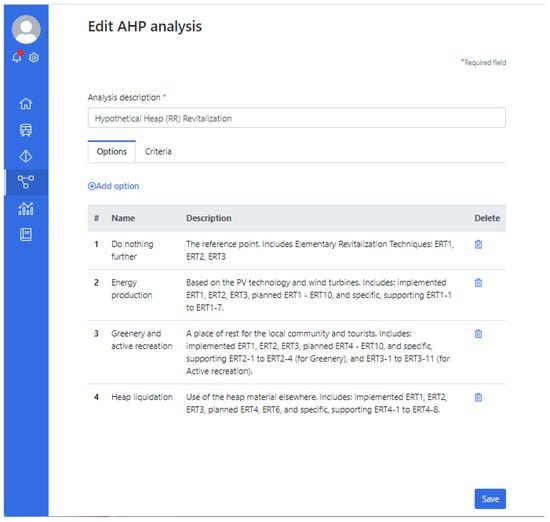
Figure 6.
The list of alternatives in the AHP tool.
- RVA[1] “Energy production based on the PV technology and wind turbines”;
- RVA[2] “Simple greenery”;
- RVA[3] “Active recreation”;
- RVA[4] “Heap liquidation by the use of the heap material elsewhere”.
Each alternative can be a subset of the Elementary Revitalization Techniques (ERTs) as described in [15]. The CTR tool adaptation embraces domain data: the options and decision criteria. The AHP implemented in the CTR tool is based on the Saaty approach [49]. Generally, it is domain neutral—it can work in different domains of application, including railway management processes (including security, safety management) as well as the environment protection and revitalization domain.
5.2. Defining Decision Criteria
The next research question is to define the AHP criteria based on the expert knowledge. This can even be decided ad hoc on someone’s expectation, but it will be better to define the criteria using results of the detailed object exploration, analyses, evidence or managed processes.
The SUMAD methodology is presented in the paper [15]. Readers are encouraged to see this paper. It presents more details dealing with three kinds of analyses (RRA, CBA and QCA) for the considered Revitalization Alternatives and their results, both detailed and aggregated (Table 6 in [15]). It is the input for the SUMAD decision-maker. The decision about the target Revitalization Alternative for implementation is manual and heuristic, but it is based on results obtained from analyses. This paper proposes to enhance this decision-making process by adding an additional step—the AHP.
The aggregated results are the basis to define a reasonable set of criteria for the AHP. It is relatively easier to aggregate information about risk and cost–benefits, than about non-financial issues represented by QCA. The QCA criteria are numerous, have diversified kinds of impacts (positive, negative, mixed positive and negative, some have a threshold value) in the SUMAD methodology. It would be difficult to define the AHP criteria at this detail level. The QCA criteria are configured and thematically grouped, e.g., society, politics, technology and science, environment and economics. For each group the analyst obtains a cumulative values from the QCA utility function. These groups can be used to define, even straightforwardly, non-financial criteria for the AHP: here, e.g., economic opportunities, positive impact on the environment and positive perception by societal groups.
Preliminary examples of such criteria were proposed in the paper [15]:
- Ability to reduce risk;
- Implementation period;
- Investment cost;
- Operational cost;
- Direct benefits;
- The length of the payback period;
- Indirect benefits (image, improved natural environment, …);
- Feasibility, ease of implementation;
- Laws and regulations;
- Positive perception by societal groups;
- Positive political impact;
- Positive relationships with technology and science;
- Positive impact on natural environment;
- Economic opportunities.
To construct the decision criteria for the AHP tool, the authors propose two requirements that ought to be satisfied:
- 1.
- Number of criteria.At first glance, a huge number of criteria, e.g., 14 as on the above list, seem to be promising, in the hope to obtain precise results, but due to the practical limitations of the AHP, the number of criteria ought to be decreased. Criteria are used by people, who have certain cognitive limitations when considering a huge number of issues. These limitations related to the Miller’s Law are considered in cognitive psychology, which is out of the scope of this paper. This issue was discussed within the AHP context too [50,51]. It is caused by the pairwise comparisons and to preserve the consistency ratio. It is hard to operate with a huge number of criteria. Usually, the number of criteria (as well as options) are 7(+/−2). Too few criteria decrease the preciseness and quality, making decisions trivial. With a deeper aggregation of criteria based on trade-offs, all relevant information related to the decision-making process should be preserved.
- 2.
- Balance.The criteria should be neutral and well balanced. They cannot favor a certain option. The criteria should be agreed on by stakeholders balancing their priorities. The decision process objectives should be satisfied. The criteria should express all issues needed to obtain impartial and objective decisions.
With respect to above requirements, the number of criteria is reduced. All risk-related issues (such as number of identified risks, risk levels before and after the RVA implementation) are represented here by one criterion Risk reduction ability, which concerns the risk picture for a given alternative. The financial picture (cost–benefit analysis and information about investment/operational costs, direct benefits, the length of the payback period) is represented by the criterion Costs (investments, implementation, operational costs). The so-called “soft”, intangible, non-financial parameters are very diversified and were aggregated into three criteria focused on three generally non-overlapping and very important issues:
- Economic, technological, political and other opportunities, which concern, e.g., additional funds, sources of financing, compensation, penalties, environmental fees, impact on financial situation of citizens, on the property market and on trade relations, NGO compatibility, trust in authorities, compliance with political activities, plans and programmes;
- Positive impact on the environment concerns, e.g., direct impact on the natural environment, climate conditions, waste management;
- Positive perception by societal groups and legal compliance concern, e.g., social reception of applied revitalization techniques, social cohesion, living conditions, physical and mental health, impact on social behavior, on a local job market, lawfulness, compliance with development strategies and plans, revitalization durability, time of implementation.
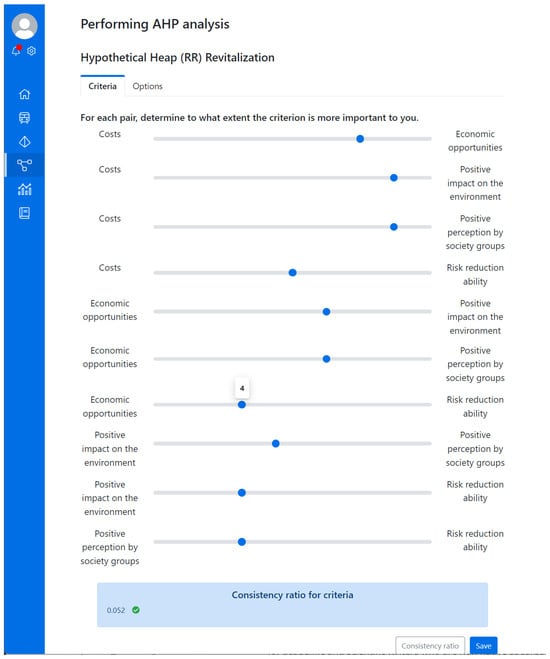
Figure 7 presents these criteria introduced into the AHP tool.
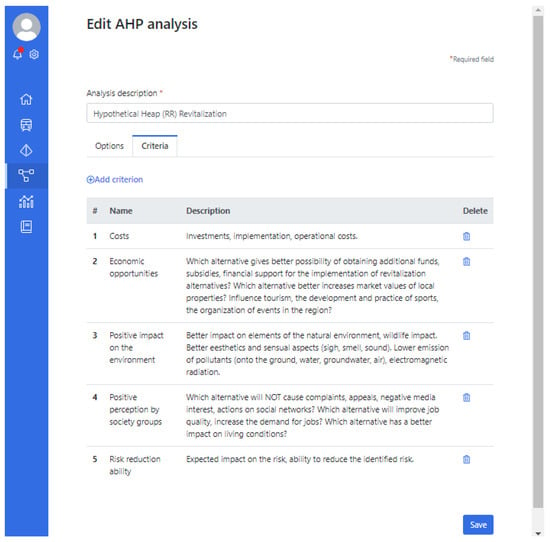
Figure 7.
The list of alternatives in the AHP tool.
5.3. Decision Process Supported by the CTR Tool
The AHP tool supports collective decisions. The geometric mean method was chosen to aggregate individual results. This basic approach is based on the solution presented in [47]. The decision-maker can be a well-balanced collective body represented by stakeholders of different interests and views on the decision problem. In this case study, the team consists of the representatives of the following:
- Investors;
- Landowners;
- Local community, NGOs;
- Local government—environmental protection department.
They obtain their own links according to their roles to the AHP tool to perform two important tasks:
The decision-makers should watch the consistency indexes (Figure 10) for whether they are smaller than 0.1. When an index is too high, the decision-maker is warned and makes his/her assessment more consistent. After setting the importance criteria, the decision-making team member starts an exhaustive process of mutual comparisons of options. Going from one criterion to another, the mutual comparison of options is performed.
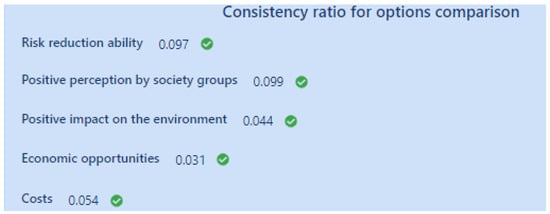
Figure 10.
Consistency indexes.
The AHP tool allows us to assign more individuals to the given interest group and the number of such groups can be higher. The decision team composition influences the decision. For this reason, the team should be balanced and managed. For example, if decision teams were represented only by investors, decisions could not be beneficial for people living locally or for the natural environment.
The AHP module has been added to the CTR system in such a way that its use does not require additional work when used in other application areas. The decision problem described by the criteria and evaluated alternatives can be freely defined. One has to determine a list of people that are experts who are to take part in the analysis. It requires only creating an “Expert” account in the CTR system. A person logging into this account has access to the AHP analysis module, where the analyses that have been assigned to him/her are visible. However, the use of the CTR system for risk management, threats and vulnerabilities assessment, and selection of security measures in areas other than railways, requires adaptation of the remaining system components. This primarily includes adapting dictionaries of specific industry terms, including typical threats, vulnerabilities, security measures, threat classification, adjustment of risk levels, probability scale, impact assessment and scope of event description.
5.4. Decision Support Process Results
The AHP tool provides assessment results. Figure 11 shows partial results after local and government representative voting. At this stage of the decision process, the most preferable by the decision-makers team is the alternative RVA[3] “Active recreation”. Very close to it is RVA[4] “Heap liquidation by the use of the heap material elsewhere”.
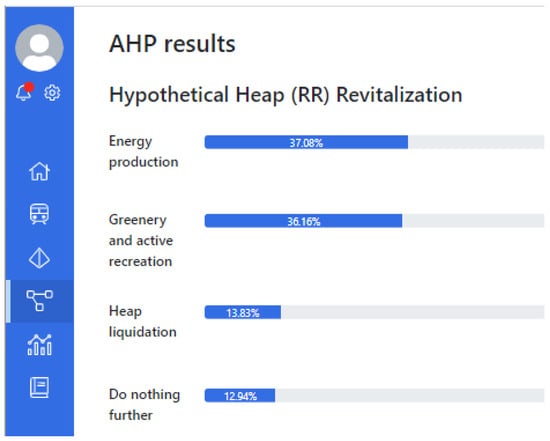
Figure 11.
AHP result.
When all decision-makers perform their assessments, the final results are obtained, which can be used to approve the target revitalization alternative for implementation.
6. Conclusions and Further Works
This paper presents a complex tool to supporting decision-making based on the AHP analysis. The tool was originally designed for railway transportation issues. The AHP method implemented as part of the CTR tool was validated by railway safety managers working with safety management systems on a daily basis at railway companies in Poland.
Designed for decision support in the area of railway risk and threat management, the tool can also be used in other areas of railway management than originally intended. It can also be used to assess and make decisions on environmental, social and expected utility aspects.
As outlined in this article, the same tool was then proposed and used to support decision-making in the selection of revitalization techniques in post-industrial areas, i.e., the revitalization of heap areas after mining activities.
An attempt to use the MCDM tool and method also resulted from the location of the EMAG Institute in a mining region, where the problem of revitalization and use of heap areas is significant. As confirmed in the framework of scientific and research projects [14,52] carried out at the EMAG Institute, this type of decision support, multi-criteria decision-making methods, although known and proposed in many scientific publications, are rarely used in practice in the above-mentioned areas. Proposing a universal tool for security management, building into it a method of decision support and applying it to different areas will help spread the concept of supporting decision-making processes by methods dedicated to this purpose.
The provided new environmental case, related with the post-industrial area revitalization, proves the generality of the AHP module and confirms the implementation potential. Using the module is just a matter of defining the decision problem, defining evaluation criteria and alternatives, as well as organizing a balanced evaluation team that will represent the point of view of each stakeholder group.
As mentioned in the article, the possibility of using the AHP module in combination with another solution was checked in combination with the SUMAD tool. The SUMAD methodology [14] and the AHP methodology built-in CTR tool support each other, as it was shown in this case study.
The proposed approach is based on the SUMAD-related domain data. They are identified by the SUMAD project team and placed into the SUMAD knowledge base. The data describe the post-mining heap properties (as revitalized object properties), elementary revitalization techniques, related risk factors (threats/hazards, vulnerabilities, impacts, cost–benefit factors, qualitative criteria ordered by groups, kinds of utility functions). The SUMAD project demonstrated that the analyses based on these data provides input for the decision-maker to manually select the target Revitalization Alternative for implementation.
The SUMAD process provides ordered and detailed information related to the revitalization process. It is not subjective, but worked out through detailed analyses of the revitalized object, risk reduction, financial and non-financial factors. The SUMAD process allows deeper identification of the domain where decisions are made. These data can be used as input to define the AHP criteria. The AHP options are elaborated in the SUMAD process directly. Reports from the SUMAD process can be provided to decision-makers, helping them understand better the decision context. According to the authors’ opinion, the AHP decision can have more solid foundations.
On the other hand, the AHP extends and enhances the roughly defined manual decision process in SUMAD. Now it is more formalized and well balanced. The AHP tool allows one to structure the decision process and to organize the decisions team, which represents a well-balanced group of stakeholders of different interests and views on the decision problem.
The SUMAD methodology adaptation to other application domains (e.g., to urban revitalization) requires identification of data from this domain, but this issue has not been researched yet. The methodology allows one to configure data and calculations to facilitate such adaptation. The adaptation is a rather extensive task when no domain knowledge is available and can be considered in the future.
For the revitalization test case, the assessment was carried out by people representing various stakeholder groups (investors, owners of the land where the heap is located, representatives of the local community and local government). The final ranking of alternatives resulting from their assessments shows the basic two favored alternatives (energy production, greenery and active recreation solution). The case is typical, representative of this type of problem, and the results are consistent with the social mood, views and expectations of individual stakeholder groups. The results only confirmed the correctness and applicability of the method. The validated solution was perceived as easy to use, acceptable and understandable to AHP assessors.
Current work focuses on full component internationalization and providing a self-existing component, ready to be applied in any domain.
Author Contributions
Conceptualization, A.B., M.S. and J.B.; methodology, M.S., A.B. and J.B.; software, J.B.; validation, J.B. and A.B.; formal analysis, M.S. and A.B.; investigation, M.S., J.B., A.B. and M.M.; resources, A.B.; data curation, J.B.; writing—original draft preparation, M.M., J.B. and A.B.; writing—review and editing, M.M., J.B. and A.B.; visualization, J.B.; supervision, M.S. and A.B.; project administration, M.S., A.B. and A.K.; funding acquisition, M.S., A.B. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Polish National Centre for Research and Development (NCBiR) within the Smart Growth Operational Program: grant no. POIR.04.01.02-00-0024/17-00 (Central Threat Register—The management system of information and expertise knowledge about threats for railway transportation safety), and partially funded by the EU Research Fund for Coal and Steel, grant agreement No. 847227 (Sustainable use of mining waste dumps).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dionne, G. Risk Management: History, Definition, and Critique. Risk Manag. Insur. Rev. 2013, 16, 147–166. [Google Scholar] [CrossRef]
- Liu, P.; Wu, Y.; Li, Y.; Wu, X. An improved FMEA method based on the expert trust network for maritime transportation risk management. Expert Syst. Appl. 2024, 238. [Google Scholar] [CrossRef]
- Elhoseny, M.; Darwiesh, A.; El-Baz, A.; Rodrigues, J.J.P.C. Enhancing Cryptocurrency Security Using AI Risk Management Model. IEEE Consum. Electron. Mag. 2024, 13, 48–53. [Google Scholar] [CrossRef]
- Yang, M.; Alballa, T.; Khalifa, H.A.E.W. A comprehensive data analytics framework for risk management in photovoltaic system design projects. Optik 2023, 295, 171411. [Google Scholar] [CrossRef]
- Michalak, M.; Górka, W.; Bagiński, J.; Rogowski, D.; Socha, M.; Stęclik, T.; Flisiuk, B.; Leśniak, D.; Sikora, M. Central threat register—A complex system for risk analysis and decision support in railway transport. IET Intell. Transp. Syst. 2020, 14, 970–981. [Google Scholar] [CrossRef]
- Górka, W.; Baginski, J.; Socha, M.; Steclik, T.; Lesniak, D.; Wojtas, M.; Flisiuk, B.; Michalak, M. Cloud Decision Support System for Risk Management in Railway Transportation. In Proceedings of the 14th International Conference on Software Technologies, ICSOFT 2019, Prague, Czech Republic, 26–28 July 2019; van Sinderen, M., Maciaszek, L.A., Eds.; SciTePress: Setúbal, Portugal, 2019; pp. 475–482. [Google Scholar] [CrossRef]
- Baginski, J.; Flisiuk, B.; Górka, W.; Rogowski, D.; Steclik, T. Multi-criteria Decision Analysis in the Railway Risk Management Process. In Proceedings of the Beyond Databases, Architectures and Structures, Paving the Road to Smart Data Processing and Analysis—15th International Conference, BDAS 2019, Ustroń, Poland, 28–31 May 2019; Communications in Computer and Information Science. Kozielski, S., Mrozek, D., Kasprowski, P., Malysiak-Mrozek, B., Kostrzewa, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1018, pp. 126–138. [Google Scholar] [CrossRef]
- Stoilova, S.; Nikolova, R. An application of AHP method for examining the transport plan of passenger trains in Bulgarian railway network. Transp. Probl. 2018, 13, 37–48. [Google Scholar] [CrossRef]
- Ergun, M.; Iyinam, S.; Iyinam, A. An assessment of transportation alternatives for Istanbul Metropolitan City for year 2000. In Proceedings of the 8th Meeting of the Euro Working Group Transportation, Rome, Italy, 12–15 September 2000; pp. 183–190. [Google Scholar]
- Bureika, G.; Bekintis, G.; Liudvinavičius, L.; Vaičiūnas, G. Applying analytic hierarchy process to assess traffic safety risk of railway infrastructure. Eksploat. Niezawodn. Maint. Reliab. 2013, 15, 376–383. [Google Scholar]
- Sang, K.; Fontana, G.L.; Piovan, S.E. Assessing Railway Landscape by AHP Process with GIS: A Study of the Yunnan-Vietnam Railway. Remote Sens. 2022, 14, 603. [Google Scholar] [CrossRef]
- Cheng, B.; Chang, R.; Yin, Q.; Li, J.; Huang, J.; Chen, H. A PSR-AHP-GE model for evaluating environmental impacts of spoil disposal areas in high-speed railway engineering. J. Clean. Prod. 2023, 388, 135970. [Google Scholar] [CrossRef]
- Chen, H.; Li, H.; Wang, Y.; Cheng, B. A Comprehensive Assessment Approach for Water-Soil Environmental Risk during Railway Construction in Ecological Fragile Region Based on AHP and MEA. Sustainability 2020, 12, 7910. [Google Scholar] [CrossRef]
- SUMAD. Available online: https://www.nottingham.ac.uk/research/groups/nottingham-centre-for-geomechanics/research/sumad-project/sustainable-use-of-mining-waste-dumps.aspx (accessed on 1 October 2023).
- Bialas, A. Towards a Software Tool Supporting Decisions in Planning Heap Revitalization Processes. Sustainability 2022, 14, 2492. [Google Scholar] [CrossRef]
- Spanidis, P.M.; Roumpos, C.; Pavloudakis, F. A Multi-Criteria Approach for the Evaluation of Low Risk Restoration Projects in Continuous Surface Lignite Mines. Energies 2020, 13, 2179. [Google Scholar] [CrossRef]
- Pavloudakis, F.; Roumpos, C.; Karlopoulos, E.; Koukouzas, N. Sustainable Rehabilitation of Surface Coal Mining Areas: The Case of Greek Lignite Mines. Energies 2020, 13, 3995. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. Multi-Criteria Decision Making (MCDM) Methods and Concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Alvarez, P.A.; Ishizaka, A.; Martínez, L. Multiple-criteria decision-making sorting methods: A survey. Expert Syst. Appl. 2021, 183, 115368. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill International Book Co.: New York, NY, USA; London, UK, 1980. [Google Scholar]
- Majstorović, A.; Jajac, N. Maintenance Management Model for Nonurban Road Network. Infrastructures 2022, 7, 80. [Google Scholar] [CrossRef]
- Piratla, K.R.; Jin, H.; Yazdekhasti, S. A Failure Risk-Based Culvert Renewal Prioritization Framework. Infrastructures 2019, 4, 43. [Google Scholar] [CrossRef]
- Harputlugil, T.; Prins, M.; Gultekin, T.; Topcu, I. Conceptual Framework for Potential Implementations of Multi Criteria Decision Making (MCDM) Methods for Design Quality Assessment; Management and Innovation for a Sustainable Built Environment: Amsterdam, The Netherlands, 2011; pp. 20–23. [Google Scholar]
- Saaty, T. Decision Making with Dependence and Feedback: The Analytic Network Process: The Organization and Prioritization of Complexity; Analytic Hierarchy Process Series; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Saaty, T.; Vargas, L. Decision Making with Dependence and Feedback: The Analytic Network Process: The Organization and Prioritization of Complexity; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 1996. [Google Scholar]
- Hwang, G.; Han, J.H.; Chang, T.W. An Integrated Key Performance Measurement for Manufacturing Operations Management. Sustainability 2020, 12, 5260. [Google Scholar] [CrossRef]
- Hwang, C.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications A State-of-the-Art Survey; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Brans, J.P.; Mareschal, B. Promethee Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: New York, NY, USA, 2005; pp. 163–186. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Nguyen, T.L.; Nguyen, T.G.; Nguyen, D.T.; Tran, T.H.; Le, H.C.; Phung, H.T. A Cross-Country European Efficiency Measurement of Maritime Transport: A Data Envelopment Analysis Approach. Axioms 2022, 11, 206. [Google Scholar] [CrossRef]
- Wang, C.N.; Yang, F.C.; Vo, N.T.M.; Nguyen, V.T.T. Enhancing Lithium-Ion Battery Manufacturing Efficiency: A Comparative Analysis Using DEA Malmquist and Epsilon-Based Measures. Batteries 2023, 9, 317. [Google Scholar] [CrossRef]
- Wang, C.N.; Nguyen, T.L.; Dang, T.T. Analyzing Operational Efficiency in Real Estate Companies: An Application of GM (1,1) and DEA Malmquist Model. Mathematics 2021, 9, 202. [Google Scholar] [CrossRef]
- Stecyk, A. The AHP-TOPSIS Model in the Analysis of the Counties Sustainable Development in the West Pomeranian Province in 2010 and 2017. J. Ecol. Eng. 2019, 20, 233–244. [Google Scholar] [CrossRef] [PubMed]
- Sindhu, S.; Nehra, V.; Luthra, S. Investigation of feasibility study of solar farms deployment using hybrid AHP-TOPSIS analysis: Case study of India. Renew. Sustain. Energy Rev. 2017, 73, 496–511. [Google Scholar] [CrossRef]
- Wang, C.N.; Nguyen, N.A.T.; Dang, T.T.; Bayer, J. A Two-Stage Multiple Criteria Decision Making for Site Selection of Solar Photovoltaic (PV) Power Plant: A Case Study in Taiwan. IEEE Access 2021, 9, 75509–75525. [Google Scholar] [CrossRef]
- Opricovic, S. Programski paket VIKOR za visekriterijumsko kompromisno rangiranje. In Proceedings of the 17th International Symposium on Operational Research SYM-OP-IS, Kupari, Croatia, 9–12 October 1990. [Google Scholar]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- San Cristóbal, J. Multi-criteria decision-making in the selection of a renewable energy project in spain: The Vikor method. Renew. Energy 2011, 36, 498–502. [Google Scholar] [CrossRef]
- Soner, O.; Celik, E.; Akyuz, E. Application of AHP and VIKOR methods under interval type 2 fuzzy environment in maritime transportation. Ocean Eng. 2017, 129, 107–116. [Google Scholar] [CrossRef]
- Stević, Z.; Tanackov, I.; Vasiljević, M.; Vesković, S. Evaluation in Logistics using Combined Ahp and Edas Method. In Proceedings of the Simpozijum O Operacionim Istraživanjima, Jasikovice, Serbia, 20–23 September 2016. [Google Scholar]
- Wang, C.N.; Yang, F.C.; Vo, T.M.N.; Nguyen, V.T.T.; Singh, M. Enhancing Efficiency and Cost-Effectiveness: A Groundbreaking Bi-Algorithm MCDM Approach. Appl. Sci. 2023, 13, 9105. [Google Scholar] [CrossRef]
- Kahraman, C.; Keshavarz-Ghorabaee, M.; Zavadskas, E.; Çevik, S.; Yazdani, M.; Öztayşi, B. Intuitionistic fuzzy EDAS method: An application to solid waste disposal site selection. J. Environ. Eng. Landsc. Manag. 2017, 25, 1–12. [Google Scholar] [CrossRef]
- Ishizaka, A.; Lusti, M. How to derive priorities in AHP: A comparative study. Cent. Eur. J. Oper. Res. 2006, 14, 387–400. [Google Scholar] [CrossRef]
- Golden, B.L.; Wang, Q. An Alternate Measure of Consistency. In The Analytic Hierarchy Process: Applications and Studies; Golden, B.L., Wasil, E.A., Harker, P.T., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 68–81. [Google Scholar] [CrossRef]
- Alonso, J.; Lamata, M. Estimation of the random index in the analytic hierarchy process. In Proceedings of the Information Processing and Management of Uncertainty in Knowledge-Based Systems, Perugia, Italy, 4–9 July 2004; pp. 317–322. [Google Scholar]
- Forman, E.; Peniwati, K. Aggregating individual judgments and priorities with the analytic hierarchy process. Eur. J. Oper. Res. 1998, 108, 165–169. [Google Scholar] [CrossRef]
- Stirn, L.Z.; Groselj, P. Estimating Priorities in Group AHP Using Interval Comparison Matrices. Mult. Criteria Decis. Mak. 2013, 8, 143–159. [Google Scholar]
- Saaty, T. Decision making with the Analytic Hierarchy Process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Saaty, T.; Sagir Ozdemir, M. Why the magic number seven plus or minus two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
- Gawlik, R. Preliminary Criteria Reduction for the Application of Analytic Hierarchy Process Method. In Evolution and Revolution in the Global Economy: Enhancing Innovation and Competitiveness Worldwide; Global Business and Technology Association: New York, NY, USA, 2008; pp. 366–374. [Google Scholar]
- Centralny Rejestr Zagrożeń (Central Threat Register). Available online: https://www.emag.lukasiewicz.gov.pl/pl/szczegoly-projektow (accessed on 1 October 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).