The Structural Reliability of the Usumacinta Bridge Using InSAR Time Series of Semi-Static Displacements
Abstract
:1. Introduction
2. Case Study
3. Methodology
3.1. PS InSAR
3.2. Reliability Index
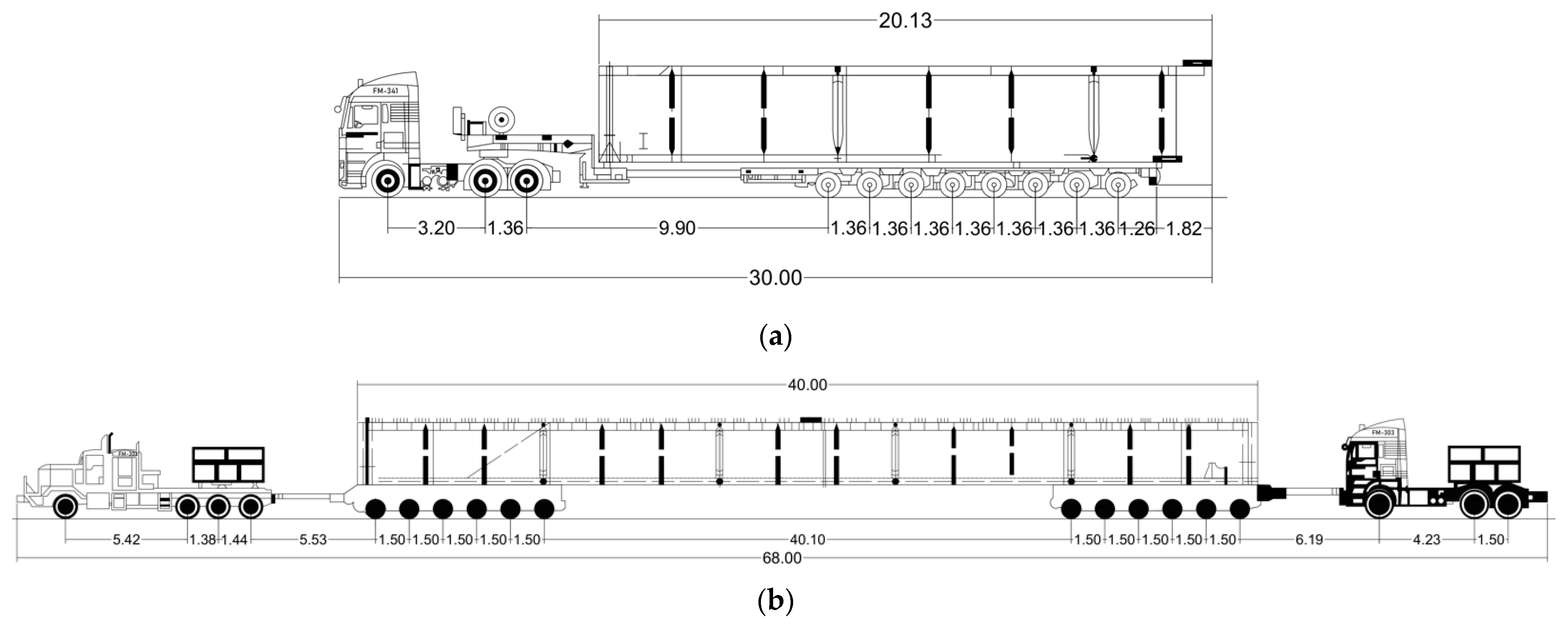
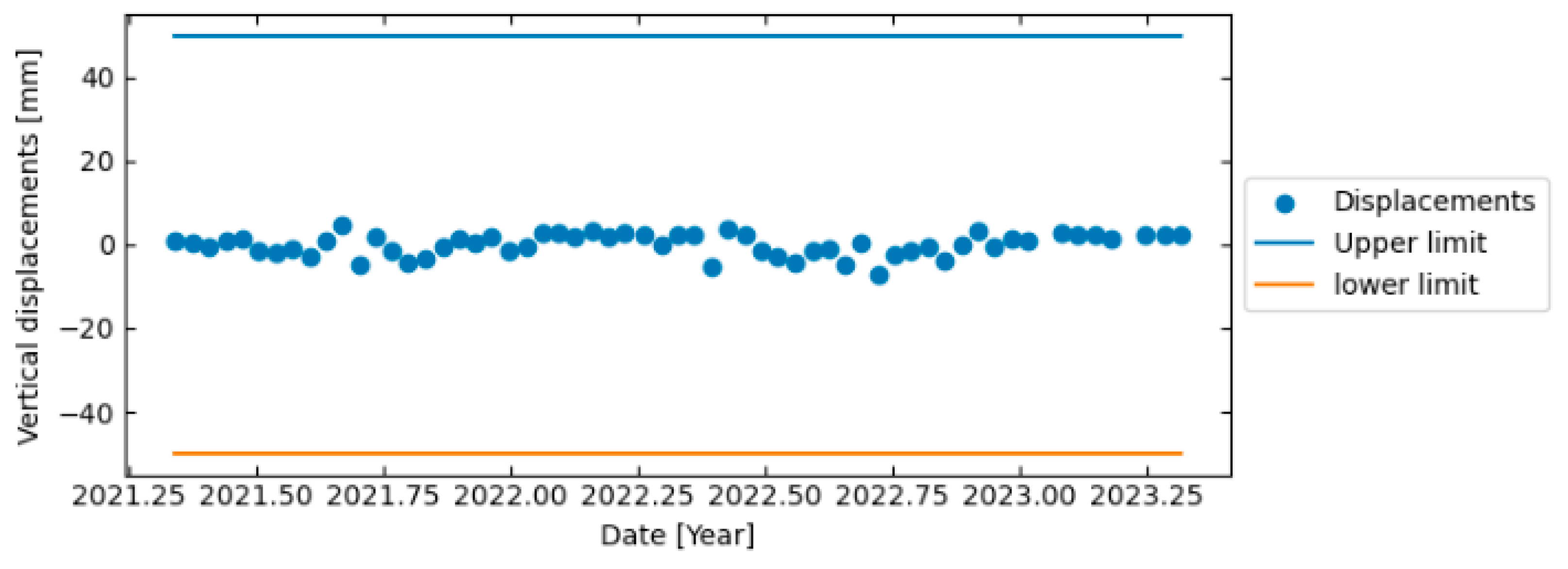
4. Controlled Testing Using CR
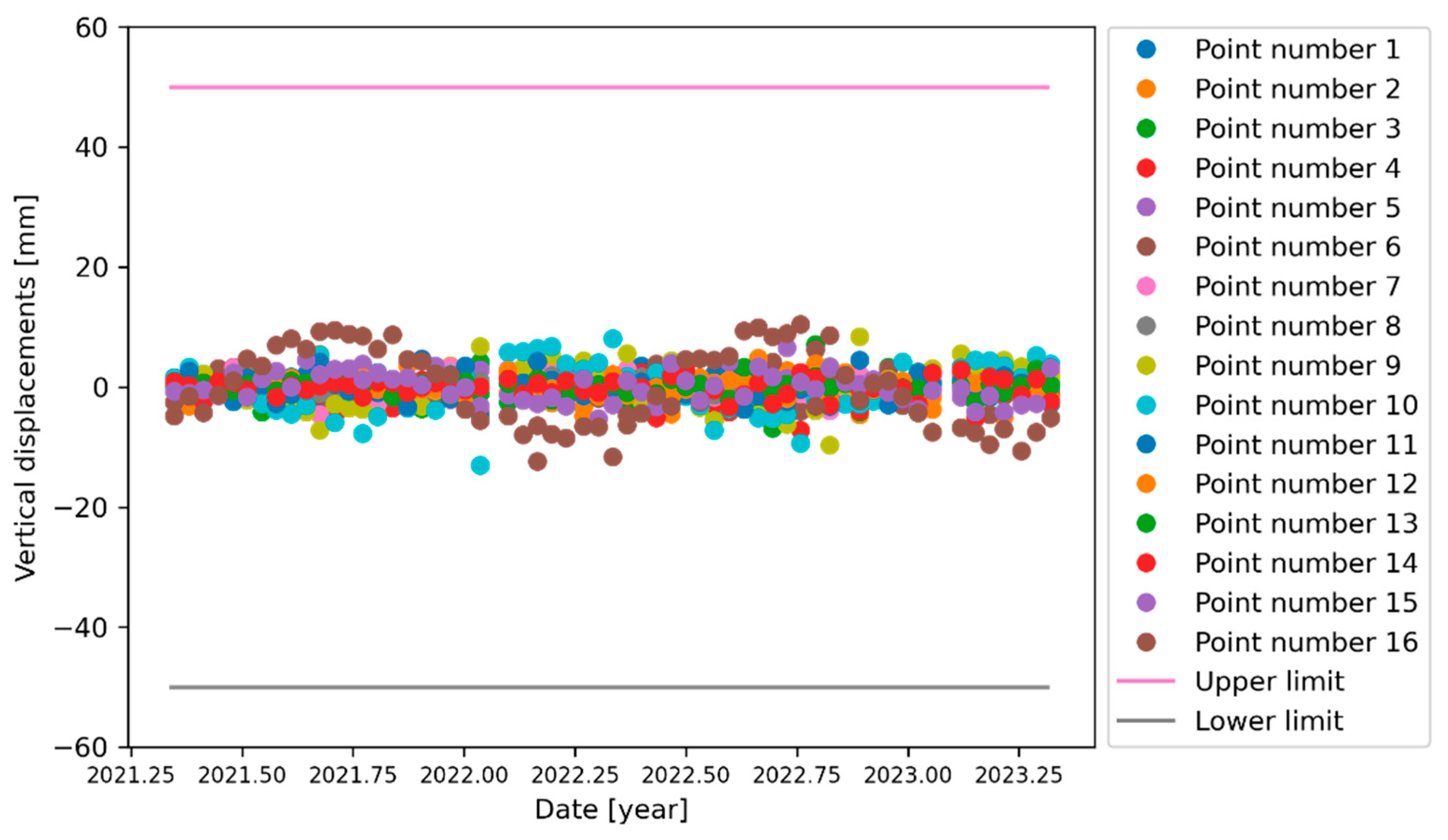
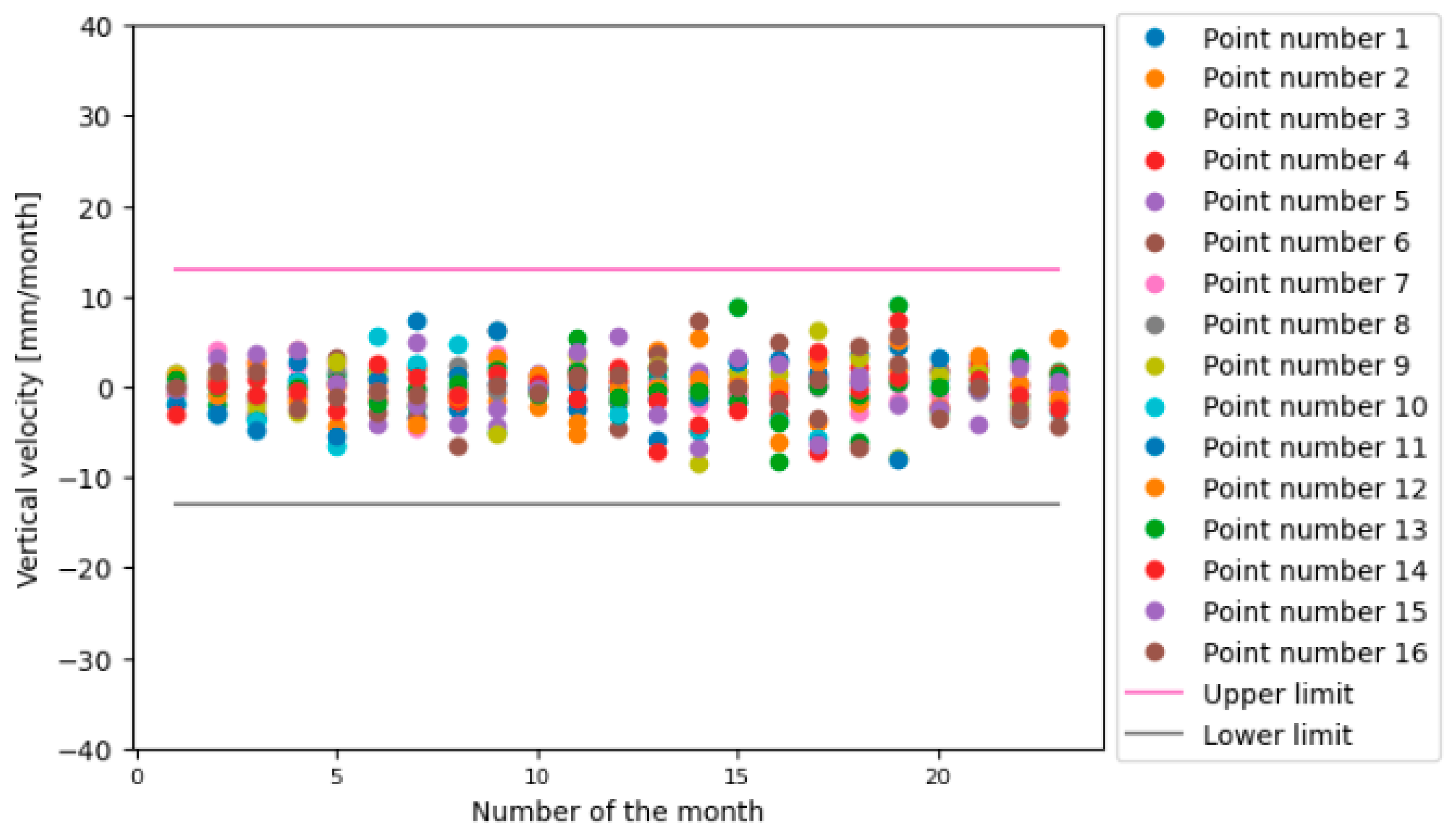
5. Field Testing on the Usumacinta Bridge
Structural Reliability of the Usumacinta Bridge
6. Discussion
7. Conclusions
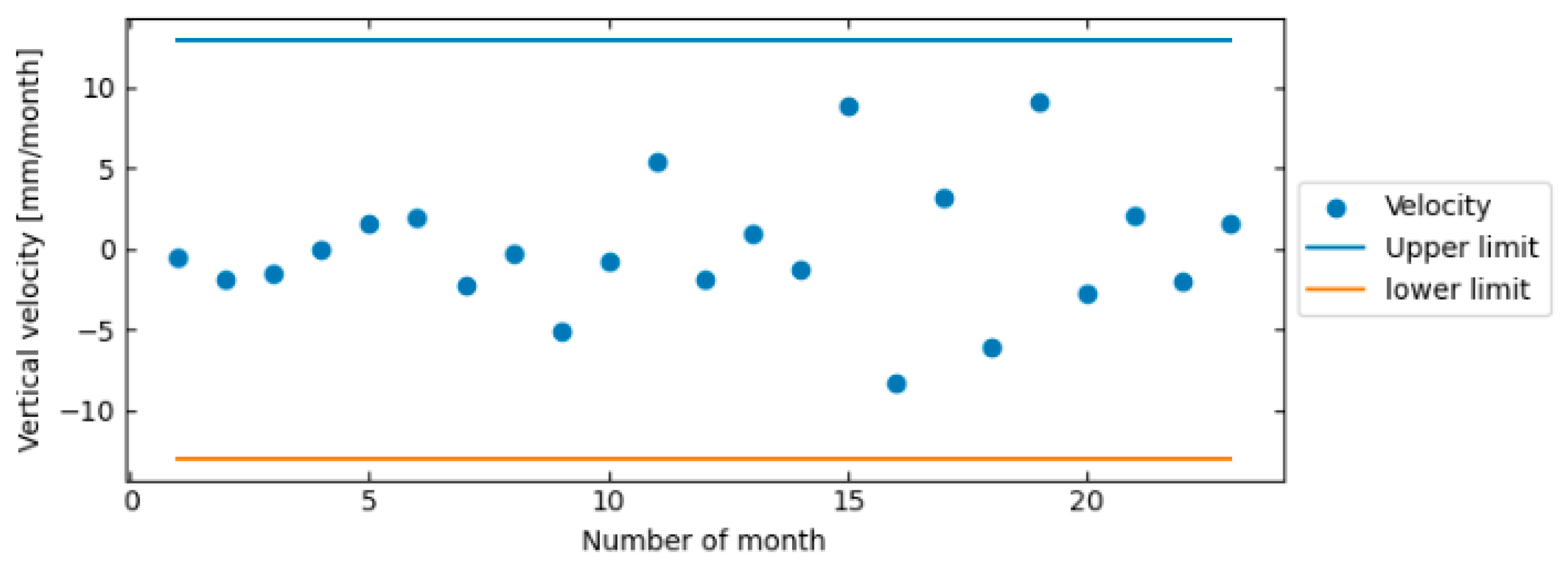
- The displacements of the Usumacinta Bridge achieved a maximum reliability index value (β) of 8.1 and a minimum one of 3.4. The mean value of β was 5.9, and the standard deviation was 1.4. On the other hand, the calculated monthly velocities presented a maximum probability of risk (PR) of 2.61%. The minimum value was 1.5 × 10−5%, the mean 0.4%, and the standard deviation 0.8%. Based on the results, it can be established that the areas of the bridge analyzed did not present damages produced by the heavy vehicles overloading the main structure.
- InSAR is a useful technology to determine the semi-static displacements of bridges and estimate their structural reliability. Therefore, a support decision system can be developed to improve the quality of the road infrastructure with the methodology presented in this manuscript.
- Due to the Sentinel-1 image resolution, a few zones of the bridge were analyzed, which represents a general idea of the actual reliability of the Usumacinta Bridge. An ideal assessment would be a study in detail of the bridge considering the relevant structural elements. This can be accomplished using commercial images and corner reflectors.
- The proposed probabilistic assessment can be improved by using specific limit states for each structure instead of employing a general one. In addition, more PDFs can be integrated into the methodology to obtain the structural risk.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vazquez-Ontiveros, J.R.; Vazquez-Becerra, G.E.; Quintana, J.A.; Carrion, F.J.; Guzman-Acevedo, G.M.; Gaxiola-Camacho, J.R. Implementation of PPP-GNSS measurement technology in the probabilistic SHM of bridge structures. Measurement 2021, 173, 108677. [Google Scholar] [CrossRef]
- Korolkov, I.V.; Zhumanazar, N.; Gorin, Y.G.; Yeszhanov, A.B.; Zdorovets, M.V. Enhancement of electrochemical detection of Pb 2+ by sensor based on track-etched membranes modified with interpolyelectrolyte complexes. J. Mater. Sci. Mater. Electron. 2020, 31, 20368–20377. [Google Scholar] [CrossRef]
- Shlimas, D.I.; Kozlovskiy, A.L.; Zdorovets, M.V. Study of the formation effect of the cubic phase of LiTiO2 on the structural, optical, and mechanical properties of Li2±xTi1±xO3 ceramics with different contents of the X component. J. Mater. Sci. Mater. Electron. 2021, 32, 7410–7422. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Algarou, N.A.; Slimani, Y.; Sadaqat, A.; Baykal, A.; Manikandan, A.; Trukhanov, S.V.; Trukhanov, A.V.; Ercan, I. Investigation of exchange coupling and microwave properties of hard/soft (SrNi0.02Zr0.01Fe11.96O19)/(CoFe2O4)x nanocomposites. Mater. Today Nano 2022, 18, 100186. [Google Scholar] [CrossRef]
- Zhumatayeva, I.Z.; Kenzhina, I.E.; Kozlovskiy, A.L.; Zdorovets, M.V. The study of the prospects for the use of Li0.15Sr0.85TiO3 ceramics. J. Mater. Sci. Mater. Electron. 2020, 31, 6764–6772. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; Machorro-Lopez, J.M.; Amezquita-Sanchez, J.P.; Dominguez-Gonzalez, A.; Alvarez-Junco, S.; Gasca-Zamora, H.M. A new damage indicator based on homogeneity and wireless accelerometers for evaluating the structural condition of a cable-stayed bridge. Dev. Built Environ. 2023, 14, 100166. [Google Scholar] [CrossRef]
- Dong, C.Z.; Catbas, F.N. A review of computer vision–based structural health monitoring at local and global levels. Struct. Health Monit. 2021, 20, 692–743. [Google Scholar] [CrossRef]
- Perissin, D. Interferometric SAR multitemporal processing: Techniques and applications. In Multitemporal Remote Sensing: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 145–176. [Google Scholar]
- Selvakumaran, S.; Plank, S.; Geiß, C.; Rossi, C.; Middleton, C. Remote monitoring to predict bridge scour failure using Interferometric Synthetic Aperture Radar (InSAR) stacking techniques. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 463–470. [Google Scholar] [CrossRef]
- Sousa, J.J.; Bastos, L. Multi-temporal SAR interferometry reveals acceleration of bridge sinking before collapse. Nat. Hazards Earth Syst. Sci. 2013, 13, 659–667. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.J.; Palanisamy Vadivel, S.K.; Yun, S.H. Long-term deflection monitoring for bridges using X and C-band time-series SAR interferometry. Remote Sens. 2019, 11, 1258. [Google Scholar] [CrossRef]
- Vadivel, S.K.P.; Kim, D.J.; Kim, Y.C. Time-series InSAR Analysis and Post-processing Using ISCE-StaMPS Package for Measuring Bridge Displacements. Korean J. Remote Sens. 2020, 36, 527–534. [Google Scholar] [CrossRef]
- Cusson, D.; Trischuk, K.; Hébert, D.; Hewus, G.; Gara, M.; Ghuman, P. Satellite-based InSAR monitoring of highway bridges: Validation case study on the North Channel Bridge in Ontario, Canada. Transp. Res. Rec. 2018, 2672, 76–86. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Pre-collapse space geodetic observations of critical infrastructure: The Morandi Bridge, Genoa, Italy. Remote Sens. 2019, 11, 1403. [Google Scholar] [CrossRef]
- Lanari, R.; Reale, D.; Bonano, M.; Verde, S.; Muhammad, Y.; Fornaro, G.; Casu, F.; Manunta, M. Comment on “pre-collapse space geodetic observations of critical infrastructure: The morandi bridge, Genoa, Italy” by Milillo et al. (2019). Remote Sens. 2020, 12, 4011. [Google Scholar] [CrossRef]
- Milillo, P.; Giardina, G.; Perissin, D.; Milillo, G.; Coletta, A.; Terranova, C. Reply to Lanari, R. et al. comment on “pre-collapse space geodetic observations of critical infrastructure: The morandi bridge, Genoa, Italy” by Milillo et al. (2019). Remote Sens. 2020, 12, 4016. [Google Scholar] [CrossRef]
- Schlögl, M.; Widhalm, B.; Avian, M. Comprehensive time-series analysis of bridge deformation using differential satellite radar interferometry based on Sentinel-1. ISPRS J. Photogramm. Remote Sens. 2021, 172, 132–146. [Google Scholar] [CrossRef]
- Ma, P.; Li, T.; Fang, C.; Lin, H. A tentative test for measuring the sub-millimeter settlement and uplift of a high-speed railway bridge using COSMO-SkyMed images. ISPRS J. Photogramm. Remote Sens. 2019, 155, 1–12. [Google Scholar] [CrossRef]
- Xiong, S.; Wang, C.; Qin, X.; Zhang, B.; Li, Q. Time-series analysis on persistent scatter-interferometric synthetic aperture radar (PS-InSAR) derived displacements of the Hong Kong–Zhuhai–Macao Bridge (HZMB) from Sentinel-1A observations. Remote Sens. 2021, 13, 546. [Google Scholar] [CrossRef]
- Huang, Q.; Crosetto, M.; Monserrat, O.; Crippa, B. Displacement monitoring and modelling of a high-speed railway bridge using C-band Sentinel-1 data. ISPRS J. Photogramm. Remote Sens. 2017, 128, 204–211. [Google Scholar] [CrossRef]
- Qin, X.; Li, Q.; Ding, X.; Xie, L.; Wang, C.; Liao, M.; Zhang, L.; Zhang, B.; Xiong, S. A structure knowledge-synthetic aperture radar interferometry integration method for high-precision deformation monitoring and risk identification of sea-crossing bridges. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102476. [Google Scholar] [CrossRef]
- JTGT H21-2011; Evaluation Standard for Technical Conditions of Highway Bridges. Highway Research Institute, Ministry of Transport: Beijing, China, 2011.
- Acton, S. InSAR Remote Sensing for Performance Monitoring of Transportation Infrastructure at the Network Level; Final Report No. RITARS-14-H-UVA; University of Virginia: Charlottesville, VA, USA, 2016. [Google Scholar]
- Cusson, D.; Rossi, C.; Ozkan, I.F. Early warning system for the detection of unexpected bridge displacements from radar satellite data. J. Civ. Struct. Health Monit. 2021, 11, 189–204. [Google Scholar] [CrossRef]
- Giordano, P.F.; Turksezer, Z.I.; Previtali, M.; Limongelli, M.P. Damage detection on a historic iron bridge using satellite DInSAR data. Struct. Health Monit. 2022, 21, 2291–2311. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Farneti, E.; Cavalagli, N.; Costantini, M.; Trillo, F.; Minati, F.; Venanzi, I.; Ubertini, F. A method for structural monitoring of multispan bridges using satellite InSAR data with uncertainty quantification and its pre-collapse application to the Albiano-Magra Bridge in Italy. Struct. Health Monit. 2023, 22, 353–371. [Google Scholar] [CrossRef]
- AASHTO. Highway Safety Manual; American Association of State and Highway Transportation Officials: Washington, DC, USA, 2010. [Google Scholar]
- Nowak, A.S.; Collins, K.R. Reliability of Structures; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Haldar, A.; Azizsoltani, H.; Gaxiola-Camacho, J.R.; Vazirizade, S.M.; Huh, J. Reliability Evaluation of Dynamic Systems Excited in Time Domain-Redset: Alternative to Random Vibration and Simulation; John Wiley Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Monjardin-Quevedo, J.G.; Valenzuela-Beltran, F.; Reyes-Salazar, A.; Leal-Graciano, J.M.; Torres-Carrillo, X.G.; Gaxiola-Camacho, J.R. Probabilistic assessment of buildings subjected to multi-level earthquake loading based on the PBSD concept. Buildings 2022, 12, 1942. [Google Scholar] [CrossRef]
- Lemaire, M. Structural Reliability; Wiley-ISTE: New York, NY, USA, 2009. [Google Scholar]
- Garthwaite, M.C. On the design of radar corner reflectors for deformation monitoring in multi-frequency InSAR. Remote Sens. 2017, 9, 648. [Google Scholar] [CrossRef]
- Adam, N.; Kampes, B.; Eineder, M. Development of a scientific permanent scatterer system: Modifications for mixed ERS/ENVISAT time series. In Proceedings of the 2004 Envisat ERS Symposium (ESA SP-572), Salzburg, Austria, 6–10 September 2004. [Google Scholar]
- Nahli, A.; Simonetto, E.; Tatin, M.; Durand, S.; Morel, L.; Lamour, V. On the combination of PsInsar and GNSS techniques for long-term bridge monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 325–332. [Google Scholar] [CrossRef]
- Qin, Y.; Perissin, D.; Lei, L. The design and experiments on corner reflectors for urban ground deformation monitoring in Hong Kong. Int. J. Antennas Propag. 2013, 2013, 191685. [Google Scholar] [CrossRef]
- Algafsh, A.; Inggs, M.; Mishra, A.K. The effect of perforating the corner reflector on maximum radar cross section. In Proceedings of the 2016 16th Mediterranean Microwave Symposium (MMS), Abu Dhabi, United Arab Emirates, 14–16 November 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Hoppe, E.J.; Novali, F.; Rucci, A.; Fumagalli, A.; Del Conte, S.; Falorni, G.; Toro, N. Deformation monitoring of posttensioned bridges using high-resolution satellite remote sensing. J. Bridge Eng. 2019, 24, 04019115. [Google Scholar] [CrossRef]
- Perissin, D.; Wang, T. Repeat-pass SAR interferometry with partially coherent targets. IEEE Trans. Geosci. Remote Sens. 2011, 50, 271–280. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter accuracy of InSAR time series: Experimental validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- SARPROZ Office Webpage. 2023. Available online: https://www.sarproz.com/ (accessed on 26 November 2023).







| Image Mode | Azimuthal Resolution (m) | Slant Range Resolution (m) | Ground Range Resolution (m) | Ground Range Resolution Area (m2) | Clutter (dB) |
|---|---|---|---|---|---|
| Interferometric wide swath | 20.0 | 5.0 | 8.7 | 174.3 | −12 |
| Number of the Test | Ground Truth (mm) | InSAR Displacements (mm) | Differences (mm) |
|---|---|---|---|
| 1 | 0 | 1 | 1 |
| 2 | 0 | 1.6 | 1.6 |
| 3 | 0 | 1 | 1 |
| 4 | 7.9 | 10 | 2.1 |
| 5 | 7.9 | 8.4 | 0.5 |
| 6 | 15.8 | 14.4 | −1.4 |
| Number of the Test | Ground Truth (mm) | InSAR Displacements (mm) | Differences (mm) |
|---|---|---|---|
| 1 | 0 | 0.2 | 0.2 |
| 2 | 0 | 0.2 | 0.2 |
| 3 | 0 | 1.2 | 1.2 |
| 4 | 7.9 | 9.1 | 1.2 |
| 5 | 7.9 | 8.2 | 0.3 |
| 6 | 15.8 | 14.6 | −1.2 |
| Number of the Point | Velocity (mm/year) | Cumulative Displacements (mm) |
|---|---|---|
| 1 | −3.5 ± 1.4 | −7 |
| 2 | −0.5 ± 0.35 | −1 |
| 3 | −0.66 ± 0.45 | −1.3 |
| 4 | −0.8 ± 0.59 | −1.6 |
| 5 | 0.37 ± 0.59 | 0.8 |
| 6 | 0.45 ± 0.59 | 0.9 |
| 7 | −0.2 ± 0.34 | −0.4 |
| 8 | −0.45 ± 0.57 | −0.9 |
| 9 | −0.19 ± 0.37 | −0.4 |
| 10 | 0.51 ± 0.4 | 1 |
| 11 | 0.37 ± 0.28 | 0.8 |
| 12 | 1.68 ± 0.8 | 3.4 |
| 13 | −0.83 ± 0.56 | −1.6 |
| 14 | 1.22 ± 0.9 | 2.4 |
| 15 | −0.29 ± 0.39 | −0.6 |
| 16 | −0.23 ± 0.49 | −0.4 |
| Number of the Point | Mean Velocity (mm/month) | Standard Deviation (mm) |
|---|---|---|
| 1 | −0.37 | 2.45 |
| 2 | 0.71 | 3.23 |
| 3 | −1.59 | 4.13 |
| 4 | −0.38 | 3.39 |
| 5 | 0.1 | 2.29 |
| 6 | −0.003 | 3.34 |
| 7 | 0.06 | 2.12 |
| 8 | 0.14 | 1.44 |
| 9 | 0.7 | 3.56 |
| 10 | 0.77 | 5.03 |
| 11 | 0.57 | 3.53 |
| 12 | 0.26 | 2.06 |
| 13 | −0.23 | 1.45 |
| 14 | −0.25 | 2.47 |
| 15 | 0.59 | 3.31 |
| 16 | 0.64 | 2.92 |
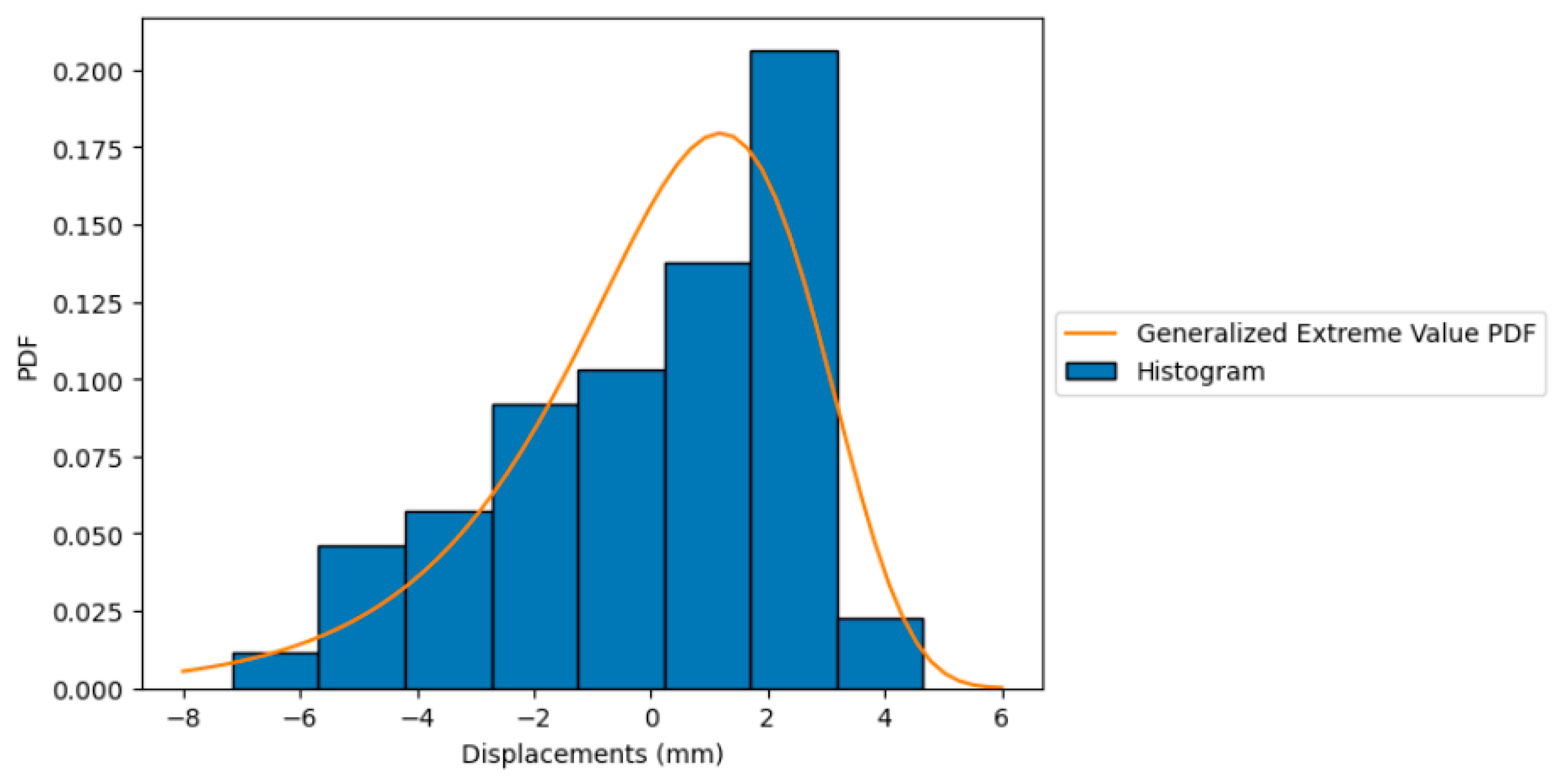
| Point | Best-Fitted PDF | β |
|---|---|---|
| 1 | Extreme Value | 8.1 |
| 2 | Extreme Value | 6.6 |
| 3 | Weibull | 6.1 |
| 4 | Generalized Extreme Value | 6.7 |
| 5 | Extreme Value | 7.5 |
| 6 | Extreme Value | 6.0 |
| 7 | Weibull | 7.6 |
| 8 | Stable | 5.2 |
| 9 | Extreme Value | 4.9 |
| 10 | Stable | 3.4 |
| 11 | Extreme Value | 6.5 |
| 12 | Weibull | 7.2 |
| 13 | T Location Scale | 5.9 |
| 14 | Stable | 3.6 |
| 15 | Extreme Value | 5.9 |
| 16 | Weibull | 3.7 |
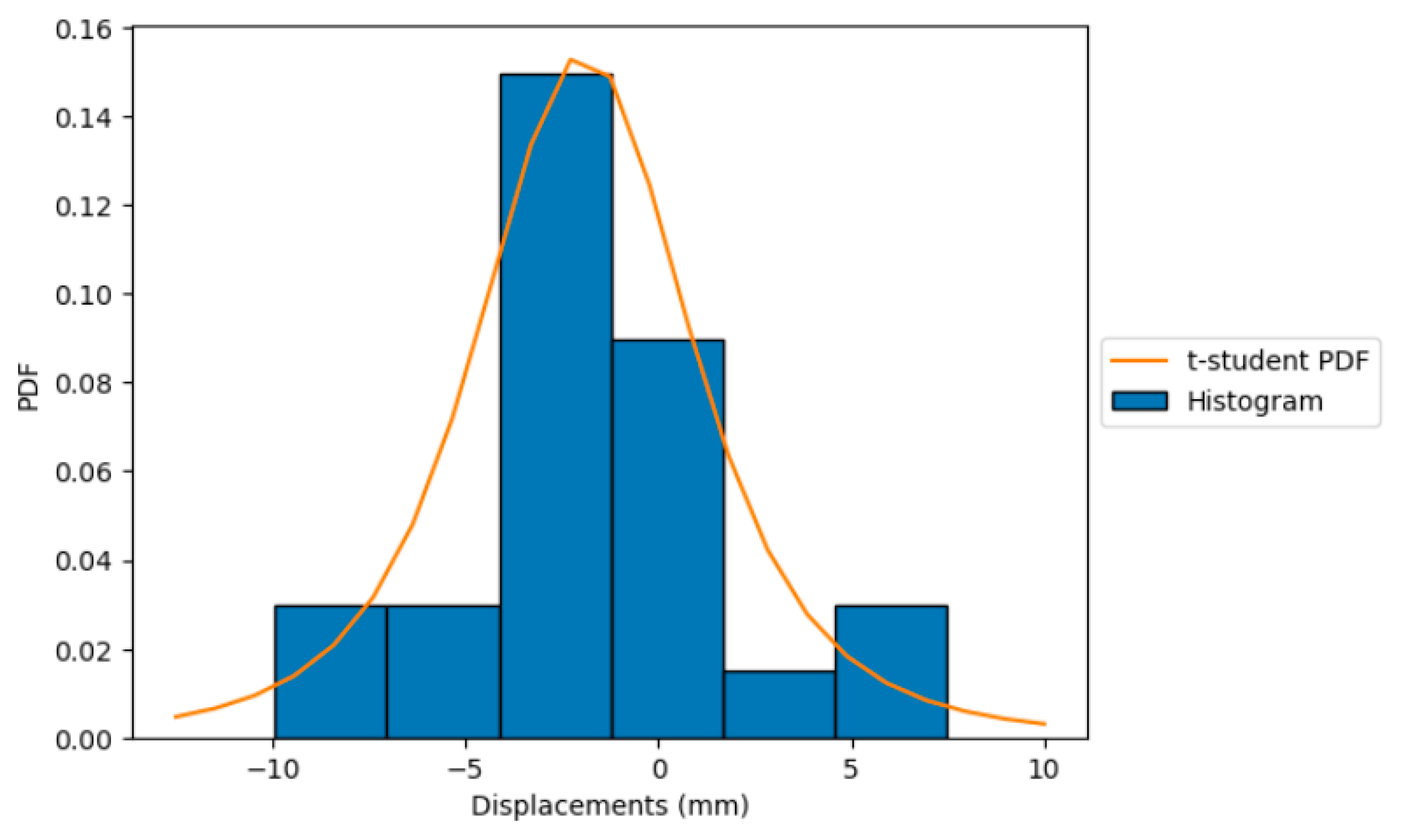
| Point | Best-Fitted PDF | PR |
|---|---|---|
| 1 | Logistic | 0.013 |
| 2 | Logistic | 0.17 |
| 3 | t student | 1.64 |
| 4 | Stable | 2.61 |
| 5 | Logistic | 0.006 |
| 6 | Fatigue life | 0.012 |
| 7 | Fisk | 0.036 |
| 8 | Logistic | 1.5 × 10−5 |
| 9 | Stable | 1.78 |
| 10 | Generalized Extreme Value | 8.4 × 10−5 |
| 11 | Logistic | 0.22 |
| 12 | Logistic | 0.002 |
| 13 | Stable | 0.001 |
| 14 | Logistic | 0.001 |
| 15 | Generalized Extreme Value | 0.03 |
| 16 | t student | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzman-Acevedo, G.M.; Quintana-Rodriguez, J.A.; Gaxiola-Camacho, J.R.; Vazquez-Becerra, G.E.; Torres-Moreno, V.; Monjardin-Quevedo, J.G. The Structural Reliability of the Usumacinta Bridge Using InSAR Time Series of Semi-Static Displacements. Infrastructures 2023, 8, 173. https://doi.org/10.3390/infrastructures8120173
Guzman-Acevedo GM, Quintana-Rodriguez JA, Gaxiola-Camacho JR, Vazquez-Becerra GE, Torres-Moreno V, Monjardin-Quevedo JG. The Structural Reliability of the Usumacinta Bridge Using InSAR Time Series of Semi-Static Displacements. Infrastructures. 2023; 8(12):173. https://doi.org/10.3390/infrastructures8120173
Chicago/Turabian StyleGuzman-Acevedo, German Michel, Juan A. Quintana-Rodriguez, Jose Ramon Gaxiola-Camacho, Guadalupe Esteban Vazquez-Becerra, Vanessa Torres-Moreno, and Jesus Guadalupe Monjardin-Quevedo. 2023. "The Structural Reliability of the Usumacinta Bridge Using InSAR Time Series of Semi-Static Displacements" Infrastructures 8, no. 12: 173. https://doi.org/10.3390/infrastructures8120173
APA StyleGuzman-Acevedo, G. M., Quintana-Rodriguez, J. A., Gaxiola-Camacho, J. R., Vazquez-Becerra, G. E., Torres-Moreno, V., & Monjardin-Quevedo, J. G. (2023). The Structural Reliability of the Usumacinta Bridge Using InSAR Time Series of Semi-Static Displacements. Infrastructures, 8(12), 173. https://doi.org/10.3390/infrastructures8120173







