A Study on the Genetic Algorithm Optimization of an Asphalt Mixture’s Viscoelastic Parameters Based on a Wheel Tracking Test
Abstract
:1. Introduction
2. Methodology
2.1. Optimization Objects
2.2. Kriging Surrogate Model
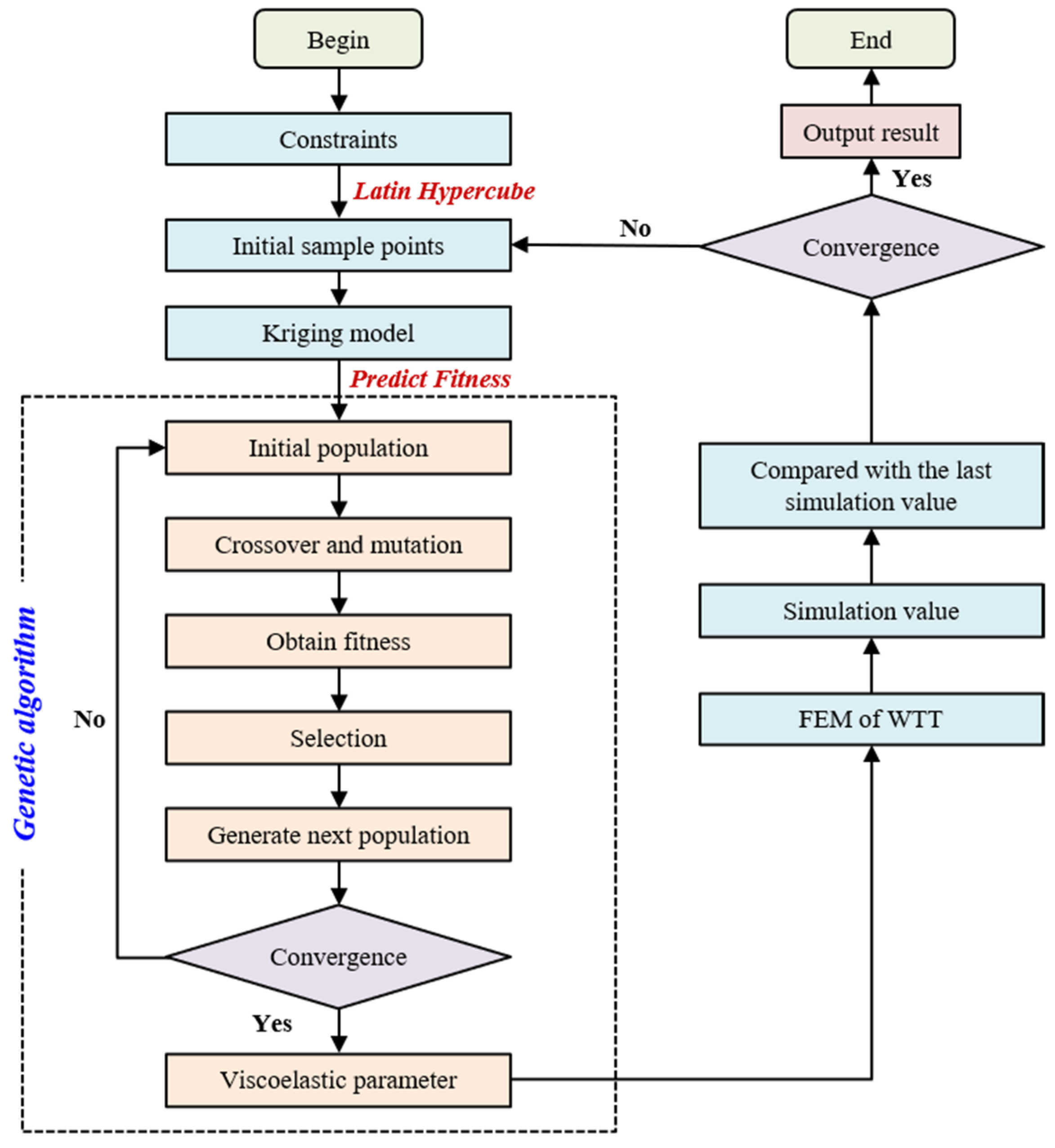
2.3. Optimal Algorithm
- (1)
- According to the constraints in the optimization model, the initial sample points selected randomly using the LHS method are used to establish the initial Kriging “response surface”.
- (2)
- Genetic algorithms are utilized to obtain the optimal solution in this “response surface”.
- (3)
- The true values of the optimization results are calculated using the FEM simulations and this set of true values is added to the initial sample points to renew the Kriging “response surface”.
- (4)
- The second and third steps are looped until the difference between the optimization results SAE of the two adjacent ones is less than 1.
3. Materials and Experiment
3.1. Material Properties
3.2. Wheel Tracking Test
3.3. Uniaxial Compression Test
4. Results and Discussion
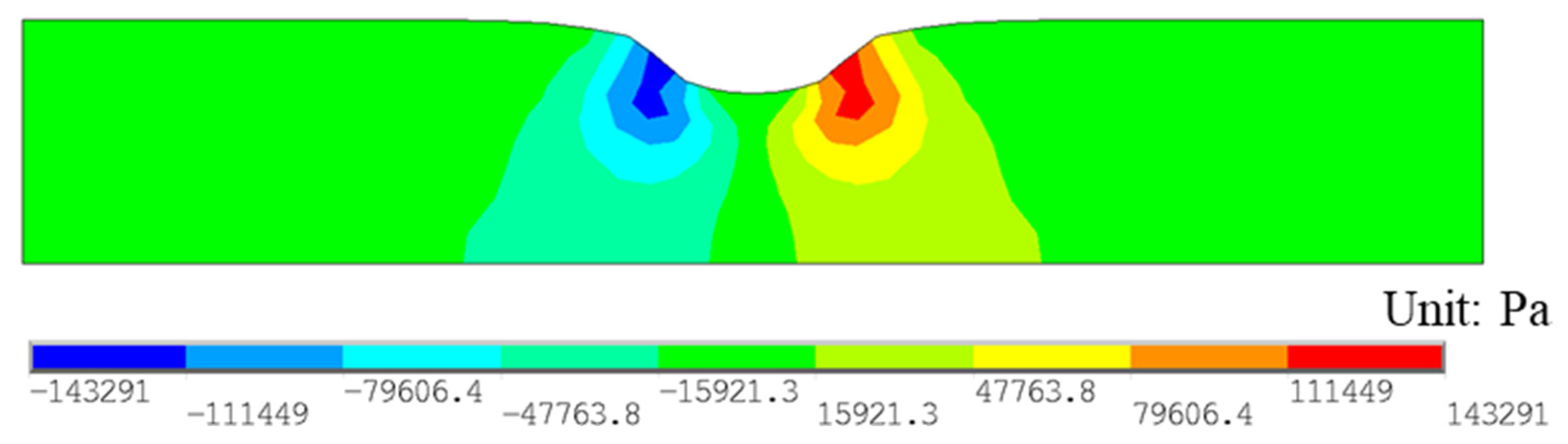
4.1. Finite Element Model Simulation of WTT
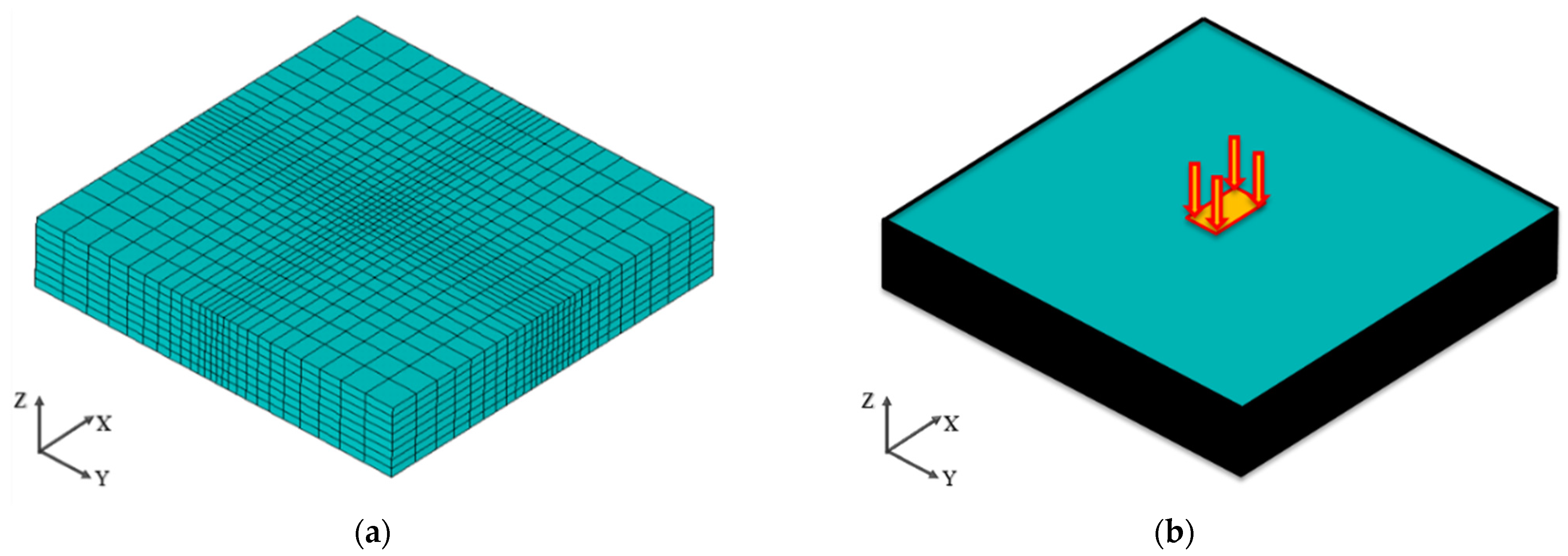
4.1.1. Elements Division
4.1.2. Loading Mode and Boundary Conditions
4.2. Implementation of the Proposed Method
4.3. Comparison of Simulation Results
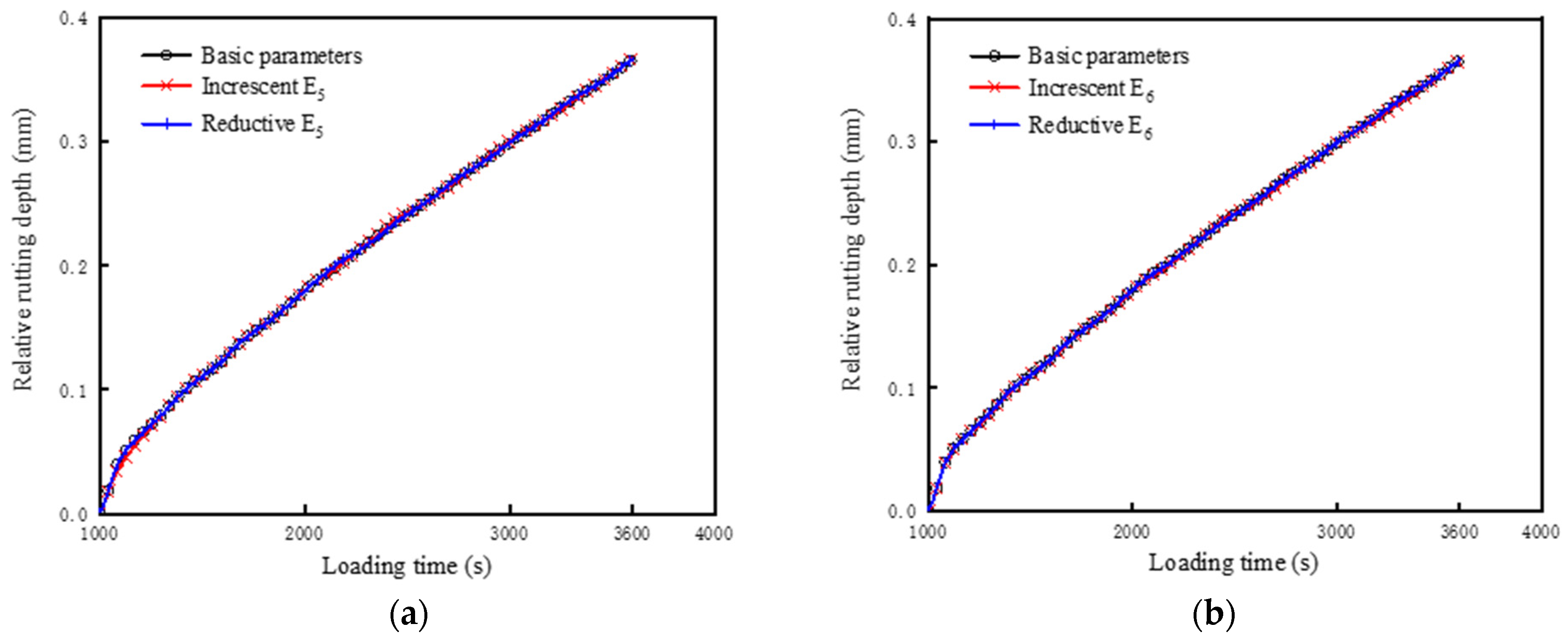
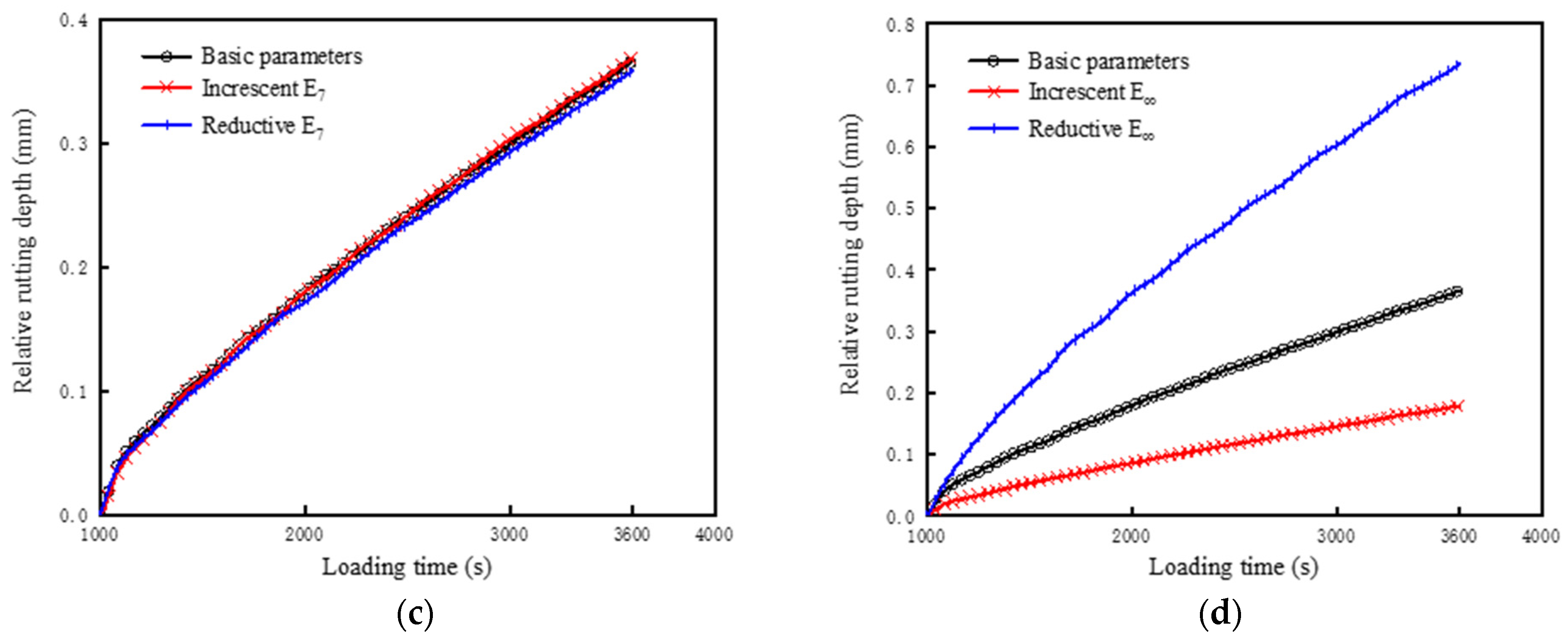
4.4. Sensitivity Analysis of Viscoelastic Parameters
5. Conclusions
- The generalized Maxwell model used in the finite element models could accurately reflect the rutting development of asphalt mixtures under high temperatures. The rutting depth variation curves obtained from the finite element models using the optimized parameters were in a high agreement with the WTT curve, showing that the proposed method could determine the viscoelastic parameters of the asphalt mixture for rutting study and prediction.
- Compared with experimental parameters, the optimized parameters could more accurately simulate the trend of the flow-type rutting depths and reflect the rutting resistance of the asphalt mixture compared to parameters from the experiment. In addition, there was a large error in the simulation of the rutting deformation with the viscoelastic parameters obtained under the uniaxial compression loading mode. This might be related to the inability of this loading mode to reflect the shear properties of the material.
- Among the 10 parameters mentioned above, the dynamic modulus corresponding to a larger relaxation time was more sensitive to the mechanical response of the asphalt mixture. The equilibrium modulus had the most significant influence on the growth rate and rutting depth. Therefore, the number of parameters can be appropriately reduced to improve the optimization efficiency in the subsequent parameters’ optimization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Zhang, Q.S.; Tan, J.Q. Investigation of Layer Contributions to Asphalt Pavement Rutting. J. Mater. Civ. Eng. 2009, 21, 181–185. [Google Scholar] [CrossRef]
- Guo, R.; Nian, T.F.; Zhou, F. Analysis of factors that influence anti-rutting performance of asphalt pavement. Constr. Build. Mater. 2020, 254, 119237. [Google Scholar] [CrossRef]
- Zhang, J.P.; Zhu, C.Z.; Li, X.Q.; Pei, J.Z.; Chen, J. Characterizing the three-stage rutting behavior of asphalt pavement with semi-rigid base by using UMAT in ABAQUS. Constr. Build. Mater. 2017, 140, 496–507. [Google Scholar] [CrossRef]
- Shan, L.Y.; Tan, Y.Q.; Zhang, H.; Xu, Y.A. Analysis of Linear Viscoelastic Response Function Model for Asphalt Binders. J. Mater. Civ. Eng. 2016, 28, 04016010. [Google Scholar] [CrossRef]
- Rameshkhah, S.; Olounabadi, M.M.; Malekzadeh, P.; Meraji, S.H. Dynamic response analysis of viscoelastic pavement using differential quadrature element method. Int. J. Pavement Eng. 2020, 21, 1321–1335. [Google Scholar] [CrossRef]
- Alimohammadi, H.; Zheng, J.X.; Buss, A.; Schaefer, V.R.; Williams, C.; Zheng, G.F. Field and simulated rutting behavior of hot mix and warm mix asphalt overlays. Constr. Build. Mater. 2020, 265, 120366. [Google Scholar] [CrossRef]
- Sun, Y.Z.; Gu, B.C.; Gao, L.; Li, L.J.; Guo, R.; Yue, Q.Q.; Wang, J.C. Viscoelastic Mechanical Responses of HMAP under Moving Load. Materials 2018, 11, 2490. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.L.; Wu, Y.; Chen, H.M.; Liu, S.N.; Huang, W.; Wang, H.Z.; Yang, J. Performance Evaluation and Structure Optimization of Low-Emission Mixed Epoxy Asphalt Pavement. Materials 2022, 15, 6472. [Google Scholar] [CrossRef]
- Chen, H.; Hoff, I.; Liu, G.; Zhang, X.M.; Barbieri, D.M.; Wang, F.S.; Liu, J.A. Development of finite element model based on indirect tensile test for various asphalt mixtures. Constr. Build. Mater. 2023, 394, 132085. [Google Scholar] [CrossRef]
- Ho, C.H.; Romero, P. Alternative Function to Represent Relaxation Modulus of Viscoelastic Materials. J. Mater. Civ. Eng. 2012, 24, 152–158. [Google Scholar] [CrossRef]
- Alae, M.; Ling, M.; Haghshenas, H.F.; Zhao, Y.Q. Three-dimensional finite element analysis of top-down crack propagation in asphalt pavements. Eng. Fract. Mech. 2021, 248, 107736. [Google Scholar] [CrossRef]
- Li, L.L.; Li, W.L.; Wang, H.; Zhao, J.N.; Wang, Z.Y.; Dong, M.S.; Han, D. Investigation of Prony series model related asphalt mixture properties under different confining pressures. Constr. Build. Mater. 2018, 166, 147–157. [Google Scholar] [CrossRef]
- Liu, H.Q.; Luo, R.; Lv, H.J. Establishing continuous relaxation spectrum based on complex modulus tests to construct relaxation modulus master curves in compliance with linear viscoelastic theory. Constr. Build. Mater. 2018, 165, 372–384. [Google Scholar] [CrossRef]
- Jamshidi, A.; White, G.; Hosseinpour, M. Revisiting the correlation between the dynamic modulus and the flexural modulus of hot mixture asphalt. Constr. Build. Mater. 2021, 296, 123697. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Partl, M.N.; Francken, L.; De La Roche Saint Andre, C. Stiffness testing for bituminous mixtures. Mater. Struct. 2001, 34, 66–70. [Google Scholar] [CrossRef]
- Chen, H.; Saba, R.G.; Liu, G.; Barbieri, D.M.; Zhang, X.M.; Hoff, I. Influence of material factors on the determination of dynamic moduli and associated prediction models for different types of asphalt mixtures. Constr. Build. Mater. 2023, 365, 130134. [Google Scholar] [CrossRef]
- Cui, L.L.; Ling, T.Q.; Sun, F.; Zhang, Z.Y.; Xin, J.Z. Study of in situ dynamic modulus prediction of asphalt mixture utilizing Ground penetrating radar technology. Constr. Build. Mater. 2022, 350, 128695. [Google Scholar] [CrossRef]
- Pronk, A.C. Calibration of 4PB Tests Taking into Account Shear Forces and other Equipment Factors. Road Mater. Pavement Des. 2009, 10, 373–386. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, C.H.; Wang, X.D. Comparison of HMA dynamic modulus between trapezoid beam test and SPT. J. Cent. South Univ. (Sci. Technol.) 2017, 48, 3092–3099. [Google Scholar]
- Ruan, L.; Luo, R.; Hu, X.D.; Pan, P. Effect of bell-shaped loading and haversine loading on the dynamic modulus and resilient modulus of asphalt mixtures. Constr. Build. Mater. 2018, 161, 124–131. [Google Scholar] [CrossRef]
- Qin, X.C.; Ma, L.; Wang, H. Comparison analysis of dynamic modulus of asphalt mixture: Indirect tension and uniaxial compression test. Transp. A-Transp. Sci. 2019, 15, 165–178. [Google Scholar] [CrossRef]
- Cheng, H.L.; Wang, Y.H.; Liu, L.P.; Sun, L.J. Effects of using different dynamic moduli on predicted asphalt pavement responses in mechanistic pavement design. Road Mater. Pavement Des. 2022, 23, 1860–1876. [Google Scholar] [CrossRef]
- Coleri, E.; Harvey, J.T.; Yang, K.; Boone, J.M. Investigation of asphalt concrete rutting mechanisms by X-ray computed tomography imaging and micromechanical finite element modeling. Mater. Struct. 2013, 46, 1027–1043. [Google Scholar] [CrossRef]
- Cheng, H.L.; Wang, Y.H.; Liu, L.P.; Sun, L.J.; Zhang, Y.N.; Yang, R.K. Estimating Tensile and Compressive Moduli of Asphalt Mixture from Indirect Tensile and Four-Point Bending Tests. J. Mater. Civ. Eng. 2021, 33, 04020402. [Google Scholar] [CrossRef]
- Phan, H.T.; Le, V.P.; Lee, H.J. Application of Dynamic Stability Criterion in Evaluating Field Rutting of Asphalt Pavements Using the Wheel Tracking Test. J. Transp. Eng. Part B-Pavements 2022, 148, 04022019. [Google Scholar] [CrossRef]
- Taherkhani, H.; Jalali, M. Investigating the performance of geosynthetic-reinforced asphaltic pavement under various axle loads using finite-element method. Road Mater. Pavement Des. 2017, 18, 1200–1217. [Google Scholar] [CrossRef]
- Tschoegl, N.W. The Phenomenological Theory of Linear Viscoelastic Behavior; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Liao, J.; Sargand, S. Viscoelastic FE Modeling and Verification of a U.S. 30 Perpetual Pavement Test Section. Road Mater. Pavement Des. 2010, 11, 993–1008. [Google Scholar] [CrossRef]
- Han, Z.H.; Gortz, S. Hierarchical Kriging Model for Variable-Fidelity Surrogate Modeling. Aiaa J. 2012, 50, 1885–1896. [Google Scholar] [CrossRef]
- Kwon, H.; Yi, S.; Choi, S. Numerical investigation for erratic behavior of Kriging surrogate model. J. Mech. Sci. Technol. 2014, 28, 3697–3707. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, W.X.; Xiao, C.N. A Kriging surrogate model coupled in simulation-optimization approach for identifying release history of groundwater sources. J. Contam. Hydrol. 2016, 185, 51–60. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.X.; Cao, D.D. Genetic algorithm optimization for cohesive zone modeling of viscoelastic asphalt mixture fracture based on SCB test. Eng. Fract. Mech. 2022, 271, 108663. [Google Scholar] [CrossRef]
- Plati, C.; Georgouli, K.; Cliatt, B.; Loizos, A. Incorporation of GPR data into genetic algorithms for assessing recycled pavements. Constr. Build. Mater. 2017, 154, 1263–1271. [Google Scholar] [CrossRef]
- Rakesh, N.; Jain, A.K.; Reddy, M.A.; Reddy, K.S. Artificial neural networks—Genetic algorithm based model for backcalculation of pavement layer moduli. Int. J. Pavement Eng. 2006, 7, 221–230. [Google Scholar] [CrossRef]
- Kouevidjin, A.B.; Barthélémy, J.F.; Somé, S.C.; Ben Dhia, H.; Mouillet, V. Modelling of viscoelastic properties and crack growth in bituminous mixtures: Application to the simulation of crack growth in semi-circular samples subjected to oxidative ageing. Eng. Fract. Mech. 2022, 271, 108580. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, J.; Cao, D.; Ding, Y.; Zhou, W. Mechanistic analysis of bottom-up crack in asphalt pavement using cohesive zone model. Theor. Appl. Fract. Mech. 2023, 125, 103904. [Google Scholar] [CrossRef]
- Dorea, C.C.Y.; Guerra, J.A.; Morgado, R.; Pereira, A.G.C. Multistage Markov Chain Modeling of the Genetic Algorithm and Convergence Results. Numer. Funct. Anal. Optim. 2010, 31, 164–171. [Google Scholar] [CrossRef]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Ministry of Transport: Beijing, China, 2011.
- AASHTO T 342-11; Standard Method of Test for Determining Dynamic Modulus of Hot Mix Asphalt Concrete Mixtures. AASHTO: Washington, DC, USA, 2001.
- Ashokan, B.K.; Kokini, J.L. Determination of the WLF constants of cooked soy flour and their dependence on the extent of cooking. Rheol. Acta 2005, 45, 192–201. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Cao, D.D.; Chen, P.S. Dynamic backcalculation of asphalt pavement layer properties using spectral element method. Road Mater. Pavement Des. 2015, 16, 870–888. [Google Scholar] [CrossRef]
- Hua, J. Finite Element Modeling and Analysis of Accelerated Pavement Testing Devices and Rutting Phenomenon. Ph.D. Thesis, ProQuest, Ann Arbor, MI, USA, 2000. [Google Scholar]
- Gao, Y.X.; Zeng, H.X.; Zhang, D.S. Research on Influencing Factors on Asphalt Mixture Shear Strength. J. Highw. Transp. Res. Dev. 2009, 26, 28–32. [Google Scholar]
- Bartolomeo, P.; Chailan, J.F.; Vernet, J.L. On the use of WLF equation to study resin curing by dielectric spectroscopy. Polymer 2001, 42, 4385–4392. [Google Scholar] [CrossRef]








| 0.001 | |
| 0.01 | |
| 0.1 | |
| 1 | |
| 10 | |
| 100 | |
| 1000 | |
| Infinity |
| Viscoelastic Parameters | Minimum Value | Maximum Value |
|---|---|---|
| 0 | 15,000 MPa | |
| 0 | 10,000 MPa | |
| 0 | 8000 MPa | |
| 0 | 5000 MPa | |
| 0 | 3000 MPa | |
| 0 | 2000 MPa | |
| 0 | 1000 MPa | |
| 0 | 100 MPa | |
| 10 | 30 | |
| 10 | 300 |
| Items | Penetration (25 °C, 0.1 mm) | Ductility (25 °C, cm) | Softening Point (°C) | Viscosity (135 °C, Pa∙s) |
|---|---|---|---|---|
| SBS-modified asphalt | 69 | >150 | 81.5 | 2.263 |
| Sieve size/mm | 16.0 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
| Passing rate/% | 100.0 | 95.0 | 76.5 | 53.0 | 37.0 | 26.5 | 19.0 | 13.5 | 10.0 | 6.0 |
| Materials | Relative Rutting Depth (mm) | Rutting Depth (mm) | DS (Times/mm) |
|---|---|---|---|
| AC-13 | 0.355 | 1.328 | 7875 |
| 0.001 | 10,445.190 |
| 0.01 | 7307.682 |
| 0.1 | 4157.773 |
| 1 | 1697.304 |
| 10 | 825.104 |
| 100 | 158.589 |
| 1000 | 203.613 |
| Infinity | 40.232 |
(MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | SAE (mm) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 14,234.66 | 7921.82 | 4879.95 | 2146.03 | 877.61 | 214.35 | 346.29 | 48.03 | 14.53 | 177.45 | 69.4 |
| 5714.47 | 9778.50 | 5249.52 | 1326.61 | 1647.28 | 312.91 | 73.13 | 37.44 | 10.49 | 252.92 | 21.0 |
| 9962.96 | 6257.96 | 3831.73 | 1882.12 | 1630.42 | 275.32 | 203.61 | 49.45 | 21.14 | 181.13 | 190.3 |
| 11,330.95 | 5723.03 | 4463.77 | 1236.60 | 1051.13 | 322.64 | 62.64 | 49.49 | 21.12 | 197.10 | 28.0 |
| 6474.03 | 7112.44 | 4693.83 | 2387.69 | 995.12 | 142.90 | 1.71 | 49.54 | 11.33 | 130.31 | 59.2 |
| 7902.77 | 1769.87 | 4880.03 | 3252.78 | 877.61 | 214.24 | 94.37 | 43.20 | 11.24 | 230.81 | 26.6 |
| 5452.40 | 5737.01 | 4754.71 | 1066.52 | 1256.93 | 493.06 | 102.91 | 34.63 | 21.01 | 270.39 | 57.6 |
| 11,707.55 | 7383.45 | 5049.70 | 2427.01 | 1462.02 | 364.57 | 41.73 | 51.06 | 15.31 | 229.41 | 32.1 |
| 13,779.47 | 6259.29 | 4879.95 | 2145.98 | 1078.85 | 111.75 | 255.83 | 51.37 | 11.24 | 135.03 | 71.1 |
| 6155.02 | 9163.47 | 3339.41 | 1472.47 | 1579.49 | 430.89 | 398.18 | 25.78 | 15.81 | 290.35 | 186.9 |
| 7033.77 | 6666.79 | 4879.95 | 2005.77 | 1152.97 | 189.89 | 75.64 | 52.89 | 17.59 | 176.57 | 45.8 |
| 11,919.99 | 5439.85 | 3735.72 | 2981.71 | 763.80 | 173.23 | 216.89 | 53.08 | 16.85 | 182.77 | 47.6 |
| 14,437.67 | 8353.78 | 4880.32 | 2126.11 | 877.61 | 214.29 | 89.85 | 54.17 | 10.01 | 133.81 | 82.0 |
| 7459.34 | 5357.24 | 3782.13 | 1389.79 | 1929.09 | 101.98 | 157.03 | 55.37 | 12.57 | 107.72 | 190.0 |
| 7658.08 | 7921.82 | 3018.70 | 2327.11 | 1293.32 | 232.09 | 199.00 | 56.18 | 24.75 | 263.28 | 51.6 |
| 5879.70 | 8965.31 | 4879.95 | 2146.03 | 877.61 | 110.91 | 249.12 | 57.54 | 10.76 | 130.31 | 29.7 |
| 7943.79 | 6229.67 | 3966.84 | 2617.61 | 835.60 | 168.14 | 86.23 | 59.18 | 19.32 | 157.79 | 104.3 |
| 9677.71 | 6152.51 | 4879.95 | 2146.03 | 1265.92 | 232.09 | 198.99 | 59.20 | 21.20 | 169.10 | 193.6 |
| 10,383.75 | 9718.84 | 3134.27 | 1497.97 | 788.03 | 386.57 | 139.89 | 31.41 | 12.44 | 122.27 | 27.9 |
| 13,369.45 | 9963.37 | 3884.26 | 2757.35 | 637.19 | 357.26 | 279.93 | 43.97 | 13.81 | 294.36 | 149.8 |
| 14,636.83 | 7818.66 | 4936.38 | 2894.79 | 587.86 | 411.26 | 131.82 | 39.96 | 23.08 | 137.14 | 32.8 |
| 13,326.93 | 5172.03 | 5783.64 | 1212.75 | 1818.82 | 328.38 | 307.02 | 49.05 | 13.89 | 280.14 | 93.8 |
| 11,445.29 | 7796.16 | 5774.63 | 2227.54 | 1788.96 | 157.95 | 445.18 | 51.95 | 13.13 | 240.10 | 23.4 |
| 7344.10 | 7338.86 | 4693.83 | 2389.09 | 690.83 | 335.25 | 93.48 | 22.07 | 12.03 | 232.62 | 22.6 |
(MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | SAE (mm) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 10,133.33 | 7753.27 | 4879.95 | 2147.25 | 877.58 | 214.29 | 255.64 | 41.21 | 11.1 | 129.2 | 6.03 |
| Items | Relative Rutting Depth (mm) | DS (Time/min) | Error Rate of Relative Rutting Depth (%) | Error Rate of DS (%) |
|---|---|---|---|---|
| WTT | 0.355 | 7875 | - | - |
| Simulation of OP | 0.366 | 7756 | 3.1 | 1.5 |
| Simulation of EP | 0.339 | 6033 | 4.5 | 23.4 |
| Items | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Correlation coefficient | −0.022 | 0.105 | −0.046 | −0.034 | 0.245 | 0.222 | −0.414 | 0.394 | 0.427 | 0.359 |
| p-value | 0.731 | 0.099 | 0.475 | 0.597 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Items | (MPa) | (MPa) | (MPa) | (MPa) | SAE (mm) | Error Rate of SAE (%) |
|---|---|---|---|---|---|---|
| Basic parameters | 877.58 | 214.29 | 255.64 | 41.21 | 6.03 | - |
| Increscent | 1755.15 | 214.29 | 255.64 | 41.21 | 6.66 | 10.45 |
| Reductive | 438.79 | 214.29 | 255.64 | 41.21 | 7.04 | 16.75 |
| Increscent | 877.58 | 428.58 | 255.64 | 41.21 | 7.18 | 19.07 |
| Reductive | 877.58 | 107.15 | 255.64 | 41.21 | 7.08 | 17.41 |
| Increscent | 877.58 | 214.29 | 511.28 | 41.21 | 6.68 | 10.78 |
| Reductive | 877.58 | 214.29 | 127.82 | 41.21 | 9.80 | 62.52 |
| Increscent | 877.58 | 214.29 | 255.64 | 82.42 | 101.01 | 1575.12 |
| Reductive | 877.58 | 214.29 | 255.64 | 20.60 | 191.58 | 3077.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhou, W.; Cao, D.; Zhang, J. A Study on the Genetic Algorithm Optimization of an Asphalt Mixture’s Viscoelastic Parameters Based on a Wheel Tracking Test. Infrastructures 2023, 8, 169. https://doi.org/10.3390/infrastructures8120169
Zhang J, Zhou W, Cao D, Zhang J. A Study on the Genetic Algorithm Optimization of an Asphalt Mixture’s Viscoelastic Parameters Based on a Wheel Tracking Test. Infrastructures. 2023; 8(12):169. https://doi.org/10.3390/infrastructures8120169
Chicago/Turabian StyleZhang, Jinxi, Weiqi Zhou, Dandan Cao, and Jia Zhang. 2023. "A Study on the Genetic Algorithm Optimization of an Asphalt Mixture’s Viscoelastic Parameters Based on a Wheel Tracking Test" Infrastructures 8, no. 12: 169. https://doi.org/10.3390/infrastructures8120169
APA StyleZhang, J., Zhou, W., Cao, D., & Zhang, J. (2023). A Study on the Genetic Algorithm Optimization of an Asphalt Mixture’s Viscoelastic Parameters Based on a Wheel Tracking Test. Infrastructures, 8(12), 169. https://doi.org/10.3390/infrastructures8120169






