Data-Driven Prediction of Cement-Stabilized Soils Tensile Properties

Abstract

The indirect tensile strength of two geomaterials treated with variable cement contents, degrees of compaction and water contents were tested after several curing times. A statistical review through an analysis of variance allows for identifying the significant variables and generating prediction models. The distribution of associated uncertainties was measured. Based on these probabilistic results, numerical models were constructed using Latin Hypercube Sampling as the space filling technique. Predictions from the numerical sampling were in accordance with the experimental results. The numerical results suggest that the net gain in accuracy was not affected by the soil type. In addition, it increases rapidly as a function of the sampling size. The proposed approach is broad. It can help to highlight the physical mechanisms involved in behaviors of multi-component materials.

1. Introduction

Adding small amounts of cement as a binder is a common technique to enhance the engineering and mechanical properties of in situ soils according to stress rates imposed by civil engineering projects [1,2]. This practice has the advantage of minimizing environmental impacts and reducing infrastructure cost [3], especially in terms of preserving quality natural resources. The use of in situ soil avoids the use of quarry materials [4].

Cement stabilization consists of incorporating a volume of cement-based additive to the soil. In the presence of water, pozzolanic reactions occur over short and long terms, and improve the stiffness and strength of the mix [5]. The current state of practice tends to limit the application of cement to coarse and low plastic soils [6,7]; however, satisfactory performances have been reported with fine-grained and even with expansive soils [8,9,10,11].

These treated materials are called Cement-Stabilized Soils (CSS). They constitute an intermediate class of geomaterials whose mechanical behavior is at the boundary between classical soil mechanics and rock mechanics [12,13]. Cement stabilization is widely used in civil engineering applications such as embankments, slope protection of dams, pavement of highways, building pads and foundation stabilization [5,14]. In the field of transportation geotechnics, CSSs are generally used in capping layers and can be used in a road base or subbase [13].

The amounts of hydraulic binder in CSSs commonly range between 5 and 10% per weight of dry material. However, cement manufacturing is one of the most significant sources of anthropogenic greenhouse gases, in particular with carbon dioxide (CO₂) emissions, and production requires the use of considerable energy and materials [15]. Total emissions from the cement industry contributes as much as 8% of global CO₂ emissions [16]. Thus, in the field of road geotechnics, due to the amount of material involved, the optimization of dosage procedures is a key issue. Decreasing cement amounts could bring a real environmental benefit.

Treated layers of land transport infrastructures are subjected to tensile stress at their bottom. This critical mechanical characteristic is generally used for material evaluation and structure design [2,17,18]. For an easy-performing, time-saving and cost-effective method, this feature is mainly ascertained from the measurement of Indirect Tensile Strength (ITS) at the laboratory scale [19].

The mechanical properties of CSSs depend on variables such as cement content, cement type, moisture content, curing time, degree of compaction, temperature during curing, aggregate type, volume of voids and porosity/binder ratio [2,14,17,18,19,20,21,22,23,24,25,26,27].

To consider the possible performance variations due to construction procedures in worksites, a laboratory test program is established during the design process by varying the mixture parameters. In France, for instance, mixture proportioning design follows a Central Composite Design (CCD) based on variations around the standard proctor values of the reference mixture, i.e., Optimum Moisture Content (OMC) and Maximum Dry Density (MDD). Performance is evaluated for a fixed curing time (long term, e.g., 90 days) [28].

This sensitivity analysis only focuses on unfavorable conditions. That limits the scope and these aspects are critical for rationalizing structure design, particularly when binder amounts are less than 5%. Unfortunately, increasing the number of variables can lead to an infeasible experimental program [29] and reducing it is unacceptable and may bias the conclusions [26]. Currently, there is a need to develop models based on a reasonable number of tests that allow a straightforward assessment of tensile properties.

Design Of Experiment (DOE) techniques have become crucial for dosage evaluations and the mixing optimization of CSSs [30,31]. DOE techniques, for example, can be implemented in numerical works to assess the influence of sampling on the accuracy of prediction models [29]. Similarly, Response Surface Methodology (RSM) as part of the DOE process has become a useful tool to rationalize cemented amounts in hydraulically bound materials. RSM is often used with innovative complex materials when interactions between constituents are not well understood [19,23,26,32,33,34,35,36].

The first aim of our work was to investigate, at the laboratory scale, the mechanical performances of CSSs treated with a low amount of binder considering the variability of field conditions. To achieve this goal, we measured the ITS of two geo-materials treated with 3% of cement. To consider the field conditions, the dosage preparations (i.e., curing time, compaction degree, cement content and water content) were varied around a reference mixture, following a CCD design. Then, an Analysis of Variance (ANOVA) and multilinear regression were applied to the experimental results to assess and predict the mechanical performance. Response surfaces and contour plots were generated to highlight the links between preparation parameters. The second aim of the study was to propose a tool to facilitate and support the selection of a given sampling in variability studies. Based on the ascertained regression models and measured uncertainties, numerical experiments were simulated using DOE. For a given number of numerical experiments, varying from 10 up to 100, 1000 samplings were carried out. Synthetic regression models were obtained and the distances between the experimental and numerical models were measured. Through this approach, we expressed the mean differences, and thus the accuracy as a function of the sampling size.

2. Materials and Methods

2.1. Materials

2.1.1. Soils

Two soils named A and B were studied. The results of the characterization are shown in Table 1 and the grain size curves are shown in Figure 1.

• Soil A

This material was cut from the covering soil of an aggregate quarry at Soignies Belgium (50°34′25.759″ N, 4°2′16.476″ E). The maximum diameter of the larger elements in this material was less than 1 mm. Through an 80 μm sieve, the cumulated undersize was 94%, which means that its mechanical behavior was controlled by its fine fraction. It is classified as a fine-grained soil [37]. The clay activity is low, A = PI/C_2μm = 0.29. Swelling potential was thus not significant.

• Soil B

This material was a quarry tailing from Chauvé, France (47°8′22.886″ N, 2°0′45.934″ W). The maximum diameter of the larger elements in this material was less than 50 mm. Through an 8 mm sieve, the cumulated undersize was 93%, and fine content, less than 80 μm, was 17%, which means that its mechanical behavior was controlled by its coarse fraction. It is classified as a coarse-grained soil [37]. Despite a high clay activity, A = 1.3, the low clay content and low PI imply a low swelling potential.

Table 1. Physical properties of soils.

Properties	Reference	Soil A	Soil B
Density of soil particles, ρs	[38]	2.59 g/cm3	2.64 g/cm3
Liquid limit, WL	[39]	30%	38%
Plastic limit, WP		17%	25%
Plasticity index, (PI = WL − WP)		13%	13%
Clay content (d < 2 μm) a, C2μm	[37]	24%	6%
Silt (2 μm < d < 63 μm) a		69%	11%
Sand (63 μm < d < 2 mm) a		6%	40%
Gravel (2 mm < d < 200 mm) a		1%	43%
AASHTO b classification	[40]	A-6(11)	A-2-6(0)
GTR c classification d	[41]	B5	A2
USCS d classification c	[42]	CL	SM-SC

^a Soil size range based on European standard NF EN ISO 14688-1 [43]; ^b American Association of State Highway and Transportation Officials; ^c French Road Earthworks Manual; ^d Unified Soils Classification System.

Table 1. Physical properties of soils.

Properties	Reference	Soil A	Soil B
Density of soil particles, ρs	[38]	2.59 g/cm3	2.64 g/cm3
Liquid limit, WL	[39]	30%	38%
Plastic limit, WP		17%	25%
Plasticity index, (PI = WL − WP)		13%	13%
Clay content (d < 2 μm) a, C2μm	[37]	24%	6%
Silt (2 μm < d < 63 μm) a		69%	11%
Sand (63 μm < d < 2 mm) a		6%	40%
Gravel (2 mm < d < 200 mm) a		1%	43%
AASHTO b classification	[40]	A-6(11)	A-2-6(0)
GTR c classification d	[41]	B5	A2
USCS d classification c	[42]	CL	SM-SC

^a Soil size range based on European standard NF EN ISO 14688-1 [43]; ^b American Association of State Highway and Transportation Officials; ^c French Road Earthworks Manual; ^d Unified Soils Classification System.

Figure 1. Particle size distribution of soils A and B. Soil size range: F (fine), M (medium) and C (coarse) [37,43].

Figure 1. Particle size distribution of soils A and B. Soil size range: F (fine), M (medium) and C (coarse) [37,43].

2.1.2. CSS—Treatment and Sample Preparation

Both soils were treated with 3% of cement (weight of dry material) CEM II/A-LL 42.5 R [44]. Lime pre-treatment was not needed due to the suitable workability in both mixtures. The OMC and the MDD relationships for both CSSs were obtained following Proctor compaction tests [45], for standard compaction effort (600 kN m/m³):

• OMC = 15.5%, MDD = 1.79 g/cm³ for mixture A
• OMC = 10.0%, MDD = 1.98 g/cm³ for mixture B

These values were taken as a reference for the sample preparation. Based on the French guidelines for soil treatment, a variability study following a fractional CDD was proposed [28]. Samples were prepared at several Varying conditions (V) around the reference mixture (V3) with four varying factors: Curing Time (CT), Cement Content (CC), Degree of Compaction (DC) and Water content (W).

Table 2. Reference values for sample preparation for the variability study.

V	Varying Factors
	Curing Time, CT (Days)	Cement Content, CC (%) a	Degree of Compaction, DC (%) b	Water Content, W (%) c
V1	7, 28, 90, 180, 360	3.0	94.0	100
V2	7, 28, 90, 180, 360	2.0	96.0	100
V3 (ref.)	7, 28, 90, 180, 360	3.0	96.0	100
V4	7, 28, 90, 180, 360	4.0	96.0	100
V5	7, 28, 90, 180	3.0	96.0	90
V6	7, 28, 90, 180	3.0	96.0	110
V7	7, 28, 90, 180, 360	3.0	98.5	100
NT	-	0.0	96.0	100

^a CC as percentage of dry material weight, ^b DC as percentage of MDD, ^c W as percentage of OMC.

shows all the parameters assessed, their definition and the levels of variation used as the reference in this work. The varied factor for each V is highlighted in bold. In total, seven treatments were proposed and for each one, at least three specimens were tested. The complete variability study included a total of 107 treated specimens for A and 106 for mixture B. Additionally, four Non-Treated (NT) samples were tested for each material.

Samples were compacted in a double static mode in one layer into a 100 mm diameter (D), 100 mm high (H) cylindrical mold and they were stored in a room with temperature regulated at 20 °C and protected with plastic films to keep constant water content. No saturation process was made before the experiments. Details of the sampling preparation are available online [46].

2.2. Indirect Tensile Strength

All tests were carried out on a Zwick/Roell Z150 press with a crosshead speed of 0.3 mm/min in absolute value. Applied load was measured with a force sensor TME F521TC (max. load = 10 kN). Specimens were placed between two diametrically opposite generators and then subjected to a compressive load until failure [47]. ITS (MPa) was then calculated using Equation (1),

$$\mathrm{I}\mathrm{T}\mathrm{S}=\frac{2{\mathrm{F}}_{\mathrm{r}}}{\mathsf{\pi }\mathrm{H}\mathrm{D}}$$

(1)

where ${\mathrm{F}}_{\mathrm{r}}$ is the applied failure load (N); H and D are the thickness and diameter of the specimen (mm).

2.3. Statistical Approach

2.3.1. Analysis of Variance

Analysis of Variance, ANOVA, is a statistical tool used to identify and establish the effect of variations of a given factor on the output variable, by grouping and comparing the mean values according to the levels of the factor under study. This analysis was considered due to the large data set obtained from the experimental program, and the number of investigated variables. This tool was applied to the experimental results to determine which factors significantly affected the ITS of both CSSs. The results of NT were not included.

An ANOVA tests the hypothesis that all group means are equal (i.e., the null hypothesis, H₀) against the alternative supposition that at least one group mean is different from the others (H₁). Null hypotheses are evaluated by a Fisher’s test (F-test) to compare the variation within groups with a significance level $\mathsf{\alpha }=0.05$ as the threshold. If the calculated probability (p-value) is lower than $\mathsf{\alpha }$, then H₀ is rejected as it inherently implies a significant effect and thus the factor is considered in the prediction model. The hypothesis of no differences in the treatment means was performed, as described by the means model (Equation (2)) [48]. It was analyzed using type II ANOVA, i.e., considering only main effects. This approach is justified because mixture parameters are independent variables [49]

$${\mathrm{y}}_{\mathrm{i}\mathrm{j}\mathrm{k}\mathrm{l}\mathrm{m}}=\overline{\mathsf{\mu }}+{\mathsf{\alpha }}_{\mathrm{i}}+{\mathsf{\beta }}_{\mathrm{j}}+{\mathsf{\gamma }}_{\mathrm{k}}+{\mathsf{\theta }}_{\mathrm{l}}+{\mathsf{\epsilon }}_{\mathrm{i}\mathrm{j}\mathrm{k}\mathrm{l}\mathrm{m}}\left\{\begin{array}{c}\mathrm{i}=1,2,3,4,5\\ \mathrm{j}=1,2,3\\ \mathrm{k}=1,2,3\\ \mathrm{l}=1,2,3\\ \mathrm{m}=1,2,3\end{array}\right.$$

(2)

where:

• ${\mathrm{y}}_{\mathrm{ijklm}}$ is the experimental measurement of ITS when the factors CT, CC, DC and W are in the $\mathrm{i}\text{-}$th, $\mathrm{j}$-th, $\mathrm{k}$-th and $\mathrm{l}$-th level, respectively, for the $\mathrm{m}$-th replicate;
• $\overline{\mathsf{\mu }}$ is the overall mean effect, ${\mathsf{\alpha }}_{\mathrm{i}}$ is the effect of the $\mathrm{i}$-th level of the CT factor, ${\mathsf{\beta }}_{\mathrm{j}}$ is the effect of the $\mathrm{j}$-th level of the CC factor, ${\mathsf{\gamma }}_{\mathrm{k}}$ is the effect of the $\mathrm{k}$-th level of the DC factor and ${\mathsf{\theta }}_{\mathrm{l}}$ is the effect of the $\mathrm{l}$-th level of the W factor;
• ${\mathsf{\epsilon }}_{\mathrm{i}\mathrm{j}\mathrm{k}\mathrm{l}\mathrm{m}}$ is the error (or residual) component. It is assumed normally distributed with a constant variance SD²_ε and zero mean (${\mathsf{\mu }}_{\mathsf{\epsilon }}=0$).

2.3.2. Regression Model

Once significant variables were identified by the ANOVA, a multilinear regression analysis was conducted to develop predictive equations for both treated soils. The least square method was employed to estimate the regression coefficients. Models for both mixtures follow Equation (3).

$${\mathrm{y}}_{\mathrm{e}}={\mathrm{a}}_0+{\mathrm{a}}_1{\log }_{10}\mathrm{C}\mathrm{T}+{\mathrm{a}}_2\mathrm{C}\mathrm{C}+{\mathrm{a}}_3\mathrm{D}\mathrm{C}+{\mathrm{a}}_4\mathrm{W}$$

(3)

where ${\mathrm{y}}_{\mathrm{e}}={\mathrm{f}}_{\mathrm{e}\left(\mathrm{A}\right)}\mathrm{o}\mathrm{r}{\mathrm{f}}_{\mathrm{e}\left(\mathrm{B}\right)}$ are the predicted ITS based on the experimental data in MPa. Predictor variables are CT (days), CC (%), DC (%) and W (%); ${\mathrm{a}}_{\mathrm{i}}$, with $\mathrm{i}=0,1,2,3,4,$ as the regression coefficients. First-order models were selected. A logarithmic relationship was proposed to represent the evolution of CT, because its effect on CSSs usually follows this pattern [2,11].

An examination of the residuals of both models allowed the construction of Probabilistic Density Functions (PDFs). The variations of residuals were considered to follow a normal distribution. The representation of variables as a PDF is convenient in geotechnical problems [50].

The Response Surface Method, RSM, [51] and contour plots were used to visualize the relationships between factors and their response according to the regression models.

2.4. Numerical Approach

2.4.1. Experimental Design

The inference space defined in the statistical approach (i.e., 7 < CT (days) < 360, 2 < CC (%) < 4, 94 < DC (%) < 98.5 and 90 < W (%) < 110) is the general frame of the numerical works. Sampling followed Latin Hypercube Sampling (LHS) [52]. This space-filling technique is based on DOE methods. One particularity of this random sampling method is that replications are avoided [29,53]. Besides this, it is computationally cheap and can cope with many input variables [54]. The use of LHS has been successfully proven for data generation in geotechnical problems when random variables are considered [55].

To match the laboratory work, the number of observations, n, varies from n = 10 to n = 100. To be statistically relevant, sampling was generated k = 10³ times. Based on a numerical toolbox for DOE [56], the LHS matrix (LHS_n,k) was constructed. At the k-th iteration, ${\mathrm{b}}_{\mathrm{n},\mathrm{k}}$ is the n-th sample (vector) whose coordinates, i.e., mixture parameters, were generated by LHS. Then, ${\mathrm{B}}_{\mathrm{n},\mathrm{k}}$ is a data subset (matrix) that contains n samples for the k-th iteration. Therefore, the LHS matrix corresponds to the merged ${\mathrm{B}}_{\mathrm{n},\mathrm{k}}$ subsets, as described by Equation (4).

$${\mathrm{L}\mathrm{H}\mathrm{S}}_{\mathrm{n},\mathrm{k}}=\left[\begin{array}{ccc}{\mathrm{B}}_{\mathrm{10,1}}& \cdots & {\mathrm{B}}_{10,\mathrm{k}}\\ ⋮& \ddots & ⋮\\ {\mathrm{B}}_{\mathrm{n},1}& \cdots & {\mathrm{B}}_{{10}^2,{10}^3}\end{array}\right],\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{\mathrm{B}}_{\mathrm{n},\mathrm{k}}=\left[\begin{array}{c}{\mathrm{b}}_{10,\mathrm{k}}\\ ⋮\\ {\mathrm{b}}_{\mathrm{n},\mathrm{k}}\\ ⋮\\ {\mathrm{b}}_{{10}^2,\mathrm{k}}\end{array}\right]\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{b}}_{\mathrm{n},\mathrm{k}}={(\mathrm{C}\mathrm{T},\mathrm{C}\mathrm{C},\mathrm{D}\mathrm{C},\mathrm{W})}_{\mathrm{n},\mathrm{k}}$$

(4)

2.4.2. Numerical ITS Values and Prediction Models

Numerical ITS values were generated following two steps: firstly, by applying the experimental prediction models ${\mathrm{f}}_{\mathrm{e}}$, (Equation (3)) to the ${\mathrm{B}}_{\mathrm{n},\mathrm{k}}$ subsets. Second, a random residual value generated from the PDF was added. From there, numerical prediction models, named ${\mathrm{f}}_{\mathrm{n},\mathrm{k}}$, i.e., ${\mathrm{f}}_{\mathrm{n},\mathrm{k}\left(\mathrm{A}\right)}\mathrm{o}\mathrm{r}{\mathrm{f}}_{\mathrm{n},\mathrm{k}\left(\mathrm{B}\right)}$, were obtained by fitting the numerical ITS values to the corresponding ${\mathrm{B}}_{\mathrm{n},\mathrm{k}}$ sampling subset obtained by LHS.

2.4.3. Model Similarity

A similarity assessment was used to compare experimental and numerical predictions [29]. A first indicator ${\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}$, defined as the absolute difference between numerical and experimental predictions for the ${\mathrm{B}}_{\mathrm{n},\mathrm{k}}$ subset, was used to quantify their distance. To generalize results, this parameter is normalized by the value of the experimental prediction on the same sampling, as presented in Equation (5). The indicator, ${\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}$, is expressed in kPa and the normalized value $\overline{{\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}}$ is expressed in percent.

$$\overline{{\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}}=\frac{{\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}}{{\mathrm{f}}_{\mathrm{e}}\left({\mathrm{B}}_{\mathrm{n},\mathrm{k}}\right)},\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}=\left|{\mathrm{f}}_{\mathrm{n},\mathrm{k}}\left({\mathrm{B}}_{\mathrm{n},\mathrm{k}}\right)-{\mathrm{f}}_{\mathrm{e}}\left({\mathrm{B}}_{\mathrm{n},\mathrm{k}}\right)\right|$$

(5)

For k iterations, both values ${\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}$ and $\overline{{\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}}$ are averaged and represented by a mean value, i.e., ${\mathsf{\delta }}_{\mathrm{n}}$ and $\overline{{\mathsf{\delta }}_{\mathrm{n}}}$, respectively. Both indicators are considered normally distributed with a constant standard deviation ${\mathrm{S}\mathrm{D}}_{\mathsf{\delta }}$ for ${\mathsf{\delta }}_{\mathrm{n}}$ and ${\mathrm{S}\mathrm{D}}_{\mathsf{\delta }-\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}}$ for $\overline{{\mathsf{\delta }}_{\mathrm{n}}}$.

All calculations were performed using Python version 4.1 [57]. The following scientific libraries were used: SciPy [58], NumPy [59], pandas [60], statsmodels [61], doePy [56], matplotlib [62] and seaborn [63].

3. Results and Discussion

3.1. Experimental Results

Hereinafter, Standard Deviation (SD) is indicated in brackets. The analysis of the experiments is based, for each case (V), on both the mean value and the SD (

Table 3. Experimental ITS results: mean ITS values and SD, in MPa.

Material	V	NT		7 Days		28 Days		90 Days		180 Days		360 Days
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
A	V1			0.116	0.008	0.154	0.009	0.152	0.014	0.162	0.013	0.230	0.010
	V2			0.092	0.006	0.093	0.005	0.101	0.008	0.144	0.007	0.187	0.012
	V3			0.140	0.019	0.151	0.009	0.176	0.010	0.226	0.003	0.215	0.031
	V4			0.141	0.009	0.203	0.029	0.292	0.022	0.318	0.041	0.354	0.030
	V5			0.125	0.009	0.155	0.009	0.204	0.006	0.211	0.014	-	-
	V6			0.117	0.010	0.138	0.014	0.194	0.020	0.215	0.011	-	-
	V7			0.144	0.016	0.162	0.009	0.218	0.004	0.272	0.032	0.258	0.011
	NT	0.019	0.004
B	V1			0.105	0.011	0.135	0.009	0.179	0.019	0.198	0.014	0.264	0.013
	V2			0.085	0.004	0.107	0.012	0.157	0.007	0.195	0.001	0.225	0.004
	V3			0.120	0.007	0.174	0.008	0.210	0.014	0.261	0.013	0.313	0.008
	V4			0.149	0.001	0.199	0.010	0.269	0.007	0.317	0.018	0.319	0.006
	V5			0.108	0.004	0.140	0.018	0.190	0.009	0.252	0.010	-	-
	V6			0.101	0.002	0.137	0.005	0.210	0.009	0.230	0.021	-	-
	V7			0.126	0.002	0.172	0.017	0.253	0.008	0.306	0.017	0.344	0.007
	NT	0.010	0.001

). Individual results can be consulted online [46]. A first analysis of ITS results shows:

Considering all variabilities, the mean ITS values for both CSSs were between 0.085 and 0.354 MPa. Uncertainties on measurements, in terms of the SD, range between 0.001 and 0.041 MPa. The Coefficient Of Variation (COV), defined as the ratio between the SD and the corresponding mean ITS value, was under 15% for all CSSs. The results from the experiments can be considered as statistically relevant.

Measured ITS values were relevant according to the literature. For instance, the values for ITS on CSSs have been reported between 0.050 and 0.300 MPa for gravel and limestone [21], 0.050 and 0.550 MPa for silt [14], 0.010 and 0.370 MPa for sand [25] when CC varied from 4 to 8% (7 < CT < 21 days), 3% to 9% (7 < CT < 28 days) and 1 to 12% (CT = 7 days), respectively. For cement-modified loess, when treated with three different hydraulic binders (CC = 5.5% and 7.0%) ITS varied between 0.330 MPa and 0.530 MPa for CT = 90 days [13]. For cemented sands [64], ITS ranged between 0.020 and 0.130 MPa (42 < CT < 90 days) when 2 < CC < 6%. To compare with similar materials, a review of recycled cement-treated mixtures [65] found that the average ITS values were 0.500 MPa, with 75% of the individual values lower than 0.650 MPa. In the case of lime-treated soils [66], with binder content varying from 3 to 5%, ITS values were reported varying between 0.310 and 0.800 MPa (CT = 7 and 28 days). For mixed treatment, reported ITS values varied between 0.200 and 0.700 MPa when soils were treated with 5 to 6% of hydraulic binder (7 < CT < 720 days) [67].

A noteworthy strength improvement with cement addition and curing time. For CT = 7 days, the ratio between the ITS for V3 and NT was 7 for mixture A and 12 for mixture B. For CT = 360 days the same ratios were, respectively, 11 and 31. A number of researchers have reported the key role of CC and CT in improving the ITS on CSSs [13,21,25]. Specifically, the enhancing of quarry waste by adding small amounts of cement (CC = 2%) has been described in the literature [68].

Lower and higher values of ITS, in bold, seem to be related to CC (V2 and V4) and DC (V1 and V7). To counterbalance the use of lower CC by increasing CD, for instance, statistical models have been proposed in cement-treated materials [22].

The effects of W (V5 and V6) are not clear. The existence of a moisture content threshold where variations can improve the performance of CSSs is suggested in the literature [2].

3.2. Statistical Approach

3.2.1. Analysis of Individual Responses

The means model from Equation (2) is represented in Figure 2. The overall mean effect ($\overline{\mathsf{\mu }}$), represented as dashed lines, show that ITS were slightly higher for mixture B than for mixture A. Effects of CT (${\mathsf{\alpha }}_{\mathrm{i}}$), CC (${\mathsf{\beta }}_{\mathrm{j}}$), DC (${\mathsf{\gamma }}_{\mathrm{k}}$) and W (${\mathsf{\theta }}_{\mathrm{l}}$) are shown as solid lines and their individual effects are related to a standardized slope.

Figure 2 shows that ITS follows a quite linear function of Log10(CT) for both materials, as usual for CSSs [2]. With the higher slopes, Figure 2 suggests that the most relevant factor for B is CT. Nevertheless, with two different slopes, the effects of CT are probably different in each mixture, varying from short- to long-term. This could illustrate different kinetics over time, i.e., that the process of cementation could be different in the two materials. At short-term (CT = 7 days), ITS_A > ITS_B, whereas for CT > 28 days, ITS_B > ITS_A.

For B, the effects of CC come after the CT ones. For A, this effect is unclear, even if it is comparable with the slope from CT. Nevertheless, in both cases, measured ITS values as a function of CC can be described as essentially linear. This behavior has already been reported in the literature [12,14,69]. It is well known that CC plays an important role to improve the cohesion in CSSs. It can be noted that for A, the slope is higher than for B.

Regarding DC, mixture B is slightly more affected than A. A linear relationship is identified for both CC and DC. Finally, with slopes close to zero, variations around the overall mean due to W seem not to be determining.

The dispersion of results can also be discussed graphically. The coefficient of variation, COV, is plotted in Figure 2 (bottom). Regardless of the studied material, COV seems to be a parameter-independent, varying around constant values.

3.2.2. ANOVA

The results of the ANOVA are summarized in

Table 4. ANOVA results for the studied factors.

CSS	Source of Variation	Degrees of Freedom	SS (×10−4)	Fo	p-Value	Percent Contribution
A	Log10 CT	1	1396.7	218.7	4.1 × 10−27	44.5
	CC	1	1514.0	237.0	2.3 × 10−28	48.2
	DC	1	225.6	35.3	3.9 × 10−8	7.2
	W	1	4.7	0.74	0.39	0.1
	Error	102	651.5
B	Log10 CT	1	3381.3	770.2	4.6 × 10−49	77.3
	CC	1	677.6	154.3	4.6 × 10−22	15.5
	DC	1	311.7	71.0	2.6 × 10−13	7.1
	W	1	2.7	0.62	0.43	0.1
	Error	101	443.4

for each source in terms of Sum of Squares (SS), F value (F_o), p-value and percent contribution (defined as the normalized SS) [48]. As degrees of freedom are one for each factor, the Mean Square Treatment (MST) are equal to SS.

With the highest contributions in both cases, CT and CC are the main factors explaining ITS variations. For CT, the percent contribution was higher for B than for A (77.3 vs. 44.5). For CC, the percent contribution was higher for A than for B (48.2 vs. 15.5). The contribution of DC was around 7% for both materials.

The influence of W, in terms of percent contribution, was negligible for both materials. In the same way, p-values related to W are higher than $\mathsf{\alpha }=0.05$. The F value (F_o), is lower than the F critical value, F_crit calculated from the degree of freedom, error and $\mathsf{\alpha }$. For mixture A, (F_o(W) = 0.39 < F_crit(1,102; 0.05) = 3.9) and B, (F_o(W) = 0.43 < F_crit(1,101; 0.05) = 3.9). This result shows that for the studied inference space, this factor does not have a significant effect on ITS values for either mixtures A or B. It was excluded from the prediction models. All these results are in accordance with observations from Figure 2.

Nevertheless, the results of the ANOVA clarify the role of each parameter variation, whose scope is limited to the studied range. In a similar investigation, it has been reported that W was the most significant variable on ITS for CSS. However, variations were conducted over a wider range (60 to 140% of OMC) [21].

3.2.3. Multilinear Regression

Multilinear regression models (Equations (6) and (7)) allowed the prediction of ITS with high accuracy for both mixtures. For A, R² is 0.842 with a number of observations, n, of 107. For B, R² = 0.923, with n = 106. The accuracy of the models can be confirmed using the observed F value, F_obs, which is higher than the F critical value. For A, F_obs = 183.2 > F_crit(3, 103;0.05) = 2.7 and for B, F_obs = 406.3 > F_crit(3, 102;0.05) = 2.7. In Equations (6) and (7), CT is the curing time (days), CC is the cement content (%), and DC is the degree of compaction, as a percentage of the MDD.

$${\mathrm{I}\mathrm{T}\mathrm{S}}_{\mathrm{A}}\left(\mathrm{M}\mathrm{P}\mathrm{a}\right)=(-131.99+6.34{\log }_{10}\mathrm{C}\mathrm{T}+6.90\mathrm{C}\mathrm{C}+1.24\mathrm{D}\mathrm{C})\times {10}^{-2}$$

(6)

$${\mathrm{I}\mathrm{T}\mathrm{S}}_{\mathrm{B}}\left(\mathrm{M}\mathrm{P}\mathrm{a}\right)=(-160.45+9.99{\log }_{10}\mathrm{C}\mathrm{T}+4.79\mathrm{C}\mathrm{C}+1.55\mathrm{D}\mathrm{C})\times {10}^{-2}$$

(7)

By comparing the regression coefficients of Equations (6) and (7), some previous analyses from Figure 2 can be quantitatively confirmed: (i) the effects of CT are stronger for mixture B than for mixture A, (ii) the influence of CC is higher in mixture A and (iii) with a similar order of magnitude, the effects of DC are comparable for both mixtures. Coefficient values are in the same range for both materials, which implies comparable values of ITS regardless of soil type.

The experimental data and the predicted ITS values from Equations (6) and (7) are compared in Figure 3. Residual values ($\epsilon$), defined in Equation (2), are the difference between measured and predicted values. They can be represented as the horizontal distances from each point to the line of equality. For both models, residuals are accurately described by a normal PDF (R² of 0.96 and 0.99 for mixtures A and B, respectively) with mean values close to zero (μ_ε(A) = −1.74 × 10⁻¹⁵ MPa and μ_ε(B) = −6.35 × 10⁻¹⁴ MPa), and a constant variance value (SD²_ε(A) = (0.0248 MPa)² and SD²_ε(B) = (0.0205 MPa)²). Thus, the underlying assumption of normality of the residual distributions was verified.

3.2.4. Coded Multilinear Regression

In order to determine which factor has the strongest effect on ITS, dimensionless models with coded units were considered. By a scale change on input variables, the magnitudes of the model’s coefficients can be directly compared as they measure the effect of changing each design factor over the same one-unit interval [−1, +1] [48]. The construction of the coded variables is presented in

Table 5. Natural and coded factors. Coded values in square brackets.

Source of Variation	Min. Level	Intermediate Level(s)			Max. Level
CT	Log10(7) [−1.00]	Log10(28) [−0.30]	Log10(90) [+0.30]	Log10(180) [+0.65]	Log10(360) [+1.00]
CC	2.0 [−1.00]		3.0 [0.00]		4.0 [+1.00]
DC	94.0 [−1.00]		96.0 [+0.11]		98.5 [+1.00]

.

Coded equations, presented below, followed the same form that the reference model described in Equation (3). In the case of mixture A, coefficients in Equation (8) show that CC has the strongest effect (6.90 × 10⁻²) on ITS, followed by CT (5.44 × 10⁻²) and DC (2.78 × 10⁻²). For mixture B, (Equation (9)), the strongest effect is due to CT (8.56 × 10⁻²), followed by CC (4.80 × 10⁻²) and DC (3.50 × 10⁻²). The relative effect of every factor agrees with the percent contribution shown in Figure 2 and the ANOVA (Table 4). In all cases, the effects are positive.

$${\mathrm{I}\mathrm{T}\mathrm{S}}_{\mathrm{C}-\mathrm{A}}\left(-\right)=(18.46+5.44{\log }_{10}\mathrm{C}\mathrm{T}+6.90\mathrm{C}\mathrm{C}+2.78\mathrm{D}\mathrm{C})\times {10}^{-2}$$

(8)

$${\mathrm{I}\mathrm{T}\mathrm{S}}_{\mathrm{C}-\mathrm{B}}\left(-\right)=(20.46+8.56{\log }_{10}\mathrm{C}\mathrm{T}+4.80\mathrm{C}\mathrm{C}+3.50\mathrm{D}\mathrm{C})\times {10}^{-2}$$

(9)

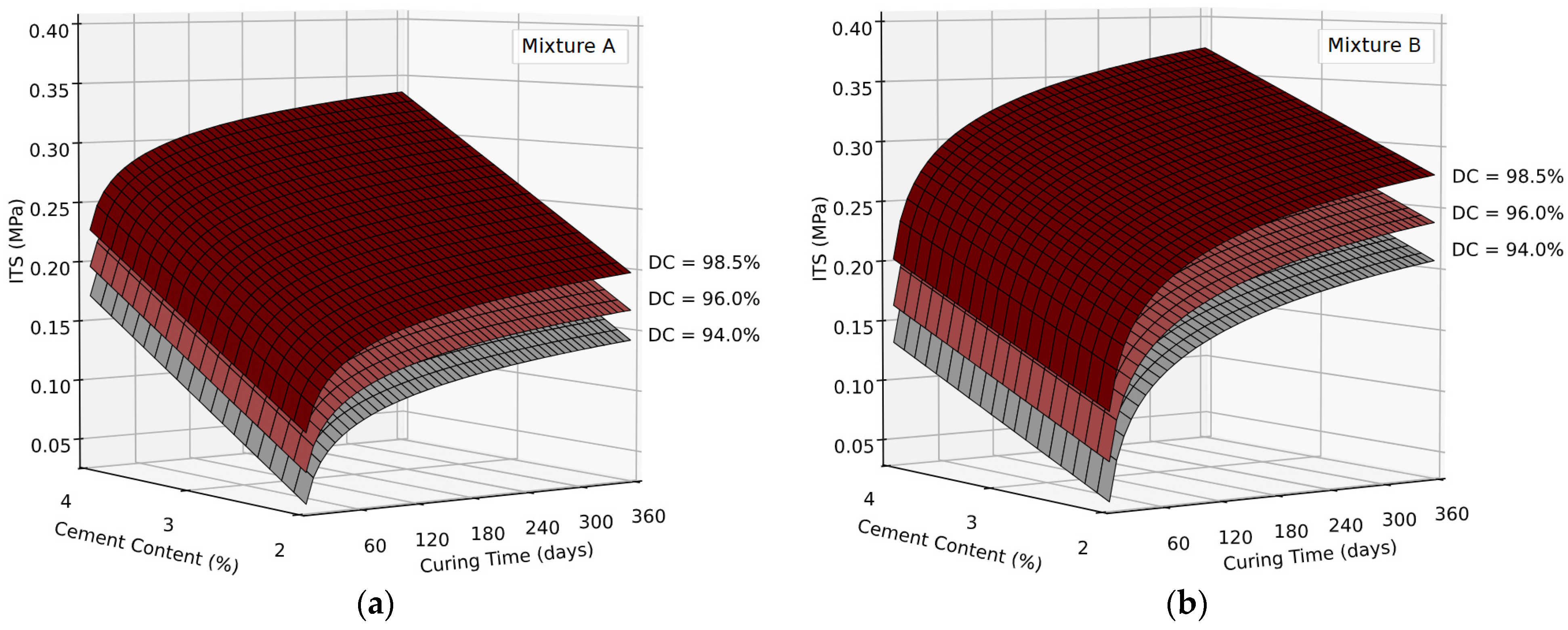
3.2.5. Response Surfaces

As the varying factors that play a significant role on ITS are limited to 3, it is possible to visualize the prediction models (Equations (6) and (7)) as response surfaces (Figure 4).

Responses surfaces (Figure 4) show the classical ITS behavior of CT for a given CC and DC. In both cases, it follows the same pattern: from quick short-term stabilization, to slow long-term effects. As pointed by Firoozi et al. [5], hydration in cement occurs quickly, which allows for an immediate strength gain at a young age. A reduction of the ITS gain at later ages for a given CC and CD can be linked to the deceleration of hydration [70] and a slow pozzolanic reaction.

For our discussion about the influence of parameters, one parameter is fixed and contour plots in 2D are generated from the response surfaces (Figure 5 and Figure 6).

In Figure 5a and Figure 6a, contours of ITS (iso-lines) as a function of CT and CC are plotted. Gradients represent the effect of CC on ITS as function of time for DC = 96% MDD. Despite the logarithmic shape of the ITS curves, ITS variation is constant and depends on CC variations. For a 1% increase of CC (e.g., 2.5% to 3.5%), the gain on ITS is around 0.069 MPa for A and 0.048 MPa for B regardless of CT. This suggests that CC governs the number of bonds between aggregates. The lower the CC, the lower the number of bonds and thus the lower ITS. However, it also suggests that the chemical kinetics were not modified.

The coarse material B (Figure 6a) exhibits higher gradients than the clayey mixture A (Figure 5a) under the same preparation conditions. This may be linked to different stabilization mechanisms. Particularly, clay content and OMC can explain these results. The higher occurrence of water in A could explain the quick reactivity with cement in the short-term. Conversely, the occurrence of clay could affect the long-term quality of cement bonds between soil aggregates. It is accepted that the best cement-stabilization results are observed on silt and coarse-grained materials [9] whereas fine-grained soil may require a higher CC [27]. For example, for a fixed CC, at DC = 96% MDD, with CT varying from 7 to 360 days, the increase in ITS is 0.109 MPa for mixture A and 0.171 MPa for mixture B.

To achieve a required ITS value with lower quantities of cement, it is necessary to have a higher CT. For instance, in Figure 5a for material A, to obtain ITS = 0.200 MPa we consider both CT = 360 days and CC = 2.5%, or CT = 7 days and CC = 4%. This is an important point, especially in the short term, when ITS values are critical issues on practice (e.g., opening to traffic for road structures). Finally, this relationship can be used to support the choice of smaller amounts of binder in applications where the CT is not a critical factor. It also could be used, in the field, for estimating mechanical performance variations due to dosage fluctuations.

Figure 5b and Figure 6b plot ITS contours as a function of CT and DC. Regardless of the materials, contour plots present the same pattern previously described for the interaction between CT and CC. For instance, when the DC ranges from 94.0 to 98.5% of MDD (at CC = 3%), the gain on ITS is 0.056 MPa for A and 0.070 for B, regardless of CT.

In the same way, a higher DC would lead to achieving a given value of ITS with a lower CT. Specifically, the effects of the DC are stronger for mixture B. In Figure 6b (CC = 3%), for B, for example, to obtain ITS = 0.250 MPa we can consider both CT = 65 days and DC = 98.5% MDD, or CT = 320 days and DC = 94% MDD. The mechanism might be the following: the higher the DC, the higher the contact points between aggregates in the matrix and thus the creation of more cemented bonds. With a higher importance of DC for the coarse material (mixture B), this suggestion is in accordance with previous observations [71]. These remarks support the importance of compaction control and their consequence even in long term.

Figure 5c and Figure 6c plot ITS contours as a function of DC and CC. As the effects of both DC and CC are linear, the contour plots are straight lines. In mixture B at CT = 90 days (Figure 6c), the contour plots show that a reduction of 1% on CC (e.g., from 3 to 2%) can be compensated by increasing the DC on 3.1% (e.g., from 94% to 97.1% MDD). In practice, cement savings could be expected with good compaction.

A practical example to use these contour plots could be the following. For a given level of expected ITS performance (e.g., material A, ITS = 0.200 MPa), several combinations are possible. For instance, for regular field practices (CC = 3%, DC = 96%), this performance is achieved normally for CT = 100 days (Figure 5a). The curing time can be reduced by increasing DC for the same CC of 3% (CT = 40 days when DC = 98%, in Figure 5b). Increasing the DC also allows CC to be reduced. For a given curing time (e.g., CT = 90 days, Figure 5c), varying DC from 96% to 98% allows CC to be reduced from 3% to 2.7% to achieve the aimed performance.

3.3. Numerical Approach

An example of one numerical experiment for the mixture A is illustrated in Figure 7, for a set of n = 100 observations at the k = 10³ iteration (${\mathrm{B}}_{{10}^2,{10}^3}$). Numerical ITS values are generated and presented as a function of dosage variables. In Figure 7, the hue and marker size represent the numerical ITS values. The LHS sampling is illustrated with the points scattering. In spite of the addition of noise, the effects of dosage variables on ITS can be identified. When compared with iso-lines from the contour plot of A (Figure 5), the ITS increase due to CT, CC and DC is clear. The introduction of noise on the numerical data generates variations around the reference model.

The parameter ${\mathsf{\delta }}_{\mathrm{n},\mathrm{k}}$ as defined in Equation (5) represents the distance between the noised numerical model and the experimental model. Once all the iterations are complete, the mean (${\mathsf{\delta }}_{\mathrm{n}}$) and normalized ($\overline{{\mathsf{\delta }}_{\mathrm{n}}}$) indicators, and their respective standard deviations, can be calculated. Figure 8 illustrates that for both materials, the COV of ${\mathsf{\delta }}_{\mathrm{n}}$ and $\overline{{\mathsf{\delta }}_{\mathrm{n}}}$ are nearly constant (in average, 37%) which implies a proportional reduction of the SD as function of n for both indicators.

The higher the number of samples n, the lower ${\mathsf{\delta }}_{\mathrm{n}}$ as shown in Figure 8a. For the studied range (10 < n < 100), ${\mathsf{\delta }}_{\mathrm{n}}$ decreases from 12.1 (4.6) to 3.9 (1.4) kPa for A and from 10.0 (3.9) to 3.2 (1.1) kPa for mixture B. That is, there is a total net gain on accuracy of 8.2 kPa for A and 6.8 kPa for B. The lower values of ${\mathsf{\delta }}_{\mathrm{n}}$ for B than for A are related to the error of experimental residuals, which is lower for B than for A (SD²_ε(B) < SD²_ε(A)). The numerical results are in accordance with the experimental ones. This is clearer in Figure 8b with the normalized indicator $\overline{{\mathsf{\delta }}_{\mathrm{n}}}$ (Equation (5)). For the range of observations analyzed (10 < n < 100), $\overline{{\mathsf{\delta }}_{\mathrm{n}}}$ decreases from 6.8 (2.8)% to 2.0 (0.7)% for A and from 4.8 (2.1)% to 1.4 (0.5)% for B material. For both indicators and both materials, the rate of decline slows as n increases (Figure 8).

A curve that represents the gain in accuracy for both materials is presented in Figure 9. The net gain for a given n is described as the ratio between ${\mathsf{\delta }}_{10}-{\mathsf{\delta }}_{\mathrm{n}}$ and ${\mathsf{\delta }}_{10}-{\mathsf{\delta }}_{100}$. For the studied range of n, regardless of the material, both curves exhibit the same increasing pattern as a function of n. Most of the improvement (82%) is achieved when n varies from 10 to 50 observations. That corresponds approximately to half of the experimental sampling. Moreover, 43% of the total net gain is obtained when n is varied from 10 to 20 observations. This implies that good accuracy in the numerical models can be rapidly achieved, e.g., with less than 50 samples by LHS. This result can be used to optimize the sampling of experimental procedures.

4. Conclusions

We have experimentally and numerically assessed the impact of dosage in two CSSs in a fixed inference space. Based on a conventional approach, an experimental variability study on ITS was planned for both materials. Curing time, cement content, degree of compaction and water content were the dosage variables. An ANOVA was used to identify the significant dosage variables and to build prediction models. A numerical approach was used to iteratively generate synthetic ITS values from statistical prediction models. An LHS space-filling technique was used. Experimental and numerical predictions were compared. Based on the experimental results, statistical analysis and numerical results, within the inference space, the following conclusions can be drawn:

• The addition of a few percentage points of cement significantly increased the overall performance of both sandy and clayey soils. Mean treated ITS values for the reference mixture varied from 7 up to 11 times the non-treated ITS for mixture A, and from 12 up to 31 times for mixture B.
• The content of water variations in the interval we studied (±10% OMC) showed no significant effects on ITS values for both mixtures. Once this variable was excluded, density was identified as the factor with the lowest effect. Conversely, CC and CT proved to be most significant variable on mixture A and B, respectively.
• The experimental ITS was described accurately by using dosage variables and curing time as predictors on multilinear regression models: R² of 0.84 and 0.92 for mixture A and B, respectively. The effects of CC were stronger on the clayey soil (A) whereas the influence of CT and DC showed to be higher on the sandy mixture (B).
• The ANOVA proved to be a straightforward method to construct experimental prediction models. These models can be used to interpolate conditions that were not explicitly evaluated in the experimental program. Preparation parameters are ranked regarding their effect on ITS values.
• The combined effects of dosage variables were assessed by means of contour plots. These tools can be used for mixture optimization according to technical specifications and operating conditions.
• The combined effects of dosage variables were observed on the response of surfaces and associated contour plots. These tools can be used to assess specifications for mixture optimization, and operating conditions from short to long-term.
• Long-term results can be achieved in several days by increasing CC. Reducing the binder consumption can be achieved by increasing CT or DC. Specifically, the effects of compaction were shown to be relevant even in the long-term in both materials.
• The residual values of experimental models are well described with normal PDFs. These statistical descriptions were used to generate numerical data.
• LHS as space-filling technique was a powerful method to generate efficiently numerical sampling data.
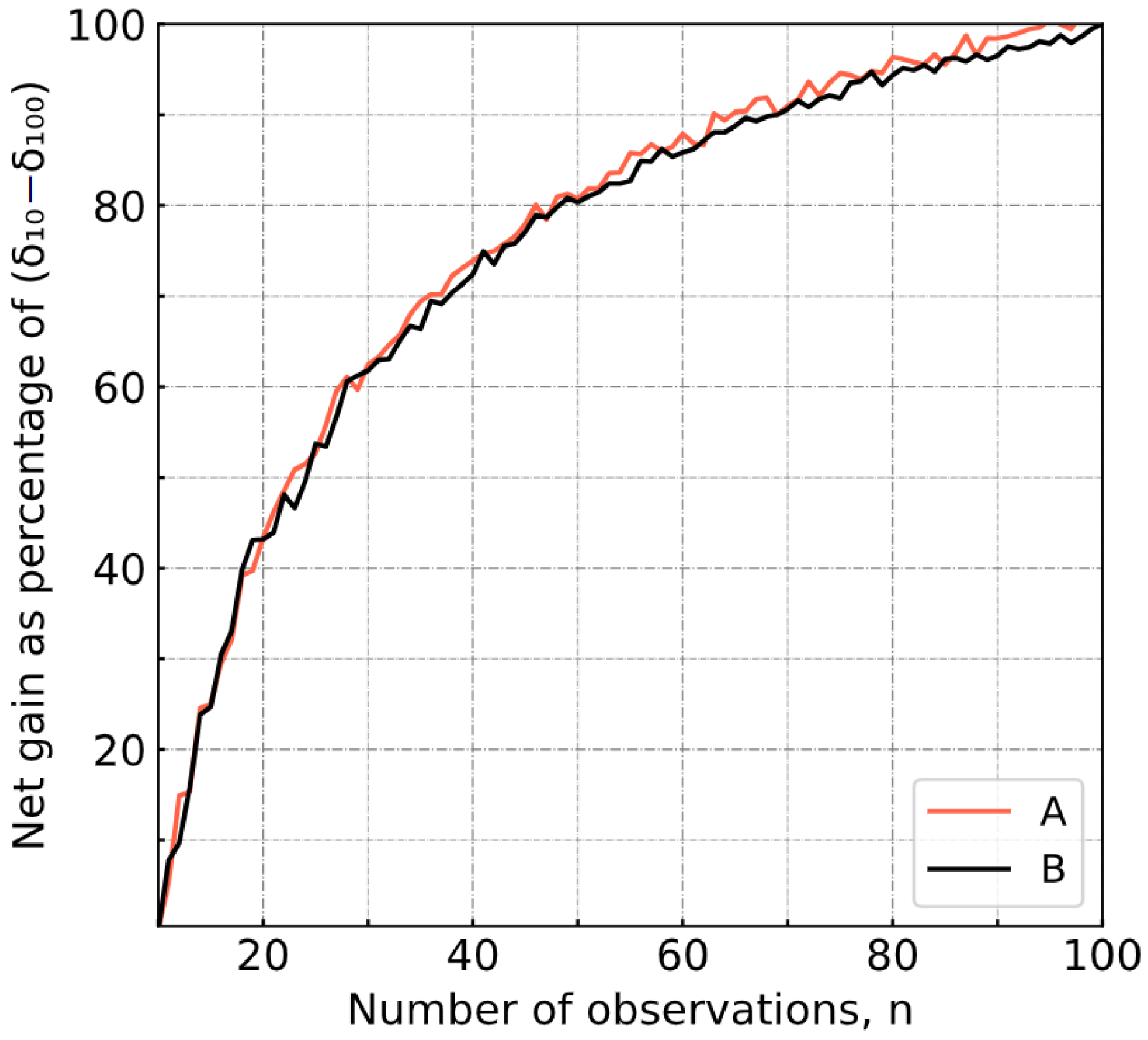
• As expected, the number of observations was critical in explaining the differences between experimental and numerical models. The results showed that regardless of material type, the complete sampling size (n~100) may not be necessary for achieving a similar degree of accuracy. A net accuracy gain of 43% was measured when the number of observations varied from 10 to 20 for both mixtures. This gain reached 82% in both cases when n varied from 10 to 50. This supports the optimization of the experimental work in terms of the reduction of sampling. Moreover, the proposed methodology associates a number of experimental observations with a given degree of uncertainty on ITS.
• Finally, the proposed methodology can be generalized to other experimental scientific fields.